理论力学第一章习题
1-8章的习题答案理论力学.doc

第一章静力学公理和物体的受力分析一、选择题与填空题1.C2.ACD3.A, B两处约束力的方向如图所示60°第二章平面力系一、选择题与填空题■1. B; D。
2. B。
3. F;向上。
4. B。
5. 4^M;方向与水平线成60角,指向 23L右下。
6. 10kN; 10kN ; 5kN; 5kN。
7. 100kN;水平向右。
二•计算题1. F B - -70 KN F AX =70 KN ,F Ay =120 KN , M A二-30KN m2. F AX - -qa F BX二 F qa F Ay =qa F F By 二 qa - F3. F= -5kN F Dy = 4.33kN F E-4.33kN F C =24.41kND xF B^ -17.08kN F AX=F BX = -5kN l^y = -14.08kN M A=T4.66kN mF AX =10N FAy =20N M A =15N mF CD =14.1N6F Ax=2.5kN F Ay=—2.16kN M A=」kN ,m F c =20.33kN7 F B=40kNF AX = —10kNFA ^-20kN M -50kN m F cx = 40kNF ey = 0F HX =300N F Hy =100N第三章空间力系少2(-8. F A ^ = -100N F Ay 二-300N F Ex 二-300N F Ey =100N F °y 二 200N整=一一A > X Y m 一:J E £c X一、选择题与填空题f—- - Fa 6 Fa 1.B。
2.B。
3. M x(F)=O ; M y(F) —H2 44.F x=-40.2N; F y=30-2N; M z=240.2 N m。
5.F z= F sin :;F y= F cos :cos :;M x(F)二 F(ccos'cos : bsin )。
理论力学习题答案

第三章 空间力系
一、是非题判断题
3.1.1对一空间任意力系,若其力多边形自行封闭,则该力系的主矢为零。 (∨)
平面力系中,若其力多边形自行闭合,则力系平衡。(×)
3.1.2只要是空间力系就可以列出6 个独立的平衡方程。 (×)
2.3.4悬臂式吊车的结构简图如图所示,由DE、AC二杆组成,A、B、C为铰链连接。已知P1=5kN,P2=1kN,不计杆重,试求杆AC杆所受的力和B点的支反力。
(答案:FBx=3.33kN,FBy=0.25kN,FAC=6.65kN)
2.3.5由AC和CD构成的组合粱通过铰链C连接,它的支承和受力如图所示,已知均布载荷强度q=10kN/m,力偶矩M=40kN.m,不计梁重,求支座A、B、D的约束反力和铰链C处所受的力。
3.1.3若由三个力偶组成的空间力偶系平衡,则三个力偶矩矢首尾相连必构成自行封闭的三角形。(∨)
3.1.4空间汇交力系平衡的充分和必要条件是力系的合力为零;空间力偶系平衡的充分和必要条件是力偶系的合力偶矩为零。(∨)
二、填空题
3.2.1若一空间力系中各力的作用线平行于某一固定平面,则此力系有5个独立的平衡方程。
3.3.3如图所示,三圆盘A、B、C的半径分别为15cm、10cm、5cm,三根轴OA、OB、OC在同一平面内,∠AOB为直角,三个圆盘上分别受三个力偶作用,求使物体平衡所需的力F和α角。
3.3.4某传动轴由A、B两轴承支承。圆柱直齿轮的节圆直径d=17.3cm,压力角 =20º,在法兰盘上作用一力偶矩为M=1030N.m的力偶,如轮轴的自重和摩擦不计,求传动轴匀速转动时A、B两轴承的约束反力。(答案:FAx=4.2kN,FAz=1.54kN,FBz=7.7kN,FBz.=2.79kN)
(最新整理)1-8章习题答案 理论力学.doc

第一章 静力学公理和物体的受力分析一、选择题与填空题 1.C 2.ACD3.A ,B 两处约束力的方向如图所示。
4.5F ,方向与5F 方向相反。
5.60°。
6. 铅直向上。
第二章 平面力系一、选择题与填空题 1.B ;D 。
2.B 。
3.2F ;向上。
4.B 。
5.LM 334;方向与水平线成︒60角,指向右下。
6.10kN ;10kN ;5kN ;5kN 。
7. 100kN ;水平向右。
二.计算题1. 70-=BF KN 70=AxF KN ,120=Ay F KN ,30A M KN m =-⋅ 2. qa F Ax -= qa F F Bx += F qa F Ay += F qa F By -=3. kN5-=Dx FkN33.4=Dy FkN33.4=E FkN41.24=C FkN08.17-=By FkN 5-='=BxAx F FkN08.14-=Ay F m kN 66.14⋅-=A M4.5.N10=Ax FN20=Ay F m N 15⋅=A M N 1.14=CD F6.kN5.2=AxF kN 16.2-=Ay F m kN 8⋅-=A M kN33.20=C F7. kN 40=B FkN10-=Ax FkN20-=Ay F m kN 50⋅-=A MkN40=Cx F 0=Cy F8. N100-=Ax F N300-=Ay FN300-=Ex F N100=Ey F N200=Dy FN 300=Hx F N100=Hy F第三章 空间力系一、选择题与填空题1.B 。
2.B 。
3. 0)(=F M x ;2)(FaF M y -= ;46)(Fa F M z = 。
4. F x =240-N ;F y =302N ;M z =2402m N ⋅。
5.sin z F F ϕ=;cos cos y F F ϕβ=;()(cos cos sin )x M F F c b ϕβϕ=+。
理论力学习题答案

理论力学习题答案(总26页)--本页仅作为文档封面,使用时请直接删除即可----内页可以根据需求调整合适字体及大小--2第一章 静力学公理和物体的受力分析一、是非判断题在任何情况下,体内任意两点距离保持不变的物体称为刚体。
( ∨ ) 物体在两个力作用下平衡的必要与充分条件是这两个力大小相等、方向相反,沿同一直线。
( × ) 加减平衡力系公理不但适用于刚体,而且也适用于变形体。
( × ) 力的可传性只适用于刚体,不适用于变形体。
( ∨ ) 两点受力的构件都是二力杆。
( × ) 只要作用于刚体上的三个力汇交于一点,该刚体一定平衡。
( × ) 力的平行四边形法则只适用于刚体。
( × ) 凡矢量都可以应用平行四边形法则合成。
( ∨ ) 只要物体平衡,都能应用加减平衡力系公理。
( × ) 凡是平衡力系,它的作用效果都等于零。
( × ) 合力总是比分力大。
( × ) 只要两个力大小相等,方向相同,则它们对物体的作用效果相同。
( × )若物体相对于地面保持静止或匀速直线运动状态,则物体处于平衡。
( ∨ )当软绳受两个等值反向的压力时,可以平衡。
( × )静力学公理中,二力平衡公理和加减平衡力系公理适用于刚体。
( ∨ )静力学公理中,作用力与反作用力公理和力的平行四边形公理适用于任何物体。
( ∨ )凡是两端用铰链连接的直杆都是二力杆。
( × )如图所示三铰拱,受力F ,F 1作用,其中F 作用于铰C 的销子上,则AC 、BC 构件都不是二力构件。
( × )图3二、填空题力对物体的作用效应一般分为 外 效应和 内 效应。
对非自由体的运动所预加的限制条件称为 约束 ;约束力的方向总是与约束所能阻止的物体的运动趋势的方向 相反 ;约束力由 主动 力引起,且随 主动 力的改变而改变。
理论力学第一章习题

理论力学第一章习题
1-1重力为P的圆球放在板AC与墙壁AB之间,如图所示。
设板AC自重不计,试画出板和球的受力图。
1-2梁AB的A端为滚动铰链支座,B端为固定铰链支座。
杆CD的C端靠在光滑墙壁上,两杆在D处用铰链连接,如图所示。
如果在E处作用铅直力F,不计重力,分别画出杆CD和AB的受力图。
1-3平面承重支架如图所示,在C点上作用荷载F,若不计各杆件的重力,试分别画出杆AC 和BD的受力图。
1-4球体的重力为G,放在如图所示的光滑接触面上,今在球心O作用水平向左的力P后使球处于静止状态。
画出球体的受力图。
1-5匀质杆AB的重力为G,放在光滑的半圆槽内,并在如图所示的位置处于静止状态。
画出杆AB在平衡时的受力图。
1-6图为汽车制动机构的示意图。
已知司机脚踏制动蹬的力为P,平衡时拉杆CD为水平。
A 和D均为固定铰链支座,C处为铰链连接。
如果不计机构的重量和摩擦,画出制动蹬AB 的受力图。
理论力学习题解答第一章

第一章 静力学基本概念
1-1 考虑力对物体作用的运动效应,力是( A )。
A.滑动矢量
B.自由矢量
C.定位矢量
1-2 如图1-18所示,作用在物体A 上的两个大小不等的力1F 和2F ,沿同一直线但方向相反,则其合力可表为( C )。
A.1F –2F
B.2F - 1F
C.1F +2F
图1-18 图1-19 1-3 F =100N ,方向如图1-19所示。
若将F 沿图示x ,y 方向分解,则x 方向分力的大小 x F = C N ,y 方向分力的大小y F = ___B __ N 。
A. 86.6
B. 70.0
C. 136.6
D.25.9
1-4 力的可传性只适用于 A 。
A. 刚体
B. 变形体
1-5 加减平衡力系公理适用于 C 。
A. 刚体;
B. 变形体;
C. 刚体和变形体。
1-6 如图1-20所示,已知一正方体,各边长a ,沿对角线BH 作用一个力F ,则该力在x 1轴上的投影为 A 。
A. 0
B. F/2
C. F/6
D.-F/3
1-7如图1-20所示,已知F=100N ,则其在三个坐标轴上的投影分别为:
Fx Fy Fz
图1-20 图1-21。
理论力学习题
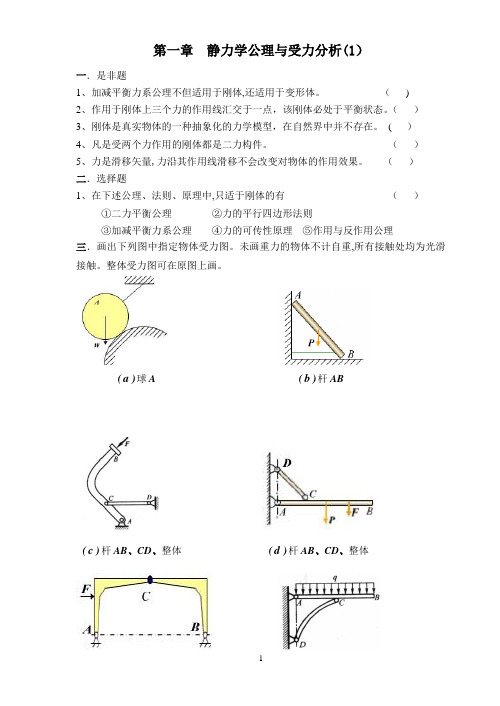
第一章静力学公理与受力分析(1)一.是非题1、加减平衡力系公理不但适用于刚体,还适用于变形体。
()2、作用于刚体上三个力的作用线汇交于一点,该刚体必处于平衡状态。
()3、刚体是真实物体的一种抽象化的力学模型,在自然界中并不存在。
( )4、凡是受两个力作用的刚体都是二力构件。
()5、力是滑移矢量,力沿其作用线滑移不会改变对物体的作用效果。
()二.选择题1、在下述公理、法则、原理中,只适于刚体的有()①二力平衡公理②力的平行四边形法则③加减平衡力系公理④力的可传性原理⑤作用与反作用公理三.画出下列图中指定物体受力图。
未画重力的物体不计自重,所有接触处均为光滑接触。
整体受力图可在原图上画。
)a(球A )b(杆ABd(杆AB、CD、整体)c(杆AB、CD、整体)- 1 -)e(杆AC、CB、整体)f(杆AC、CD、整体四.画出下列图中指定物体受力图。
未画重力的物体不计自重,所有接触处均为光滑接触.多杆件的整体受力图可在原图上画。
)a(球A、球B、整体)b(杆BC、杆AC、整体- 2 -- 3 -第一章 静力学公理与受力分析(2)一.画出下列图中指定物体受力图。
未画重力的物体不计自重,所有接触处均为光滑接触。
整体受力图可在原图上画。
WADB CE Original FigureAD B CEWWFAxF AyF BFBD of the entire frame)a (杆AB 、BC 、整体)b (杆AB 、BC 、轮E 、整体)c (杆AB 、CD 、整体)d (杆BC 带铰、杆AC 、整体)e(杆CE、AH、整体)f(杆AD、杆DB、整体)g(杆AB带轮及较A、整体)h(杆AB、AC、AD、整体- 4 -- 5 -第二章 平面汇交和力偶系一.是非题1、因为构成力偶的两个力满足F = — F ',所以力偶的合力等于零。
( )2、用解析法求平面汇交力系的合力时,若选用不同的直角坐标系,则所求得的合力不同。
理论力学习题及答案(全)

第一章静力学基础一、是非题1.力有两种作用效果,即力可以使物体的运动状态发生变化,也可以使物体发生变形。
()2.在理论力学中只研究力的外效应。
()3.两端用光滑铰链连接的构件是二力构件。
()4.作用在一个刚体上的任意两个力成平衡的必要与充分条件是:两个力的作用线相同,大小相等,方向相反。
()5.作用于刚体的力可沿其作用线移动而不改变其对刚体的运动效应。
()6.三力平衡定理指出:三力汇交于一点,则这三个力必然互相平衡。
()7.平面汇交力系平衡时,力多边形各力应首尾相接,但在作图时力的顺序可以不同。
()8.约束力的方向总是与约束所能阻止的被约束物体的运动方向一致的。
()二、选择题1.若作用在A点的两个大小不等的力F1和F2,沿同一直线但方向相反。
则其合力可以表示为。
①F1-F2;②F2-F1;③F1+F2;2.作用在一个刚体上的两个力F A、F B,满足F A=-F B的条件,则该二力可能是。
①作用力和反作用力或一对平衡的力;②一对平衡的力或一个力偶。
③一对平衡的力或一个力和一个力偶;④作用力和反作用力或一个力偶。
3.三力平衡定理是。
①共面不平行的三个力互相平衡必汇交于一点;②共面三力若平衡,必汇交于一点;③三力汇交于一点,则这三个力必互相平衡。
4.已知F1、F2、F3、F4为作用于刚体上的平面共点力系,其力矢关系如图所示为平行四边形,由此。
①力系可合成为一个力偶;②力系可合成为一个力;③力系简化为一个力和一个力偶;④力系的合力为零,力系平衡。
5.在下述原理、法则、定理中,只适用于刚体的有。
①二力平衡原理;②力的平行四边形法则;③加减平衡力系原理;④力的可传性原理;⑤作用与反作用定理。
三、填空题1.二力平衡和作用反作用定律中的两个力,都是等值、反向、共线的,所不同的是。
2.已知力F沿直线AB作用,其中一个分力的作用与AB成30°角,若欲使另一个分力的大小在所有分力中为最小,则此二分力间的夹角为度。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第一章习题细杆OL 绕O 点以角速ω转动,并推动小环C 在固定的钢丝AB 上滑动。
图中的d 为已知常数,试求小球的速度及加速度的量值。
解 如题1.4.1图所示,A BOCLxθd 第1.4题图OL 绕O 点以匀角速度转动,C 在AB 上滑动,因此C 点有一个垂直杆的速度分量22x d OC v +=⨯=⊥ωωC 点速度dx d d v v v 222sec sec cos +====⊥⊥ωθωθθ 又因为ωθ=&所以C 点加速度θθθω&⋅⋅⋅⋅==tan sec sec 2d dt dv a ()2222222tan sec 2d x d x d +==ωθθω矿山升降机作加速度运动时,其变加速度可用下式表示:⎪⎭⎫ ⎝⎛-=T t c a 2sin1π 式中c 及T 为常数,试求运动开始t 秒后升降机的速度及其所走过的路程。
已知升降机的初速度为零。
解 由题可知,变加速度表示为⎪⎭⎫ ⎝⎛-=T t c a 2sin1π 由加速度的微分形式我们可知dtdv a =代入得dtT t c dv ⎪⎭⎫ ⎝⎛-=2sin 1π 对等式两边同时积分dt T t c dv t v⎰⎰⎪⎭⎫ ⎝⎛-=002sin 1π可得 :D Ttc T ct v ++=2cos2ππ(D 为常数)代入初始条件:0=t 时,0=v ,故cT D π2-=即⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛-+=12cos 2T t T t c v ππ 又因为dtds v =所以dt T t T t c ⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛-+12cos 2ππ =ds对等式两边同时积分,可得:⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛-+=t T t T T t c s 2sin 22212πππ一质点沿位失及垂直于位失的速度分别为r λ及μθ,式中λ及μ是常数。
试证其沿位矢及垂直于位失的加速度为⎪⎭⎫ ⎝⎛+-r rr μλμθθμλ,222解 由题可知质点的位矢速度r λ=//v (1)沿垂直于位矢速度μθ=⊥v (2)又因为 , 即 r r λ=& (3)μθθ==⊥r v &rμθθ=& (4) 对③求导(5) 对④求导θμμθθ&&&&rr r +-=2(6)根据课本的推导可知 沿位矢方向加速度()2θ&&&r r a -= (7) 垂直位矢方向加速度()θθ&&&&r r a 2+=⊥ (8)把(3)(4)(5)(6)代入(7)(8)式中可得rr a 222//θμλ-=⎪⎭⎫ ⎝⎛+=⊥r a μλμθr r// v rr r 2试自θθsin ,cos r y r x ==出发,计算x &&及y &&。
并由此推出径向加速度r a 及横向加速度θa 。
解 由题可知⎩⎨⎧==θθsin cos r y r x ①②对①求导θθθ&&&sin cos r r x -= ③ 对③求导 θθθθθθθcos sin sin 2cos 2&&&&&&&&&r r r r x ---=④对②求导 θθθcos sin &&&r r y +=⑤对⑤求导 θθθθθθθsin cos cos 2sin 2&&&&&&&&&r r r r y -++=⑥对于加速度a ,我们有如下关系见题1.7.1图题1.7.1图θθsin cos y x a r &&&&+= ⑾把④⑥代入 ⑾得2θ&&&r r a r -= 同理可得θθθ&&&&r r a 2+=一飞机在静止空气中每小时的速率为100千米。
如果飞机沿每边为6千米的正方形飞行,2()cos (2)sin x r r r r θθθθθ=--+&&&&&&&&&即2()sin (2)cos y r r r r θθθθθ=--+&&&&&&&&&即sin cos a x y θθθ=-+&&&&且风速为每小时28千米,方向与正方形的某两边平行,则飞机绕此正方形飞行一周,需时多少?解 正方形如题1.14.1图。
CD3v由题可知h km v v /28==风牵设风速B A →,h km v /100=相,当飞机B A →,h km h km v /128/)28100(1=+= h km h km v D B /96/28100,222=-=→h km h km v D C /72/)28100(,3=-=→=→4,v A D h km h km /96/2810022=-故飞机沿此边长6h km /正方形飞行一周所需总时间min 16515192499667269661286==⎪⎭⎫ ⎝⎛+++=h h t2风v 相题1.14.2图风v v 题1.14.3图小船M 被水冲走后,由一荡桨人以不变的相对速度朝岸上A 点划回。
假定河流速度1 2沿河宽不变,且小船可以看成一个质点,求船的轨迹。
解 以A 为极点,岸为极轴建立极坐标如题.图.题1.17.1图船沿垂直于r 的方向的速度为,船沿径向r 方向的速度为和沿径向的分量的合成,即①--② ②/①得 ,对两积分: 设为常数,即C r k k +=+-αα11cos 2sin ln ln 代入初始条件0r r =时,0ϕϕ=.设,200αϕ=有,cos 2sin ln ln 01010αα+--=k k r C 得101110sin cos cos sin αααα-++-⋅=k kk k r r将质量为m 的质点竖直抛上于有阻力的媒质中。
设阻力与速度平方成正比,即22gv mk R =。
如上抛时的速度为0v ,试证此质点又落至投掷点时的速度为Ck, 2,12Crsin ln 2 tan ln ln 12 d rdrcot sin 1 22 1 1 cos sin dtdr dtd r12sin 122011vk v v +=解 质点从抛出到落回抛出点分为上升和下降阶段.取向上为正各力示意图如题1.19.1图,上升时 下降时 题1.19.1图则两个过程的运动方程为: 上升22yg mk mg y m &&&--= ① 下降:②对上升阶段:()221v k g dtdv+-= ()221v k g dyvdvdt dy dy dv +-== 即gdy vk vdv-=+221 对两边积分gdy vk vdv h v ⎰⎰-=+022010所以()2221ln 21v k gk h +=③ 即质点到达的高度. 对下降阶段:2 2 y g mk mgy m即()21221ln 21v k gk h --= ④ 由③=④可得202011vk v v +=重为W 的不受摩擦而沿半长轴为a 、半短轴为b 的椭圆弧滑下,此椭圆的短轴是竖直的。
如小球自长2轴的端点开始运动时,其初速度为零,试求小球在到达椭圆的最低点时它对椭圆的压力。
gdy v kvdv h v2 2 0 12 2 gv k -g dyvdvdt dy dy dv解 建立如题1.28.1图所示直角坐标.题1.28.1图椭圆方程 12222=+by a x ① 从A 滑到最低点B ,只有重力做功.机械能守恒.即221mv mgb =②设小球在最低点受到椭圆轨道对它的支持力为N 则有:③ρ为B 点的曲率半径. B A →的轨迹:221axb y --=得2221ax abx y -=';2322211⎪⎪⎭⎫ ⎝⎛-⋅=''a x ab y 又因为()223211ab y y k ='+''==ρ所以⎪⎪⎭⎫ ⎝⎛+=⨯+=+=2222212a b W mgh a b mg mv mg N ρ 故根据作用力与反作用力的关系小球到达椭圆最低点对椭圆压力为⎪⎪⎭⎫ ⎝⎛+2221a b W 方向垂直轨道向下.检验下列的力是否是保守力。
如是,则求出其势能。
()a 233206y bx y abz F x -=,y bx abxz F y 43106-=,218abxyz F z =()b ()()()z F y F x F z y x k j i F ++=2v mmgN解 (a )保守力F 满足条件0F =⨯∇对题中所给的力的表达式 ,代入上式 即()()()22=+--+-+-=⎪⎪⎭⎫ ⎝⎛∂∂-∂∂+⎪⎭⎫ ⎝⎛∂∂-∂∂+⎪⎪⎭⎫ ⎝⎛∂∂-∂∂=∂∂∂∂∂∂=⨯∇kj i kj i F F F k j i F zyxy 40abx 6abz y 40bx 6abzy 18abz y 18abz 18abxz 18abxz y F x F x F z F z F y F z y x 333322x y z x y z所以此力是保守力,其势为()()()()()()()()()()()324,,0,,20,,0,0,4300000233z y,x,0,0,0x6518106d 206F abxyz y bx dz abxyz dy y bx abxzx y bx y abz dz F dy F dx V z y x y x y x x ,x,,,zy-=-----++-=⋅-=⎰⎰⎰⎰⎰drF(b)同(a ),由=⎪⎪⎭⎫ ⎝⎛∂∂-∂∂+⎪⎭⎫ ⎝⎛∂∂-∂∂+⎪⎪⎭⎫ ⎝⎛∂∂-∂∂=∂∂∂∂∂∂=⨯∇k j i k j i F y F x F x F z F z F y F F F F z y x x y zx y z zyx所以此力F 是保守力,则其势能为dzF dy F dx F d V BABABx Az z z y y y x x ⎰⎰⎰⎰---=⋅-=rF已知作用在质点上的力为za y a x a F z a y a x a F z a y a x a F z y x 333231232221131211++=++=++= 式中系数()3,2,1,=j i a ij 都是常数。
问这些ij a 应满足什么条件,才有势能存在?如这些条件满足,试计算其势能。
解 要满足势能的存在,即力场必须是无旋场,亦即力为保守力,所以0=⨯∇F 即⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧∂∂=∂∂∂∂=∂∂∂∂=∂∂x F zF x F yF z F yF zx yx yz 得⎪⎩⎪⎨⎧===311321122332aa a a a a ()3,2,1,=j i a ij 为常数满足上式关系,才有势能存在。
