第35次课纯弯曲时梁的正应力
梁的纯弯曲正应力实验报告

梁的纯弯曲正应力实验报告梁的纯弯曲正应力实验报告一、实验目的本实验旨在通过对实验材料进行纯弯曲加载,测量其正应力和弯曲角度,从而掌握材料在纯弯曲状态下的应力特性,并探究材料性能的影响因素。
二、实验原理当梁在纯弯曲时,受到的载荷可以分解为一个弯矩和一个剪力。
由于实验中去除了外部作用力,剪力为零,因此我们只需要考虑弯矩作用下的应力情况。
在梁的截面上,由于受到弯曲,不同位置的应变不同,因此会形成不同大小的应力。
在正常情况下,当梁未发生破坏时,梁的内部应力呈线性分布,即受到的弯矩越大,所受到的应力也会相应增大。
三、实验设备本实验所使用的设备包括:1.纯弯曲实验台2.测力仪3.梁材料(一定长度的圆形钢管或方管)四、实验步骤1. 选择一段合适材质的梁进行实验。
2. 将梁固定在纯弯曲实验台上。
3. 在梁的一端加上一定荷载。
4. 通过测力仪测量在梁部位不同位置受到的正应力。
5. 在梁的另一端加上一定数量的荷载,并重复步骤4,记录正应力。
6. 重复以上操作,直到梁发生破坏。
五、实验结果在实验过程中,我们记录了梁不同位置受到的正应力,并根据实验数据分析了不同弯矩下的应力分布曲线。
实验结果表明,在纯弯曲状态下,梁的内部应力呈线性分布,随着弯矩的增大,所受应力也会逐渐增大,直到梁发生破坏。
六、实验分析根据实验结果,我们可以发现梁的性能会受到材料的影响。
不同的材料具有不同的弯曲特性,不同的性能和抗断性能。
而在实验中,我们也可以通过调整材料的材质和长度来控制弯曲的程度,从而控制梁的应力分布和破坏点位置。
七、实验结论本实验通过纯弯曲实验台对梁进行弯曲测试,得到了不同弯矩下的应力分布曲线。
实验结论表明,梁在纯弯曲状态下,其内部应力呈线性分布,随着弯矩的增大,所受应力也会逐渐增大,直到梁发生破坏。
同时,不同材质和长度的材料在弯曲状态下具有不同的弯曲特性和抗断性能。
纯弯曲时梁横截面上的正应力

(2) a点的正应力
a点到中性轴的距离为
ya
560 2
21
259
mm
所以a点的正应力为
a
M max ya Iz
375103 259103 65600108
148.1 MPa
例3 图示梁由工字钢制成。许用弯曲正应力[]
=152 MPa, F=75 kN,试选择工字钢的型号 。
解: 求约束反力, 作弯矩图 F F F
5.2 纯弯曲时梁横截面上的正应力 E E y
M z
y dA M
A
E y2dA EIz M
A
Iz
y2dA 为横是梁中性层的曲率表达式。
EIz称为梁的抗弯刚度。
5.2 纯弯曲时梁横截面上的正应力
E E y
1 M
EIz
My
示。铸铁的抗拉许用应力为[t]=30MPa, 抗压 许用应力为[c]=160 MPa。已知截面对形心轴
z的Iz=763 cm4, y1=52 mm。校核梁的强度。
80
20
F1=9 kN F2=4 kN
AC
B
D
1m 1m 1m
y1
C
z
120
y2
20
y
80
120 20
y1
解:求约束反力
FA=2.5 kN, FB=10.5 kN
52 mm。
B截面
y2
y1
80
C
z
t max
M B y1 Iz
4000 0.052 763 108
27.2 MPa [ t]
FA F1=9 kN
y 20
FB F2=4 kN
y2 120 20 52 88 mm
3.3纯弯曲时梁横截面上的正应力详解

剪切弯曲:横截面上既有剪力 又有弯矩。 纯弯曲:横截面上只有弯矩而 无剪力。
4
《化工设备设计基础》
3.3.1 纯弯曲时的变形现象与假设
1、变形现象 ① 两条横向线mm nn不再相互平行,而是相互 倾斜,但仍然是直线,且仍与梁的轴线垂直。 ② 两条纵向线aa、 bb 变成 曲线 梁的轴线 内凹一侧的纵向线aa缩短了, 外凸一侧的纵向线bb伸长了。 中性层既不伸长也不缩短。
①纯弯曲 ( pure bending )
2
《化工设备设计基础》
3.3纯弯曲时梁横截面上的正应力
1.纯弯曲和横力弯曲
②横力弯曲
3
《化工设备设计基础》
3.3纯弯曲时梁横截面上的正应力
1.纯弯曲和横力弯曲
纯弯曲 ( pure bending )
横力弯曲 ( transverse load bending )
W I /y
Z z
max
14
《化工设备设计基础》
第三章 直梁的弯曲
3.1 平面弯曲的概念 3.2 直梁弯曲时的内力分析 3.3纯弯曲时梁横截面上的正应力 3.4 截面惯性矩和抗弯截面模量 3.5 梁的弯曲强度计算 3.7 提高梁弯曲强度的主要途径 3.8 梁的弯曲变形与刚度校核
1
《化工设备设计基础》
3.3纯弯曲时梁横截面上的正应力
1.纯弯曲和横力弯曲
3.3.2 弯曲变形与应力的关系
4.弯曲应力
横力弯曲正应力公式
弹性力学精确分析表明,当跨 度 l 与横截面高度 h 之比 l / h > 5 (细长梁)时,纯弯曲正应力公 式对于横力弯曲近似成立。 危险点应力:
max
M max ymax Iz
Mmax:在梁的所有横截面中,选择弯矩为峰值的截面 ymax: 在指定的横截上,选择离中性轴最远的点
纯弯曲梁的正应力实验参考书报告
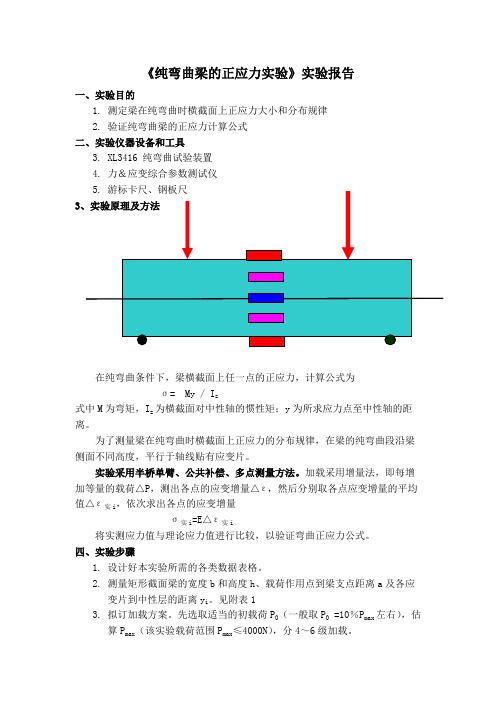
《纯弯曲梁的正应力实验》实验报告一、实验目的1.测定梁在纯弯曲时横截面上正应力大小和分布规律2.验证纯弯曲梁的正应力计算公式二、实验仪器设备和工具3.XL3416 纯弯曲试验装置4.力&应变综合参数测试仪5.游标卡尺、钢板尺3、实验原理及方法在纯弯曲条件下,梁横截面上任一点的正应力,计算公式为σ= My / I z式中M为弯矩,I z为横截面对中性轴的惯性矩;y为所求应力点至中性轴的距离。
为了测量梁在纯弯曲时横截面上正应力的分布规律,在梁的纯弯曲段沿梁侧面不同高度,平行于轴线贴有应变片。
实验采用半桥单臂、公共补偿、多点测量方法。
加载采用增量法,即每增加等量的载荷△P,测出各点的应变增量△ε,然后分别取各点应变增量的平均值△ε实i,依次求出各点的应变增量σ实i=E△ε实i将实测应力值与理论应力值进行比较,以验证弯曲正应力公式。
四、实验步骤1.设计好本实验所需的各类数据表格。
2.测量矩形截面梁的宽度b和高度h、载荷作用点到梁支点距离a及各应变片到中性层的距离y i。
见附表13.拟订加载方案。
先选取适当的初载荷P0(一般取P0 =10%P max左右),估算P max(该实验载荷范围P max≤4000N),分4~6级加载。
4.根据加载方案,调整好实验加载装置。
5. 按实验要求接好线,调整好仪器,检查整个测试系统是否处于正常工作状态。
6.加载。
均匀缓慢加载至初载荷P 0,记下各点应变的初始读数;然后分级等增量加载,每增加一级载荷,依次记录各点电阻应变片的应变值εi ,直到最终载荷。
实验至少重复两次。
见附表27.作完实验后,卸掉载荷,关闭电源,整理好所用仪器设备,清理实验现场,将所用仪器设备复原,实验资料交指导教师检查签字。
附表1 (试件相关数据)附表2 (实验数据)P 50010001500200025003000载荷N △P 500500500500500εP -33-66-99-133-166△εP -33-33-34-334平均值-33.25εP -16-33-50-67-83△εP -17-17-17-162平均值16.75εP 00000△εP 00001平均值0εP 1532476379△εP 171516163平均值16εP 326597130163△εP 33323333 各 测点电阻应变仪读数µε5平均值32.75五、实验结果处理1.实验值计算根据测得的各点应变值εi 求出应变增量平均值△εi ,代入胡克定律计算应变片至中性层距离(mm )梁的尺寸和有关参数Y 1-20宽 度 b = 20 mm Y 2-10高 度 h = 40 mm Y 30跨 度 L = 620mm (新700 mm )Y 410载荷距离 a = 150 mm Y 520弹性模量 E = 210 GPa ( 新206 GPa )泊 松 比 μ= 0.26惯性矩I z =bh 3/12=1.067×10-7m 4 =106667mm 4。
纯弯曲时梁横截面上的正应力

材料力学
缩)时的胡克定律,即
E 将式(5-4)中的 代入上式,即得
E E y
(5-5)
式(5-5)表达了梁横截面上正应力的变化规律。由于 E 是常量,故由式(5-5) 可知,横截面上任一点处的正应力与该点到中性轴的距离 y 成正比,而与中性轴
等距离的各点处的正应力均相同。正应力在梁横截面上的分布规律如图 5-19(b) 所示。在中性轴上,各点的 y 坐标等于零,故中性轴上的正应力等于零。
材料力学
图5-16(a)中外伸梁上的两个外 力F对称地作用于梁的纵向对称面内。
(a)
其剪力图和弯矩图分别如图5-16(b)、
(c)所示。AB和CD段梁的各横截面上
同时存在有剪力和弯矩,因此这些截面 (b)
上既有切应力又有正应力。该两段梁的
弯曲变形称为横力弯曲或剪切弯曲。在
BC段梁上剪力等于零,而弯矩为常量, (c)
因而横截面上就只有正应力而无切应力。
这种情况称为纯弯曲。
图5-16
一、变形几何关系
取一矩形截面梁段,在变形前梁的侧表面画上纵向线 aa 和 bb,并做垂直 于纵向线的横向线 mm 和 nn,如图 5-17(a)所示。然后在梁的两端加一对转 向相反且作用在梁的纵向对称面内的弯矩 M,梁发生纯弯曲变形,如图 5-17 (b)所示。此时可以观察到如下现象。
形后的长度 bb 应为
bb ( y)d
原长 OO dx d ,所以上述距中性层为 y 处的纵向纤维的线应变为
( y)d d y
d
(5-4)
式(5-4)表明,线应变 随 y 按线性规律变化。
二、物理关系
假设纵向纤维之间不存在相互挤压,于是各纵向纤维只有轴向拉伸或压缩
纯弯曲梁的正应力实验

纯弯 曲梁 的正 应力 实验
(1)梁的基本参数。 (2)实验记录表格。 (3)将各点的σ实和σ理描绘在同一个σOy 坐标系中,分别作出σ实-y和σ理-y分布曲线, 以便进行比较,从而检验梁的弯曲正应力理论公 式的正确性。
15.4 材料 剪切 弹性 模量G 的测
定
实验用到的仪器包括WSG-80型纯弯曲正应力试 验台、静
实验梁为低碳钢制成的矩形截面梁,根据实验装置 图、实验受力图可知,施加的砝码重量通过杠杆以一定 的比例作用于副梁的中央并通过两个挂杆作用于实验梁 C,D处,其荷载各为F/2。CD段处于纯弯曲状态。
(1)测定矩形截面梁的宽度b和高度h,荷载作用点 至梁支座距离a,并测量各应变片距中性层的距离y。
(2)正确地将各测点应变片和温度补偿片分别接到 电阻应变仪的相应接线柱上。
(3)接通应变仪的电源,完成预热工作后,设置应 变仪的灵敏系数,并将各窗口读数清零。
(4)加载。首先挂上砝码托作为初荷载,记录各测 点的应变值εi。采用增量法逐级加载,分四次加载,每加 载一次记录一次应变值,直至加载完毕。
在梁中CD段任选一截面,距中性层不同高度处,等 距离地粘贴五片电阻应变片,每片相距h/4,此外还布 设一个温度补偿片。试验中,采用半桥接线法将各测点 的工作应变片和温度补偿片连接在应变电桥的相邻桥臂 上,按照电阻应变仪的操作规程将电桥预调平衡,加载 后即可从应变仪上读出各测点的应变值ε实。
纯弯 曲梁 的正 应力 实验
1.1实验目的及仪器设备
纯弯曲梁的正 应力实验
1.2实验原理 1.3实验步骤
1.4实验数据处理
理论分析可知,梁发生纯弯曲变形时,横截面 上只有正应力,以中性轴为界,一侧为拉应力,一 侧为压应力,且正应力的大小与点到中性轴的距离 成正比。本节用实验测定矩形截面简支梁承受纯弯 曲时横截面上正应力的大小及其分布规律,并与理 论值进行比较,以验证弯曲正应力公式,并初步掌 握电测法原理和静态电阻应变仪的使用方法。
第35次课纯弯曲时梁的正应力
课时授课计划第三十五次课【教学课题】:§3-7纯弯曲的梁的正应力【教学目的】:掌握纯弯曲的梁的正应力【教学重点及处理方法】:纯弯曲的梁的正应力处理方法:详细讲解【教学难点及处理方法】:纯弯曲的梁的正应力的应用处理方法:结合例题分析讲解【教学方法】: 讲授法【教具】:【时间分配】:引入新课5min新课80 min小结、作业5min第三十五次课【提示启发引出新课】在上次课中已经讨论剪力图和弯矩图的绘制及他们之间的关系。
在这次课中讨论纯弯曲的梁的正应力的计算。
【新课内容】§3-10 纯弯曲时梁的正应力在平面弯曲时,工程上近似地认为梁横截面上的弯矩是由截面上的正应力形成的,而剪力则由截面上的切应力所形成。
本章将在梁弯曲时的内力分析的基础上,导出梁弯曲时的应力与变形的计算,建立梁的强度和刚度条件。
为了研究梁横截面上的正应力分布规律,取一矩形截面等直梁,在表面画些平行于梁轴线的纵线和垂直干梁轴线的横线。
在梁的两端施加一对位于梁纵向对称面内的力偶,梁则发生弯曲。
梁任意横截面上的内力只有弯矩而无剪力,这种弯曲称为纯弯曲,这种梁称为纯弯曲梁。
通常从变形的几何关系、物理关系和静力平衡条件三个方面来推导出纯弯曲梁横截面上的正应力公式。
一、实验观察梁发生弯曲变形后,我们可以观察到以下现象:1、横向线仍是直线且仍与梁的轴线正交,只是相互倾斜了一个角度2、纵向线(包括轴线)都变成了弧线。
3、梁横截面的宽度发生了微小变形,根据上述现象,可对梁的变形提出如下假设:① 平面假设:梁弯曲变形时,其横截面仍保持平面,且绕某轴转过了一个微小的角度。
② 单向受力假设:设梁由无数纵向纤维组成,则这些纤维处于单向受拉或单向受压状态。
可以看出,梁下部的纵向纤维受拉伸长,上部的纵向纤维受压缩短,其间必有一层纤维既不伸长也木缩短,这层纤维称为中性层。
中性层和横截面的交线称为中性轴,即图中的Z轴。
梁的横截面绕Z轴转动一个微小角度。
纯-弯曲梁的正应力实验
纯-弯曲梁的正应力实验本实验旨在研究弯曲梁在受力时的正应力分布情况,通过实验数据的测量及分析,探讨影响梁正应力分布的因素,并对梁的强度进行评估。
1. 实验原理1.1 弯曲梁正应力分析弯曲梁是一种常用的结构元件,例如桥梁、楼层结构等,她受到外力的作用会发生弯曲形变,产生正应力和剪应力。
弯曲梁的正应力是沿着截面法向的应力,在梁的顶部为拉应力,底部为压应力。
正应力的计算公式如下:$$\sigma = \frac{My}{I}$$其中,$\sigma$为正应力,$M$为弯矩,$y$为受力点到截面重心的距离,$I$为截面惯性矩。
弯曲梁正应力的分布情况受到多种因素的影响,主要包括:① 梁材料的弹性模量:弹性模量越大,弯曲梁的刚度越大,相同外力作用下,梁的形变和正应力都会相应减小。
② 梁截面形状和尺寸:梁截面的惯性矩影响正应力的大小和分布情况。
截面抗弯性能越强,正应力越小。
③ 受力位置和方向:受力位置和作用方向是影响正应力大小和分布情况的重要因素。
不同位置和方向的外力作用会导致不同的正应力分布规律。
2. 实验设备和方法本实验采用的主要设备有:弯曲梁试验机、电子天平、千分尺等。
2.2 实验步骤1. 准备弯曲梁样品,将其加工成常用的矩形截面和半圆形截面,分别测量其截面形状和尺寸。
2. 调整弯曲梁试验机,设置好取样位置和取样方式。
3. 将弯曲梁放入试验机,设置试验参数,包括荷重大小、位移速率等。
4. 开始试验,记录每个荷载下的跨中挠度和荷载大小,并计算出弯矩大小。
5. 在试验过程中,用电子天平测量梁的重量,并用千分尺对梁的跨中直径和截面高度进行测量,计算出截面惯性矩。
6. 根据测量数据,计算出每个荷载下的正应力,并绘制出正应力分布图。
3. 结果分析3.1 实验数据记录本实验用常见的矩形和半圆形弯曲梁进行了试验,记录了不同工况下的荷载和跨中挠度等数据。
根据数据计算得出弯矩以及正应力等数据,具体数据结果如下表:1. 矩形截面弯曲梁(1)弯曲梁在起始荷载下出现了微小的振动,但并未发生失稳。
纯弯曲梁的正应力实验报告
姓名: 班级: 学号:实验陈述 纯曲折梁的正应力实验一.实验目标:1.测定梁在纯曲折时横截面上正应力大小和散布纪律2.验证纯曲折梁的正应力公式 二.实验装备及对象:1.材料力学多功效实验台中的纯曲折梁实验装配2.数字测力仪.电阻应变仪 三.实验道理及办法:在纯曲折前提下,依据平面假设和纵向纤维间无挤压的假设,可得到梁横截面上随意率性一点的正应力,盘算公式:zM yI σ⋅=为测量梁横截面上的正应力散布纪律,在梁的曲折段沿梁正面不合高度,平行于轴线贴有应变片.贴法:中性层一片,中性层高低1/4梁高处各一片,梁高低两侧各一片,共计五片.采取增量法加载,每增长等量荷载△P (500N )测出各点的应变增量△ε,求的各点应变增量的平均值△ε实i ,从而求出应力增量:σ实i =E △ε实i将实验应力值与理论应力值进行比较,已验证曲折正应力公式. 四.原始数据:五.实验步调:1. 打开应变仪.测力仪电源开关2.连策应变仪上电桥的连线,肯定第一测点到第五测点在电桥通道上的序号.3. 检讨测力仪,选择力值加载单位N或kg,按动按键直至显示N 上的红灯亮起.按清零键,使测力计显示零.4.应变仪调零.按下“主动均衡”键,使应变仪显示为零.5.转着手轮,按铭牌指导加载,加力的学生要迟缓匀速加载,到测力计上显示500N,读数的学生读下5个测点的应变值,(留意记载下正.负号).用应变仪右下角的通道切换键来显示第5测点的读数.今后,加力每次500N,到3000N为止.6.读完3000N应变读数后,卸下载荷,封闭电源.六.实验成果及处理:1.各点实验应力值盘算依据上表数据求得应变增量平均值△εPi,带入胡克定律盘算各点实验值:σ实i=E△εPi×10-62.各点理论应力值盘算载荷增量△P = 500N弯矩增量△M = △P/2×L P应力理论值盘算(验证的就是它)3.绘出实验应力值和理论应力值的散布图以横坐标暗示各测点的应力σ实和σ理,以纵坐标暗示各测点距梁中性层的地位.将各点用直线衔接,实测用实线,理论用虚线.σy4.实验值与理论值比较,验证纯曲折梁的正应力公式。
弯曲应力—纯弯曲时的正应力(材料力学)
§5-2 正应力计算公式
3、物理关系
σ Eε
M
?
所以 σ E y
z
O
x
应力分布规律:
?
y
直梁纯弯曲时横截面上任意一点的正应力,与它到中性轴的距离成正比。待解决问题中性轴的位置?
中性层的曲率半径
§5-2 正应力计算公式
4、静力关系
横截面上内力系为垂直于横截面的空 间平行力系,这一力系简化得到三个内力分 M 量。
y t max
M
z
y
σtmax
σ cmax My cmax Iz
§5-2 正应力计算公式
二、横力弯曲时梁横截面上的正应力
实际工程中的梁,其横截面上大多同时存在着弯矩和剪力,为横 力弯曲。但根据实验和进一步的理论研究可知,剪力的存在对正应力 分布规律的影响很小。因此对横力弯曲的情况,前面推导的正应力公 式也适用。
(2)最大正应力发生在横截面上离中性轴最远的点处。
σ max M y max Iz
引用记号
Wz
Iz ymax
—抗弯截面系数
则公式改写为
σ max
M Wz
§5-2 正应力计算公式
对于中性轴为对称轴的横截面
矩形截面
Wz
Iz h/2
bh3 / 12 h/2
bh2 6
实心圆截面
Wz
Iz d /2
πd 4 / 64 d /2
推论:必有一层变形前后长度不变的纤维—中性层
⊥ 中性轴 横截面对称轴
中性层
中性轴
横截面对称轴
§5-2 正应力计算公式
2、变形几何关系
d
dx
图(a)
O’
b’ z
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
课时授课计划
第三十五次课
【教学课题】:§3-7纯弯曲的梁的正应力
【教学目的】:掌握纯弯曲的梁的正应力
【教学重点及处理方法】:纯弯曲的梁的正应力处理方法:详细讲解
【教学难点及处理方法】:纯弯曲的梁的正应力的应用处理方法:结合例题分析讲解
【教学方法】: 讲授法
【教具】:
【时间分配】:引入新课5min
新课80 min
小结、作业5min
第三十五次课
【提示启发引出新课】
在上次课中已经讨论剪力图和弯矩图的绘制及他们之间的关系。
在这次课中讨论纯弯曲的梁的正应力的计算。
【新课内容】
§3-10 纯弯曲时梁的正应力
在平面弯曲时,工程上近似地认为梁横截面上的弯矩是由截面上的正应力形成的,而剪力则由截面上的切应力所形成。
本章将在梁弯曲时的内力分析的基础上,导出梁弯曲时的应力与变形的计算,建立梁的强度和刚度条件。
为了研究梁横截面上的正应力分布规律,取一矩形截面等直梁,在表面画些平行于梁轴线的纵线和垂直干梁轴线的横线。
在梁的两端施加一对位于梁纵向对称面内的力偶,梁则发生弯曲。
梁任意横截面上的内力只有弯矩而无剪力,这种弯曲称为纯弯曲,这种梁称为纯弯曲梁。
通常从变形的几何关系、物理关系和静力平衡条件三个方面来推导出纯弯曲梁横截面上的正应力公式。
一、实验观察
梁发生弯曲变形后,我们可以观察到以下现象:
1、横向线仍是直线且仍与梁的轴线正交,只是相互倾斜了一个角度
2、纵向线(包括轴线)都变成了弧线。
3、梁横截面的宽度发生了微小变形,
根据上述现象,可对梁的变形提出如下假设:
① 平面假设:梁弯曲变形时,其横截面仍保持平面,且绕某轴转过了一个微小的角度。
② 单向受力假设:设梁由无数纵向纤维组成,则这些纤维处于单向受拉或单向受压状态。
可以看出,梁下部的纵向纤维受拉伸长,上部的纵向纤维受压缩短,其间必有一层纤维既不伸长也木缩短,这层纤维称为中性层。
中性层和横截面的交线称为中性轴,即图中的Z轴。
梁的横截面绕Z轴转动一个微小角度。
二、变形的几何关系
图中梁的两个横截面之间距离为dx,变形后中性层纤维长度仍为dx且dx=ρdθ。
距中性层为y的某一纵向纤维的线应变ε为:
即梁内任一纵向纤维的线应变ε与它到中性层的距离y成正比。
三、变形的物理关系
由单向受力假设,当正应力不超过材料的比例极限时,将虎克定律代入上式,得:
可见矩形截面梁在纯弯曲时的正应力的分布有如下特点:
① 中性轴上的线应变为零,所以其正应力亦为零。
② 到中性轴距离相等的各点,其线应变相等。
根据虎克定律,它们的正应力也相等。
③ 在图示的受力情况下,中性轴上部各点正应力为负值,中性轴下部各点正应力为正值。
④ 正应力沿y轴线性分布。
最大正应力(绝对值)在离中性轴最
四、梁纯弯曲时横截面上正应力的分布规律
1、纯弯曲时梁横截面上只有正应力而无切应力。
由于梁横截面保持平面,所以沿横截面高度方向纵向纤维从缩短到伸长是线性变化的,因此横截面上的正应力沿横截面高度方向也是线性分布的。
以中性轴为界,凹边是压应力,使梁缩短,凸边是拉应力,使梁伸长,横截面上同一高度各点的正应力相等,距中性轴最远点有最大拉应力和最大压应力,中性轴上各点正应力为零。
2、梁纯弯曲时正应力计算公式
在弹性范围内,经推导可得梁纯弯曲时横截面上任意一点的正应力为
式中,M为作用在该截面上的弯矩(Nmm);y 为计算点到中性轴的距离(mm); I为横截面对中性轴z的惯性矩
(mm4)。
在中性轴上y=0,所以σ=0;当y=y max时,σ=σmax。
最大正应力产生在离中性轴最远的边缘处,
或
__________横截面对中性轴z的抗弯截面模量mm3)
计算时,M和y均以绝对值代入,至于弯曲正应力是拉应力还是压应力,则由欲求应力的点处于受拉侧还是受压侧来判断。
受拉侧的弯曲正应力为正,受压侧的为负。
弯曲正应力计算式虽然是在纯弯曲的情况下导出的,但对于剪切弯曲的梁,只要其跨度L与横截面高度h之比L/h>5,仍可运用这些公式计算弯曲正应力。
5、惯性矩和抗弯截面模量
简单截面的惯性矩和抗弯截面模量计算公式
6、梁纯弯曲时的强度条件
对于等截面梁,弯矩最大的截面就是危险截面,其上、下边缘各点的弯曲正应力即为最大工作应力,具有最大工作应力的点一般称为危险点。
梁的弯曲强度条件是:梁内危险点的工作应力不超过材料的许用应力。
运用梁的弯曲强度条件,可对梁进行强度校核、设计截面和确定许可载荷。
例7-6 在例7-3中的简支梁,若选用D=100mm,d=60mm的空心圆形截面钢制造,已知梁的跨度l=3m,a=1m,b=2m,集中载荷
F=25kN,许用正应力[ ]=200MPa。
不计梁的自重,试校核该梁的强度。
【小结】:纯弯曲的梁的正应力【作业】:5
【后记】:。
