中考复习----五种基本尺规作图
人教版数学中考复习课件第七章第一节 尺规作图

尺规作图题常见考查类型 1.直接作图,如作角平分线,线段的垂直平分线,作一个角等于已 知角等,直接利用五种基本的尺规作图来解答. 2.给出作图痕迹或步骤,判断结论正误或进行相关计算,对于此种 类型的题目,平时要对五种基本尺规作图了熟于心,从而判断是哪种基 本作图,再根据作图依据进行结论判断或计算.
5.★(2020·郴州)如图,在矩形 ABCD 中,AD=4,AB=8.分别以点 B,D 为圆心,以大于12BD 的长为半径画弧,两弧相交于点 E 和 F.作直线 EF 分别与 DC,DB,AB 交于点 M,O,N,则 MN= 2 5 .
6.(2020·扬州)如图,在△ABC 中,按以下步骤作图: ①以点 B 为圆心,任意长为半径作弧,分别交 AB,BC 于点 D,E. ②分别以点 D,E 为圆心,大于12DE 的长为半径作弧,两弧交于点 F. ③作射线 BF 交 AC 于点 G. 如果 AB=8,BC=12,△ABG 的面积为 18,则△CBG 的面积为 27 .
∴∠DBA=∠ACD=45°, ∵AC=6,BC=8,∴AB=10, ∴AD=BD=AB·sin 45°=10× 22=5 2.
7.(2020·青海)如图,在 Rt△ABC 中,∠C=90°.
(1)尺规作图:作 Rt△ABC 的外接圆⊙O;作∠ACB 的角平分线交⊙O 于点 D,连接 AD;(不写作法,保留作图痕迹)
解:如图,Rt△ABC 的外接圆⊙O,线段 CD 即为所求.
(2)若 AC=6,BC=8,求 AD 的长. 解:连接 BD, ∵∠C=90°. ∴AB 是⊙O 的直径, ∴∠BDA=90°, ∵CD 平分∠ACB, ∴∠ACD=∠BCD=45°,
命题点:尺规作图及相关的证明与计算(2020 年考查 2 次,2019 年考 查 2 次,2018 年考查 2 次,2017 年考查 1 次)
2023中考数学复习:尺规作图

1
栏目导航
数据聚焦
2
3
考点梳理
数据剖析
数据链接
题型突破
真题试做
第27讲
返回栏目导航
尺规作图— 教材链接
1
数据聚焦
考点梳理
教材链接
人教:七上第四章P126.
冀教:七上第二章P69-P70,P79,八上第十三章P52-P54,第十六章P112P123.
北师:七下第二章P55-P60,第四章P105-P107.
直平分线 点N;
MN
返回栏目导航
(2)过点M,N作直线MN,直线MN即为线
段AB的垂直平分线
图形示例
第27讲
返回思维导图
尺规作图— 考点梳理
返回栏目导航
续表
1.五种尺规作图
作图内容
作图步骤
作
过直线 (1)以点O为圆心,任意长为半径向点O两侧
直
上一点 作弧,分别交直线l于A,B两点;
线l
O作直
(2)分别以点A,B为圆心,以大于AB的长为半
即为所求
图示
第27讲
尺规作图— 考点梳理
返回思维导图
返回栏目导航
3.作三角形的内切圆和外接圆
作图要求
续表
作法
作三角形 (1)分别作AB,BC的⑥___________,
垂直平分线
的外接圆 交点为O;
(2)以O为圆心,OA的长为半径画
圆,☉O即为所求
图示
第27讲
尺规作图— 考点梳理
4.作特殊四边形的方法
于点P2.故符合题意的点P有两处.
1
2
13
4
5
第27讲
尺规作图— 题型突破
中考尺规作图专题

中考专题复习:尺规作图最基本,最常用的尺规作图,通常称基本作图。
一些复杂的尺规作图都是由基本作图组成的。
五种基本作图:1、作一条线段等于已知线段:2、作一个角等于已知角;3、作已知线段的垂直平分线:4、作已知角的角平分线:5、过一点作已知直线的垂线:专题训练;1 •已知:线段/ b求作:A ABC,使AB=a, BC二b, AC二2a・(尺规作图,不写作法,保留作图痕迹)| b分析:首先画线段AC二2a,再以A为圆心,a长为半径画弧,再以C为圆心,b长为半径画弧,两弧交于点B, 连接AB、BC即可.解:如图所示:AABC即为所求.点评:此题主要考査了作图,关键是掌握作一条线段等于已知线段的方法.2•如图(1),已知直线及直线外一点C,过点C作CD//AB(写出作法,画出图形). 分析:根据两直线平行的性质,同位角相等或内错角相等,故作一个角ZECD=ZEFB即可. 作法:如图(2).(1)过点C作直线FF,交于点(2 )以点F为圆心,以任意长为半径作弧,交FB于点P,交EF于点、Q;(3)以点C为圆心,以"为半径作弧,交CE于M点;(4)以点M为圆心,以PQ为半径作弧,交前弧于点0(5)过点D作直线CD, CD就是所求的直线.3•已知:ZAOB,求作:ZA r O' B r =ZA0B (用尺规作图,保留作图痕迹,不写步骤).O BA图()b1分析:(1)作射线L B r :(2) 以0为圆心,以任意长为半径画弧,交0A 于点C,交0B 于点D :(3) 以0'为圆心,以0C 的长为半径画弧,交O' A'于点C':(4) 以点D'为圆心,以CD 的长为半径画弧,交前弧于点C':(5) 过C ,作射线0, A f .则O' B'就是所求作的角.解:ZA‘ 0’ B'就是所求作的角.4•画出ZA0B 的角平分线(要求:尺规作图,不写作图过程保留作图痕迹).分析:以点0为圆心,以任意长为半径画弧,与边0A 、0B 分别相交于点M. N,再以点N 为圆心,以大 于1/2 MN 长为半径,画弧,在ZA0B 内部相交于点C,作射线0C 即为ZA0B 的平分线.解:如图所示,0C 即为所求作的ZA0B 的平分线.5•尺规作图:线段MN 的垂直平分线(不写作法•保留作图痕迹)分析:分别以M 、N 点为圆心,以大于1/2 MN 的长为半径作弧,两弧相交于A, B 两点:作直线AB, AB 即 为线段AB 的垂直平分线.解:如图所示:AB 即为所求.6 •经过已知宜线外一点作这条直线的垂线“的尺规作图过程: 已知:直线I 和I 外一点P ・求作:直线I 的垂线,使它经过点P・作法:如图:(2)在直线I上任取两点A、B:(2)分别以点A、B为圆心,AP, BP长为半径画弧,两弧相交于点Q:(3)作直线PQ.参考以上材料作图的方法,解决以下问题:(1)以上材料作图的依据是:线段垂直平分线上的点到线段两端点的距离相等7. 尺规作图:画一个三角形与AABC全等,要求用尺规作图,保留作图痕迹. 分析:根据全等三角形的判立SSS左理分别作DF二BC, DE二AB, EF二AC即可. 解:如图所示:A E8. 尺规作图:作三角形的外接圆.分析:由于三角形的外心是三角形三边中垂线的交点,可作AABC的任意两边的垂直平分线,它们的交点即为AABC的外接圆的圆心(设圆心为0):以0为圆心、0B长为半径作圆,即可得出AABC的外接圆.解:如图所示:00即为AABC的外接圆.9. 利用尺规作岀AABC的内切圆(不写作法,保留作图痕迹)分析:首先作岀三角形的内角平分线进而得岀得出内切圆圆心位置,利用圆心到三角形边的距离为半径画圆得岀即可.解:如图所示:00即为所求.A10•尺规作图,找出圆的圆心,不要求写作法,保留作图痕迹.分析:画出两条弦,分别作岀两条弦的垂直平分线,两垂直平分线的交点就是圆心位置. 解:如图所示:11 •如图,已知00・用尺规作00的内接正四边形ABCD.(写岀结论,不写作法,保留作图痕迹,并把作图痕迹用黑色签字笔描黑・)解:作O0的任意一条直径AC.作AC 的垂直平分线,与€>0相交于B, D 两点.顺次连接AB, BC, CD, DA 得到正四边形ABCD.四边形ABCD 就是所要求作的图形.强化练习:1.已知:ZAOB,点M 、N.求作:点P,使点P 到OA 、0B 的距离相等,且PM=PN.(要求:用尺规作图,保 留作图痕迹,不写作法.)分析:首先作岀ZAOB 的平分线,作H 点关于对角线对称点W,连接WN,作WN 的垂直平分线,交角平分 线的点就是P 点.2•如图,在 RtAABC 中,ZBAC=9O C ・(1)先作ZACB 的平分线交AB 边于点P,再以点P 为圆心,PA 长为半径作OP :(要求:尺规作图,保 留作图痕迹,不写作法)(2)请你判断(1)中BC 与OP 的位宜关系,并证明你的结论3•如图,AABC 中,ZBAC=90% AD 丄BC,垂足为D ・求作ZABC 的平分线,分别交AD, AC 于P, Q 两点; 并证明AP 二AQ.(要求:尺规作图,保留作图痕迹,不写作法)5 D C4.已知:直线AB 和AB±一点C.求作:AB 的垂线,使它经过点C.A C 中小艾的作法如下:如图,(1)在直线AB 上取一点D,使点D 与点C 不重合,以点C 为圆心,CD 长为半径作弧,交AB 于D, E 两点;(2)分別以点D 和点E 为圆心.大于2°E 长为半径作弧,两弧相交于点F ;(3)作直线CF.所以直线CF 就是所求作的垂线.作图如右:A C B这样作图的依据是一等腰三角形的"三线合一”,两点确立一条直如图,5.下而是"经过已知宜线外一点作这条直线的平行线”的尺规作图过程.已知:如图1,直线I和直线I外一点P.求作:直线I的平行直线,使它经过点P.作法:如图2.(1)过点P作直线m与直线I交于点0:(2)在直线m上取一点A (0A<0P),以点0为圆心,0A长为半径画弧,与直线I交于点B:(3)以点P为圆心,0A长为半径画弧,交直线m于点C,以点C为圆心,AB长为半径画弧,两弧交于点D:(4)作直线PD.所以直线PD就是所求作的平行线.该作图的依据是三边分别相等的两个三角形全等:全等三角形的对应角相等;同位角相等,两直线平行・6•如图,ZkABC是直角三角形,ZACB=90°.(1)尺规作图:作©C,使它与AB相切于点D,与AC相交于点E,保留作图痕迹,不写作法,请标明字母. (2)在你按(2)中要求所作的图中,若BC=3, ZA=30°,求五的长.7•如图:(1)如图,已知ZAOB及点C、D两点,请利用直尺和圆规作一点P,使得点P到射线OA. 0B的距离相等,且P点到点c、D的距离也相等.(2)利用方格纸画岀AABC关于直线I的对称图形△A8U.(3)如图,已知在AABC中,AB二AC, AD是BC边上的高,P是AB边上的一点,试在高AD ±找一点E,使得APEB的周长最短.解:(1)如图1所示,点P即为所求:(2)如图2所示:△A,BC即为所求:8 •如图,在平面直角坐标系中,AABC三个顶点的坐标分别为A ( -2, 4), B (・4, 1), C (0, 1).(1)画出与AABC关于x轴对称的厶AiBiCn并写出点G的坐标:(2)画出以G为旋转中心,将厶AiBiCi逆时针旋转90。
中考尺规作图大全-(含练习答案)

中考尺规作图大全-(含练习答案)尺规作图是一种使用没有刻度的直尺和圆规的方法。
基本作图是尺规作图的最基本、最常用的方法,而一些复杂的尺规作图都是由基本作图组成的。
基本作图包括五种:作一条线段等于已知线段、作一个角等于已知角、作已知线段的垂直平分线、作已知角的角平分线、过一点作已知直线的垂线。
题目一要求作一条线段等于已知线段a。
作法是先作射线AP,然后在射线AP上截取AB=a,这样线段AB就是所求作的图形。
题目二要求作已知线段MN的垂直平分线,即找到点O 使得MO=NO(即O是MN的中点)。
作法是分别以M、N 为圆心,以大于MN的相同线段为半径画弧,两弧相交于P、Q,然后连接PQ交MN于O,这样点PQ就是所求作的MN 的垂直平分线。
题目三要求作已知角AOB的角平分线OP。
作法是以O 为圆心,任意长度为半径画弧,分别交OA、OB于M、N,然后以M、N为圆心,以大于MN的线段长为半径画弧,两弧交∠AOB内于P,最后作射线OP,这样射线OP就是∠AOB的角平分线。
题目四要求作一个角等于已知角AOB。
作法是先作射线O’A’,然后以O为圆心,任意长度为半径画弧,交OA于M,交OB于N,接着以O’为圆心,以OM的长为半径画弧,交O’A’于M’,再以M’为圆心,以MN的长为半径画弧,交前弧于N’,最后连接O’N’并延长到B’,这样∠A’O’B’就是所求作的角。
题目五要求经过直线AB上一点P做已知直线CD的垂线。
作法是以P为圆心,任意长为半径画弧,交AB于M、N,然后分别以M、N为圆心,以大于MN的长为半径画弧,两弧交于点Q,最后连接CQ、DQ即可得到所求作的CD。
3.删除明显有问题的段落(无问题段落为1、2、4、5)4.改写每段话3)过D、Q作直线CD。
则直线CD是求作的直线。
改写为:作直线CD,使其经过点P并垂直于直线AB,方法如下:6)题目六:经过直线外一点作已知直线的垂线已知:如图,直线AB及外一点P。
求作:直线CD,使CD经过点P,且CD⊥AB。
陕西中考题尺规作图题(含答案)
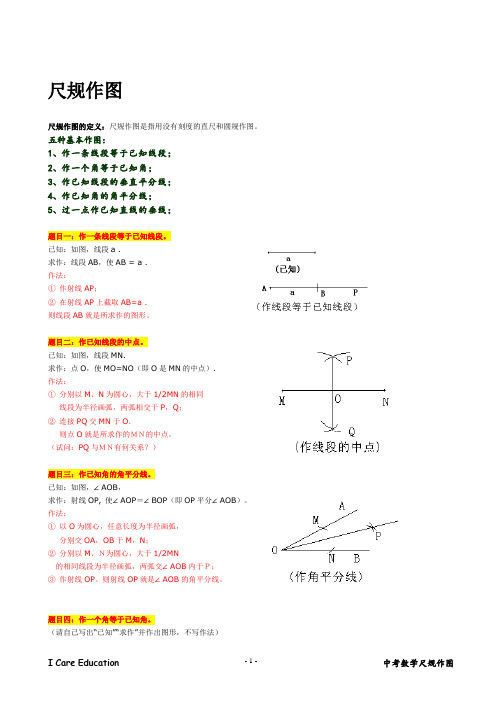
尺规作图尺规作图的定义:尺规作图是指用没有刻度的直尺和圆规作图。
五种基本作图:1、作一条线段等于已知线段;2、作一个角等于已知角;3、作已知线段的垂直平分线;4、作已知角的角平分线;5、过一点作已知直线的垂线;题目一:作一条线段等于已知线段。
已知:如图,线段a .求作:线段AB,使AB = a .作法:①作射线AP;②在射线AP上截取AB=a .则线段AB就是所求作的图形。
题目二:作已知线段的中点。
已知:如图,线段MN.求作:点O,使MO=NO(即O是MN的中点).作法:①分别以M、N为圆心,大于1/2MN的相同线段为半径画弧,两弧相交于P,Q;②连接PQ交MN于O.则点O就是所求作的MN的中点。
(试问:PQ与MN有何关系?)题目三:作已知角的角平分线。
已知:如图,∠AOB,求作:射线OP, 使∠AOP=∠BOP(即OP平分∠AOB)。
作法:①以O为圆心,任意长度为半径画弧,分别交OA,OB于M,N;②分别以M、N为圆心,大于1/2MN的相同线段为半径画弧,两弧交∠AOB内于P;③作射线OP。
则射线OP就是∠AOB的角平分线。
题目四:作一个角等于已知角。
(请自己写出“已知”“求作”并作出图形,不写作法)题目五:已知三边作三角形。
已知:如图,线段a,b,c.求作:△ABC,使AB = c,AC = b,BC = a.作法:①作线段AB = c;②以A为圆心b为半径作弧,以B为圆心a为半径作弧与前弧相交于C;③连接AC,BC。
则△ABC就是所求作的三角形。
题目六:已知两边及夹角作三角形。
已知:如图,线段m,n, ∠α.求作:△ABC,使∠A=∠α,AB=m,AC=n.作法:①作∠A=∠α;②在AB上截取AB=m ,AC=n;③连接BC。
则△ABC就是所求作的三角形。
题目七:已知两角及夹边作三角形。
已知:如图,∠α,∠β,线段m .求作:△ABC,使∠A=∠α,∠B=∠β,AB=m. 作法:①作线段AB=m;②在AB的同旁作∠A=∠α,作∠B=∠β,∠A与∠B的另一边相交于C。
中考专题复习——初中最基本的尺规作图总结与典型例题

初中基本尺规作图总结与典型例题一、理解“尺规作图”的含义1.在几何中,我们把只限定用直尺(无刻度)和圆规来画图的方法,称为尺规作图.其中直尺只能用来作直线、线段、射线或延长线段;圆规用来作圆和圆弧.由此可知,尺规作图与一般的画图不同,一般画图可以动用一切画图工具,包括三角尺、量角器等,在操作过程中可以度量,但尺规作图在操作过程中是不允许度量成分的.2.基本作图:(1)用尺规作一条线段等于已知线段;(2)用尺规作一个角等于已知角. 利用这两个基本作图,可以作两条线段或两个角的和或差.二、熟练掌握尺规作图题的规范语言1.用直尺作图的几何语言:①过点×、点×作直线××;或作直线××;或作射线××;②连结两点××;或连结××;③延长××到点×;或延长(反向延长)××到点×,使××=××;或延长××交××于点×;2.用圆规作图的几何语言:①在××上截取××=××;②以点×为圆心,××的长为半径作圆(或弧);③以点×为圆心,××的长为半径作弧,交××于点×;④分别以点×、点×为圆心,以××、××的长为半径作弧,两弧相交于点×、×. 三、了解尺规作图题的一般步骤尺规作图题的步骤:1.已知:当作图是文字语言叙述时,要学会根据文字语言用数学语言写出题目中的条件;2.求作:能根据题目写出要求作出的图形及此图形应满足的条件;3.作法:能根据作图的过程写出每一步的操作过程.当不要求写作法时,一般要保留作图痕迹.对于较复杂的作图,可先画出草图,使它同所要作的图大致相同,然后借助草图寻找作法.在目前,我们只要能够写出已知,求作,作法三步(另外还有第四步证明)就可以了,而且在许多中考作图题中,又往往只要求保留作图痕迹,不需要写出作法,可见在解作图题时,保留作图痕迹很重要.尺规作图的定义:尺规作图是指用没有刻度的直尺和圆规作图。
中考数学基础复习第22课尺规作图课件
解得,x=5或-3(舍弃),∴BE=5.
变式2.(202X·长沙)人教版初中数学教科书八年级上册第48页告知我们一种 作已知角的平分线的方法: 已知:∠AOB. 求作:∠AOB的平分线. 作法:(1)以点O为圆心,适当长为半径画弧,交OA于点M,交OB于点N; (2)分别以点M,N为圆心,大于 1 MN的长为半径画弧,两弧在∠AOB的内部相交
4.(202X·北京)已知:如图,△ABC为锐角三角形,AB=AC,CD∥AB. 求作:线段BP,使得点P在直线CD上,且∠ABP= ∠BAC. 作法:①以点A为圆心,AC长为半径画圆,交直线CD于C,P两点;②连接BP.线段BP 就是所求作线段. (1)使用直尺和圆规,依作法补全图形.(保留作图痕迹)
2
∠CBA内交于点F;作射线BF交AC于点G.若CG=1,P为AB上一动点,则GP的最小值
为
(C)
A.无法确定
B. 1
2
C.1
D.2
5.(202X·河北)如图1,已知∠ABC,用尺规作它的角平分线.
如图2,步骤如下,
第一步:以B为圆心,以a为半径画弧,分别交射线BA,BC于点D,E;
第二步:分别以D,E为圆心,以b为半径画弧,两弧在∠ABC内部交于点P;
【解析】(1)则四边形ABCD就是所求作的四边形.
(2)∵AB∥CD,∴∠ABP=∠CDP,∠BAP=∠DCP,∴△ABP∽△CDP,∴ AB . AP
【考点3】尺规作图拓展应用
例3.(202X·苏州)如图,已知∠MON是一个锐角,以点O为圆心,任意长为半径画 弧,分别交OM,ON于点A,B,再分别以点A,B为圆心,大于 1 AB长为半径画弧,两
2
弧交于点C,画射线OC.过点A作AD∥ON,交射线OC于点D,过点D作DE⊥OC,交ON于
(完整版)初中最基本的尺规作图总结
尺规作图一、理解“尺规作图”的含义1.在几何中,我们把只限定用直尺(无刻度)和圆规来画图的方法,称为尺规作图.其中直尺只能用来作直线、线段、射线或延长线段;圆规用来作圆和圆弧.由此可知,尺规作图与一般的画图不同,一般画图可以动用一切画图工具,包括三角尺、量角器等,在操作过程中可以度量,但尺规作图在操作过程中是不允许度量成分的.2.基本作图:(1)用尺规作一条线段等于已知线段;(2)用尺规作一个角等于已知角. 利用这两个基本作图,可以作两条线段或两个角的和或差.二、熟练掌握尺规作图题的规范语言1.用直尺作图的几何语言:①过点×、点×作直线××;或作直线××;或作射线××;②连结两点××;或连结××;③延长××到点×;或延长(反向延长)××到点×,使××=××;或延长××交××于点×;2.用圆规作图的几何语言:①在××上截取××=××;②以点×为圆心,××的长为半径作圆(或弧);③以点×为圆心,××的长为半径作弧,交××于点×;④分别以点×、点×为圆心,以××、××的长为半径作弧,两弧相交于点×、×. 三、了解尺规作图题的一般步骤尺规作图题的步骤:1.已知:当作图是文字语言叙述时,要学会根据文字语言用数学语言写出题目中的条件;2.求作:能根据题目写出要求作出的图形及此图形应满足的条件;3.作法:能根据作图的过程写出每一步的操作过程.当不要求写作法时,一般要保留作图痕迹.对于较复杂的作图,可先画出草图,使它同所要作的图大致相同,然后借助草图寻找作法.在目前,我们只要能够写出已知,求作,作法三步(另外还有第四步证明)就可以了,而且在许多中考作图题中,又往往只要求保留作图痕迹,不需要写出作法,可见在解作图题时,保留作图痕迹很重要.尺规作图的定义:尺规作图是指用没有刻度的直尺和圆规作图。
中考数学专题复习导学案尺规作图》(含答案)
中考数学专题练习《尺规作图》【知识归纳】一)尺规作图1.定义只用没有刻度的和作图叫做尺规作图.2.步骤①根据给出的条件和求作的图形,写出已知和求作部分;②分析作图的方法和过程;③用直尺和圆规进行作图;④写出作法步骤,即作法.二)五种基本作图1.作一条线段等于已知线段;2.作一个角等于已知角;3.作已知角的平分线;4.过一点作已知直线的垂线;5.作已知线段的垂直平分线.三)基本作图的应用1.利用基本作图作三角形(1)已知三边作三角形;(2)已知两边及其夹角作三角形;(3)已知两角及其夹边作三角形;(4)已知底边及底边上的高作等腰三角形;(5)已知一直角边和斜边作直角三角形.2.与圆有关的尺规作图(1)过不在同一直线上的三点作圆(即三角形的外接圆).(2)作三角形的内切圆.【基础检测】1.如图,在平面直角坐标系中,以O 为圆心,适当长为半径画弧,交x 轴于点M ,交y 轴于点N ,再分别以点M 、N 为圆心,大于MN 的长为半径画弧,两弧在第二象限交于点P .若点P 的坐标为(2a ,b +1),则a 与b 的数量关系为( )A .a =bB .2a +b =﹣1C .2a ﹣b =1D .2a +b =12.如图,已知△ABC ,以点B 为圆心,AC 长为半径画弧;以点C 为圆心,AB 长为半径画弧,两弧交于点D ,且点A ,点D 在BC 异侧,连结AD ,量一量线段AD 的长,约为( )A .2.5cmB .3.0cmC .3.5cmD .4.0cm3.如图,已知△ABC ,∠BAC=90°,请用尺规过点A 作一条直线,使其将△ABC 分成两个相似的三角形(保留作图痕迹,不写作法)4.如图,在边长为1的正方形网格中,△ABC 的顶点均在格点上,点A 、B 的坐标分别是A (4,3)、B (4,1),把△ABC 绕点C 逆时针旋转90°后得到△A 1B 1C .(1)画出△A 1B 1C ,直接写出点A 1、B 1的坐标;(2)求在旋转过程中,△ABC 所扫过的面积.5.如图,在边长为1个单位长度的小正方形组成的12×12网格中,给出了四边形ABCD 的两条边AB 与BC ,且四边形ABCD 是一个轴对称图形,其对称轴为直线AC .(1)试在图中标出点D ,并画出该四边形的另两条边;(2)将四边形ABCD 向下平移5个单位,画出平移后得到的四边形A′B′C′D′.6.已知:线段a 及∠ACB .求作:⊙O ,使⊙O 在∠ACB 的内部,CO=a ,且⊙O 与∠ACB 的两边分别相切.7.如图,OA=2,以点A 为圆心,1为半径画⊙A 与OA 的延长线交于点C ,过点A 画OA 的垂线,垂线与⊙A 的一个交点为B ,连接BC(1)线段BC 的长等于 ; (2)请在图中按下列要求逐一操作,并回答问题:A B C①以点为圆心,以线段的长为半径画弧,与射线BA交于点D,使线段OD的长等于②连OD,在OD上画出点P,使OP得长等于,请写出画法,并说明理由.【达标检测】一、选择题1.如图,在△ABC中,∠B=55°,∠C=30°,分别以点A和点C为圆心,大于AC的长为半径画弧,两弧相交于点M,N,作直线MN,交BC于点D,连接AD,则∠BAD的度数为()A.65°B.60°C.55°D.45°2.如图,已知钝角△ABC,依下列步骤尺规作图,并保留作图痕迹.步骤1:以C为圆心,CA为半径画弧○1;步骤2:以B为圆心,BA为半径画弧○2,将弧○1于点D;步骤3:连接AD,交BC延长线于点H.下列叙述正确的是()第10题图A.BH垂直分分线段AD B.AC平分∠BAD=BC·AH D.AB=ADC.S△ABC二、填空题3.如图,已知线段AB,分别以点A和点B为圆心,大于AB的长为半径作弧,两弧相交于C、D 两点,作直线CD交AB于点E,在直线CD上任取一点F,连接FA,FB.若FA=5,则FB=.4.如图,在△ABC中,∠C=90°,∠B=30°,以A为圆心,任意长为半径画弧分别交AB、AC于点M和N,再分别以M、N为圆心,大于MN的长为半径画弧,两弧交于点P,连结AP并延长交BC于点D,则下列说法中正确的是。
2020年中考数学人教版专题复习:尺规作图
2020年中考数学人教版专题复习:尺规作图基本作图1.最基本、最常用的尺规作图,通常称为基本作图.2.基本作图有五种:(1)作一条线段等于已知线段;(2)作一个角等于已知角;(3)作一个角的平分线;(4)作一条线段的垂直平分线;(5)过一点作已知直线的垂线.典例精析典例1如图,在△ABC中,∠ACB=90°,分别以点A和B为圆心,以相同的长(大于AB)为半径作弧,两弧相交于点M和N,作直线MN交AB于点D,交BC于点E,连接CD,下列结论错误的是A.AD=BD B.BD=CDC.∠A=∠BED D.∠ECD=∠EDC【答案】D【解析】∵MN为AB的垂直平分线,∴AD=BD,∠BDE=90°,∵∠ACB=90°,∴CD=BD,∵∠A+∠B=∠B+∠BED=90°,∴∠A=∠BED,∵∠A≠60°,AC≠AD,∴EC≠ED,∴∠ECD≠∠EDC.故选D.典例2如图,已知∠MAN,点B在射线AM上.(1)尺规作图:①在AN上取一点C,使BC=BA;②作∠MBC的平分线BD,(保留作图痕迹,不写作法)(2)在(1)的条件下,求证:BD∥AN.1 2【解析】(1)①以B点为圆心,BA长为半径画弧交AN于C点;如图,点C即为所求作;②利用基本作图作BD平分∠MBC;如图,BD即为所求作;(2)先利用等腰三角形的性质得∠A=∠BCA,再利用角平分线的定义得到∠MBD=∠CBD,然后根据三角形外角性质可得∠MBD=∠A,最后利用平行线的判定得到结论.∵AB=AC,∴∠A=∠BCA,∵BD平分∠MBC,∴∠MBD=∠CBD,∵∠MBC=∠A+∠BCA,即∠MBD+∠CBD=∠A+∠BCA,∴∠MBD=∠A,∴BD∥AN.拓展1.根据下图中尺规作图的痕迹,可判断AD一定为三角形的A.角平分线B.中线C.高线D.都有可能2.(1)请你用尺规作图,作AD平分∠BAC,交BC于点D(要求:保留作图痕迹);(2)∠ADC的度数.复杂作图利用五种基本作图作较复杂图形.典例精析典例2如图,在同一平面内四个点A,B,C,D.(1)利用尺规,按下面的要求作图.要求:不写画法,保留作图痕迹,不必写结论.①作射线AC;②连接AB,BC,BD,线段BD与射线AC相交于点O;③在线段AC上作一条线段CF,使CF=AC–BD.(2)观察(1)题得到的图形,我们发现线段AB+BC>AC,得出这个结论的依据是__________.【答案】见解析.【解析】(1)①如图所示,射线AC即为所求;②如图所示,线段AB,BC,BD即为所求;③如图所示,线段CF即为所求;(2)根据两点之间,线段最短,可得AB+BC>AC.故答案为:两点之间,线段最短.拓展3.作图题:学过用尺规作线段与角后,就可以用尺规画出一个与已知三角形一模一样的三角形来.比如给定一个△ABC,可以这样来画:先作一条与AB相等的线段A′B′,然后作∠B′A′C′=∠BAC,再作线段A′C′=AC,最后连接B′C′,这样△A′B′C′就和已知的△ABC一模一样了.请你根据上面的作法画一个与给定的三角形一模一样的三角形来.(请保留作图痕迹)同步测试1.根据已知条件作符合条件的三角形,在作图过程中主要依据是A.用尺规作一条线段等于已知线段B.用尺规作一个角等于已知角C.用尺规作一条线段等于已知线段和作一个角等于已知角D.不能确定2.下列作图属于尺规作图的是A.画线段MN=3 cmB.用量角器画出∠AOB的平分线C.用三角尺作过点A垂直于直线l的直线D.已知∠α,用没有刻度的直尺和圆规作∠AOB,使∠AOB=2∠α3.如图,已知钝角△ABC,依下列步骤尺规作图,并保留作图痕迹.步骤1:以C为圆心,CA为半径画弧①;步骤2:以B为圆心,BA为半径画弧②,交弧①于点D;步骤3:连接AD,交BC延长线于点H.下列叙述正确的是A .BH 垂直平分线段ADB .AC 平分∠BAD C .S △ABC =BC ·AHD .AB =AD4.如图,点C 在∠AOB 的OB 边上,用尺规作出了∠AOB =∠NCB ,作图痕迹中,弧FG 是A .以点C为圆心,OD 为半径的弧 B .以点C 为圆心,DM 为半径的弧 C .以点E 为圆心,OD 为半径的弧 D .以点E 为圆心,DM 为半径的弧5.如图,△ABC 中,∠C =90°,∠CAB =50°.按以下步骤作图:①以点A 为圆心,小于AC 长为半径画弧,分别交AB 、AC 于点E 、F ; ②分别以点E 、F 为圆心,大于EF 长为半径画弧,两弧相交于点G ; ③作射线AG 交BC 边于点D . 则∠ADC 的度数为A .65°B .60°C .55°D .45°6.如图,△ABC 为等边三角形,要在△ABC 外部取一点D ,使得△ABC 和△DBC 全等,下面是两名同学做法: 甲:①作∠A 的角平分线l ;②以B 为圆心,BC 长为半径画弧,交l 于点D ,点D 即为所求;12乙:①过点B作平行于AC的直线l;②过点C作平行于AB的直线m,交l于点D,点D即为所求.A.两人都正确B.两人都错误C.甲正确,乙错误D.甲错误,乙正确交于两点M,N;②作直线MN交AC于点D,连接BD.若CD=BC,∠A=35°,则∠C=__________.8.如图,在△ABC中,AB=A C.以点C为圆心,以CB长为半径作圆弧,交AC的延长线于点D,连接BD.若∠A=32°,则∠CDB的大小为__________度.9.按要求用尺规作图(要求:不写作法,但要保留作图痕迹,并写出结论)已知:线段AB;求作:线段AB的垂直平分线MN.10.如图,已知△ABC,∠BAC=90°,(1)尺规作图:作∠ABC的平分线交AC于D点(保留作图痕迹,不写作法)(2)若∠C=30°,求证:DC=DB.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
D
A
C
B
l
②.如图,如果点C不在直线l上,应采取怎样的步骤,过 点C画出直线l的垂线?
图 24.4.10
A D
B
五种基本作图:
►做一条线段等于已知线段
►做一个角等于已知角
►做一条线段的垂直平分线
►做一个角的角平分线
►过一点做已知线段的垂线
构扒初中
魏利
做一条线段等于已知线段
做一个角等于已知角
五种 基本 作图
做一条线段的垂直平分线
做一个角的角平分线
过一点做已知线段的垂线
1.作一条线段等于已知线段
已知:线段AB. 求作:线段A′B′, 使A′B′=AB. 作法与示范:
A B
A′
B′
C′
2、作一个角等于已知角
已知: ∠AOB。
求作: ∠A`O`B`,使∠A`O`B`= ∠AOB。
B
D D`
B`
O
C
A
O`
C`
A`
3、画已知线段的垂直平分线
已知:线段AB。
求作:O.
C A B
D
4、平分已知角
►已知: ∠AOB。
►求作:射线OC,使
∠
AOC= ∠ BOC。
B
E
C
O
D
A
5.过定点作已知直线的垂线
