圆柱和圆锥的体积ppt
合集下载
人教版六年级下册数学《圆柱的体积》圆柱与圆锥说课教学复习课件

(1)帽子的侧面积:3.14×20×30=1884(平方厘米)
比计算结果
(2)帽顶的面积:3.14×(20÷2)2 =314(平方厘米)
以这类问题
(3)需要用的材料:1884+314=2198 ≈ 2200(平方厘米)
答:做这样一顶帽子至少需要用2200平方厘米的材料。
多一些,所
往往用“进
一法”取近
手抄报:课件/shouchaobao/
课件
课件 课件
课件 课件
课件
课件
课件 课件
课件
课件
UNDERSTANDING
课件
OF
CYLINDER
两个底面 ——圆
一个侧面 ——曲面
侧面展开是一个长方形。
你知道怎么计算
涂色的面积吗?
涂色面积就是圆柱的表面积。
圆柱表面积 = 侧面积 + 两个 2× 底面积
想一想:计算圆柱表面积需要知道哪些量?
也就是求前轮的侧面积。
前轮的侧面积:
3.14×1.2×2=7.536(m2)
答:压路的面积是7.536平方米。
2m
做一个无盖的圆柱形铁皮水桶,高是5分米。底面直径4分米,至少需要
多大面积的铁皮?
(1)水桶的侧面积:
求水桶的侧面积
和一个底面积。
4dm
5dm
3.14×4×5=62.8(平方分米)
(2)水桶的底面积:
面直径6cm的饮料
罐的长度。
箱子的宽是4个底
面直径6cm的饮料
罐的长度。
12c
m
圆柱的侧面积=底面周长×高
底面周长:C
高:h
半径:r
S侧 = Ch
圆柱的表面积=侧面积 + 两个底面的面积
最新圆柱和圆锥-圆柱的体积-课件(1)课件ppt

谢谢
联合用药大纲 胆囊炎、肝病类
湖南益丰大药房医药连锁有限公司
通 用 名:复方胆通 类 别:胆囊炎用药 作 用:清热利胆,解痉止痛。用于急、慢性胆囊炎,胆管炎, 胆囊、胆道结石合并感染,胆囊术后综合征,胆道功能性疾患等。 不良反应:有致过敏性休克者 联合用药:复方胆通胶囊+曲匹布通+抗生素+胆舒胶囊 注意事项:无
V=Sh
圆柱形包装盒的体积是多少立方厘米?
底面积=3.14×(12÷2)²=113.04(cm²) 体 积=113.04×20=2260.8(cm³) 答:圆柱形包装盒的体积是2260.8立方厘米。3.14×3²×10源自3.14×(4÷2)²×10
=3.14×9×10
=282.6(cm³) 3.14×(8÷2)²×8 =3.14×4×10
采购分类 自代
品名 利胆排石片
规格 0.43*96s
厂家 山东绿因
卖点
1)消炎、排石,双管齐下,疗效一流 2)品牌厂家,质量有保证 3)纯中药,安全无副作用
通 用 名:肝速康 类 别:治疗肝病中成药 作 用:本品具有降酶,降浊,调整机体免疫功能,改善代谢障 碍,肝病症状及加速肝功能恢复等作用。用于急、慢性肝炎。 不良反应:偶有胃区不适,停药后即可消失。 联合用药: 1.急性肝炎: 肝速康+干扰素+护肝片+维生素c+降酶灵 2.慢性肝炎: 肝速康+阿德福韦酯+维生素c+慢肝养阴 注意事项: 1.合并消化道出血的病人禁用。 2.忌食辛辣食品
=3.14×16×8
=12.56×10
=50.24×8
=125.6(cm³)
=401.92(cm³)
第一根木料: 3.14×(0.4÷2)²×10
=3.14×0.04×10 =1.256(m³)
8.3.2 圆柱、圆锥、圆台、球表面积和体积(课件)2022-2023学年高一下学期数学(人教A版2

解:当球内切于正方体时用料最省 此时棱长=直径=5cm
答:至少要用纸150cm2
练习
解析 设球 O 的半径为 r,则圆柱的底面半径为 r, 高为 2r,所以VV12=π43rπ2·r23r=32.
三、课堂小结:
1.圆柱、圆锥、圆台的表面积公式
1).圆柱 2).圆锥
S 2r 2 rl
S r 2 rl
如果圆台的上、下底面半径分别为r和R,母线长为l,你能计算它的
表面积吗?
r O’
RO
圆台的侧面展开图是扇环
x x
r 'O’
rO
xl r x r' l rr' x r'
xl 1 r 1 x r'
x r' l r r'
∵圆台侧面展开图是一个扇环
S侧面积
1 2
2 r( x
l)
1 2
2 r
'
x
r( x l ) r ' x rx rl r ' x
A
B
D
C
A1 D1
B1 C1
变式 球的内接长方体的长、宽、高分别为3、2、 3 ,求此球体的表面积 和体积。
分析:长方体内接于球,则由球和长方体都是中心对称图形可知,它们 中心重合,则长方体对角线与球的直径相等。
内切球问题
例题3 把直径为5cm钢球放入一个正方体的有盖纸盒中,至少要用多少纸? 分析:用料最省时,球与正方体有什么位置关系? 球内切于正方体
解:一个浮标的表面积为
2π×0.15×0.6 + 4π×0.152 =0.8478(m2) 所以给1000个这样的浮标涂防水漆约需涂料
0.8478×0.5×1000 =423.9(kg).
答:至少要用纸150cm2
练习
解析 设球 O 的半径为 r,则圆柱的底面半径为 r, 高为 2r,所以VV12=π43rπ2·r23r=32.
三、课堂小结:
1.圆柱、圆锥、圆台的表面积公式
1).圆柱 2).圆锥
S 2r 2 rl
S r 2 rl
如果圆台的上、下底面半径分别为r和R,母线长为l,你能计算它的
表面积吗?
r O’
RO
圆台的侧面展开图是扇环
x x
r 'O’
rO
xl r x r' l rr' x r'
xl 1 r 1 x r'
x r' l r r'
∵圆台侧面展开图是一个扇环
S侧面积
1 2
2 r( x
l)
1 2
2 r
'
x
r( x l ) r ' x rx rl r ' x
A
B
D
C
A1 D1
B1 C1
变式 球的内接长方体的长、宽、高分别为3、2、 3 ,求此球体的表面积 和体积。
分析:长方体内接于球,则由球和长方体都是中心对称图形可知,它们 中心重合,则长方体对角线与球的直径相等。
内切球问题
例题3 把直径为5cm钢球放入一个正方体的有盖纸盒中,至少要用多少纸? 分析:用料最省时,球与正方体有什么位置关系? 球内切于正方体
解:一个浮标的表面积为
2π×0.15×0.6 + 4π×0.152 =0.8478(m2) 所以给1000个这样的浮标涂防水漆约需涂料
0.8478×0.5×1000 =423.9(kg).
圆柱和圆锥的体积
长方体的底面积等于圆柱体的底面积 长方体的高等于圆柱体的高
长方体的体积=长×宽×高 圆柱的体积=底面积×高 V=Sh V=πr ² h
20厘米 25厘米
20)2=314(cm2) (1)水桶的底面积:3.14×( 2 3 (2)水桶的容积: 314×25=7850(cm )
4分米 10分米
把一个棱长是6厘米的正方体木 块,加工成一个最大的圆锥体, 圆锥的体积是多少立方厘米?
0.8米
求各圆柱的 体积。
0.5分米
求下面各圆柱的体积。
1、底面半径3cm,高5cm。 2、底面直径8m,高10m。 3、底面周长25.12dm,高2dm。
圆柱体积=底面积
高
圆柱体积=底面积
高
圆柱体积=底面积 圆锥体积=
高
圆柱体积=底面积 圆锥体积= 底面积
高
高
圆柱体积=底面积 圆锥体积= 底面积
高
高
1 3
圆柱与圆锥的体积之间有什么关系?
等底等高圆锥体积是圆柱体积的三分之一 等底底面周 长31.4米,高15米,这个玻璃罩的容积 是多少立方米?(玻璃厚度忽略不计)
高
圆柱体积=底面积 圆锥体积=
高
圆柱体积=底面积 圆锥体积=
高
圆柱体积=底面积 圆锥体积=
高
圆柱体积=底面积 圆锥体积=
高
圆柱体积=底面积 圆锥体积=
高
圆柱体积=底面积 圆锥体积=
高
圆柱体积=底面积 圆锥体积=
高
圆柱体积=底面积 圆锥体积=
高
圆柱体积=底面积 圆锥体积=
高
圆柱体积=底面积 圆锥体积=
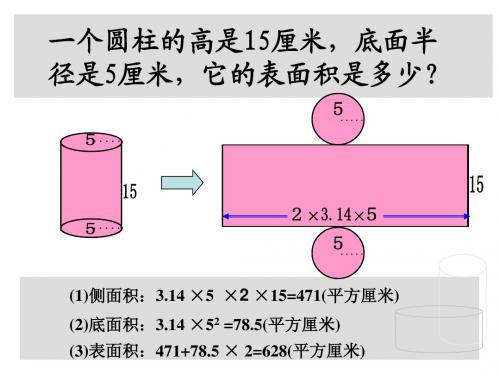
一个圆柱的高是15厘米,底面半 径是5厘米,它的表面积是多少?
【课件】圆柱、圆锥、圆台的表面积与体积+课件高一下学期数学人教A版(2019)必修第二册

设圆台的上底面面积为S',下底面面积为S
r O
1
1
2
2
2
2
V圆台 (r r r r )h ( S S S S )h
3
3
1
这和V棱台 ( S S S S )h是一致的。
3
1
因而得 V台体 = ( S S S S )h
3
【练习】 如图,在直角梯形 ABCD 中,BC∥AD,∠ABC=90°,AB=5,
1
V锥体 Sh
3
1 2
r h
3
1
V台体 = ( S SS S )h
3
1
= h(r 2 rr r 2 )
3
2
感谢聆听
S圆柱 =πr +πr +2πrl 2πr (r l )
2
2
(1)圆柱的表面积、体积
圆柱的侧面展开图是什么?如何计算它的表面积?
r O
l
2 r
O
圆柱的侧面展开图是一个矩形,
S圆柱表面积 2r 2rl 2r (r l ).
2
V圆柱 = πr h
2
例1 将一个边长分别为4π,8π的矩形卷成一个圆柱的侧面,则
圆台的表面积为(
A.81π
)
B.100π
C.168π
D.169π
解 圆台的轴截面如图所示,
设上底面半径为 r,下底面半径为 R,则它的母线长为
l= h2+R-r2= 4r2+3r2=5r=10,
所以 r=2,R=8。
故 S 侧=π(R+r)l=π(8+2)×10=100π,
S 表=S 侧+πr2+πR2=100π+4π+64π=168π。故选 C。
苏教版六年级下册数学《圆柱的体积》圆柱和圆锥PPT(第3课时)

教学新知
例二:计算圆柱的表面积。(单位:cm)(π取3.14)
S=2π×0.8+2π≈11.304 S=2π×0.5×3.5+2π×0.5²≈12.56
教学新知
例三:一个圆柱形油桶,底面直径是0.6米,高是1米。做这个油桶至少 需要铁皮多少平方米?(得数保留两位小数)
S=2π×0.3×1+2π×0.3²≈2.45(㎡)
能想到一些什么? (2)全部浸入,水面上升9厘米,你又能想到什么?怎样
计算出这个圆钢的体积? (3)这题还可以怎样思考?
教学新知
例一:一个圆柱形水桶的容积是80立方分米,里面装了2/5的水。 已知它的底面积是10平方分米,里面水的深度是多少?
【讲解】根据“水桶的容积是80立方分米”和“里 面装了 2/5的水”这两个条件,我们可以求出水桶 内水的体积,然后用水的体积除以水桶底面积得出 水桶内水的深度。 80× =32(立方分米)……水桶内水的体积 32÷10=3.2(分米)……水桶平均剖成两片,其中一片如图所示。(单位:厘米) (1)剖面面积是多少平方厘米? (2)这片木料的表面积和体积各是多少?
(1)S1=20×12=240(cm²) (2)S2=πrh+πr²+S1=3.14×6×20+3.14×6²+240=792.84(cm²)
V=1/2S3h=1/2×3.14×6²×20=1130.4(cm³)
课后习题
7.把一根长2.4米的圆柱形状的木料锯成4段,表面积增加了 0.18平方米。
这根木料原来的体积是多少立方米?
S=0.18÷6=0.03(m²)
V=sh=0.03×2.4=0.072(m³)
8.一个圆柱高4厘米,底面半径是2厘米。如果将它的底面平均分成若干份,
圆柱圆锥圆台体积和表面积.ppt

1
1
A.4
B.2
3 C. 6
3 D. 4
[答案] D
[解析]
三棱锥B1-ABC的高h=3,底面积S=S△ABC=
3 4
×12= 43,
则VB1-ABC=13Sh=13×
43×3=
3 4.
5.若一圆柱与圆锥的高相等,且轴截面面积也相等,那
么圆柱与圆锥的体积之比为( )
A.1
1 B.2
3
3
C. 2
D.4
例题解析
命题方向 多面体与旋转体的面积
【例1】圆台的上、下底面半径分别是10 cm和20 cm,它的侧 面展开图的扇环的圆心角是180°,那么圆台的表面积是多少?
命题方向 多面体的体积
[例 2] 长方体相邻三个面的面积分别为 2、3、6 求它的
体积.
[解析] 设长方体的长、宽、高分别为a、b、c则有
据条件得到
1 2
πl2=2π,解得母线长l=2,2πr=πl=2π,r=1所以
该圆锥的体积为:V圆锥=13Sh=13×
22-12π=
3 3 π.
[点评] 本题主要考查空间几何体的体积公式和侧面展开 图.审清题意,所求的为体积,不是其他的量,分清图形在 展开前后的变化;其次,对空间几何体的体积公式要记准记 牢,属于中低档题.
[解析]
三棱台ABC-A1B1C1的上、下底面积之比为4:9.连接 A1B、BC1和AC1,把棱台分为三个棱锥B-A1B1C1,C1- ABC,A1-ABC1.则这三个棱锥体积之比为________.
[答案] 4:9:6
[解析] 如图,设三棱锥B-A1B1C1,C1-ABC,A1- ABC1体积分别为V1、V2、V3,又设棱台的高为h,上、下底面 积分别为S1、S2.依题意,得
《圆柱的体积》圆柱和圆锥PPT教学课件下载

返回
圆柱和圆锥 圆柱的体积
课堂练习
1.求下列图形的体积。(单位:厘米)
3.14×32×10 = 282.6(cm³)
3.14×(8÷2)2×8
3.14×(4÷2)2×10
= 401.92(cm³)
= 125.6(cm³)
返回
圆柱和圆锥 圆柱的体积
2.哪根木料的体积大?
3.14×(0.4÷2)2×10 = 3.14×0.04×10 = 1.256(m3)
πr
S =πr×r=πr2 S =πr2
返回
圆柱和圆锥 圆柱的体积
是不是可以把圆柱转化成近似的长方体来推导圆柱 的体积公式呢?
?
返回
圆柱和圆锥 圆柱的体积
?
返回
圆柱和圆锥 圆柱的体积
……
圆柱等分的份数越多,拼成的图形越接近长方体。
返回
圆柱和圆锥 圆柱的体积
拼成后的长方体和圆柱体有什么关系呢? 长方体的体积和圆柱体的体积相等。
青圆岛柱版和五圆年锥制圆柱数的学体积五年级 下册
4 圆柱和圆锥
圆柱的体积
圆柱和圆锥 圆柱的体积
情境导入
从图中,你知道了哪些数学信息?
圆柱形包装盒的底面直径是12cm, 高是20cm。
圆柱形包装盒的体积是多少立方厘米?
返回
圆柱和圆锥 圆柱的体积
探究新知
圆柱形包装盒的体积是多少立方厘米? 求包装盒的体积就是求圆柱的体积。圆的面积公式是把圆转 化成近似的长方形推导出来的。
长方体的体积=底面积 × 高
圆柱的体积 = 底面积 × 高
V = Sh
返回
圆柱和圆锥 圆柱的体积
圆柱形包装盒的体积是多少立方厘米?
底面积: 3.14×(12÷2)2 = 3.14×36 = 113.04(平方厘米)
圆柱和圆锥 圆柱的体积
课堂练习
1.求下列图形的体积。(单位:厘米)
3.14×32×10 = 282.6(cm³)
3.14×(8÷2)2×8
3.14×(4÷2)2×10
= 401.92(cm³)
= 125.6(cm³)
返回
圆柱和圆锥 圆柱的体积
2.哪根木料的体积大?
3.14×(0.4÷2)2×10 = 3.14×0.04×10 = 1.256(m3)
πr
S =πr×r=πr2 S =πr2
返回
圆柱和圆锥 圆柱的体积
是不是可以把圆柱转化成近似的长方体来推导圆柱 的体积公式呢?
?
返回
圆柱和圆锥 圆柱的体积
?
返回
圆柱和圆锥 圆柱的体积
……
圆柱等分的份数越多,拼成的图形越接近长方体。
返回
圆柱和圆锥 圆柱的体积
拼成后的长方体和圆柱体有什么关系呢? 长方体的体积和圆柱体的体积相等。
青圆岛柱版和五圆年锥制圆柱数的学体积五年级 下册
4 圆柱和圆锥
圆柱的体积
圆柱和圆锥 圆柱的体积
情境导入
从图中,你知道了哪些数学信息?
圆柱形包装盒的底面直径是12cm, 高是20cm。
圆柱形包装盒的体积是多少立方厘米?
返回
圆柱和圆锥 圆柱的体积
探究新知
圆柱形包装盒的体积是多少立方厘米? 求包装盒的体积就是求圆柱的体积。圆的面积公式是把圆转 化成近似的长方形推导出来的。
长方体的体积=底面积 × 高
圆柱的体积 = 底面积 × 高
V = Sh
返回
圆柱和圆锥 圆柱的体积
圆柱形包装盒的体积是多少立方厘米?
底面积: 3.14×(12÷2)2 = 3.14×36 = 113.04(平方厘米)
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
感谢下载
99
3.14×3²×10 =3.14×9×10 =282.6(cm²)
3.14×(8÷2)²×8 =3.14×16×8 =50.24×8 =401.92(cm²)
3.14×(4÷2)²×10
=3.14×4×10 =12.56×10 =125.6(cm²)
感谢下载
100
底面积
感谢下载
32
长方体的体积=底面积 ×高
圆柱体的体积= 底面积 ×高
感谢下载
33
感谢下载
34
感谢下载
35
感谢下载
36
感谢下载
37
感谢下载
38
感谢下载
39
感谢下载
40
感谢下载
41
感谢下载
42
感谢下载
43
感谢下载
44
感谢下载
45
感谢下载
46
感谢下载
47
感谢下载
48
感谢下载
22
感谢下载
23
感谢下载
24
感谢下载
25
感谢下载
26
长方体的体积=底面积 × 高
底面积
感谢下载
27
长方体的体积=底面积 ×高
底面积
感谢下载
28
长方体的体积=底面积 ×高
底面积
感谢下载
29
长方体的体积=底面积 ×高
底面积
感谢下载
30
长方体的体积=底面积 x 高
底面积
感谢下载
31
长方体的体积=底面积 x 高
感谢下载
高
93
圆柱体积=底面积 圆锥体积=
感谢下载
高
94
圆柱体积=底面积 圆锥体积=
感谢下载
高
95
圆柱体积=底面积 高
圆锥体积=底面积 高
感谢下载
96
圆柱体积=底面积 高
圆锥体积=底面积
高
1 3
感谢下载
97
圆柱体积=底面积 圆锥体积=底面积
感谢下载
高
高
1 3
98
圆锥的体积= 1 ×底面积×高 3
49
感谢下载
50
感谢下载
51
感谢下载
52
感谢下载
53
感谢下载
54
感谢下载
55
感谢下载
56
感谢下载
57
感谢下载
58
感谢下载
59
感谢下载
60
感谢下载
61
感谢下载
62
感谢下载
63
感谢下载
64
感谢下载
65
感谢下载
66
感谢下载
感谢下载
68
感谢下载
69
感谢下载
70
感谢下载
感谢下载
高
86
圆柱体积=底面积 圆锥体积=
感谢下载
高
87
圆柱体积=底面积 圆锥体积=
感谢下载
高
88
圆柱体积=底面积 圆锥体积=
感谢下载
高
89
圆柱体积=底面积 圆锥体积=
感谢下载
高
90
圆柱体积=底面积 圆锥体积=
感谢下载
高
91
圆柱体积=底面积 圆锥体积=
感谢下载
高
92
圆柱体积=底面积 圆锥体积=
圆柱与圆锥的体积
感谢下载
1
感谢下载
2
感谢下载
3
感谢下载
4
感谢下载
5
感谢下载
6
感谢下载
7
感谢下载
8
感谢下载
9
感谢下载
10
感谢下载
11
感谢下载
12
感谢下载
13
感谢下载
14
感谢下载
15
感谢下载
16
感谢下载
17
感谢下载
18
感谢下载
19
感谢下载
20
感谢下载
21
感谢下载
71
感谢下载
72
感谢下载
73
感谢下载
74
感谢下载
75
感谢下载
76
感谢下载
77
感谢下载
78
感谢下载
79
感谢下载
80
感谢下载
81
圆柱体积=底面积 高
感谢下载
82
圆柱体积=底面积 高
感谢下载
83
圆柱体积=底面积 高
感谢下载
84
圆柱体积=底面积 圆锥体积=
感谢下载
高
85
圆柱体积=底面积 圆锥体积=
