推求Gardner-Russo持水曲线模型参数的简单入渗法
土壤水分特征曲线(研究)综述

土壤水分特征曲线(研究)综述卢常磊(学号:1001064113)(系别:农学系专业:种子科学与工程班级:一班)前言:土壤水的基质势(或土壤水吸力)随土壤含水量而变化,其关系曲线称为土壤水分特征曲线。
该曲线反映了土壤水分能量和数量之间的关系,是研究土壤水动力学性质比不可少的重要参数,在生产实践中具有重要意义。
几十年来,人们投入了大量的精力来发展确定该曲线的方法,这些方法归纳起来可分为两大类:一类是直接测定法,另一类是间接推算法(或参数估计法)。
这些方法各有优缺点,而在生产实践中有的方法几乎没有实际应用价值。
基于这一点,本文针对这些方法以及近年来发展的新方法进行了比较和综述。
关键词:土壤水分特征曲线 van Genuchten模型1.土壤水分特征曲线1.1概念土壤水的基质势(或土壤水吸力)随土壤含水量的变化而变化,其关系曲线称为土壤水分特征曲线,英文名称为soil watercharacteristic curve。
在实际中人们也使用土壤持水曲线或土壤pF曲线。
一般,该曲线以土壤含水量Q(以体积百分数表示)为横坐标,以土壤水吸力 S(以大气压表示)为纵坐标。
如右图是一不同质地土壤水分特征曲线图。
1.2意义土壤水分对植物的有效程度最终决定于土水势的高低,而不是自身的含水量。
如果测得土壤的含水量,可根据土壤水分土特征曲线查得基质势值,从而可判断该土壤含水量对植物的有效程度。
1.3应用土壤水分特征曲线主要有以下几方面的应用[1]:①进行基质势和含水量的相互换算。
根据土壤水分特征曲线可将土壤湿度换算成土壤基质势,依据基质势可判断土壤水分对作物的有效度。
也可将基质势换算成含水量,根据土壤水分特征曲线可查得田间持水量、凋萎湿度和相应的有效水范围。
②表示比水容重。
土壤水分特征曲线斜率的倒数,即单位基质势变化所引起含水量的变化,称之为比水容重,是衡量土壤水分对植物的有效性和反映土壤持水性能的一个重要重要指标。
③可以间接反映土壤孔隙的分布。
土壤持水曲线vanGenuchten模型求参的一种新方法_刘贤赵

*国家自然科学基金项目(No.40101005,No.50609022)资助作者简介:刘贤赵(1970~),男,湖南隆回人,教授,博士,主要从事区域水土资源高效利用研究。
E -mail:xianz haoliu@ 收稿日期:2006-09-21;收到修改稿日期:2007-03-23土壤持水曲线van Genuchten 模型求参的一种新方法*刘贤赵 李嘉竹 张振华(鲁东大学地理与规划学院,山东烟台 264025)A NEW METHOD TO ES TIMATING PARAMETERS OF VAN GENUCHTEN MODEL FORSOIL WATER RETENTIONLiu Xianzhao Li Jiazhu Zhang Zhe nhua(Colleg e o f Geogra ph y a n d Pla nn in g ,Lu don g U ni versit y ,Yan tai,Shan don g 264025,Chin a )关键词 土壤持水曲线;van Genuchten 模型;DPS 数据处理系统;Marquardt 方法中图分类号 S15217 文献标识码 A土壤持水曲线是研究土壤水动力学性质必不可少的重要参数。
在已经建立的众多数学模型中,van Genuchten 模型以其与实测数据拟合程度好而得到广泛的应用,而运用该模型的关键是如何获得其中的4个参数。
仅就我国而言,不少学者投入大量的精力发展了确定van Genuchten 模型参数的方法。
邵明安等[1~3]基于一维土壤水分运动的Richards 方程提出了推求土壤van Genuchten 模型和Brooks -Corey 模型参数的简单入渗法;王金生等[4]将最小二乘法和非线性单纯形法相结合拟合了van Genuchten 模型参数;徐绍辉等[5]也借助最小二乘法并结合P-i card 迭代法拟合了砂质黏壤土的van Genuchten 模型参数;李春友等[6]也利用单纯形调优法拟合van Genuchten 模型的参数;魏义长等[7]运用Matlab 编程软件对辽西淋溶褐土van Genuchten 模型的参数进行了推导估算。
空间均化分层土壤入渗模型

进行积分, 得到平均累计入渗量 F 和入渗率 f . 由于
326
GGA 模型中的参数的 Am, Bm, tm−1, tpm 和 Fpm 与地表开 始积水时和计算时刻 t 湿润锋所在土层有关, 所以需 要确定在计算时刻 t, 对于任意 K 值, 地表是否积水, 若积水还需确定湿润锋在地表开始积水时刻所在土 层 i 和 t 时刻所在土层 j.
收稿日期: 2007-05-29; 接受日期: 2008-08-03 国家自然科学基金面上项目(批准号: 50579031)和国家自然科学基金创新研究群体基金项目(批准号: 50721006)资助
摘要 以通用 Green-Ampt 模型为基础, 用概率密度函数和垂向分层分别描述了土壤饱和 导水率在水平和垂直方向上的空间变异性, 通过面积均化建立了宏观尺度上的空间均化分层 土壤入渗模型(SAI 模型). 针对典型土壤入渗过程的数值实验表明了 SAI 模型具有较高的精 度, 能够充分反映饱和导水率空间变异性对入渗的影响. 分析表明在暴雨期土壤的平均入渗 率随水平方向的变异性增强而减小, 目前采用的垂向平均方法将低估入渗量. SAI 模型本身 包含了土壤的非均匀性, 是一个宏观尺度的模型, 在保持模型物理机理和参数物理意义的同 时, 有效避免了由于入渗模型非线性和土壤非均匀性引起的模型适用尺度和应用尺度不匹配 问题, 在空间均化水文模型中的初步应用表明, SAI 模型可以用于宏观尺度水文或气象模型 中暴雨期或者灌溉条件下的入渗模拟.
当湿润锋处于第 m 层土壤, 地表积水后 GGA 模 型[25,26]可以写为
f
⎛ = km ⎜1+
⎝
Am Bm + F
⎞ ⎟, ⎠
(1)
F = kmt + Am ln ( Am + Bm + F ) + C ,
土壤水分运动特征及其参数确定

摘要土壤水分运动特征及其参数确定学科名称: 水文学及水资源答辩日期:2003.3作者: 来剑斌作者签名:导师: 王全九教授导师签名:摘要在总结国内外有关土壤水分运动特征及参数确定方法研究成果的基础上,采取理论分析与室内试验相结合的方法,研究了四种不同质地土壤水平一维入渗、垂直一维入渗、点源自由积水入渗及负压盘式吸渗等的入渗模型及土壤水分运动参数的确定方法,获得以下研究结果。
1. 对常用的土壤水分特征曲线公式特点和相互关系进行了分析,获得了土壤质地与水分特征曲线常用表达式中参数之间的相关关系。
研究表明土壤质地与分形理论预测土壤水分特征曲线结果较好。
采用积分方法与入渗特性法确定的土壤水分特征曲线,在土壤低吸力段,与实测值吻合良好。
2. 由水平一维入渗资料计算土壤水分扩散率,结果表明,扩散率与含水率间符合指数函数变化关系,扩散率系数D0随土壤粘性增加而减小。
采用Burdine模式和Mualem模式计算的土壤水分扩散率表达式中的系数和指数随着土壤质地由细变粗而逐渐变大。
3. 利用实测资料分析Philip入渗公式与Kostiakov经验公式间的关系表明,二者在某种程度上具有一致性。
分析获得了Green-Ampt入渗模型与Philip模型参数间的相关关系表达式。
利用垂直一维入渗资料分别计算了四种不同质地土壤的导水率,结果表明,土壤导水率与含水率间关系符合乘幂函数变化关系。
比较分析了不同方法确定饱和导水率K s。
4. 对负压盘吸渗的稳定性分析表明,用改进的盘式吸渗仪进行土壤吸渗实验具有一定的稳定性和可靠度。
入渗时间相同时,不同负压水头下的累积入渗量随着负压的增大而减小。
利用负压盘式入渗资料,采用不同方法,分别计算并对比分析西安理工大学硕士学位论文了四种不同质地土壤的吸湿率及导水率。
结果表明,负水头越大土壤吸湿率及导水率越小。
对于同一个负压值,土壤吸湿率与导水率随土壤粘性增加而减小。
5. 除榆林土外,其余三种不同质地的土,渗透仪与点源入渗确定的土壤导水率接近,而一维入渗与盘式吸渗确定的土壤导水率接近,且比渗透仪及点源入渗测定值大。
土中水与土的渗透及其计算
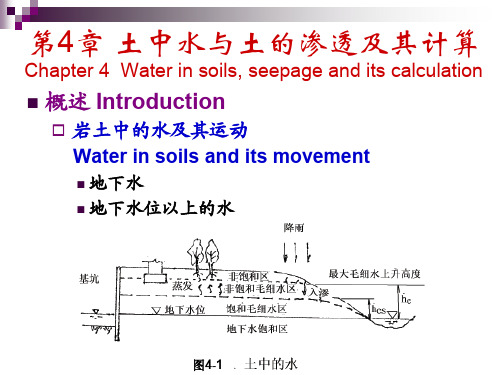
Chapter 4 Water in soils, seepage and its calculation
概述 Introduction
岩土中的水及其运动 Water in soils and its movement
地下水 地下水位以上的水
图4-1
渗流的工程意义 Engineering significance of seepage
非饱和土的渗透性
Permeability of unsaturated soil 非饱和土中孔隙水与气的三种不同形态
水封闭 双开敞 气封闭
图4-16
水和气体流动的广义达西定律
ka a va kaia a y k w w vw k wiw w y
渗漏 水利工程
渗透破坏 石油和采矿工程、环境工程
土中水和渗流问题的研究历史
Research history of water in soils and seepage
土中水的研究
年Low给出了粘土颗粒表面结合水形成的机理; 1960 年Martin得出了不同厚度结合水的密度分布, 1959年给出了物理模型以说明土的冻胀机理; 1975 年Mitchell在出版的Fundamentals of Soil Behavior一书中,对于土中水的形态及其对土性的 影响作了较全面的总结和阐述。
通过土体1和2的流量相等,得 则 则微分方程在土体1 中的定解为: (b) 土体2 的边界条件为 可求得微分方程在土体2中的定解为: (c)
若将测管水头基准面选在 h2的水面位置,微分方程的 解可进一步简化为
土体1中
地下水渗流基本方程及数学模型总结

V Qt vt m V vt
§5 描述地下水运动的数学模型及解算方法
X方向流入流出差
( v x ) |( x , y , z ,t ) yzt ( v x ) |( x x , y , z ,t ) yzt
y方向流入流出差
( v y ) |( x , y , z ,t ) xzt ( v y ) |( x , y y , z ,t ) xzt
流入- 流出=V
研究对象可以是大区域的,也可以是微分单元体 大区域的水均衡计算经常用于区域的水资源评价 地下水渗流的连续性方程就是质量守恒方程,也称为水
均衡方程。现在基于微分单元体做水均衡分析,推导渗 流连续性方程。
(一)渗流连续性方程的推导
在渗流场中任意取一点P(x, y, z),以P为 中心沿直角坐标轴取一微小的六面体,体 积为 ,称为特征单元体,设单元 体无限小,但保证单元体中地下水穿过介 质骨架和空隙。 假设:水是可压缩的,固体颗粒不能被压 缩,多孔介质骨架在垂直方向(Z)可压 缩,x、y为常量。因此,只有水的密 度、孔隙度n和单元体高度z三个量随压 力而变化。
( v y ) xyzt y
y 0
z方向流入流出差 单元体内地下 水质量变化量 地下水运动的 连续性方程:
( v z ) xyzt z
z 0
( v x ) ( v y ) ( v z ) ( nz ) x y z xy y K xx ) x x x
H ( K yy ) y y ( v z ) H ( K zz ) z z z
( v y ) y
§5 描述地下水运动的数学模型及解算方法
( nz ) 第二步:化简方程右端项: t
2地下水渗流基本方程及数学模型

安徽理工大学 地球与环境学院 水资源与规划系
Ch2 地下水渗流微分方程及数学模型
地下水动力学
安徽理工大学 地球与环境学院 水资源与规划系
Ch2 地下水渗流微分方程及数学模型
*范围值:n×10-3~ n×10-5; 范围值:0.05~ 0.30。实际测出的值往往小于理论值。
上述两参数之间的不同,还在于潜水含水层存在滞后疏干现象。 弹性释水与重力给水: 对于含水层而言,由于受埋藏条件的限制,抽水时,水的给 出存在着不同。 潜水含水层在抽水过程中,大部分水在重力作用下排出,疏干作用于水位变动带(
为反映含水层地下水运动的普遍规律,我们选定在各向异性多孔介 质中建立地下三维不稳定流动连续性方程。
地下水动力学
安徽理工大学 地球与环境学院 水资源与规划系
Ch2 地下水渗流微分方程及数学模型
由于渗流场中各点的渗流速度大小、方向都不同,为了反映液体运动的 质量守恒关系,需要在三维空间中建立微分方程形式表达的连续性方程。
则有:
即:
将
代入整理得:
地下水动力学
安徽理工大学 地球与环境学院 水资源与规划系
Ch2 地下水渗流微分方程及数学模型
所以有
上式为三维流微分方程,也可写成:
物理意义:渗流空间内任一单位体积含水层在单位时间内流入与流出该体 积含水层中的弹性水量的变化量,即单位体积含水层的水量均衡方程。
地下水动力学
安徽理工大学 地球与环境学院 水资源与规划系
= =
由含水层状态方程,
地下水动力学
安徽理工大学 地球与环境学院 水资源与规划系
Ch2 地下水渗流微分方程及数学模型
因为 则可得到: 所以有 ,Z为定值,则
于是连续性方程变为:
间接推求非饱和土壤导水参数的方法

间接推求非饱和土壤导水参数的方法【摘要】本文介绍了四种间接推求非饱和土壤导水参数的方法,包括土壤水分再分布过程法、土壤水分特征曲线拟合模型法、简单入渗法和土壤转换函数法,并对四种方法出归纳,提出了进一步研究的方向。
【关键词】非饱和土壤导水参数;水分再分布;水分特征曲线;简单入渗法;PTFs确定非饱和土壤导水参数的方法有两大类:直接法和间接法。
鉴于直接法,耗时多,价格昂贵,所得精度难以保证,空间差异性大,间接法成为许多专家学者研究的焦点。
本文通过介绍推求非饱和土壤导水参数的主要几种间接方法,做出归纳,以期为非饱和土壤导水参数间接法的进一步研究起到推动作用。
1.土壤水分再分布过程法邵明安[1]提出的一种土壤导水参数模型,将一维垂直和水平土壤水分再分布过程结合起来,根据土壤湿润锋湿度与湿润剖面平均湿度之间的函数关系,推出非饱和导水率K(θ)的解析表达式。
这样,只要利用土壤水分再分布的湿润过程,确定表达式中的常数,就可直接算出土壤的非饱和导水率。
根据湿润锋湿度与平均湿度拟合关系的不同,推出K(θ)有不同的表达式,本文采用湿润锋湿度与平均湿度为幂函数关系:K(θ)=(θ-θinm■■-Z■■-n■m■■■-X■■)上式:θ为体积含水率,θi为初始含水率,H为水深,Z、X分别为垂直和水平方向水分运移的距离,Z■和X■为所加其水面刚刚消失时初始湿润深度,m、n、m1、n1、a、b均为拟合参数。
2.土壤水分特征曲线拟合模型法2.1 Mualem模型Mualem模型关于相对导水率的表达式如下:Kr(Θ)=Θ1/2■■/■■■(1)式中:Kr为相对导水率,即K/Ks,h为水头值,Θ为无量纲含水量。
无量纲含水量表达式Θ=■(2)求解方程(1)时需要建立无量纲含水量与水头值的关系式,采用幂函数形式:Θ=(ah)-b(3)将(3)式代入方程(1)积分得:Kr(Θ)=Θ5/2+2/b(4)2.2 Burdine模型Burdine建立的相对导水率表达式如下:Kr(Θ)=Θ2■■/■■(5)将(3)式代入方程(5)积分得:Kr(Θ)=Θ3+2/b(6)2.3 Van Genuchten模型[2]Van Genuchten水分特征曲线模型为:Θ=[1+(ah)n]-m(7)式中:α是标定参数,与土壤平均孔隙半径成正比,n和m是土壤水分特征曲线的形状参数或孔隙分布指数,且有m=1-1/n。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
基金项目
作者简介
湖北监利人博士生
主要研究方向为地面水资源与地下水资源及环境
推求持水曲线模型参数的简单入渗法
薛绪掌张仁铎
武汉大学水资源与水电工程科学国家重点实验室湖北武汉
国家农业信息化工程技术研究中心
北京
中山大学环境科学与工程学院广东
广州
摘要本文基于水平一维非饱和土壤水分运动规律
推求了
用模拟的结果进行拟合其决定系数
为
利用数值模拟数据和实验数据检验该方法将用此方法
结果表明本研究所求得的参数有较高的精度关键词土壤水分渗流运动
参数数值模拟
等和
直接测量土壤水分特征曲线和非饱和土壤导水率的方法
土壤水力特性土壤质地资料被成功地用来预测非饱和土壤水力特性
和
描述非饱和土壤水力特性模型中的参数该方法是在假
等模型中的参
法来推求更多描述土壤水分运动模型中的参数基本理论
水平一维非饱和土壤水分运动建立在
其表达式为
其表达式如下
是土壤饱和体积
方程描述如下
式中
其初始和边界条件其中为土壤初始体积含水率
式中为任意位置
则湿润峰位置的土壤水基质势
很低有
式中为湿润峰
由于
可得
变化的函数表达式
该式右边须乘以一个
参数
式中
当时入渗通量
和湿润峰厚度
此公式相似于表征的水分入渗模型
当土壤湿润峰为时其相对应的土壤水累积入渗量
其中
其中
其中
土壤饱和水
力传导度和土壤饱和体积含水率取
风干土含水量和
根据入渗率和湿润峰之间的关系
?利用迭代法求得可得参数
和
本研究应用程序
模拟中用到列出了土柱长度为
用到
分别为和
体积含水率和土壤饱和导水率和后借助求解
和为了验证所推导的计算
算得到的参数值和输入的参数值进行比较和参数敏感性分析并将参数估计值代入模型中得到的
表土壤类型水力特性参数
土壤???
实验方法年
验室温度控制在土壤为风干散装土系采自北京昌平小汤山国家精准农业基地个土壤剖面层
次和土壤样品自然风干且过表
表供试土壤的基本性质
土壤剖面层次深度有机质团粒结构状况
将各种供试土壤按照装土容重分成
在实验前取自然分干土样利用烘干法测定供试土壤的重
和初始体积含水率
在实验室内进行了传统的的有机
试验土柱是界面直径为将供试土壤按设
计容重分层均匀装入圆筒在实验过程中
结果和讨论
数值分析湿润峰
为了验证其结果将模拟结果点绘在二维坐标中和图
图和图分别描述了
其拟合结果见表
入渗率湿润峰
累积入渗量湿润峰
图入渗时间湿润峰
表
土壤
为拟合累积入渗量与湿润峰的决
定系数
种土壤水分特征曲线估计值和
理论值的比较
渗时间之间的关系系数
和
率
和土壤饱和
导水率
数
和
表其中
的最
大相对误差为
最低则达到了
的最大相对误差为
为了证明估计参数值的
种模拟土壤的水分特征曲
线
数
和
图为参数和和
代入
种模拟
种土壤体积含水率均随土
结果表明由和
表
水力特性参数估计值与理论值的比较
土壤
理论值
计算值
?
?
求解
因此假设条件的正确性非常关为了证明其正确性
置
的导水率
?
在利用
将新方法估计的参数
和代入
为了进行假设条件检验将任意位置
导水率
估计值的比较
种不同土壤水分入渗湿润峰为时任意位置导水率的
湿润峰为
土壤
从图中可知模拟
的导水率和估计的导水率在湿润峰达到的增大呈减
以及基于此假设条件利用简单的水平一维水分入渗法推求模型中
实验验证
有一定程度差异
为供试土壤参数实验测定结果其中参数和为
供试土壤水力特性参数值
土壤
???
图
和图分别描述了供试土壤入渗率
与湿润峰
与湿润峰以及入渗时间
与湿润峰
从表可知
决定系数从
入渗率
湿润峰
累积入渗量
湿润峰
入渗时间
湿润峰
当关系系数和
含水率和土壤饱和导水率
和对于供试土和
的相对误差分别为
参数的相对误差分别为和
正如数值结果所证明
曲线影响不大从图进一步证
供试土壤水分特征曲线实测值与估计值的比较
表
土壤
为拟合累积入渗量与湿润峰的决定系数
结论
本文基于利用简单入渗理论确定非饱和土壤导水力特性的思想假设土壤水动力特性可用
理论基于这些理论实现利用数值模拟和实验数据验证了该方法的
总之应用本文提出
对于广范围的土壤类型水分
参考文献
王全九王文焰。
