晶体管模型
qe 和 qc（VA和VB）反映了基区宽度调变效应 qf 和 qf（IKF和IKR）反映了大注入效应
半导体器件 3.5 23
I KF =
QB 0
F
IKF正是大注入临界电流。
2002.4 半导体器件 3.5 24
2002.4
4
3.5.2 GP模型 qb通常的描述方式：
3.5.2 GP模型 9 发射系数的影响 定义参数： nF —— 正向电流发射系数 nR —— 反向电流发射系数 发射系数反映了pn结电流~ 电压关系的非理想成 分 qV I
5 2002.4 半导体器件 3.5 6
2002.4
1
3.5.1 EM模型 2. 大信号模型 BJT储存的自由载流子电荷的描述方式： 正向工作： QDE = QE + QJE + QBF + QJC = (τE +τEB +τBF +τD ) ICC ≡τF ICC
3.5.1 EM模型
反向工作： QDC = QC + QJC + QBR + QJE = (τC +τD +τBR +τEB ) IEC ≡τR IEC
2002.4
半导体器件 3.5
2ቤተ መጻሕፍቲ ባይዱ
3.5.1 EM模型 1. 直流模型 2.4节EM方程反映了BJT的理想直流特性
I E = − (1 + 1 β F ) I S ( e qVBE / kT − 1) + I S e qVBC / kT − 1 qVBE / kT − 1) − (1 + 1 β R ) I S e qVBC / kT − 1 IC = I S ( e
3.5.2 GP模型 定义参数： VA —— 正向Early电压 VB —— 反向Early电压 IKF —— 正向共作区膝点电流（knee current） IKR —— 反向共作区膝点电流 τF ——理想正向渡越时间 τR ——理想反向渡越时间 比较
I CI = QB 0
B
Q QF τ F I CC I SS 1 qV = = exp B ' E ' − 1 I KF = B 0 τF QB 0 QB 0 I KF qb kT QB 0 QR τ R I EC I SS 1 qVB 'C ' qr = = = exp − 1 I KR = τ QB 0 QB 0 I KR qb kT R
xC xE 2002.4 半导体器件 3.5 21 2002.4 半导体器件 3.5 22
3.5.2 GP模型
qb = 1 + qe + qc + q f + qr qe = qc = qf = QE CTEVB ' E ' VB ' E ' = ≡ QB 0 QB 0 VB QC CTCVB 'C ' VB 'C ' = ≡ QB 0 QB 0 VA VB ≡ VA ≡ QB 0 CTE QB 0 CTC
E0 C
IS = 用电荷来描述集电极电流：
qADnB ni2
xC xE
∫
p pB ( x)dx
注意：IS不是一个与器件结构、尺寸有关的基本 常数，而是注入强度VB'E'和VB'C'的函数。 定义一个与外电压无关的基本常数：
I SS ≡
xC 0 2 nB i
xC 0
非平衡状态下基区多子电荷： Q = qA x p ( x)dx B E ∫x pB 归一化基区多子电荷：
3.5.2 GP模型 QB = QB0 + QE + QC + QF + QR
3.5.2 GP模型 归一化基区多子电荷可描述成：
qb = 1 + QE QC QF Q + + + R = 1 + qe + qc + q f + qr QB 0 QB 0 QB 0 QB 0
xE 0
这几项基区电荷的表示形式：
QE ≡ ∫
xE xC
N AB ( x)dx = ∫
VB ' E '
0
CTE (V )dV CTC (V )dV
QC ≡ ∫ qAN A ( x)dx = ∫
xC 0 xC xE
VB ' C '
0
QF ≡ ∫ qA [ ∆pF ( x) ] dx = τ F I CC QR ≡ ∫ qA [ ∆pR ( x)] dx = τ R I EC
2
β F (VB 'C ' ) =
考虑基区宽度调变效应， 引入参数： VA ——正向Early电压
半导体器件 3.5
E' rE E
V τ F (VB 'C ' ) = τ F (0) 1 − B 'C ' VA
描述EM模型的直流参数有7个： IS ， βF ， βR ，rBB' ， rE ， rC ，VA
2002.4
半导体器件 3.5
7
2002.4
半导体器件 3.5
8
3.5.1 EM模型 引入电容来描述BJT的电荷储存效应： 两个非线性势垒电容CJE和CJC 两个非线性扩散电容CDE和CDC 集电极-衬底电容CJS
C JE = CDE = CJE (0) (1 − VB' E ' ϕ E )mE C JC = CJC (0) (1 − VB'C ' ϕ C ) mC
2002.4 半导体器件 3.5 13
2002.4
半导体器件 3.5
14
3.5.2 GP模型 定义参数： nEL —— 非理想小电流基极-发射极发射系数 nCL —— 非理想小电流基极-集电极发射系数 C2 —— 正向小电流非理想基极电流系数 C4 —— 反向小电流非理想基极电流系数
3.5.2 GP模型 考虑到基极电流其它成分的GP模型
2002.4 半导体器件 3.5 11
3.5.1 EM模型 考虑模型随温度的变化以及噪声模型，增加参数： Eg ——禁带宽度 XTβ ——正向βF 和反向βR 的温度系数 XTI ——饱和电流的温度指数因子 Kf ——闪烁噪声系数 Af ——闪烁噪声指数因子 3. 小信号模型 混合π等效电路
2002.4 半导体器件 3.5 12
)
三个参数： IS ——饱和电流 βF ——理想的最大正向电流增益 βR ——理想的最大反向电流增益 以上EM方程忽略了基极、集电极和发射极的寄生 电阻；忽略了 Early效应；忽略了基区和集电区的 大注入效应；同时认为βF 和βR 是与电流无关的
2002.4 半导体器件 3.5 3 2002.4 半导体器件 3.5
E
qAD n
∫
2002.4
xE 0
N AB ( x)dx
式中 xE0、xC0 代表外加电 压都等于零时的基区空间 电荷区边界。
半导体器件 3.5 17
qb
QB QB 0
EM方程中的 IS 可以用 ISS/qb 替代。 （ISS反映了BJT的结构参数，qb反映了工作状态）
2002.4 半导体器件 3.5 18
3.5.1 EM模型 大信号模型参数： CJE(0) ——零偏压发射结势垒电容 CJC(0) ——零偏压集电结势垒电容 CJS(0) ——零偏压集电极-衬底电容 ϕ E ——发射结内建电势 ϕ C ——集电结内建电势 —— 衬底结内建电势 m E ——发射结梯度因子 ϕS mC ——集电结梯度因子 mS ——衬底结梯度因子 τF ——理想正向渡越时间 τR ——理想反向渡越时间 FC —— 正偏压势垒电容公式中的系数（当正向偏压 V > FC•kT/q 时，势垒电容公式要作相应的修改）
用q2描述基区储存的过剩载流子电荷：
q2 = I SS I KF qVB ' E ' I SS exp kT − 1 + I KR
2
3.5.2 GP模型
3.5.2 GP模型 1. 直流模型 与EM模型相比，GP模型考虑了以下几个物理效应 9 小电流时β值下降 正向工作：发射结空间电荷区复合；基区表面复合 反向工作：集电结空间电荷区复合；基区表面复合 复合电 流导致基极 C I exp qVB ' E ' − 1 对β 而言 F 2 S 电流 IB 增大，增加 nEL kT 的成分 可以用两个 qVB 'C ' 非线性 pn 结来等效： C4 I S exp n kT − 1 对β R而言
非平衡状态下基区多子电荷的组成： QB = QB0 + QE + QC + QF + QR QE ，QC 为发射结和集电结空间电荷区宽度变化 引起的多子电荷增量。 QF ，QR 为发射结和集电结正向偏置时基区中多 子电荷增量。
2002.4
半导体器件 3.5
19
2002.4
半导体器件 3.5
20
4
3.5.1 EM模型
3.5.1 EM模型
考虑基极、集电极和发射极的寄生电阻，引入 三个电阻参数： C rC ——集电极电阻 rC rE ——发射极电阻 C' rB ——零偏压基极电阻 rB 理想
B B'
模型
基区宽度调变效应对其它参数的影响
I S (VB 'C ' ) = V I S (0) ≈ I S (0) 1 − B 'C ' 1 + VB 'C ' VA VA V β F (0) ≈ β F (0) 1 − B 'C ' 1 + VB 'C ' VA VA
晶体管h参数模型
晶体管h参数模型
晶体管是现代电子技术中最常用的器件之一，是将微弱的信号放大或开关的重要元器件。
为了更好地研究和设计晶体管电路，需要建立精确的数学模型。
其中，h参数模型是一种最为常用的晶体管模型之一。
h参数模型是通过对晶体管输入输出端口的电流和电压之间的关系进行建模得到的。
其中，h11参数表示输入电阻；h12参数表示反向传输电导；h21参数表示正向放大系数；h22参数表示输出导纳。
通过这些参数，可以计算得到晶体管的各种电路参数。
在具体的应用中，h参数模型可以用于计算晶体管的输入输出阻抗、放大系数、稳定性等性能指标。
并且，h参数模型还具有较好的可靠性和实用性，因此在工程实践中得到广泛应用。
总之，晶体管h参数模型是一种重要的数学模型，可以用于分析和设计各种晶体管电路。
对于电子工程师来说，了解和掌握h参数模型，是提高设计水平和解决实际问题的重要基础。
- 1 -。
集成电路晶体管模型及参数提取研究
集成电路晶体管模型及参数提取研究随着数字化、智能化时代的到来，集成电路技术得到了快速发展和广泛应用。
而晶体管作为集成电路的基石，所扮演的角色愈发重要。
因此，研究晶体管模型及其参数提取技术，成为了当前集成电路领域的重要研究方向。
本文将介绍集成电路晶体管模型及参数提取技术的相关背景和进展。
晶体管模型概述晶体管作为集成电路中占有重要地位的元器件，其模型的建立是必不可少的。
早期，为了更好地理解晶体管的物理特性，人们提出了一些粗略的模型。
如饱和型模型、中心线模型、T型模型和Ebers-Moll模型等。
其中，饱和型模型和中心线模型缺乏实用性，而T型模型过于复杂，难以得到可靠的参数。
Ebers-Moll模型则成为了主流。
Ebers-Moll模型是一种二极管模型，它将晶体管等价成两个PN 结串联形成的四层结构。
它的模型方程为：$I_C=I_S\left(e^{\frac{V_{BE}}{V_T}}-1\right)\left(e^{\frac{V_{BC}}{V_T}}-1\right) $其中，$I_C$为输出电流，$I_S$为饱和电流，$V_{BE}$为发射极与基极之间的电位差，$V_{BC}$为集电极与基极之间的电位差，$V_T$为热电压。
Ebers-Moll模型能够准确地描述晶体管的电流特性，并且其模型参数易于测量。
但是，它无法描述晶体管的高频特性和非线性特性。
因此，在实际应用中，需要对其进行改进或采用其他模型。
晶体管参数提取技术为了更好地描述晶体管的性能，我们需要测量出其相关的参数。
晶体管的参数主要分为直流参数和交流参数两类。
如下图所示：直流参数包括：$I_B$、$I_C$、$V_{CE}$等。
测量方法一般采用示波器、电流表、万用表等仪器，通过变化控制电流和电压，进行参数测量。
交流参数包括：$h_{fe}$、$C_{ob}$、$C_{ib}$等。
测量方法一般采用网络分析仪或频谱仪，通过对频率进行变化，测出晶体管的频率响应特性及电容等参数。
10晶体管的直流模型及Q点的估算
E4a02241 晶体管的直流模型及 Q点的估算
1. 晶体管的直流模型的建立
晶体管的直流模型用于放大电路的静态分析和工作 点Q的计算。 晶体管的直流模型可以从晶体管的特性曲线转换而 来，见图02. 。 由晶体管的输入特性曲线，可得理想二极管和开启 电压UD串联的模型。由晶体管的输出特性曲线，可得 理想二极管和电流源 I BQ 串联的模型。
iB
I BQ b
+
β I BQ
iC
I CQ
β I B5
I B5 I B4 I B3 I B2 I B1 u CE
UBEQ _
O
UD e
c + β I B3 UCEQ β I B2 _ β I B1
O
β I B4
UD
u BE
2. 静态工作点的估算
2.1 对于固定偏置共射基本放大电路
对于图02. 所示的固定偏置共射组态基本放大电 路，其基极电流IBQ为
基本放大电路的组成包括： 1。三极管 2。偏置电阻 3。负载电阻 4。耦合电容 5。直流电源
i
R b2
Re
RL
Uo
Ce
V CC
三极管VT：放大信号，起 的能量控制的作用； 偏置电路Rb1、 Rb2、Re ： 使三极管发射结正偏，集 电结反偏，保证三极管具 有放大能力； 负载电阻：包括三极管的 集电极负载电阻Rc，放大 电路的负载电阻RL； 耦合电容C1、 C2：耦合电容 对放大的交流信号可视为短 路， C1、 Ce可保证信号加到 发射结， Ce 称旁路电容。 C2可保证信号加到负载电阻 RL上；
R b1
C1
+
Rc
+
mos管的平方率模型
mos管的平方率模型MOS管的平方率模型MOS管（Metal-Oxide-Semiconductor Field-Effect Transistor）是一种常见的场效应晶体管，广泛应用于集成电路和电子设备中。
平方率模型是用于描述MOS管工作特性的一种数学模型。
本文将介绍MOS管的平方率模型以及其应用。
平方率模型是基于MOS管的三个重要参数：栅极电压（Vgs）、漏极电压（Vds）和漏极电流（Id）之间的关系。
平方率模型通过电流-电压特性曲线来描述MOS管的工作状态。
在平方率模型中，电流与电压的关系可以表示为：Id = k(Vgs - Vth)^2其中，Id为漏极电流，k为常数，Vgs为栅极电压，Vth为阈值电压。
根据平方率模型，当栅极电压小于阈值电压时，MOS管处于截止区，漏极电流非常小。
随着栅极电压的增加，当栅极电压超过阈值电压时，MOS管进入放大区，漏极电流呈指数增长。
当栅极电压继续增加时，MOS管进入饱和区，漏极电流与栅极电压的平方成正比。
平方率模型的应用非常广泛。
首先，平方率模型可以用于电路设计和仿真。
在设计电路时，我们可以利用平方率模型来计算MOS管的电流和电压，从而确定电路的性能和稳定性。
其次，平方率模型可以用于分析MOS管的非线性特性。
由于平方率模型能够较准确地描述MOS管的工作状态，因此可以用来分析MOS管的非线性失真情况，进而优化电路设计。
此外，平方率模型还可以用于MOS 管的模拟和数字电路设计、功耗估算等方面。
除了平方率模型，还有其他一些模型用于描述MOS管的工作特性，如线性模型和对数模型。
线性模型适用于MOS管的小信号分析，对于小幅度变化的信号响应较为准确。
而对数模型则适用于描述MOS管的大信号工作状态，对于大幅度变化的信号响应更为准确。
不同的模型适用于不同的应用场景，根据具体需求选择合适的模型进行分析和设计。
平方率模型是描述MOS管工作特性的一种重要数学模型。
它通过电流-电压特性曲线来描述MOS管的工作状态，可以应用于电路设计、分析非线性特性以及模拟和数字电路设计等方面。
晶体管的小信号模型
跨导为
iD
I
DO
( uGS U GS(th)
1) 2
gm
2I DO U GS(th)
( U GSQ U GS(th)
1)
第5章 基本放大电路
2010.02
5.4.2 双极型晶体管低频小信号模型
5.4.2.1 低频模型的建立
双极型晶体管的微变等效电路的推导可以从晶体管的特 性曲线得出，从输入特性曲线可以模拟出输入侧的模型；从 输出特性曲线可以模拟出输出侧的等效电路模型。
模型中的主要参数是跨导gm，跨导可以查手册，通过转 移特性曲线或漏极输出特性曲线求解，也可以通过转移特性 曲线方程式求导得到。
在转移特性曲线上求低频跨导gm ，单位是mS(毫西门子)。
gm
iD uGS
U DS const
ID /mA
U GS ID Q
6 5 IDSS 4 3 2
4 3 2 1 UGS(off)
IC1
3
IC IC1 IC2
ICQ2
IC2
1
ICEO
O
Q IBQ
80 μA IB1
60 μA
IB IB1 IB2
40 μA IB2 20 μA
IB =0
3
6
9
12 uCE / V
UCE
图5.4.5 的图解
第5章 基本放大电路
2010.02
第5章 基本放大电路
2010.02
晶体管微变等效电路与线性模型是同一问题的不同称谓。
g dd
开U路 gsg
s
g
mU
VCCS
gs
rds
s
图5.4.1 场效应管低频小信号模型
晶体管π等效模型
晶体管π等效模型
晶体管是一种电子元件，它可以被用作放大器、开关、振荡器等。
为了更好地理解晶体管的工作原理，需要使用一种等效模型来描述它的行为。
其中最常用的模型就是π等效模型。
π等效模型是一种简化模型，它把晶体管看做是一个由基极、集电极和发射极构成的三端口网络。
这个网络的输入端是基极，输出端是集电极，发射极则充当了中间节点的作用。
在π等效模型中，晶体管的行为可以看做是一个由输入电阻、输出电导和反向放大系数组成的电路。
通过π等效模型，可以更好地理解晶体管的工作原理。
例如，在放大器中，如果需要提高放大倍数，可以通过增大输入电阻或减小输出电导的方式来实现。
而在开关电路中，可以通过调整输入信号的幅值来控制晶体管的开关状态。
总之，π等效模型是理解晶体管工作原理的重要工具，它可以帮助工程师们更好地设计电路，实现各种功能。
- 1 -。
最新双极晶体管模型PPT课件
Chapter 2: BJT Junction
微电子学院
4. EM-2模型和EM-1模型
对EM－2模型，RB、RE、RC、CTE0、CTC0、 CTS0、TF和TR这8个参数的内定值均为0。
若全部采用内定值，EM－2模型将简化为EM－1模型 。
三、EM－2模型
四、EM－3模型
EM－1和EM－2是描述晶体管直流和交流特性的基本模型 。
进一步考虑晶体管的二阶效应，包括基区宽度调制、小电 流下复合电流的影响、大注入效应等，就成为EM－3模型。
微电子学院
Chapter 2: BJT Junction
微电子学院
Chapter 2: BJT Junction
微电子学院
Chapter 2: BJT Junction
微电子学院
Chapter 2: BJT Junction
微电子学院
Chapter 2: BJT Junction
微电子学院
下表总结了上述29个模型参数对应的物理模型，以 及在哪种工作状态下必需考虑该参数。
基 本 的 双 极 晶 体 管 模 型 参 数
六、其他效应的考虑
在PSpice模拟软件采用的双极晶体管模型中，还同时考虑 许多其他问题。例如：
模型参数随温度的变化(包括晶体管饱和电流、漏电流、电 流放大系数、串联电阻、势垒内建电势、结电容等参数)；
I4＝ISC[exp(qVb’c’/NckT)-1] 相当于等效电路中IB增加两个电流分量。 因此，要考虑基区复合电流的影响，需新增下述4个模型参数描 述小电流下复合电流对电流放大系数的影响：
ISE(发射结漏饱和电流) ISC(集电结漏饱和电流) NE(发射结漏电流发射系数) NC(集电结漏电流发射系数)
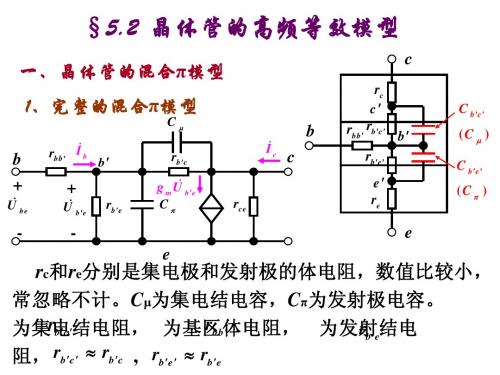
5.2 晶体管的高频等效模型
b
rbc
Ic c
rce
be
rbe
gmUbe C
e
-
Ib 和 Ic 的大小、相角与频率有关，即 是频率的函数。 U 根据半体物理的分析， 与 Ic 成线性关系，与频率无 be U 关。gm为跨导，一个常数，表明 对 be 的控制关系， Ic Ic gmUbe
1 f 2 rbe C (C C C )
fT 1 求Cπ的值。 0 f
2
3、共基截止频率fα 0 0 1 jf / f 0 1 0 1 jf / f 0 1 0 jf / f 1 1 1 jf / f 1 0 0 f (1 0 ) f
0
rbe
0 1 1 jC rbe j C
rbe
0
的频率响应与低通电路相似，fβ为 的截止频率，
称为共射截止频率。
1 f 2 2 rbe C
1
(C C C )
2 f 20 lg 20 lg 20 lg 1 0 f 0 f f 1 j act tan f f
b
f
U be的幅值下
降，相移增大
相移增大
Ic 的幅值下降，
高频时，频率变化时 Ib与 Ic 的关系是频率的函数 也随着变化，电流放大系数不是常量，是频率的函数。
b
+ U rbb
b
c
rbe
be
+ U be -
C
e
gmUbe
1、电流放大系数的幅频特性和相频特性
2.2晶体管模型
2.2.3晶体管伏安特性曲线各极电压与电流之间的关系-------外部特性各极电压：V BE 、V CB 、V CE ，由于V BE + V CB = V CE ，所以两个是独立的。
各极电流：I E 、I B 、I C 。
由于I B + I C = I E ，所以两个是独立的。
一、 共E 输入特性曲线共E ： 输入：I B 、V BE 。
输出：I C 、V CE 。
共E 输入特性曲线：当V CE 维持不同的定值，输入电流I B 随输入电压V BE 变化的特性1()CE B E BE VI f V =定值V BE 是自变量 I B 是因变量 V CE 是参变量 测试原理图：是一族曲线，每根都类似二极管的伏安特性曲线。
特点：（1） 当V CE = 0时，两PN 结并联，I B 较大 （2） 当V CE 从0→0.3V 时，曲线右移。
（3） 当V CE >0.3V 后，曲线基本重合（V CE 的影响很小），不完全重合的原因：基区宽度调制效应。
当V CE ↑，集电结空间电荷区宽度↑，基区宽度↓，复合几率↓，I B ↓。
实际影响很小，所以一般只画一根。
（4） 存在发射结正向导通电压V BE(on) ,类似二极管正向导通电压V D(on) 。
即发射结正向导通时，不管I B 多大，V BE = V BE(on) 基本不变（分析外电路时）。
()0.60.7:(0.60.7)BE on V N PNSi V V PN P ⎧=⎨-⎩:: 例：如右上图求I B 。
等效电路如右下图()B B B E on B BV V I R -=（5） 反向特性 V BE <0 (NPN)发射结反偏，集电结反偏反向电流 I B =－（I EBO + I CBO ） 很小 I EBO ：发射结反向饱和电流I C I V V V VV BECE CECE B=0=0.3V=10V(BR)BEOCBBCCR V V I BBBBBE(o n)R VV I CCEBE/V饱和10V（6） 击穿特性当反向电压大到V （BR ）BEO 时，反向电流↑↑ 二、共E 输出特性曲线（P68）当I B 维持不同的定值，输出电流I C 随输出电压V CE 变化的特性2()C E CE I f V =BI 定值分四个区：放大区、饱和区、截止区、击穿区1、 放大区：发射结正偏，集电结反偏0,0BE CB V V >>()C B C E BE C E BE BE on V V V V V V =-∴>=Q特点：（1） 满足C B CEO B I I I I ββ=+≈，I B 对I C 有正向控制作用（2） 当I B 是等间隔时，曲线是平行等距的。
射频调制第五章低噪放4-2晶体管模型
小信号跨导与管子特性及工作点偏置有关 小信号等效电路 输入阻抗呈容性 极限工作频率 极限工作频率
f T －－
输出电阻很大
由等效电路中的电容引起 gm gm fT = ≈ 2π (C gS + C gd ) 2πC gS
CMOS ——噪声低、线性好、与数字集成电路兼容 噪声低、 噪声低 线性好、 3GHz以上 以上
5.2.1 双极型晶体管共射小信号等效电路
共射放大器原理图 共射放大器原理图 基极偏置 基极偏置VBEQ 偏置 决定基极偏置电流 IBQ 集电极电源 VCC 负载电阻 RL 输入信号为 输入信号为 共同决定工作点 共同决定工作点Q 工作点
5.2
晶体管高频等效电路
射频集成电路主要工艺 最高频率达到100~50GHz 砷化钾 GaAs——最高频率达到 最高频率达到 超高速微电子学和光电子学 双极（ 双极（Bipolar） ）
工艺技术 Bipolar BiCMOS SiGe HBT 截止频率
f T (GHZ)
25 – 50 10 – 20 40 - 80
I BQ
iB
vs ,
v BE = VBEQ + v s
q v BE kT
输出电流公式 输出电流公式 iC = I S e 当 Vsm << VT (
VT =
= I CQe
)时
q vs kT
VCC RL
VBEQ
kT ≈ 26mV q
I CQ
I BQ
晶体管可用其等效电路代替 晶体管可用其等效电路代替 等效电路
v DS 大小划分
可变电阻区
v DS 很小） 很小）
i D = β n [( vGS − VGS ( th ) )v DS ]