麦克斯韦速率分布函数的物理意义
北京化工大学 普通物理学 习题课上(热学).

致冷机的致冷系数定义为:
A Q1 Q2 1 Q2
Q1
Q1
Q1
e Q2 A
Q2 Q1 Q2
七、热力学第二定律的两种表述 不可能从单一热源吸取热量,使它完全变为有用功
而不引起其它变化(即热全部变为功的过程是不可能 的) 热力学第二定律的开尔文表述。
不可能把热量从低温物体自动传到高温物体而不引 起其它变化(即热量不可能自动地从低温物体传向高 温物体) 热力学第二定律的克劳修斯表述。
dQp dT
i2 2
R
迈耶公式:
比热容比:
C p,m CV ,m R
Cp,m i 2
CV ,m
i
CV ,m
1
dE dT
i 2
R
C p,m
i2 2
R,
i
i
2
单原子气体:
CV ,m
3R 2
双原子气体:
CV ,m
5R 2
单原子分子气体: CV ,m 12.47
卡诺循环的效率: T1 T2 1 T2
T1
T1
卡诺致冷机的致冷系数:e Q2 T2
Q1 Q2 T1 T2
七、热力学第二定律
四种热力学过程的主要公式
过程 过程方程 E2 E1
等体 p C
T
M Mm
CV
(T2
T1)
等压 V C
T
M Mm
CV
(T2
T1)
1.25 20.81J 0.028
929J
所以气体在这一过程中所吸收的热量为
211-麦克斯韦速率分布律、三种统计速率

211麦克斯韦速率分布律、三种统计速率1、选择题1,麦克斯韦速率分布曲线如图所示,图中A ,B 两部分面积相等,则该图表示 (A )0v 为最概然速率(B )0v 为平均速率 (C )0v 为方均根速率(D )速率大于和小于0v 的分子数各占一半[ ]2,麦克斯韦速率分布函数)(v f 的物理意义是 (A )它是气体分子处于v 附近单位速率区间的概率 (B )它是气体分子处于v 附近的频率(C )它是气体分子处于dv v v +~速率区间内的分子数(D )它是气体分子处于dv v v +~速率区间内的相对分子数[ ]3,气体的三种统计速率:最概然速率p v 、平均速率v 、方均根速率2v ,它们之间的大小关系为 (A )2v v v p >> (B )2vv v p ==(C )2vv v p << (D )无法确定[ ]4,设在平衡状态下,一定量气体的分子总数为N ,其中速率在dv v v +~区间内的分子数为dN ,则该气体分子的速率分布函数的定义式可表示为 (A )NdN v f =)( (B )dv dN N v f 1)(= (C )vdvdN N v f 1)(=(D )dvv dNN v f 21)(=[ ]5,空气中含有氮分子和氧分子,它们两者的平均速率关系为 (A )22O N v v > (B )22O N v v = (C )22O N v v < (D )无法确定 [ ]6,已知n 为单位体积分子数,)(x v f 为麦克斯韦速度分量的分布函数,则xx dv v nf )(表示为(A )单位时间内碰到单位面积器壁上的速度分量x v 处于x x x dv v v +~区间的分子数(B )单位体积内速度分量x v 处于x x x dv v v +~区间的分子数 (C )速度分量在x v 附近,x dv 区间内的分子数占总分子数的比率 (D )速度分量在x v 附近,x dv 区间内的分子数[ ]7,设氢分子在温度为300 K 时的平均速率为1v ,在温度为2.7 K (星际空间温度)时的平均速率为2v ,则平均速率1v 和2v 的大小分别为 (A )211069.1⨯=v m/s ,321079.1⨯=v m/s (B )311079.1⨯=v m/s ,221069.1⨯=v m/s (C )211083.1⨯=v m/s ,221093.1⨯=v m/s (D ))311058.1⨯=v m/s ,321050.1⨯=v m/s ,[ ]8,设氢分子在温度为300 K 时的最概然速率为1p v ,在温度为2.7 K (星际空间温度)时的最概然速率为2p v ,则最概然速率1p v 和2p v 的大小分别为 (A )211069.1⨯=p v m/s ,321078.1⨯=p v m/s (B )311078.1⨯=p v m/s ,221069.1⨯=p v m/s (C )311057.1⨯=p v m/s ,221049.1⨯=p v m/s (D ))211050.1⨯=p v m/s ,321058.1⨯=p v m/s ,[ ]9,设氢分子在温度为300 K 时的方均根速率为21v ,在温度为2.7 K (星际空间温度)时的方均根速率为22v ,则方均根速率21v 和22v 的大小分别为 (A )3211078.1⨯=v m/s ,2221069.1⨯=v m/s (B )3211058.1⨯=v m/s ,2221050.1⨯=v m/s(C )3211093.1⨯=v m/s ,3221083.1⨯=v m/s(D ))3211093.1⨯=v m/s ,2221083.1⨯=v m/s ,[ ](A )3.18 m/s (B )3.37 m/s (C )4.00 m/s (D )5.00 m/s [ ]11,理想气体的温度由27︒C 升高到927︒C ,其最概然速率将增大到原来的 (A ) 2倍 (B ) 4倍 (C ) 6倍 (D ) 34倍[ ]12,已知n 为单位体积的分子数,)(v f 为麦克斯韦速率分布函数,则)(v nf 表示 (A ) 速率v 附近,dv 区间内的分子数(B ) 单位体积内速率在dv v v +~区间内的分子数 (C )速率v 附近,dv 区间内的分子数占总分子数的比率(D ) 单位时间内碰到单位器壁上,速率在dv v v +~区间内的分子数[ ]13,已知一定量的某种理想气体,在温度为1T 和2T 时分子的最概然速率分别为1p v 和2p v ,分子速率分布函数的最大值分别为)(1p v f 和)(2p v f ,已知1T >2T ,则在下列几个关系式中正确的是(A ) 1p v >2p v ,)(1p v f >)(2p v f (B ) 1p v <2p v ,)(1p v f >)(2p v f (C ) 1p v >2p v ,)(1p v f <)(2p v f (D ) 1p v <2p v ,)(1p v f <)(2p v f[ ]则其方均根速率为(A )3.18 m/s (B )3.37 m/s (C )4.00 m/s (D )2.41 m/s[ ]15,某理想气体处于平衡状态,其速率分布函数为)(v f ,则速率分布在速率间隔21~v v 内的气体分子的算术平均速率的计算式为(A )⎰⎰=2210)()(v v v dvv f dvv vf v (B )⎰⎰∞=121)()(v v v dv v f dvv vf v(C )⎰⎰∞=)()(21dvv f dv v vf v v v (D )⎰⎰=2121)()(v v v v dvv f dvv vf v[ ](A )3.18 m/s (B )3.37 m/s (C )4.00 m/s (D )0.68 m/s [ ]2、判断题1,理想气体分子的最概然速率,就是麦克斯韦速率分布曲线峰值对应的速率。
热学-统计物理3 第3章 气体分子热运动速率和能量的统计分布律
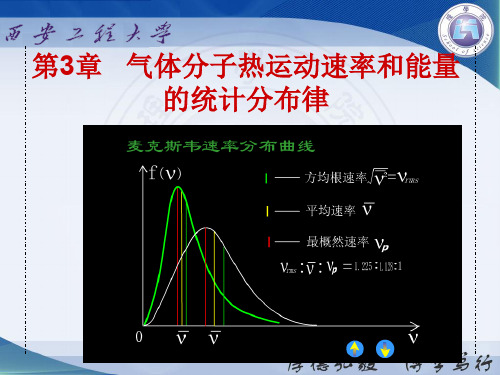
v v pv v 2
讨论
麦克斯韦速率分布中最概然速率 vp 的概念
下面哪种表述正确?
(A) vp 是气体分子中大部分分子所具有的速率. (B) vp 是速率最大的速度值. (C) vp 是麦克斯韦速率分布函数的最大值.
(D) 速率大小与最概然速率相近的气体分子的比 率最大.
例1 计算在 27 C 时,氢气和氧气分子的方均
M
3.方均根速率 v2
v2
N
0
v2dN N
0
v2Nf N
(v)dv
o
v
v2 v2 f (v)dv 4 ( m )3 2 e mv2 2kT v4dv
0
2 kT
0
v4ev2 dv 3
0
8 5
v2 3kT m
v2 3kT 3RT
2kT
v
麦克斯韦速率分布函数的物理意义: f (v) dNv
Nd v
既反映理想气体在热动平衡条件下,分布在速率 v 附近单
位速率区间内的分子数占总分子数的百分比,又表示任意
一分子的速率出现在 v附近单位速率区间内的概率。
如果以速率为横坐标轴,速率分布函数为纵坐标轴,画 出的一条表示f(v) —v之间关系的曲线,称为气体分子的麦 克斯韦速率分布曲线。 ,它形象地描绘出气体分子按速率 分布的情况。
大量分子的速率的算术平均值叫做分子的平均速率.
v
vNf (v)dv
0
vf (v)dv
v 4 (
m
)3 e2 mv2 2kT v2dv
N
0
0
热学补充题

热学补充题热学补充题一、单一选择题:1.下列关于平衡态的说法中,正确的是A.系统状态参量不随时间变化的状态B.系统内各处均匀一致的状态C.热力学系统的宏观性质不随时间变化的状态D.系统在不受外界影响的条件下,宏观性质不随时间变化的状态2.金属杆的一端与沸水接触,另一端与冰接触,当沸水和冰的温度都维持不变时,杆的温度虽然不同,但不随时间改变,下面说法中正确的是A.杆处于平衡状态,因为杆各处的温度不随时间改变B.杆不处于平衡状态,因为杆的温度各处不同C.杆不处于平衡状态,因为杆受外界影响D.不能确定杆是否处于平衡态3.一个水银温度计,一个酒精温度计,两者都在冰点校正了零度,在水的沸点校正了100度,然后在0度和100度之间等分成100份,现在分别用这两个温度计测量两个物体的温度,结果它们都指示在30度处,则知两物体的温度A.相同B.不一定相同C.一定不相同D.无法判断4. 理想气体状态方程pV = RT适用于A.1cm3的理想气体B.任意体积的理想气体C.1g 的理想气体D.1mol 理想气体5.相等质量的氢气和氧气被密封在一粗细均匀的玻璃管内,并由一水银滴所隔开,当玻璃管平放时,氢气柱和氧气柱的长度比为A.16:1B.1:1C.1:16D.32:16. 1mol 的范德瓦耳斯方程为A. (p-a / V m2)( V m-b) = RTB. (p + a / V m 2)( V m—b) = RTC. (p + a / V m 2)( V m + b) = RTD. (p-a / V m 2)( V m+ b) = RT7.范德瓦耳斯方程(p + a / V m 2)( V m—b) = RT 中的V m是A.气体可被压缩的体积B.气体分子自由活动的体积C.容器的容积D.气体分子本身的体积8.按麦克斯韦速率分布率,一个分子精确的具有一定速率的比率是A. 1B. 0.5C.0 D. 比0.5大9.在一定速率v 附近,麦克斯韦速率分布函数f (v ) 的物理意义是:一定量的气体在给定的温度下处于平衡时的A.速率为v 的分子数B.分子数随速率v 的变化C.速率为v 的分子数占总分子数的百分比D.速率在v 附近单位速率区间内的分子数占总分子数的百分比10. f (v )为麦克斯韦速率分布函数,那么⎰21)(v v dv v f 表示A.速率在v 1~v 2之间的分子数B.速率在v 1~v 2 之间的分子数占总分子数的百分比C.速率在 v 1~v 2 之间的平均速率D.无明确的物理意义 11.根据能量均分定理,理想气体分子的平均总能量为A.()kT v r t 221++ B.()RT v r t 221++C.()kT v r t ++21D.()kT v r t 223++12.如果氢气和氦气的温度相同,摩尔数也相同,则这两种气体的A.平均动能相同B.平均平动动能相同D.内能相等 C.势能相等13.理想气体等压过程中,其分子的平均碰撞平率Z 与温度T 的关系是A. T Z ∝B. T Z 1∝ C. T Z ∝D. TZ 1∝ 14.体积固定的容器中有一定量的气体,设分子有效直径不变,当温度逐渐升高时,分子的平均碰撞平率和平均自由程的变化为 A.Z 增大,λ增大 B.Z 增大,λ减小 C.Z 增大,λ不变 D.Z 和λ均保持不变15.如果每立方厘米约有3×1019个分子,空气分子的有效直径为2×109s -1cm ,则在00C 和1atm下,空气分子的平均自由程的量值是A. 2×105cmB. 2×10-6cmC.2×10-5cm D. 2.1×10-2cm16.如果空气分子的平均速率为1×105cm·S -1,而平均自由程的量值为1×10-5cm ,那么空气碰撞频率为A. 1s -1B. 1×1010 s-1 C.1×10-10s -1 D. 1×10-5s -117.下列有关热量的说法,哪些是正确的A.热是一种特殊物质B.热传递是改变系统内能的一种方式C.热量是表征系统固有属性的物理量D.系统温度越高,所含热量越多18.在p -V 图上理想气体系统由平衡态I 到达平衡态II ,如图1所示,无论经历过什么样的过程系统必然 A.对外作功 B.内能增加 C.吸收热量 D.放出热量19.如图1所示,一系统从同一初态E 分别经过三个不同过程R 1,R 2,R 3变化到相同末态下,则在三个系统中对外作的功的关系为A . W 1 < W 2 < W 3B .C . W 2 < W 3 < W 1D . 20.内能相等的1mol VO 图1 . . I Ip V O 图1气A.热接触时,它们之间会发生热传递B.质量必定相等C.温度必定相等D.温度可能相等,也可能不等21.一定量的某种理想气体作如图2所示的循环,则下列说法正确的是A .气体在2-3过程中气体不作功B .在4-1过程中气体不作功C .整个循环中气体所作的功为负值D .气体在1-2过程中及3-4过程中所作的功数值相同 22.如图3所示,p -V 图上有两条曲线 abc 和adc,由此知 A .其中一条是绝热线,一条是等温线B .两过程吸收的热量相等C .两过程中系统对外作的功相等D .两过程中系统内能变化相等23.理想气体经历了一个由等温过程、绝热过程和等压过程组成的逆循环,在此循环过程中,理想气体p VO 1 234 图2 图3 V p O a b c dA .从外界吸收热量 B.向外界放出热量C.对外界作功D.内能减少24.绝热过程的过程方程是A.=-γγ/)1(Tp恒量 B.=-T p //)2(γγ恒量 C.=--γγT p1恒量 D.=γpT 恒量25.设热源的热力学温度是冷源的热力学温度的n 倍,则一卡诺循环中,气体将把从热源得到的热量交给冷源A. n 倍B. (n –1)倍C. 1/n 倍 D. (n +1) / n 倍26.卡诺热机的效率A.仅依赖于高温热源的温度B.仅依赖于低温热源的温度C.仅依赖于高温热源和低温热源的温度D.仅依赖于高温热源与低温热源的温度差27.在327 0C 的高温热源和27 0C 的低温热源间工作的热机,理论上的最大效率是A. 100%B. 92%C. 50%D. 25%28.在327 0C 的高温热源和27 0C 的低温热源间工作的热机,理论上的最大效率是A. 100%B. 92%C. 50%D. 25%29.在功与热的转变过程中,下列叙述中不正确的是A.不可能制成一种循环动作的热机,它只从一个热源吸取热量,使之完全变为有用功,而其他物体不发生任何变化。
麦克斯韦速率分布

麦克斯韦速率分布律、三种统计速率1、选择题题号:21111001分值:3分难度系数等级:1麦克斯韦速率分布曲线如图所示,图中A,B两部分面积相等,则该图表示<A)为最概然速率<B)为平均速率<C)为方均根速率<D)速率大于和小于的分子数各占一半[ ]答案:< D )题号:21111002分值:3分难度系数等级:1麦克斯韦速率分布函数的物理意义是,它是气体分子<A)处于附近单位速率区间的概率 <B)处于附近的频率<C)处于速率区间内的概率 <D)处于速率区间内的相对分子数[ ]答案:< A )题号:21111003分值:3分难度系数等级:1气体的三种统计速率:最概然速率、平均速率、方均根速率,它们之间的大小关系为<A) <B)<C) <D)无法确定[ ]答案:< C )题号:21111004分值:3分难度系数等级:1设在平衡状态下,一定量气体的分子总数为,其中速率在区间内的分子数为,则该气体分子的速率分布函数的定义式可表示为b5E2RGbCAP<A) <B)<C) <D)[ ]答案:< B )题号:21112005分值:3分难度系数等级:2空气中含有氮分子和氧分子,它们两者的平均速率关系为<A) <B) <C) <D)无法确定[ ]答案:< A )题号:21112006分值:3分难度系数等级:2已知n为单位体积分子数,为麦克斯韦速度分量的分布函数,则表示为<A)单位时间内碰到单位面积器壁上的速度分量处于区间的分子数<B)单位体积内速度分量处于区间的分子数<C)速度分量在附近,区间内的分子数占总分子数的比率<D)速度分量在附近,区间内的分子数[ ]答案:< B )题号:21112007分值:3分难度系数等级:2设氢分子在温度为300 K时的平均速率为,在温度为2.7 K<星际空间温度)时的平均速率为,则平均速率和的大小分别为p1EanqFDPw<A) m/s, m/s<B) m/s, m/s<C) m/s, m/s<D)) m/s, m/s,[ ]答案:< B )题号:21112008分值:3分难度系数等级:2设氢分子在温度为300 K时的最概然速率为,在温度为2.7 K<星际空间温度)时的最概然速率为,则最概然速率和的大小分别为DXDiTa9E3d<A) m/s, m/s<B) m/s, m/s<C) m/s, m/s<D)) m/s, m/s,[ ]答案:< C )题号:21112009分值:3分难度系数等级:2设氢分子在温度为300 K时的方均根速率为,在温度为2.7K<星际空间温度)时的方均根速率为,则方均根速率和的大小分别为RTCrpUDGiT<A) m/s, m/s<B) m/s, m/s<C) m/s, m/s<D)) m/s, m/s,[ ]答案:< D )题号:21112018分值:3分难度系数等级:2设有一群粒子按速率分布如下:粒子数速率则其最概然速率为<A)3.18 m/s <B)3.37 m/s <C)4.00 m/s <D)5.00 m/s5PCzVD7HxA[ ]答案:< C )题号:21113011分值:3分难度系数等级:3理想气体的温度由27︒C升高到927︒C,其最概然速率将增大到原来的<A) 2倍 <B) 4倍 <C)6倍 <D)34倍[ ]答案:< A )题号:21113012分值:3分难度系数等级:3已知为单位体积的分子数,为麦克斯韦速率分布函数,则表示<A)速率附近,区间内的分子数<B)单位体积内速率在区间内的分子数<C)速率附近,区间内的分子数占总分子数的比率<D)单位时间内碰到单位器壁上,速率在区间内的分子数[ ]答案:< B )题号:21113013分值:3分难度系数等级:3已知一定量的某种理想气体,在温度为和时分子的最概然速率分别为和,分子速率分布函数的最大值分别为和,已知>,则在下列几个关系式中正确的是jLBHrnAILg<A)>,><B)<,><C)>,<<D)<,<[ ]答案:< C )题号:21113014分值:3分难度系数等级:3设有一群粒子按速率分布如下:粒子数速率则其方均根速率为<A)3.18 m/s <B)3.37 m/s <C)4.00 m/s <D)2.41 m/sxHAQX74J0X[ ]答案:< B )题号:21113015分值:3分难度系数等级:3某理想气体处于平衡状态,其速率分布函数为,则速率分布在速率间隔内的气体分子的算术平均速率的计算式为<A) <B)<C) <D)[ ]答案:< D )题号:21113016分值:3分难度系数等级:3设有一群粒子按速率分布如下:粒子数速率则其平均速率为<A)3.18 m/s <B)3.37 m/s <C)4.00 m/s <D)0.68 m/sLDAYtRyKfE[ ]答案:< A )题号:21114017分值:3分难度系数等级:4如右下图所示,两条曲线分别表示在相同温度下氧气和氢气分子速率分布曲线,和分别表示氧气和氢气的最概然速率,则下列表述正确的是Zzz6ZB2Ltk<A)图中表示氧气分子的速率分布曲线,且<B)图中表示氧气分子的速率分布曲线,且<C)图中表示氧气分子的速率分布曲线,且<D)图中表示氧气分子的速率分布曲线,且[ ]答案:< C )题号:21114018分值:3分难度系数等级:4如右图所示,两条曲线分别表示在相同温度下氧气和氢气分子速率分布曲线,和分别表示氧气和氢气的最概然速率,则下列表述正确的是dvzfvkwMI1<A)图中表示氧气分子的速率分布曲线,且<B)图中表示氢气分子的速率分布曲线,且<C)图中表示氧气分子的速率分布曲线,且<D)图中表示氢气分子的速率分布曲线,且[ ]答案:< D )题号:21114019分值:3分难度系数等级:4一氧气瓶的容积为,充了气未使用时的压强为,温度为,使用后瓶内氧气的质量减少为原来的一半,其压强降为,则使用前后分子热运动平均速率之比为 rqyn14ZNXI<A) <B) <C) <D)[ ]答案:< B )题号:21115020分值:3分难度系数等级:5处于平衡状态的理想气体,其分子的速率分布曲线如图所示,设表示最概然速率,表示速率分布在之间的分子数占总分子数的百分比,当温度降低时,则EmxvxOtOco<A)减小,也减小 <B)增大,也增大<C)减小,增大 <D)增大,减小[ ]答案:< C )2、判断题题号:21121001分值:2分难度系数等级:1理想气体分子的最概然速率,就是麦克斯韦速率分布曲线峰值对应的速率。
麦克斯韦速率分布

exp(
mv
2
) v dv
2
2kT
⑶ N个分子的气体处于平衡态,以容器为参考系速率在v ~ v+dv 间的分子占总分子数N的百分比(概率)
dN N f (v )dv 4 ( m 2 kT
3 )2
exp(
mv
2
2kT
) v dv 概率
2
2. 麦氏速率分布函数曲线: ⑴
但速率很大 或很小的分子数较少
N
( v ~ v v的分子数 )
则在总分子中分子速率介于
v ~ v+∆v 的分子的概率为:
N N
Pv v v
当∆v→0 时,即得分子速率分布的概率密度函数:
F (v ) dN N dv
相应地,分子速率介于v ~ v+dv的概率即为:
d Pv v d v F ( v ) d v
(三)最概然速率vp:
vp 2kT m
2 RT Mm
vrms
f (v )
v
2
3kT m
3 RT Mm
(四)三种速率之比:
v p : v : v rms 1 : 1 . 128 : 1 . 224
v
o
v p v v2
1. 前面讨论理想气体 和 P 时曾用到 vrms v
v rms v 1.085 误差 8.5%
2 RT Mm
vp
意义: 若把整个可能的速率范围分为许多等间隔的小区间, 则在最可几速率vp所在区间中分子数所占比率最大。
3. 称概率密度取极大值时的速率为 最概然速率vp,也称最可几速率
vp
vp
速率分布

1、选择题题号: 分值:3分 难度系数等级:1麦克斯韦速率分布曲线如图所示,图中A ,B 两部分面积相等,则该图表示 (A )0v 为最概然速率 (B )0v 为平均速率 (C )0v 为方均根速率(D )速率大于和小于0v 的分子数各占一半[ ] 答案:( D ) 题号: 分值:3分 难度系数等级:1麦克斯韦速率分布函数)(v f 的物理意义是 (A )它是气体分子处于v 附近单位速率区间的概率 (B )它是气体分子处于v 附近的频率(C )它是气体分子处于dv v v +~速率区间内的分子数 (D )它是气体分子处于dv v v +~速率区间内的相对分子数[ ] 答案:( A ) 题号: 分值:3分 难度系数等级:1气体的三种统计速率:最概然速率p v 、平均速率v 、方均根速率2v ,它们之间的大小关系为 (A )2v v v p >> (B )2v v v p == (C )2v v v p << (D )无法确定[ ] 答案:( C ) 题号: 分值:3分 难度系数等级:1设在平衡状态下,一定量气体的分子总数为N ,其中速率在dv v v +~区间内的分子数为dN ,则该气体分子的速率分布函数的定义式可表示为(A )N dNv f =)( (B )dv dNN v f 1)(= (C )vdvdNN v f 1)(= (D )dvv dNN v f 21)(=[ ] 答案:( B ) 题号: 分值:3分 难度系数等级:2空气中含有氮分子和氧分子,它们两者的平均速率关系为(A )22O N v v > (B )22O N v v = (C )22O N v v < (D )无法确定 [ ] 答案:( A ) 题号:分值:3分 难度系数等级:2已知n 为单位体积分子数,)(x v f 为麦克斯韦速度分量的分布函数,则x x dv v nf )(表示为(A )单位时间内碰到单位面积器壁上的速度分量x v 处于x x x dv v v +~区间的分子数(B )单位体积内速度分量x v 处于x x xdv v v +~区间的分子数(C )速度分量在x v 附近,x dv 区间内的分子数占总分子数的比率 (D )速度分量在x v 附近,x dv 区间内的分子数[ ] 答案:( B ) 题号: 分值:3分 难度系数等级:2设氢分子在温度为300 K 时的平均速率为1v ,在温度为 K (星际空间温度)时的平均速率为2v ,则平均速率1v 和2v 的大小分别为(A )211069.1⨯=v m/s ,321079.1⨯=v m/s (B )311079.1⨯=v m/s ,221069.1⨯=v m/s (C )211083.1⨯=v m/s ,221093.1⨯=v m/s (D ))311058.1⨯=v m/s ,321050.1⨯=v m/s ,[ ] 答案:( B ) 题号: 分值:3分难度系数等级:2设氢分子在温度为300 K 时的最概然速率为1p v ,在温度为 K (星际空间温度)时的最概然速率为2p v ,则最概然速率1p v 和2p v 的大小分别为 (A )211069.1⨯=p v m/s ,321078.1⨯=p v m/s (B )311078.1⨯=p v m/s ,221069.1⨯=p v m/s (C )311057.1⨯=p v m/s ,221049.1⨯=p v m/s (D ))211050.1⨯=p v m/s ,321058.1⨯=p v m/s ,[ ] 答案:( C ) 题号: 分值:3分 难度系数等级:2设氢分子在温度为300 K 时的方均根速率为21v ,在温度为 K (星际空间温度)时的方均根速率为22v ,则方均根速率21v 和22v 的大小分别为 (A )3211078.1⨯=v m/s ,2221069.1⨯=v m/s (B )3211058.1⨯=v m/s ,2221050.1⨯=v m/s (C )3211093.1⨯=v m/s ,3221083.1⨯=v m/s (D ))3211093.1⨯=v m/s ,2221083.1⨯=v m/s ,[ ] 答案:( D ) 题号: 分值:3分 难度系数等级:2设有一群粒子按速率分布如下: 粒子数i N 2 4 6 8 2 速率i v (m/s )则其最概然速率为(A )3.18 m/s (B )3.37 m/s (C )4.00 m/s (D )5.00 m/s [ ] 答案:( C ) 题号: 分值:3分 难度系数等级:3理想气体的温度由27C 升高到927C ,其最概然速率将增大到原来的 (A ) 2倍 (B ) 4倍 (C ) 6倍 (D ) 34倍[ ] 答案:( A ) 题号: 分值:3分 难度系数等级:3已知n 为单位体积的分子数,)(v f 为麦克斯韦速率分布函数,则)(v nf 表示 (A ) 速率v 附近,dv 区间内的分子数(B ) 单位体积内速率在dv v v +~区间内的分子数 (C )速率v 附近,dv 区间内的分子数占总分子数的比率(D ) 单位时间内碰到单位器壁上,速率在dv v v +~区间内的分子数[ ] 答案:( B )分值:3分 难度系数等级:3已知一定量的某种理想气体,在温度为1T 和2T 时分子的最概然速率分别为1p v 和2p v ,分子速率分布函数的最大值分别为)(1p v f 和)(2p v f ,已知1T >2T ,则在下列几个关系式中正确的是 (A ) 1p v >2p v ,)(1p v f >)(2p v f (B ) 1p v <2p v ,)(1p v f >)(2p v f (C ) 1p v >2p v ,)(1p v f <)(2p v f (D ) 1p v <2p v ,)(1p v f <)(2p v f[ ] 答案:( C ) 题号: 分值:3分 难度系数等级:3设有一群粒子按速率分布如下: 粒子数i N 2 4 6 8 2 速率i v (m/s )则其方均根速率为(A )3.18 m/s (B )3.37 m/s (C )4.00 m/s (D )2.41 m/s [ ] 答案:( B )分值:3分 难度系数等级:3某理想气体处于平衡状态,其速率分布函数为)(v f ,则速率分布在速率间隔21~v v 内的气体分子的算术平均速率的计算式为(A )⎰⎰=2210)()(v v v dv v f dvv vf v (B )⎰⎰∞=121)()(v v v dv v f dvv vf v(C )⎰⎰∞=0)()(21dv v f dvv vf v v v (D )⎰⎰=2121)()(v v v v dvv f dvv vf v[ ]答案:( D ) 题号: 分值:3分难度系数等级:3设有一群粒子按速率分布如下:则其平均速率为(A )3.18 m/s (B )3.37 m/s (C )4.00 m/s (D )0.68 m/s [ ] 答案:( A ) 题号: 分值:3分 难度系数等级:4如右下图所示,两条曲线分别表示在相同温度下氧气和氢气分子速率分布曲线,2)(o p v 和2)(H p v 分别表示氧气和氢气的最概然速率,则下列表述正确的是(A )图中a 表示氧气分子的速率分布曲线,且4)()(22=H p O p v v(B )图中b 表示氧气分子的速率分布曲线,且4)()(22=Hp O p v v (C )图中a 表示氧气分子的速率分布曲线,且41)()(22=H p O p v v (D )图中b 表示氧气分子的速率分布曲线,且41)()(22=Hp O p v v [ ] 答案:( C ) 题号: 分值:3分 难度系数等级:4如右图所示,两条曲线分别表示在相同温度下氧气和氢气分子速率分布曲线,2)(o p v 和2)(H p v 分别表示氧气和氢气的最概然速率,则下列表述正确的是(A )图中a 表示氧气分子的速率分布曲线,且2000)(2=O p v m/s (B )图中a 表示氢气分子的速率分布曲线,且2000)(2=H p v m/s (C )图中b 表示氧气分子的速率分布曲线,且2000)(2=O p v m/s (D )图中b 表示氢气分子的速率分布曲线,且2000)(2=H p v m/s[ ] 答案:( D )题号: 分值:3分 难度系数等级:4一氧气瓶的容积为V ,充了气未使用时的压强为1p ,温度为1T ,使用后瓶内氧气的质量减少为原来的一半,其压强降为2p ,则使用前后分子热运动平均速率之比21v v 为 (A )212p p (B )212p p (C )122p p (D )122p p [ ] 答案:( B ) 题号: 分值:3分 难度系数等级:5处于平衡状态的理想气体,其分子的速率分布曲线如图所示,设p v 表示最概然速率,p N ∆表示速率分布在v v v p p ∆+~之间的分子数占总分子数的百分比,当温度降低时,则(A )p v 减小,p N ∆也减小 (B )p v 增大,p N ∆也增大 (C )p v 减小,p N ∆增大 (D )p v 增大,p N ∆减小[ ] 答案:( C )2、判断题题号: 分值:2分难度系数等级:1理想气体分子的最概然速率,就是麦克斯韦速率分布曲线峰值对应的速率。
经典:第四讲-速度分布函数-麦克斯韦速率

f (v) dN Ndv
速率分布函数
理解分布函数的几个要点:
1.条件:一定温度(平衡态)和确定的气体系统,T和m是一定的; 2.范围:(速率v附近的)单位速率间隔,所以要除以dv;
3.数学形式:(分子数的)比例,局域分子数与总分子数之比。
8
物理意义:
速率在 v 附近,单位速率区间的分子数占总分子数
• dN/N 是 v 的函数; •当速率区间足够小时(宏观小,微观大), dN/N还应与
区间大小成正比。
为此,规定以单位速率间隔为比较标准,即 dN ,这样,比
Ndv
值 dN
Ndv
就反映出了分布随速率v的改变而改变。为此我们规定;
7
定义:处于一定温度下的气体,分布在速率v附近的
单位速率间隔内的分子数占总分子数的百分比只是
(2) 氢气在该温度时的最概然速率和方均根速率
解 (2)
vp
2RT
M
RT 2 103
1000
m/s
RT
f(v)
(v p )H2 103
1.41 103 m/s
( v 2 )H2
3RT M
1.73103 m/s
He H2
1000
v
29
例2 有N 个粒子,其速率分布函数为
f (v )
(2) 因为速率分布曲线下的面积代表一定速率区间内 的分子与总分子数的比率,所以
v v0 的分子数与总分子数的比率为
N
N
v0a
v0
2 3v 0
2 3
N 2 N
3
因此, v>v0 的分子数为 ( 2N/3 ) f (v )
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
在平衡状态下,当分子的相互作用可以忽略时,分布在任一速率区间v~v+△v间的分子数dN 占总分子数N的比率(或百分比)为dN / N .
dN / N是v 的函数,在不同速率附近取相等的区间,此比率一般不相等.当速率区间足够小时(宏观小,微观大),dN / N 还应与区间大小成正比:
其中f(v)是气体分子的速率分布函数.分布函数f(v)的物理意义是:速率在v 附近,单位速率区间的分子数占总分子数的比率.
分布函数f(v)满足归一化条件:
大量分子的系统处于平衡态时,可以得到速率分布函数的具体形式:
式中T是热力学温度,m为分子质量,k为玻尔兹曼常数.上式就是麦克斯韦速率分布律.
麦克斯韦速率分布是大量分子处于平衡态时的统计分布,也是它的最概然分布.大量分子的集合从任意非平衡态趋于平衡态,其分子速率分布则趋于麦克斯韦速率分布,其根源在于分子间的频繁碰撞.
上图是麦克斯韦速率分布函数f(v)示意图,曲线下面宽度为dv 的小窄条面积等于分布在此速率区间内的分子数占总分子数的比率dN/N .
我们可以看到:同一种理想气体在平衡状态下,温度升高时速率分布曲线变宽、变平坦,但曲线下的总面积不变.随着温度的升高,速率较大的分子在分子总数中的比率增大.同一温度下,分子质量m越小,曲线越宽越平坦,在分子总数中速率较大的分子所占比率越高.。
