无源RLC网络与阻抗变换
合集下载
无源网络的分析

9911991142222122???????????ss?sssksssksssshsz22用部分分式法综合无源网络83941s12212122?????s?????ssssszk85149s92292222?????s?????ssssszk222182582391zzzzsssskssksz????????????由此可得
现代电路理论与设计
第2章
无源网络的分析与设计
2.1 用直接法综合无源网络
2.1 用直接法综合无源网络
2.1 用直接法综合无源网络
2.1.1
1
LC网络的输入阻抗
LC网络的输入阻抗及其零极点分布 常用的六种LC网络的输入阻抗及其零极点 分布如图所示。
LC网络
输入阻抗
零、极点的位置
(a)
L
Z sL
( s )(s ) Z (s) H 2 2 s ( s )(s )
2 2 z1 2 p1 2 2 z2 2 p2
(0 z1 p1 z 2 p 2 )
2.2 用部分分式法综合无源网络
将Z(s)的表达式展开为部分分式,并将复共轭 项组合,得:
2.2 用部分分式法综合无源网络
d. Z(s)的每一个极点对应一个元件;
e. 电容和电感的数目要么相等,要么差值为1;
f. 该网络实现了Z(s)的全部各种极点:第一个串 联电感实现了无穷大处的极点;第一个串联电 容实现了原点处的极点;第一个并联LC电路 实现了±jωp1处的极点;第n个并联LC电路实 现了±jωpn处的极点; g. 从福斯特1型网络不能看出零点的分布情况。
2.2 用部分分式法综合无源网络
也可以根据Z(∞) 值确定网络的第一个串联元 件是电感还是电容。 如果Z(∞)=0, 则网络的第一个串联元件是电容。 如果Z(∞)= ∞,则网络的第一个串联元件是电感。 (b) 如果元件的数目为偶数,则网络的串联电 感和串联电容要么都需要,要么都不需要。 如果Z(0)= ∞或Z(∞)= ∞, 则网络的串联电感 和串联电容都需要。 如果Z(0)=0或Z(∞)=0, 则网络的串联电感和 串联电容都不需要。
现代电路理论与设计
第2章
无源网络的分析与设计
2.1 用直接法综合无源网络
2.1 用直接法综合无源网络
2.1 用直接法综合无源网络
2.1.1
1
LC网络的输入阻抗
LC网络的输入阻抗及其零极点分布 常用的六种LC网络的输入阻抗及其零极点 分布如图所示。
LC网络
输入阻抗
零、极点的位置
(a)
L
Z sL
( s )(s ) Z (s) H 2 2 s ( s )(s )
2 2 z1 2 p1 2 2 z2 2 p2
(0 z1 p1 z 2 p 2 )
2.2 用部分分式法综合无源网络
将Z(s)的表达式展开为部分分式,并将复共轭 项组合,得:
2.2 用部分分式法综合无源网络
d. Z(s)的每一个极点对应一个元件;
e. 电容和电感的数目要么相等,要么差值为1;
f. 该网络实现了Z(s)的全部各种极点:第一个串 联电感实现了无穷大处的极点;第一个串联电 容实现了原点处的极点;第一个并联LC电路 实现了±jωp1处的极点;第n个并联LC电路实 现了±jωpn处的极点; g. 从福斯特1型网络不能看出零点的分布情况。
2.2 用部分分式法综合无源网络
也可以根据Z(∞) 值确定网络的第一个串联元 件是电感还是电容。 如果Z(∞)=0, 则网络的第一个串联元件是电容。 如果Z(∞)= ∞,则网络的第一个串联元件是电感。 (b) 如果元件的数目为偶数,则网络的串联电 感和串联电容要么都需要,要么都不需要。 如果Z(0)= ∞或Z(∞)= ∞, 则网络的串联电感 和串联电容都需要。 如果Z(0)=0或Z(∞)=0, 则网络的串联电感和 串联电容都不需要。
射频集成电路设计第3章 无源RLC网络和阻抗匹配

使用双分支匹配电路可以把任意有耗负载ZL(阻 抗实数部分不为零)匹配到输入阻抗Zin。
3.5 总结
• • • • 无源RLC网络的基本特性 串并联阻抗等效变换 阻抗匹配网络 阻抗匹配设计方法
第三章
3.1 3.2 3.3 3.4 3.5
无源RLC网络和阻抗匹配
无源RLC网络 串并联阻抗变换 抽头回路阻抗变换 阻抗匹配 总结
3.1
3.1.1
无源RLC网络
串联RLC网络
3.1
无源RLC网络
谐振:
L C
1 LC
L C
即
0
串联RLC网络的阻抗特性
3.1
谐振时:
无源RLC网络
50.0
25.0
100
200 10.0
ZL Z0
0.08 0.2 0.04 0.02 0.01 0.004 0.04 100 200
500.0
0.2
500.0
0.004 0.08 50.0 25.0 10.0 0.01 0.02
3.4.2 匹配禁区和频率响应
确定匹配禁区的过程
并电容后阻抗的变化范围
共轭匹配
3.4 阻抗匹配
• 匹配电路的概念 • 目的:
获得最大功率传输 获得最小系统噪声 获得最佳频率响应 获得最大功率容量等多种标准
• 应用:
低噪声放大电路 宽频带放大电路 功率放大电路等射频电路中
3.4.1 集总参数L形匹配电路
分立元件的8种电路结构
Smith圆图匹配的方法
• 目的
– 从负载点出发向匹配点移动;
再串电感后阻抗ZMS的范围
确定匹配禁区的过程
50.0 25.0 100
第一章无源阻抗变换4-2要点
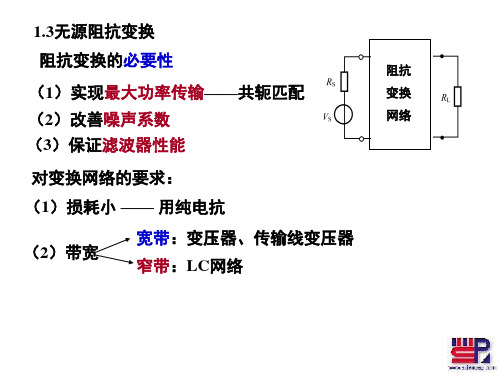
XS 2 ) ) RL (1 Q 2 ) RL R 1 X S (1 ( L ) 2 ) X S (1 2 ) XS Q
由变换电阻可求出Q
Q
RS 1 RL
( 条件: Rs > R L )
已知 o
则:
X S QRL , X P RS Q
L、C
当 Rs < R L 时
PC C1 C1 C 2 RL Rin
1 1 C 63.7 PF 9 0 X C 2 10 2.5
0.774
C1 281.7PF
C2 82.3PF
1.3.3 L网络阻抗变换 特征:① 两电抗元件组成 --结构形式同 L ② 窄带网络--两电抗元件不同性质,有选频滤波性能
V I SV2 I S
IS IS V2 Pc I S V RS RS 2 P c
例1-3-1 用电容部分接入方式设计一个窄带阻抗变换网络, 工作频率为1GHz,带宽为 50MHz,将 RL 30 变换为阻抗 Rin 50 解:阻抗变换网络如图示, 注意:此处有两个不同的 Q
源端并联电容支路有
RS 10 X C1 4.263 Q1 2.346
fo 3.75MHz
C1 9955PF
源端串联电感支路有 X L1 Q1Rint er 2.346 1.538 3.608
总电感为: L
XL 3.608 12.30 0.675 6 2f o 2 3.75 10
根据已知带宽计算出
(1) 并联回路L、C 1、C 2的 Q (2) 并联支路R L 、C 2的 Q2_ 决定计算阻抗变换 采用高Q法,还是低Q法 由回路的等效负载决定
现代电路设计第2章无源网络的分析与设计

2.2 用部分分式法综合无源网络
电路理论与设计
2.2 用部分分式法综合无源网络
利用部分分式法综合实现的网络称为福斯特网络。其中, 只包含电感和电容元件的福斯特网络称为LC福斯特网络。 只包含电阻和电容元件的福斯特网络称为RC福斯特网络。 这些网络都是通过网络的端口特性进行设计的。网络的端口特性可以用阻抗表示,也可以用导纳表示。根据阻抗表示式实现的福斯特网络称为福斯特1型网络,根据导纳表示式实现的福斯特网络称为福斯特2型网络。
现代电路理论与设计
单击添加副标题
第2章 无源网络的分析与设计
2.1 用直接法综合无源网络
电路理论与设计
2.1 用直接法综合无源网络
PART 01
电路理论与设计
LC网络
L
C
C
L
L
C
C2
L2
L1
C1
C2
L2
输入阻抗
零、极点的位置
(a)
(b)
(c)
(d)
(e)
(f)
LC网络输入阻抗Z(s)零点和极点的特点:
2.1 用直接法综合无源网络
电路理论与设计
从电抗曲线可知,当ω=1时,Z(ω)=-1.于是可求得: H=8/3
(3)所求的阻抗函数为:
2.1 用直接法综合无源网络
(2) 求H: 令s=jω,沿虚轴计算Z(s):
C1
C2
比较
和
可得如下关系:
求得各元件值为:
可用如下电路实现:
2.1 用直接法综合无源网络
例2.5 (a)已知网络的阻抗函数 假设H=1, 求对应的LC福斯特1型网络; (b)假设H=10, 求对应的LC福斯特1型网络; (c)如果Z(s)的表达式中的s用10s代替,求对应的LC福斯特1型网络 。
电路理论与设计
2.2 用部分分式法综合无源网络
利用部分分式法综合实现的网络称为福斯特网络。其中, 只包含电感和电容元件的福斯特网络称为LC福斯特网络。 只包含电阻和电容元件的福斯特网络称为RC福斯特网络。 这些网络都是通过网络的端口特性进行设计的。网络的端口特性可以用阻抗表示,也可以用导纳表示。根据阻抗表示式实现的福斯特网络称为福斯特1型网络,根据导纳表示式实现的福斯特网络称为福斯特2型网络。
现代电路理论与设计
单击添加副标题
第2章 无源网络的分析与设计
2.1 用直接法综合无源网络
电路理论与设计
2.1 用直接法综合无源网络
PART 01
电路理论与设计
LC网络
L
C
C
L
L
C
C2
L2
L1
C1
C2
L2
输入阻抗
零、极点的位置
(a)
(b)
(c)
(d)
(e)
(f)
LC网络输入阻抗Z(s)零点和极点的特点:
2.1 用直接法综合无源网络
电路理论与设计
从电抗曲线可知,当ω=1时,Z(ω)=-1.于是可求得: H=8/3
(3)所求的阻抗函数为:
2.1 用直接法综合无源网络
(2) 求H: 令s=jω,沿虚轴计算Z(s):
C1
C2
比较
和
可得如下关系:
求得各元件值为:
可用如下电路实现:
2.1 用直接法综合无源网络
例2.5 (a)已知网络的阻抗函数 假设H=1, 求对应的LC福斯特1型网络; (b)假设H=10, 求对应的LC福斯特1型网络; (c)如果Z(s)的表达式中的s用10s代替,求对应的LC福斯特1型网络 。
3-无源RLC网络解析

2020/3/2
31
互连线效应(1)
• 互连线(看作传输线)模型
2020/3/2
32
互连线效应(2)
2020/3/2
33
互连线效应(3)
• 传输线的特性阻抗
2020/3/2
34
传输线阻抗变换
2020/3/2
35
二端口网络与S 参数
2020/3/2
36
二端口网络与S 参数
2020/3/2
37
二端口网络与S 参数
2020/3/2
38
二端口网络与S 参数
2020/3/2
39
二端口网络与S 参数
2020/3/2
40
二端口网络与S 参数
2020/3/2
41
S 参数与参考平面
2020/3/2
42
2020/3/2
43
2020/3/2
5
第三章 无源RLC网络
• 并联RLC谐振回路
Q R LC
特征阻抗
此时,导纳为纯实数
2020/3/2
6
第三章 无源RLC网络
• 并联RLC谐振回路
2020/3/2
7
无源元件(Passiv 无源RLC网络
• 并联RLC谐振回路
2020/3/2
23
• 1、L匹配
4.6举例
2020/3/2
24
Π型匹配
2020/3/2
25
抽头电容匹配
2020/3/2
26
无源阻抗变换
2020/3/2
27
无源阻抗变换
2020/3/2
28
实例
• 第三章作业:第二题,第十二题
1高频-LC选频与阻抗变换-少公式
LC谐振回路的选频特性和阻抗变换
根据电流比值画出相应的曲线如下图所示,该曲线称 为串联谐振回路的谐振曲线。由图可知回路的品质因数越 高,谐振曲线越尖锐,回路的选择性越好。在高频中通常 Q值远大于1(一般电感线圈的Q值为几十到一二百)。在 串联回路中,电阻、电感、电容上的电压值与电抗值成正 比,因此串联谐振时的电感及电容上的电压为最大,其值 为电阻上电压值的Q值,也就是恒压源的电压值的Q值。 发生谐振时的物理意义是,电容和电感中储存的最大能量 相等。
注意:在实际电路分析与计算中,为了简便,仍然将其当 作理想电阻。
2 电感线圈
图3 理想电感
图4 实际电感的等效电路
LC谐振回路的选频特性和阻抗变换
电感线圈在高频频段除表 现电感L的特性外,还具有一 定的损耗电阻r和分布电容。
但是在分析一般中、长、 短波频段电路时,通常忽略分 布电容的影响。因而电感线圈 的等效电路可以表示为电感L 和电阻r的串联。如图所示。
LC谐振回路的选频特性和阻抗变换
高频电路中的元器件 简单LC谐振回路 阻抗的串、并联等效转换 阻抗变换电路 集中选频滤波器
LC谐振回路的选频特性和阻抗变换
高频电路中的元器件
1 电阻器
图1 纯电阻
一个实际的电阻器,在低频 时主要表现为电阻特性,但在高 频使用时不仅表现为电阻特性的 一面,而且表现有电抗特性的一 面。电阻器的电抗特性反映的就 是高频特性。
LC谐振回路的选频特性和阻抗变换
4 二极管 半导体二极管在高频中主要用于检波、调制解调电
路等非线性变换电路中,工作在低电平。高频电路中主 要用点接触式二极管和表面势垒二极管,它们的极间电 容小,工作频率高。如常用的点接触式二极管,工作频 率可达100~200MHz。
无源阻抗变换

分析方法:分解为两个 L 网络, 设置一个假想中间电阻 Rint er 两个L网络的Q分别是
Q1 RS 1 Rint er
Q2 RL 1 Rint er
由于 Rint er 是未知数,因此可以假设一个 Q 1 或 Q 2 假设Q 的原则:根据滤波要求,设置一个高Q 当 R L > R S 时,Q2 = Q
磁芯变压器可近似为理想变压器
部分接入进行阻抗变换 电抗元件部分接入 (
x1 与 x2 为同性质电抗 )
分析方法: 将部分阻抗折合到全部,
x1 、 x2
值不变, R
R
电感部分接入:
*
*
电容部分接入:
定义参数——接入系数 n n=
接入部分阻抗 同性质的总阻抗 =
X2
X1+ X2
<1
电容部分接入系数
变压器种类:
空心变压器 磁芯变压器——耦合紧,漏感小( k
1 ),
磁芯损耗随频率升高增大
理想变压器:无损耗、耦合系数为1,
初级电感量为无穷
理想变压器阻抗变换:
电压
V1 N1 V2 N 2
电流
阻抗
I1 N2 I2 N1
' RL
N1 2 ( ) RL N2
注意电流方向(负号、图中方向)
XS 2 ) ) RL (1 Q 2 ) RL RL 2 1 X S (1 ( ) ) X S (1 2 ) XS Q
由变换电阻可求出Q
Q
RS 1 RL
( 条件: Rs > R L )
已知 o
则:
X S QRL , X P RS Q
L、C
当 Rs < R o ,欲将 R L变换为 Rs , 求:电路结构 和 X S 、X P
阻抗变换原理

阻抗变换原理
阻抗变换原理,又称为阻抗匹配原理,是电路中常用的一种技术,用于将电路的输入和输出阻抗匹配,以提高电路的性能和效果。
阻抗变换的基本原理是利用电路元件的特性,将一种阻抗转换为另一种阻抗,使得输入阻抗和输出阻抗之间能够达到最佳匹配。
这种匹配可以通过适当地选择电阻、电容、电感等元件的数值来实现。
在电路中,当输入和输出之间的阻抗不匹配时,会出现反射和功率损耗等问题。
阻抗变换可以通过将输入和输出之间的阻抗变换为相等或者接近的数值,减小阻抗不匹配带来的问题。
阻抗变换常用于放大器、滤波器、天线系统等电子电路中。
在放大器中,阻抗变换可以提高输入和输出之间的耦合效率,增加信号的传输效果。
而在滤波器中,阻抗变换可以实现滤波器对特定频率范围的阻抗适配,提高滤波器的精确度和性能。
总之,阻抗变换原理是一种重要的电路设计技术,能够利用电路元件的特性,实现输入和输出阻抗之间的匹配,从而提高电路的性能和效果。
通过合理选择电阻、电容、电感等元件的数值,能够实现阻抗的变换,使得电路能够更好地适应不同的工作条件和需求。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
串并联阻抗等效互换
R:电感引入的寄生
• 在谐振频率周围进行等效
串并联阻抗等效互换(续)
串联电路的有效品质因子:
谐振频率下,串联电路转换为等效并联电路后,电抗 XP的性质与XS相同,在QS较高的情况下,其电抗X基本 保持不变,而并联电路的电阻RP比串联电路的电阻RS 增大了QS2倍
串并联阻抗等效互换(续)
阻抗匹配的重要性
• 最大功率传输 • 前置滤波器要求50欧姆的负载终端
3dB
40dB
Matched Termination
Unmatched Termination
• PCB连线需要:传输线走线,匹配终端情况下 不用考虑走线长度
功率匹配
ZS
VS
VL
ZL
1 V PL Re VL 2 Z
串并联阻抗等效互换(续)
提要
• 并联RLC网络 • 串并联阻抗等效互换 • 回路抽头时的阻抗变换 • 阻抗匹配(L匹配、Pi匹配和T匹配)
回路抽头时的阻抗变换
• 输入阻抗:
• 谐振频率:
提要
• 并联RLC网络 • 串并联阻抗等效互换 • 回路抽头时的阻抗变换 • 阻抗匹配(L匹配、Pi匹配和T匹配)
清华大学微电子学研究所
April 0ห้องสมุดไป่ตู้, 2014
无源RLC网络和阻抗匹配
池保勇 清华大学微电子学研究所设计室
参考书:池保勇等编,《CMOS射频集成电路分析与 设计》, §3
提要
• 并联RLC网络 • 串并联阻抗等效互换 • 回路抽头时的阻抗变换 • 阻抗匹配(L匹配、Pi匹配和T匹配)
并联RLC网络的阻抗特性
1 | | VSWR 1 | |
• 带宽与元件值灵敏度:中间各节点的阻抗在 SMITH原图上不能太接近单位圆(要求低Q值) • 考虑直流偏置:不能因阻抗匹配网络影响直流 特性; • 实现代价:尽量少用电感;
– L:1nH~10nH, C: 0.3pF~5pF
总结
• 并联RLC网络 • 串并联阻抗等效互换 • 回路抽头时的阻抗变换 • 阻抗匹配(L匹配、Pi匹配和T匹配)
PL max ( Z L ) Z L Z
* S
L匹配
降阻型
升阻型
例子
Pi匹配
中间节点的品质因子为可选量
例子
T匹配
中间节点的品质因子为可选量
例子
阻抗匹配设计考虑
• 匹配性能:匹配度的要求与应用相关,通常在 整个工作频带内VSWR位于2:1~1.5:1认为是可以 接受的,这时反射系数约为-15dB~-10dB
* L * L
1 VS ZL 2 Re Z * Z Z L S L
2
2
PL PL 2 2 2 2 0 RS RL (XS 2X S X L X L ) 0, X L ( X S X L ) 0 RL X L
• 最大功率传输条件:负载阻抗与源阻抗共轭
感性 容性
品质因子
• 回路谐振:
• 回路谐振时,流过电感和电容的电流大小 相等、方向相反,流过电阻的电流为外加 激励电流 • 品质因子:电感/电容上的电流放大倍数 • 本质定义:
R QP = =ω0 CR ω0 L
品质因子(续)
• 回路阻抗:
• 当
• 3dB带宽:
提要
• 并联RLC网络 • 串并联阻抗等效互换 • 回路抽头时的阻抗变换 • 阻抗匹配(L匹配、Pi匹配和T匹配)
