选频网络
合集下载
第3讲-选频网络
r 时，则
0 L 02 L2
0
b
0C
1
0 L
0
0
1 LC
可见，谐振时，回路旳感抗和容抗近似相等。
回路旳品质因数：
.
Q 0L 1 1 L Is r 0Cr r C
Cr L
谐振时，因为电纳b=0,总导纳只包括电导部分,
称为谐振电导,用gp表达
gp
r2
r
0L2
r
0 L 2
r L
2
r L
Cr L
LC C
其谐振后旳等效阻抗为一种纯电阻，即 Zp Rp
其电路图如图所示：
.
Is
C L RRp
Rp
1 gp
r2
0L2
r
L ( Cr
Q2r)
Y
1 R
j
ωC
1 ωL
Z1
1
Y
1 R
j
ωC
1 ωL
|Z|
φ
Rp
π/ 2
O －π/ 2
O
ω0
ω
ω0
ω
频率特征
所谓回路旳频率特征就是
回路端电压 U 与频率旳关系。
为了取得工作频率高度稳定、带阻衰减特征十 分陡峭旳滤波器，就要求滤波器元件旳品质因数Q 很高。LC型滤波器旳品质因数一般在100～200范 围内，不能满足上述旳要求。用石英晶体切割成旳 石英谐振器，其品质因数可达几万甚至几百万，因 而能够构成工作频率稳定度极高、阻带衰减特征很 陡峭、通带衰减很小旳滤波器。
r
.
C
Is
L
Y
r
1
jL
jC
r2
r
2L2
j C
0 L 02 L2
0
b
0C
1
0 L
0
0
1 LC
可见，谐振时，回路旳感抗和容抗近似相等。
回路旳品质因数：
.
Q 0L 1 1 L Is r 0Cr r C
Cr L
谐振时，因为电纳b=0,总导纳只包括电导部分,
称为谐振电导,用gp表达
gp
r2
r
0L2
r
0 L 2
r L
2
r L
Cr L
LC C
其谐振后旳等效阻抗为一种纯电阻，即 Zp Rp
其电路图如图所示：
.
Is
C L RRp
Rp
1 gp
r2
0L2
r
L ( Cr
Q2r)
Y
1 R
j
ωC
1 ωL
Z1
1
Y
1 R
j
ωC
1 ωL
|Z|
φ
Rp
π/ 2
O －π/ 2
O
ω0
ω
ω0
ω
频率特征
所谓回路旳频率特征就是
回路端电压 U 与频率旳关系。
为了取得工作频率高度稳定、带阻衰减特征十 分陡峭旳滤波器，就要求滤波器元件旳品质因数Q 很高。LC型滤波器旳品质因数一般在100～200范 围内，不能满足上述旳要求。用石英晶体切割成旳 石英谐振器，其品质因数可达几万甚至几百万，因 而能够构成工作频率稳定度极高、阻带衰减特征很 陡峭、通带衰减很小旳滤波器。
r
.
C
Is
L
Y
r
1
jL
jC
r2
r
2L2
j C
Chapter2 选频网络
f0 ⋅ L 1 ω0 L 1 = = ⋅ = ⋅Q R 2π R 2π
回路储能 ∴Q = 2π ⋅ 每周耗能
2010-12-23 Copyrights yaoping. All rights reserved. 8
二、谐振曲线和通频带
谐振曲线: 谐振曲线:串联谐振回路中电流 幅值与外加电动势频 率之间的关系曲线。 率之间的关系曲线。
一般 ωL>> R
Is
.
代入上式 ： Z = RC 1 + j(ωC − )
L C G
1
L
ωL
1 RC 1 ： = G = 为电导 B = ωC − 为电纳 ， 其中 L ωL Rp
2010-12-23 Copyrights yaoping. All rights reserved. 14
2010-12-23
Copyrights yaoping. All rights reserved.
3
一、谐振条件、谐振特性 谐振条件、
Zs = R + jX = R + jωL + 1 jωC
2
= R + j(ωL −
1
ωC
) =| Zs | e
jϕ
| Zs |=
R +X
2
2
=
R + (ωL −
谐振时的阻抗特性： 谐振时的阻抗特性：
并联谐振时，回路呈纯电阻性， 并联谐振时，回路呈纯电阻性， 且阻抗为最大值； 且阻抗为最大值； ω < ωp ,呈现感性 . I L C G0 ω > ωp ,呈现容性 因此回路谐振时： 因此回路谐振时：
s
|Z|,Re,Xe
3 选频网络
3选频网络选频网络在高频电子线路中，应用广泛。
它能选出所需要的频率分量和滤除不需要的频率分量。
通常选频网络分为两大类：◆LC振荡回路（单振荡回路和耦合振荡回路）◆各种滤波器（LC集中滤波器、石英晶体滤波器、陶瓷滤波器和声表面声波滤波器等。
）3.1串联谐振回路由电感线圈和电容器组成的单个振荡电路，称为单振荡回路。
信号源与电容和电感串接，就构成中联振荡回路。
电感的感抗值(wL)随信号频率的升高而增大，电容的容抗值1／wC则随信号频率的升高而减小。
与感抗或容抗的变化规律不同，串联振荡回路的阻抗在其一特定频率上具有最小值，而偏离特定频率时的阻抗将迅速增大，单振荡回路的这种特性称为谐振特性，这特定的频率称为谐振频率。
因而上述的串联单振荡回路又可称为串联谐振因路。
由于串联谐振回路在谐振时阻抗具有最小值，因而在谐振频率处信号源在串联谐振因路中产生的电流达到最大但，而在其他频率处回路电流都要下降,所以谐振回路有选频或滤波作用。
它在高频电子线路中得到了广泛的应用。
本节重点：串联谐振回路的谐振及谐振条件、谐振特性、谐振曲线和通频带。
3.1.1基本原理（如图1所示）图3.1.1 串联谐振回路及其矢量图由图知：()wCwLjRZ/1-+=ϕj eZ=2222)1(wCwLRXRZ-+=+=X＝wCwL/1-,RwCwL/1arctan-=ϕjXRVjwCjwLRVZVI SSS+=-+==∙∙∙∙/1★在其一特定角频率w0时，若回路电抗满足下列条件X＝wCwL/1-=0, Z为最小值R，则电流I max＝I0＝Vs/R为最大值，回路发生谐振。
所以式X=0称为串联谐振回路的谐振条件。
★由此可以导出回路发生串联谐振的角频率w0和频率f0分别为LCw/1=,LCfπ21=谐振时，L和C上的电压大小相等，相位差180O，外加电压∙SV等于R上的电压降∙RV。
根据图3.1.1 可知，当w<w0时，wL<1/wC，∙∙<CLVV，此时，电流∙I超前∙SV，ϕ<0。
第2章选频网络
微亨（μH）为单位， 上式可变为一实用计算公式:
L ( 1 )2
2
1 f02C
10 6
25330 f02C
将f0=fs=10 MHz代入, 得 L 5.07u
(2) 回路谐振电阻和带宽。
Rp Q0L 100 2 107 5.07106 3.18104
31.8k
X1 R1
R2 X2
00:13
第2章 选频网络
R1
R2 1（R2 /
X
）2
2
R2 1 Q2
L1
R2 （1 QL21）R1
X1
X2 1（X 2 /
R2）2
X2
1
1 Q2
L1
X2
X（1 1
1 Q2
）
L1
如果QL1值较大（大于10或更大），则
R2
Q R 2 L1 1
X2 X1
00:13
第2章 选频网络
1、串、并联阻抗等效互换
等效互换 等效互换前的电路与等效互换后的电路阻抗相等
R1
jX1
R2 ( jX 2 ) R2 jX 2
R2
X
2 2
R22
X
2 2
j
R2 2
X
2
R22
X
2 2
=
所以2
X
2 2
X1
R2 2
X
2
R22
X
2 2
串联电路的有效品质因数为：QL1
4）电流源的折合公式
L ( 1 )2
2
1 f02C
10 6
25330 f02C
将f0=fs=10 MHz代入, 得 L 5.07u
(2) 回路谐振电阻和带宽。
Rp Q0L 100 2 107 5.07106 3.18104
31.8k
X1 R1
R2 X2
00:13
第2章 选频网络
R1
R2 1（R2 /
X
）2
2
R2 1 Q2
L1
R2 （1 QL21）R1
X1
X2 1（X 2 /
R2）2
X2
1
1 Q2
L1
X2
X（1 1
1 Q2
）
L1
如果QL1值较大（大于10或更大），则
R2
Q R 2 L1 1
X2 X1
00:13
第2章 选频网络
1、串、并联阻抗等效互换
等效互换 等效互换前的电路与等效互换后的电路阻抗相等
R1
jX1
R2 ( jX 2 ) R2 jX 2
R2
X
2 2
R22
X
2 2
j
R2 2
X
2
R22
X
2 2
=
所以2
X
2 2
X1
R2 2
X
2
R22
X
2 2
串联电路的有效品质因数为：QL1
4）电流源的折合公式
第3章选频网络
= R[ 1 + j
ωo L ω ωo ( − )] R ωo ω
1 ) ωC
又由于: 又由于 Q =
ωo L
R
，而
∴
其中： 其中 ： ∆ω = ω −ωo Rp Rp = Zp = = Z 2∆ω 1+ jξ 00:23 + jQ 1 ωo
ω 2 − ω o2 ( ω − ω 0 )(ω + ω o ) 2∆ω ω ωo ( − )= ≈ = ωo ω oω ωo ω ω oω
00:23
= jQii
电容端电压： 1 ui uc = ii =−j = − jQui jω oC ω oCR
7．谐振曲线
定义： 定义： 谐振回路： 并联 谐振回路： 回路电压与工作频率之间的关系
ii Z p ui 1 αp = = = uio ii Z po 1+ξ 2
第3章 选频网络 章
谐振回路： 串联 谐振回路 ： 回路电流与工作频率之间的关系
ui uio
由定义可得： ξ = Q 由定义可得：
ωo
或=
fo Q
1
1 2
ii iio
1
1 2
00:23
ωo
ω
ωo
ω
第3章 选频网络 章
概论 列表
00:23
第3章 选频网络 章
3.2 串并联阻抗的等效互换
LC串、并联谐振回路在高频率低阻负载工作时，难以达到良好的 串 并联谐振回路在高频率低阻负载工作时， 阻抗匹配与选频作用，因此还必须采用这类电路的变形电路， 阻抗匹配与选频作用，因此还必须采用这类电路的变形电路，其设计基 础是串、并联阻抗的等效互换与回路抽头时的阻抗变换。 础是串、并联阻抗的等效互换与回路抽头时的阻抗变换。
选频网络
2.1.1谐振及谐振条件
x 容性 感性
z
L
x=L– 1 C
O
0
– 1 C
R
0
串联振荡回路电抗与频率的关系
阻抗模值与频率的关系
> 0 ，x > 0，电路呈感性
< 0，x < 0，电路呈容性 = 0，x = 0，|z| = R，电路达到串联谐振
当 0时，|z| >R 当 = 0时，|z|min =R
五、通频带
回路外加电压的幅值不变时，改变频率，回路电流 I 下降 到 Io 的 时所对应的频率范围称为谐振回路的通频带。 1 2
B0.7 20.7 2 1或B0.7 2f0.7 f2 f1
通信电子线路(Ⅱ)
第二章 选频网络
第二章 选频网络
• 2.1 串联谐振回路
• 2.2 并联谐振回路 • 2.3 串并联阻抗等效互换和抽头变换 • 2.4 谐振回路的相频特性—群时延特性 • 2.5 耦合回路 • 2.6 滤波器的其它形式
2选频网络
• 超外差式接收机方框图
2选频网络
选频的基本概念：
各种滤波器 石英晶体滤波器
陶瓷滤波器 声表面波滤波器
2.1串联谐振回路
由电感线圈和电容器组成的单个振荡
电路，称为单振荡回路。
信号源、电容和电感串联连接，就构 成串联振荡回路。 串联振荡回路的阻抗在某一特定频率 上具有最小值，而偏离这个特定频率 的时候阻抗将迅速增大。单振荡回路 的这种特性称为谐振特性，这个特定 频率就叫做谐振频率。 谐振回路具有选频和滤波作用。
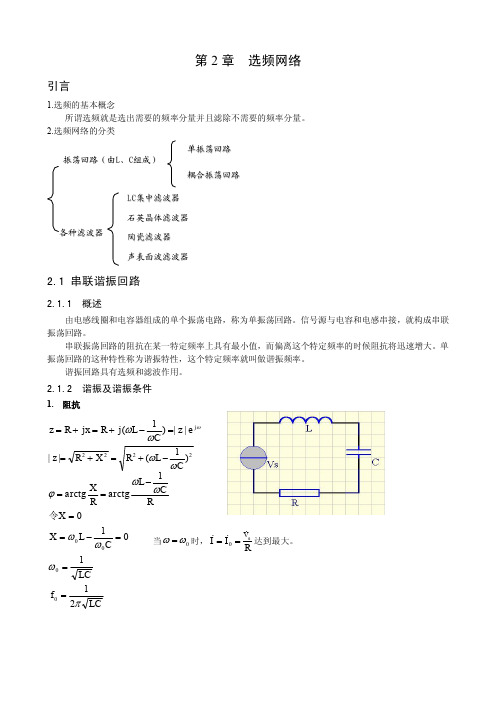
1)谐振时阻抗最小，且为纯电阻 0 X 0
Z R 为最小值，且为纯电阻
选频网络
X L0
X C0
0L
1 0C
L C
2.1.3 谐振特性
1) 0 X 0
Z R 为最小值，且为纯电阻
0 X 0
X L XC呈现感性
0 X 0
X
L
X
呈
C
现
容
性
2) 谐振时电流最大且与电压源同相 3)
VL0
I0
j0 L
VS R
P
P
QP
p p P
QP
2 p
在小失谐时：
V V0
结论：
1
1
QP
2 P
2
a
r
c
t
aQn p
2 p
1)当
时
p
:
0
V V0 1为最大， 0为纯阻性
2)当
到 G最P为大最值小且值与I。S同
相
其 RP
中：L GRPC为R谐C
L为谐振 振电阻
电
导
2.2.3 谐振特性
2.谐振频率 f0
B 0时，回路端电 压
ISRp
L CR
IS，V与IS同 相。
谐振条件:
B 0
C 1 L
p
1 LC
,
fp
2
1 LC
若 L R 不成立
谐振时回路端电压
vo Is Rp Is / GP
由此可作出谐振曲线
选频网络
ωC
1 ωL − X ωC ϕ = arctan = arctan R R
幅角： 幅角：
感性和容性
§3.1 串联谐振回路
二、谐振及谐振条件
设外加电压： 设外加电压：vs=Vsmsinω t 回路电流： 路电流： 谐振条件： 谐振条件：
ɺ ɺ Vs Vs ɺ I = = = 1 R + jX Z R + j( ω L − ) ωC 1 X = ω0 L − =0 ω 0C ɺ Vs
§3.2 并联谐振回路
三、谐振特性
CR 电纳B 最小(G 为谐振电导，＝ ♦电纳 = 0，导纳 = Gp ，最小 p为谐振电导，＝ ) ． ，导纳Y L
电压达到最大，并且与电流相同． 电压达到最大，并且与电流相同．
品质因数： 品质因数： p = Q
1 1 L L ( 特性阻抗)． = = ρ ，特性阻抗 ． R ωpCR R C C 2 2 1 L ωp L 1 1 谐振电阻： 谐振电阻： Rp = = = = Qpωp L = 2 2 = Qp Gp CR R ωp C R ω pC =
§3.1 串联谐振回路
六、能量关系（谐振时） 能量关系（谐振时）
2 w 上的瞬时能量（磁能）： 电感Ｌ上的瞬时能量（磁能）： L = 1 Li 2 = 1 LI 0m sin 2 ωt 2 2
wC = 1 CVC = 1 CVC2m cos2 ωt 上的瞬时能量（电能）： 电容Ｃ上的瞬时能量（电能）： 2 2
和电容C并联组成 ♦由电感L和电容 并联组成，电阻 由电感 和电容 并联组成，电阻R 通常为电感线圈损耗的等效电阻． 通常为电感线圈损耗的等效电阻．
L R
C ɺ Ic
−
♦信号源为电流源，适合信号源内阻 信号源为电流源， 很大的情况． 很大的情况．
1 ωL − X ωC ϕ = arctan = arctan R R
幅角： 幅角：
感性和容性
§3.1 串联谐振回路
二、谐振及谐振条件
设外加电压： 设外加电压：vs=Vsmsinω t 回路电流： 路电流： 谐振条件： 谐振条件：
ɺ ɺ Vs Vs ɺ I = = = 1 R + jX Z R + j( ω L − ) ωC 1 X = ω0 L − =0 ω 0C ɺ Vs
§3.2 并联谐振回路
三、谐振特性
CR 电纳B 最小(G 为谐振电导，＝ ♦电纳 = 0，导纳 = Gp ，最小 p为谐振电导，＝ ) ． ，导纳Y L
电压达到最大，并且与电流相同． 电压达到最大，并且与电流相同．
品质因数： 品质因数： p = Q
1 1 L L ( 特性阻抗)． = = ρ ，特性阻抗 ． R ωpCR R C C 2 2 1 L ωp L 1 1 谐振电阻： 谐振电阻： Rp = = = = Qpωp L = 2 2 = Qp Gp CR R ωp C R ω pC =
§3.1 串联谐振回路
六、能量关系（谐振时） 能量关系（谐振时）
2 w 上的瞬时能量（磁能）： 电感Ｌ上的瞬时能量（磁能）： L = 1 Li 2 = 1 LI 0m sin 2 ωt 2 2
wC = 1 CVC = 1 CVC2m cos2 ωt 上的瞬时能量（电能）： 电容Ｃ上的瞬时能量（电能）： 2 2
和电容C并联组成 ♦由电感L和电容 并联组成，电阻 由电感 和电容 并联组成，电阻R 通常为电感线圈损耗的等效电阻． 通常为电感线圈损耗的等效电阻．
L R
C ɺ Ic
−
♦信号源为电流源，适合信号源内阻 信号源为电流源， 很大的情况． 很大的情况．
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
+ L C 1/G Is – Vo L C R
一、阻抗
一般 L>> R
1 1 R jL R jL jC jL Z 1 1 R jL R j L jC C
L C 1 RC 1 j C L L
B 0
C
1 L
p
1 LC
, fp
1 2 LC
若L R 不成立
1 L jC Z 1 CR R j L 1 C
谐振时Z为实数,故
1 j R L
R jL
1 L j R CR
X L0 X C0
1 0 L 0 C
L
C
退出
2.1 谐振回路
二、谐振特性 1) 0 X 0
Z R 为最小值，且为纯电阻 0 X 0
X L X C呈现感性 0 X 0 X L X C呈现感性
2) 谐振时电流最大且与电源同相 3)
其中：G P R C L 为谐振电导
电纳B 0，回路导纳Y G P为最小值。 R P L R C 为谐振电阻 电压V I / G 相应达到最大值且与 I 同相
0 S P S
退出
2.2并联谐振回路
二、并联谐振特性：
ISRp L I ，V 与I 同相。 B 0时， V S S CR 谐振条件:
L C
一般Q为几十到几百，因此信号源的电流不是很大，而支路 内的电流却是很大。
谐振时电感支路或者电容支路的电流幅值为外加电流源IS的 QP倍。因此，并联谐振又称为电流谐振。
退出
C R p L L 1 1 j C I CP V j C V I Q jQ P IS 0 p 0 p S P jp C P C IQ L I LP V0 R jP L V0 jP L S P P jQ P IS jP L QP Rp
Vs V Vs Q s R r
因此串联谐振时，电感L和电容C上的电压达到最大值且为 输入信号电压的Q倍，故串联谐振也称为电压谐振。因此，必须 预先注意回路元件的耐压问题。
退出
2.1 谐振回路
结论： ①电感线圈与电容器两端的电压模值相等，且等于外加电压 的Q倍。 ②Q值一般可以达到几十或者几百，故电容或者电感两端的 电压可以是信号电压的几十或者几百倍，称为电压谐振， 在实际应用的时候要加以注意。 ③串联谐振时电路中的电流或者电压可以绘成向量图。 注意：损耗电阻是包含在R中的，所以
代入上式：Z
1 R j L C
退出
2.2并联谐振回路
CR 1 为电导，B c 为电纳 L L
其中：G
谐振时的ห้องสมุดไป่ตู้抗特性：
并联谐振时，呈现纯电 阻， 且阻抗为最大值
p , 呈现感性 p , 呈现容性
因此回路谐振时：
f0 Q1> Q2
1
1
L
Q值不同即损耗R不同时，对曲线有很大影响， Q值大曲线尖锐，选择性好，Q值小曲线钝， 通带宽。
退出
1 C R
1 1 j
2.1 谐振回路
六、通频带
当回路外加电压的幅值不变时，改变频率，回路电流I下 1 降到Io 的 2 时所对应的频率范围称为谐振回路的通频带 用B表示， B 2 0.7 2 1或B 2f 0.7 f 2 f1
电路R上消耗的平均功率为：
P
1 2 RI om 2
Q 2
回路储能 每周耗能
退出
2.1 谐振回路
九、信号源内阻及负载对串联谐振回路的影响
通常把没有接入信号源内阻和负载电阻时回路本身的Q值叫做无 载Q（空载Q值） o L Q Qo 如式
R
把接入信号源内阻和负载电阻的Q值叫做有载Q值，用QL表示： QL
jQV V C0 S
退出
2.1 谐振回路
三、品质因数Q： 谐振时回路感抗值（或容抗值）与回路电阻R的比值称为回路 的品质因数，以Q表示，它表示回路损耗的大小。
1 1 L Q R o cR R R C
当谐振时：
o L
o L
oc
1
Lo v Co I o v
o
o
当 0即失谐不大时：
Q0
2
0
Q0
2 f f0
当谐振时： = 0。
退出
2.1 谐振回路 五、谐振曲线： 串联谐振回路中电流幅值与外加电动势 频率之间的关系曲线称为谐振曲线。 可用N(f)表示谐振曲线的函数。
N(f) Q1
Q2 f
s v 失谐处电流 I N( f ) 谐振点电流 Io R j (L s v R 1 ) C R 1 R j( L ) C
j z = R + jx = R+ j (L – c ) = z e 1 Z R 2 X 2 R 2 (L ) 2 C
arctg
令X 0
X arctg R
L R
1 C
X 0 L 0
1 0 0 C
当 0 时
v I I0 s R
I 1 1 2 Io 2 1 时
1
0 2 0 7 Q
当 而
N(f )
Q
2
I N(f)= I0 1
2
Q2 Q1 (f)
o
所以
也可用线频率f0表示，即 B= 2 f 0 .7
f0 Q
1' 1 2 '2
0 (f0) Q1> Q2
③外加电源只是提供回路电阻所消耗的能量，以维持回路的 等幅振荡，谐振时振荡器回路中的电流最大。
1 2 1 2 1 W P T I R T I R 每一周期时间内消耗在电阻上的能量为： R om om 2 2 fo
WC W L f L 1 o L 1 o Q 1 2 1 WR R 2 R 2 RI om 2 fo 1 2 LI om 2
其中R为回路本身的损耗，RS为信号源内阻，RL为负载
L Rs + – Vs R C RL
0 L R RS R L
可见Q L Q Q L为有载时的品质因数 Q为空载时的品质因数
结论：串联谐振回路通常适用于信号源内阻Rs很小 （恒压源）和负载电阻RL也不大的情况。
退出
2.2并联谐振回路
概述： 对于信号源内阻和负载比较大的情 况，宜采用并联谐振回路。 结构：电感线圈、电容C、外加 信号源相互并联的振荡回路。 Is 如图所示：其中由于外加信号源内 阻很大，为了分析方便采用恒流源。
Vcom I com R 2 2 L2 Vsm R R 2 2 L2 Vsm 1 Q 2
o
超前 V I 0 的角度小于 90 故： L0
退出
2.1 谐振回路 四、广义失谐系数： 广义失谐是表示回路失谐大小的量， 其定义为：
1 L o L o ( 失谐时的抗) X C Qo R R R o
Wc 1 2 I om L cos 2 wt 2
Q
1 R
L C
1 1 1 1 L 2 1 2 2 2 CVcm CQ 2Vsm C 2 Vsm LI 0 m 2 2 2 R C 2
1 2 I om L 2 1 1 2 WL Li 2 LI om sin 2 t 2 2 1 2 WLm I om L 2 1 2 1 2 1 2 W WL WC LI om sin 2 t LI om cos 2 t LI om 2 2 2 Wcm
达到最大
1 LC 1 f0 2 LC
退出
2.1串联谐振回路
x 容性 感性
z
L
x=L– 1 C
z
2 O
0
O
0
– 1 C
R
0
2
当 0时节|z| >R， 1 > =0，x > 0呈感性，电流滞后电压，i < 0 x L c < 0，x<0呈容性，电流超前电压，i > 0 = 0 |z| = R x = 0达到串联谐振。 当回路谐振时的感抗或容抗，称之为特性阻抗。用表示
退出
2.1 谐振回路 七、相频特性曲线：
回路电流的相角随频率变化的曲线。
I 1 1 I o 1 j 1 j x R
o
Q1 2 Q2
回路电流的相频特性曲线为
0
2
o x 2 因为 arctg R arctgQ arctgQ arctg o o
p L R 1 p L R p RC p 1 R2 2 LC L
即谐振电阻为感抗或者容抗的Qp倍，当Qp很大时，这个 电阻值是很大的。
退出
2.2并联谐振回路
p L 三、品质因数： 定义： R
Qp p L R 1 L 1 LC R R
1 R Q p为并联振荡回路品质因 数 p C
s v sm e jo v j ( ) j I I e I e m m j z ze
所以回路电流的相角为阻抗幅角的负值， = –回路电 流的相角是与外加电压相比较而言的。若超前，则 > 0 若滞后，则 < 0。 Q值不同时，相频特性曲线的陡峭 程度不同，Q1>Q2