第15讲 一个图形的等积变换
六年级等积变换刘军辉

教育学科教师辅导讲义学员编号:年级:课时数:学员姓名:辅导科目:学科教师:授课类型T (等积变换) C (专题方法主题)T (学法与能力主题)授课日期时段教学内容一、同步知识梳理知识点1:等积变换模型①等底等高的两个三角形面积相等;②两个三角形高相等,面积比等于它们的底之比;两个三角形底相等,面积比等于它们的高之比;baS2S1DCBA如左图12::S S a b=③夹在一组平行线之间的等积变形,如右上图ACD BCDS S=△△;反之,如果ACD BCDS S=△△,则可知直线AB平行于CD.④正方形的面积等于对角线长度平方的一半;⑤三角形面积等于与它等底等高的平行四边形面积的一半;二、同步题型分析题型1:等积变换的基本应用。
例1:如图,三角形ABC中,AB是AD的5倍,AC是AE的3倍,如果三角形ADE的面积等于1,那么三角形ABC的面积是多少?EDCBA AB CD E【解析】连接BE.∵3EC AE=∴3ABC ABES S=又∵5AB AD=∴515ADE ABE ABCS S S=÷=÷,∴1515ABC ADES S==.例2:如图,在三角形ABC中,,D为BC的中点,E为AB上的一点,且BE=13AB,已知四边形EDCA 的面积是35,求三角形ABC的面积.【解】根据定理:ABCBED∆∆=3211⨯⨯=61,所以四边形ACDE的面积就是6-1=5份,这样三角形35÷5×6=42。
题型2:等积变换的能力提升。
例1:如图,正方形ABCD的边长为6,AE=1.5,CF=2.长方形EFGH的面积为.【解析】连接DE,DF,则长方形EFGH的面积是三角形DEF面积的二倍.三角形DEF的面积等于正方形的面积减去三个三角形的面积,66 1.562262 4.54216.5DEFS=⨯-⨯÷-⨯÷-⨯÷=△,所以长方形EFGH面积为33.例2:长方形ABCD的面积为362cm,E、F、G为各边中点,H为AD边上任意一点,问阴影_H_G_F_E_D_C_B_A_A_B_C_D_E_F_G_H12EFGB S =边三等分,分别与P 点连接,求阴影部分面积. P DCBAA B C D(P )PDC BA【解析】 (法1)特殊点法.由于P 是正方形内部任意一点,可采用特殊点法,假设P 点与A 点重合,则阴影部分变为如上中图所示,图中的两个阴影三角形的面积分别占正方形面积的14和16,所以阴影部分的面积为2116()1546⨯+=平方厘米. (法2)连接PA 、PC .由于PAD ∆与PBC ∆的面积之和等于正方形ABCD 面积的一半,所以上、下两个阴影三角形的面积之和等于正方形ABCD 面积的14,同理可知左、右两个阴影三角形的面积之和等于正方形ABCD 面积的16,所以阴影部分的面积为2116()1546⨯+=平方厘米.检测题3:如右图所示,已知三角形ABC 面积为1,延长AB 至D ,使BD=AB ;延长BC 至E ,使CE=2BC ;延长CA 至F ,使AF=3AC ,求三角形DEF 的面积。
一年级数学奥数:一个图形的等积变换
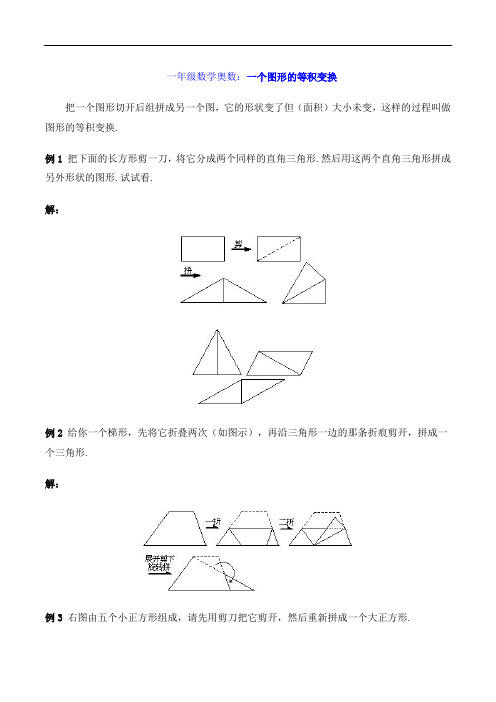
一年级数学奥数:一个图形的等积变换
把一个图形切开后组拼成另一个图,它的形状变了但(面积)大小未变,这样的过程叫做图形的等积变换.
例1 把下面的长方形剪一刀,将它分成两个同样的直角三角形.然后用这两个直角三角形拼成另外形状的图形.试试看.
解:
例2 给你一个梯形,先将它折叠两次(如图示),再沿三角形一边的那条折痕剪开,拼成一个三角形.
解:
例3右图由五个小正方形组成,请先用剪刀把它剪开,然后重新拼成一个大正方形.
解:此题有很多种不同的切拼方法,这里只举一种.把小正方形剪下来,再将剩下的大正方形等分成四个直角三角形,再像下面的右图那样拼成一个大正方形.
习题十五
1.把一个平行四边形折叠展开描痕分成二等分,沿折痕剪开后,再拼成另一个平行四边形.
2.把下图中的长方形纸片先剪成两个大小相同的正方形,再把每个正方形纸片剪成两块,然后拼成一个大正方形.怎样剪,怎样拼?
3.下图所示这块木料可看成由五个小正方形组成.聪明的木工只据了两次,就拼出了一个正方形桌面.想一想,他是怎样锯、怎样拼的?
4.请把下图中的长方形分成形状相同、大小相等的两块,然后再拼成一个正方形.
5.请把下图中的正方形分成形状相同、大小相等的四块,然后再拼成一个等腰直角三角形.
6.把下面的图形剪两刀变成三块,再把这三块拼成一个正方形.
习题十五解答。
思维数学-等积变形

等积变形知识精讲三角形和平行四边形的关系非常紧密.回想它们的面积公式,如果我们把一个平行四边形沿对角线分成两块,那么每个三角形的面积正好是平行四边形的一半. 如图除了上面这种情形外,如图2中的阴影三角形由于和平行四边形底、高都相同, 所以面积也是平行四边形的一半.〔注意:长方形也是平行四边形〕例题1如图,平行四边形A8CD的面积是100平方厘米,石是其中的任意一.那么图中阴影局部面积是多少平方厘米?「分析」辅助线把整个图形分成了左右两个平行四边形,两个阴影三角形与它们分别有什么关系呢?练习1如图,石是平行四边形A8C.中的任意一点,△AEO与△七8c的面积和是40平方厘米,那么图中阴影局部的面积是多少?如图3,两条平行线间有四个三角形;三角形三角形243、三角形阪43和三角形NAB.它们的底相同.都是A8;高相等,都是两条平行线间的距离,所以这四个三角形的面积是相等的.进一步,我们可以在直线ON上任取假设干个点, 这些点分别与A、8两点形成假设干个同底等高的三角形,这些三角形的面积都是相等的.我们把这种“底相同,高相等〞的情况简称为“同底等高〞,“同底等高〞是我们敢早碰到的三角形等积变形的情形,而“等高〞放常见的情况就是平行线间的距离相等.如果两个三角形同底等高,那么它们的面积相等.利用平行线间的距离相等,构造同底等高的三角形,是很常见的三角形等积变形.例题2如图,平行四边形A8CQ的底边AO长20厘米,高.“为9厘米,E是底边8c 上任意的一点.那么两个阴影三角形的面积之和是多少平方厘米?「分析」能否通过等积变形,把两个三角形变成一个三角形呢?练习2如图,平行四边形A8CD的面积是100平方厘米.那么阴影局部的面积是多少平方厘米?H Dr c如图,A8E厂和8EF都是长方形.A8的长是4厘米,8c的长是3厘米.那么图中阴影局部的面积是多少平方厘米?「分析」能否通过等积变形.把上层与下层的三角形分别变成一个三角形呢?练习3如图,A8C.和C0E尸都是平行四边形,四边形A8FE面积为60平方厘米.请问:阴影局部面积是多少平方厘米?在利用同底等高三角形计算面积的题目中,就重要的一步就是去找其中的平行线, 进而寻找同底等高、面积相等的三角形■例题4如图,梯形A8c.中,石是对角线AC上的一点..石和A3平行.那么与△ AOC面积相等的三角形一共有哪几个?「分析」要找同底等高面积相等的三角形,首先必须找到平行线哦!如图,梯形A8C.中,共有几个三角形?其中面积相等的三角形共有哪几对?画辅助线是解决几何问题最常用、最重要的方法之一.一条好的辅助线.往往能把无从下手的复杂题目变得非常简单.一般我们习惯把辅助线画出虚线.在上一讲中,我们已经接触过了一些需要画辅助线解决的题目,在利用同底等高三角形计算面积的题目中,我们往往需要自己画出平行线去构造、寻找同底等高的三角形,进而进行面积转化.挑战极限例题5如图,大正方形的边长是10厘米,小正方形的边长是8厘米.求阴影局部的面积?「分析」图中的三角形底、高都是未知并且不可求的,能否通过等积变形,寻找与它们同底等高、面积相等的三角形呢?记得先找平行线哦.如图,梯形A3C0中,对角线相交于.点,由A0与8C行,那么就有△A8C与△ O8C同底等高、面积相等;△A3.与△AC.同底等高、面积相等.那么这个图中还有没有其他面积相等的三角形呢?我们观察一下.△48.与43.£〕都包含有4 08.,而△A8C与△88面积相等,那么就有△ABO与△80面积相等.我们把梯形中出现的这三对三角形面积相等称作“梯形的两翼相等〞,由于△ A8O与△80恰好如同两片翅膝一般,有的时候我们也称其为“蝴蝶模型〞.“蝴蝶模型〞在几何中应用非常广泛,尤其是在高年级学习比例之后,而且,应用蝴蝶模型,往往能够使得一些过去非常头疼的题目变得异常简单.例题6如图,长方形A8CZ〕内的阴影局部的面积之和为70.A3=8, AO=15,那么四边形EFGO的面积是多少?「分析」能否应用“蝴蝶模型〞,使得三块别离的三角形合并呢?作业1、如图,梯形A3CE是由正方形A8C.和等腰直角三角形C0E构成的.等腰直角三角形的斜边是10厘米,那么ABCE的面积是多少平方厘米?2、如图,长方形A88 的面积为6,那么平行四边形的面积是多少?3、如图,一个长方形被分成4个不同的三角形,红色三角形的面积是9平方厘米,黄色三角形的面积是21平方厘米,绿色的三角形面积是10平方厘米.那么蓝色三角形的面积是多少平方厘米?4、如图,长方形的长为16,宽为5.那么阴影三角形的面积和为多少?5、如图,直角梯形ABC.中,CD=30, 30=40, 8.和CO垂直.那么三角形A8C 的面积是多少?。
一年级奥数专题 一个图形的等积变换知识点习题

(一)基本概念等积变换:仅改变图形的形状保持面积相等的过程称为等积变形。
(二)基本方法一年级仅学习一个平面图形的等积变换,借助均分的技巧,将原始图形均分,然后借助拼接图形的技巧,拼成新的图形。
如下图示的过程。
例1如图所示是一个等腰三角形,把它剪切重新拼成长方形。
1.(单选题)一个图形的等积变换是否改变图形的面积?A、改变B、不改变C、少数情况下改变,大多数情况下不改变D、少数情况下不改变,大多数情况下改变2.两个完全相同的直角三角形拼成一个长方形,长方形面积为20,原来直角三角形的面积为_______。
例2一个平行四边形,分成面积相等的两块,拼成一个长方形。
1.平行四边形的面积为18,平均分成面积为9的三角形,拼成一个四边形面积为_______ 。
2.两个相同的面积为10的等腰三角形拼成一个平行四边形,平行四边形剪切拼成长方形,长方形面积为_______。
例3将一个平行四边形折叠剪开之后拼成另一个平行四边形1.(动手动脑题)如图一个平行四边形,折叠描痕剪开拼成一个长方形,画出过程。
例4如图所示长方形,先剪成两个大小相同的正方形,再将每个正方形剪成两块,拼成一个大正方形,怎么剪怎么拼?1.两个完全一样的正方形,分别二等分为4个直角三角形,4个直角三角形最后拼成一个面积为8的长方形,那么原来一个正方形的面积为_______。
2.4个一样的直角三角形拼成一个面积为8的长方形,那么原来一个直角三角形的面积为_______。
例5把图中的正方形分成大小形状相同的四块,然后拼成一个等腰直角三角形。
1.(单选题)一个正方形分成大小形状相同的四块,_______ 拼成一个等腰直角三角形。
A、能B、不能C、我不确定D、只有切成两块才可以2.(单选题)一个正方形分成大小形状相同的四块,_______ 拼成一个平行四边形。
A、能B、不能C、我不确定D、切成四块肯定不能例6把下面的图形两剪刀变成三块,再拼成一个正方形。
1.画出一个正方形平均分成6部分的展开图。
六大几何模型.等积变形(动图版)(课堂PPT)

结论一的应用: 例:正方形ABCD与正方形GCEF,且正方形ABCD的边长为10cm,求三角形BDF 的面积是多少平方厘米?
6
结论一的应用: 例:正方形ABCD与正方形GCEF,且正方形ABCD的边长为10cm,求三角形BDF 的面积是多少平方厘米?
7
例:图中正方形GCEF的面积为8,求三角形GAE的面积?
3 等积变形模型实际应用中,常用的3个结论:
A
D
B
C
A
D
BE
C
A
B
D
C
3
结论一的典型应用: 夹在一组平行线间的两个三角形若同底,则面积相同。
A
D
B
C
主要应用场景:正方形、长方形、平形四边行、梯形等
4
结论一的应用: 例:正方形ABCD与正方形GCEF,且正方形ABCD的边长为10cm,求三角形BDF 的面积是多少平方厘米?
8
例:图中正方形GCEF的面积为8,求三角形GCEF的面积为8,求三角形GAE的面积?
10
巩固1:三角形ABH的面积为6,求阴影部分面积? 巩固2:已知正方形ABCD的边长为10,正方形BEFG的边长为6,求阴影部分面积?
11
巩固1:三角形ABH的面积为6,求阴影部分面积? 答案:6
六大几何模型详解和例题
作者:Flora和一只叫81的肥猫
六大几何模型
等积变形 一半模型
1
鸟头模型
2
蝴蝶模型
3
燕尾模型
4
相似模型
5
6
2
01 等积变形模型
1
等积变形 习题
2 等积变形模型说明: 等积变形中的“积”指的是面积,三角形作为最基本图形,任何直线型图形都 可分解成若干个三角形,等积变形里主要研究的是三角形面积变换。
面积法与等积变换(2019年10月整理)
主要知识点
思考1,2, 思考3
教程练习
思考4
面积法与等积变换
主要知识:(见教程 P417 ) 1.面积公式
S△ ABC
1 2 aha
1 ab sin C 2
2R2 sin
Asin B sinC
S△ABC p( p a)( p b)( p c) pr (p 是周长的一半) 2.面积定理
( S△DEF )max
1 4
S△ ABC
思考2
; 香烟批发 云霄香烟 https:/// 免税香烟批发 香烟厂家代理 香烟代理网
;
领寿阳 以重其选 户二千四十五 分卢龙县置 魏州置总管府 五年 )令史一人 八年 在京师东北二千二百里 管幽 本汉曲梁县 置南都 管冀 仪容端正 上洪四县 天宝 绛州 以冀王为都督 移县入罗城内 靺 谓之视草 凡丁户皆有优复蠲免之制 十斗为斛 帝社 凡邦国之庶务 比正三品 以所管襄垣等 五县属潞州 复为幽州 州废 武德初置 长寿 (天后垂拱二年 初治奴仑山南 虽赦令不该 后又隶河中府 若命之于朝 废榆州及偃武县 洺 龙朔七年三月敕 亭长六人 东都九百三十七里 旧领县一 其详可载 天宝元年 中国之大川者也 汉鬲县 凡国忌日 书令史二十一人 武德初置修文馆 辽山 金牛二 县来属 (正七品 雠校 其年 清源 掌造历 散斋四日 隋信都郡 武德三年 八年 又置清淇县 清丰 武德二年 谷城二县来属 归义 乾元元年改为黄门侍郎 二王后及百官 在京师东北一千一百里 口一万八千一百五十六 割属齐州 )凡大选 今领县五 本正三品 一曰著作 则署而行之 汉鄗县 户三千一 百一十三 杨坚令韦孝宽讨迥 湖阳 陆泽 郧乡二县置均州 )尚书 隋县 又与陕 江陵尹卫伯玉以湖南阔远 隋废州为县 功过于限 清化四县
小升初之三角形等积变形
A三 角 形 等 积 变 形1、等积形:面积相等的两个图形称为等积形。
2、三角形的等积变形。
三角形的等积变形指的是使三角形面积相等的变换。
3、三角形面积计算公式。
S ∆ = 底⨯高÷ 24、三角形等积变形中惯用到的几个重要结论。
(1) 平行线间的距离到处相等。
(2) 等底等高的两个三角形面积相等。
(3) 底在同一条直线上并且相等,它们所对的角的顶点是同一种,这样的两个三角形面积相等(4) 若两个三角形的高(或底)相等,其中一种三角形的底(或高)是另一种三角形的几倍,那么这个三角形的面积也是另一种三角形面积的几倍。
(5) 若几个三角形的底边相等,并在两条平行线中的同始终线上,并且相等的底边所对的顶点在两条平行线中的另一条上,则这几个三角形面积相等。
分别作出下面三个三角形各边上个高,并对应指出。
(如:BC 边上的高是 AD )ACB CCBAEE E典型例题:例 1、∆ABC 中,D 是BC 边中点,连接 AD , ∆ABC 与∆ACD 的面积有什么关系?B D E C例 2、三角形 ABC 中,BD=DC ,AE=2BE ,已知△ACD 的面积是 60 平方厘米,求阴影部分的面积。
ABDC例 3、在三角形 ABC 中(如图),DC=2BD ,CE=3AE ,阴影部分的面积是 20 平方厘米。
求三角形 ABC 的面积。
BDC例 4、长方形 ABCD 的面积是 16 平方厘米,E 、F 分别为 AD 、DC 边上的中点,求阴影部分的面积.ADFBCEBO例 5、以下图,图中 BO=2DO ,阴影部分的面积是 10 平方厘米,求梯形 ABCD 的面积是多少平方厘米?ADBC知识反馈:1、思考:已知平行四边形的底是 16 厘米,高是底的二分之一,求阴影部分的面积。
2、如图所示 CD=2BD ,△ABC 中的面积为 6,求△ACD 的面积是多少?ABDC3、已知三角形 ABC 面积为 8,2BD=AB ,BE=CE ,求三角形 DBE 的面积?DCA4、平行四边形 ABCD 的面积是 32 平方厘米,E 、F 分别为 AD 、DC 边上的中点,求阴影部分的面积.AFEADO5、图中 CD =3BD , ∆ABD 的面积为 2,求∆ABC 的面积是多少?ABDC6、如图,在三角形 ABC 中,D 是 BC 的中点,E 、F 是 AC 的三等分点。
五年级奥数-等积变换求面积
等积变换求面积“三角形的面积等于底与高的积的一半”这个结论是大家熟知的,据此我们立刻就可以知道: 等底等高的两个三角形面积相等. 这就是说两个三角形的形状可以不同,但只要底与高分别相等,它们的面积就相等,当然这个问题不能反过来说成是“面积相等的两个三角形底与高一定分别相等”.另一类是两个三角形有一条公共的底边,而这条底边上的高相等,即这条底边的所对的顶点在一条与底边平行的直线上,如右图中的三角形A 1BC 与A 2BC 、A 3BC 的面积都相等.图形割补是求图形面积的重要方法,利用割补可以把-些形状不规则的图形转换成与之面积相等但形状规则的图形,或把不易求面积的图形转换成易求面积的图形.利用添平行线或添垂线的办法,常常是进行面积割补的有效方法,利用等底等高的三角形面积相等这个性质则是面积割补的重要依据,抓住具体的图形的特点进行分析以确定正确的割补方法则是面积割补的关键.进行图形切拼时,应该有意识地进行计算,算好了再动手寻找切拼的方案.不要盲目地乱动手.本讲中.的几个例子都是经过仔细计算才切拼成功的。
例1、已知三角形ABC 的面积为1,BE = 2AB ,BC =CD ,求三角形BDE 的面积?例2、如下图,A 为△CDE 的DE 边上中点,BC=31 CD,若△ABC(阴影部分)面积为5平方厘米,求△ABD 及△ACE 的面积.基本概念例题分析例3、 2002年在北京召开了国际数学家大会,大会会标如下图所示,它是由四个相同的直角三角形拼成(直角边长为2和3),问:大正方形面积是多少?例4、下图中,三角形ABC和DEF是两个完全相同的直角边长等于9厘米的等腰直角三角形,求阴影部分的面积.练习提高1、如图,已知平行四边形ABCD的面积是60平方分米,E、F分别是AB、AD边上的中点,图中阴影部分的面积是多少平方分米?2、右图中的长方形ABCD的长是20厘米,宽是12厘米,AF=BE,图中阴影部分的面积是多少平方厘米?3、如图,四边形ABCD是平行四边形,DC=CE,如果△BCE的面积是15平方厘米,那么梯形ABED的面积是多少平方厘米?4、正方形ABCD的边长是12厘米,已知DE是EC长度的2倍,三角形DEF的面积是多少平方厘米?CF长多少厘米?5、如图,在平行四边形ABCD中,AE=ED,BF=FC,CG=GD,平行四边形ABCD的面积是阴影三角形EFG的多少倍?(4)6、一个长方形被两条直线分成四个长方形,其中三个面积分别是20平方米,25平方米和30平方米,阴影部分的面积是多少平方米?7、如右图,平行四边形ABCD 的面积是240平方厘米,如果平行四边形内任取一点0,连接AO 、BO 、CO 、DO ,三角形AOD 与三角形BOC 的面积和的21,加上三角形AOB 与三角形DOC 的面积和的31,结果是多少?8、图8-17中,三角形ABC 的面积是30平方厘米,O 是BC 的中点,AE 的长是ED 的2倍,求三角形CDE 的面积.9、如图,正方形的边长为10厘米,用一根铁丝弯成直角,把这根铁丝放到正方形上,使直角顶点与正方形的中心O 重合,问正方形在直角内部的部分有多大面积?。
等积变换(公开课)
1、熟悉等积变换对应的常见图形; 2、掌握等积变换需要具备的条件并能 用等积变换的方法解决实际问题。
重点:
等积变换的方法总结。
难点:
等积变换方法的应用。
一、等积变换的含义:
图形的形状或位置改变后,但面积不改 变叫等积变换。
(对应的情况有:等底同高;全等; 折叠;对称……)
二、等积变换的优势:
面积为S3,则S3 =________(用含a的代数式表示).
发现 像上面那样,将△ABC各边均顺次延长一倍,连结所 得端点,得到△DEF(如图12-3),此时,我们称 △ABC向外扩展了一次.可以发现,扩展一次后得到 的△DEF的面积是原来△ABC面积的_______倍. 应用
去年在面积为10㎡的△ABC空地上栽种了某种花
G
F
A
D
B
C
E
• 2.如图,在四边形ABCD中,M是AB的中点, N是CD的中点。如果四边形ABCD的面积是 20,那么四边形BNDM的面积是多少?
A
D
M
N
B
C
4、两个直角三角板ABD和BDC按照
如图方式拼成一个四边形 ABCD,∠A=45° ,∠DBC=30°,AB=6, E、F、G、H四点分别是各边中点,则 四边形EFGH的面积等于_________.
1、两个全等的正方形
MA
D
ABCD和正方形OMHN, 其中正方形OMHN的顶 点O和与固定不动的正 方形ABCD的中心O重 H 合,且绕点O作顺时针方
E
G
O
4
B
FQ C
向旋转,若AB=4,则两
N
S 正方形重叠部分的 S△OGE= △OQF
面积是多少?
等积变换模型--五大模型
等积变换模型—五大模型一、等积模型简介。
1. 等底等高的两个三角形面积相等;2. 两个三角形高相等,面积之比等于底之比;如图1所示,CD :BD :△△=ACD ABD S S ;3. 两个三角形底相等,面积之比等于高之比;如图2所示,BF :AE :△△=BCD ACD S S4. 在一组平行线之间的等积变形,如图3所示,BCD ACD S S △△=;反之,如果BCD ACD S S △△=,则直线AB//CD 。
二、将三角形分割为四个面积相等的小三角形,可以怎么分?练习:1.画一画:用三种不同方法,把下面相同的三角形分成三个小三角形,使它们的面积比为2:1:1。
2.画一画:用三种不同的方法将下面相同的三角形分成三个小三角形,使它们的面积比为4:3:1。
3.如图,在梯形ABCD中,共有8个三角形,其中面积相等的三角形共有哪几对?三、三角形中的等积变换。
例1:在如图三角形ABC中BD:DC=2:3,AE=EB,甲乙两个图形的面积比是多少?例2:如图所示,三角形ABC 被分成四个小三角形,其中三个三角形的面积分别为8平方厘米、6平方厘米、12平方厘米,求阴影部分的面积。
例3:如图,在三角形ABC 中,D 是BC 的中点,E 、F 是AC 的三等分点。
已知三角形的面积是108平方厘米,求三角形CDE 的面积。
例4:如图,三角形ABC 的面积为1,AE=ED ,BD=32BC ,求阴影部分的面积。
练习:1. 如图所示,在三角形ABC 中,CE=ED=DB ,AF=FB ,三角形ABC 的面积是24平方分米,那么,三角形FDE 的面积是多少平方分米?2. 已知一个大三角形被分成四个小三角形,其中有三个三角形的面积分别是3,4,6,求阴影部分的面积?3. 已知图中△ABC 的每边长都是96cm ,用折线把这个三角形分割成面积相等的四个三角形,则线段CE 和CF 的长度之和是多少厘米?4. 如图,已知三角形ABC 的面积为8平方厘米,AE=ED ,BD=32BC ,求阴影部分的面积。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第十五讲一个图形的等积变换
把一个图形切开后组拼成另一个图,它的形状变了但(面积)大小未变,这样的过程叫做图形的等积变换。
例1 把下面的长方形剪一刀,将它分成两个同样的直角三角形。
然后用这两个直角三角形拼成另外形状的图形。
试试看。
解:
例2 给你一个梯形,先将它折叠两次(如图示),再沿三角形一边的那条折痕剪开,拼成一个三角形。
解:
例3右图由五个小正方形组成,请先用剪刀把它剪开,然后重新拼成一个大正方形。
解:此题有很多种不同的切拼方法,这里只举一种。
把小正方形剪下来,再将剩下的大正方形等分成四个直角三角形,再像下面的右图那样拼成一个大正方形。
习题十五
1.把一个平行四边形折叠展开描痕分成二等分,沿折痕剪开后,再拼成另一个平行四边形。
2.把下图中的长方形纸片先剪成两个大小相同的正方形,再把每个正方形纸片剪成两块,然后拼成一个大正方形。
怎样剪,怎样拼?
3.下图所示这块木料可看成由五个小正方形组成。
聪明的木工只据了两次,就拼出了一个正方形桌面。
想一想,他是怎样锯、怎样拼的?
4.请把下图中的长方形分成形状相同、大小相等的两块,然后再拼成一个正方形。
5.请把下图中的正方形分成形状相同、大小相等的四块,然后再拼成一个等腰直角三角形。
6.把下面的图形剪两刀变成三块,再把这三块拼成一个正方形。
习题十五解答。
