基于最小势能原理的变截面压杆临界压力的计算方法
测量压杆临界压力的理论与实验

摘要提出了新的力矩分配思想,将角位移和线位移综合考 虑,使力矩分配法能直接应用于有侧移结构,且在计算内力 的同时还能计算结构的位移,使力矩分配法具有多功能.实 例计算表明,该方法正确、简单,有利用价值. 关键词多功能力矩分配法,结构内力,结构位移,有侧移 结构,无侧移结构
当结构中刚结点较多时,宜采用位移法.力矩分配法是 位移法的一种近似计算,原理易懂,使用方便,但美中不足的 是以前的力矩分配法不能直接用于有侧移的结构,当结构有 侧移时只能通过采取加连杆的方法,将力矩分配法和位移法
2005—12—30收到第1稿,2006--09-30收到修改稿
万方数据 1)E-mail:wxwwxw2002@sohu.corn
联合起来进行求解,但该方法比较繁琐,用起来不太方便; 对于比较特殊的结构,可用无剪力分配法求解,但此法难于 理解,且条件苛刻,使应用大受限制.此外以前的力矩分配法 只能计算结构的内力,而不能计算结构的位移.本文提出了 新的力矩分配思想,将角位移和线位移综合考虑,使力矩分 配法能直接用于有侧移的结构,同时还能计算结构的位移, 使其应用范围更加广泛.
UA 2 UB
式(4)也可以表述为
—d—PFAC一=u×r~AG dt
这说明表征刚体的连体矢量对时间的一阶变化率的泊松公式 具有一般性.以式(4)为基础,还可容易说明微小转角为矢 量这一概念以及方便地导出角速度的合成公式.
这种讲授方法,便于组织从一般到特殊的教学体系,符 合教改的要求,不仅减少了教学学时,而且使学生对一般运动 刚体角速度概念的理解更加深刻,取得了更好的教学效果.
74
力 学与 实践
2007年第29卷
刚体上的任意一点P,有
Up=t,A+uA×”AP, t,B=t,A+uA×PAB
压杆临界力

压杆临界力压杆临界力是指压杆在受力作用下能够保持平衡的最大力量。
压杆是一种直杆,两端固定,用于承受压力或压缩力。
压杆临界力的计算是力学中的重要问题,它与材料的强度、结构的稳定性等密切相关。
我们需要明确压杆的受力情况。
压杆在受力作用下,会产生两种力,分别是压缩力和弯曲力。
压缩力是指压杆两端产生的压力,而弯曲力是指压杆在受力作用下发生的弯曲变形所产生的力。
在压杆的受力分析中,我们主要关注压缩力对压杆的影响。
压杆临界力的计算涉及到材料的强度。
材料的强度是指材料能够承受的最大应力。
在计算压杆临界力时,我们需要知道压杆的长度、横截面积和材料的强度。
当所施加的力小于或等于压杆临界力时,压杆可以保持平衡;而当所施加的力大于压杆临界力时,压杆将发生破坏。
压杆临界力的计算公式为:F = σA其中,F表示压杆的临界力,σ表示材料的强度,A表示压杆的横截面积。
由此可见,压杆临界力与材料的强度和压杆的横截面积密切相关。
在实际应用中,我们需要根据具体情况来计算压杆的临界力。
首先,我们需要测量压杆的长度和横截面积。
然后,我们需要确定材料的强度。
根据上述公式,我们可以计算出压杆的临界力。
如果所施加的力小于临界力,说明压杆可以保持平衡;而如果所施加的力大于临界力,说明压杆将发生破坏。
压杆临界力的计算对于设计和制造工程结构非常重要。
在实际应用中,我们需要根据结构的要求和材料的特性来确定压杆的尺寸和材料。
通过合理的设计和计算,可以确保压杆在受力作用下能够保持稳定,不发生破坏。
压杆临界力是指压杆在受力作用下能够保持平衡的最大力量。
它与压杆的长度、横截面积和材料的强度密切相关。
通过合理的设计和计算,可以确保压杆在受力作用下能够保持稳定,不发生破坏。
压杆临界力的计算对于设计和制造工程结构非常重要,它能够确保结构的安全性和稳定性。
因此,在工程实践中,我们需要重视压杆临界力的计算,以确保工程结构的质量和可靠性。
压杆的临界载荷

π 2 EI ( μl ) 2
F
F
F
F
F
μl=l
μl=0.5l
μl=0.7l μl=2l μl=l
F
F 两端固支
F 一端铰支 一端固定 μ=0.7 一端自由 一端固定 μ=2.0 二端不能转动 但可相对移动 μ=1.0
两端铰支
μ=1.0
μ=0.5
最后可以推得欧拉(Euler)公式:
式中 Pcr 一压杆的临界力;E 一压杆材料的弹性模量;I 一压杆横截面的最小惯 矩;l 一压杆的长度。依此式可计算两端铰支压杆的临界力。 杆端约束对临界力的影响
在工程实践中,压杆除两端铰支的约束形式外,还存在其他各种不同的端 部约束情况,这些压杆的临界力计算公式,可以仿照上述方法,由挠曲线近似 微分方程式及边界条件求得,也可利用挠曲线相似的特点将两端铰支压杆的结 果推广得到: Pcr =
10-2 压杆的临界载荷
细长压杆的临界载荷——欧拉公式
确定临界力可以从研究杆的微弯曲变形的挠曲线着手。对两端为铰支座的 细长杆,当它处于弯曲平衡的临界状态时,若杆内应力不超过材料的比例极 限,则压杆任一截面 m-n 处的弯曲变形与截面弯矩的关系仍为
其弯矩 M(x)是在轴向力 PHale Waihona Puke 作用下因有弯曲变形 y 而产生的,即
压杆临界压力的测定
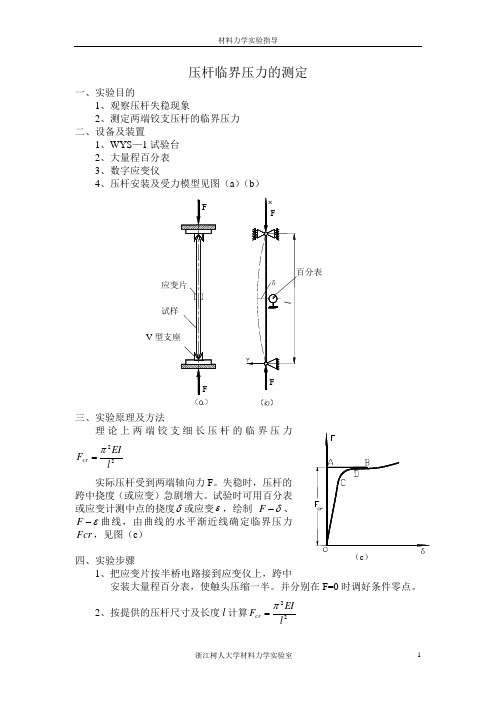
压杆临界压力的测定一、实验目的1、观察压杆失稳现象2、测定两端铰支压杆的临界压力二、设备及装置1、WYS —1试验台2、大量程百分表3、数字应变仪4、压杆安装及受力模型见图(a )(b )三、实验原理及方法理论上两端铰支细长压杆的临界压力22l EIF cr π=实际压杆受到两端轴向力F 。
失稳时,压杆的跨中挠度(或应变)急剧增大。
试验时可用百分表或应变计测中点的挠度δ或应变ε,绘制 δ-F 、ε-F 曲线,由曲线的水平渐近线确定临界压力Fcr ,见图(c )四、实验步骤1、把应变片按半桥电路接到应变仪上,跨中安装大量程百分表,使触头压缩一半。
并分别在F=0时调好条件零点。
2、按提供的压杆尺寸及长度l 计算22l EIF cr π=试样V3、取F的70%~80%按四~五级加载分别测出δ及εcr4、以后按小等级加载例如∆F=100N,50N,20N,10N甚至1 N加载,观察并记录δ、ε的变化。
当δ或ε出现明显变化而载荷几乎不变时停止试验。
5、作F-ε及F-δ曲线可求出实际测量值F'。
cr五、实验注意事项及实验报告。
1、加载时,应变仪读数不可超过3000με,以防产生塑性变形。
2、用坐标纸作F-ε及F-δ曲线,求出F'。
并与用欧拉公式计算结果作cr比较。
3、若在V型支架中加上橡皮则F'将提高或降低?cr4、若两端V型支座底线不在压杆的同一纵向对称平面内,实测临界压力是提高还是降低?。
能量法求压杆的临界载荷-概述说明以及解释

能量法求压杆的临界载荷-概述说明以及解释1.引言1.1 概述在工程结构设计中,压杆是一种常见的承载结构,其在受力作用下可能会达到临界载荷而发生屈曲破坏。
为了有效地预测压杆的临界载荷,本文将采用能量法来进行求解。
能量法是一种基于能量守恒原理的力学分析方法,通过建立适当的应变能和外力做功的关系,可以求解出结构的稳定性问题。
本文将针对压杆的临界载荷进行能量法求解,并通过数学推导和实例分析,展示其在工程实践中的应用价值和意义。
通过本文的研究,读者将能够深入了解压杆临界载荷的求解方法,为工程结构设计提供理论支持和指导。
1.2 文章结构:本文将围绕能量法求压杆的临界载荷展开讨论。
首先在引言部分概述了本文的背景和意义,引出了文章的主要内容。
接下来在正文部分,将介绍能量法的基本原理及应用,然后详细讨论如何利用能量法求解压杆的临界载荷。
最后通过具体的应用与实例,展示了该方法在工程实践中的应用。
在结论部分,将对全文进行总结,展望未来可能的研究方向,并给出最终的结论。
整个文章结构清晰、逻辑性强,旨在为读者提供对能量法求解压杆临界载荷的全面理解与应用指导。
1.3 目的本文旨在探讨利用能量法求解压杆的临界载荷的方法。
通过引入能量法这一新的分析工具,我们可以更加深入地理解压杆在承受外载荷时的力学性质。
通过对压杆的临界载荷进行研究和求解,我们可以揭示压杆在受力状态下可能出现的失稳现象,从而为压杆结构设计和工程实践提供重要的参考依据。
同时,本文还将通过具体的应用与实例,验证能量法在解决压杆问题中的有效性和可行性,为读者提供实用的参考信息。
通过本文的深入分析,旨在推动工程领域对压杆问题的探讨和研究,在理论和实践上取得新的突破和进展。
2.正文2.1 能量法介绍能量法是一种通过考虑结构内部潜在能量的分布情况,来求解结构受力状态的方法。
在力学领域中,能量法经常被用来分析和计算结构的稳定性和承载能力。
在应用能量法求解压杆的临界载荷时,我们首先需要建立压杆的应变能和外部载荷对其做功的关系。
利用能量法求解变截面压杆的临界压力

班级:力学(1)班
姓名:喻光安
学号:1203040122
指导教师:黄志强
利用能量法求解变截面压杆的临界压力
摘要
目前计算变截面压杆的临界压力通常采用以下四种方法:最小截面的等截面法、静力分析法、能量法、有限单元法。本文主要采用能量法,根据结构的受力条件计算杆件的应变能增量和外力做的功,当二者相等时,即建立了杆件临界状态下的方程,由此解出的外力即为临界压力值。该方法简洁明了,在解决此类问题中可以广泛使用。
参考文献:
【1】徐芝纶.弹性力学.4版.北京:高等教育出版社,2006.
【2】同济大学数学系.高等数学.6版.高等教育出版社,2007.
若令上式中的 ,此时该阶梯杆件即变成了等截面杆件,可化简上式得到该杆件的临界压力为:
即总所周知的等截面杆的临界压力,从而表明了本文计算的正确性。
(三)、结论
利用能量法,可以对各种约束条件下的变截面杆进行临界压力的求解。计算过程简单明了,可以在工程中得到广泛的应用,但读者也可以看到,此种方法会遇到复杂的积分运算,即使杆件不等截面的段数较少,计算的工作量仍较大,建议采用该方法时配合MATLAB等相关计算软件辅助运算。
(1)
所以得到的临界条件是:在弹性体系对其平衡位置的微小偏移中,体系的变形能增量与外力所做的功相等,根据这一条件即可求出临界载荷,这种方法称为 。
对于杆件的轴线由直线变为曲线后,力作用点竖向位移λ应为:
将上式中的 展开为级数, :
上式代入λ中得: ,而外力所做的功为:
变截面压杆因弯曲而增加的变形能为: ,对于压杆一维问题,取应变能增量:
关键词:能量法;变截面压杆;临界压力;
正文:
(1)、理论分析
怎样推导压杆的临界力和临界应力公式

06、基本知识 怎样推导压杆的临界力和临界应力公式(供参考) 同学们学习下面内容后,一定要向老师回信(****************),说出你对本资料的看法(收获、不懂的地方、资料有错的地方),以便考核你的平时成绩和改进我的工作。
回信请注明班级和学号的后面三位数。
1* 问题的提出及其对策 (1)1.1 问题的提出及其对策 ........................................................................................................ 1 1.2 压杆稳定分析概述——与强度、刚度分析对比 ............................................................ 2 2压杆临界压力F cr 的计算公式 ................................................................................................. 3 2.1 压杆稳定的力学模型——弯曲平衡 ................................................................................ 3 2.2梁的平衡理论——梁的挠曲微分方程 ............................................................................. 4 2.3 按梁的平衡理论分析两端铰支的压杆临界压力 ............................................................ 6 2.4 按梁的平衡理论分析一端固定一端自由的压杆临界压力 ............................................ 8 2.5 按梁的平衡理论分析一端固定一端铰支的压杆临界压力 .......................................... 10 2.6 按梁的平衡理论分析两端固定的压杆临界压力 .......................................................... 14 2.7 将四种理想压杆模型的临界力公式及其推导分析图示的汇总 .. (18)1* 问题的提出及其对策1.1 问题的提出及其对策试计算长度为400mm ,宽度为10mm ,厚度为1mm 的钢锯条,在一端固定、一端铰支的情况下,许用的轴向压力。
压杆临界压力fcr的计算公式

压杆临界压力fcr的计算公式
压杆临界压力fcr的计算公式是根据美国工程学杂志《工程学杂志》(Engineering Science)上一篇2019年的文章所推导得出的。
该文章中,作者使用了一个称为“BRDF(辐射传输模型)”的模拟工具,来估算压杆周围的表面温度分布和表面辐射率。
压杆临界压力fcr的计算公式如下:
fcr = 0.85 * (0.5 * r3 - 0.25 * r22) + 0.3 * r1 其中,r1和r2分别是压杆两个接触点的距离,r3是压杆表面的面积。
这个公式可以理解为,压杆临界压力fcr是一个与压杆表面温度和接触点温度相关的非线性函数,它随着接触点温度的变化而变化。
当压杆表面温度接近临界温度时,压杆临界压力会逐渐增加,而当温度降下去时,压力会迅速下降。
这个公式可以用于设计和优化压杆的性质,以提高其安全性和效率。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
摘
要: 基 于弹性 力学的最小势能 变分原理 , 对一类具有连 续 变截 面的压 杆进行 了稳 定性 计算 , 得 到 了临界 压
力的表 达式 。该解能够适应可 变截 面形状和边界 约束 的压杆 , 计 算 简单方便 , 精 确度较 高 , 能够在 工程 q - 得 到较 为
广泛的应用。
关键 词 :变截 面压杆 ;稳定性 ;最小势能原理 ;临界压力
e 一 一
一
y 一
面压杆 进行 稳 定分 析 。
1 临界压力的最小势 能变分计 算
对变形体材料 , 基 于能 量 的变分 原理是 现代 计算
收稿 日 期: 2 o 1 2 一O 6 —1 4 作者 简介 : 谢
其 中 Y为 Y轴方向上的挠度 , P 为曲率半径 。 由式 ( 3 )可 以得 到压杆 横截 面上 的应 力 为 :
文 章 编 号 :1 6 7 3 — 3 8 5 1( 2 0 1 3 ) 0 卜0 0 8 7 — 0 3
基 于最小 势 能原理 的变 截面压 杆 I 界 压 力 的计 算方 法
谢 海。 寿开荣 , 李 龙, 李剑敏
( 浙江理 工大学机械与 自动控制 学院 , 杭州 3 1 0 0 1 8 )
直 杆进 行分 析 的 。近年 来 , 实际 工程 中 , 由于各 种 工 艺 或造 型需 要 , 出现 了很 多变 截 面杆 , 而且 , 不 同 于
即在此弯曲状态下平衡 。 取位移试 函数系数为:
1
( z) , 2 ( z) , … ( z)
( 1 )
这里 , 每一 个 函数均 需要 有 2阶以上 的导数 。 同 时, 根 据压 杆 的 约束情 况 , 该 试 函数 须 满 足 边 界
浙 江理 工 3年 1月
J o u r n a l o f Z h e j i a n g S c i — T e c h Un i v e r s i t y
Vo 1 . 3 O ,No . 1, J a n .2 0 1 3
一
层一 一E f ∑ ( z ) 1 Y
( 4 )
海( 1 9 8 5 一) , 男, 湖北武汉人 , 硕士研 究生 , 主要从事机械动力学方面的研究 。
通信作 者:李剑敏 , 电子邮箱 : l j mz r z @1 6 3 . c o n r
8 8
浙
江
理
工
大
学
学
报
2 0 1 3年
中图分类号 : THl 1 4 文 献 标 志码 : A
0 引 言
压 杆 在 工 程 中有 着 极 其 广泛 的应 用 , 如 建 筑结
构 中的承压 柱 、 汽车 起 重机 的 吊臂 、 多 级液 压 油缸 的
力学的基本原理。虚位移原理、 最小势能原理等都可 以归结为能量泛函的变分原理。最小势能原理在有限 元分析 中 的应用 得 到广 泛 的认 同。最 小 势 能原 理 指 出, 变形体结构平衡的条 件是其势能泛 函取驻值[ ] 。 假 设变 截 面压杆 的惯性 矩 为 J ( z ) , 当压 杆受 到
第3 0卷
其 中 E为 弹性模 量 。
而各 待定 系数 , 。 , …, A 与积 分无 关 , 则 可 以 定 义如下参 数 :
由式 ( 3 ) 、 式( 4 ) 可 以计算 得 到压杆 的应 变能 为
—
l f a e d  ̄ = 吉 - 『 : 』 E y 2 ( ∑ ( z ) ) d A d 一
试 函数集 的线性组合 , 由试 函数 I 生 质 可知 , 挠度 也满足
压杆 的边界 约束条件 。 压杆 此时 的变形是 在压力 载荷 作用下 的弯 曲变形 , 在小 变形情况下 , 压杆的应 变为
e 一 一 』 D 一 一 努Y : = : = 一 f ( ∑ ( z ) ) Y( 3 )
专 E J ) ( ∑ ) ) d r ( 5 )
为:
j 。 k z 出
: 户
∽
其 中 n 为压杆 的体 积 , A 为压 杆 的横 截 面 积 , z
为压杆 长度 。
} 一
一F N b u
则方 程 ( 9 )可 以用 式 ( I O )所 定 义 的 参 数 表 达
压力 作 用发 生微 小 的 弯 曲 而处 于临 界 平 衡 时 , 压 杆
活 塞杆 等 , 其 工 作 时受 到较大 的压力作 用 , 且长 细 比 较大 , 因此 , 稳定 性是 这类 杆件 分 析 中需 主 要考 虑 的 问题 [ 1 ] 。但 通 常 的稳定 性 计算 , 压 杆 是 作 为 等 截 面
O
0
● ● ●
另外 , 可 以计算外载荷在此变形中所做功, 由于
线 性 稳定 的计 算公 式 , 从 而可 以对 一 般 意 义 的 变截
假 设压 杆 在载荷 作 用下 的挠 度为 :
一 1 1 ( z)+ 2 2 ( )+ … + A ( )= = =
∑ 乒 ( z )
i
( 2 )
其中, , z , …, 为待定系数。 即, 挠度为所取得
条件。
机械类 阶梯轴那样 的间断变化 , 其截面是连续的变 化 。这类杆 在新 型 建 筑 中应 用 较 广 , 但 其 设计 的 主 要问题仍然是稳定性问题 。目前工程 中对变截面杆
可 以采用有 限元 等 数 值 方 法 进 行 离散 分 析 , 但 需 要 用 到大 型专 业软 件 , 且建 模 、 分 析 等耗 时较 多 E 2 3 。因 此, 工 程界试 图寻 找具 有 足够 精 度 的解 析 解 或 半解 析解 , 以对 变截 面压 杆 的稳定 性 进行 简单 、 方便 的计 算 与设 计 。本 文采 用 弹 性 理 论 的 最小 势 能原 理 , 通 过 对假 设位 移 函数 的变 分 运 算 , 来 得 到 变 截 面压 杆
