图形旋转精彩试题附问题详解
初三旋转试题及答案

初三旋转试题及答案一、选择题1. 将一个图形绕着某一点旋转一定角度后,与原图形重合,这种图形称为()。
A. 轴对称图形B. 中心对称图形C. 旋转对称图形D. 相似图形答案:C2. 一个图形绕着某一点旋转180°后,与原图形重合,这种图形称为()。
A. 轴对称图形B. 中心对称图形C. 旋转对称图形答案:B3. 一个图形绕着某一条直线旋转180°后,与原图形重合,这种图形称为()。
A. 轴对称图形B. 中心对称图形C. 旋转对称图形D. 相似图形答案:A4. 一个图形绕着某一点旋转90°后,与原图形重合,这种图形称为()。
A. 轴对称图形B. 中心对称图形C. 旋转对称图形答案:C5. 一个图形绕着某一点旋转120°后,与原图形重合,这种图形称为()。
A. 轴对称图形B. 中心对称图形C. 旋转对称图形D. 相似图形答案:C二、填空题6. 一个图形绕着某一点旋转180°后,与原图形重合,这种图形称为中心对称图形,这个点称为____。
答案:对称中心7. 一个图形绕着某一条直线旋转180°后,与原图形重合,这种图形称为轴对称图形,这条直线称为____。
答案:对称轴8. 一个图形绕着某一点旋转一定角度后,与原图形重合,这种图形称为旋转对称图形,这个角度称为____。
答案:旋转角9. 一个图形绕着某一点旋转360°后,与原图形重合,这种图形称为____。
答案:旋转对称图形10. 一个图形绕着某一点旋转360°/n后,与原图形重合,这种图形称为n次旋转对称图形,这个点称为____。
答案:旋转中心三、解答题11. 已知一个图形绕着某一点旋转90°后,与原图形重合,求这个图形的旋转角。
答案:旋转角为90°。
12. 已知一个图形绕着某一条直线旋转180°后,与原图形重合,求这个图形的对称轴。
答案:对称轴为该直线。
人教版九年级数学上册23.1.1《图形的旋转》试题及答案
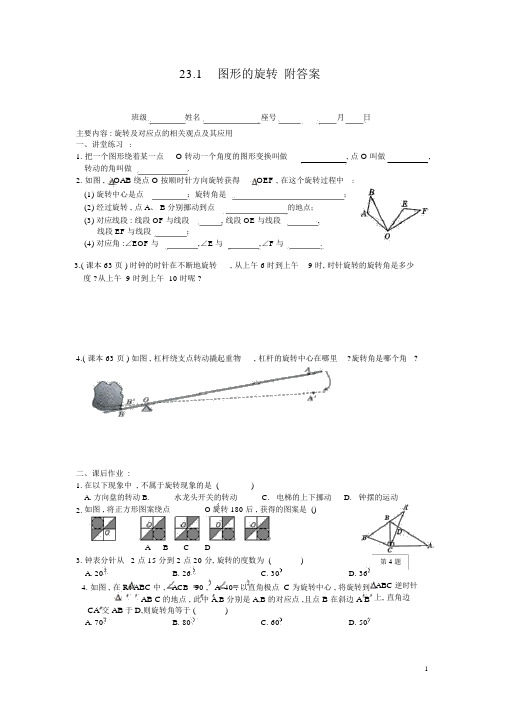
23.1图形的旋转附答案班级姓名座号月日主要内容 : 旋转及对应点的相关观点及其应用一、讲堂练习:1. 把一个图形绕着某一点O 转动一个角度的图形变换叫做, 点O叫做,转动的角叫做.2. 如图 ,OAB 绕点 O 按顺时针方向旋转获得OEF ,在这个旋转过程中:(1) 旋转中心是点;旋转角是;(2) 经过旋转 , 点 A、 B 分别挪动到点的地点;(3) 对应线段 : 线段 OF 与线段, 线段 OE 与线段,线段 EF 与线段;(4) 对应角 :∠EOF 与,∠E与,∠F与.3.( 课本 63 页 ) 时钟的时针在不断地旋转, 从上午 6 时到上午9 时, 时针旋转的旋转角是多少度 ?从上午 9 时到上午 10 时呢 ?4.( 课本 63 页 ) 如图 , 杠杆绕支点转动撬起重物, 杠杆的旋转中心在哪里?旋转角是哪个角?二、课后作业 :1.在以下现象中 , 不属于旋转现象的是 ()A. 方向盘的转动B.水龙头开关的转动C. 电梯的上下挪动D. 钟摆的运动2.如图 , 将正方形图案绕点O旋转 180 后 , 获得的图案是 ()A B C D3. 钟表分针从 2 点 15 分到 2 点 20 分, 旋转的度数为 ()A. 20B. 26C. 30D. 364. 如图 , 在Rt ABC中 , ACB 90 , A 40 , 以直角极点C为旋转中心 , 将旋转到AB C的地点,此中A,B分别是A,B的对应点,且点 B 在斜边 A B CA 交 AB于D,则旋转角等于()A. 70B. 80C. 60D. 50第 4 题ABC 逆时针上, 直角边15. 如图 ,ABC 与ADE 都是等腰直角三角形, C 和AED 都是直角,点 E 在 AB 上,假如ABC 经逆时针旋转后能与ADE 重合,那么旋转中心是点;旋转的度数是.6. 如图 ,ABC 为等边三角形, D 为ABC 内一点,ABD 经过旋转后抵达ACP 的地点,则(1) 旋转中心是点;(2)旋转角度是;(3)ADP 是三角形.第5题第6题7.( 课本 66 页 ) 如图 , 说出压水机压水时的旋转中心和旋转角.8.( 课本 66 页 ) 如图 , 吃米的小鸡是站立的小鸡经过旋转获得的, 旋转中心是O .从图上量一量旋转角是多少度.三、新课预习 :1.对应点到旋转中心的距离;对应点与旋转中心所连线段的夹角等于;旋转前、后的图形.2.如图 , OAB绕O点按顺时针方向旋转获得OEF ,在这个旋转过程中,找出图中相等的角和相等的线段 .3. 如图 , E 是正方形ABCD 中, CD 边上随意一点,以点 B 为中心,把 EBC 逆时针旋转90 ,画出旋转后的图形 .2参照答案一、讲堂练习:1. 把一个图形绕着某一点O 转动一个角度的图形变换叫做旋转, 点O叫做旋转中心,转动的角叫做旋转角.2. 如图 ,OAB 绕点 O 按顺时针方向旋转获得OEF ,在这个旋转过程中:(1) 旋转中心是点O;旋转角是∠ AOE、∠ BOF;(2) 经过旋转 , 点 A、 B 分别挪动到点E、F的地点;(3) 对应线段 : 线段 OF 与线段OB, 线段 OE 与线段OA,线段 EF 与线段AB;(4) 对应角 :∠EOF 与∠AOB,∠E与∠A,∠F 与∠B.3.( 课本 63 页 ) 时钟的时针在不断地旋转, 从上午 6 时到上午9 时, 时针旋转的旋转角是多少度 ?从上午 9 时到上午 10 时呢 ?解:时针1小时转30 ,从上午6时到9时,时针要旋转30 3 90 ;从 9时到 10时,时针要旋转 30 .4.( 课本 63 页 ) 如图 , 杠杆绕支点转动撬起重物, 杠杆的旋转中心在哪里?旋转角是哪个角?解 : 杠杆的旋转中心在点O,旋转角是∠ AOA .二、课后作业:1.在以下现象中 , 不属于旋转现象的是 ( C )A. 方向盘的转动B.水龙头开关的转动C.电梯的上下挪动D.钟摆的运动2. 如图 , 将正方形图案绕点O旋转 180 后, 获得的图案是( D )A B C D3.钟表分针从 2 点 15分到 2点 20分, 旋转的度数为 ( C )第 4 题A. 20B. 26C. 30D. 364. 如图 , 在Rt ABC中 ,ACB90, A 40, 以直角极点C为旋转中心 , 将ABC逆时针旋转到ABC的地点,此中A,B分别是 A,B 的对应点 , 且点B在斜边A B上, 直角边CA 交 AB于D ,则旋转角等于( B )A. 70B. 80C. 60D. 505.如图,ABC 与ADE 都是等腰直角三角形, C和AED都是直角 ,点E在 AB上,假如ABC 经逆时针旋转后能与ADE 重合,那么旋转中心是点A;旋转的度数是45°.6. 如图,ABC 为等边三角形, D 为ABC 内一点, ABD 经过旋转后抵达ACP 的地点,则(1) 旋转中心是点A; (2)旋转角度是60°;(3)ADP是等边三角形 .第5题第6题37.( 课本 66 页 ) 如图 , 说出压水机压水时的旋转中心和旋转角.解 : 压水机的旋转中心为把手柄与机体的连结点, 旋转角为把手柄旋转的角度 .8.( 课本 66 页 ) 如图 , 吃米的小鸡是站立的小鸡经过旋转获得的, 旋转中心是O .从图上量一量旋转角是多少度.解 : 经丈量旋转角AOA 约等于85.三、新课预习 :1.对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等 .2.如图 , OAB绕O点按顺时针方向旋转获得OEF ,在这个旋转过程中, 找出图中相等的角和相等的线段 .答 : 相等的角是 :A E , B F ,AOBEOF ,AOE BOF .相等的线段是 : AB EF ,OA OE,OB OF .3.如图 , E 是正方形ABCD中 , CD边上随意一点 , 以点B为中心 , 把 EBC 逆时针旋转 90 , 画出旋转后的图形 .答 : E BA是由EBC逆时针旋转90后获得的 .4。
初一数学图形的旋转试题

初一数学图形的旋转试题1.如图,若正六边形ABCDEF绕着中心O旋转角α得到的图形与原来的图形重合,则α最小值为()A.180°B.120°C.90°D.60°【答案】D【解析】根据旋转对称图形和旋转角的概念作答.解:正六边形被平分成六部分,因而每部分被分成的圆心角是60°,并且圆具有旋转不变性,因而旋转60度的整数倍,就可以与自身重合.则α最小值为60度.故选D.2.如图是一个旋转对称图形,以O为旋转中心,以下列哪一个角为旋转角旋转,能使旋转后的图形与原图形重合()A.60°B.90°C.120°D.180°【答案】C【解析】根据旋转对称图形的概念:把一个图形绕着一个定点旋转一个角度后,与初始图形重合,这种图形叫做旋转对称图形,这个定点叫做旋转对称中心,旋转的角度叫做旋转角.解:O为圆心,连接三角形的三个顶点,即可得到∠AOB=∠BOC=∠AOC=120°,所以旋转120°后与原图形重合.故选C.3.下列图形中,是中心对称图形的是()A.平行四边形B.正五边形C.等腰梯形D.直角三角形【答案】A【解析】根据中心对称的定义,结合所给图形即可作出判断.解:A、是中心对称图形,故本选项正确;B、不是中心对称图形,是轴对称图形,故本选项错误;C、不是中心对称图形,是轴对称图形,故本选项错误;D、不是中心对称图形,故本选项错误;故选:A.4.下列图形是中心对称图形的是()A.B.C.D.【答案】B【解析】根据中心对称的定义,结合所给图形进行判断即可.解:A、不是中心对称图形,故本选项错误;B、是中心对称图形,故本选项正确;C、不是中心对称图形,故本选项错误;D、不是中心对称图形,故本选项错误;故选B.5.下列图标中,属于中心对称的是()A.B.C.D.【答案】C【解析】根据中心对称图形的概念逐项分析求解即可.解:根据中心对称图形的概念,知A、B、D都不是中心对称图形,不符合题意;C是中心对称图形,符合题意.故选C.6.小明把如图所示的扑克牌放在一张桌子上,请一位同学避开他任意将其中一张牌倒过来,然后小明很快辨认出被倒过来的那张扑克牌是()A.方块5B.梅花6C.红桃7D.黑桃8【答案】A【解析】根据中心对称图形的概念和各图的特点解答.解:根据题意,知黑桃8、红桃7、梅花6在旋转后,花色发生了变化,只有方块5没有变化.故选A.7.把图中的五角星图案,绕着它的中心旋转,旋转角至少为()时,旋转后的五角星能与自身重合.A.30°B.45°C.60°D.72°【答案】D【解析】五角星图案,可以被平分成五部分,因而每部分被分成的圆心角是72°,并且圆具有旋转不变性,因而旋转72度的整数倍,就可以与自身重合.解:该图形被平分成五部分,旋转72度的整数倍,就可以与自身重合,因而A、B、C都错误,能与其自身重合的是D.故选D.8.如图,香港特别行政区区旗中央的紫荆花团由5个相同的花瓣组成.它是由其中的一瓣经过4次旋转得到的,每次旋转的角度是°.【答案】72【解析】根据旋转的性质和周角是360°求解即可.解:观察图形可知,中心角是由五个相同的角组成,∴旋转角度是360°÷5=72°,∴这四次旋转中,旋转角度最小是72°.故答案为:72°.9.如图所示的图案中,弧AD=弧DC=弧CB=弧AE=60°,绕中心O至少旋转度后,能与原来的图案重合.【答案】120°【解析】根据旋转对称图形的概念,把一个图形绕着一个定点旋转一个角度后,与初始图形重合,这种图形叫做旋转对称图形,旋转的角度叫做旋转角进行计算即可.解:该图形围绕自己的旋转中心,最少顺时针旋转360°﹣4×60°=120°后,能与其自身重合.故答案为:120°.10.设将一张正方形纸片沿图中虚线剪开后,能拼成下列四个图形,则其中是中心对称图形的是(填序号)【答案】(2)【解析】根据中心对称图形的概念求解.解:由图中观察,知(1)、(3)、(4)都只是轴对称图形;只有(2)是中心对称图形.故选(2).。
小学旋转测试题及答案

小学旋转测试题及答案一、选择题(每题2分,共10分)1. 一个正方形旋转90度后,它的形状会改变吗?A. 会B. 不会C. 不确定答案:B2. 一个圆在平面内旋转360度后,它的位置会改变吗?A. 会B. 不会C. 不确定答案:B3. 一个等边三角形绕着它的一个顶点旋转120度后,它的位置会改变吗?A. 会B. 不会C. 不确定答案:B4. 一个矩形绕着它的中心点旋转180度后,它的形状和位置会改变吗?A. 形状和位置都会改变B. 形状不会改变,位置会改变C. 形状和位置都不会改变答案:C5. 如果一个图形绕着一个点旋转了360度,那么这个图形的位置会回到原来的位置吗?A. 会B. 不会C. 不确定答案:A二、填空题(每题2分,共10分)1. 一个图形绕着一个点旋转____度后,会回到原来的位置。
答案:3602. 一个图形旋转后,它的形状____改变。
答案:不会3. 一个图形绕着它的中心点旋转,它的形状和位置____改变。
答案:不会4. 一个图形旋转180度后,它的位置____改变。
答案:会5. 一个图形绕着一个点旋转90度后,它的位置____改变。
答案:会三、判断题(每题2分,共10分)1. 一个正方形旋转180度后,它的形状和位置都会改变。
()答案:×2. 一个圆在平面内旋转任意角度后,它的形状都不会改变。
()答案:√3. 一个矩形绕着它的一个顶点旋转90度后,它的形状不会改变。
()答案:√4. 一个等边三角形绕着它的中心点旋转120度后,它的位置不会改变。
()答案:√5. 一个图形旋转360度后,它的位置一定会回到原来的位置。
()答案:√四、简答题(每题5分,共20分)1. 请简述旋转对称图形的特点。
答案:旋转对称图形是指一个图形绕着一个点旋转一定角度后,能够与自身重合的图形。
这样的图形在旋转过程中,其形状和大小不会发生改变,只是位置发生了变化。
2. 为什么一个圆在平面内旋转任意角度后,它的形状不会改变?答案:一个圆在平面内旋转任意角度后,它的形状不会改变,因为圆是所有点到圆心距离相等的点的集合,无论旋转多少角度,这些点到圆心的距离都保持不变,因此圆的形状不会发生改变。
图形的旋转测试题(含答案)
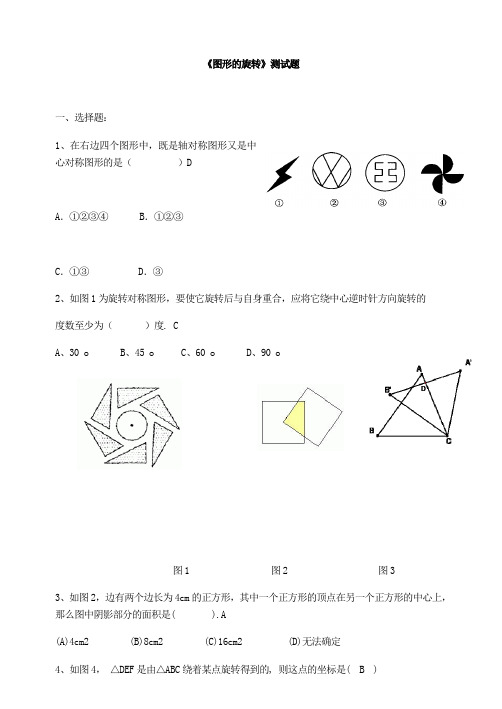
《图形的旋转》测试题一、选择题:1、在右边四个图形中,既是轴对称图形又是中心对称图形的是()DA.①②③④ B.①②③C.①③ D.③2、如图1为旋转对称图形,要使它旋转后与自身重合,应将它绕中心逆时针方向旋转的度数至少为()度. CA、30 oB、45 oC、60 oD、90 o图1 图2 图33、如图2,边有两个边长为4cm的正方形,其中一个正方形的顶点在另一个正方形的中心上,那么图中阴影部分的面积是( ).A(A)4cm2 (B)8cm2 (C)16cm2 (D)无法确定4、如图4,△DEF是由△ABC绕着某点旋转得到的, 则这点的坐标是( B )图5 图4 A. (1,1) B. (0,1) C. (−1,1) D. (2,0)二、填空题5、点a 4(,)与3b (,)关于原点对称,则a b += .-76、如图3,把三角形△ABC 绕着点C 顺时针旋转350,得到△A 'B 'C ,A 'B '交AC 于点D ,若∠A 'DC=900,则∠A 的度数是__________。
5507、如图5, △ABC 中, (ACB = 90(, (B = 30(, BC = 6, 三角板绕C 逆时针旋转, 当点A的对应点A' 落在AB 边上时即停止转动, 则BM 的长为 3 .8、如图6,△ABC 中, 已知∠C=90°, ∠B=50°, 点D 在边BC 上, BD=2CD. 把△ABC 绕着点D逆时针旋转m (0(<m<180()度后, 如果点B 恰好落在初始Rt △ABC 的边上, 那么m = _______.80(或120(.三、解答题9、作图题(1)如图7,画出△ABC 绕点O 顺时针旋转60°所得到的图形.图6 BA CO图7 图8(2)如图8,在直角坐标系中,点P 的坐标为(3,4),将OP 绕原点O 逆时针旋转90°得到线段OP ′,(1)在图中画出线段OP ′;(2)P ′的坐标为 ______. (-4,3)1、如图,在△ABC 中,∠B=900,∠C=300,AB=1,将△ABC 绕顶点A 旋转1800,点C 落在C1处,则C C1的长为( )A .24B .4C .32D .522、如图,△ABC 中,∠ACB=1200,将它绕着点C 旋转300 后得到△DCE ,则∠ACE=∠A+∠E=3、如图,在Rt △ABC 中,∠ACB=90°,∠A=35°,以直角顶点C•为旋转中心,将△ABC 旋转到△A ′B ′C 的位置,其中A ′、B ′分别是A 、B 的对应点,且点B 在斜边A ′B ′上,直角边CA ′交AB 于D ,求∠BDC 的度数.4,如图,正方形ABCD 中,E 在BC 上,F 在AB 上且∠FDE=45°,•△DEC 按顺时针方向转动一个角度后成为△DGA .(1)图中哪一个点是旋转中心?(2)旋转了多少度?(3)指出图中的对应点,对应线段和对应角;(4)求∠GDF 的度数.5、已知如图,正方形ABCD 中,E 为CD 边上一点,F 为BC 边上一点,CE=CF:(1)EBC FDC ∠∠与相等吗?(2)△DCF 能与△BCE 重合吗?(3)试判断BE 与DF 的位置关系并说明理由,6.如图所示,四边形ABCD 中,∠BAD=∠C=90°,AB=AD ,AE ⊥BC 于E ,△BEA 旋转后能与△DFA 重合.(1)旋转中心是哪一点?(2)旋转了多少度?(3)若AE=5cm ,求四边形ABCD 的面积.7,如图,K是正方形ABCD内一点,以AK为一边作正方形AKLM,使L,M,D在AK的同旁,连结BK和DM,试用旋转的思想说明线段BK与DM的关系.,8,.如图所示,等边△ABC中,D是AB边上的动点(不与A、B重合),以CD为一边,向上作等边△EDC。
(完整版)图形的旋转测试题(含答案)
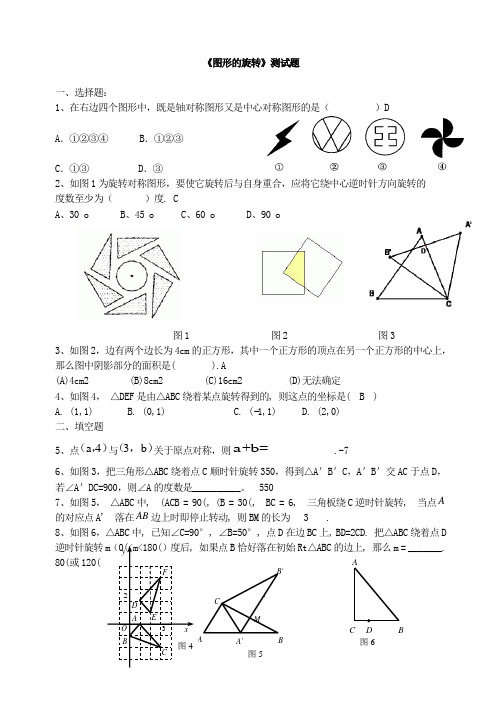
MB' A'C A B 图5 图4 《图形的旋转》测试题一、选择题:1、在右边四个图形中,既是轴对称图形又是中心对称图形的是( )DA .①②③④B .①②③C .①③D .③2、如图1为旋转对称图形,要使它旋转后与自身重合,应将它绕中心逆时针方向旋转的度数至少为( )度. CA 、30 oB 、45 oC 、60 oD 、90 o图1 图2 图33、如图2,边有两个边长为4cm 的正方形,其中一个正方形的顶点在另一个正方形的中心上,那么图中阴影部分的面积是( ).A(A)4cm2 (B)8cm2 (C)16cm2 (D)无法确定4、如图4, △DEF 是由△ABC 绕着某点旋转得到的, 则这点的坐标是( B )A. (1,1)B. (0,1)C. (−1,1)D. (2,0)二、填空题5、点a 4(,)与3b (,)关于原点对称,则a b += .-76、如图3,把三角形△ABC 绕着点C 顺时针旋转350,得到△A 'B 'C ,A 'B '交AC 于点D ,若∠A 'DC=900,则∠A 的度数是__________。
5507、如图5, △ABC 中, (ACB = 90(, (B = 30(, BC = 6, 三角板绕C 逆时针旋转, 当点A的对应点A' 落在AB 边上时即停止转动, 则BM 的长为 3 .8、如图6,△ABC 中, 已知∠C=90°, ∠B=50°, 点D 在边BC 上, BD=2CD. 把△ABC 绕着点D逆时针旋转m (0(<m<180()度后, 如果点B 恰好落在初始Rt △ABC 的边上, 那么m = _______. 80(或.O A B C D E F x y2 3图6 A C BD三、解答题9、作图题(1)如图7,画出△ABC 绕点O 顺时针旋转60°所得到的图形.图7 图8(2)如图8,在直角坐标系中,点P 的坐标为(3,4),将OP 绕原点O 逆时针旋转90°得到线段OP ′,(1)在图中画出线段OP ′;(2)P ′的坐标为 ______. (-4,3)1、如图,在△ABC 中,∠B=900,∠C=300,AB=1,将△ABC 绕顶点 A 旋转1800,点C 落在C1处,则C C1的长为( )A .24B .4C .32D .522、如图,△ABC 中,∠ACB=1200,将它绕着点C 旋转300 后得到△DCE ,则∠ACE=∠A+∠E=3、如图,在Rt △ABC 中,∠ACB=90°,∠A=35°,以直角顶点C•为旋转中心,将△ABC 旋转到△A ′B ′C 的位置,其中A ′、B ′分别是A 、B 的对应点,且点B 在斜边A ′B ′上,直角边CA ′交AB 于D ,求∠BDC 的度数.E DC BA B A C O ABC B C4,如图,正方形ABCD 中,E 在BC 上,F 在AB 上且∠FDE=45°,•△DEC 按顺时针方向转动一个角度后成为△DGA .(1)图中哪一个点是旋转中心?(2)旋转了多少度?(3)指出图中的对应点,对应线段和对应角;(4)求∠GDF 的度数.5、已知如图,正方形ABCD 中,E 为CD 边上一点,F 为BC 边上一点,CE=CF:(1)EBC FDC ∠∠与相等吗?(2)△DCF 能与△BCE 重合吗?(3)试判断BE 与DF 的位置关系并说明理由,6.如图所示,四边形ABCD 中,∠BAD=∠C=90°,AB=AD ,AE ⊥BC 于E ,△BEA 旋转后能与△DFA 重合.(1)旋转中心是哪一点?(2)旋转了多少度?(3)若AE=5cm ,求四边形ABCD 的面积.7,如图,K 是正方形ABCD 内一点,以AK 为一边作正方形AKLM ,使L ,M ,D 在AK 的同旁,连结BK 和DM ,试用旋转的思想说明线段BK 与DM 的关系. C FEDB A,8,.如图所示,等边△ABC中,D是AB边上的动点(不与A、B重合),以CD为一边,向上作等边△EDC。
数学旋转测试题附答案

第3题图ED C BA 第4题图O D CBA 第5题AB 旋转测试题一、 选择题:1.一个图形经过旋转变化后,发生改变的是 .A.旋转中心B.旋转角度C.图形的形状D.图形的位置 2.下列图形中绕某个旋转180°后能与自身重合的有 .①正方形; ②长方形; ③等边三角形; ④线段; ⑤角; ⑥平行四边形 A. 5个 B. 2个 C. 3个 D. 4个3.如图所示,△ABC 中,AC =5,中线AD =7,△EDC 是由△ADB 旋转180°所得,则AB 边的取值范围是 .A. 1<AB <29B. 4<AB <24C. 5<AB <19D. 9<AB <194.如图,已知△OAB 绕点O 沿逆时针方向旋转80°到△OCD 的位置,且∠A =110°,∠D =40°,则∠AOD 的度数为 .A. 30°B. 40°C. 50°D. 60°5.将方格纸中的图形(如图所示)绕点O 沿顺时针方向旋转90°后,得到的图形是6.下列图形中,是中心对称图形而不是轴对称图形的是 . A.等边三角形 B.矩形 C.平行四边形 D.菱形7.点A (-3,2)关于x 轴的对称点为点B ,点B 关于原点的对称点为C ,则点C 的坐标是 .A.(3,2)B.(-3,2)C.(3,-2)D.(-2,3) 8.已知点A 的坐标为(a ,b ),O 为原点,连结OA ,将线段OA 绕点O 按逆时针方向旋转90°得OA 1,则点A 1的坐标为 .A.(-a ,b )B.(a ,-b )C.(-b ,a )D.(b ,-a ) 9.如图,△ABC 为等腰三角形,AB =AC ,∠A =38°,现将△ABC 绕点旋转,使BC 的对应边落在AC 上,则其旋转角为 .A. 38°B. 52°C. 71°D. 81°10.如图所示,在直角三角形ABC 中,∠C =90°,AC =6,BC =8,将△ABC 绕点B 旋第9题图EDCB A 第10题图CB A 第16题图C /B /()A /C B A 第17题图B /A /C B A转90°,得到关于点A 的对称点D ,则AD 的长是 .A. 20B. 10√2C. 10D. 20√211.平面直角坐标系中有一图案,如果将图案中各点的横、纵坐标都乘以-1,所得图案与原图案相比 .A.向下平移了一个单位长度B.向左平移了一个单位长度C.关于坐标轴成轴对称D.关于坐标原点成中心对称12.在正方形ABCD 中,E 是CD 上一点,F 是BC 上一点,且EF =BF +DE ,则∠EAF 的度数是 .A. 30°B. 60°C. 45°D. 小于60° 二、填空题:13.线段的对称中心是 ,平行四边形的对称中心是 ,圆的对称中心是 .14.已知A 、B 、O 三点不在同一直线上,A 、A /关于点O 对称,B 、B /关于点O 对称,那么线段AB 与A /B /的关系是 .16.如图在Rt △ABC 中,∠C =90°,∠A =60°,AC =3cm ,将△ABC 绕B 点旋转到 △A /B /C /的位置且使A 、B 、C /三点在同一直线上,则A 点经过的最短路线长是 cm.17.如图,将Rt △ABC 绕C 点逆时针旋转得到△A /B /,若∠A /CB =160°,则此图形旋转角是 度.18.若矩形ABCD 的对称中心恰为原点O ,且点B 坐标为(-2,-3), 则点D 坐标为 .19.点(1,-3)绕原点顺时针旋转90°得到的点的坐标是 ;直线y =-3x 绕原点顺时针旋转90°得到的直线的解析式为 . 20.阅读课题学习:“如果一个图形绕着某点O 旋转α后所得的图形与原图形重合,则称此图形关于点O 有角α的旋转对称。
初三旋转测试题卷子及答案

初三旋转测试题卷子及答案一、选择题(每题3分,共15分)1. 一个点绕原点旋转90度后,其坐标变为原来的什么?A. 相反数B. 倒数C. 两倍D. 四倍2. 一个图形绕某点旋转180度后,与原图形的关系是?A. 完全重合B. 完全相反C. 部分重合D. 没有关系3. 一个图形绕某点旋转60度后,其面积和周长会如何变化?A. 面积不变,周长不变B. 面积变小,周长变小C. 面积不变,周长变长D. 面积变小,周长变大4. 一个图形绕其对称轴旋转180度后,图形的位置会如何变化?A. 完全重合B. 完全相反C. 部分重合D. 没有变化5. 如果一个图形绕某点旋转了θ度,那么它的旋转矩阵是什么?A. [cosθ -sinθ; sinθ cosθ]B. [cosθ sinθ; -sinθ cosθ]C. [sinθ cosθ; cosθ -sinθ]D. [sinθ -sinθ; cosθ cosθ]二、填空题(每题2分,共10分)6. 一个点P(x, y)绕原点旋转θ度后,其新坐标为_________。
7. 若一个图形绕点(a, b)旋转θ度,其旋转后的图形与原图形的对应点坐标变化关系为_________。
8. 一个正方形绕其中心点旋转45度后,其四个顶点的坐标变化情况是_________。
9. 一个圆绕其圆心旋转任意角度,其形状和大小_________。
10. 旋转矩阵可以表示为_________,其中θ为旋转角度。
三、解答题(每题5分,共20分)11. 给定一个点P(1, 2),求该点绕原点旋转120度后的坐标。
12. 一个矩形ABCD,其中A(-1, 1),B(1, 1),C(1, -1),D(-1, -1),求该矩形绕点A旋转90度后的顶点坐标。
13. 描述一个正方形绕其对称轴旋转90度后,四个顶点的坐标变化情况。
14. 解释旋转矩阵在图形旋转变换中的作用。
四、综合题(每题5分,共10分)15. 一个正六边形绕其中心点旋转60度后,求其顶点坐标的变化。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一.教学容:图形的旋转(一)课程标准要求1. 知识与技能:(1)通过具体的实例认识图形的旋转变换,探索它的基本特征,理解“对应点到旋转中心的距离相等”以及“对应线段相等,对应角相等”等基本性质;(2)认识旋转对称图形,并能按要求作出简单的平面图形旋转后的图形。
2. 过程与方法灵活运用轴对称、平移与旋转或它们的组合进行图案设计,认识和欣赏这些图形变换在现实生活中的应用。
3. 情感、态度与价值观:在观察、操作、推理、归纳等探索过程中,发展学生的合情推理能力,进一步培养学生的数学说理的习惯与能力。
(二)知识点1. 图形的旋转(1)定义:在平面,将一个圆形绕一个定点沿某个方向(顺时针或逆时针)转动一个角度,这样的图形运动叫做旋转,这个定点叫做旋转中心,转动的角称为旋转角。
(2)生活中的旋转现象大致有两大类:一类是物体的旋转运动,如时钟的时针、分针、秒针的转动,风车的转动等;另一类则是由某一基本图形通过旋转而形成的图案,如香港特别行政区区旗上的紫荆花图案。
(3)图形的旋转不改变图形的大小和形状,旋转是由旋转中心和旋转角所决定,旋转中心可以在图形上也可以在图形外。
(4)会找对应点,对应线段和对应角。
2. 旋转的基本特征:(1)图形在旋转时,图形中的每一个点都绕旋转中心旋转了同样大小的角度。
(2)图形在旋转时,对应点到旋转中心的距离相等,对应线段相等,对应角相等; (3)图形在旋转时,图形的大小和形状都没有发生改变。
3. 几点说明:(1)在理解旋转特征时,首先要对照图形,找出旋转中心、旋转方向、对应点、旋转角。
(2)旋转的角度是对应线段的夹角或对应顶点与旋转中心连线的夹角。
(3)旋转中心的确定分两种情况,即在图形上或在图形外,若在图形上,哪一点旋转过程中位置没有改变,哪一点就是旋转中心;若在图形外,对应点连线的垂直平分线的交点就是旋转中心。
【典型例题】例1. 如图,把一块砖ABCD 直立于地面上,然后将其轻轻推倒,在这个过程中A 点保持不动,四边形ABCD 旋转到AD ’C ’B ’位置。
(1)指出在这个过程中的旋转中心,并说出旋转角度是多大? (2)指出图中的对应线段。
C ’B A D ’分析:因为四边形'''B C AD 是由四边形ABCD 旋转得到的,A 保持不动,因此A 是旋转中心,又因为AB 、'AD 在同一平面上,且AD 垂直于地面,对应线段AB 与'AB 成︒90,因此旋转角度是︒90;(2)中由于点A 、B 、C 、D 的对应点分别是A 、'''D C B 、、,找出了对应点,对应线段也就不难找了。
答案:(1)旋转中心是A ,旋转角度是︒90(2)对应线段分别是:CD 与''D C ,AB 与'AB ,AD 与'AD ,BC 与''C B方法提炼:解答这类题目,应该看哪个点不动,在旋转过程中,图形中的点都动,哪个点不动,哪个点就是旋转中心,只要找出了对应点,对应线段自然可得,抓住“动”与“不动”。
难点:运用旋转的特征解决一些实际问题,培养分析问题和解决问题的能力,突破难点的途径应多动手操作,充分认识“图形在旋转过程中每一点与该对应点到旋转中心的距离都相等”这一性质去理解和运用旋转的其它性质。
例2.分析:得到的,'ABE ∆答案:(1)相等的线段有:''BE DE AE AE CB DC AD AB =====,, 相等的角有:'''BAE DAE BA E EDA E E ∠=∠∠=∠∠=∠,,(除直角外) (2)ADE ∆与'ABE ∆的形状和大小都一样。
方法提炼:解答这类题目,应考虑旋转的特征,是绕什么点旋转的,图形中的每个点都旋转相同的角度,对应线段相等,对应角相等,关键是是否旋转。
例3. 如图,小华同学正在黑板上画ABC ∆绕ABC ∆外一点P 旋转︒45的旋转图,当他画完A 、B 两点旋转后的对应点''B A 、时,不小心将旋转中心P 擦掉了,没有旋转中心P ,小明不知道如何画下去,你能帮助小明找到旋转中心P ,使他继续完成剩下的图形吗?A ’B ’分析:因为旋转中心在对应点连线的垂直平分线上,所以旋转中心是对应点连线垂直平分线的交点。
答案:先连结''BB AA 、,然后分别画线段''BB AA 、的垂直平分线,则它们的交点就是。
方法提炼:解这种类型的题,弄清楚它是一种什么样的题,联系所学知识,灵活使用所学的知识来解答问题,这个题目是旋转方面的题,应联系旋转的特征等。
例4. 如图,ABC ∆和ADE ∆都是等边三角形,B 在AD 上,试利用旋转说明BE=CD 。
D分析:因为此题是利用旋转说明,所以应考虑应用旋转的一些特征来解题。
答案:因为ABC ∆和ADE ∆都是等边三角形,所以︒=∠=∠60EAD BAC ,AB=AC ,AE=AD ,所以线段AB 绕A 点逆时针转︒60后与AC 重合,AE 绕A 点逆时针旋转︒60后与AD 重合,即ABE ∆绕A 点逆时针旋转︒60后与ACD ∆重合,此时BE 与CD 重合,所以BE=CD 。
方法提炼:把题目中的结论与条件互换,即已知BE=CD ,问哪两个三角形可以通过旋转得到,这样的题目就是抓住旋转的特征去寻找思路。
例5. (2001年)同学们曾玩过万花筒,它是由三块等长的玻璃片围成,如图所示,是万花筒的一个图案,图中所有的小三角形均是形状、大小相同的等边三角形,其中的菱形AEFG 可以看成是菱形ABCD 以A 为中心( )A. 顺时针旋转︒60得到的B. 顺时针旋转︒120得到的C. 逆时针旋转D. 逆时针旋转解析:AD GAD ∠∴ 图中所有小三角形均是形状、大小相同的等边三角形︒=︒+︒=∠+∠=∠∴1206060EAD GAE GAD∴选D评注:本题的关键是确定对应边,而对应边的夹角就是旋转角。
例6. 如图,AEB ACD ∆∆,都是等腰直角三角形,︒=∠=∠90EAB CAD ,画出ADB ∆以A 为旋转中心,顺时针方向旋转︒90后的三角形。
解答:根据旋转的特征,点D 绕点A 顺时针旋转︒90到点C ,点B 绕A 顺时针旋转︒90到E 点,从而ADB ∆以A 为旋转中心,顺时针方向旋转︒90后的三角形是ACE ∆。
思维方式:找出ADB ∆中顶点旋转后的对应点。
【模拟试题】(答题时间:40分钟)一、选择题1. A. 30°B. 45° 2. A. 36°B. 45° 3. (基础题)如图,把直角三角形ABC 绕直角顶点顺时针方向旋转90°后到达C B A ''∆,延长AB 交''B A 于D ,则'ADA ∠的度数是( ) A. 30°B. 60°C. 75°D. 90°A CB ’4. (基础题)下列图形中,既是轴对称图形,又是旋转对称图形的是( )A. 等腰三角形B. 平行四边形C. 等边三角形D. 三角形5. (能力题)如图,O 是等边三角形的旋转中心,EOF EOF ∠︒=∠,120绕点O 进行旋转,在旋转过程中,OE 、OF 与ABC ∆的边构成的图形面积( )A. 等于ABC ∆面积的31B. 等于ABC ∆面积的21C. 等于∆ 6. ︒=∠15BAD A. 15°二、填空题:7. (基础题)如图,旋转角是_________,AO 8. (基础题)如图,按________方向旋转了B CE9. (基础题)如图,ABC ∆绕点C 旋转后得到CDE ∆,则A ∠的对应角是___________,=∠B ________,AB=_________,AC=_________。
AED三、解答题:10. 11.向旋转一个角度后成DGA ∆。
(1)图中哪一个点是旋转中心,旋转角等于多少? (2)指出图中旋转图形的对应线段和对应角。
(3)求GDF ∠的度数。
G A F BE12. (探究题)如图,画出ABC ∆关于直线OM 的轴对称图形'''C B A ∆;再画出'''C B A ∆关于ON 的轴对称图形''''''C B A ∆,观察ABC ∆与''''''C B A ∆,你能从中发现这两个三角形有什么关系吗?MNB13. (综合题)如图,点C 是线段AB 上任意一点,分别以AC 、BC 为边在同侧作等边ACD ∆和等边BCE ∆,连结BD 、AE ,试找出图中能够通过旋转完全重合的图形,它是绕哪一点旋转?旋转了多少度?A C B14. (创新题)如图,ABC ∆是等腰三角形,︒=∠90ACB ,延长BC 到D ,连接AD ,作AD BE ⊥于E ,交AC 于F ,在这个图形中,哪两个三角形可以看成是一个三角形沿某一点旋转而得到的?试说明理由。
AE FB C D2 1315. (开放题)请你用几个基本图形设计一个图案,并用一句话说明你所设计图案的创意(要求至少用一次轴对称,一次平移和一次旋转)。
【试题答案】1. C导解:旋转对称图形的概念。
2. D导解:将圆五等分,每一等份的圆心角是︒72。
3. D导解:图形中的每个点都旋转了相同的度数。
4. C导解:等边三角形旋转︒60后与自身重合。
5. A导解:因为是旋转,所以旋转的角度一样,对应线段相等。
6. C7. 点O ,AOD ∠,相等,相等导解:旋转角度一样,对应角相等,对应点到旋转中心距离相等。
8. 点C ,顺时针,909.D ,∠ 导解: 10. 导解:'''B D A ,,11. (1)点D 是旋转中心 ︒90导解:关键是看动与不动。
(2)DC 与DA ,DE 与DG ,EC 与GA ,∠CDE 与∠GDA ,∠C 与∠DAG ,∠DEC 与∠G 。
(3)︒=∠︒=∠4545FDE GDF ,,由于旋转,CDE GDA ∠=∠∴, ︒=∠∠+∠=∠∴45FDE CDE ADF GDF ,又ABCD 是正方形,︒=∠+∠∴45CDE ADF导解:旋转过程对应角相等,应抓住旋转的特征。
12. 图略。
ABC ∆可以旋转2倍MON ∠,得到''''''C B A ∆。
13. DCB ∆与ACE ∆,绕C 点旋转,旋转了︒60。
14. BCF ∆与ACD ∆,绕点C 旋转了︒90。
