8.晶体的各向异性和多晶型性
国科大材料化学复习资料

第二章晶体学终极重点:1、晶体特征,晶体与非晶体区别 2、晶向与晶面指数确定步骤1.晶体的性能特征:均一性,各向异性,自限性,对称性,最小内能性;2.对称操作与对称要素:对称轴,对称面,对称中心,倒转轴;3.晶向指数与晶面指数:确定步骤;4.球体的堆积:六方,面心立方,体心立方5.鲍林规则;6.各种典型晶体构型;7.硅酸盐晶体结构与实例:岛状,链状,层状,架状;8.同质多晶现象:可逆转变,不可逆转变,重建型转变,位移型转变。
1.晶体的性能特征:均一性,各向异性,自限性,对称性,最小内能性(1)晶体的基本特征晶体的性能特征结晶均一性:在晶体内部任意部位上具有相同的性质;各向异性:在晶体不同方向上表现出的性质差异;自限性:能够自发形成封闭的凸几何多面体外形的特性;对称性:晶体中的相同部分(晶面,晶棱,等等)以及晶体的性质能够在不同方向或位置上有规律地重复;最小内能性:在相同的热力学条件下,晶体与同组成的气体、液体及非晶态固体相比具有最小内能,即最为稳定。
(2)对称操作与对称要素:对称操作:使晶体的点阵结构和性质经过一定程序后能够完全复原的几何操作;对称要素:实施对称操作所依赖的几何要素(点,线,面等);1.旋转操作与对称轴:一个晶体如能沿着某一轴线旋转360 / n(n = 1, 2, 3, 4, 6)后使晶体位置完全回复原状,则该晶体具有n 重对称轴;2.反映操作和对称面:一个晶体中如果存在某一个平面,使平面两边进行反映操作,而令晶体复原,则这个平面称为对称面;3.反演操作和对称中心:一个晶体中央在某一个几何点,使晶体外形所有晶面上各点通过该几何点延伸到相反方向相等距离时,能够使晶体复原的操作。
该几何点称为对称中心。
4.旋转反演操作和对称反轴:旋转之后进行反演使晶体复原的操作;只有4¯是新的独立对称要素。
(3)晶向指数与晶面指数:确定步骤晶向指数:以晶胞的某一阵点O为原点,过原点O的晶轴为坐标轴x,y,z,以晶胞点阵矢量的长度作为坐标轴的长度单位;过原点O作一直线OP,使其平行于待定晶向;在直线OP上选取距原点O最近的一个阵点P,确定P点的3个坐标值;将这3个坐标值化为最小整数u,v,w,加以方括号,[ u v w ]即为待定晶向的晶向指数。
晶体中的各向异性

2 结晶生长的微观描述
如图 1 所示,晶体生长体系的组成从溶液相到晶相经历了三个区间,即液相区、过渡相区与晶相区。在
液相区, 溶质与溶剂以离子水平均匀混合。晶体的
组成原子在溶液中通过彼此之间很强的化学键相互键
合,从而形成众多的生长单元 ( 离子、分子或 团 簇) 。
在过渡相区,生长单元经扩散逐步接近晶体,在靠近晶
( 1. State Key Laboratory of Rare Earth Resource Utilization,Changchun Institute of Applied Chemistry,Chinese Academy of Sciences, Changchun 130022,China; 2. School of Chemical Engineering,Dalian University of Technology,Dalian 116024,China)
人工晶体学报
JOURNAL OF SYNTHETIC CRYSTALS
Vol. 41 Supplement August,2012
晶体中的各向异性研究
孙丛婷1,2 ,李克艳2 ,宋术岩1 ,薛冬峰1,2
( 1. 中国科学院长春应用化学研究所稀土资源利用国家重点实验室,长春 130022; 2. 大连理工大学化工学院,大连 116024)
此,有效地设计表面键合环境有利于调节各向异性生
长形态。在 Cu2 O 结晶过程中,EDTA 被证实起到了还 原剂和螯合剂的双重作用 。 [12,13,20] EDTA 的浓度决定
了 Cu2 O 生长过程中的控制步骤。在高 Cu( II) / EDTA
浓度比的结晶条件下,Cu2 O 的结晶习性主要受到反应 图 3 控制,结晶环境中的 EDTA Fig. 1 Schematics of three phase zone
材料科学基础第2章
可编辑ppt
10
2.3.1 固溶体
固溶体(solid solution) :
合金组元通过溶解形成一种成分和性能均匀的、 且结构与组元之一相同的固相称为固溶体。
➢ 固溶体的最大特点是保持溶剂的晶体结构。
➢ 与固溶体晶格相同的组元为溶剂,一般在合金中 含量较多;另一组元为溶质,含量较少。
✓ 各向异性:由于在不同方向上的原子排列的紧密程 度不同使晶体在不同方向上的物理、化学和力学性 能不同。而一般整个晶体不显示各向异性,称为伪 等向性。
✓ 晶粒:组成晶体的结晶颗粒。 ✓ 多晶体:凡由两颗以上晶粒组成的晶体一般金属都
是多晶体。。
可编辑ppt
4
晶粒
可编辑ppt
5
Байду номын сангаас
多相合金
可编辑ppt
6
可编辑ppt
12
(3)按溶质原子在溶剂中的分布特点分类 无序固溶体:溶质原子在溶剂中任意分布, 无规律性。
有序固溶体:溶质原子按一定比例和有规 律分布在溶剂晶格的点阵或间隙里。
(4)按基体类型分类: 一次固溶体:以纯金属为基形成的固溶体。
二次固溶体:以化合物为基形成的固溶体。
可编辑ppt
13
固溶体的两种类型(置换和间隙)
中间相可以用分子式来大致表示其组成。
合金相的性质由以下三个因素控制: (1)电化学因素(电负性或化学亲和力因素)
电负性—化学亲和力越大越容易形成化合物,电负性 相近的元素容易形成固溶体。
(2)原子尺寸因素 △r=(rA-rB)/rA △r越大,越易形 成中间相。 △r越小,越易形成固溶体
(3)原子价因素(电子浓度因素): C电子=[A(100-x) +Bx]/100 C越大,越易形成
材料科学基础名词解释

材料科学基础名词解释第一章固体结构1、晶体 :原子按一定方式在三维空间内周期性地规则重复排列,有固定熔点、各向异性。
非晶体 :原子没有长程的周期排列,无固定的熔点,各向同性等。
2、中间相 : 两组元 A 和 B 组成合金时,除了形成以 A 为基或以 B 为基的固溶体外,还可能形成晶体结构与 A,B 两组元均不相同的新相。
由于它们在二元相图上的位置总是位于中间,故通常把这些相称为中间相。
3、晶体点阵:由实际原子、离子、分子或各种原子集团,按一定几何规律的具体排列方式称为晶体结构或晶体点阵。
4、配位数 :晶体结构中任一原子周围最近邻且等距离的原子数。
5、晶格:描述晶体中原子排列规律的空间格架称之为晶格。
6、晶胞 :在点阵中取出一个具有代表性的基本单元(最小平行六面体)作为点阵的组成单元,称为晶胞。
7、空间点阵:由周围环境相同的阵点在空间排列的三维列阵成为空间点阵。
8、晶向:在晶格中,穿过两个以节点的任一直线,都代表晶体中一个原子列在空间的位向,称为晶向。
9、晶面:由节点组成的任一平面都代表晶体的原子平面,称为晶面。
10、晶向指数(晶面指数):为了确定晶面、晶向在晶体中的相对取向、就需要一种符号,这种符号称为晶面指数和晶向指数。
国际上通用的是密勒指数。
一个晶向指数并不是代表一个晶向,二十代表一组互相平行、位向相同的晶向。
11、晶向族:原子排列相同但空间位向不同的所有晶向称为晶向族,以<uvw>表示。
12、晶面间距:相邻两个平行晶面之间的垂直距离。
低指数晶面的面间距较大,而高指数晶面的面间距较小。
晶面间距越大,则该晶面上原子排列越紧密,该原子密度越大。
13、配位数:每个原子周围最近邻且等距离的原子数目,称为配位数。
14、多晶型性:有些金属固态在不同温度或不同压力范围内具有不同的晶体结这种性质构,称为晶体的多晶型性。
15、多晶型性转变:具有多晶型性的金属在温度或压力变化由一种结构转变为另一种结时,构的过程称为多晶型性转变,也称为同素异构转变。
1-2 金属的晶体结构

c
a3
a1
a2
六方晶系晶向指数的确定
解析法: 用三轴坐标先求出待标晶向的三个指数U,V,W, 再利用下列三轴与四轴坐标系晶向指数的关系, 换算出四周坐标系的晶向。
1 u 2U V 3 1 v 2V U 3 t (u v ) w W
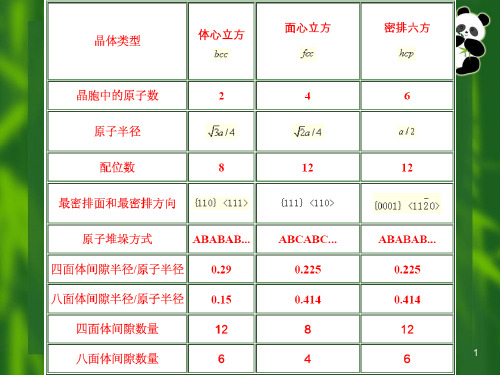
3种典型金属的晶体结构
刚球模型 晶胞原子数 原子半径 配位数和 原子堆垛顺序 致密度
体心 立方
CN=8 k=0.68
ABABAB…
面心 立方
CN=12 k=0.74
ABCABC…
密排 六方
CN=12 k=0.74
ABABAB…
四、晶向指数和晶面指数
晶面——晶体结构中,由一系列原子所构成的平面。
晶向——晶体中任意两个原子中心之间连线所指的
八面体间隙rB=0.414rA 有6个 四面体间隙rB=0.225rA 有12个
描述晶胞从以下几个方面: 晶胞中原子的排列方式 (原子所处的位置) 点阵参数 (晶格常数和晶轴间夹角) 晶胞中原子数 原子半径 R(原子的半径)(和点阵常数关系) 配位数 和致密度 密排方向和密排面 晶体结构中间隙 (大小和数量) 原子的堆垛方式
1 1 x , y ,z 1 2 2
[1 1 2]
例一、已知某过原点晶向上一点的坐标为1、1.5、2,
求该直线的晶向指数。 将三坐标值化为最小整数加方括弧得[234]。
[234]
例二、已知晶向指数为[110],
画出该晶向。
找出1、1、0坐标点,连接 原点与该点的直线即所
为什么单晶体具有各向异性

为什么单晶体具有各向异性,而多晶体在一般情况下不显示各向异性?答:在单晶体中不同晶面和晶向上的原子密度不同,原子间的结合力就不同,因而晶体在不同方向上性能各异。
而多晶体是由许多位向不同的单晶体组成的,各个晶粒在整块金属内的空间位向是任意的,整个晶体各个方向上的性能则是大量位向各不相同的晶粒性能的均值,所以一般不显示各向异性。
综述晶体缺陷对金属强度的作用和机理。
答:①空位、置换原子、间隙原子均提高材料强度(固溶强化)。
点缺陷造成晶格畸变,与位错相互作用,增大了位错运动阻力。
间隙原子的作用最大,置换原子次之,空位的作用最小。
②当位错密度非常低时,位错降低强度,因为位错破坏了晶体的完整性,通过位错滑移比完整晶体的滑移更容易进行。
但当位错密度较高时,随位错密度的增大强度提高,因为位错与位错交割时增大了位错阻力。
③位错不能直接通过大角度晶界、相界、孪晶界,所以提高强度(细晶强化),小角度晶界对位错运动也有一定阻碍作用也能提高强度,但效果很小。
1.假设过冷液体中出现一个立方体晶胚,证明形核功ΔGc=1/3Ac σ(Ac 为临界晶核表面积)。
说明形核功和临界晶核尺寸的意义。
证明:设晶核边长为a ,则 σ⨯⨯+∆=∆236a G a G vσσσσσσσσσσc c v v v c v c c vv c v A a G G G a G a G G G a a G a daG d 312)(32)(96)(64643120123222323232==∆=∆+∆-=+∆=∆∆-=∆-==+∆=∆得: 3.简述湿润角θ,杂质粒子的晶体结构和表面形态对异质形核的影响。
答:①θ角越小,形核率越大。
②杂质粒子的晶体结构与固相晶体结构越相似,形核率越大。
③凹面比凸面形核率大。
4.根据形核理论说明变质处理细化晶粒的机理。
答:根据形核理论,形核需要一定的形核功,变质处理减小了形核功,因而更容易形核,提高了形核率,或者降低长大速度,增大形核率与长大速率的比值,使晶粒细化,从而使铸件的晶粒细化。
8.晶体的各向异性和多晶型性

五,晶体的各向异性晶体具有各向异性的原因是由于在不同品向上的原子紧密程度不同所致。
原子的紧密程度不同,意味着原子之间的距离不同,则导致原子间结合力不同,从而使晶体在不同晶向上的物理,化学和力学性能不同具体性能即无论是弹性模量、断裂抗力,屈服强度,还是电阻率、磁导率、线膨胀系数以及在酸中的溶解度等方面都表现出明显的差异例如具有体心立方晶格的Fe -α单晶体100晶向的原子密度即单位长度的原子数为a 1,110晶向为a7.0,而111晶向为a16.1,所以111为最大原子密度晶向,其弹性模量GPa E 290=,100晶向的GPa E 135=,前者是后者的两倍多。
同样,沿原子密度最大的晶向的屈服强度,磁导率等性能,也显示出明显的优越性。
在工业用的金属材料中通常却见不到这种各向异性特征如上述Fe -α的弹性模量不论方向如何其弹性模量E 均在GPa 210左右这是因为,一般固态金属均是由很多结晶颗粒所组成,这些结晶颗粒称为晶粒。
由于多晶体中的晶粒位向是任意的,晶粒的各向异性被互相抵消,因此在一般情况下整个晶体不显示各向异性,称之为伪等向性一般固态金属均是由很多结晶颗粒所组成这些结晶颗粒称为晶粒图1-27为纯铁的显微组织图1-28为纯铜的显微组织图中的每一颗晶粒由大量的位向相同的晶胞组成晶粒与晶粒之间存在着位向上的差别如图1.29所示凡由两颗以上晶粒所组成的晶体称为多晶体一般金属都是多晶体只有用特殊的方法才能获得单个的晶体即单晶体特殊的加工工艺获得各向异性已在工业生产中得到了应用:如果用特殊的加工处理工艺,使组成多晶体的每个晶粒的位向大致相同,那么就将表现出各向异性,这点已在工业生产中得到了应用用特殊的工艺可以制备单个的晶体即单晶体少数金属以单晶体形式使用单晶铜:伸长率高电阻率低和极高的信号传输性能,可作为生产集成电路微型电子器件及高保真音响设备所需的高性能材料六,多晶型性多晶型性和同素异构转变:● 大部分金属只有一种晶体结构,但也有少数金属如Sn Be Ti Mn Fe ,,,,等具有两种或几种晶体结构,即具有多晶型。
金属的晶体结构

引言金属学是研究金属及合金的成分、组织、结构与力学性能之间关系的科学。
所谓力学性能主要指材料的强度、硬度和塑性。
通常用来承受载荷的零件要求材料具有一定的力学性能,我们称这类材料为结构材料。
与结构材料对应的另一类材料是功能材料,它一般不要求承受载荷,主要使用它的物理性能,如光、电、磁性能等。
功能材料利用它对光、电、磁的敏感特性制作各类传感器。
金属学只讨论金属材料的力学性能,不涉及物理性能。
固态金属通常是晶体,金属学研究的最小结构单元是原子。
原子通过不同的排列可构成各种不同的晶体结构,产生不同的性能。
原子结构不是金属学研究的范畴。
第1章金属的晶体结构1-1金属及金属键金属的定义根据学科的不同有多种划分方法。
本人倾向按结合键的性质来划分,即金属是具有金属键的一类物质。
这种分类的好处是有利于解释与金属力学性能相关的现象。
例如,为什么金属具有较好的塑性?什么是金属键、离子键、共价键我们早就熟知,金属键的最大特点是无饱和性、无方向性。
以后我们将会看到,正是这些特点使金属具有较好的塑性。
研究表明,固态金属通常是晶体,且其结构趋于密堆积结构。
这是为什么?下面我们用双原子模型来说明。
当两个原子相距很远时,它们之间不发生作用。
当它们逐渐靠近时,一个原子的原子核与另一个原子的核外电子之间将产生引力;而两原子的原子核及电子之间产生斥力。
研究表明,引力是长程力,斥力是短程力,即距离较远时,引力大于斥力,表现为相互吸引。
随着原子距离的减小,斥力增加的速度逐渐大于引力增加的速度。
显然这样作用的结果必然存在一个平衡距离d0,此时,引力等于斥力,偏离这一距离时,都将受到一个恢复力,如P3图2。
d c对应最大恢复引力,即最大结合力,它对应着金属的理论抗拉强度。
下面,我们从能量的角度来考虑系统的稳定性。
在引力作用下原子移近所做的功使原子的势能降低,所以吸引能是负值。
相反,排斥能是正值。
吸引能和排斥能的代数和是结合能。
由P3图2可以看出,当原子移至平衡距离d0时,其结合能达到最低值,此时系统的势能最低,状态最稳定。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
五,晶体的各向异性
晶体具有各向异性的原因
是由于在不同品向上的原子紧密程度不同所致。
原子的紧密程度不同,意味着原子之间的距离不同,则导致原子间结合力不同,从而使晶体在不同晶向上的物理,化学和力学性能不同
具体性能
即无论是弹性模量、断裂抗力,屈服强度,还是电阻率、磁导率、线膨胀系数以及在酸中的溶解度等方面都表现出明显的差异
例如具有体心立方晶格的Fe -α单晶体
100晶向的原子密度即单位长度的原子数为a 1,110晶向为a
7.0,而111晶向为a
16.1,所以111为最大原子密度晶向,其弹性模量GPa E 290=,100晶向的GPa E 135=,前者是后者的两倍多。
同样,沿原子密度最大的晶向的屈服强度,磁导率等性能,也显示出明显的优越性。
在工业用的金属材料中通常却见不到这种各向异性特征如上述Fe -α的弹性模量不论方向如何其弹性模量E 均在GPa 210左右
这是因为,一般固态金属均是由很多结晶颗粒所组成,这些结晶颗粒称为晶粒。
由于多晶体中的晶粒位向是任意的,晶粒的各向异性被互相抵消,因此在一般情况下整个晶体不显示各向异性,称之为伪等向性
一般固态金属均是由很多结晶颗粒所组成这些结晶颗粒称为晶粒
图1-27为纯铁的显微组织图1-28为纯铜的显微组织
图中的每一颗晶粒由大量的位向相同的晶胞组成
晶粒与晶粒之间存在着位向上的差别如图1.29所示
凡由两颗以上晶粒所组成的晶体称为多晶体
一般金属都是多晶体
只有用特殊的方法才能获得单个的晶体即单晶体
特殊的加工工艺获得各向异性已在工业生产中得到了应用:
如果用特殊的加工处理工艺,使组成多晶体的每个晶粒的位向大致相同,那么就将表现出各向异性,这点已在工业生产中得到了应用
用特殊的工艺可以制备单个的晶体即单晶体
少数金属以单晶体形式使用
单晶铜:
伸长率高电阻率低和极高的信号传输性能,可作为生产集成电路微型电子器件及高保真音响设备所需的高性能材料
六,多晶型性
多晶型性和同素异构转变:
● 大部分金属只有一种晶体结构,但也有少数金属如Sn Be Ti Mn Fe ,,,,等具有两
种或几种晶体结构,即具有多晶型。
● 当外部条件(如温度和压强)改变时,金属内部由一种晶体结构向另一种晶
体结构的转变称为多晶型转变或同素异构转变。
● 如Fe 在912度以下为体心立方晶格称为Fe -α,在912~1394时具有面心立方
晶格称为Fe -γ,而从1394至熔点,又转变为体心立方晶格称为Fe -δ。
同素异构转变或多晶型转变时的体积变化:
由于不同的晶体结构具有不同的致密度,因而当发生多晶型转变时,将伴有比容或体积的突变。
图1-30为纯铁加热时膨胀曲线
Fe -α的致密度小,Fe -γ的致密度大,Fe -δ的致密度又小,所以在912度由Fe -α转变为Fe -γ时体积突然减小,而Fe -γ在1394度转变为Fe -δ时体积又突然增大,在曲线上出现了明显的转折点。
其他:
除体积变化外,多晶型转变还会引起其它性能的变化。
