图像几何变换PPT课件
合集下载
几何变换思想-PPT

第一,对一些概念得准确把握
平移、旋转、轴对称变换与生活中物体得平移、旋转和轴对 称现象不是一个概念。数学来源于生活,但不等于生活,是生活现 象得抽象和概括。生活中得平移和旋转现象往往都是物体得运动, 如推拉窗、传送带、电梯、钟摆、旋转门等物体得运动,都可以 称为平移现象或旋转现象。而中小学中得几何变换都是指平面图 形在同一平面得变换,也就是说原图形和变换后得图形都是平面 图形,而且都在同一平面内。几何中得平移、旋转和轴对称现象 来自于生活中物体得平移现象、旋转现象和轴对称现象,如果把 生活中这些物体画成平面图形,并且在同一平面上运动,就可以说 成是几何中得平移、旋转和轴对称变换了。
3、几何变换思想得具体应用 图形变换作为空间与图形领域得重要
内容之一,在图形得性质得认识、面积公 式得推导、面积得计算、图形得设计和欣 赏、几何得推理证明等方面都有重要得应 用。
小学数学中几何变换思想得应用
4、几何变换思想得教学 (1)课程标准关于图形变换得数学要求
课程标准关于图形变换得内容和目标分为以下几个层次:
以保持,但通过改变其位置,组合成新得图形,便于计算和证 明。
(3)反射变换 在同一平面内,若存在一条定直线L,使对于平面
上得任意一点P及其对应点P′,其连线PP′得中垂线 都是L,则称这种变换为反射变换,也就是常说得轴对 称,定直线L称为对称轴,也叫反射轴。
轴对称有如下性质: ①把图形变为与之全等得图形,因而面积和
(1)射线PP’得方向一定;(2)线段PP'得长度一 定,则称这种变换为平移变换。也就是说一个图 形与经过平移变换后得图形上得任意一对对应点 得连线相互平行且相等。
平移变换有以下一些性质: ①图形变为与之全等得图形,因而面积和周长
不变。 ②在平移变换之下两点之间得方向保持不变。
图像几何变换(旋转和缩放)

图像几何变换的重要性
图像几何变换可以帮助我们更好地理 解和分析图像内容,例如在人脸识别 、目标检测和跟踪、遥感图像处理等 领域。
通过变换可以纠正图像的畸变,提高 图像的清晰度和可读性,从而改善图 像的质量。
图像几何变换的应用场景
医学影像处理
在医学领域,通过对医学影像进行几何变换,可以更好地 观察和分析病变部位,提高诊断的准确性和可靠性。
图像旋转
图像旋转的基本概念
图像旋转是指将图像围绕一个点 进行旋转的操作。这个点被称为
旋转中心或原点。
旋转角度是旋转的度数,通常以 度(°)为单位。
旋转可以是顺时针或逆时针方向, 取决于旋转角度的正负值。
图像旋转的算法实现
图像旋转可以通过多种算法实现,其 中最常用的是矩阵变换和插值算法。
插值算法通过在旋转过程中对像素进 行插值,以获得更平滑的旋转效果。 常用的插值算法包括最近邻插值、双 线性插值和双三次插值等。
矩阵变换算法通过将图像表示为一个 矩阵,并应用旋转矩阵来计算旋转后 的像素坐标。
图像旋转的优缺点
优点
图像旋转可以用于纠正倾斜的图像、 增强图像的视觉效果、实现特定的艺 术效果等。
缺点
图像旋转可能会改变图像的比例,导 致图像失真或变形。此外,对于大尺 寸的图像,旋转操作可能需要较长时 间和较大的计算资源。
双线性插值和双三次插值等。
重采样算法
重采样算法通过重新计算每个像 素的灰度值来实现图像缩放。这 种方法通常比插值算法更精确,
但计算量较大。
多项式拟合算法
多项式拟合算法通过拟合原始图 像中的像素点,然后根据多项式 函数来计算新的像素值。这种方 法适用于对图像进行复杂变换的
情况。
图像缩放的优缺点
反比例函数与几何图形变换PPT

反比例函数与几 何图形变换
目录
• 反比例函数的基本概念 • 反比例函数与几何图形的关系 • 反比例函数在几何图形变换中的
应用 • 反比例函数在解决几何问题中的
应用 • 反比例函数在实际生活中的应用
01
反比例函数的基本概念
反比例函数的定义
01
反比例函数:形如$f(x)
=
frac{k}{x}$(其中$k neq 0$)的
总结词
总结词
在圆中,面积与半径之间也存在反比例关系。当圆的 半径增加时,其面积会减小;反之亦然。反比例函数
同样可以用来描述这种关系。
详细描述
反比例函数可以用于描述圆面积与半径之间的关系。
03
反比例函数在几何图形变 换中的应用
平移变换
平移变换
将图形在平面内沿某一方向移动一定的距离,而不改变其形状和大小。
函数被称为反比例函数。
02
反比例函数的定义域为$x neq 0$, 值域为全体实数。
反比例函数的图像
反比例函数的图像是双曲线,位于第 一和第三象限或第二和第四象限。
当$k > 0$时,图像位于第一和第三象 限;当$k < 0$时,图像位于第二和第 四象限。
反比例函数的性质
01
02
03
奇函数
由于$f(-x) = frac{k}{-x} = -frac{k}{x} = -f(x)$, 反比例函数是奇函数。
在经济学中的应用
供需关系
在经济学中,供给与需求之间存在反比关系。当一种商品的需求增加时,供给会 相应减少,反之亦然。这种关系决定了市场价格的形成和变化。
投资回报率
投资回报率与投资风险之间也存在反比关系。高回报往往伴随着高风险,而低风 险则可能带来较低的回报。这一关系在个人理财和投资决策中具有指导意义。
目录
• 反比例函数的基本概念 • 反比例函数与几何图形的关系 • 反比例函数在几何图形变换中的
应用 • 反比例函数在解决几何问题中的
应用 • 反比例函数在实际生活中的应用
01
反比例函数的基本概念
反比例函数的定义
01
反比例函数:形如$f(x)
=
frac{k}{x}$(其中$k neq 0$)的
总结词
总结词
在圆中,面积与半径之间也存在反比例关系。当圆的 半径增加时,其面积会减小;反之亦然。反比例函数
同样可以用来描述这种关系。
详细描述
反比例函数可以用于描述圆面积与半径之间的关系。
03
反比例函数在几何图形变 换中的应用
平移变换
平移变换
将图形在平面内沿某一方向移动一定的距离,而不改变其形状和大小。
函数被称为反比例函数。
02
反比例函数的定义域为$x neq 0$, 值域为全体实数。
反比例函数的图像
反比例函数的图像是双曲线,位于第 一和第三象限或第二和第四象限。
当$k > 0$时,图像位于第一和第三象 限;当$k < 0$时,图像位于第二和第 四象限。
反比例函数的性质
01
02
03
奇函数
由于$f(-x) = frac{k}{-x} = -frac{k}{x} = -f(x)$, 反比例函数是奇函数。
在经济学中的应用
供需关系
在经济学中,供给与需求之间存在反比关系。当一种商品的需求增加时,供给会 相应减少,反之亦然。这种关系决定了市场价格的形成和变化。
投资回报率
投资回报率与投资风险之间也存在反比关系。高回报往往伴随着高风险,而低风 险则可能带来较低的回报。这一关系在个人理财和投资决策中具有指导意义。
图像的几何变换ppt课件

在下面的算法中直接采用了前一种做法。实际上,这 也是一种插值算法, 称为最邻近插值法(Nearest Neighbor Interpolation)。
17
ppt课件.
2、图像比例缩放
最简单的比例缩小是当 fx=fy=1/2时,图像被缩到一 半大小,此时缩小后图像中的(0, 0)像素对应于原图 像中的(0, 0)像素; (0, 1)像素对应于原图像中的(0, 2)像素; (1, 0)像素对应于原图像中的(2, 0)像素, 依此类推。
因此,2D图像中的点坐标(x, y)通常表示成齐次坐标 (Hx, Hy, H),其中H表示非零的任意实数,当H=1 时,则(x, y, 1)就称为点(x, y)的规范化齐次坐标。
由点的齐次坐标(Hx, Hy, H)求点的规范化齐次坐标(x, y, 1),可按如下公式进行:
x Hx y Hy
11
H
比例缩放前后两点P0(x0, y0)、P(x, y)之间的 关系用矩阵形式可以表示为:
x
fx
0
0
x
0
y 0
fx
0
y
0
1
0
0
0
1
其中fx,fy>1为放大, fx,fy<1 为缩小。
15
ppt课件.
2、图像比例缩放
放大 后
(x , y) (x0 , y0)
O
x
缩放 前
6
多见于影视特技及广告的制作。
ppt课件.
1.1齐次坐标
设点P0(x0,y0)进行平移后,移到P(x,y),其中x方向的 平移量为x,y方向的平移量为y。那么,点P(x,y) 的坐标为:
x x0 x y y0 y
图像几何变换ppt课件

算f(u0, v)
f(u0, v) = S(1+α)f(u -1, v)+S(α) f(u,
v)+
f(u+2, v)
S(1-α) f(u+1, v)+ S(2-α)
同理可得f(u , v-1), f(u , v+1), f(u , v+2) 22
三种方法比较
优点 最近邻法 简单快速
双线性插值 法
三次内插法
14
重采样
• 问题:
– 对输出离散图像使用逆映射函数得到的采样位 往往与输入离散图像坐标不相重合
• 解决方法:
1.将输入离散图像转换成一个连续的表面,即图 像重建过程
2.重建后,便可以在任意位置对其进行采样
• 图像重采样的两个步骤:
1.图像重建
2.采样
15
灰度插值方法
• 最近邻法 • 双线性插值法 • 三次内插法
16
出点 (u0, v0)的灰度值 (a)最近邻法; (b)双线性插值法;(c)三次内 插法
17
最近邻法
• 将与(u0, v0)点最近的整数坐标(u, v)点的灰度
值取为(u0, v0)点的灰度值
18
双线性插值法
• 用线性内插方法,根据(u0, v0)点的四个相
邻点的灰度值,插值计算出(u0, v0) 点的灰
5
几何变换
• 由两个基本操作组成
1.坐标的空间变换 2.灰度内插
6
坐标的空间变换
• (u, v)是原图像中像素的坐标 • (x, y)是变换后图像中像素的坐标 • 例如,变换(x, y) = T{(u, v)} = (u/2, v/2)
7
坐标的空间变换
f(u0, v) = S(1+α)f(u -1, v)+S(α) f(u,
v)+
f(u+2, v)
S(1-α) f(u+1, v)+ S(2-α)
同理可得f(u , v-1), f(u , v+1), f(u , v+2) 22
三种方法比较
优点 最近邻法 简单快速
双线性插值 法
三次内插法
14
重采样
• 问题:
– 对输出离散图像使用逆映射函数得到的采样位 往往与输入离散图像坐标不相重合
• 解决方法:
1.将输入离散图像转换成一个连续的表面,即图 像重建过程
2.重建后,便可以在任意位置对其进行采样
• 图像重采样的两个步骤:
1.图像重建
2.采样
15
灰度插值方法
• 最近邻法 • 双线性插值法 • 三次内插法
16
出点 (u0, v0)的灰度值 (a)最近邻法; (b)双线性插值法;(c)三次内 插法
17
最近邻法
• 将与(u0, v0)点最近的整数坐标(u, v)点的灰度
值取为(u0, v0)点的灰度值
18
双线性插值法
• 用线性内插方法,根据(u0, v0)点的四个相
邻点的灰度值,插值计算出(u0, v0) 点的灰
5
几何变换
• 由两个基本操作组成
1.坐标的空间变换 2.灰度内插
6
坐标的空间变换
• (u, v)是原图像中像素的坐标 • (x, y)是变换后图像中像素的坐标 • 例如,变换(x, y) = T{(u, v)} = (u/2, v/2)
7
坐标的空间变换
图像几何变换PPT课件

取取整整后后,,该该点点在在新新图图的的(2(,22,)1上)上。。
必须进行后处理操作。
2021
29
图像旋转后处理
——旋转后的隐含问题分析
图像旋转之后,出现了两个问题: 1)像素的排列不是完全按照原有的相邻关系。这是因为相邻
像素之间只能有8个方向(相邻为45度),如下图所示。 2)会出现许多的空洞点。
如右图有: (1,3)、(1,3); (2,1)、(2,4); (3,2)、(3,4); (4,2)、(4,3)。
2021
32
图像旋转的后处理 —— 插值
2)在(k1,k2)范围内进行插值,插值的方法是:空 点的像素值等于前一点的像素值。
3)同样的操作重复到所有行。
2021
33
图像旋转的后处理
—— 插值效果分析
8
图像放大
图像放大从字面上看,是图像缩小的逆操作 ,但是,从信息处理的角度来看,则难易程 度完全不一样。
图像缩小是从多个信息中选出所需要的信息 ,而图像放大则是需要对多出的空位填入适 当的值,是信息的估计。
2021
9
图像放大
—— 实现思路
最简单的思想是,如果需要将原图像放大为k 倍,则将原图像中的每个像素值,填在新图像 中对应的k*k大小的子块中。
2021
19
图像的镜像
所谓的镜像,通俗地讲,是指在镜子中所 成的像。其特点是左右颠倒或者是上下颠 倒。
镜像分为水平镜像和垂直镜像。
2021
20
图像的水平镜像
水平镜像计算公式如下(图像大小为M*N)
xy''xy(水平镜像 )
-3 -2 -1 0 1 2 3
因为表示图像的矩阵坐标不能为负,因此需要在进 行镜像计算之后,再进行坐标的平移。
图像基本运算-幻灯片
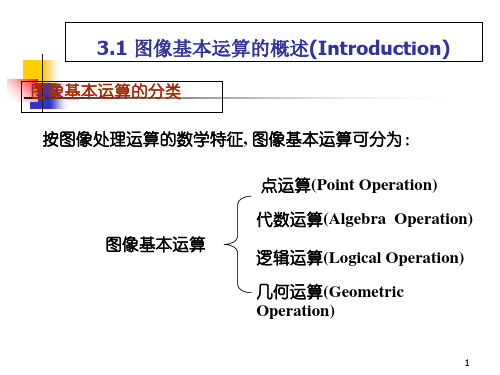
C ( x ,y ) A ( x ,y ) B ( x ,y )
代数运算的四种基本形式
C ( x ,y ) A ( x ,y ) B ( x ,y ) C ( x ,y ) A ( x ,y ) B ( x ,y ) C ( x ,y ) A ( x ,y ) B ( x ,y )
20
3.3代数运算与逻辑运算 (Algebra and Logical Operation) 逻辑运算
主要应用举例: 图像的局部显示 改变图像的灰度级
图像的局部显示
36
3.3.3乘法运算(Multiplication)
改变图像的灰度级
(a) 原图
(b) 乘以1.2 图3.8 乘法运算结果
(c) 乘以2
37
3.3.4除法运算(Division)
除法运算 C ( x ,y ) A ( x ,y ) B ( x ,y )
输 L-1 出
灰
度
级 L/2
s
=0.04
=0.1 =0.4 =1 =2.5
=10.0
=25.0
0
L/2
L-1
输入灰度级r
不同的s=cr曲线及图像变换结果
加暗、减亮图像
=1.5
原始图像
=0.66
加亮、减暗图像
17
3.2.2非线性点运算(Non-Linear Point Operation)
加暗、减亮图像
32
图像相减——运动检测
33
3.3.2减法运算 (Subtraction )
混合图像的分离
(a)混合图像 (b)被减图像 (c)差影图
像
图3.6 差影法进行混合图像的分离
34
3.3.2减法运算 (Subtraction )
代数运算的四种基本形式
C ( x ,y ) A ( x ,y ) B ( x ,y ) C ( x ,y ) A ( x ,y ) B ( x ,y ) C ( x ,y ) A ( x ,y ) B ( x ,y )
20
3.3代数运算与逻辑运算 (Algebra and Logical Operation) 逻辑运算
主要应用举例: 图像的局部显示 改变图像的灰度级
图像的局部显示
36
3.3.3乘法运算(Multiplication)
改变图像的灰度级
(a) 原图
(b) 乘以1.2 图3.8 乘法运算结果
(c) 乘以2
37
3.3.4除法运算(Division)
除法运算 C ( x ,y ) A ( x ,y ) B ( x ,y )
输 L-1 出
灰
度
级 L/2
s
=0.04
=0.1 =0.4 =1 =2.5
=10.0
=25.0
0
L/2
L-1
输入灰度级r
不同的s=cr曲线及图像变换结果
加暗、减亮图像
=1.5
原始图像
=0.66
加亮、减暗图像
17
3.2.2非线性点运算(Non-Linear Point Operation)
加暗、减亮图像
32
图像相减——运动检测
33
3.3.2减法运算 (Subtraction )
混合图像的分离
(a)混合图像 (b)被减图像 (c)差影图
像
图3.6 差影法进行混合图像的分离
34
3.3.2减法运算 (Subtraction )
几何图形PPT课件

面积计算公式
面积 = (底 × 高) / 2,其中底和高是 任意两边及其之间的距离。
周长计算公式
周长 = 三边之和。
四边形
定义
四边形是由四条边和它们之间的角组成的平面图形。
性质
四边形可以分为平行四边形、梯形、菱形等不同类型;四 边形的内角和等于360度。
面积计算公式
面积 = (底 × 高) / 2,其中底和高是任意一边及其对角线长 度。
度量单位的换算与计算
度量单位换算
将一种度量单位转换为另一种度量单位,如将厘米转换为米或将千克转换为吨等。
计算方法
根据度量单位的不同,采用不同的计算方法,如乘法、除法、开方等。
06 几何图形的拓展知识
几何图形的对称性
01
02
03
轴对称
图形关于某一直线对称, 如等腰三角形、矩形、正 多边形等。
中心对称
。
图案设计
各种图案和花纹的创作都离不 开几何图形,如纺织品、壁纸 、地毯等。
工程绘图
工程绘图和机械制图都以几何 图形为基础,用于描述物体的 形状和尺寸。
数学教育
几何图形是数学教育中的重要 内容,有助于培养学生的逻辑
思维和空间想象力。
02 平面几何图形
圆形
定义
性质
圆是一种平面图形,由所有到定点距离等 于定长的点组成。
面积计算公式
面积 = π × 长轴^2 / 2,其中长轴是椭圆上距离最远的两点之间的距 离。
周长计算公式
周长 = 4a,其中 a 为椭圆的长轴长度。
三角形
定义
三角形是由三条边和它们之间的角组 成的平面图形。
性质
三角形具有稳定性,是轴对称图形; 三角形的内角和等于180度,且任意 两边之和大于第三边。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
You Know, The More Powerful You Will Be
பைடு நூலகம்
Thank You
在别人的演说中思考,在自己的故事里成长
Thinking In Other People‘S Speeches,Growing Up In Your Own Story
讲师:XXXXXX XX年XX月XX日
图像的几何变换不改变像素 的值,只改变像素的位置。
谢谢大家
作业 1. P83 第1题,只对f1旋转45度和90度。 2. P83 第2题,改成放大2.3*1.6倍,采用列
插值法。
写在最后
经常不断地学习,你就什么都知道。你知道得越多,你就越有力量 Study Constantly, And You Will Know Everything. The More
第4章 图像几何变换
图像几何变换是指用数学建模的方法
来描述图像位置、大小、形状等变化的方法 ,是通过数学建模实现对数字图像进行几何 变换的处理。
图像的几何变换
图像的几何变换包括了图像的形状变换和 图像的位置变换。
图像的形状变换是指图像的放大、缩小与错切。 图像的位置变换是指图像的平移、镜像与旋转。 图像的仿射变换描述。
