专题复习空间中的平行关系

合集下载

空间中的平行与垂直例题和知识点总结

空间中的平行与垂直例题和知识点总结在立体几何的学习中，空间中的平行与垂直关系是非常重要的内容。

理解和掌握这些关系，对于解决相关的几何问题具有关键作用。

下面我们通过一些例题来深入探讨，并对相关知识点进行总结。

一、平行关系（一）线线平行1、定义：如果两条直线在同一平面内没有公共点，则这两条直线平行。

2、判定定理：如果平面外一条直线与此平面内的一条直线平行，那么该直线与此平面平行。

例 1：在正方体 ABCD A₁B₁C₁D₁中，E，F 分别是 AB，BC 的中点，求证：EF∥A₁C₁。

证明：连接 AC，因为 E，F 分别是 AB，BC 的中点，所以 EF∥AC。

又因为正方体中，AC∥A₁C₁，所以 EF∥A₁C₁。

（二）线面平行1、定义：如果一条直线与一个平面没有公共点，则称这条直线与这个平面平行。

2、判定定理：平面外一条直线与此平面内的一条直线平行，则该直线与此平面平行。

例 2：已知四棱锥 P ABCD 的底面是平行四边形，M 是 PC 的中点，求证：PA∥平面 MBD。

证明：连接 AC 交 BD 于 O，连接 MO。

因为四边形 ABCD 是平行四边形，所以 O 是 AC 的中点。

又因为 M 是 PC 的中点，所以MO∥PA。

因为 MO⊂平面 MBD，PA⊄平面 MBD，所以 PA∥平面MBD。

（三）面面平行1、定义：如果两个平面没有公共点，则称这两个平面平行。

2、判定定理：一个平面内的两条相交直线与另一个平面平行，则这两个平面平行。

例 3：在正方体 ABCD A₁B₁C₁D₁中，求证：平面 A₁BD∥平面 B₁D₁C。

证明：因为 A₁B∥D₁C，A₁D∥B₁C，且 A₁B 和 A₁D 是平面A₁BD 内的两条相交直线，D₁C 和 B₁C 是平面 B₁D₁C 内的两条相交直线，所以平面 A₁BD∥平面 B₁D₁C。

二、垂直关系（一）线线垂直1、定义：如果两条直线所成的角为 90°，则这两条直线垂直。

1.2.2空间中的平行关系4

五、定理运用形成技能
例2、已知点P 是平行四边形ABCD所在平面外一点，
分别是 E, F上的点，
① 若E、F分别为PA、BD的中点，求证：EF // 面PBC
P
P
E
E
N
D
C
D
C
F
A
B
F
M
A
B
五、定理运用形成技能
例2、已知点P 是平行四边形ABCD所在平面外一点，
分别是 E, F上的点，
① 若E、F分别为PA、BD的中点，求证：EF // 面PBC
D1
S
C1
A1
P •
N
B1 R
Q
M
D
C
A
B
六、收获感悟总结提高
一、直线与平面平行的判定定理二、证明直线与平面平行的方法三、运用判定定理时的几个要点四、运用定理的关键：找平行线五、立体几何的基本思想：化归
七、分层作业共同进步
谢谢！
a // c
又由P a, P c a c P
故假设不成立，所以a //
矛盾！
五、定理运用形成技能
例1、空间四边形ABCD中，E,F分别AB,AD的中点．判断并证明EF与平面BCD的位置关系.
变式1、把上题中“△ABD”改为“梯形BDHG”，E、F 分别是BG、DH的中点，判断并证明 EF与平面BCD 的位置关系．
一、复习回顾
在空间中，直线与平面有哪几种位置关系？
一、复习回顾
在空间中，直线与平面有哪几种位置关系？
文字语言图形语言符号语言
直线在
平面内 α a
a
直线与平面直线与的位置关系平面相交
a A

高考数学一轮复习考点知识专题讲解52---直线、平面平行的判定与性质

高考数学一轮复习考点知识专题讲解直线、平面平行的判定与性质考点要求1.理解空间中直线与直线、直线与平面、平面与平面的平行关系，并加以证明.2.掌握直线与平面、平面与平面平行的判定与性质，并会简单应用．知识梳理1．线面平行的判定定理和性质定理文字语言图形语言符号语言判定定理平面外一条直线与此平面内的一条直线平行，那么该直线与此平面平行错误!⇒a∥α性质定理一条直线与一个平面平行，则过这条直线的任一平面与此平面的交线与该直线平行错误!⇒a∥b2．面面平行的判定定理和性质定理文字语言图形语言符号语言判定定理一个平面内的两条相交直线与另一个平面平行，那么这两个平面平行错误!⇒β∥α性质定理如果两个平行平面同时和第三个平面相交，那么它们的交线平行错误!⇒a∥b常用结论(1)垂直于同一条直线的两个平面平行，即若a⊥α，a⊥β，则α∥β.(2)平行于同一个平面的两个平面平行，即若α∥β，β∥γ，则α∥γ.(3)垂直于同一个平面的两条直线平行，即a⊥α，b⊥α，则a∥b.(4)若α∥β，a⊂α，则a∥β.思考辨析判断下列结论是否正确(请在括号中打“√”或“×”)(1)若一条直线平行于一个平面内的一条直线，则这条直线平行于这个平面．(×)(2)若直线a∥平面α，P∈α，则过点P且平行于直线a的直线有无数条．(×)(3)若直线a⊂平面α，直线b⊂平面β，a∥b，则α∥β.(×)(4)如果两个平面平行，那么分别在这两个平面内的两条直线平行或异面．(√)教材改编题1．下列说法中，与“直线a∥平面α”等价的是()A．直线a上有无数个点不在平面α内B．直线a与平面α内的所有直线平行C．直线a与平面α内无数条直线不相交D．直线a与平面α内的任意一条直线都不相交答案D解析因为a∥平面α，所以直线a与平面α无交点，因此a和平面α内的任意一条直线都不相交．2．已知不重合的直线a，b和平面α，则下列选项正确的是()A．若a∥α，b⊂α，则a∥bB．若a∥α，b∥α，则a∥bC．若a∥b，b⊂α，则a∥αD．若a∥b，a⊂α，则b∥α或b⊂α答案D解析若a∥α，b⊂α，则a∥b或异面，A错；若a∥α，b∥α，则a∥b或异面或相交，B错；若a∥b，b⊂α，则a∥α或a⊂α，C错；若a∥b，a⊂α，则b∥α或b⊂α，D对．3.如图是长方体被一平面所截得的几何体，四边形EFGH为截面，则四边形EFGH的形状为______．答案平行四边形解析∵平面ABFE∥平面DCGH，又平面EFGH∩平面ABFE＝EF，平面EFGH∩平面DCGH＝HG，∴EF∥HG.同理EH∥FG，∴四边形EFGH是平行四边形．题型一直线与平面平行的判定与性质命题点1直线与平面平行的判定例1如图，在四棱锥P－ABCD中，底面ABCD是平行四边形，E，F分别是BC，PD的中点，求证：(1)PB∥平面ACF；(2)EF∥平面PAB.证明(1)如图，连接BD交AC于O，连接OF，∵四边形ABCD 是平行四边形， ∴O 是BD 的中点，又∵F 是PD 的中点， ∴OF ∥PB ，又∵OF ⊂平面ACF ，PB ⊄平面ACF ， ∴PB ∥平面ACF .(2)取PA 的中点G ，连接GF ，BG . ∵F 是PD 的中点， ∴GF 是△PAD 的中位线， ∴GF 綉12AD ，∵底面ABCD 是平行四边形，E 是BC 的中点， ∴BE 綉12AD ，∴GF 綉BE ，∴四边形BEFG 是平行四边形， ∴EF ∥BG ，又∵EF ⊄平面PAB ，BG ⊂平面PAB ， ∴EF ∥平面PAB .命题点2直线与平面平行的性质例2如图所示，在四棱锥P －ABCD 中，四边形ABCD 是平行四边形，M 是PC 的中点，在DM上取一点G，过G和PA作平面交BD于点H.求证：PA∥GH.证明如图所示，连接AC交BD于点O，连接OM，∵四边形ABCD是平行四边形，∴O是AC的中点，又M是PC的中点，∴PA∥OM，又OM⊂平面BMD，PA⊄平面BMD，∴PA∥平面BMD，又平面PAHG∩平面BMD＝GH，∴PA∥GH.教师备选如图，四边形ABCD是矩形，P∉平面ABCD，过BC作平面BCFE交AP于点E，交DP于点F，求证：四边形BCFE是梯形．证明∵四边形ABCD为矩形，∴BC∥AD.∵AD⊂平面PAD，BC⊄平面PAD，∴BC∥平面PAD.∵平面BCFE∩平面PAD＝EF，BC⊂平面BCFE，∴BC∥EF.∵AD＝BC，AD≠EF，∴BC≠EF，∴四边形BCFE是梯形．思维升华(1)判断或证明线面平行的常用方法①利用线面平行的定义(无公共点)．②利用线面平行的判定定理(a⊄α，b⊂α，a∥b⇒a∥α)．③利用面面平行的性质(α∥β，a⊂α⇒a∥β)．④利用面面平行的性质(α∥β，a⊄β，a∥α⇒a∥β)．(2)应用线面平行的性质定理的关键是确定交线的位置，有时需要经过已知直线作辅助平面确定交线．跟踪训练1如图所示，已知四边形ABCD是正方形，四边形ACEF是矩形，M是线段EF的中点．(1)求证：AM∥平面BDE；(2)若平面ADM∩平面BDE＝l，平面ABM∩平面BDE＝m，试分析l与m的位置关系，并证明你的结论．(1)证明如图，记AC与BD的交点为O，连接OE.因为O，M分别为AC，EF的中点，四边形ACEF是矩形，所以四边形AOEM是平行四边形，所以AM∥OE.又因为OE⊂平面BDE，AM⊄平面BDE，所以AM∥平面BDE.(2)解l∥m，证明如下：由(1)知AM∥平面BDE，又AM⊂平面ADM，平面ADM∩平面BDE＝l，所以l∥AM，同理，AM∥平面BDE，又AM⊂平面ABM，平面ABM∩平面BDE＝m，所以m∥AM，所以l∥m.题型二平面与平面平行的判定与性质例3如图所示，在三棱柱ABC－A1B1C1中，过BC的平面与上底面A1B1C1交于GH(GH与B1C1不重合)．(1)求证：BC∥GH；(2)若E，F，G分别是AB，AC，A1B1的中点，求证：平面EFA1∥平面BCHG.证明(1)∵在三棱柱ABC－A1B1C1中，∴平面ABC∥平面A1B1C1，又∵平面BCHG∩平面ABC＝BC，且平面BCHG∩平面A1B1C1＝HG，∴由面面平行的性质定理得BC∥GH.(2)∵E，F分别为AB，AC的中点，∴EF∥BC，∵EF⊄平面BCHG，BC⊂平面BCHG，∴EF∥平面BCHG.又G，E分别为A1B1，AB的中点，A1B1綉AB，∴A1G綉EB，∴四边形A1EBG是平行四边形，∴A1E∥GB.∵A1E⊄平面BCHG，GB⊂平面BCHG，∴A1E∥平面BCHG.又∵A 1E ∩EF ＝E ，A 1E ，EF ⊂平面EFA 1， ∴平面EFA 1∥平面BCHG .延伸探究在本例中，若将条件“E ，F ，G 分别是AB ，AC ，A 1B 1的中点”变为“点D ，D 1分别是AC ，A 1C 1上的点，且平面BC 1D ∥平面AB 1D 1”，试求ADDC的值．解如图，连接A 1B 交AB 1于O ，连接OD 1.由平面BC 1D ∥平面AB 1D 1，且平面A 1BC 1∩平面BC 1D ＝BC 1，平面A 1BC 1∩平面AB 1D 1＝D 1O ，所以BC 1∥D 1O ，则A 1D 1D 1C 1＝A 1OOB ＝1.又由题设A 1D 1D 1C 1＝DC AD，所以DC AD＝1，即ADDC＝1.如图，在三棱柱ABC －A 1B 1C 1中，E ，F ，G 分别为B 1C 1，A 1B 1，AB 的中点．(1)求证：平面A 1C 1G ∥平面BEF ；(2)若平面A1C1G∩BC＝H，求证：H为BC的中点．证明(1)∵E，F分别为B1C1，A1B1的中点，∴EF∥A1C1，∵A1C1⊂平面A1C1G，EF⊄平面A1C1G，∴EF∥平面A1C1G，又F，G分别为A1B1，AB的中点，∴A1F＝BG，又A1F∥BG，∴四边形A1GBF为平行四边形，则BF∥A1G，∵A1G⊂平面A1C1G，BF⊄平面A1C1G，∴BF∥平面A1C1G，又EF∩BF＝F，EF，BF⊂平面BEF，∴平面A1C1G∥平面BEF.(2)∵平面ABC∥平面A1B1C1，平面A1C1G∩平面A1B1C1＝A1C1，平面A1C1G与平面ABC有公共点G，则有经过G的直线，设交BC于点H，如图，则A1C1∥GH，得GH∥AC，∵G为AB的中点，∴H为BC的中点．思维升华证明面面平行的常用方法(1)利用面面平行的判定定理．(2)利用垂直于同一条直线的两个平面平行(l⊥α，l⊥β⇒α∥β)．(3)利用面面平行的传递性，即两个平面同时平行于第三个平面，则这两个平面平行(α∥β，β∥γ⇒α∥γ)．跟踪训练2如图，四棱柱ABCD－A1B1C1D1的底面ABCD是正方形．(1)证明：平面A1BD∥平面CD1B1；(2)若平面ABCD∩平面CD1B1＝直线l，证明：B1D1∥l.证明(1)由题设知BB1綉DD1，所以四边形BB1D1D是平行四边形，所以BD∥B1D1.又BD⊄平面CD1B1，B1D1⊂平面CD1B1，所以BD∥平面CD1B1.因为A1D1綉B1C1綉BC，所以四边形A1BCD1是平行四边形，所以A1B∥D1C.又A1B⊄平面CD1B1，D1C⊂平面CD1B1，所以A1B∥平面CD1B1.又因为BD∩A1B＝B，BD，A1B⊂平面A1BD，所以平面A1BD∥平面CD1B1.(2)由(1)知平面A1BD∥平面CD1B1，又平面ABCD∩平面CD1B1＝直线l，平面ABCD∩平面A1BD＝直线BD，所以直线l∥直线BD，在四棱柱ABCD－A1B1C1D1中，四边形BDD1B1为平行四边形，所以B1D1∥BD，所以B1D1∥l.题型三平行关系的综合应用例4如图，在正方体ABCD－A1B1C1D1中，E为DD1的中点．(1)求证：BD1∥平面AEC；(2)CC1上是否存在一点F，使得平面AEC∥平面BFD1，若存在，请说明理由．(1)证明如图，连接BD交AC于O，连接EO.因为ABCD－A1B1C1D1为正方体，底面ABCD为正方形，对角线AC，BD交于O点，所以O为BD的中点，又因为E为DD1的中点，所以在△DBD1中，OE是△DBD1的中位线，所以OE∥BD1.又因为OE⊂平面AEC，BD1⊄平面AEC，所以BD1∥平面AEC.(2)解当CC1上的点F为中点时，即满足平面AEC∥平面BFD1.连接BF，D1F，因为F为CC1的中点，E为DD1的中点，所以CF綉ED1，所以四边形CFD1E为平行四边形，所以D1F∥EC，又因为EC⊂平面AEC，D1F⊄平面AEC，所以D1F∥平面AEC.由(1)知BD1∥平面AEC，又因为BD1∩D1F＝D1，BD1，D1F⊂平面BFD1，所以平面AEC∥平面BFD1.教师备选如图，四边形ABCD与ADEF均为平行四边形，M，N，G分别是AB，AD，EF的中点．求证：(1)BE∥平面DMF；(2)平面BDE∥平面MNG.证明(1)如图，连接AE，则AE必过DF与GN的交点O，连接MO，则MO为△ABE的中位线，所以BE∥MO.又BE⊄平面DMF，MO⊂平面DMF，所以BE∥平面DMF.(2)因为N，G分别为平行四边形ADEF的边AD，EF的中点，所以DE∥GN，又DE⊄平面MNG，GN⊂平面MNG，所以DE∥平面MNG.又M为AB的中点，所以MN为△ABD的中位线，所以BD∥MN，又MN⊂平面MNG，BD⊄平面MNG，所以BD∥平面MNG，又DE，BD⊂平面BDE，DE∩BD＝D，所以平面BDE∥平面MNG.思维升华证明平行关系的常用方法熟练掌握线线、线面、面面平行关系间的相互转化是解决线线、线面、面面平行的综合问题的关键．面面平行判定定理的推论也是证明面面平行的一种常用方法．跟踪训练3如图所示，四边形EFGH为空间四边形ABCD的一个截面，若截面为平行四边形．(1)求证：AB∥平面EFGH；(2)若AB＝4，CD＝6，求四边形EFGH周长的取值范围．(1)证明∵四边形EFGH为平行四边形，∴EF∥HG.∵HG ⊂平面ABD ，EF ⊄平面ABD ， ∴EF ∥平面ABD . 又∵EF ⊂平面ABC ，平面ABD ∩平面ABC ＝AB ， ∴EF ∥AB ，又∵AB ⊄平面EFGH ，EF ⊂平面EFGH ， ∴AB ∥平面EFGH . (2)解设EF ＝x (0<x <4)，由(1)知EF ∥AB ， ∴CF CB ＝EF AB ＝x 4，与(1)同理可得CD ∥FG ， ∴FG CD ＝BF BC，则FG 6＝BF BC ＝BC －CF BC ＝1－x 4， ∴FG ＝6－32x .∴四边形EFGH 的周长L ＝2⎝ ⎛⎭⎪⎫x ＋6－32x ＝12－x . 又∵0<x <4， ∴8<L <12，故四边形EFGH 周长的取值范围是(8,12)．课时精练1．(2022·宁波模拟)下列命题中正确的是()A．若a，b是两条直线，且a∥b，那么a平行于经过b的任何平面B．若直线a和平面α满足a∥α，那么a与α内的任何直线平行C．平行于同一条直线的两个平面平行D．若直线a，b和平面α满足a∥b，a⊂α，b⊄α，则b∥α答案D解析A中，a可以在过b的平面内；B中，a与α内的直线也可能异面；C中，两平面可能相交；D中，由直线与平面平行的判定定理知b∥α，正确．2．设l是直线，α，β是两个不同的平面，则下列能判断l∥α的是()A．l∥β，α∥βB．l与平面α内无数条直线平行C．l⊂β，α∥βD．l⊥β，α⊥β答案C解析对于A，l可能在α内，故不能判断l∥α，故A不正确；对于B，l可能在α内，故不能判断l∥α，故B不正确；对于C，因为l⊂β，α∥β，由面面平行的定义得l∥α，故C正确；对于D，l可能在α内，故不能判断l∥α，故D不正确．3．(2022·成都模拟)如图，在三棱柱ABC－A1B1C1中，AM＝2MA1，BN＝2NB1，过MN作一平面分别交底面△ABC的边BC，AC于点E，F，则()A．MF∥EB B．A1B1∥NEC．四边形MNEF为平行四边形 D．四边形MNEF为梯形答案D解析由于B，E，F三点共面，F∈平面BEF，M∉平面BEF，故MF，EB为异面直线，故A错误；由于B1，N，E三点共面，B1∈平面B1NE，A1∉平面B1NE，故A1B1，NE为异面直线，故B错误；∵在平行四边形AA1B1B中，AM＝2MA1，BN＝2NB，1∴AM∥BN，AM＝BN，故四边形AMNB为平行四边形，∴MN∥AB.又MN⊄平面ABC，AB⊂平面ABC，∴MN∥平面ABC.又MN⊂平面MNEF，平面MNEF∩平面ABC＝EF，∴MN∥EF，∴EF∥AB，显然在△ABC中，EF≠AB，∴EF≠MN，∴四边形MNEF为梯形，故C错误，D正确．4．(2022·杭州模拟)已知P为△ABC所在平面外一点，平面α∥平面ABC，且α交线段PA，PB，PC于点A′，B′，C′，若PA′∶AA′＝2∶3，则S∶S△ABC等于()△A′B′C′A．2∶3 B．2∶5C．4∶9 D．4∶25答案D解析∵平面α∥平面ABC，∴A′C′∥AC，A′B′∥AB，B′C′∥BC，∴S△A′B′C′∶S△ABC＝(PA′∶PA)2，又PA′∶AA′＝2∶3，∴PA′∶PA＝2∶5，∴S△A′B′C′∶S△ABC＝4∶25.5．如图，在下列四个正方体中，A，B为正方体的两个顶点，M，N，Q为所在棱的中点，则在这四个正方体中，直线AB与平面MNQ不平行的是()答案D解析A项，由正方体性质可知AB∥NQ，NQ⊂平面MNQ，AB⊄平面MNQ，AB∥平面MNQ，排除；B，C项，由正方体性质可知AB∥MQ，MQ⊂平面MNQ，AB⊄平面MNQ，AB∥平面MNQ，排除；D项，由正方体性质易知，直线AB与平面MNQ不平行，满足题意．6．如图，透明塑料制成的长方体容器ABCD－A1B1C1D1内灌进一些水，固定容器一边AB于地面上，再将容器倾斜，随着倾斜程度的不同，有下面几个结论，其中正确的是()①没有水的部分始终呈棱柱形；②水面EFGH所在四边形的面积为定值；③随着容器倾斜程度的不同，A1C1始终与水面所在平面平行；④当容器倾斜如图(3)所示时，AE·AH为定值．A．①② B．①④C．②③ D．③④答案B解析根据棱柱的特征(有两个面互相平行，其余各面都是四边形，并且每相邻两个四边形的公共边都互相平行)，结合题中图形易知①正确；由题图可知水面EFGH的边EF的长保持不变，但邻边的长却随倾斜程度而改变，可知②错误；因为A1C1∥AC，AC⊂平面ABCD，A 1C 1⊄平面ABCD ，所以A 1C 1∥平面ABCD ，当平面EFGH 不平行于平面ABCD 时，A 1C 1不平行于水面所在平面，故③错误；当容器倾斜如题图(3)所示时，因为水的体积是不变的，所以棱柱AEH －BFG 的体积V 为定值，又V ＝S △AEH ·AB ，高AB 不变，所以S △AEH 也不变，即AE ·AH 为定值，故④正确．7．考查①②两个命题，①⎭⎪⎬⎪⎫m ⊂αl ∥m ⇒l ∥α；②⎭⎪⎬⎪⎫l ∥m m ∥α⇒l ∥α，它们都缺少同一个条件，补上这个条件就可以使其构成真命题(其中l ，m 为直线，α为平面)，则此条件为__________．答案l ⊄α解析①由线面平行的判定定理知l ⊄α；②由线面平行的判定定理知l ⊄α.8.如图所示，在正四棱柱ABCD －A 1B 1C 1D 1中，E ，F ，G ，H 分别是棱CC 1，C 1D 1，D 1D ，DC 的中点，N 是BC 的中点，点M 在四边形EFGH 及其内部运动，则M 只需满足条件______，就有MN ∥平面B 1BDD 1.(注：请填上你认为正确的一个条件即可，不必考虑全部可能情况)答案点M 在线段FH 上(或点M 与点H 重合) 解析连接HN ，FH ，FN (图略)，则FH ∥DD 1，HN ∥BD ，∴平面FHN ∥平面B 1BDD 1，只需M ∈FH ，则MN ⊂平面FHN ，∴MN ∥平面B 1BDD 1.9.如图，在正方体ABCD －A 1B 1C 1D 1中，E ，F ，G ，H 分别是BC ，CC 1，C 1D 1，AA 1的中点，求证：(1)BF ∥HD 1； (2)EG ∥平面BB 1D 1D ； (3)平面BDF ∥平面B 1D 1H . 证明如图．(1)取B 1B 的中点M ，连接HM ，MC 1，易证四边形HMC 1D 1是平行四边形， ∴HD 1∥MC 1. 又MC 1∥BF ， ∴BF ∥HD 1.(2)取BD 的中点O ，连接OE ，OD 1，则OE 綉12DC .又D 1G 綉12DC ，∴OE綉D1G.∴四边形OEGD1是平行四边形，∴EG∥D1O.又D1O⊂平面BB1D1D，EG⊄平面BB1D1D，∴EG∥平面BB1D1D.(3)由(1)知BF∥HD1，由题意易证B1D1∥BD.又B1D1，HD1⊂平面B1D1H，BF，BD⊂平面BDF，且B1D1∩HD1＝D1，DB∩BF＝B，∴平面BDF∥平面B1D1H.10.如图，在四棱锥P－ABCD中，AD∥BC，AB＝BC＝12AD，E，F，H分别为线段AD，PC，CD的中点，AC与BE交于O点，G是线段OF上一点．(1)求证：AP∥平面BEF；(2)求证：GH∥平面PAD.证明(1)如图，连接EC，因为AD∥BC，BC＝12 AD，所以BC∥AE，BC＝AE，所以四边形ABCE是平行四边形，所以O为AC的中点．又因为F是PC的中点，所以FO ∥AP ，因为FO ⊂平面BEF ，AP ⊄平面BEF ，所以AP ∥平面BEF .(2)连接FH ，OH ，因为F ，H 分别是PC ，CD 的中点，所以FH ∥PD ，因为PD ⊂平面PAD ，FH ⊄平面PAD ，所以FH ∥平面PAD .又因为O 是BE 的中点，H 是CD 的中点，所以OH ∥AD ，因为AD ⊂平面PAD ，OH ⊄平面PAD ，所以OH ∥平面PAD .又FH ∩OH ＝H ，FH ，OH ⊂平面OHF ，所以平面OHF ∥平面PAD . 又因为GH ⊂平面OHF ，所以GH ∥平面PAD .11．(2022·福州检测)如图所示，正方体ABCD －A 1B 1C 1D 1中，点E ，F ，G ，P ，Q 分别为棱AB ，C 1D 1，D 1A 1，D 1D ，C 1C 的中点，则下列叙述中正确的是()A．直线BQ∥平面EFGB．直线A1B∥平面EFGC．平面APC∥平面EFGD．平面A1BQ∥平面EFG答案B解析过点E，F，G的截面如图所示(H，I分别为AA1，BC的中点)，连接A1B，BQ，AP，PC，易知BQ与平面EFG相交于点Q，故A错误；∵A1B∥HE，A1B⊄平面EFG，HE⊂平面EFG，∴A1B∥平面EFG，故B正确；AP⊂平面ADD1A1，HG⊂平面ADD1A1，延长HG与PA必相交，故C错误；易知平面A1BQ与平面EFG有交点Q，故D错误．12.如图所示，正方体ABCD－A1B1C1D1的棱长为3，M，N分别是棱A1B1，B1C1的中点，P是棱AD上的一点，AP＝1，过P，M，N的平面交上底面于PQ，Q在CD上，则PQ＝________.答案2 2解析因为平面ABCD∥平面A1B1C1D1，平面ABCD∩平面PQNM＝PQ，平面A1B1C1D1∩平面PQNM＝MN，所以MN∥PQ，又因为MN∥AC，所以PQ∥AC.又因为AP＝1，所以PDAD＝DQCD＝PQAC＝23，所以PQ＝23AC＝23×32＝2 2.13．在正四棱柱ABCD－A1B1C1D1中，O为底面ABCD的中心，P是DD1的中点，设Q是CC1上的点，则点Q满足条件________时，有平面D1BQ∥平面PAO.答案Q为CC1的中点解析如图所示，设Q为CC1的中点，因为P为DD1的中点，所以QB∥PA.连接DB，因为P，O分别是DD1，DB的中点，所以D1B∥PO，又D1B⊄平面PAO，QB⊄平面PAO，PO⊂平面PAO，PA⊂平面PAO，所以D1B∥平面PAO，QB∥平面PAO，又D1B∩QB＝B，D1B，QB⊂平面D1BQ，所以平面D 1BQ ∥平面PAO .故Q 为CC 1的中点时，有平面D 1BQ ∥平面PAO .14．在三棱锥P －ABC 中，PB ＝6，AC ＝3，G 为△PAC 的重心，过点G 作三棱锥的一个截面，使截面平行于PB 和AC ，则截面的周长为________．答案8解析如图，过点G 作EF ∥AC ，分别交PA ，PC 于点E ，F ，过点E 作EN ∥PB 交AB 于点N ，过点F 作FM ∥PB 交BC 于点M ，连接MN ，则四边形EFMN 是平行四边形(平面EFMN 为所求截面)，且EF ＝MN ＝23AC ＝2，FM ＝EN ＝13PB ＝2，所以截面的周长为2×4＝8.15．(2022·合肥市第一中学模拟)正方体ABCD －A 1B 1C 1D 1的棱长为1，点M ，N 分别是棱BC ，CC 1的中点，动点P 在正方形BCC 1B 1(包括边界)内运动，且PA 1∥平面AMN ，则PA 1的长度范围为()A.⎣⎢⎡⎦⎥⎤1，52B.⎣⎢⎡⎦⎥⎤324，52C.⎣⎢⎡⎦⎥⎤324，32 D.⎣⎢⎡⎦⎥⎤1，32答案B解析取B 1C 1的中点E ，BB 1的中点F ，连接A 1E ，A 1F ，EF ，取EF 的中点O ，连接A 1O ，如图所示，∵点M ，N 分别是棱长为1的正方体ABCD －A 1B 1C 1D 1中棱BC ，CC 1的中点， ∴AM ∥A 1E ，MN ∥EF ，∵AM ∩MN ＝M ，A 1E ∩EF ＝E ，AM ，MN ⊂平面AMN ，A 1E ，EF ⊂平面A 1EF ， ∴平面AMN ∥平面A 1EF ，∵动点P 在正方形BCC 1B 1(包括边界)内运动，且PA 1∥平面AMN ， ∴点P 的轨迹是线段EF ， ∵A 1E ＝A 1F ＝12＋⎝ ⎛⎭⎪⎫122＝52，EF ＝1212＋12＝22， ∴A 1O ⊥EF ，∴当P 与O 重合时，PA 1的长度取最小值A 1O ，A 1O ＝⎝ ⎛⎭⎪⎫522－⎝ ⎛⎭⎪⎫242＝324，当P 与E (或F )重合时，PA 1的长度取最大值A 1E 或A 1F ，A 1E ＝A 1F ＝52.∴PA 1的长度范围为⎣⎢⎡⎦⎥⎤324，52.16．(2022·郑州模拟)如图，在三棱锥P －ABC 中，AC ，BC ，PC 两两垂直，AC ＝BC ，E ，F 分别是AC ，BC 的中点，△ABC 的面积为8，四棱锥P －ABFE 的体积为4.(1)若平面PEF ∩平面PAB ＝l ，求证：EF ∥l ； (2)求三棱锥P －ABC 的表面积． (1)证明∵E ，F 分别是AC ，BC 的中点， ∴EF ∥AB ，∵AB ⊂平面PAB ，EF ⊄平面PAB ， ∴EF ∥平面PAB .又平面PEF ∩平面PAB ＝l ，EF ⊂平面PEF ， ∴EF ∥l .(2)解∵AC ，BC ，PC 两两垂直，AC ∩BC ＝C ，AC ，BC ⊂平面ABC ， ∴PC ⊥平面ABC ，即PC 是四棱锥P －ABFE 的高． ∵S △ABC ＝8，AC ＝BC ，AC ⊥BC ， ∴AC ＝BC ＝4.∵E ，F 分别是AC ，BC 的中点，V P －ABFE ＝4， ∴13×34×12AC ×BC ×PC ＝4，即PC ＝2. ∴PA ＝42＋22＝25，PB ＝42＋22＝25，AB ＝42＋42＝4 2.∴△PAB的面积为12×42×(25)2－⎝⎛⎭⎪⎫4222＝4 6.∴三棱锥P－ABC的表面积S＝2×12×4×2＋8＋46＝16＋4 6.。

立体几何复习专题及答案-高中数学

立体几何复习专题姓名：班级：考点一、空间中的平行关系1．如图，在三棱锥P ABC -中，02,3,90PA PB AB BC ABC ====∠=,平面PAB ⊥平面ABC ，D 、E 分别为AB 、AC 的中点． (1)求证：DE //平面PBC ； (2)求证：AB PE ⊥；(3)求三棱锥B PEC -的体积．2．如图，在四棱锥P ABCD -中，底面ABCD 为平行四边形，PCD △为等边三角形，平面PAC ⊥平面PCD ，PA CD ⊥，2CD =，3AD =，（Ⅰ）设G H ，分别为PB AC ，的中点，求证：GH ∥平面PAD ；（Ⅱ）求证：PA ⊥平面PCD ；3．如图，七面体ABCDEF 的底面是凸四边形ABCD ，其中2AB AD ==，120BAD ∠=︒，AC ，BD 垂直相交于点O ，2OC OA =，棱AE ，CF 均垂直于底面ABCD .（1）证明：直线DE 与平面BCF 不．平行；4.（2014新课标Ⅱ）如图，四棱锥P ABCD -中，底面ABCD 为矩形，PA ⊥平面ABCD ，E 为PD 的中点．（Ⅰ）证明：PB ∥平面AEC ；（Ⅱ）设二面角D AE C --为60°，AP =1，AD =3，求三棱锥E ACD -的体积．考点二、空间中的垂直关系5．如图，在四面体ABCD 中，E ，F 分别是线段AD ，BD 的中点，90ABD BCD ∠=∠=，2EC =，2AB BD ==，直线EC 与平面ABC 所成的角等于30．（1）证明：平面EFC ⊥平面BCD ；6．已知某几何体的直观图和三视图如下图所示，其中正视图为矩形，侧视图为等腰直角三角形，俯视图为直角梯形．（1）求证：BN ⊥平面11C B N ；（2）设M 为AB 中点，在C B 边上求一点P ，使//MP 平面1C NB ，求CBPP 的值．7．（2016全国I ）如图，在以A ，B ，C ，D ，E ，F 为顶点的五面体中，面ABEF为正方形，2AF FD =，90AFD ∠=，且二面角D AF E --与二面角C BE F --都是60．（I ）证明：平面ABEF⊥平面EFDC ；（II ）求二面角E BC A --的余弦值．考点三、折叠问题和探究性问题中的位置关系8．如图 1，在直角梯形ABCD 中， //,AB CD AB AD ⊥，且112AB AD CD ===．现以AD 为一边向外作正方形ADEF ，然后沿边AD 将正方形ADEF 翻折，使ADEF 平面与平面ABCD 垂直， M 为ED 的中点，如图 2．（1）求证： //AM 平面BEC ；（2）求证： BC ⊥平面BDE ； .9．如图，在边长为4的正方形ABCD 中，点E,F 分别是AB,BC 的中点，点M 在AD 上，且14AM AD =，将AED,DCF 分别沿DE,DF 折叠，使A,C 点重合于点P ，如图所示2.()1试判断PB 与平面MEF的位置关系，并给出证明；()2求二面角M EF D --的余弦值.10．如图所示，直角梯形ABCD 中，//AD BC ，AD AB ⊥，22AB BC AD ===，四边形EDCF 为矩形，3CF =，平面EDCF ⊥平面ABCD ． (1)求证：DF //平面ABE ；(2)求平面ABE 与平面EFB 所成锐二面角的余弦值． (3)在线段DF 上是否存在点P ，使得直线BP 与平面ABE 所成角的正弦值为34，若存在，求出线段BP 的长，若不存在，请说明理由．11．如图1，在边长为4的正方形ABCD中，E是AD的中点，F是CD的中点，现-.将三角形DEF沿EF翻折成如图2所示的五棱锥P ABCFE（1）求证：AC//平面PEF；（2）若平面PEF⊥平面ABCFE，求直线PB与平面PAE所成角的正弦值.12．（2011•浙江）如图，在三棱锥P﹣ABC中，AB=AC，D为BC的中点，PO⊥平面ABC，垂足O落在线段AD上，已知BC=8，PO=4，AO=3，OD=2（1）证明：AP⊥BC；（2）在线段AP上是否存在点M，使得二面角A﹣MC﹣β为直二面角？若存在，求出AM的长；若不存在，请说明理由．13．如图，在直三棱柱111ABC A B C -中，底面ABC 为等边三角形，122CC AC ==.（Ⅰ）求三棱锥11C CB A -的体积；（Ⅱ）在线段1BB 上寻找一点F ，使得1CF AC ⊥，请说明作法和理由.考点四、知空间角求空间角问题14．（2014天津）如图四棱锥P ABCD -的底面ABCD 是平行四边形，2BA BD ==2AD =,5PA PD ==E ,F 分别是棱AD ,PC 的中点．（Ⅰ）证明: EF ∥平面PAB ；（Ⅱ）若二面角P AD B --为60°，（ⅰ）证明：平面PBC ⊥平面ABCD（ⅱ）求直线EF 与平面PBC 所成角的正弦值． PCDBF15．四棱锥P ABCD -中，底面ABCD 为矩形，PA ABCD ⊥平面，E 为PD 的中点．(1)证明：//E PB A C 平面；(2)设13AP AD ==，，三棱锥P ABD -的体积34V =，求二面角D -AE -C 的大小16．如图，四棱锥P ABCD -中， PA ⊥底面ABCD ，底面ABCD 是直角梯形，90ADC ∠=︒， //AD BC ， AB AC ⊥， 2AB AC ==，点E 在AD 上，且2AE ED =．（Ⅰ）已知点F 在BC 上，且2=CF FB ，求证：平面PEF ⊥平面PAC ；（Ⅱ）当二面角--A PB E 的余弦值为多少时，直线PC 与平面PAB 所成的角为45︒？立体几何专题参考答案1． (1)证明：∵在△ABC 中，D 、E 分别为AB 、AC 的中点，∴DE ∥BC . ∵DE ⊄平面PBC 且BC ⊂平面PBC ，∴DE ∥平面PBC . (2)证明：连接PD .∵PA ＝PB ，D 为AB 的中点，∴PD ⊥AB .∵DE ∥BC ，BC ⊥AB ，∴DE ⊥AB .又∵PD 、DE 是平面PDE 内的相交直线， ∴AB ⊥平面PDE .∵PE ⊂平面PDE ，∴AB ⊥PE .(3)解：∵PD ⊥AB ，平面PAB ⊥平面ABC ，平面PAB ∩平面ABC ＝AB ，∴PD ⊥平面ABC ，可得PD 是三棱锥P －BEC 的高．又∵33,2BECPD S==，1332B PEC P BEC BEC V V S PD --∆∴==⨯=. 2．（I ）见解析；（II ）见解析；（III ）33. （I ）证明：连接BD ，易知AC BD H ⋂=，BH DH =，又由BG PG =，故GHPD ，又因为GH ⊄平面PAD ，PD ⊂平面PAD ，所以GH ∥平面PAD .（II ）证明：取棱PC 的中点N ，连接DN ，依题意，得DN PC ⊥，又因为平面PAC ⊥平面PCD ，平面PAC平面PCD PC =，所以DN ⊥平面PAC ，又PA ⊂平面PAC ，故DN PA ⊥，又已知PA CD ⊥，CD DN D =，所以PA ⊥平面PCD . 3．（1）见解析；（2）23535本卷由系统自动生成，请仔细校对后使用，答案仅供参考。

高二数学复习1：空间中的平行与垂直关系

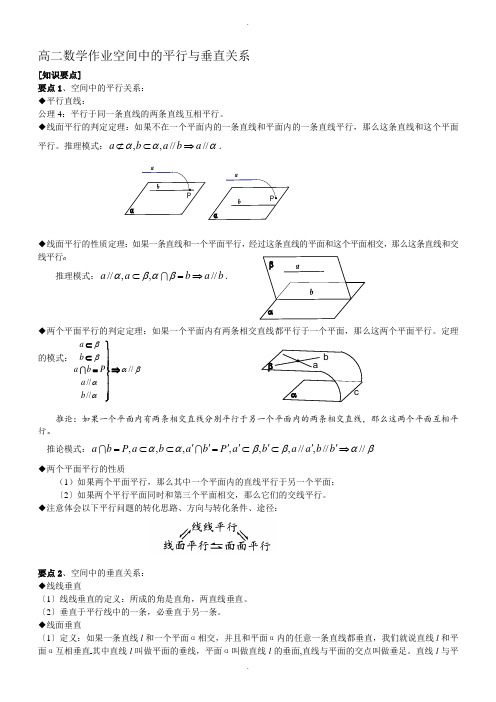
.高二数学作业空间中的平行与垂直关系[知识要点]要点1、空间中的平行关系： ◆平行直线：公理4：平行于同一条直线的两条直线互相平行。

◆线面平行的判定定理：如果不在一个平面内的一条直线和平面内的一条直线平行，那么这条直线和这个平面平行。

推理模式：,,////a b a b a ααα⊄⊂⇒．◆线面平行的性质定理：如果一条直线和一个平面平行，经过这条直线的平面和这个平面相交，那么这条直线和交线平行推理模式：//,,//a a b a b αβαβ⊂=⇒．◆两个平面平行的判定定理：如果一个平面内有两条相交直线都平行于一个平面，那么这两个平面平行。

定理的模式：//////a b a b P a b ββαβαα⊂⎫⎪⊂⎪⎪=⇒⎬⎪⎪⎪⎭推论：如果一个平面内有两条相交直线分别平行于另一个平面内的两条相交直线，那么这两个平面互相平行。

推论模式：,,,,,,//,////a b P a b a b P a b a a b b ααββαβ'''''''=⊂⊂=⊂⊂⇒◆两个平面平行的性质（1）如果两个平面平行，那么其中一个平面内的直线平行于另一个平面；〔2〕如果两个平行平面同时和第三个平面相交，那么它们的交线平行。

◆注意体会以下平行问题的转化思路、方向与转化条件、途径：要点2、空间中的垂直关系： ◆线线垂直〔1〕线线垂直的定义：所成的角是直角，两直线垂直。

〔2〕垂直于平行线中的一条，必垂直于另一条。

◆线面垂直〔1〕定义：如果一条直线l 和一个平面α相交，并且和平面α内的任意一条直线都垂直，我们就说直线l 和平面α互相垂直其中直线l 叫做平面的垂线，平面α叫做直线l 的垂面,直线与平面的交点叫做垂足。

直线l 与平bab aααP P ab βαc b a βα2面α垂直记作：l ⊥α。

〔2〕直线与平面垂直的判定定理：如果一条直线和一个平面内的两条相交直线都垂直，那么这条直线垂直于这个平面。

高一数学空间中的平行关系

Байду номын сангаас
济南市长清第一中学
考点二平面与平面平行的判定与性质
1、设直线l，m，平面α，β，下列条件能得出α∥β的有( )
①l⊂α，m⊂α，且l∥β，m∥β； ②l⊂α，m⊂α，且l∥m，l∥β，m∥β； ③l∥α，m∥β，且l∥m； ④l∩m＝P，l⊂α，m⊂α，且l∥β，m∥β. A．1个 B．2个 C．3个 D．0个
高中数学一年级
空间中的平行关系复习课
目录
1 知识回顾 2 考点一直线与平面平行的判定与性质 3 考点二平面与平面平行的判定与性质 4 考点三线面、面面平行的综合应用
知识回顾：
一、直线与直线平行
1、基本事实4：平行于同一条直线的两条直线平行。
2、判定直线与直线平行的常用方法：（1）三角形中利用中位线定理（2）构造平行四边形（3）平行线的传递性（4）平行线分线段成比例
故面GFH∥面ACD
方法二取BE的中点M,连接GM,FM
G, M , F分别是CE, BE, AE的中点
GM // BC, FM // AB
又 GM 面GMF , FM 面GMF , AB 面ABC, BC 面ABC
GM FM M, AB BC B 面GMF // 面ABC
GF 面GMF
GF // 面ABC
考点一直线与平面平行的判定与性质
1.“直线与平面内无数条直线平行”是“直线//平面”
的（）
A．充要条件
B．充分不必要条件
C．必要不充分条件 D．既不充分也不必要条件
答案：C
2．如图，已知四边形ABCD是平行四边形，点P是平面ABCD外一点，M是PC的中点，在DM上取一点G，过G和AP作平面交平面BDM于GH．求证：

高中数学《空间的平行关系》复习和习题课件PPT

过关练习
巩固练习
过关练习
ห้องสมุดไป่ตู้固练习
过关练习
同学们！再见！
课后一定要多练习哦！
(2)直线与平面平行的判定定理：平面α外的一条直线l与平面α内的一条直线m
平行，则直线l与平面α平行.(线线平行线面平行)
(3)直线与平面平行的性质定理：已知直线l与平面α平行，且经过直线l的平面β
与平面α相交于直线m，则直线l与直线m平行.(线面平行线线平行)
知识清单
知识点四平面与平面的平行
典例精析
例
变式训练
变式训练3
下列说法正确的是（）. A．经过平面外一点有且仅有一条直线平行于这个平面 B．经过平面外一点有且仅有一条直线垂直于这个平面 C．经过直线外一点有且仅有一个平面平行于这条直线 D．经过直线外一点有且仅有一条直线垂直于这条直线
巩固练习
过关练习
巩固练习
过关练习
巩固练习
知识清单
知识点二直线与平面的位置关系
直线与平面的三种位置关系：直线在平面内、直线与平面相交、直线与平面平行.
(1)直线在平面内：直线上的所有点都在平面内. (2)直线与平面相交：直线与平面只有唯一一个公共点. (3)直线与平面平行：直线与平面没有公共点.
知识清单
知识点三直线与平面的平行
(1)直线与平面平行的定义：若直线l与平面α没有公共点，则称直线l与平面α平行.
线都与另一个平面平行.(面面平行线面平行)
典例精析
例
变式训练
变式训练1
如图92所示，AB、CD是夹在两个平行平面α、β之间的线段，M、N分别为AB、CD的中点. 求证：MN∥平面α．
典例精析
例
变式训练

专题复习：空间中的平行关系

3、线线平行
中位线定理
平行四边形性质平行公理线面平行性质定理（2）空间中的线线平行：面面平行性质定理线面垂直性质定理
（1）平面中的线线平行：比例关系
P F P F
M
E B A C
D
B
E
A C
D
N
空间平行关系的常见判定方法：
1、线面平行（1）利用线面平行的定义（无公共点）；（2）利用线面平行的判定定理；（3）利用面面平行的性质.
空间平行关系的常见判定方法：
2、面面平行
（1）利用面面平行的定结论：垂直于同一条直线的两个平面
A1 G
H
C1
B1
A E
F B
C
探究：如图，已知三棱柱ABC-A1B1C1中，底面为正三角形，侧棱与底面垂直，点E，F分别是CC1，BB1上的点，点M是棱AC上的动点，且EC=2FB，当M在何位置时，BM//平面AEF？
当堂检测
1、如图，在直三棱柱ABC A1 B1C1中，AB AC， D为BC中点，四边形B1 BCC1是正方形，求证：A1 B //平面AC1 D.
a // a // b
；
；
（3） , b , a // , b // a
//
；
（4）
// , a , b a // b .
空间中的平行关系
判定定理
线线平行
线面平行
判定定理定义
面面平行
性质定理性质定理
例1、如图，已知点P是平行四边形ABCD所在平面外一点，E，F分别是AB，PD的中点，求证：AF//平面PCE
M
N
2、如图，在正方体ABCD A1 B1C1 D1中，E、F 分别为棱AD、AB的中点．求证：EF //平面CB1 D1.

高考一轮复习第七章第四节空间中的平行关系

[答案] 2
返回
[巧练模拟]——————(课堂突破保分题，分分必保！)
1．(2012· 抚顺模拟)已知 m，n 表示两条不同直线，α，β，γ 表示不同平面，给出下列三个命题：
m⊥α (1) n⊥α m⊥α (3) n∥α
⇒m∥n；
m⊥α (2) m⊥n
⇒n∥α
⇒α∥β
行，那么这两个平
面平行
返回
2.两平面平行的性质定理：文字语言性如果两个平行平面时质与第三个平面相交，定那么它们的交线平理行图形语言符号语言 α∥β α∩γ＝a β∩γ＝b
⇒a∥b
返回
返回
1．(教材习题改编)下列条件中，能判断两个平面平行的是 ( )
返回
返回
[考题范例] (12分)(2012· 太原模拟)如图，在四棱锥S－ABCD中，已知底面 ABCD为直角梯形，其中AD∥BC，∠BAD＝90° ，SA⊥底面 ABCD，SA＝AB＝BC＝2.tan∠SDA＝ (1)求四棱锥S－ABCD的体积； (2)在棱SD上找一点E，使CE∥平面SAB，并证明． 2 3
⇒a∥α
定理
2．性质定理：文字语言性质定理如果一条直线和一个平面平行，经过这条 a∥α a⊂β α∩β＝b
⇒a∥b
图形语言
符号语言
直线的平面和这个平
面相交，那么这条直线就和交线平行.
返回
四、平面与平面平行 1．判定定理：文字语言如果一个平面内有判定定理两条相交直线平行于另一个平面平图形语言符号语言 a⊂α b⊂α a∩b＝P a∥β b∥β
返回
[步步满分] 2 (1)∵SA⊥底面ABCD，tan∠SDA＝3，SA＝2， ∴AD＝3.(3分) 由题意知四棱锥S－ABCD的底面为直角梯形，且SA＝AB＝BC＝2， 1 1 VS－ABCD＝3×SA×2×(BC＋AD)×AB 1 1 10 ＝3×2×2×(2＋3)×2＝ 3 .(6分)

空间中的平行关系

【答案】 B 【解析】如图所示，联结BE,BD. 因为点 N 为正方形 ABCD的中心， △ ECD为正三角形，平面 ECD 平面 ABCD， M 是线段 ED的中点，所以 BM 平面 BDE， EN BDE 平面，因为 BM 是 △ BDE中 DE边上的中线， EN 是 △ BDE中 BD边上的中线，直线 BM ， EN 是相交直线，
BM=EN,且直线BM、EN 是相交直线
已知m,n,l是不同的直线,α,β是不同的平面,以下命题正确的是( )
AE CF 同理可得MQ∥BD,又MN⊥QM,则AC⊥BD,故A、B正确. 【解析】如图 ,由得 AC//EF. ①若m∥n,m⊂α,n⊂β,则α∥β; ②若m⊂α,n⊂β,α∥β,l⊥m,则l⊥n; EB FB 因为D点为AB的中点,
A.
B.
C.
D.
【答案】A 【解析】选项B,由AB∥MQ,则直线AB∥平面MNQ; 选项C,由AB∥MQ,则直线AB∥平面MNQ; 选项D,由AB∥NQ,则直线AB∥平面MNQ.
11.如图,在三棱柱ABC-A1B1C1中,各个侧面均是边长为2的正方形,D为线段AC的中点.求证:直线AB1∥平面BC1D.
专题训练
1.已知m,n,l是不同的直线,α,β是不同的平面,以下命题正确的是( )
①若m∥n,m⊂α,n⊂β,则α∥β; ②若m⊂α,n⊂β,α∥β,l⊥m,则l⊥n;
③若m⊥α,n⊥β,α∥β,则m∥n; ④若α⊥β,m∥α,n∥β,则m⊥n.
A.①③
B.③④
C.②④
D.③
【答案】D 【解析】 ①若m∥n,m⊂α,n⊂β,则α∥β或α,β相交; ②若m⊂α,n⊂β,α∥β,l⊥m,则l⊥n或l∥n或l,n异面; ③正确; ④若α⊥β,m∥α,n∥β,则m⊥n或m∥n或m,n异面.

空间几何的平行与垂直关系知识点总结

空间几何的平行与垂直关系知识点总结在空间几何中，平行与垂直关系是非常重要的概念，它们贯穿于整个几何学习的始终。

理解和掌握这些关系对于解决空间几何问题至关重要。

下面，我们就来详细总结一下空间几何中平行与垂直关系的相关知识点。

一、线线平行1、平行线的定义在同一平面内，不相交的两条直线叫做平行线。

2、线线平行的判定定理（1）同位角相等，两直线平行。

（2）内错角相等，两直线平行。

（3）同旁内角互补，两直线平行。

3、线线平行的性质定理（1）两直线平行，同位角相等。

（2）两直线平行，内错角相等。

（3）两直线平行，同旁内角互补。

4、空间中直线平行的传递性如果两条直线都与第三条直线平行，那么这两条直线也互相平行。

二、线面平行1、线面平行的定义如果一条直线与一个平面没有公共点，那么这条直线与这个平面平行。

2、线面平行的判定定理如果平面外一条直线与此平面内的一条直线平行，那么该直线与此平面平行。

3、线面平行的性质定理如果一条直线与一个平面平行，经过这条直线的平面与这个平面相交，那么这条直线与交线平行。

三、面面平行1、面面平行的定义如果两个平面没有公共点，那么这两个平面平行。

2、面面平行的判定定理（1）如果一个平面内有两条相交直线都平行于另一个平面，那么这两个平面平行。

（2）如果两个平面都平行于同一条直线，那么这两个平面平行。

3、面面平行的性质定理（1）如果两个平面平行，那么其中一个平面内的直线平行于另一个平面。

（2）如果两个平行平面都和第三个平面相交，那么它们的交线平行。

四、线线垂直1、线线垂直的定义如果两条直线所成的角为直角，那么这两条直线互相垂直。

2、线线垂直的判定定理（1）如果一条直线垂直于一个平面，那么这条直线垂直于平面内的任意一条直线。

（2）如果两条平行线中的一条垂直于一条直线，那么另一条也垂直于这条直线。

五、线面垂直1、线面垂直的定义如果一条直线与一个平面内的任意一条直线都垂直，那么这条直线与这个平面垂直。

【精编】高考复习课件第53讲空间中的平行关系-精心整理

点评：证面面平行的基本方法是利用面面平行的判定定理，即转化为证线面平行．
【变式探究】
2．如图，已知 ABC-A1B1C1 是正三棱柱，E，F 分别是 AC， A1C1 的中点．求证：平面 AB1F∥平面 BEC1.
证明：因为 E、F 分别是 AC、A1C1 的中点，所以 AE＝FC1.又因为 AE∥FC1，所以四边形 AEC1F 是平行四边形，所以 AF∥EC1. 因为 EC1⊂平面 BEC1，AF⊄平面 BEC1，所以 AF∥平面 BEC1. 连接 EF.因为 EF∥BB1，EF＝BB1，所以四边形 BB1FE 是平行四边形，所以 B1F∥BE，B1F⊄平面 BEC1，BE⊂平面 BEC1，所以 B1F∥平面 BEC1. 因为 AF，B1F 是平面 AB1F 内的相交直线，所以平面 AB1F∥平面 BEC1.
制作不易尽请参考
(4)如果一条直线与两个平行平面中的一个相交，那么它与另一个也相交．
(5)一条直线垂直于两个平行平面中的一个平面，必垂直于另一个平面．
(6)夹在两个平行平面间的平行线段相等． (7)两平行平面间的距离处处相等． (8)平行于同一条直线的两条直线平行． (9)平行于同一个平面的两个平面平行． (10)平行于同一直线的两个平面平行或相交． (11)平行于同一个平面的两条直线平行、相交或异面．
(2)平面 BEG∥平面 ACH.证明如下：因为 ABCD-EFGH 为正方体，所以 BC∥FG，BC＝FG. 又 FG∥EH，FG＝EH，所以 BC∥EH，BC＝EH，于是四边形 BCHE 为平行四边形，所以 BE∥CH. 又 CH⊂平面 ACH，BE⊄平面 ACH，所以 BE∥平面 ACH. 同理 BG∥平面 ACH. 又 BE∩BG＝B，所以平面 BEG∥平面 ACH.

空间中的平行关系(复习带有详细答案)

空间中的平行关系1．设α，β，γ是三个互不重合的平面，m，n是两条不重合的直线，则下列命题中正确的是A、若α⊥β，β⊥γ，则α⊥γB、若α//β，m⊄β，m//α，则m//βC、若α⊥β，m⊥α，则m//βD、若m//α，n//β，α⊥β，则m⊥n 【答案】B【解析】解：利用平面的线面的位置关系，可知，两个平行平面，如果不在平面内的一条直线平行于其中一个平面，必定平行与另一个平面。

选项A还可能平行。

选项C，线可能在面内。

选项D中，线线的位置关系不定。

2．若直线a与平面α相交与一点Ａ，则下列结论正确的是（）A.α内的所有直线与a异面Ｂ.α内不存在与a平行的直线Ｃ.α内存在唯一的直线与a平行Ｄ.α内的直线与a都相交【答案】B【解析】略3．已知直线l、m 、n 与平面α、β给出下列四个命题：①若m∥l，n∥l，则m∥n；②若m⊥α，m∥β，则α⊥β；③若m∥α，n∥α，则m∥n；④若m⊥β，α⊥β，则m∥α其中，假命题的个数是（）A、1B、2C、3D、4【答案】B【解析】略4．若直线l平行于平面α内的无数条直线，则下列结论正确的是A、//⊂lαB、lαC、lα⊄D、lα与不相交【答案】D【解析】略5．下列命题中lα①若直线l上有无数点不在平面α内，则//②若直线l 与平面α平行，则l 与平面α内任意一条直线平行③若直线l 与平面α平行，则l 与平面α内的任意一条直线都没有公共点 ④若直线l 平行于α内无数条直线，则//l α⑤如果两条平行线中的一条与一个平面平行，那么另一条也与这个平面平行其中正确的个数是（）A 、0B 、1C 、2D 、3 【答案】B 【解析】略6．给定下列四个命题：①若一个平面内的两条直线与另一个平面都平行，那么这两个平面相互平行；②若一个平面经过另一个平面的垂线，那么这两个平面相互垂直； ③垂直于同一直线的两条直线相互平行；④若两个平面垂直，那么一个平面内与它们的交线不垂直的直线与另一个平面也不垂直．其中，为真命题的是( )A ．①和②B ．②和③C ．③和④D ．②和④ 【答案】D 【解析】略7．α、β是两个不重合的平面，a 、b 是两条不同直线，在下列条件下，可判定α∥β的是( )A ．α、β都平行于直线a 、bB ．α内有三个不共线点A 、B 、C 到β的距离相等 C ．a 、b 是α内两条直线，且a ∥β，b ∥βD ．a 、b 是两条异面直线且a ∥α，b ∥α，a ∥β，b ∥β 【答案】A 【解析】略8．已知直线平面，则“平面平面”是“”的A.充要条件B.充分不必要条件C.必要不充分条件D.既不充分也不必要条件【答案】B 【解析】略9．空间可以确定一个平面的是（）A.两条直线B.一点和一条直线C.一个三角形D.三个点m ⊂α//αβ//m β【解析】略10．已知直线a//平面α,则a 与平面α内的直线的位置关系（） A ．相交 B. 异面 C. 平行 D. 异面或平行【答案】C 【解析】略11．已知a 、b 为直线，γβα、、为平面，有下列四个命题： ①b a b a //////，则，αα ②βαγβγα//，则，⊥⊥ ③βαβα//////，则，a a ④αα////a b b a ，则，⊂其中正确命题的个数有（）Ａ.0个 B.1个 C.2个 D.3个【答案】A 【解析】略12．已知,αβ为互不重合的平面，,m n 为互不重合的直线，给出下列四个命题：①,,m n n m αα⊂若则；②,,,,m n m n m n ααββ⊂⊂若则； ③,,,m n m n αβαβ⊂⊂若则；④,,,,m n m n n αβαβαβ⊥=⊂⊥⊥若则. 其中正确命题的序号是____ ▲ __ __．【答案】④ 【解析】略13．设,m n 是两条不同的直线，βα,是两个不同的平面，有下列四个命题: ①若n m n m //,//,则αα⊂ ②βαβα⊥⊥⊥⊥则,,,n m n m ③若,//,n m n αβ=则m ∥,α且m ∥β④若βαβα//,,则⊥⊥m m其中正确的命题是 ▲ ．（写出所有真命题的序号）．【答案】②④14．设,l m 为两条不同的直线，,αβ为两个不同的平面，下列命题中正确的是．（填序号）①若,//,,l m αβαβ⊥⊥则l m ⊥；②若//,,,l m m l αβ⊥⊥则//αβ； ③若//,//,//,l m αβαβ则//l m ；④若,,,,m l l m αβαββ⊥=⊂⊥则l α⊥．【答案】②④ 【解析】略15．．如图是正方体的表面展开图，在这个正方体中有如下命题：①；②与是异面直线；③与成角；④与成角。

[最新]专题一空间中平行关系的相互转化

专题一空间中平行关系的相互转化一．线面平行的判定定理：①文字语言表述：平面外一条直线与此平面内的一条直线平行，则该直线与此平面平行。

②图形语言表述：③符号语言表述：,,////a b a b a ααα⊄⊂⇒④作用：线线平行⇒线面平行二．面面平行的判定定理：①文字语言表述：一个平面内的两条相交直线与另一个平面平行，则这两个平面平行。

②图形语言表述：③符号语言表述：//,//,,,//a b a b P a b ββαααβ=⊂⊂⇒④作用：线面平行⇒面面平行三．线面平行的性质定理：①文字语言表述：一条直线与一个平面平行，则过这条直线的任一平面与此平面的交线与该直线平行。

②图形语言表述：③符号语言表述：//,,//a a b a b αβαβ⊂=⇒④作用：线面平行⇒线线平行四．面面平行的性质定理：①文字语言表述：如果两个平行平面同时和第三个平面相交，则它们的交线平行。

②图形语言表述：③符号语言表述：//,,//a b a b αβαγβγ==⇒④作用：面面平行⇒线线平行五．面面平行性质的推论：①文字语言表述：两个平面平行，则一个平面内的任何一条直线都与另一个平面平行。

②图形语言表述：③符号语言表述：//,//a a αβαβ⊂⇒④作用：面面平行⇒线面平行小结：线线平行线面平行面面平行专题练习：一、选择题线面平行的判定：1．已知两条相交直线a 、b ，a ∥平面α，则b 与平面α的位置关系 ( )A ｂ∥αB ｂ与α相交C ｂ⊂αD ｂ∥α或ｂ与α相交2．不同直线,m n 和不同平面,αβ，给出下列命题： ( )①////m m αββα⎫⇒⎬⊂⎭ ② //////m n n m ββ⎫⇒⎬⎭③ ,m m n n αβ⊂⎫⇒⎬⊂⎭异面其中假命题有A 0个B 1个C 2个D 3个 3．若将直线、平面都看成点的集合，则直线l ∥平面α可表示为 ( )A l ∉αB l ⊂αC l ≠αD l ∩α＝∅4．平行于同一个平面的两条直线的位置关系是 ( )A 平行B 相交C 异面D 平行或相交或异面5．已知直线l 1、l 2，平面α，l 1∥l 2，l 1∥α，则l 2与α的位置关系是 ( )A l 2∥αB l 2⊂αC l 2∥α或l 2⊂αD l 2与α相交面面平行的判定：6．设直线l,m,平面α,β,下列条件能得出α∥β的有 ( )①l ⊂α,m ⊂α,且l ∥β,m ∥β；②l ⊂α,m ⊂α,且l ∥m ；③l ∥α,m ∥β,且l ∥mA 1个B 2个C 3个D 0个7．已知：命题：P ：α内存在着不共线的三点到平面β的距离均相等；命题：Q ：α∥β，则下面成立的是（） A P ⇒Q ，P ⇐Q B P ⇐Q ，P ⇒Q C P ⇔Q ， D P ⇒Q ， P ⇐Q 8．下列命题中，可以判断平面α∥β的是（）①α，β分别过两条平行直线；②a ，b 为异面直线，α过a 平行b ，β过b 平行a ；A ①B ②C ①②D 无9．下列命题中为真命题的是（） A 平行于同一条直线的两个平面平行 B 垂直于同一条直线的两个平面平行C 若—个平面内至少有三个不共线的点到另—个平面的距离相等，则这两个平面平行．D 若三条直线a 、b 、c 两两平行，则过直线a 的平面中，有且只有—个平面与b ，c 都平行．10．下列命题中正确的是( )①平行于同一直线的两个平面平行； ②平行于同一平面的两个平面平行；③垂直于同一直线的两个平面平行； ④与同一直线成等角的两个平面平行A ①②B ②③C ③④D ②③④线面、面面平行的性质：11．平面α∩平面β＝a ，平面β∩平面γ＝b ，平面γ∩平面α＝c ，若a ∥b ，则c 与a ，b的位置关系是（）A ．c 与a ，b 都异面B ．c 与a ，b 都相交C ．c 至少与a ，b 中的一条相交D ．c 与a ，b 都平行12．如果两个相交平面分别经过两条平行线中的一条，那么它们的交线和这两条平行线的位置关系是（）A ．都平行B ．都相交C ．一个相交，一个平行D ．都异面13．对于直线m 、n 和平面α，下面命题中的真命题是A ．如果m n m ,,αα⊄⊂、n 是异面直线，那么α//nB ．如果m n m ,,αα⊄⊂、n 是异面直线，那么α与n 相交C ．如果m n m ,//,αα⊂、n 共面，那么n m //D ．如果m n m ,//,//αα、n 共面，那么nm //14．已知m 、n 是不重合的直线，α、β是不重合的平面，有下列命题①若m ⊂α，n ∥α，则m ∥n ；②若m ∥α，m ∥β，则α∥β；③若α∩β=n ，m ∥n ，则m ∥α且m ∥β；其中真命题的个数是A ．0B ．1C ．2D ．315．A 、B 是不在直线l 上的两点，则过点A 、B 且与直线l 平行的平面的个数是（）A ．0个B ．1个C ．无数个D ．以上三种情况均有可能二、填空题线面、面面平行的判定：1．经过直线外一点有平面和已知直线平行；2．经过直线外一点直线与已知直线平行；3．经过两条异面直线中的一条与另一条直线平行；4．有以下命题，正确命题的序号是 .①直线与平面没有公共点，则直线与平面平行；②直线与平面内的任何一条直线都不相交，则直线与平面平行；③直线上有两点，它们到平面的距离相等，则直线与平面平行；④直线与平面内的无数条直线不相交，则直线与平面平行5．下列命题中正确的是（填序号）；①一个平面内两条直线都平行于另一个平面，那么这两个平面平行；②如果一个平面内任何一条直线都平行于另一个平面，那么这两个平面平行；③平行于同一直线的两个平面一定相互平行；④如果一个平面内的无数多条直线都平行于另一个平面，那么这两个平面平行；线面、面面平行的性质：6．三个平面两两相交，有三条交线，则这三条交线的位置关系为__________；7．过正方体ABCD—A1B1C1D1的顶点A1、C1、B的平面与底面ABCD所在平面的交线为l，则l与A1C1的位置关系是__________；三、解答题；1．已知四面体ABCD中，M，N分别是△ABC和△ACD的重心，P为AC上一点，且AP：PC=2：1，求证：（1）BD∥面CMN；（2）平面MNP//平面BCD.2．空间四边形ABCD，平行于AD与BC的截面分别交AB，AC，CD，BD于E、F、G、H．求证：四边形EFGH为平行四边形；3 如图：S 是平行四边形A B C D 平面外一点，,M N 分别是,SA BD 上的点，且SM AM =NDBN，求证：//MN 平面SCDC。

空间平行关系课件-2025届高三数学一轮复习

空间平行关系
兹能
基础知识1：直线与平面平行的判定和性质
基础知识2：平面与平面平行的判定和性质
答案解析
【创新方案选题】如图所示，在三棱柱 ABCA1B1C1 中，E，F，G，H 分别是 AB，AC，A1B1， A1C1 的中点，求证：（1）B，C，H，G 四点共面；（2）平面 EFA1∥平面 BCHG. 证明：（1）∵G，H 分别是 A1B1，A1C1 的中点，∴GH 是△A1B1C1 的中位线，∴GH∥B1C1. 又∵B1C1∥BC，∴GH∥BC，∴B，C，H，G 四点共面．（2）∵E，F 分别是 AB，AC 的中点，∴EF∥BC.∵EF⊄平面 BCHG，BC⊂平面 BCHG，
02 答案解析
(2014·安徽)如图，四棱锥 P－ABCD 的底面是边长为 8 的正方形，四条侧棱长均为 2 7.点 G，E，F，H 分别是棱 PB，AB，CD，PC 上共面的四点，平面 GEFH⊥ 平面 ABCD，BC∥平面 GEFH.证明：GH∥EF；证明：因为 BC∥平面 GEFH，BC 平面 PBC，且平面 PBC∩平面 GEFH＝GH，所以 GH∥BC.同理可证：EF∥BC，因此 GH∥EF.
AP
03 答案解析
(2016·北京)如图，在四棱锥 P－ABCD 中，平面 PAD⊥平面 ABCD，PA⊥PD，
PA＝PD，AB⊥AD，AB＝1，AD＝2，AC＝CD＝ 5.在棱 PA 上是否存在点 M；
使得 BM∥平面 PCD？若存在，求AM的值；若不存在，说明理由. AP
解：设 M 是棱 PA 上一点，则存在λ∈[0，1]使得A→M＝λA→P，因此点 M(0，1－λ，
接 EH.
∵H 为 AB1 的中点，且 B1H＝1C1D，B1H∥C1D，而 EF＝1C1D，

高考数学一轮总复习：空间中的平行关系

空间中的平行关系[基础梳理]1．直线与平面平行的判定定理和性质定理因为l∥a，aα，lα，所以l∥α一条直线与一个平面平行，因为l∥α，lβ，α∩β＝b，所以l∥b 2.平面与平面平行的判定定理和性质定理因为a∥β，b∥β，a∩b＝P，aα，bα，所以α∥β1．判定定理续表2.性质定理α∥β且aα⇒a∥β3.线线平行、线面平行、面面平行的相互转化利用线线平行、线面平行、面面平行的相互转化，解决平行关系的判定时，一般遵循从“低维”到“高维”的转化，即从“线线平行”到“线面平行”，再到“面面平行”；而应用性质定理时，其顺序正好相反．在实际应用中，判定定理和性质定理一般要相互结合，灵活运用．[四基自测]1．下列命题中正确的是()A．若a，b是两条直线，且a∥b，那么a平行于经过b的任何平面B．若直线a和平面α满足a∥α，那么a与α内的任何直线平行C．平行于同一条直线的两个平面平行D．若直线a，b和平面α满足a∥b，a∥α，bα，则b∥α答案：D2．下列四个正方体图形中，A，B为正方体的两个顶点，M，N，P分别为其所在棱的中点，能得出AB∥平面MNP的图形的序号是()A．①③B．②③C．①④D．②④答案：C3．在正方体ABCD－A1B1C1D1中，点E是DD1的中点，则BD1与平面ACE的位置关系为________．答案：平行4．(2017·高考全国卷Ⅰ)如图所示，正方体ABCD A1B1C1D1中，M、N、E、F 分别为棱的中点，则面AMN与面DBEF的关系为________．答案：平行考点一直线与平面平行的判定与性质◄考基础——练透[例1](1)(2019·河北石家庄模拟)过三棱柱ABC－A1B1C1的任意两条棱的中点作直线，其中与平面ABB1A1平行的直线共有()A．4条B．6条C．8条D．12条解析：如图所示，H，G，F，I是相应线段的中点，故符合条件的直线只能出现在平面HGFI中，有FI，FG，GH，HI，HF，GI共6条直线，故选B.答案：B(2)如图所示，四边形ABCD是平行四边形，点P是平面ABCD外一点，M是PC的中点，在DM上取一点G，过G和AP作平面交平面BDM于GH.求证：GH∥平面P AD.解析：证明：如图所示，连接AC交BD于点O，连接MO，因为四边形ABCD是平行四边形，所以O是AC的中点，又M是PC的中点，所以AP∥OM.根据直线和平面平行的判定定理，则有P A∥平面BMD.因为平面P AHG∩平面BMD＝GH，根据直线和平面平行的性质定理，所以P A∥GH.因为GH平面P AD，P A平面P AD，所以GH∥平面P AD.方法关键适用题型利用线面平行的判定定理证线面平行在该平面内找或作一直线，证明其与已知直线平行平行线易作出利用面面平行的性质证线面平行过该线找或作一平面，证明其与已知平面平行面面平行较明显利用线面平行性质证线线平行过线作平面，产生交线已知线面平行如图所示，四棱锥P ABCD 中，底面ABCD 是边长为3的菱形，∠ABC ＝60°.P A ⊥平面ABCD ，且P A ＝3.F 在棱P A 上，(1)若F 为P A 的中点，求证PC ∥平面BDF ；(2)若AF ＝1，E 在棱PD 上，且CE ∥平面BDF ，求PE ∶ED 的值．解析：(1)证明：连接AC ，AC ∩BD＝O ，由ABCD 为菱形知O 为AC 的中点， F 为P A 的中点，∴OF ∥PC .OF 平面BDF ，PC 平面BDF .∴PC ∥平面BDF .(2)过E 作EG ∥FD 交AP 于G ，连接CG ，FO .∵EG ∥FD ，EG 平面BDF ，FD 平面BDF ，∴EG ∥平面BDF ，又EG∩CE＝E，CE∥平面BDF，EG，CE平面CGE，∴平面CGE∥平面BDF，又CG平面CGE，∴CG∥平面BDF，又平面BDF∩平面P AC＝FO，CG平面P AC，∴FO∥CG.又O为AC的中点，∴F为AG中点，∴FG＝GP＝1，∴E为PD的中点，PE∶ED＝1∶1.考点二平面平行的判定与性质◄考能力——知法[例2]如图所示，在多面体ABCDEF中，底面ABCD是菱形，四边形BDEF是矩形，平面BDEF⊥平面ABCD，G和H 分别是CE和CF的中点．求证：平面BDGH∥平面AEF.证明：在△CEF中，因为G，H分别是CE，CF的中点，所以GH∥EF，又因为GH平面AEF，EF平面AEF，所以GH∥平面AEF，设AC∩BD＝O，连接OH，在△ACF中，因为OA＝OC，CH＝HF，所以OH∥AF，又因为OH 平面AEF ，AF 平面AEF ，所以OH ∥平面AEF .又因为OH ∩GH ＝H ，OH ，GH 平面BDGH ，所以平面BDGH ∥平面AEF .判定面面平行的4种方法(1)面面平行的定义，即判断两个平面没有公共点． (2)面面平行的判定定理．(3)垂直于同一条直线的两平面平行．(4)平面平行的传递性，即两个平面同时平行于第三个平面，则这两个平面平行．(2019·豫北六校联考)如图所示，正方体ABCD －A 1B 1C 1D 1中，M ，N 分别是A 1B 1，A 1D 1的中点，E ，F 分别是B 1C 1，C 1D 1的中点．(1)求证：四边形BDFE 为梯形； (2)求证：平面AMN ∥平面EFDB . 证明：(1)连接B 1D 1（图略）.∵在△B 1D 1C 1中，E ，F 分别是B 1C 1，C 1D 1的中点， ∴EF ∥B 1D 1且EF ＝12B 1D 1，又知四边形BDD1B1为矩形，∴四边形BDFE为梯形．(2)连接FM（图略），在△A1B1D1中，M，N分别为A1B1，A1D1的中点，∴MN ∥B1D1.由(1)知，EF∥B1D1，∴MN∥EF.在正方形A1B1C1D1中，F为C1D1的中点，M为A1B1的中点，，又∵四边形ADD1A1为正方形，∴四边形ADFM为平行四边形．又∵AM∩MN＝M，DF∩FE＝F，∴平面AMN∥平面EFDB.考点三平行关系的探索问题◄考基础——练透[例3](1)(2019·福建泉州模拟)如图所示，在正方体ABCD－A1B1C1D1中，O为底面ABCD的中点，P是DD1的中点，设Q是CC1上的点，当点Q________时，平面D1BQ∥平面P AO()A．与C重合B．与C1重合C．为CC1的三等分点D．为CC1的中点解析：在正方体ABCD－A1B1C1D1中，∵O为底面ABCD的中心，P是DD1的中点，∴PO∥BD1，当点Q为CC1的中点时，连接PQ，，∴四边形ABQP是平行四边形，∴AP∥BQ，∵AP∩PO＝P，BQ∩BD1＝B，AP、PO平面P AO，BQ、BD1平面D1BQ，∴平面D1BQ∥平面P AO.故选D.答案：D(2)如图所示，在斜三棱柱ABC-A1B1C1中，D，D1分别是AC，A1C1上的点，当AD DC，A1D1D1C1分别为何值时，平面BC1D∥平面AB1D1.解析：如图所示，连接A1B与AB1交于点O，连接OD1.因为平面BC1D∥平面AB1D1，且平面A1BC1∩平面BDC1＝BC1，平面A1BC1∩平面AB1D1＝OD1，所以BC1∥OD1.同理AD1∥DC1.由BC 1∥OD 1，得A 1D 1D 1C 1＝A 1O OB ＝1，即A 1D 1＝D 1C 1. 由AD 1∥DC 1，AD ∥D 1C 1，得四边形ADC 1D 1是平行四边形，所以AD ＝D 1C 1，所以A 1D 1＝DC .所以DC AD ＝A 1D 1D 1C 1＝1，即当AD DC ＝A 1D 1D 1C 1＝1时，平面BC 1D ∥平面AB 1D 1.对于此类问题往往采取逆向思维(1)对命题条件的探索常采用以下三种方法：①先猜后证，即先观察与尝试给出条件再证明；②先通过命题成立的必要条件探索出命题成立的条件，再证明其充分性； ③把几何问题转化为代数问题，探索命题成立的条件．(2)对命题结论的探索常采用以下方法：首先假设结论存在，然后在这个假设下进行推理论证，如果通过推理得到了合乎情的结论，就肯定假设，如果得到了矛盾的结论，就否定假设．在三棱柱ABCA 1B 1C 1中，设D ，E 分别是线段BC ，CC 1的中点，在线段AB 上是否存在一点M ，使直线DE ∥ 平面A 1MC ？请证明你的结论．解析：存在一点M ∈AB ，使DE ∥平面A 1MC .证明如下：取AB的中点M，A1C的中点N，连接EN，DM，MN(图略)．∴四边形DENM为平行四边形，∴MN∥DE，又DE平面A1MC，MN平面A1MC，∴DE∥平面A1MC.故存在点M为AB的中点，使DE∥平面A1MC.直观想象——空间平行关系中的学科素养空间中的平行关系的应用其实质就是转化．甚至可以通过直观想象去理解或找出平行的线或面．[例](2018·高考全国卷Ⅰ)已知正方体的棱长为1，每条棱所在直线与平面α所成的角都相等，则α截此正方体所得截面面积的最大值为()A.334 B.233C.324 D.32解析：如图所示，在正方体ABCD－A1B1C1D1中，平面AB1D1与棱A1A，A1B1，A1D1所成的角都相等，又正方体的其余棱都分别与A1A，A1B1，A1D1平行，故正方体ABCD－A1B1C1D1的每条棱所在直线与平面AB1D1所成的角都相等．如图所示，取棱AB，BB1，B1C1，C1D1，DD1，AD的中点E，F，G，H，M，N，则正六边形EFGHMN所在平面与平面AB1D1平行且面积最大，此截面面积为S正六边形EFGHMN ＝6×12×22×22sin 60°＝334.故选A.答案：A点评：本题是通过直观想象找到最值时的图形位置，再结合线面平行、面面平行的性质求得需要的量.课时规范练A组基础对点练1．(2019·益阳市、湘谭市调研)下图中，G，N，M，H分别是正三棱柱(两0底面为正三角形的直棱柱)的顶点或所在棱的中点，则表示直线GH，MN是异面直线的图形有()A．①③B．②③C．②④D．②③④解析：由题意，可知题图①中，GH∥MN，因此直线GH与MN共面；题图②中，连接GN，G，H，N三点共面，但M平面GHN，因此直线GH与MN异面；题图③中，连接MG，则GM∥HN，因此直线GH与MN共面；题图④中，连接GN，G，M，N三点共面，但H平面GMN，所以直线GH 与MN异面．故选C.答案：C2．如图所示，在下列四个正方体中，A，B为正方体的两个顶点，M，N，Q为所在棱的中点，则在这四个正方体中，直线AB与平面MNQ不平行的是()解析：对于选项A，设正方体的底面对角线的交点为O(图略)，连接OQ，则OQ∥AB，因为OQ与平面MNQ有交点，所以AB与平面MNQ有交点，即AB与平面MNQ不平行，故选A.3．(2019·银川模拟)已知m，n是两条不同的直线，α，β是两个不同的平面，若m⊥α，n⊥β，且β⊥α，则下列结论一定正确的是()A．m⊥n B．m∥nC．m与n相交D．m与n异面解析：若β⊥α，m⊥α，则直线m与平面β的位置关系有两种：mβ或m ∥β.当mβ时，又n⊥β，所以m⊥n；当m∥β时，又n⊥β，所以m⊥n，故m ⊥n，故选A.答案：A4．(2019·济宁模拟)如图所示，在三棱柱ABC－A1B1C1中，侧棱AA1⊥底面A1B1C1，底面三角形A1B1C1是正三角形，E是BC的中点，则下列叙述正确的是()A．CC1与B1E是异面直线B．AC⊥平面ABB1A1C．AE⊥B1C1D．A1C1∥平面AB1E解析：对于A，CC1与B1E均在侧面BCC1B1内，又两直线不平行，故相交，A错误；对于B，AC与平面ABB1A1所成的角为60，所以AC不垂直于平面ABB1A1，故B错误；对于C，AE⊥BC，BC∥B1C1，所以AE⊥B1C1，故C正确；对于D，AC与平面AB1E有公共点A，AC∥A1C1，所以A1C1与平面AB1E相交，故D错误．答案：C5．已知互相垂直的平面α，β交于直线l，若直线m，n满足m∥α，n⊥β，则() A．m∥l B．m∥nC．n⊥l D．m⊥n解析：因为α∩β＝l，所以lβ，又n⊥β，所以n⊥l.故选C.答案：C6．(2019·重庆六校联考(一))设a，b是两条不同的直线，α，β是两个不同的平面，则α∥β的一个充分条件是()A．存在一条直线a，a∥α，a∥βB．存在一条直线a，aα，a∥βC．存在两条平行直线a，b，aα，bβ，a∥β，b∥αD．存在两条异面直线a，b，aα，bβ，a∥β，b∥α解析：对于选项A，若存在一条直线a，a∥α，a∥β，则α∥β或α与β相交，若α∥β，则存在一条直线a，使得a∥α，a∥β，所以选项A的内容是α∥β的一个必要条件；同理，选项B，C的内容也是α∥β的一个必要条件而不是充分条件；对于选项D，可以通过平移把两条异面直线平移到一个平面中，成为相交直线，则有α∥β，所以选项D的内容是α∥β的一个充分条件．故选D.答案：D7．(2019·宜昌调研)如图所示，在棱长均相等的四棱锥P－ABCD中，O为底面正方形的中心，M，N分别为侧棱P A，PB的中点，有下列结论：①PC∥平面OMN；②平面PCD∥平面OMN；③OM⊥P A；④直线PD与MN所成角的大小为90．其中正确结论的序号是________．(写出所有正确结论的序号)解析：如图所示，连接AC，易得PC∥OM，所以PC∥平面OMN，结论①正确．同理PD∥ON，所以平面PCD∥平面OMN，结论②正确．由于四棱锥的棱长均相等，所以AB2＋BC2＝P A2＋PC2＝AC2，所以PC⊥P A，又PC∥OM，所以OM⊥P A，结论③正确．由于M，N分别为侧棱P A，PB的中点，所以MN∥AB，又四边形ABCD为正方形，所以AB ∥CD，又三角形PDC为等边三角形，所以∠PDC＝60，所以直线PD与MN所成的角即∠PDC，故④错误．故正确的结论为①②③.答案：①②③8．如图所示，四棱锥P ABCD中，四边形ABCD为正方形，PD⊥平面ABCD，PD＝DC＝2，点E，F分别为AD，PC的中点．(1)证明：DF∥平面PBE；(2)求点F到平面PBE的距离．解析：(1)证明：取PB的中点G，连接EG，FG，则FG∥BC，且FG＝12BC，∵DE∥BC且DE＝12BC，∴DE∥FG且DE＝FG，∴四边形DEGF为平行四边形，∴DF∥EG，又DF平面PBE，EG平面PBE，∴DF∥平面PBE.(2)由(1)知DF∥平面PBE，∴点D到平面PBE的距离与F到平面PBE的距离是相等的，故转化为求点D到平面PBE的距离，设为d.连接BD.∵V D PBE＝V P BDE，∴13S△PBE·d＝13S△BDE·PD，由题意可求得PE＝BE＝5，PB＝23，∴S△PBE ＝12×23×(5)2－⎝⎛⎭⎪⎫2322＝6，又S△BDE＝12DE·AB＝12×1×2＝1，∴d＝6 3.9．(2019·昆明七校模拟)一个正方体的平面展开图及该正方体直观图的示意图如图所示，在正方体中，设BC的中点为M，GH的中点为N.(1)请将字母F，G，H标记在正方体相应的顶点处(不需说明理由)；(2)证明：直线MN∥平面BDH；(3)过点M，N，H的平面将正方体分割为两部分，求这两部分的体积比．解析：(1)点F，G，H的位置如图所示．(2)证明：连接BD，设O为BD的中点，连接OM，OH，AC，BH，MN.∵M，N分别是BC，GH的中点，∴OM∥CD，且OM＝12CD，NH∥CD，且NH＝12CD，∴OM∥NH，OM＝NH，则四边形MNHO是平行四边形，∴MN∥OH，又MN平面BDH，OH平面BDH，∴MN∥平面BDH.(3)由(2)知OM∥NH，OM＝NH，连接GM，MH，过点M，N，H的平面就是平面GMH，它将正方体分割为两个同高的棱柱，高都是正方体的棱长，∴体积比等于底面积之比，即3∶1.B组能力提升练10．(2019·荆州模拟)如图所示，在三棱柱ABC－A′B′C′中，点E，F，H，K 分别为AC′，CB′，A′B′，B′C′的中点，G为△ABC的重心．从K，H，G，B′中取一点作为P，使得该棱柱恰有2条棱与平面PEF平行，则P 为()A．K B．HC．G D．B′解析：取A′C′的中点M，连接EM，MK，KF，EF，则EM，得四边形EFKM为平行四边形，若P＝K，则AA′∥BB′∥CC′∥KF，故与平面PEF平行的棱超过2条；HB′∥MK⇒HB′∥EF，若P＝H或P＝B′，则平面PEF与平面EFB′A′为同一平面，与平面EFB′A′平行的棱只有AB，不满足条件；连接BC′，则EF∥A′B′∥AB，若P＝G，则AB，A′B′与平面PEF平行．故选C.答案：C11．(2019·洛阳统考(一))正方形ABCD和等腰直角三角形DCE组成如图所示的梯形，M，N分别是AC，DE的中点，将△DCE沿CD折起(点E始终不在平面ABCD内)，则下列说法一定正确的是()A．MN∥平面BCEB．在折起过程中，一定存在某个位置，使MN⊥ACC．MN⊥AED．在折起过程中，不存在某个位置，使DE⊥AD解析：折起后的图形如图所示，取CD的中点O，连接MO，NO，则在△ACD中，M，O分别是AC，CD的中点，∴MO∥AD∥BC，同理NO∥CE，又BC∩CE＝C，∴平面MON∥平面BCE，∴MN∥平面BCE，故A正确；易知MO⊥CD，NO⊥CD，又MO∩NO＝O，∴CD⊥平面MNO，∴MN⊥CD，若MN⊥AC，又AC∩CD＝C，∴MN⊥平面ABCD，∴MN⊥MO，又MO＝12AD＝12EC＝NO，∴MN不可能垂直于MO，故MN⊥AC不成立，故B错误；取CE 的中点Q，连接MQ，则在△ACE中，M，Q分别是AC，CE的中点，∴MQ∥AE，由图知MQ与MN不可能始终垂直，故C错误，当平面CDE⊥平面ABCD时，又平面CDE∩平面ABCD＝CD，AD⊥CD，AD平面ABCD，∴AD⊥平面CDE，∴AD⊥DE，故D错误．答案：A12．下列命题正确的是()A．若两条直线和同一个平面平行，则这两条直线平行B．若一条直线与两个平面所成的角相等，则这两个平面平行C．若一条直线与两个相交平面都平行，则这条直线与这两个平面的交线平行D．若两个平面垂直于同一个平面，则这两个平面平行解析：A选项中两条直线可能平行也可能异面或相交；对于B选项，如图所示，在正方体ABCD－A1B1C1D1中，平面ABB1A1和平面BCC1B1与B1D1所成的角相等，但这两个平面垂直；D选项中两平面也可能相交．C正确．答案：C13．(2019·杭州模拟)如图所示，在正方体ABCD－A1B1C1D1中，AB＝2，E为AD 的中点，点F在CD上，若EF∥平面AB1C，则EF＝________.解析：根据题意，因为EF∥平面AB1C，所以EF∥AC.又E是AD的中点，所以F是CD的中点．因为在Rt△DEF中，DE＝DF＝1，故EF＝ 2.答案：214．(2019·唐山统一考试)在三棱锥P ABC中，PB＝6，AC＝3，G为△P AC的重心，过点G作三棱锥的一个截面，使截面平行于直线PB和AC，则截面的周长为________．解析：过点G作EF∥AC，分别交P A、PC于点E、F，过E、F分别作EN∥PB、FM∥PB，分别交AB、BC于点N、M，连接MN(图略)，则四边形EFMN是平行四边形，所以EF3＝23，即EF＝MN＝2，FMPB＝FM6＝13，即FM＝EN＝2，所以截面的周长为2×4＝8.答案：815.如图所示，四棱锥P ABCD的底面是边长为8的正方形，四条侧棱长均为217 .点G，E，F，H分别是棱PB，AB，CD，PC上共面的四点，平面GEFH⊥平面ABCD，BC∥平面GEFH .(1)证明：GH∥EF；(2)若EB＝2，求四边形GEFH的面积．解析：(1)证明：因为BC∥平面GEFH，BC平面PBC，且平面PBC∩平面GEFH＝GH，所以GH∥BC.同理可证EF∥BC，因此GH∥EF.(2)如图所示，连接AC，BD交于点O，BD交EF于点K，连接OP，GK.因为P A＝PC，O是AC的中点，所以PO⊥AC，同理可得PO⊥BD.又BD∩AC＝O，且AC，BD都在底面内，所以PO⊥底面ABCD.又平面GEFH⊥平面ABCD，且PO平面GEFH，所以PO∥平面GEFH.因为平面PBD∩平面GEFH＝GK，所以PO∥GK，且GK⊥底面ABCD，从而GK⊥EF，所以GK是梯形GEFH的高．由AB＝8，EB＝2，得EB∶AB＝KB∶DB＝1∶4，从而KB＝14DB＝12OB，即K为OB的中点．由PO∥GK得GK＝12PO，即G是PB的中点，且GH＝12BC＝4.由已知可得OB＝42，PO＝PB2－OB2＝68－32＝6，所以GK＝3.故四边形GEFH的面积S＝GH＋EF2·GK＝4＋82×3＝18.。

高三数学总复习《空间中的平行关系》课件

3.直线与平面平行的性质定理:一条直线与一个平面平行,则过这条直线的任一平面与此平面的交线与该直线平行. 符号表示:a∥α,a⊂β,α∩β=b⇒a∥b.
图形:
说明:注意定理中有三个条件:直线a∥平面α,α∩β=b,a⊂β,这三个条件缺一不可.
4.平面与平面平行的性质
(1)定理:如果两个平行平面同时和第三个平面相交,那么它们的交线平行. 符号表示:α∥β,α∩γ=a,β∩γ=b⇒a∥b. 图形:
解析:①②显然正确,命题③,直线b有可能在平面M内,对于命
题④,直线b可能与平面M平行或斜交,图所示,在四棱锥P—ABCD 中,∠ABC=∠ACD=90°,∠BAC=∠CAD=60°,PA⊥平面 ABCD,E为PD的中点,PA=2AB=2.
(1)若F为PC的中点,求证:PC⊥平面AEF;
④若两个平面垂直,那么一个平面内与它们的交线不垂直的
直线与另一个平面也不垂直. 其中,为真命题的是( )
A.①和② B.②和③ C.③和④ D.②和④ 解析:①错,应该为一个平面内的两条相交直线与另一个平面平行,那么这两个平面相互平行.
③错,两直线可能相交,也可能异面.
故②④正确,选D. 答案:D
回归教材
1.直线与平面平行的判定定理
平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行. 符号表示:a⊄α,b⊂α,且a∥b⇒a∥α. 图形:
说明:(1)直线与平面平行的判定定理具备三个条件:
平面外的一条直线、平面内的一条直线、两直线平行,三个
条件缺一不可. (2)定理充分体现了转化的思想,它将线面平行问题转化为线
解法二:如图所示,延长DC,AB,设它们交于点N,连接PN. ∵∠NAC=∠DAC=60°,

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

空间中的平行关系
线线平行
判定定理
判定定理
线面平行
面面平行
性质定理
定义
性质定理
例1、如图，已知点P是平行四边形ABCD所
在平面外一点，E，F分别是AB，PD的中
点，求证：AF//平面PCE
P
P
EA B
F
M
D E
A
CB
F
D
N
C
空间平行关系的常见判定方法：
1、线面平行（1）利用线面平行的定义（无公共点）；（2）利用线面平行的判定定理；（3）利用面面平行的性质.
判定定理
判定定理
线//线
线//面
面//面
性质定理
性质
性质定理
2、空间中的平行关系的常用判定方法
线线平行？线面平行？面面平行？
空间平行关系的常见判定方法：
3、线线平行
中位线定理
（1）平面中的线线平行：比例关系
平行四边形性质
平行公理线面平行性质定理
（2）空间中的线线平行：面面平行性质定理
线面垂直性质定理
当堂检测
1、如图，在直三棱柱ABC A1B1C1中，AB AC， D为BC中点，四边形B1BCC1是正方形，求证：A1B //平面AC1D.
M
N
2、如图，在正方体ABCD A1B1C1D1中，E、F分别为棱AD、AB的中点．求证：EF //平面CB1D1.
课堂小结 1、空间中的平行关系
求证：A1E//平面ADC1
A1
C1 A1
C1
E
E
B1
B1
A
CA
C
D
D
B
B
变式：如图，已知在三棱柱ABC-A1B1C1 中， E,F,G,H分别是AB,AC,A1B1,A1C1的中点，求证：（1）B,C,H,G四点共面；
（2）平面EFA1//平面BCHG
A1HBiblioteka C1GB1
A
F
C
E B
探究：如图，已知三棱柱ABC-A1B1C1中，底面为正三角形，侧棱与底面垂直，点E，F分别是CC1，BB1上的点，点M是棱AC上的动点，且EC=2FB，当M在何位置时，BM//平面AEF？
如何学好立体几何
学好立体几何需注意的几个方面： 1、立足课本，夯实基础
2、建立数学模型，培养空间想象能力
3、规范解答，学会转化，总结规律，提高逻辑论证能力
例：已知不重合的直线a，b和平面，，
试判断下列命题的真假.
（1）a // b,b a // ；（2）a //,b a // b ；（3）a ,b , a // ,b // // ；（4） // , a ,b a // b .
空间平行关系的常见判定方法：
2、面面平行（1）利用面面平行的定义；（2）利用面面平行的判定定理；（3）利用结论：垂直于同一条直线的两个平面
平行；（4）利用结论：两个平面同时和第三个平面平
行，那么这两个平面平行
练习：如图，已知在三棱柱ABC-A1B1C1中， D，E分别是BC，B1C1的中点，