第2章 双变量回归模型(2)
合集下载
第二章 双变量模型
概念： 概念：
在给定解释变量Xi条件下被解释变量Yi的期 望轨迹称为总体回归线 总体回归线（population 总体回归线 regression line），或更一般地称为总体回 总体回 归曲线（population regression curve）。 归曲线 相应的函数： E (Y | X i ) = f ( X i ) 称为（双变量）总体回归函数（population 总体回归函数（ 总体回归函数 regression function, PRF）。 ）
变量间的关系
经济变量之间的关系，大体可分为两类： （1）确定性关系 函数关系：研究的是确定 确定性关系或函数关系 确定性关系 函数关系： 现象非随机变量间的关系。
相关关系： （2）统计依赖 相关关系： 研究的是非确定现 ）统计依赖或相关关系 象随机变量间的关系。
回归与相关
相关分析的主要目的在于研究变量之间统计 线性关联的程度，将变量均视为随机变量。 回归分析的主要目的在于研究变量之间统计 关联的形式，目的在于揭示被解释变量如何依赖 解释变量的变化而变化的规律，将解释变量视为 确定性的，而将被解释变量视为随机变量。
二、回归分析的基本概念
回归分析(regression analysis)是研究一个变量关 回归分析 是研究一个变量关 于另一个（ 于另一个（些）变量的具体依赖关系的计算方法 和理论。 和理论 其用意：在于通过后者的已知或设定值， 其用意：在于通过后者的已知或设定值，去估计和 预测前者的（总体）均值。 （或）预测前者的（总体）均值 这里：前一个变量被称为被解释变量（Explained 被解释变量（ 被解释变量 Variable）或应变量（Dependent Variable）， 应变量（ ） 应变量 ）， 后一个（些）变量被称为解释变量 解释变量 （Explanatory Variable）或自变量 ） 自变量 （Independent Variable）。 ）
计量经济学第二章经典线性回归模型
Yt = α + βXt + ut 中 α 和 β 的估计值 和
,
使得拟合的直线为“最佳”。
直观上看，也就是要求在X和Y的散点图上
Y
* * Yˆ ˆ ˆX
Yt
* **
Yˆt
et * *
*
*
**
*
**
**
*
Xt
X
图 2.2
残差
拟合的直线 Yˆ ˆ ˆX 称为拟合的回归线.
对于任何数据点 (Xt, Yt), 此直线将Yt 的总值 分成两部分。
β
K
βK
β1 β1
...
βK
βK
Var(β 0 )
Cov(β1 ,β
0
)
Cov(β 0 ,β1 )
Var(β1 )
...
Cov(β
0
,β
K
)
...
Cov(β1
,β
K
)
...
...
...
...
Cov(β
K
,β
0
)
Cov(β K ,β1 )
...
Var(β K )
不难看出，这是 β 的方差-协方差矩阵，它是一 个(K+1)×(K+1)矩阵，其主对角线上元素为各 系数估计量的方差，非主对角线上元素为各系 数估计量的协方差。
ut ～ N (0, 2 ) ，t=1,2,…n
二、最小二乘估计
1. 最小二乘原理
为了便于理解最小二乘法的原理，我们用双
变量线性回归模型作出说明。
对于双变量线性回归模型Y = α+βX + u， 我 们
的任务是，在给定X和Y的一组观测值 (X1 ,
第2章：线性回归的基本思想：双变量模型
如： P(Y=460|X=5000）=1/5。
因此，给定收入X的值Xi，可得分数Y的条件均值 （ conditional mean ） 或 条 件 期 望 （ conditional
expectation）：
2-17
E(Y|X=Xi)
2.2 总体归函数（PRF）：假想一例
描出散点图发现：随着收入的增加，成绩“平均 地说”也在增加，且Y的条件均值均落在一根正斜 率的直线上。这条直线称为总体回归线。
皮尔逊收集过一些家庭群体的1千多名成员的身 高记录。他发现，对于一个父亲高的群体，儿 辈的平均身高低于他们父辈的身高，而对于一 个父亲矮的群体，儿辈的平均身高则高于其父 辈的身高。这样就把高的和矮的儿辈一同“回 归”到所有男子的平均身高。用加尔顿的话说， 这是“回归到中等”。
2-2
2.1 回归的含义
对变量间统计依赖关系的考察主要是通过相关分析 (correlation analysis) 和 回 归 分 析 (regression analysis)来完成的：
正相关
线性相关 不相关 相关系数：
统计依赖关系
2-4
负相关 1 XY 1
正相关 非线性相关 不相关
负相关
有因果关系 无因果关系
回归分析 相关分析
经济变量之间的关系，大体可分为两类： （1）确定性关系或函数关系：研究的是
确定现象非随机变量间的关系。
（2）统计依赖或相关关系：研究的是非确 定现象随机变量间的关系。
2-3
2.1 回归的含义
例如：
函数关系： 圆面积 f ,半径 半径2
统计依赖关系/统计相关关系：
农作物产量 f 气温, 降雨量, 阳光, 施肥量
2-23
2.3 总体回归函数的统计或随机设定
因此，给定收入X的值Xi，可得分数Y的条件均值 （ conditional mean ） 或 条 件 期 望 （ conditional
expectation）：
2-17
E(Y|X=Xi)
2.2 总体归函数（PRF）：假想一例
描出散点图发现：随着收入的增加，成绩“平均 地说”也在增加，且Y的条件均值均落在一根正斜 率的直线上。这条直线称为总体回归线。
皮尔逊收集过一些家庭群体的1千多名成员的身 高记录。他发现，对于一个父亲高的群体，儿 辈的平均身高低于他们父辈的身高，而对于一 个父亲矮的群体，儿辈的平均身高则高于其父 辈的身高。这样就把高的和矮的儿辈一同“回 归”到所有男子的平均身高。用加尔顿的话说， 这是“回归到中等”。
2-2
2.1 回归的含义
对变量间统计依赖关系的考察主要是通过相关分析 (correlation analysis) 和 回 归 分 析 (regression analysis)来完成的：
正相关
线性相关 不相关 相关系数：
统计依赖关系
2-4
负相关 1 XY 1
正相关 非线性相关 不相关
负相关
有因果关系 无因果关系
回归分析 相关分析
经济变量之间的关系，大体可分为两类： （1）确定性关系或函数关系：研究的是
确定现象非随机变量间的关系。
（2）统计依赖或相关关系：研究的是非确 定现象随机变量间的关系。
2-3
2.1 回归的含义
例如：
函数关系： 圆面积 f ,半径 半径2
统计依赖关系/统计相关关系：
农作物产量 f 气温, 降雨量, 阳光, 施肥量
2-23
2.3 总体回归函数的统计或随机设定
双变量回归模型估计问题
i 1
^
n
这说明 1 是 Yi 的一个线性函数，它是以 k 为
i
^
权的一个加权平均数，从而它是一个线性估计
量。同理， 0 也是一个线性估计量。
^
（2）无偏性
^ E 0 0
^ E 1 1
^
1 就是说，虽然由不同的样本得到的 0 ， 1，但平均 可能大于或小于它们的真实值 0， 1 。 起来等于它们的真实值 0 ，
2 i 2 i i
yi Yi Y
2
式(3-13)可表示为
TSS=ESS+RSS
（3-14）
这说明 Yi 的观测值围绕其均值的总变异
可分解为两部分，一部分来自回归线，而另 一部分则来自扰动项ui 。
Y
ui =来自残差
Yi
2
SRF
Yi 0 1 X i
n i 1 i i
3.2 高斯-马尔可夫定理
最小二乘估计量有何优良的统计性质呢？ 假定5：同方差性
Var ui X i E ui E ui X i
E ui X i
2
f Y X i
2
Y
2
E Y X i 0 1 X i
X
2
i
se 1
x
i 1
n
n
2
i
var ( 0 )
X
i 1
2 i 2
n xi
2
se 0 i 1n 2 n xi
i 1
X
2 i
^
n
这说明 1 是 Yi 的一个线性函数，它是以 k 为
i
^
权的一个加权平均数，从而它是一个线性估计
量。同理， 0 也是一个线性估计量。
^
（2）无偏性
^ E 0 0
^ E 1 1
^
1 就是说，虽然由不同的样本得到的 0 ， 1，但平均 可能大于或小于它们的真实值 0， 1 。 起来等于它们的真实值 0 ，
2 i 2 i i
yi Yi Y
2
式(3-13)可表示为
TSS=ESS+RSS
（3-14）
这说明 Yi 的观测值围绕其均值的总变异
可分解为两部分，一部分来自回归线，而另 一部分则来自扰动项ui 。
Y
ui =来自残差
Yi
2
SRF
Yi 0 1 X i
n i 1 i i
3.2 高斯-马尔可夫定理
最小二乘估计量有何优良的统计性质呢？ 假定5：同方差性
Var ui X i E ui E ui X i
E ui X i
2
f Y X i
2
Y
2
E Y X i 0 1 X i
X
2
i
se 1
x
i 1
n
n
2
i
var ( 0 )
X
i 1
2 i 2
n xi
2
se 0 i 1n 2 n xi
i 1
X
2 i
双变量回归
第三章
双变量回归模型：估计问题
简单的线性回归模型
Yi = 1 + 2 X i + ui
Yi = 每周家庭支出 X i = 每周家庭收入
对于给定的 xi的水平, 预期的食物支 出将是: E(Yi|X i) = 1 + 2 X i
参数
1和 2是未知常数.
^ ^ ) 的公 产生样本估计量 b1 (或 1)和 b2(或 2 式就是 1 和 2的估计。
b1 和b2的预期值
简单线性回归下的估计量的公式:
b2 =
nXiYi - XiYi nX2 -(Xi)2 i
xiyi = xi2
b1 = Y - b2X
这里
Y = Yi / n 和 X = Xi / n
将 Yi = 1 + 2xi + 替代到 b2 公式中并得:
ui
nxi ui - xi ui b2 = 2 + 2 2 nxi -(xi)
)2
=
yi
i
2
=
^
xi2 yi2
Sx2 Sy2
xiyi)2 xiyi 2 xi2 = = 2 2 xi2yi2 xi yi
Y
当R2 = 0 SRF
哪个是SRF ?Leabharlann X Y当 R2 = 1
SRF
SRF 通过所有点
X
高斯马尔可夫定理
在经典的线性回归模型条件下, 最小二乘 (OLS) 估计量 b1 和 b2 是1和 2 的最优线 性无偏估计量 (BLUE). 这意味着 b1和 b2 在1 和2所有线性无偏估计量中拥有 最小 方差.
错误的模型设定 先前的无偏结果假定使用了正确 的设定形式
双变量回归模型：估计问题
简单的线性回归模型
Yi = 1 + 2 X i + ui
Yi = 每周家庭支出 X i = 每周家庭收入
对于给定的 xi的水平, 预期的食物支 出将是: E(Yi|X i) = 1 + 2 X i
参数
1和 2是未知常数.
^ ^ ) 的公 产生样本估计量 b1 (或 1)和 b2(或 2 式就是 1 和 2的估计。
b1 和b2的预期值
简单线性回归下的估计量的公式:
b2 =
nXiYi - XiYi nX2 -(Xi)2 i
xiyi = xi2
b1 = Y - b2X
这里
Y = Yi / n 和 X = Xi / n
将 Yi = 1 + 2xi + 替代到 b2 公式中并得:
ui
nxi ui - xi ui b2 = 2 + 2 2 nxi -(xi)
)2
=
yi
i
2
=
^
xi2 yi2
Sx2 Sy2
xiyi)2 xiyi 2 xi2 = = 2 2 xi2yi2 xi yi
Y
当R2 = 0 SRF
哪个是SRF ?Leabharlann X Y当 R2 = 1
SRF
SRF 通过所有点
X
高斯马尔可夫定理
在经典的线性回归模型条件下, 最小二乘 (OLS) 估计量 b1 和 b2 是1和 2 的最优线 性无偏估计量 (BLUE). 这意味着 b1和 b2 在1 和2所有线性无偏估计量中拥有 最小 方差.
错误的模型设定 先前的无偏结果假定使用了正确 的设定形式
第二章 双变量回归分析(计量经济学,南开大学)
ˆ 和 ˆ 1 2
i
为Yi的线性函数
i 2 i
ˆ
2
xY x
(
xi )Yi 2 x i
k Y
i
i
其中k i
xi xi2 1 xi2
ki k i2
x
2
i
0
2 xi
1 xi2 1 xi2
i
1 xi2
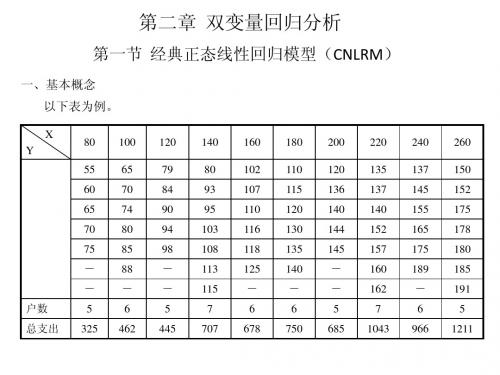
6、样本回归函数（SRF） 由于在大多数情况下，我们只知道变量值得一个样本，要用样本信息的基础 上估计PRF。(表） 样本1
X（收入） Y（支出） 80 55 100 65 120 79 140 80 160 102 180 110 200 120 220 135 240 137 260 150
样本2
ˆ ) VAR( 2
x
2 i
2
2 i
x
ˆ： 对于 1
ˆ Y ˆ X 1 ˆ X Yi 1 2 2 n 1 ˆ X ( 1 2 X i ui ) 2 n u 1 i X k i ui n ˆ ) E[( ui X 方差：VAR( k i ui ) 2 ] 1 n
ˆ ) E( ki E (ui ) 2 2 2 ˆ Y ˆ X 1 2 ( 1 2 X i ui ) ( 1 k i u i ) X 1 u i X k i u i ˆ ) E( 1 1
1 1 2 21
估计量（Estimator）：一个估计量又称统计量(statistic)，是指一个规则、公式 或方法，以用来根据已知的样本所提供的信息去估计总体参数。在应用中，由估 计量算出的数值称为估计（值）（estimate)。 样本回归函数SRF的随机形式为：
第2章习题
3. 美国各航空公司业绩的统计数据公布在《华尔街日报 1999 年年鉴》（The Wall Street Journal Almanac 1999）上。航班正点到达的比率和每 10 万名乘客投诉的次数的数据如下。
航空公司名称
航班正点率（%）
投诉率（次/10 万名乘客）
西南(Southwest)航空公司
D （X，Y）
16. 以 Y 表示实际观测值， Yˆ 表示 OLS 估计回归值，则用 OLS 得到的样本回归直线
Yˆ i＝βˆ0 + βˆ1Xi 满足（ ）
∑ A （Yi－Yˆ i）＝0 ∑ B （Yi－Yi）2＝0 ∑ C （Yi－Yˆ i）2＝0 ∑ D （Yˆ i－Yi）2＝0
17. 若一正常商品的市场需求曲线向下倾斜，则可断定（ ） A 它具有不变的价格弹性 B 随需求量增加，价格下降 C 随需求量增加，价格上升 D 需求无弹性
6. 在总体回归直线 E（Yˆ ）＝β0 + β1X 中， β1表示（ ） A 当 X 增加一个单位时，Y 增加 β1 个单位 B 当 X 增加一个单位时，Y 平均增加 β1 个单位 C 当 Y 增加一个单位时，X 增加 β1 个单位 D 当 Y 增加一个单位时，X 平均增加 β1 个单位
7. 最小二乘准则是指使（
C Yi＝βˆ0 + βˆ1Xi + ei
D Yˆ i＝βˆ0 + βˆ1Xi + ei
E E(Yi )＝βˆ0 + βˆ1Xi
4. Yˆ 表示 OLS 估计回归值，u 表示随机误差项。如果 Y 与 X 为线性相关关系，则下列哪些
是正确的（
）
A Yi＝β0 + β1Xi
B Yi＝β0 + β1Xi＋ui
第2章_线性回归的基本思想：双变量模型 (2)
200 35 31 30 28 26 22 20
225 36 34 31 29 27 26 23
250 38 36 33 30 28 25 23
275 40 37 32 30 29 27 25
300 42 39 34 31 30 29 26
325 43 35 31 30 29 33 32
350 375 45 39 33 30 27 30 28 46 40 34 31 28 32 30
2019/2/21
R 2 0.99
2
回归分析可以用来：
1、找到被解释变量(Y)与解释变 量(X)运动的相互关系，并检验 某些假设 如：固定其它条件不变，施肥 量每增加一单位, 收成变化多 少？是增收还是减产？ 2、在已知解释变量(X)的基础上， 估计或预测被解释变量(Y)的均 值 如：估计身高170的父亲，其 儿子的平均身高 3、综合分析、指导决策
随机干扰项的性质和意义 Yi B1 B2 X i ui
它是从模型中省略下来，但又集体地影
响着Y的全部变量的替代物。
博 彩 支 出
系统成分/定性：可支配收入（X） 其它变量的影响 如性格、年龄、 性别
B1＋B2 X i
非系统/随机成分:
ui
另外一些说不清的随机事件： 如某几天心情好，多买点
slope
Regression coefficients
12
2019/2/21
度量了X每变动一单位，Y（条件） 均值的变化率
2、总体回归函数（PRF）
（Population Regression Function）
条件回归分析
E（Y Xi ）＝B1＋B2 X i
E（ Y ）
B1
第2章 双变量回归模型(2)
小结：
计量经济学模型有两种类型：一是总体回归模型，另一是 样本回归模型。两类回归模型都具有确定的形式与随机形式两 种： 总体回归模型的确定形式——总体回归函数
EY X B1 B2 X
总体回归模型的随机形式——总体回归模型
很难知道
Y B1 B2 X
样本回归模型的确定形式——样本回归函数
因此，由该样本估计的回归方程为：
ˆ Yi 103.172 0.777X i
即可支配收入每上升一个百分点，则消费支出上升0.777个百 分点；截距-103.172表明没有收入是负支出，这里没有经济意义。 另一样本结果
ˆ Yi 99.978 0.757 X i
综合图示
不同可支配收入水平组家庭消费支出的条件分布图
1、用OLS法得出的样本回归线经过样本均值点，即
Y b1 b2 X
2、残差的均值总为0，即
e e
n
i
0
3、对残差与解释变量的积求和，其值为0，即
e X
i
i
0
三、用EXCEL和Eviews实现最小二乘法
以“美国高年级学生平均智能测试结果”建立词汇分数 与数学分数的关系，用数学分数(X) 来预测词汇分数(Y) 。
3500 每 月 消 费 支 出 (元) 3000 2500 2000 1500 1000 500 0 0 500 1000 1500 2000 2500 3000 3500 4000 每月可支配收入(元) 每月家庭消费支出Y 条件均值Y* 样本1 预测 样本 样本2 预测 样本2
问题：如何检验？
二、普通最小二乘估计量的一些重要性质
一、参数的普通最小二乘估计（OLS）
建立双变量总体回归模型PRF
计量经济学模型有两种类型：一是总体回归模型，另一是 样本回归模型。两类回归模型都具有确定的形式与随机形式两 种： 总体回归模型的确定形式——总体回归函数
EY X B1 B2 X
总体回归模型的随机形式——总体回归模型
很难知道
Y B1 B2 X
样本回归模型的确定形式——样本回归函数
因此，由该样本估计的回归方程为：
ˆ Yi 103.172 0.777X i
即可支配收入每上升一个百分点，则消费支出上升0.777个百 分点；截距-103.172表明没有收入是负支出，这里没有经济意义。 另一样本结果
ˆ Yi 99.978 0.757 X i
综合图示
不同可支配收入水平组家庭消费支出的条件分布图
1、用OLS法得出的样本回归线经过样本均值点，即
Y b1 b2 X
2、残差的均值总为0，即
e e
n
i
0
3、对残差与解释变量的积求和，其值为0，即
e X
i
i
0
三、用EXCEL和Eviews实现最小二乘法
以“美国高年级学生平均智能测试结果”建立词汇分数 与数学分数的关系，用数学分数(X) 来预测词汇分数(Y) 。
3500 每 月 消 费 支 出 (元) 3000 2500 2000 1500 1000 500 0 0 500 1000 1500 2000 2500 3000 3500 4000 每月可支配收入(元) 每月家庭消费支出Y 条件均值Y* 样本1 预测 样本 样本2 预测 样本2
问题：如何检验？
二、普通最小二乘估计量的一些重要性质
一、参数的普通最小二乘估计（OLS）
建立双变量总体回归模型PRF
双变量回归模型分析案例及模型形式的探讨
双变量回归模型分析案例及模型形式的探讨双变量回归模型是一种用于分析两个变量之间关系的统计模型。
它可以用来预测一个变量（因变量）受另一个变量（自变量）的影响程度，或者研究两个变量之间的相关性。
本文将探讨一个双变量回归模型的分析案例，并探讨该模型的形式。
假设我们想要分析一个人的身高和体重之间的关系。
我们收集了一组数据，包括100个人的身高和体重数据。
我们想要建立一个双变量回归模型，来预测一个人的体重受其身高的影响程度。
首先，我们需要将收集到的数据进行整理和描述性统计分析。
我们可以计算身高和体重的平均值、方差和相关系数等指标。
这些指标可以提供有关数据的整体特征和两个变量之间的关系强度的信息。
接下来，我们可以使用散点图来可视化身高和体重之间的关系。
散点图可以显示每个人的身高和体重，并观察它们之间的模式和趋势。
基于散点图的观察，我们可以大致判断两个变量之间是否存在线性关系。
然后，我们可以使用最小二乘法来估计回归方程的系数。
回归方程的形式可以表示为：Y=β0+β1X，其中Y代表体重，X代表身高，β0和β1分别是回归方程的截距和斜率。
最小二乘法的目标是最小化实际观测值和回归方程预测值之间的误差平方和。
在估计回归系数之后，我们可以对回归方程进行模型拟合和评估。
拟合优度指标，如R平方和调整后的R平方，可以用来评估模型的拟合程度。
R平方的取值范围在0到1之间，越接近1说明模型对数据的解释能力越强。
最后，我们可以使用回归模型进行预测和推断。
通过将新的身高值代入回归方程，我们可以预测对应的体重。
此外，我们还可以进行假设检验和置信区间估计，以评估回归系数的显著性和区间估计。
总之，双变量回归模型可以用于分析两个变量之间的关系，并进行预测和推断。
在实际应用中，我们需要注意模型的前提假设、数据的合理性和模型的解释力。
另外，还可以通过添加交互项、多项式项或考虑其他模型形式来扩展双变量回归模型。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
-973 1314090 1822500 947508 -929 975870 1102500 863784 -445 334050 562500 198381 -412 185580 202500 170074 -159 23910 22500 25408 28 4140 22500 762 402 180720 202500 161283 511 382950 562500 260712 1018 1068480 1102500 1035510 963 1299510 1822500 926599 5769300 7425000 4590020
可支配收入与消费支出的样本图
消费支出Y 3000 2500 2000 1500 1000 500 0 0
ˆ Yi 103.172 0.777 X i
b2
x y x
i 2 i
i
5769300 0.777 7425000
可支配收入X 1000 2000 3000 4000
b1 Y b2 X 1567 0.777 2150 103.172
3500 每 月 消 费 支 出 (元) 3000 2500 2000 1500 1000 500 0 0 500 1000 1500 2000 2500 3000 3500 4000 每月可支配收入(元) 每月家庭消费支出Y 条件均值Y* 样本1 预测 样本 样本2 预测 样本2
问题：如何检验？
二、普通最小二乘估计量的一些重要性质
选择的直线处于样本数据的中心位置最合理。怎样用数学 语言描述“处于样本数据的中心位置”？ 普通最小二乘法（Ordinary least squares, OLS）给出的判 断标准是： 选择参数b1,b2，使得残差平方和最小。
ˆ Q Yi Yi
i 1 n
Y b b X
ˆ Yi 380.4791.6418X i
说明：男生的数学分数每增加1 分，平均而言，其词汇将增加1.64 分，-380.479没有什么实际意义。
Coefficients 准误差 t Stat P-value Lower 95%Upper 95% 标 下限 95.0% 限 95.0% 上 Intercept -380.479 63.32969 -6.00791 4.78E-06 -511.817 -249.141 -511.817 -249.141 男生 1.641791 0.126648 12.96341 8.9E-12 1.379139 1.904443 1.379139 1.904443
条件均值Y*
样本
E(Y | X i ) B1 B2 X i
或都说使bi (i=0,1)
尽可能接近Bi (i=0,1)。
1000 500 0 0 500 1000 1500 2000 2500 3000
PRF
收入X 3500 4000
§2.2 一元线性回归模型的参数估计
一、参数的普通最小二乘估计（OLS）
640000 352836 1210000 407044 1960000 1258884 2890000 1334025 4000000 1982464 5290000 2544025 6760000 3876961 8410000 4318084 10240000 6682225 12250000 6400900 53650000 29157448
小结：
计量经济学模型有两种类型：一是总体回归模型，另一是 样本回归模型。两类回归模型都具有确定的形式与随机形式两 种： 总体回归模型的确定形式——总体回归函数
EY X B1 B2 X
总体回归模型的随机形式——总体回归模型
很难知道
Y B1 B2 X
样本回归模型的确定形式——样本回归函数
一、参数的普通最小二乘估计（OLS）
建立双变量总体回归模型PRF
P105
Yi B1 B2 X i ui
用下面的样本回归模型SRF来估计它。
Yi b1 b2 X i ei
估计PRF的要求是：
残差
求B1，B2的估计量b1,b2，使得残差ei尽可能小。
ˆ ei 实际的Yi 估计的Yi ˆ Yi Yi Yi b1 b2 X i
引例分析：利用公式计算回归参数
在上述家庭可支配收入-消费支出例中，对于所抽出的一 组样本数，参数估计的计算可通过下面的表2.2.1进行。
表 2.2.1 参数估计的计算表
xi yi b2 xi2 b1 Y b2 X
Xi
Yi
xi
yi
xi y i
xi2
y i2
X i2
ˆ Y b1 b 2 X
样本回归模型的随机形式——样本回归模型
Y b1 b2 X e
Y表示“真实 其中带“＾”者表示“估计值”。 值”。
用来估计总体 回归模型
表示“误差”。
▼回归分析的主要任务：
根据样本回归函数SRF，估计总体回归函数PRF。
ˆ 即，根据 Yi Yi ei b1 b2 X i ei
因此，由该样本估计的回归方程为：
ˆ Yi 103.172 0.777X i
即可支配收入每上升一个百分点，则消费支出上升0.777个百 分点；截距-103.172表明没有收入是负支出，这里没有经济意义。 另一样本结果
ˆ Yi 99.978 0.757 X i
综合图示
不同可支配收入水平组家庭消费支出的条件分布图
二、最小二乘估计量的性质
三、利用EXCEL和Eviews回归步骤
四、实例
单方程计量经济学模型分为两大类
线性模型中，变量之间的关系呈线性关系
非线性模型中，变量之间的关系呈非线性关系
直线上各点斜率相同
2 需 1.5 求 1 量 0.5 0 0 0.5 1 价格 1.5 2
15 需 10 求 量 5 0 0 0.5 价格 1
1、用“EXCEL实现最小二乘法”步骤
①调出EXCEL中“美国高年级学生平均智能测试”工作表
②利用菜单中“工具→数据分析→回归” 出现如下对话框
③把 “男生词汇成绩送入Y值输入区域”，把 “男生数学成绩 送入X值输入区域”，点中“输出区域”，选择一空白格，选择 线性拟合图选项，出现如下对话框。
男生数学分数(X) 与词汇分数(Y)的回归方程为：
上式表明：残差是Y的真实值与估计值之差。
步骤
给定一组样本观测值（Xi, Yi）（i=1,2,…n）要求样本回 可支配收入与消费支出的样本图 归函数尽可能好地拟合这组值.
消费支出Y 3000
ˆ Yi b1 b2 X i
2000 1000 0 0 1000 2000 3000 可支配收入X 4000
2 n i 1 i 1 2 i
2
问题转化为:在给定的样本观测值下，b1=?,b2=? 时，Q最小？
推导：
Q b 2 (Yi b1 b2 X i ) (1) 0 1 Q 2 (Y b b X ) ( X ) 0 i 1 2 i i b2
估计
样本回归模型 总体回归模型
ˆ Yi b1 b2 X i
Yi E(Y | X i ) ui B1 B2 X i ui
消费Y
▼这就要求：
散点图
3500 3000 2500 2000 1500
设计一”方法”构
造SRF,以使SRF尽可 能”接近”PRF。
SRF
每月家庭பைடு நூலகம்费支出Y
( X i X )(Yi Y ) X iYi nXY b2 ( X i X )2 X i2 nX 2 得b1 , b2的求解公式为： b1 Y b2 X
变形公式
在计量经济学中，往往以小写字母表示对均值的离差。 记
1 2 x (X i X ) X n X i
1、用OLS法得出的样本回归线经过样本均值点，即
Y b1 b2 X
2、残差的均值总为0，即
e e
n
i
0
3、对残差与解释变量的积求和，其值为0，即
e X
i
i
0
三、用EXCEL和Eviews实现最小二乘法
以“美国高年级学生平均智能测试结果”建立词汇分数 与数学分数的关系，用数学分数(X) 来预测词汇分数(Y) 。
Yi 2
1 800 594 -1350 2 1100 638 -1050 3 1400 1122 -750 4 1700 1155 -450 5 2000 1408 -150 6 2300 1595 150 7 2600 1969 450 8 2900 2078 750 9 3200 2585 1050 10 3500 2530 1350 求和 21500 15674 平均 2150 1567
曲线上各点斜率不同
(1)解释变量线性：
(2)参数线性：
EY B1 B X i
2 2
1 E Y B1 B2 Xi
EY B1 B2 X
2 i
非线性
非线性
双变量线性回归模型的特征
只有一个解释变量
Yi B1 B2 X i ui
i=1,2,…,n
Yi为被解释变量，Xi为解释变量，B1与B2为待估参数，ui为 随机干扰项 估计方法有多种，其中最广泛使用的是普通最小二乘法 （ordinary least squares, OLS）。 为保证参数估计量具有良好的性质，通常对模型提出若干 基本假设。（即普通最小二乘法是有条件的，在下一章讲解）
④单击确定，出现如下结果：
SUMMARY OUTPUT 回归统计 Multiple R0.940341 R Square 0.884241 Adjusted R0.878979 Square 标准误差 4.146637 观测值 24 方差分析 df 回归分析 残差 总计 SS MS 1 2889.552 2889.552 22 378.2811 17.1946 23 3267.833 F Significance F 168.05 8.9E-12