有向图的最小树形图解剖
图论课件-有向图

例3 求下图D的强连通分支、单向连通分支。
2
3
4
5
1
9
8
7
6
D
14
1
0.5 n 0
0.5
1 2 1.5 t1
0.5
00
1 0.8
0.6 0.4 x 0.2
(1) D的强连通分支
2
3
4
5
{1} {2, 3, 9, 8, 4, 7} {5} {6}
1
9
8
7
6
D
上面点集导出的子图是 D的强 连通分支。
2
证明:“必要性”
设V(D)={v1,v2,…,vn}。由于D是强连通图,所以,对任 意两点vi与vj, 都存在(vi, vj)路,同时也存在(vj ,vi)路。所以 存在如下闭途径:v1→v2→…→vn→v1。这是一条包含D的 所有顶点的回路。
12
1
0.5 n 0
0.5
1 2 1.5 t1
0.5
00
1
0.5 n 0
0.5
1 2 1.5 t1
0.5
00
1 0.8
0.6 0.4 x 0.2
(2) 在L中取v7, U中取点v6 , 作边<v7, v6>。令l (v6)=l (v7)+1=3, L ={v1,v7,v6}, U={v2,v3,…,v5}, A={ <v1, v7>, <v7, v6> }
6
1
0.5 n 0
0.5
1 2 1.5 t1
0.5
00
1 0.8
0.6 0.4 x 0.2
对 v V (D) ,有
d (v) d (v) 1
最小生成树的构造离散数学

最小生成树的构造离散数学
最小生成树的构造是离散数学技术的重要组成部分,用于解决图形中的最小树问题。
能够有效地构造最小生成树,有助于我们解决复杂的网络优化等问题。
最小生成树是指一个边数最少的连接结点的树,即所有点之间只建立最少的边,使得所有点都连接在一起,称为一棵生成树。
最小生成树建立在图上,是多重图G(V,E)的一棵子树,它满足以下三个条件:1、包含G中的所有n个结点;2、只包含G中m-n+1条边;3、权值最小。
使用最小生成树的边,可以把n个节点连接成一个树,所有边的权重总和最小。
最小生成树的步骤是:1、选择一个结点作为树的根,将它加入到树中;2、以选定的结点为根,从剩余结点中选择权值最小的边,加入到树中;3、继续重复步骤2,直到n-1条边全部加入到树中,从而完成树的构造。
最小生成树有多种构造方式,如Prim和Kruskal算法、动态规划算法等,可以快速和有效地构建最小生成树。
Prim算法从图中原始结点出发,每一步都把一条最短边加入进去;Kruskal算法从图中原始边出发,每次都把一条最短边加入进去;动态规划算法是在Graph-MST网络上使用的,可以用来解决复杂的路径优化等问题。
总之,最小生成树的构造是离散数学的重要技术,能够有效地构建最小生成树,从而解决复杂的网络优化问题。
最小生成树的构造有不同的方法,要想更好地理解和使用,就需要深刻掌握其原理和实现方法。
图最小生成树

是按逐个将顶点连通的方式来构造最
小生成树的。
10
从连通网络 N = { V, E }中的某一顶点 u0 出 发,选择与它关联的具有最小权值的边( u0, v), 将其顶点加入到生成树的顶点集合U中。 以后每一步从一个顶点在 U 中,而另一个顶点不 在U中的各条边中选择权值最小的边(u, v),把该 边加入到生成树的边集TE中,把它的顶点加入到 集合 U 中。如此重复执行,直到网络中的所有顶 点都加入到生成树顶点集合U中为止。
for (i=0; i<G.vexnum; ++i)
// 建零入度顶点栈S
if (!indegree[i]) Push(S, i); // 入度为0者进栈 count = 0; // 对输出顶点计数
while (!StackEmpty(S)) { Pop(S, i); printf(i, G.vertices[i].data); ++count; // 输出i号顶点并计数 for (p=G.vertices[i].firstarc; p; p=p->nextarc) { k = p->adjvex; // 对i号顶点的每个邻接点的入度减1
23
由于AOV网中有些活动之间没有次序要求,它们在拓扑序列的 位置可以是任意的,因此拓扑排序的结果不唯一。
C1 C3 C4
对右图进行拓扑排序,可得一个拓扑序列: C1,C3,C2,C4,C7,C6,C5 也可得到另一个拓扑序列: C2,C7,C1,C3,C4,C5,C6
C7 C2
C6 C5
还可以得到其它的拓扑序列。学生按照任何一个拓扑序列都可 以完成所要求的全部课程学习。 在AOV网中不应该出现有向环。因为环的存在意味着某项活动 将以自己为先决条件,显然无法形成拓扑序列。 判定网中是否存在环的方法:对有向图构造其顶点的拓扑有序 序列,若网中所有顶点都出现在它的拓扑有序序列中,则该 AOV网中一定不存在环。
最小生成树解法

最小生成树解法
最小生成树(Minimum Spanning Tree, MST)是指一棵图的生成树,其所有边的权值之和最小。
在计算最小生成树问题时,切图算法(Prim)和克鲁斯卡尔算法(Kruskal)是两种常用的解法。
切图算法从一个源点开始,依次将与源点相连的边加入树中,同
时将与该边相连的节点加入集合,然后在新集合中选取一条连接已选
节点和未选节点的最短边加入树,并将新的节点也加入集合中。
直至
所有节点都被加入树中。
克鲁斯卡尔算法则是将边按照权值从小到大排序,依次取边加入
树中,在加入前需判断该边是否会形成环,若不会则加入树中,并将
该边的两个节点视为已连接。
直至所有节点都被加入树中。
两种算法时间复杂度均为O(ElogE),其中E为边数。
但Prim算法更适合求解稠密图,而Kruskal算法则比较适合求解稀疏图。
最小树与最小树形图(数学建模)讲解

最小树与最小树形图(数学建模)讲解一、最小树的定义及性质1. 定义:最小树,又称最小树,是指在给定的带权无向图中,包含图中所有顶点的一个树形结构,且树中所有边的权值之和最小。
2. 性质:(1)最小树中不存在回路;(2)对于最小树中的任意两个顶点,它们之间有且仅有一条路径;(3)最小树中边的数量等于顶点数量减一;(4)在最小树中添加任意一条边,都会形成一条回路;(5)最小树不唯一,但权值之和相同。
二、求解最小树的方法1. Prim算法Prim算法是一种贪心算法,其基本思想是从图中的一个顶点开始,逐步添加边和顶点,直到形成最小树。
具体步骤如下:(1)初始化:选择一个顶点作为最小树的起点,将其加入最小树集合;(2)迭代:在最小树集合和非最小树集合之间,寻找一条权值最小的边,将其加入最小树集合;(3)重复步骤2,直到所有顶点都加入最小树集合。
2. Kruskal算法Kruskal算法同样是一种贪心算法,其基本思想是将图中的所有边按权值从小到大排序,然后依次选择权值最小的边,判断是否形成回路,若不形成回路,则将其加入最小树集合。
具体步骤如下:(1)初始化:将所有顶点视为独立的树;(2)按权值从小到大排序所有边;(3)迭代:选择权值最小的边,判断其是否形成回路,若不形成回路,则将其加入最小树集合;(4)重复步骤3,直到所有顶点都在同一棵树中。
三、最小树形图的定义及求解方法1. 定义:最小树形图,又称最优树形图,是指在给定的有向图中,找到一个包含所有顶点的树形结构,使得树中所有边的权值之和最小。
2. 求解方法:朱刘算法(Edmonds' Algorithm)朱刘算法是一种用于求解最小树形图的算法,其基本思想是通过寻找图中的最小权值环,进行收缩和扩展操作,最终得到最小树形图。
具体步骤如下:(1)寻找最小权值环;(2)对最小权值环进行收缩操作,将环中的顶点合并为一个新顶点;(3)在新图中寻找最小树形图;(4)将新图中的最小树形图扩展回原图,得到原图的最小树形图。
最小生成树问题(共7张PPT)

个,所以支撑树是有不唯一]。
C n1 m
求最小树的Kruskal算法
赋权的连通图G=(V,E)中m=|E|,n=|V|,
S1:对E中各边的权排序,设 w1≤w2≤…≤wm,wi=w(ei)
S2:初始化: w←0,T←φ,k←1,t←0
S3:若t=n-1则转S6,否则转S4
Y
N
T’←T∪{ek}
T’成圈? N END
Y
T←T+ {ek},
k←k+1 w←w+wk,
t←t+1,k←k+1
用Kruskal算法求最小树
用Kruskal算法(避圈法)求赋权连通图G的最小树
V2
5
V6
Kruskal法盯住边,而Prim法更注意顶点:
T为最小树,w为T的权。
4
T={v1,v2,v3,v5}
Prim法求最小支撑树 E的权排序w1≤w2≤…≤wm w←0,T←φ,k←1,t←0
对要m让条程边序的读边懂长“图排”,序S程3,:序m如个何元判素断排是序否较成好“的圈算”?法谈是何基容于易分,治时策间略、的空快间速复排杂序性(Q绝u不ick应S小or看ting),其时间复杂性是O(m㏒m)。
min S2:初始化:w←0,T←φ,k←1,t←0 设: {w(vv )}w(vv ) 简对称m条最边小的树边或长最排短序树,[管vvm线ij个 铺ST 元设素]。排序较好的i算法j是基于分治策略的快l速排k序(Quick Sorting),其时间复杂性是O(m㏒m)。
S4:若T∪{ek}有圈则k←k+1转S4,否则 转S5
S5: T←T∪{ek},w←w+wk, t←t+1, k←k+1,转S3
图论_5_树

• 图——基本概念
– 图、路与连通、最短路、有向图、图的矩阵
• Euler图与Hamilton图 • 树
– 树、生成树、有向树
• 平面图 图的着色
– 平面图、对偶图、顶点着色、面着色
• 网络 匹配 独立集
树
• 树的概念 • 生成树 • 有向树
树
• 定义1 连通无回路的图称为树,树中度为 1的点称为树叶,度大于1的点称为分枝点 或内点,每个连通分支均为树的图称为森 林。
Kruskal算法
(1)选取G的一边e1,使w(e1)=min{w(e)|e∈E},令E1 ={e1} (2)若已选出Ei={e1,…,ei},那么,从E-Ei中 e 选取一边ei+1,使 (Ⅰ)Ei∪{ei+1}的导出子图中不含回路; (Ⅱ)w(ei+1)=min{w(e)|e∈E-Ei , Ei∪{e}的导 出子图无回路} (3)若ei+1存在,令Ei+1=Ei∪{ei+1},i+1→i,转 (2),若ei+1不存在,则停止。
• 定理2 任意一棵非平凡树 T 中,至少有 两片树叶。
• • •
作业 证明 非平凡树中最长路的起点和终点 均为树叶。 证明 一棵树恰有2片树叶,则此树为 路。
生成树
• 定义1 若图G的生成子图T是树,则称T为 G的生成树。
• 定理1 G是连通图当且仅当G有生成树。
• 权图G中带权最小的生成树称为最小生成树 • Kruskal算法 • 输入:简单连通图G ,权函数w 。 • 输出:最小生成树T
(a)
b1
b2
(b)
b3
• 定义4 设u是有根树T的一个顶点,Vu是u 及其子孙构成的顶点集,Vu的导出子图称为 T的以u为根的子树。 • 定
1
详解图的应用(最小生成树、拓扑排序、关键路径、最短路径)
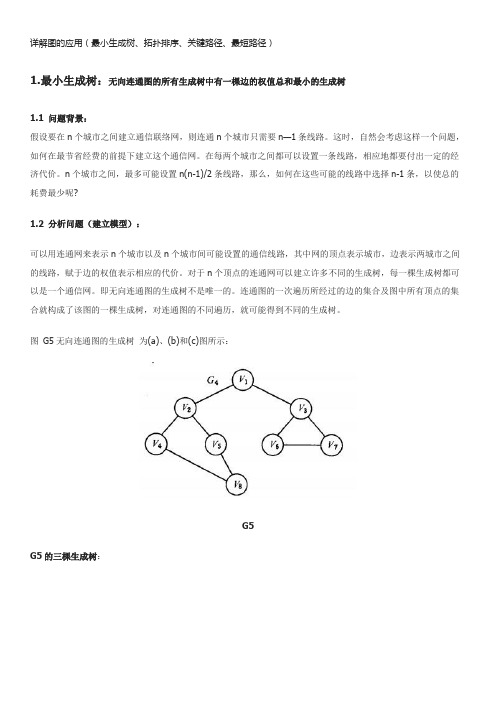
详解图的应用(最小生成树、拓扑排序、关键路径、最短路径)1.最小生成树:无向连通图的所有生成树中有一棵边的权值总和最小的生成树1.1 问题背景:假设要在n个城市之间建立通信联络网,则连通n个城市只需要n—1条线路。
这时,自然会考虑这样一个问题,如何在最节省经费的前提下建立这个通信网。
在每两个城市之间都可以设置一条线路,相应地都要付出一定的经济代价。
n个城市之间,最多可能设置n(n-1)/2条线路,那么,如何在这些可能的线路中选择n-1条,以使总的耗费最少呢?1.2 分析问题(建立模型):可以用连通网来表示n个城市以及n个城市间可能设置的通信线路,其中网的顶点表示城市,边表示两城市之间的线路,赋于边的权值表示相应的代价。
对于n个顶点的连通网可以建立许多不同的生成树,每一棵生成树都可以是一个通信网。
即无向连通图的生成树不是唯一的。
连通图的一次遍历所经过的边的集合及图中所有顶点的集合就构成了该图的一棵生成树,对连通图的不同遍历,就可能得到不同的生成树。
图G5无向连通图的生成树为(a)、(b)和(c)图所示:G5G5的三棵生成树:可以证明,对于有n 个顶点的无向连通图,无论其生成树的形态如何,所有生成树中都有且仅有n-1 条边。
1.3最小生成树的定义:如果无向连通图是一个网,那么,它的所有生成树中必有一棵边的权值总和最小的生成树,我们称这棵生成树为最小生成树,简称为最小生成树。
最小生成树的性质:假设N=(V,{ E}) 是个连通网,U是顶点集合V的一个非空子集,若(u,v)是个一条具有最小权值(代价)的边,其中,则必存在一棵包含边(u,v)的最小生成树。
1.4 解决方案:两种常用的构造最小生成树的算法:普里姆(Prim)和克鲁斯卡尔(Kruskal)。
他们都利用了最小生成树的性质1.普里姆(Prim)算法:有线到点,适合边稠密。
时间复杂度O(N^2)假设G=(V,E)为连通图,其中V 为网图中所有顶点的集合,E 为网图中所有带权边的集合。
