条件极值答案
导数与函数的极值、最值(经典导学案及练习答案详解)

§3.3导数与函数的极值、最值学习目标1.借助函数图象,了解函数在某点取得极值的必要和充分条件.2.会用导数求函数的极大值、极小值.3.会求闭区间上函数的最大值、最小值.知识梳理1.函数的极值(1)函数的极小值函数y=f(x)在点x=a的函数值f(a)比它在点x=a附近其他点的函数值都小,f′(a)=0;而且在点x=a附近的左侧f′(x)<0,右侧f′(x)>0,则a叫做函数y=f(x)的极小值点,f(a)叫做函数y=f(x)的极小值.(2)函数的极大值函数y=f(x)在点x=b的函数值f(b)比它在点x=b附近其他点的函数值都大,f′(b)=0;而且在点x=b附近的左侧f′(x)>0,右侧f′(x)<0,则b叫做函数y=f(x)的极大值点,f(b)叫做函数y=f(x)的极大值.(3)极小值点、极大值点统称为极值点,极小值和极大值统称为极值.2.函数的最大(小)值(1)函数f(x)在区间[a,b]上有最值的条件:如果在区间[a,b]上函数y=f(x)的图象是一条连续不断的曲线,那么它必有最大值和最小值.(2)求y=f(x)在区间[a,b]上的最大(小)值的步骤:①求函数y=f(x)在区间(a,b)上的极值;②将函数y=f(x)的各极值与端点处的函数值f(a),f(b)比较,其中最大的一个是最大值,最小的一个是最小值.常用结论对于可导函数f(x),“f′(x0)=0”是“函数f(x)在x=x0处有极值”的必要不充分条件.思考辨析判断下列结论是否正确(请在括号中打“√”或“×”)(1)函数f(x)在区间(a,b)上不存在最值.(×)(2)函数的极小值一定是函数的最小值.(×)(3)函数的极小值一定不是函数的最大值.(√)(4)函数y=f′(x)的零点是函数y=f(x)的极值点.(×)教材改编题1.如图是f (x )的导函数f ′(x )的图象,则f (x )的极小值点的个数为( )A .1B .2C .3D .4答案 A解析 由题意知只有在x =-1处f ′(-1)=0,且其两侧导数符号为左负右正.2.函数f (x )=x 3-ax 2+2x -1有极值,则实数a 的取值范围是( )A .(-∞,-6]∪[6,+∞)B .(-∞,-6)∪(6,+∞)C .(-6,6)D .[-6,6]答案 B解析 f ′(x )=3x 2-2ax +2,由题意知f ′(x )有变号零点,∴Δ=(-2a )2-4×3×2>0, 解得a >6或a <- 6.3.若函数f (x )=13x 3-4x +m 在[0,3]上的最大值为4,则m =________. 答案 4解析 f ′(x )=x 2-4,x ∈[0,3],当x ∈[0,2)时,f ′(x )<0,当x ∈(2,3]时,f ′(x )>0,所以f (x )在[0,2)上单调递减,在(2,3]上单调递增.又f (0)=m ,f (3)=-3+m .所以在[0,3]上,f (x )max =f (0)=4,所以m =4.题型一 利用导数求函数的极值问题命题点1 根据函数图象判断极值例1 (2022·广州模拟)设函数f (x )在R 上可导,其导函数为f ′(x ),且函数y =(x -1)f ′(x )的图象如图所示,则下列结论中正确的是( )A .函数f (x )有极大值f (-3)和f (3)B .函数f (x )有极小值f (-3)和f (3)C.函数f(x)有极小值f(3)和极大值f(-3)D.函数f(x)有极小值f(-3)和极大值f(3)答案 D解析由题图知,当x∈(-∞,-3)时,y>0,x-1<0⇒f′(x)<0,f(x)单调递减;当x∈(-3,1)时,y<0,x-1<0⇒f′(x)>0,f(x)单调递增;当x∈(1,3)时,y>0,x-1>0⇒f′(x)>0,f(x)单调递增;当x∈(3,+∞)时,y<0,x-1>0⇒f′(x)<0,f(x)单调递减.所以函数有极小值f(-3)和极大值f(3).命题点2求已知函数的极值例2已知函数f(x)=x-1+ae x(a∈R,e为自然对数的底数).(1)若曲线y=f(x)在点(1,f(1))处的切线平行于x轴,求a的值;(2)求函数f(x)的极值.解(1)因为f(x)=x-1+ae x,所以f′(x)=1-ae x,又因为曲线y=f(x)在点(1,f(1))处的切线平行于x轴,所以f′(1)=0,即1-ae1=0,所以a=e.(2)由(1)知f′(x)=1-ae x,当a≤0时,f′(x)>0,所以f(x)在(-∞,+∞)上单调递增,因此f(x)无极大值与极小值;当a>0时,令f′(x)>0,则x>ln a,所以f(x)在(ln a,+∞)上单调递增,令f′(x)<0,则x<ln a,所以f(x)在(-∞,ln a)上单调递减,故f(x)在x=ln a处取得极小值,且f(ln a)=ln a,但是无极大值,综上,当a≤0时,f(x)无极大值与极小值;当a>0时,f(x)在x=ln a处取得极小值ln a,但是无极大值.命题点3已知极值(点)求参数例3(1)(2022·大庆模拟)函数f(x)=x3+ax2+bx+a2在x=1处取得极值10,则a+b等于()A .-7B .0C .-7或0D .-15或6答案 A 解析 由题意知,函数f (x )=x 3+ax 2+bx +a 2,可得f ′(x )=3x 2+2ax +b ,因为f (x )在x =1处取得极值10,可得⎩⎪⎨⎪⎧ f ′(1)=3+2a +b =0,f (1)=1+a +b +a 2=10, 解得⎩⎪⎨⎪⎧ a =4,b =-11,或⎩⎪⎨⎪⎧a =-3,b =3, 检验知,当a =-3,b =3时,可得f ′(x )=3x 2-6x +3=3(x -1)2≥0,此时函数f (x )单调递增,函数无极值点,不符合题意;当a =4,b =-11时,可得f ′(x )=3x 2+8x -11=(3x +11)(x -1),当x <-113或x >1时, f ′(x )>0,f (x )单调递增;当-113<x <1时,f ′(x )<0,f (x )单调递减, 当x =1时,函数f (x )取得极小值,符合题意.所以a +b =-7.(2)(2022·南京模拟)已知函数f (x )=x (ln x -ax )在区间(0,+∞)上有两个极值,则实数a 的取值范围为( )A .(0,e)B.⎝⎛⎭⎫0,1eC.⎝⎛⎭⎫0,12 D.⎝⎛⎭⎫0,13 答案 C解析 f ′(x )=ln x -ax +x ⎝⎛⎭⎫1x -a=ln x +1-2ax ,由题意知ln x +1-2ax =0在(0,+∞)上有两个不相等的实根,2a =ln x +1x, 设g (x )=ln x +1x, 则g ′(x )=1-(ln x +1)x 2=-ln x x 2.当0<x <1时,g ′(x )>0,g (x )单调递增;当x >1时,g ′(x )<0,g (x )单调递减,所以g (x )的极大值为g (1)=1,又当x >1时,g (x )>0,当x →+∞时,g (x )→0,当x →0时,g (x )→-∞,所以0<2a <1,即0<a <12. 教师备选 1.(2022·榆林模拟)设函数f (x )=x cos x 的一个极值点为m ,则tan ⎝⎛⎭⎫m +π4等于( ) A.m -1m +1B.m +1m -1C.1-m m +1D.m +11-m 答案 B解析 由f ′(x )=cos x -x sin x =0,得tan x =1x ,所以tan m =1m, 故tan ⎝⎛⎭⎫m +π4=1+tan m 1-tan m =m +1m -1. 2.已知a ,b ∈R ,若x =a 不是函数f (x )=(x -a )2(x -b )·(e x -1-1)的极小值点,则下列选项符合的是( )A .1≤b <aB .b <a ≤1C .a <1≤bD .a <b ≤1 答案 B解析 令f (x )=(x -a )2(x -b )(e x -1-1)=0,得x 1=a ,x 2=b ,x 3=1.下面利用数轴标根法画出f (x )的草图,借助图象对选项A ,B ,C ,D 逐一分析.对选项A ,若1≤b <a ,由图可知x =a 是f (x )的极小值点,不符合题意; 对选项B ,若b <a ≤1,由图可知x =a 不是f (x )的极小值点,符合题意; 对选项C ,若a <1≤b ,由图可知x =a 是f (x )的极小值点,不符合题意; 对选项D ,若a <b ≤1,由图可知x =a 是f (x )的极小值点,不符合题意. 思维升华 根据函数的极值(点)求参数的两个要领(1)列式:根据极值点处导数为0和极值这两个条件列方程组,利用待定系数法求解;(2)验证:求解后验证根的合理性.跟踪训练1 (1)(2022·长沙模拟)若x =1是函数f (x )=(x 2+ax -1)e x-1的极值点,则f (x )的极大值为( )A .-1B .-2e -3C .5e -3D .1 答案 C解析 因为f (x )=(x 2+ax -1)e x -1,故可得f ′(x )=(2x +a )e x -1+(x 2+ax -1)e x -1=e x -1[x 2+(a +2)x +a -1],因为x =1是函数f (x )=(x 2+ax -1)e x-1的极值点,故可得f ′(1)=0,即2a +2=0,解得a =-1.此时f ′(x )=e x -1(x 2+x -2)=e x -1(x +2)(x -1).令f ′(x )=0,解得x 1=-2,x 2=1,由f ′(x )>0可得x <-2或x >1;由f ′(x )<0可得-2<x <1,所以f (x )在区间(-∞,-2)上单调递增,在(-2,1)上单调递减,在(1,+∞)上单调递增,故f (x )的极大值点为x =-2.则f (x )的极大值为f (-2)=(4+2-1)e -3=5e -3.(2)(2022·芜湖模拟)函数f (x )=ln x +12x 2-ax (x >0)在⎣⎡⎦⎤12,3上有且仅有一个极值点,则实数a 的取值范围是( )A.⎝⎛⎭⎫52,103B.⎣⎡⎭⎫52,103C.⎝⎛⎦⎤52,103D.⎣⎡⎦⎤2,103 答案 B解析 ∵f (x )=ln x +12x 2-ax (x >0), ∴f ′(x )=1x+x -a , ∵函数f (x )=ln x +12x 2-ax (x >0)在⎣⎡⎦⎤12,3上有且仅有一个极值点, ∴y =f ′(x )在⎣⎡⎦⎤12,3上只有一个变号零点.令f ′(x )=1x +x -a =0,得a =1x+x . 设g (x )=1x +x ,则g (x )在⎣⎡⎦⎤12,1上单调递减,在[1,3]上单调递增,∴g (x )min =g (1)=2,又g ⎝⎛⎭⎫12=52,g (3)=103, ∴当52≤a <103时,y =f ′(x )在⎣⎡⎦⎤12,3上只有一个变号零点. ∴实数a 的取值范围为⎣⎡⎭⎫52,103.题型二 利用导数求函数最值例4 已知函数g (x )=a ln x +x 2-(a +2)x (a ∈R ).(1)若a =1,求g (x )在区间[1,e]上的最大值;(2)求g (x )在区间[1,e]上的最小值h (a ).解 (1)∵a =1,∴g (x )=ln x +x 2-3x ,∴g ′(x )=1x +2x -3=(2x -1)(x -1)x, ∵x ∈[1,e],∴g ′(x )≥0,∴g (x )在[1,e]上单调递增,∴g (x )max =g (e)=e 2-3e +1.(2)g (x )的定义域为(0,+∞),g ′(x )=a x +2x -(a +2)=2x 2-(a +2)x +a x=(2x -a )(x -1)x. ①当a 2≤1,即a ≤2时,g (x )在[1,e]上单调递增,h (a )=g (1)=-a -1; ②当1<a 2<e ,即2<a <2e 时,g (x )在⎣⎡⎭⎫1,a 2上单调递减,在⎝⎛⎦⎤a 2,e 上单调递增,h (a )=g ⎝⎛⎭⎫a 2=a ln a 2-14a 2-a ; ③当a 2≥e ,即a ≥2e 时,g (x )在[1,e]上单调递减,h (a )=g (e)=(1-e)a +e 2-2e. 综上,h (a )=⎩⎪⎨⎪⎧ -a -1,a ≤2,a ln a 2-14a 2-a ,2<a <2e ,(1-e )a +e 2-2e ,a ≥2e.教师备选已知函数f (x )=ln x -ax -2(a ≠0).(1)讨论函数f (x )的单调性;(2)若函数f (x )有最大值M ,且M >a -4,求实数a 的取值范围.解 (1)f (x )的定义域为(0,+∞),由f (x )=ln x -ax -2(a ≠0)可得f ′(x )=1x-a , 当a <0时,f ′(x )>0,所以f (x )在(0,+∞)上单调递增;当a >0时,令f ′(x )=0,得x =1a, 所以当x ∈⎝⎛⎭⎫0,1a 时, f ′(x )>0,f (x )单调递增;当x ∈⎝⎛⎭⎫1a ,+∞时,f ′(x )<0,f (x )单调递减, 综上所述,当a <0时,f (x )在(0,+∞)上单调递增;当a >0时,f (x )在⎝⎛⎭⎫0,1a 上单调递增,在⎝⎛⎭⎫1a ,+∞上单调递减. (2)由(1)知,当a <0时,f (x )在(0,+∞)上单调递增,无最大值,当a >0时,f (x )在⎝⎛⎭⎫0,1a 上单调递增,在⎝⎛⎭⎫1a ,+∞上单调递减, 所以当x =1a时,f (x )取得最大值, 即f (x )max =f ⎝⎛⎭⎫1a =ln 1a -a ×1a-2 =ln 1a-3=-ln a -3, 因此有-ln a -3>a -4,得ln a +a -1<0,设g (a )=ln a +a -1,则g ′(a )=1a+1>0, 所以g (a )在(0,+∞)上单调递增,又g (1)=0,所以g (a )<g (1),得0<a <1,故实数a 的取值范围是(0,1).思维升华 (1)求函数f (x )在闭区间[a ,b ]上的最值时,在得到极值的基础上,结合区间端点的函数值f (a ),f (b )与f (x )的各极值进行比较得到函数的最值.(2)若所给的闭区间[a ,b ]含参数,则需对函数f (x )求导,通过对参数分类讨论,判断函数的单调性,从而得到函数f (x )的最值.跟踪训练2 某村庄拟修建一个无盖的圆柱形蓄水池(不计厚度),设该蓄水池的底面半径为r米,高为h 米,体积为V 立方米.假设建造成本仅与表面积有关,侧面的建造成本为100元/平方米,底面的建造成本为160元/平方米,该蓄水池的总建造成本为12 000π元(π为圆周率).(1)将V 表示成r 的函数V (r ),并求该函数的定义域;(2)讨论函数V (r )的单调性,并确定r 和h 为何值时该蓄水池的体积最大.解 (1)∵蓄水池的侧面的总成本为100×2πrh =200πrh (元),底面的总成本为160πr 2元,∴蓄水池的总成本为(200πrh +160πr 2)元.由题意得200πrh +160πr 2=12 000π,∴h =15r (300-4r 2).从而V (r )=πr 2h =π5(300r -4r 3).由h >0,且r >0,可得0<r <5 3.故函数V (r )的定义域为(0,53).(2)由(1)知V (r )=π5(300r -4r 3), 故V ′(r )=π5(300-12r 2),令V ′(r )=0,解得r 1=5,r 2=-5(舍).当r ∈(0,5)时,V ′(r )>0,故V (r )在(0,5)上单调递增;当r ∈(5,53)时,V ′(r )<0,故V (r )在(5,53)上单调递减.由此可知,V (r )在r =5处取得最大值,此时h =8,即当r =5,h =8时,该蓄水池的体积最大.课时精练1.若函数f (x )=x 2+2xe x 的极大值点与极小值点分别为a ,b ,则a +b 等于() A .-4 B. 2C .0D .2答案 C解析 f ′(x )=2-x 2e x ,当-2<x <2时,f ′(x )>0;当x <-2或x >2时,f ′(x )<0.故f (x )=x 2+2x ex 的极大值点与极小值点分别为2,-2, 则a =2,b =-2,所以a +b =0.2.如图是函数y =f (x )的导函数的图象,下列结论中正确的是( )A .f (x )在[-2,-1]上单调递增B .当x =3时,f (x )取得最小值C .当x =-1时,f (x )取得极大值D .f (x )在[-1,2]上单调递增,在[2,4]上单调递减答案 D解析 根据题图知,当x ∈(-2,-1),x ∈(2,4)时,f ′(x )<0,函数y =f (x )单调递减;当x ∈(-1,2),x ∈(4,+∞)时,f ′(x )>0,函数y =f (x )单调递增.所以y =f (x )在[-2,-1]上单调递减,在(-1,2)上单调递增,在(2,4)上单调递减,在(4,+∞)上单调递增,故选项A 不正确,选项D 正确;故当x =-1时,f (x )取得极小值,选项C 不正确;当x =3时,f (x )不是取得最小值,选项B 不正确.3.已知函数f (x )=2ln x +ax 2-3x 在x =2处取得极小值,则f (x )的极大值为( )A .2B .-52C .3+ln 2D .-2+2ln 2 答案 B解析 由题意得,f ′(x )=2x+2ax -3, ∵f (x )在x =2处取得极小值,∴f ′(2)=4a -2=0,解得a =12, ∴f (x )=2ln x +12x 2-3x , f ′(x )=2x +x -3=(x -1)(x -2)x ,∴f (x )在(0,1),(2,+∞)上单调递增,在(1,2)上单调递减,∴f (x )的极大值为f (1)=12-3=-52. 4.(2022·重庆联考)函数f (x )=x +2cos x 在[0,π]上的最大值为( )A .π-2B.π6 C .2D.π6+ 3 答案 D解析 由题意得,f ′(x )=1-2sin x ,∴当0≤sin x ≤12,即x 在⎣⎡⎦⎤0,π6和⎣⎡⎦⎤5π6,π上时,f ′(x )≥0,f (x )单调递增; 当12<sin x ≤1,即x 在⎝⎛⎭⎫π6,5π6上时, f ′(x )<0,f (x )单调递减,∴f (x )有极大值f ⎝⎛⎭⎫π6=π6+3,有极小值f ⎝⎛⎭⎫5π6=5π6-3,而端点值f (0)=2,f (π)=π-2,则f ⎝⎛⎭⎫π6>f (0)>f (π)>f ⎝⎛⎭⎫5π6, ∴f (x )在[0,π]上的最大值为π6+ 3. 5.(多选)已知x =1和x =3是函数f (x )=ax 3+bx 2-3x +k (a ,b ∈R )的两个极值点,且函数f (x )有且仅有两个不同零点,则k 值为( )A .-43B.43 C .-1D .0 答案 BD解析 f ′(x )=3ax 2+2bx -3,依题意1,3是f ′(x )=0的两个根, 所以⎩⎨⎧ 1+3=-2b 3a ,1×3=-33a,解得a =-13,b =2. 故f (x )=-13x 3+2x 2-3x +k . 易求得函数f (x )的极大值为f (3)=k 和极小值为f (1)=-43+k .要使函数f (x )有两个零点,则f (x )极大值k =0或f (x )极小值-43+k =0, 所以k =0或k =43. 6.(多选)已知函数f (x )=x +sin x -x cos x 的定义域为[-2π,2π),则( )A .f (x )为奇函数B .f (x )在[0,π)上单调递增C .f (x )恰有4个极大值点D .f (x )有且仅有4个极值点答案 BD解析 因为f (x )的定义域为[-2π,2π),所以f (x )是非奇非偶函数,故A 错误;因为f (x )=x +sin x -x cos x ,所以f ′(x )=1+cos x -(cos x -x sin x )=1+x sin x ,当x ∈[0,π)时,f ′(x )>0,则f (x )在[0,π)上单调递增,故B 正确;显然f ′(0)≠0,令f ′(x )=0,得sin x =-1x, 分别作出y =sin x ,y =-1x在区间[-2π,2π)上的图象,由图可知,这两个函数的图象在区间[-2π,2π)上共有4个公共点,且两图象在这些公共点上都不相切,故f (x )在区间[-2π,2π)上的极值点的个数为4,且f (x )只有2个极大值点,故C 错误,D 正确.7.(2022· 潍坊模拟)写出一个存在极值的奇函数f (x )=________.答案 sin x (答案不唯一)解析 正弦函数f (x )=sin x 为奇函数,且存在极值.8.(2021·新高考全国Ⅰ)函数f (x )=|2x -1|-2ln x 的最小值为________.答案 1解析 函数f (x )=|2x -1|-2ln x 的定义域为(0,+∞).①当x >12时,f (x )=2x -1-2ln x , 所以f ′(x )=2-2x =2(x -1)x,当12<x <1时,f ′(x )<0, 当x >1时,f ′(x )>0,所以f (x )min =f (1)=2-1-2ln 1=1;②当0<x ≤12时,f (x )=1-2x -2ln x 在⎝⎛⎦⎤0,12上单调递减, 所以f (x )min =f ⎝⎛⎭⎫12=-2ln 12=2ln 2=ln 4>ln e =1.综上,f (x )min =1. 9.已知函数f (x )=ln x -2x -2x +1. (1)求函数f (x )的单调区间;(2)设g (x )=f (x )-4+a x +1+2(a ∈R ),若x 1,x 2是函数g (x )的两个极值点,求实数a 的取值范围. 解 (1)由题知函数f (x )的定义域为(0,+∞),f ′(x )=1x -2(x +1)-2(x -1)(x +1)2=(x -1)2x (x +1)2≥0对任意x ∈(0,+∞)恒成立, 当且仅当x =1时,f ′(x )=0,所以f (x )的单调递增区间为(0,+∞),无单调递减区间.(2)因为g (x )=f (x )-4+a x +1+2=ln x -a x +1, 所以g ′(x )=1x +a (x +1)2=x 2+(2+a )x +1x (x +1)2(x >0). 由题意知x 1,x 2是方程g ′(x )=0在(0,+∞)内的两个不同的实数解.令h (x )=x 2+(2+a )x +1,又h (0)=1>0,所以只需⎩⎪⎨⎪⎧-2-a >0,Δ=(2+a )2-4>0,解得a <-4,即实数a 的取值范围为(-∞,-4). 10.(2022·珠海模拟)已知函数f (x )=ln x -ax ,x ∈(0,e],其中e 为自然对数的底数.(1)若x =1为f (x )的极值点,求f (x )的单调区间和最大值;(2)是否存在实数a ,使得f (x )的最大值是-3?若存在,求出a 的值;若不存在,说明理由. 解 (1)∵f (x )=ln x -ax ,x ∈(0,e],∴f ′(x )=1-ax x, 由f ′(1)=0,得a =1.∴f ′(x )=1-x x, ∴x ∈(0,1),f ′(x )>0,x ∈(1,+∞),f ′(x )<0,∴f (x )的单调递增区间是(0,1),单调递减区间是(1,e];f (x )的极大值为f (1)=-1,也即f (x )的最大值为f (1)=-1.(2)∵f (x )=ln x -ax ,∴f ′(x )=1x -a =1-ax x , ①当a ≤0时,f (x )在(0,e]上单调递增,∴f (x )的最大值是f (e)=1-a e =-3,解得a =4e >0,舍去;②当a >0时,由f ′(x )=1x -a =1-axx =0,得x =1a ,当0<1a <e ,即a >1e 时,∴x ∈⎝⎛⎭⎫0,1a 时,f ′(x )>0;x ∈⎝⎛⎭⎫1a ,e 时,f ′(x )<0,∴f (x )的单调递增区间是⎝⎛⎭⎫0,1a ,单调递减区间是⎝⎛⎭⎫1a ,e ,又f (x )在(0,e]上的最大值为-3,∴f (x )max =f ⎝⎛⎭⎫1a =-1-ln a =-3,∴a =e 2;当e ≤1a ,即0<a ≤1e 时,f (x )在(0,e]上单调递增,∴f (x )max =f (e)=1-a e =-3,解得a =4e >1e ,舍去.综上,存在a 符合题意,此时a =e 2.11.若函数f (x )=(x 2-a )e x 的两个极值点之积为-3,则f (x )的极大值为() A.6e 3 B .-2eC .-2e D.4e 2答案 A解析 因为f (x )=(x 2-a )e x ,所以f ′(x )=(x 2+2x -a )e x ,由f′(x)=(x2+2x-a)e x=0,得x2+2x-a=0,由函数f(x)=(x2-a)e x的两个极值点之积为-3,则由根与系数的关系可知,-a=-3,即a=3,所以f(x)=(x2-3)e x,f′(x)=(x2+2x-3)e x,当x<-3或x>1时,f′(x)>0;当-3<x<1时,f′(x)<0,故f(x)在(-∞,-3)上单调递增,在(-3,1)上单调递减,在(1,+∞)上单调递增,所以f(x)的极大值为f(-3)=6 e3.12.函数f(x)=ax3-6ax2+b在区间[-1,2]上的最大值为3,最小值为-29(a>0),则a,b的值为()A.a=2,b=-29 B.a=3,b=2C.a=2,b=3 D.以上都不对答案 C解析函数f(x)的导数f′(x)=3ax2-12ax=3ax(x-4),因为a>0,所以由f′(x)<0,计算得出0<x<4,此时函数单调递减,由f′(x)>0,计算得出x>4或x<0,此时函数单调递增,即函数在[-1,0]上单调递增,在[0,2]上单调递减,即函数在x=0处取得极大值同时也是最大值,则f(0)=b=3,则f(x)=ax3-6ax2+3,f(-1)=-7a+3,f(2)=-16a+3,则f(-1)>f(2),即函数的最小值为f(2)=-16a+3=-29,计算得出a=2,b=3.13.(2021·全国乙卷)设a≠0,若x=a为函数f(x)=a(x-a)2(x-b)的极大值点,则() A.a<b B.a>bC.ab<a2D.ab>a2答案 D解析当a>0时,根据题意画出函数f(x)的大致图象,如图1所示,观察可知b>a.图1当a <0时,根据题意画出函数f (x )的大致图象,如图2所示,观察可知a >b .图2综上,可知必有ab >a 2成立.14.(2022·河南多校联考)已知函数f (x )=2ln x ,g (x )=x +2,若f (x 1)=g (x 2),则x 1-x 2的最小值为______.答案 4-2ln 2解析 设f (x 1)=g (x 2)=t ,即2ln x 1=t ,x 2+2=t ,解得x 1=2e t ,x 2=t -2,所以x 1-x 2=2e t -t +2,令h (t )=2e t -t +2,则h ′(t )=21e 2t -1, 令h ′(t )=0,解得t =2ln 2,当t <2ln 2时,h ′(t )<0,当t >2ln 2时,h ′(t )>0,所以h (t )在(-∞,2ln 2)上单调递减,在(2ln 2,+∞)上单调递增,所以h (t )的最小值为h (2ln 2)=e ln 2-2ln 2+2=4-2ln 2,所以x 1-x 2的最小值为4-2ln 2.15.(多选)已知函数f (x )=x ln x +x 2,x 0是函数f (x )的极值点,以下几个结论中正确的是( )A .0<x 0<1eB .x 0>1eC .f (x 0)+2x 0<0D .f (x 0)+2x 0>0答案 AD解析 函数f (x )=x ln x +x 2(x >0),∴f ′(x )=ln x +1+2x ,∵x 0是函数f (x )的极值点,∴f ′(x 0)=0,即ln x 0+1+2x 0=0,∴f ′⎝⎛⎭⎫1e =2e >0,当x >1e时,f ′(x )>0, ∵当x →0时,f ′(x )→-∞,∴0<x 0<1e,即A 正确,B 不正确; f (x 0)+2x 0=x 0ln x 0+x 20+2x 0=x 0(ln x 0+x 0+2)=x 0(1-x 0)>0,即D 正确,C 不正确.16.已知函数f (x )=x 2-2x +a ln x (a >0).(1)求函数f (x )的单调递增区间;(2)若函数f (x )有两个极值点x 1,x 2,x 1<x 2,不等式f (x 1)≥mx 2恒成立,求实数m 的取值范围.解 (1)f ′(x )=2x -2+a x =2x 2-2x +a x,x >0, 一元二次方程2x 2-2x +a =0的Δ=4(1-2a ),①当a ≥12时,f ′(x )≥0,f (x )在(0,+∞)上单调递增; ②当0<a <12时,令f ′(x )=0, 得x 1=1-1-2a 2>0,x 2=1+1-2a 2>0, 所以当0<x <1-1-2a 2时, f ′(x )>0,f (x )单调递增, 当1-1-2a 2<x <1+1-2a 2时, f ′(x )<0,f (x )单调递减,当x >1+1-2a 2时,f ′(x )>0,f (x )单调递增. 综上所述,当a ≥12时,f (x )的单调递增区间为(0,+∞),当0<a <12时,f (x )的单调递增区间为⎝ ⎛⎭⎪⎫0,1-1-2a 2,⎝ ⎛⎭⎪⎫1+1-2a 2,+∞. (2)由(1)知,0<a <12,x 1+x 2=1,x 1x 2=a 2,则0<x 1<12<x 2, 由f (x 1)≥mx 2恒成立,得x 21-2x 1+a ln x 1≥mx 2,即(1-x 2)2-2(1-x 2)+2(1-x 2)x 2ln(1-x 2)≥mx 2,即m ≤x 2-1x 2+2(1-x 2)ln(1-x 2), 记h (x )=x -1x+2(1-x )ln(1-x ), 1>x >12, 则h ′(x )=1x 2-2ln(1-x )-1>0⎝⎛⎭⎫1>x >12, 故h (x )在⎝⎛⎭⎫12,1上单调递增,h ⎝⎛⎭⎫12=-32-ln 2, 故m ≤-32-ln 2.。
《高等数学》习题答案

《高等数学》习题答案二〇一四年六月三日《高等数学》习题答案第1章 函数练习题1.11.(1)不是。
定义域不相同。
函数x y =的定义域为R ,函数xx y 2=的定义域为}{0≠x x 。
(2)不是。
对应法则不相同。
x x y ==2。
2.(1)⎩⎨⎧>-≠-0120)12lg(x x ∴定义域为⎭⎬⎫⎩⎨⎧≠>121x x x 且。
(2)022≥-x }2-x 2x {x ≤≥∴或定义域为。
(3)⎪⎩⎪⎨⎧>≥-⇒⎩⎨⎧>-≥-⇒⎩⎨⎧>-≥-321230231ln )23ln(0230)23ln(x x x x x x {}1≥∴x x 定义域为。
3.25)23(,23)21(==f f 。
4.[()]12xf f x x=- 5.(1)⎩⎨⎧≥-≠0102x x {}011≠≤≤-∴x x x 且定义域为 (2)1211≤-≤-x {}31≤≤-∴x x 定义域为 (3)⎩⎨⎧≠≥-003x x {}03≠≤∴x x x 且定义域为6. 不是。
定义域不相同。
{}{}0lg 2)(,0lg )(2>=≠=x x x x g x x x x f 的定义域为的定义域为。
练习题1.21.(1)偶函数(2)偶函数(3)奇函数2.(1)π2=T (2)ππ==-=-==22,2cos 212122cos 1sin 2T x x x y (3)ππ==22T练习题1.31.(1)x y 2tan = (2))1sin(2+=xe y2.(1)23,10+==x u u y (2)21,x u u y -==(3)x u y u-==,10 (4)2,2x u y u== (5)1,log 22+==x u u y (6)x u u y 5,sin == (7)5,sin x u u y == (8)x u u y sin ,5== (9) x v v u u y lg ,lg ,lg === (10)2,arcsin x u u y == 3.(1)由)(21,2112R x x y y x x y ∈-=-=+=故其反函数为可得 (2)由)(2,22333R x x y y x x y ∈-=-=+=故其反函数为可得练习题1.41.(1)R (2)⎩⎨⎧>>⇒⎩⎨⎧>>⇒⎩⎨⎧>>0101lg lg 00lg x x x x x x {}1>∴x x 定义域为 (3)⎪⎩⎪⎨⎧>≥-⇒⎩⎨⎧>-≥-⇒⎩⎨⎧>-≥-321230231ln )23ln(0230)23ln(x x x x x x {}1≥∴x x 定义域为 (4)1211≤-≤-x {}31≤≤-∴x x 定义域为第一章复习题一、判断题:1.√2.×3.√4.√5.√6.√ 二、填空题:1. 0>x2. e 、13. 5,,tan -===x v v u u y4. 22-x 5. {}122±≠≤≤-x x x 且 三、解答题:42)(,4)0(3++-=-=x x x f f第2章 极限练习题2.11.(1)极限为0 (2)极限为0 (3)极限为1 (4)极限为1(5)当n 无限增大时,n)1(1-+无休止地反复取0和2两个数,而不会无限接近于任何一个确定的常数,故该数列当∞→n 时没有极限(6)数列{}n n)1(-即为-1,2,-3,4,-5…… ,故该数列当∞→n 时没有极限(7)极限为22. 该数列的奇子数列为1,2,3,…,n … 没有极限 偶子数列为111,,23n⋅⋅⋅⋅⋅⋅, 极限为0 所以该数列的极限不存在。
高三数学利用导数求最值和极值试题答案及解析

高三数学利用导数求最值和极值试题答案及解析1.已知函数 (R).(1)当时,求函数的极值;(2)若函数的图象与轴有且只有一个交点,求的取值范围.【答案】(1)当时, 取得极大值为;当时, 取得极小值为.(2)a的取值范围是.【解析】(1)遵循“求导数,求驻点,讨论驻点两侧导数值符号,确定极值”.(2)根据= ,得到△= = .据此讨论:①若a≥1,则△≤0,此时≥0在R上恒成立,f(x)在R上单调递增 .计算f(0),,得到结论.②若a<1,则△>0,= 0有两个不相等的实数根,不妨设为.有.给出当变化时,的取值情况表.根据f(x1)·f(x2)>0, 解得a>.作出结论.试题解析:(1)当时,,∴.令="0," 得. 2分当时,, 则在上单调递增;当时,, 则在上单调递减;当时,, 在上单调递增. 4分∴当时, 取得极大值为;当时, 取得极小值为. 6分(2)∵= ,∴△= = .①若a≥1,则△≤0, 7分∴≥0在R上恒成立,∴ f(x)在R上单调递增 .∵f(0),,∴当a≥1时,函数f(x)的图象与x轴有且只有一个交点. 9分②若a<1,则△>0,∴= 0有两个不相等的实数根,不妨设为.∴.当变化时,的取值情况如下表:x x(x,x)x++11分∵,∴.∴=.同理. ∴.令f(x1)·f(x2)>0, 解得a>.而当时,, 13分故当时, 函数f(x)的图象与x轴有且只有一个交点.综上所述,a的取值范围是. 14分【考点】应用导数研究函数的极值、单调性及函数的图象,分类讨论思想.2.函数的极小值是 .【答案】.【解析】,令,解得,列表如下:极大值极小值故函数在处取得极小值,即.【考点】函数的极值3.已知a≤+lnx对任意的x∈[,2]恒成立,则a的最大值为________.【解析】令f(x)=+lnx,f′(x)=,当x∈[,1)时,f′(x)<0,当x∈(1,2]时,f′(x)>0,∴f(x)min=f(1)=0,∴a≤0,故a最大值为0.4.已知函数,是函数的导函数,且有两个零点和(),则的最小值为()A.B.C.D.以上都不对【答案】B【解析】,由题意,当或时,,当时,,因此的最小值是,选B.【考点】函数的极值与最值.5.已知e为自然对数的底数,设函数f(x)=(e x-1)(x-1)k(k=1,2),则 ().A.当k=1时,f(x)在x=1处取到极小值B.当k=1时,f(x)在x=1处取到极大值C.当k=2时,f(x)在x=1处取到极小值D.当k=2时,f(x)在x=1处取到极大值【答案】C【解析】当k=1时,f′(x)=e x·x-1,f′(1)≠0,∴x=1不是函数f(x)的极值点.当k=2时,f′(x)=(x-1)(xe x+e x-2),显然f′(1)=0,且x在1的左边附近f′(x)<0,x在1的右边附近f′(x)>0,∴f(x)在x=1处取到极小值.6.已知函数f(x)=x3+ax2+x+2(a>0)的极大值点和极小值点都在区间(-1,1)内,则实数a的取值范围是______.【答案】(,2)【解析】由题意可知f′(x)=0的两个不同解都在区间(-1,1)内.因为f′(x)=3x2+2ax+1,所以根据导函数图象可得又a>0,解得<a<2.7.设函数f(x)=x e x,则().A.x=1为f(x)的极大值点B.x=1为f(x)的极小值点C.x=-1为f(x)的极大值点D.x=-1为f(x)的极小值点【答案】D【解析】∵f(x)=x e x,∴f′(x)=e x+x e x=e x(1+x).∴当f′(x)>0时,则x>-1,函数y=f(x)是增函数,同理可求,x<-1时函数f(x)为减函数.∴x=-1时,函数f(x)取得极小值.8.已知函数f(x)=x3+ax2+x+2(a>0)的极大值点和极小值点都在区间(-1,1)内,则实数a的取值范围是().A.(0,2]B.(0,2)C.[,2)D.(,2)【答案】D【解析】由题意可知f′(x)=0的两个不同解都在区间(-1,1)内.因为f′(x)=3x2+2ax+1,所以根据导函数图象可得又a>0,解得<a<2,故选D.9.若函数在区间内有极值,则实数的取值范围是 .【答案】【解析】因为函数在区间内有极值,所以导数在区间内必有零点,于是.【考点】1.导数的公式与法则;2.函数的零点.10.某人进行了如下的“三段论”推理:如果,则是函数的极值点,因为函数在处的导数值,所以是函数的极值点.你认为以上推理的 ( ) A.大前提错误B.小前提错误C.推理形式错误D.结论正确【答案】A【解析】本题中,如果,则是函数的极值点是错误的.若是函数的极值点,则函数在的左右两侧异号,而否则尽管有,都不能说明是函数的极值点.如,其导数,函数在上是增函数.所以不是函数的极值点.因此本题是大前提错误.【考点】推理与证明、导数、函数的极值11.在处有极小值,则实数为 .【答案】1【解析】由得,又在处有极小值,故,解得或,当时,有,函数在单调递增,在单调递减,故在处有极小值;当时,有,函数在单调递增,在单调递减,故在处有极大值.综上可知.【考点】利用导数处理函数的极值12.已知函数.(1)当时,求函数的极值;(2)求函数的单调区间.【答案】(1),无极大值;(2)见解析.【解析】(1)先找到函数的定义域,在定义域内进行作答,在条件下求出函数的导函数,根据函数的单调性与导数的关系,判断函数的极值;(2)先求出函数的导函数,其导函数中含有参数,所以要进行分类讨论,对分三种情况,,进行讨论,分别求出每种情况下的函数的单调增区间和单调减区间.试题解析:(1)函数的定义域是, 1分当时,,所以在上递减,在上递增,所以函数的极小值为,无极大值; 4分(2)定义域, 5分①当,即时,由,得的增区间为;由,得的减区间为; 7分②当,即时,由,得的增区间为和;由,得的减区间为; 9分③当,即时,由,得的增区间为和;由,得的减区间为; 11分综上,时,的增区间为,减区间为;时,的增区间为和,减区间为;时,的增区间为和,减区间为. 13分【考点】1、对数函数的定义域;2、含参数的分类讨论思想;3、函数的单调性与导数的关系;4、解不等式;5、求函数的极值.13.已知函数(,,且)的图象在处的切线与轴平行. (1)确定实数、的正、负号;(2)若函数在区间上有最大值为,求的值.【答案】(1),;(2).【解析】(1)先求导数,因为切线与轴平行,所以导数为0,列出等式,判断出的符号;(2)求导数,令导数为0,解出方程的根,利用导数的正负判断出函数的单调性,通过分类讨论的方法找到最大值,让最大值等于,解出的值.试题解析:(1) 1分由图象在处的切线与轴平行,知,∴. 2分又,故,. 3分(2) 令,得或. 4分∵,令,得或令,得.于是在区间内为增函数,在内为减函数,在内为增函数.∴是的极大值点,是极小值点. 5分令,得或. 6分分类:①当时,,∴ .由解得, 8分②当时,, 9分∴.由得 . 10分记,∵, 11分∴在上是增函数,又,∴, 12分∴在上无实数根. 13分综上,的值为. 14分【考点】1.用导数求切线的斜率;2.用导数求函数最值.14.已知函数,当时取得极小值,则等于()A.B.C.D.【答案】D【解析】由,解得,当;当;当,故在处取得最小值,即,则,所以,故选D.【考点】导数的极值点求法,导数的极值求解.15.对于三次函数,给出定义:设是函数的导数,是函数的导数,若方程有实数解,则称点为函数的“拐点”。
多元函数的极值

x yz xy z x y z定理1 (必要条件)函数偏导数,证:据一元函数极值的必要条件可知定理结论成立.0),(,0),(0000=′=′y x f y x f yx 取得极值,取得极值取得极值且在该点取得极值,则有),(),(00y x y x f z 在点=存在),(),(00y x y x f z 在点因=在),(0y x f z =0x x =故在),(0y x f z =0y y =zox y对于三元函数,若M 0是f (x , y , z )的驻点,f (x , y , z )在M 0处所有的二阶偏导数连续,则当矩阵在M 0处为正定阵时( ),M 0为极小值点,为负定阵时( ),M 0为极大值点.类似的,可以将以上结论推广到三元以上的函数.H=xx xy xz xyyy yz xz yz zz f f f f f f f f f ⎡⎤⎢⎥⎢⎥⎢⎥⎣⎦112233H 0,H 0,H 0>>>112233H 0,H 0,H 0<><αcos 24x αcos 22x −)sin (cos 222−+ααx =x A αsin 24αsin 4x −0cos sin 2=+ααx =αA 解得:由题意知,最大值在定义域D 内达到,而在域D 内只有一个驻点,故此点即为所求.,0sin ≠α0≠x ααααsin cos sin 2sin 2422x x x A +−=)0,120:(2πα<<<<x D 0cos 212=+−αx x 0)sin (cos cos 2cos 2422=−+−ααααx x (cm)8,603===x D πα作业P121 4, 6, 7, 13。
6函数的极值与导数答案

函数的极值与导数讲义1.极值点与极值(1)极小值点与极小值如图,函数y=f(x)在点x=a的函数值f(a)比它在点x=a附近其他点的函数值都小,f′(a)=0;而且在点x=a附近的左侧,右侧,则把点a叫做函数y=f(x)的极小值点,f(a)叫做函数y=f(x)的极小值.(2)极大值点与极大值如图,函数y=f(x)在点x=b的函数值f(b)比它在点x=b附近其他点的函数值都大,f′(b)=0;而且在点x=b的左侧,右侧,则把点b叫做函数y=f(x)的极大值点,f(b)叫做函数y=f(x)的极大值.、统称为极值点,和统称为极值.2.求函数y=f(x)的极值的方法解方程f′(x)=0,当f′(x0)=0时:(1)如果在x0附近的左侧f′(x)>0,右侧f′(x)<0,那么f(x0)是.(2)如果在x0附近的左侧f′(x)<0,右侧f′(x)>0,那么f(x0)是.想一想:若求得某点处的导数值为0,此点一定是极值点吗?提示一个点为函数的极值点不但满足此点处导数值为零,还要判断函数在此点附近左右两侧的单调性,只有单调性相反,才能作为函数的极值点,单调性一致时,不能作为极值点,如f(x)=x3,x=0就不是极值点.2.求函数f(x)极值的方法解方程f′(x)=0,当f′(x0)=0时:(1)如果在x0附近的左侧f′(x)0,右侧f′(x)0,那么,f(x0)是极大值.(2)如果在x0附近的左侧f′(x)0,右侧f′(x)0,那么,f(x0)是极小值.想一想:极值点与单调区间有什么关系?提示极大值点可以看成函数单调递增区间过渡到递减区间的转折点,极小值点可以看成函数单调递减区间过渡到单调递增区间的转折点.名师点睛1.正确理解函数极值的概念(1)函数的极值是函数的局部性质,它反映了函数在某一点附近的大小情况.(2)由函数极值的定义知道,函数在一个区间的端点处一定不可能取得极值,即端点一定不是函数的极值点.(3)在一个给定的区间上,函数可能有若干个极值点,也可能不存在极值点;函数可能只有极大值,没有极小值,或者只有极小值没有极大值,也可能既有极大值,又有极小值.极大值不一定比极小值大,极小值也不一定比极大值小.2.极值点与导数的关系(1)可导函数的极值点一定是导数为0的点,但导数为0的点不一定是函数的极值点.(2)导数为0的点可能是函数的极值点,如y=x2,y′(0)=0,x=0是极小值.导数为0的点也可能不是函数的极值点,如y=x3,y′(0)=0,x=0不是极值点.探究点一函数的极值与导数的关系问题1如图观察,函数y=f(x)在d、e、f、g、h、i等点处的函数值与这些点附近的函数值有什么关系?y=f(x)在这些点处的导数值是多少?在这些点附近,y=f(x)的导数的符号有什么规律?问题2函数的极大值一定大于极小值吗?在区间内可导函数的极大值和极小值是唯一的吗?问题3若某点处的导数值为零,那么,此点一定是极值点吗?举例说明.思考函数f(x)的定义域为开区间(a,b),导函数f′(x)在(a,b)内的图象如图所示,则函数f(x)在开区间(a,b)内有________个极小值点.题型一求函数的极值【例1】求下列函数的极值.(1)f(x)=3x+3ln x;(2)f(x)=2xx2+1-2.[思路探索] 求出f′(x)和使f′(x)=0成立的点,再结合定义域研究这些点附近左右两侧的单调性,进而判断极值.解 (1)函数f (x )=3x+3ln x 的定义域为(0,+∞),f ′(x )=-3x 2+3x =3(x -1)x 2,令f ′(x )=0得x =1.当x 变化时,f ′(x ),f (x )的变化情况如下表:(2)函数的定义域为R .f ′(x )=2(x 2+1)-4x 2(x 2+1)2=-2(x -1)(x +1)(x 2+1)2. 令f ′(x )=0,得x =-1,或x =1.当x 变化时,f ′(x ),f (x )的变化情况如下表:由上表可以看出:当x =-1时,函数有极小值,且极小值为f (-1)=-3; 当x =1时,函数有极大值,且极大值为f (1)=-1.规律方法 求函数的极值必须严格按照求函数极值的方法步骤进行,其重点是列表.解题时注意导数为零的点的左、右两侧的导数值是否是异号的,若异号,则是极值;否则,则不是极值.题型二 已知极值求参数值 【例2】已知函数f (x )=ax 3+bx 2+cx (a ≠0)在x =±1处取得极值,且f (1)=-1. (1)求常数a ,b ,c 的值; (2)判断x =±1是函数的极大值点还是极小值点,试说明理由,并求出极值. [思路探索] 先求f ′(x ),再由函数f (x )在x =±1处取得极值,且f (1)=-1建立关于a ,b ,c 的方程组.求出a ,b ,c 值,再由判定极值的方法判定其极值情况.解 (1)f ′(x )=3ax 2+2bx +c . ∵x =±1是函数f (x )的极值点, ∴x =±1是方程f ′(x )=0的两根,即3ax 2+2bx +c =0的两根,由根与系数的关系,得⎩⎨⎧-2b3a=0, ①c3a=-1 ②又f (1)=-1,∴a +b +c =-1.③由①②③解得a =12,b =0,c =-32.(2)f (x )=12x 3-32x ,∴f ′(x )=32x 2-32=32(x -1)(x +1),当x <-1或x >1时,f ′(x )>0, 当-1<x <1时,f ′(x )<0,∴函数f (x )在(-∞,-1)和(1,+∞)上是增函数, 在(-1,1)上是减函数,∴当x =-1时,函数取得极大值f (-1)=1,当x =1时,函数取得极小值f (1)=-1.规律方法 已知函数极值情况,逆向应用确定函数的解析式,进而研究函数性质时注意两点: (1)常根据极值点处导数为0和极值两个条件列方程组,利用待定系数法求解.(2)因为导数值等于零不是此点为极值点的充要条件,所以利用待定系数法求解后必须验证根的合理性.【变式2】已知函数f (x )=x 3+ax 2+bx +c ,且知当x =-1时取得极大值7,当x =3时取得极小值,试求函数f (x )的极小值,并求a 、b 、c 的值. 解 f (x )=x 3+ax 2+bx +c ,f ′(x )=3x 2+2ax +b .∵x =-1时函数取得极大值,x =3时函数取得极小值.∴-1,3是方程f ′(x )=0的根,即为方程3x 2+2ax +b =0的两个根.由一元二次方程根与系数的关系有⎩⎨⎧-1+3=-2a3,(-1)×3=b3.∴⎩⎪⎨⎪⎧a =-3,b =-9.∴f (x )=x 3-3x 2-9x +c . ∵x =-1时取得极大值7,∴(-1)3-3(-1)2-9(-1)+c =7. ∴c =2.∴函数f (x )的极小值为f (3)=33-3×32-9×3+2=-25,a =-3,b =-9,c =2.题型三 极值的综合应用【例3】 (12分)设a 为实数,函数f (x )=-x 3+3x +a . (1)求f (x )的极值;(2)是否存在实数a ,使得方程f (x )=0恰好有两个实数根?若存在,求出实数a 的值;若不存在,请说明理由.审题指导(1)依据求函数极值的方法求解.a 的值. [规范解答] (1)令f ′(x )=-3x 2+3=0, 得x 1=-1,x 2=1.(2分) 又因为当x ∈(-∞,-1)时,f ′(x )<0;当x ∈(-1,-1)时,f ′(x )>0;当x ∈(1,+∞)时,f ′(x )<0.(4分)所以f (x )的极小值为f (-1)=a -2,f (x )的极大值为f (1)=a +2.(6分)(2)因为f (x )在(-∞,-1)上单调递减,且当x →-∞时,f (x )→+∞;又f (x )在(1,+∞)上单调递减,且当x →+∞时,f (x )→-∞;而a +2>a -2,即函数的极大值大于极小值,所以当极大值等于0时,有极小值小于0,(8分)如图(1),此时曲线f (x )与x 轴恰有两个交点,即方程f (x )=0恰好有两个实数根,所以a +2=0,a =-2.(10分)如图(2),当极小值等于0时,有极大值大于0,此时曲线f (x )与x 轴恰有两个交点,即方程f (x )=0恰好有两个实数根,所以a -2=0,a =2.综上,当a =2,或a =-2时方程恰有两个实数根.(12分)练习1求函数f(x)=x3-3x2-9x+5的极值.练习2 求函数y=x4-4x3+5的极值.解y′=4x3-12x2=4x2(x-3),令y′=4x2(x-3)=0,得x1=0,x2=3.当x变化时,y′,y的变化情况如下表:练习3已知f(x)=x3+3ax2+bx+a2在x=-1时有极值0,求常数a,b的值.练习4 设x=1与x=2是函数f(x)=a ln x+bx2+x的两个极值点.(1)试确定常数a和b的值;(2)判断x=1,x=2是函数f(x)的极大值点还是极小值点,并说明理由.练习6 已知f(x)=x3+3ax2+bx+a2在x=-1处有极值0,求常数a,b的值.[错解] ∵f (x )在x =-1处有极值0, 且f ′(x )=3x 2+6ax +b , ∴⎩⎪⎨⎪⎧f ′(-1)=0,f (-1)=0,即⎩⎪⎨⎪⎧3-6a +b =0,-1+3a -b +a 2=0, 解得⎩⎪⎨⎪⎧a =1,b =3,或⎩⎪⎨⎪⎧a =2,b =9.因此常数a =1时,b =3;a =2时,b =9.根据极值定义,函数先减后增为极小值,先增后减为极大值,此题未验证x =-1两侧导数f ′(x )的符号而致错.[正解] ∵f (x )在x =-1处有极值0, 且f ′(x )=3x 2+6ax +b , ∴⎩⎪⎨⎪⎧f ′(-1)=0,f (-1)=0.即⎩⎪⎨⎪⎧3-6a +b =0,-1+3a -b +a 2=0, 解之得⎩⎪⎨⎪⎧a =1,b =3,或⎩⎪⎨⎪⎧a =2,b =9.当a =1,b =3时,f ′(x )=3x 2+6x +3=3(x +1)2≥0. ∴f (x )在R 上为增函数,无极值,故舍去;当a =2,b =9时,f ′(x )=3x 2+12x +9=3(x +1)(x +3). 当x ∈(-3,-1)时,f (x )为减函数; 当x ∈(-1,+∞)时,f (x )为增函数,所以f (x )在x =-1处取得极小值,因此a =2,b =9.探究点三函数极值的综合应用例3设函数f (x )=x 3-6x +5,x ∈R.(1)求函数f (x )的单调区间和极值;(2)若关于x 的方程f (x )=a 有三个不同的实根,求实数a 的取值范围.跟踪训练3若函数f(x)=2x3-6x+k在R上只有一个零点,求常数k的取值范围.。
高级运筹学K-T条件极值试题(含答案)

要求:(1)库恩—塔克条件求最优解(2)写出等价的线性规划问题并化为标准形
解:标准型:
注意本题运用库恩-塔克条件解题时应该引入4个拉格朗日乘子。
当 = , = , =0, =0时可以求得最优解,
最终最优解为 = 。
(2)等价的线性规划问题:
( )-6X-3X
标准型:
10.已知目标函数 受约束于
(1)解:标准化模型得: , , , 各函数的梯度分别为: , , , 。对三个约束条件分别引入拉格朗日乘子 、 和 ,则有如下K-T条件:
,即可分解为:
, ,
பைடு நூலகம்求解得:
4.用库恩—塔克条件解非线性规划
解先将其变为问题(11.60)的形式
设K-T点为 ,各函数的梯度为
对第一个和第二个约束条件分别引入广义拉格朗日乘子 , ,则得该问题的K-T条件如下:
用库恩-塔克条件判断 是否为极小点。
解:计算目标函数和约束函数在X*点的梯度
代入
则
解得λ1=1、λ2=1、λ3=0,即λ1、λ2、λ3满足非负要求,故X*={1,0}T点满足库恩-塔克条件,该点是极小值。
解:规划问题标准化
, ,
记 , 。
①下面验证正则点:
,
显然 与 线性无关,于是 为正则点。
,
同样 与 线性无关,于是 也是正则点。
②下面验证是否满足Kuhn-Tucker条件:
得 , ,故 不满足Kuhn-Tucker条件。
得 , ,故 不满足Kuhn-Tucker条件。
6.用库恩-塔克条件解非线性规划
若 解得 ,非K-T点;
若 解得 ,非K-T点;
若 解得 , 全局最小
极值,最值(含答案)

导数的极值、最值考点一.求函数的极值1.求函数的极值:(1)612y 3++-=x x ; (2)212y 2-+=x x ; (3)x x ln 6)5(21y 2+-=; (4)x ex 2y =; 解:(1)22)2(f 10-)2(f ,220123y 2==--=∴=+-='极大极小,则或x x ;(2)1,1x 0)1(1)(1(2)1(22)1(2y 22222-=∴=++-=+⨯-+=',)x x x x x x x ,则f(-1)极小=-3;f(1)极大=-1.(3)定义域:x>0,则x x x x x x x x )3)(2(6565y 2--=+-=+-=',3ln 62)3(f ;2ln 629)2(f +=+=∴极小极大;(4)2,0x 0e2y 2=∴=-=',xx x ,0)0(f ;e 4)2(f 2==∴极小极大; (5)若bx x x +=3a )(f 在x=1处取得极值-2,求a,b 的值。
解:-3b 1,a -2b a f(1)0,3(1)f ,a 3)(f 2==∴=+==+='+=',又b a b x x 。
(6)若c bx ax x x +++=23)(f ,当x=-1时取极大值7,x=3取极小值,求极小值。
解:25-)3(f 2c -9b -3,a 7,f(-1)0(3)f 0,(-1)f ,23)(f 2====∴=='='++='极小值,,,又b ax x x 。
(7)若x e x ax --+=)1(y 2(a<0),求f(x )取极小值时,x 的值. 解:a1-2x 0)2)(1()1()1()12()(f 2或,=∴=-+-=--+++='---x ax e e x ax e ax x x x x,(1)当021-,2a 1-<<>a 即,0)(f )a1-2-,0)(f ),a 1-2--<'>'+∞∞x x 上,在(上)和(,在(,取极小值时,)(f 1x x a -=∴。
有限元方法例题解答
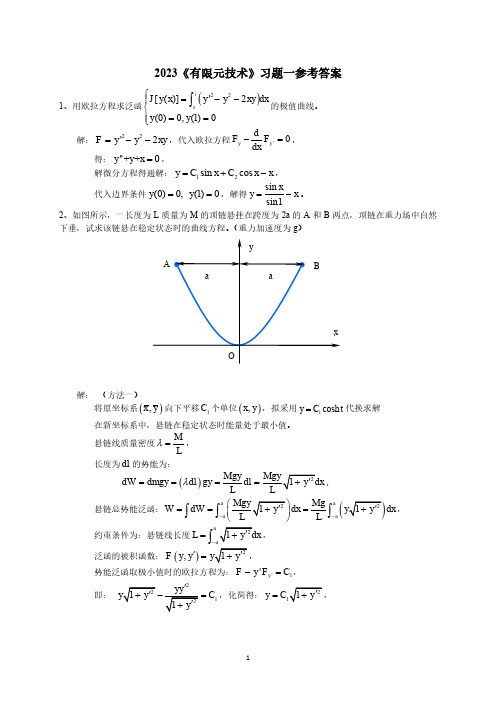
2023《有限元技术》习题一参考答案1、用欧拉方程求泛函()1022[()]'2(0)0,(1)0J y x y y xy dx y y ⎧=--⎪⎨⎪==⎩⎰的极值曲线。
解:22'2F y y xy =--,代入欧拉方程'0y y dF F dx-=, 得:''++0y y x =,解微分方程得通解:12sin cos y C x C x x =+-,代入边界条件(0)0,(1)0y y ==,解得sin sin1xy x =-。
2、如图所示,一长度为L 质量为M 的项链悬挂在跨度为2a 的A 和B 两点,项链在重力场中自然下垂,试求该链悬在稳定状态时的曲线方程。
(重力加速度为g )解: (方法一)将原坐标系(),x y 向下平移1C 个单位(),x y ,拟采用1cosh y C t =代换求解 在新坐标系中,悬链在稳定状态时能量处于最小值。
悬链线质量密度MLλ=, 长度为dl 的势能为:()Mgy dW dmgy dl gy dl L λ====,悬链总势能泛函:(a a a a Mg W dW dx dx L --===⎰⎰⎰,约束条件为:悬链线长度aL -=⎰,泛函的被积函数:(),F y y '=,势能泛函取极小值时的欧拉方程为:'1'y F y F C -=, 即:21C -=,化简得:y C =于是:dx =x =,令1cosh y C t =(在新坐标系下才能作此代换),得:1sinh sinh dy C tdt t =⎧=,代入x =,得112x C dt C t C ==+⎰所以,21x C t C -=,21cosh cosh x C t C ⎛⎫-= ⎪⎝⎭回代1cosh y C t =得:211cosh x C y C C ⎛⎫-= ⎪⎝⎭,曲线关于y 轴对称得20C =,1C由悬链线长度112sinhaaL C C -==⎰给出, 故新坐标系下所求曲线方程为11cosh x y C C ⎛⎫=⎪⎝⎭, 1C 由11sinh 2L aC C =确定。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
习题8-3答案(A )1、求下列函数的极值:(1)极小值点(0,1);极小值z=0; (2)求函数333z x y xy =+- 的极值.解:解方程组得22330330zx y xz y x y∂⎧=-=⎪∂⎪⎨∂⎪=-=∂⎪⎩,解得驻点(0,0),(1,1)由于222226,3,6z z zx y x x y y∂∂∂==-=∂∂∂∂,故在(0,0)处290AC B -=-<,函数z 不取得极值;在(1,1)处有2270AC B -=>,且60A =>,函数z 在点(1,1)处取得极值,且极小值为1z =-。
(3)极大值点(0,0),极大值1;且(0,0)点为不可导点 (4)极小值点(5,2),极小值302 要设计一个容积为a 的长方体形无盖水池 . 确定长、宽和高 , 使水池的表面积最小 .分别以x 、y 和z 表示水池的长、宽和高 , 该例可表述为 : 在约束条件xyz a =之下求函数xy yz xz z y x S ++=)(2),,(的最小值 .(,,,)2()()F x y z xz yz xy xyz a λλ=+++-对F 求偏导数, 并令它们都等于0: 20,20,2()0,0.x y z F z y yz F z x xz F x y xy F xyz a λλλλ=++=⎫⎪=++=⎪⎬=++=⎪⎪=-=⎭求上述方程组的解, 得33422,2x y z a aλ====-. 依题意, 所求水箱的表面积在所给条件下确实存在最小值. 由上可知, 当高为34a, 长与宽为高的2倍时, 表面积最小. 最小值233(2)S a =.3.提示:分别以x 、y 表示矩形的长、宽,则 222x y p +=(约束条件),所求圆柱体体积为2V x y π=构造辅助函数2(,,)(222)F x y x y x y p λπλ=++-,则2220,20,2220.x y F xy F x F x y p λπλπλ=+=⎫⎪=+=⎬⎪=+-=⎭解得2x y =,代入约束条件得:23x p =13y p =;为唯一的驻点,有实际意义知为最值点。
4.求函数u xyz =在条件222124x y z ++=之下的极值。
解:构造辅助函数222(,,,)(1)24x y F x y z xyz z λλ=+++-,则 2220,0,220,10.24x y z F yz x y F xz F xy z x y F z λλλλ=+=⎫⎪⎪=+=⎪⎬=+=⎪⎪=++-=⎪⎭前三个式子联立去掉λ,得22224x y z ==,结合第四个式子得到结果为2221243x y z ===。
所以驻点有八个(+,+,+)(+,+,-)(+,-,+)(+,-,-)(-,+,+)(-,+,-)(-,-,+)(-,-,-)。
其中1、4、6、7点为极大值点,2、3、5、8为极小值点。
(其中在三个式子联立去掉λ的过程中不需要考虑λ=0,或者x =0,y =0及z=0,因为此时它们的函数值为0,不是极值点。
5、在半径为R 的半球内求一体积为最大的内接长方体。
解:设此半球的方程为2222,0x y z R z ++=≥,内接长方体在第一象限的一个顶点坐标为(),,x y z ,则内接长方体体积22224,V xyzx y z R =++=。
考虑函数()()2222,,,4F x y z xyz x y z R λλ=+++-2222420420420yz x xz y xy z x y z Rλλλ+=⎧⎪+=⎪⎨+=⎪⎪++=⎩解此方程组得33R x y z ===,(注意0,0,0x y z >>>) 半球内体积为最大的内接长方体的体积为3439R 。
(B)1)求)2(),(22y y x e y x f x ++=的极值.解:⎪⎩⎪⎨⎧=+==+++=0)22(0)2(22222y e f e y y x e f xy xx x 解之得:⎪⎩⎪⎨⎧-==121y xe f A xx 2)1,21(=-= 0)1,21(=-=xy f B e f C yy 2)1,21(=-=故 0422>=-e B AC 而,02>=e A 故e f 21)1,21(-=-为极小值。
2.(,)sin sin sin(){(,)0,0,}(,)sin sin sin()=sin sin-sin cos cos sinsin-sin cos sin cos sinsin(1cos)sin(1cosf x y x y x yd x y x y x yf x y x y x yx y x y x yx x y y x yx y y xπ=+-+=≥≥+≤=+-++-=+-=-+-求函数在区域上的最大值最小值。
解:首先由函数在有界闭区域上连续,所以一定存在最大值和最小值,且)(,)0(,)sin sin sin()sin sin2(,)0x000.0.=(,)sin sin sin()=,,)sin sif x yx yf x y x y x y x yf x yyx yf x y x y x yx yF x y xπππλ≥≤+≤=+-+≤+≤≥≥==+=+-+⎧⎨+⎩=+由函数的定义域知又由0,初步判定2由于函数最大值只能在极值点和边界点取得。
函数在边界和时,对应函数值都为所以函数有最小值为在边界上,构造条件极值函数(n sin()(-)cos cos()0cos coscos cos()0==-=0=(,)sin sin sin()=2 =22222222.cos cos()0xyxy x y x yF x x yx yF y x yx yF x yx yx y fx yf x x yfλλπλλππππππππππ-+++=-++=⎧=⎧⎪=-++=⇒⎨⎨+⎩⎪+⎩=⎧⇒==+-+⎨+⎩=-+=,此时此时函数取得最大值在定义域的内部,函数不存在偏导数不存在的点,且cos cos()cos cos()0cos cos()(0=0,20yx x yy x y y x yx y x yx x yx yy x yπ=+⎧⎧⇒⎨⎨=-+==+⎩⎩+=+⎧⇒⇒=⎨=+⎩因为、、都在【,】内,在此区间余弦函数为单调递减的)(舍去因为已经不在区域的内部了)综上所述函数有最大值和最小值,且都在边界点取得。
3 解条件极值问题为:222(2)2x ydy x⎧--=⎪⎨⎪=⎩构造辅助函数22(2)(,,)()2x y F x y y x λλ--=+-求驻点2220(2)001214112722482x y F x y x F x y F y x x y λλλ=---=⎧⎪=---+=⎨⎪=-=⎩⎧=⎪⎪⎨⎪=⎪⎩--=解得:解得唯一的驻点,即为所求的最值点最短距离d=4 为 :2222(16)(,)2x y f x y d x y +-=++转化为求函数=的极值无偏导数不存在的点,求驻点求驻点2(16)02(16)044x y f x x y f y x y x y =++-=⎧⎨=++-=⎩=⎧⎨=⎩解得唯一的驻点:,即为所求的最值点5.证明:函数()1cos y y z e x ye =+-有无穷多个极大值点,但无极小值点。
证明:()()1sin ,cos 1y y y z ze x e x y e x y∂∂=-+=-+∂∂ 解方程组()()1sin 0cos 10yy e x e x y ⎧-+=⎪⎨--=⎪⎩可得0,0,1,2,,2k x k k y k π⎧⎪==±±=⎨-⎪⎩ 是偶数为奇数即可得驻点()()2,0,2,2k k πππ+-,其中k 为整数。
()()222221cos ,sin ,cos 2y yy y z z z A e x B e x C e x y e x x y y∂∂∂==-+==-==-+∂∂∂∂1)当2,0x k y π==时,2,0,1A B C =-==-,因为0,0AC B A -><,所以这些点是极大值点。
2)当2,2x k y ππ=+=-时,22111,0,A B C e e=+==-,因为0AC B -<,所以这些点是不是极值点。
6(1)求函数xyz f = 在条件0,1222=++=++z y x z y x 下的极值。
做辅助函数:44(,,,,)()(,,,,)10(,,,,)10(,,,,)10(,,,,)10(,,,,)0x y z tF x y z t x y z t xyzt a F x y z t yzt F x y z t xzt F x y z t xyt F x y z t xyz F x y z t xyzt a λλλλλλλλλλλλ=++++-=+=⎧⎪=+=⎪⎪=+=⎨⎪=+=⎪=-=⎪⎩解得唯一的驻点(a,a,a,a)即为所求。
(2)求函数xyz f = 在条件0,1222=++=++z y x z y x 下的极值。
解 令)()1(222z y x z y x xyz L +++-+++=μλ 02=++=μλx yz L x ,2=++=μλy xz L y ,02=++=μλz xy L z ,得 z z y y x x μλμλμλ+=+=+222222, (1)又 1222=++z y x ,(2) 0=++z y x , (3)由(1)得 )()(222x y y x -=-μλ ,)()(222y z z y -=-μλ, 当z y x ≠≠时得 μλ-=+)(2y x , μλ-=+)(2z y 故得z x =,代入(2)(3)式得 1222=+y x ,02=+y x .解得稳定点)61,62,61(1-P ,)61,62,61(2--P . 由对称性得)61,61,62(4,3±± P ,)62,61,61(6,5 ±±P 也是稳定点. 7.抛物面22y x z +=被平面1=++z y x 截成一椭圆,求原点到这椭圆的最长与最短距离.解: 设椭圆上点的坐标),,(z y x ,则原点到椭圆上的距离的平方为2222z y x d ++=其中z y x ,,需同时满足22y x z +=和1=++z y x令 =),,,,(21λλz y x F 222z y x ++)(221y x z --+λ)1(2-+++z y x λ, 则⎪⎪⎪⎩⎪⎪⎪⎨⎧=-++=--=++==+-==+-=0100202202222212121z y x y x z z F y y F x x F z y x λλλλλλ 13213223x y z ⎧-±=⎪⎪⎪-±⎪∴=⎨⎪⎪=⎪⎪⎩可得: 359min -=d , 359max +=d8.求由方程22222880x y z xz z +++-+=确定的隐函数(,)z f x y =的极值 。
