高数 对坐标的曲线积分 知识点与例题精讲
合集下载
高数-对坐标的曲面积分
z)dxdy
lim
0
i 1
R( i
,i z
,
i
)( Si
)xy n
首先将 的方程表为 z z( x, y),
z z(x, y)
Dx y 为 在 xoy 面上的投影区域
在 上任取一小块区域 Si Si 在 xoy 面上的投影区域为
o
Dxy
( i )xy , 投影为 ( Si )xy , x
y
R( x, y, z)dxdy
x
( i )xy
n
lim
0
R[i
i 1
,i
,
z(i
,i
)](
i
)
xy
R[
Dxy
x,
y,
z(
x,
y)]dxdy
n
R(
x,
y,
z)dxdy
lim
0
i 1
R( i
,i
,
i
)( Si
z)
j
R(
x,
y,
z)k
P( x, y, z)dydz Q( x, y, z)dzdx R( x, y, z)dxdy
性质: 与第二类曲线积分的性质完全相似、例如 线性性质、有限可加性等
Pdydz Qdzdx Rdxdy
1 2
Pdydz Qdzdx Rdxdy Pdydz Qdzdx Rdxdy
(Si )xy ( i )xy , i z(i ,i ),
R( x, y, z)dxdy
n
o
lim
0
R[i
i 1
,i
,
z(
i
,i
)](
高等数学 第二节 对坐标的曲线积分
第十一章 第二节
9
定积分的定限原则：起点对下限，终点对上限， 下限不一定小于上限。 {P[(t) , (t)](t) Q[(t) , (t)] (t)}dt 其他情形
(1) L : y y( x) ( x : a b)
b
L Pdx Qdy a {P[x , y( x)] Q[x , y( x)]y( x)}dx
(可推广到空间曲线 上)
第十一章 第二节
16
L Pdx Qdy L(P cos Q cos )ds : x (t) , y (t) , z (t) (t : a b)
Γ 上点( x , y , z)处的切向量的方向角为 , ,
则 Γ Pdx Qdy Rdz Γ (P cos Q cos Rcos )ds
n
3) “求和” W P (k , ηk )Δxk Q(k , ηk ) Δyk
k1 n
4) “取极限” W
lim 0 k1
P (k , ηk )Δxk Q(k , ηk ) Δyk
为所有小弧段长度的最大值
第十一章 第二节
3
2 定义 设 L 为 xOy 平面内从 A 到 B 的一条有向 光滑弧，在 L 上定义了一个向量值函数
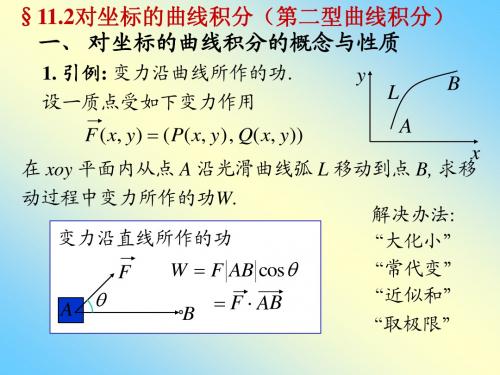
1 引例 变力沿曲线所作的功。 y L
B
设一质点受如下变力作用
F ( x , y) (P( x , y) , Q( x , y))
A
x
在 xOy 平面内从点 A 沿光滑曲线弧 L 移动到点 B ，
求移动过程中变力所作的功W。
常力沿直线所作的功
F W F AB cos
A
B F AB
第十一章 第二节
L
k
对积分域 的可加性
高数第十一章复习
第十一章
曲线积分
习题课
高等数学
1
知识梳理 一、 两类曲线积分
定义 对弧长的曲线积分 ∫ f ( x, y)ds
L
对坐标的曲线积分
∫ P( x, y)dx = lim ∑P(ξ ,η )∆x λ
L →0
n
= lim∑ f (ξi ,ηi )∆Si
λ→0
i =1
n
∫ Q( x, y)dy = lim ∑Q(ξ ,η )∆y λ
（7）求 ）
其中
是以 点 A(1,0) , B(0,1) , C(-1,0) 为 y
B (0,1)
顶点的三角形的正向边界曲线. 顶点的三角形的正向边界曲线 解 上式积分 =
C (-1,0) o
x
A(1,0)
由格林公式，得 由格林公式，
高等数学
13
例2.螺旋形弹簧一圈的方程为 螺旋形弹簧一圈的方程为
二、四个等价命题
条件：在单连通区域 内 条件：在单连通区域G内，函数P ( x , y ) , Q ( x , y ) 具有一阶 连续偏导数 以下四个命题等价： 以下四个命题等价： 内与路径无关； 1 曲线积分 ∫ Pdx + Qdy 在G 内与路径无关；
L
2
∫
∂Q ∂P 3 在 G 内恒成立 内恒成立; = ∂x ∂y 4 Pdx + Qdy = du( x , y ), 即Pdx + Qdy 为某一 u( x , y )的全微分 的全微分.
此时不能用格林公式
2 xy − 3 y x 2 − 5x dx + 2 dy 解 ∫ 2 2 2 x +y L x + y 1 = 2 ∫ (2 xy − 3 y )dx + (x 2 − 5 x )dy a L 1 = 2 ∫∫ [(2 x − 5 ) − (2 x − 3 )]dxdy a x 2 + y 2 ≤a 2
曲线积分
习题课
高等数学
1
知识梳理 一、 两类曲线积分
定义 对弧长的曲线积分 ∫ f ( x, y)ds
L
对坐标的曲线积分
∫ P( x, y)dx = lim ∑P(ξ ,η )∆x λ
L →0
n
= lim∑ f (ξi ,ηi )∆Si
λ→0
i =1
n
∫ Q( x, y)dy = lim ∑Q(ξ ,η )∆y λ
（7）求 ）
其中
是以 点 A(1,0) , B(0,1) , C(-1,0) 为 y
B (0,1)
顶点的三角形的正向边界曲线. 顶点的三角形的正向边界曲线 解 上式积分 =
C (-1,0) o
x
A(1,0)
由格林公式，得 由格林公式，
高等数学
13
例2.螺旋形弹簧一圈的方程为 螺旋形弹簧一圈的方程为
二、四个等价命题
条件：在单连通区域 内 条件：在单连通区域G内，函数P ( x , y ) , Q ( x , y ) 具有一阶 连续偏导数 以下四个命题等价： 以下四个命题等价： 内与路径无关； 1 曲线积分 ∫ Pdx + Qdy 在G 内与路径无关；
L
2
∫
∂Q ∂P 3 在 G 内恒成立 内恒成立; = ∂x ∂y 4 Pdx + Qdy = du( x , y ), 即Pdx + Qdy 为某一 u( x , y )的全微分 的全微分.
此时不能用格林公式
2 xy − 3 y x 2 − 5x dx + 2 dy 解 ∫ 2 2 2 x +y L x + y 1 = 2 ∫ (2 xy − 3 y )dx + (x 2 − 5 x )dy a L 1 = 2 ∫∫ [(2 x − 5 ) − (2 x − 3 )]dxdy a x 2 + y 2 ≤a 2
高数10-2
Γ
性质 是有向曲线弧, 反向的有向曲线弧 的有向曲线弧, （1） 设 L是有向曲线弧 − L 是与 L 反向的有向曲线弧 则 ）
∫ P( x, y)dx + Q( x, y)dy = −∫ P( x, y)dx + Q( x, y)dy
−L L
对坐标的曲线积分具有方向性. 对坐标的曲线积分具有方向性. 方向性 合并而成， （2） 设有向曲线弧 L 是由有向曲线弧 L1 , L2合并而成， 即 ）
π
2
(
)
3
∫
L
y dx = ∫ 0dx = 0
2 a
−a
此题说明：对坐标的曲线积分一般与路径有关。 一般与路径有关 此题说明：对坐标的曲线积分一般与路径有关。
11
例4 计算 I =
y = x 2上从 O (0,0 ) 到 B (1,1)的一段弧； （1）抛物线 ） 的一段弧；
∫
L
2 xydx + x 2 dy 其中 L 为：
L = L1 + L2 , 则
∫ Pdx + Qdy = ∫
L
L1
Pdx + Qdy + ∫ Pdx + Qdy
L2
对坐标的曲线积分关于积分弧段具有可加性 对坐标的曲线积分关于积分弧段具有可加性. 关于积分弧段具有可加性
6
二. 对坐标的曲线积分的计算法
x = ϕ (t ) 定理 设曲线弧 L 由参数方程 给出， 且满足下列条件： 给出， 且满足下列条件： y = ψ (t )
可简记作： ∫ P( x, y)dx + ∫ Q( x, y)dy 可简记作：∫ P( x, y)dx + Q( x, y)dy
性质 是有向曲线弧, 反向的有向曲线弧 的有向曲线弧, （1） 设 L是有向曲线弧 − L 是与 L 反向的有向曲线弧 则 ）
∫ P( x, y)dx + Q( x, y)dy = −∫ P( x, y)dx + Q( x, y)dy
−L L
对坐标的曲线积分具有方向性. 对坐标的曲线积分具有方向性. 方向性 合并而成， （2） 设有向曲线弧 L 是由有向曲线弧 L1 , L2合并而成， 即 ）
π
2
(
)
3
∫
L
y dx = ∫ 0dx = 0
2 a
−a
此题说明：对坐标的曲线积分一般与路径有关。 一般与路径有关 此题说明：对坐标的曲线积分一般与路径有关。
11
例4 计算 I =
y = x 2上从 O (0,0 ) 到 B (1,1)的一段弧； （1）抛物线 ） 的一段弧；
∫
L
2 xydx + x 2 dy 其中 L 为：
L = L1 + L2 , 则
∫ Pdx + Qdy = ∫
L
L1
Pdx + Qdy + ∫ Pdx + Qdy
L2
对坐标的曲线积分关于积分弧段具有可加性 对坐标的曲线积分关于积分弧段具有可加性. 关于积分弧段具有可加性
6
二. 对坐标的曲线积分的计算法
x = ϕ (t ) 定理 设曲线弧 L 由参数方程 给出， 且满足下列条件： 给出， 且满足下列条件： y = ψ (t )
可简记作： ∫ P( x, y)dx + ∫ Q( x, y)dy 可简记作：∫ P( x, y)dx + Q( x, y)dy
高等数学对坐标的曲线积分PPT课件
则
(2) L : x x( y) 则
第9页/共27页
x (t)
(3)
对于空间曲线
:
y
(t
),
z (t)
第10页/共27页
例 计算 xydx,其中L为抛物线 y2 x上从 L A(1,1)到B(1,1)的一段弧.
解 (1) 取 x为积分变量
y
O
x
xydx L
⌒ xydx
AO
⌒ xydx
(t), (t)在以及为端点的闭区间上具有一阶
连续导数, 且2(t) 2(t) 0, 则曲线积分
L P( x, y)dx Q( x, y)dy存在, 且
第8页/共27页
对坐标的曲线积分与曲线的方向有关. 积分下限应是起点的坐标,上限是终点的坐标. 曲线方程的其他情形 (1) L : y y( x)
B
A
•
•
12
x
xydx ( y x)dy xydx ( y x)dy
AB
BO
5 1 2 33
第14页/共27页
y
(2) AO : y 0,dy 0.
A点对应
O点对应
O
I L xydx ( y x)dy
0
2 x 0dx 0 0
A
•
•
x
12
问题: 被积函数相同, 起点和终点也相同,
沿着空间曲线L的第二型曲线积分为
其中 ds dxi dyj dzk (dx,dy,dz).
第5页/共27页
对坐标的曲线积分具有下列性质:
设 A (P( x, y),Q( x, y)),B (P1( x, y),Q1( x, y))
沿平面曲线L的第二型曲线积分存在, 则
(2) L : x x( y) 则
第9页/共27页
x (t)
(3)
对于空间曲线
:
y
(t
),
z (t)
第10页/共27页
例 计算 xydx,其中L为抛物线 y2 x上从 L A(1,1)到B(1,1)的一段弧.
解 (1) 取 x为积分变量
y
O
x
xydx L
⌒ xydx
AO
⌒ xydx
(t), (t)在以及为端点的闭区间上具有一阶
连续导数, 且2(t) 2(t) 0, 则曲线积分
L P( x, y)dx Q( x, y)dy存在, 且
第8页/共27页
对坐标的曲线积分与曲线的方向有关. 积分下限应是起点的坐标,上限是终点的坐标. 曲线方程的其他情形 (1) L : y y( x)
B
A
•
•
12
x
xydx ( y x)dy xydx ( y x)dy
AB
BO
5 1 2 33
第14页/共27页
y
(2) AO : y 0,dy 0.
A点对应
O点对应
O
I L xydx ( y x)dy
0
2 x 0dx 0 0
A
•
•
x
12
问题: 被积函数相同, 起点和终点也相同,
沿着空间曲线L的第二型曲线积分为
其中 ds dxi dyj dzk (dx,dy,dz).
第5页/共27页
对坐标的曲线积分具有下列性质:
设 A (P( x, y),Q( x, y)),B (P1( x, y),Q1( x, y))
沿平面曲线L的第二型曲线积分存在, 则
高数曲线问题
若极限 lim F ( M i *) M i 1 M i 存在 ,
n
则称此极限为函数 ( M )在有向曲线弧L上对坐标x，y F 的曲线积分 或称第二类曲线积分） ( , 记作 F ( M ) dr lim F ( M i *) ri
n
0 i 1
y
F ( i ,i )
B
求和 W W i
i 1
n i 1
n
近似值
o
L
A
M2 M1
M i 1 x i
yi
M i M n 1
[ P ( i , i ) x i Q( i , i ) y i ].
n
x
取极限 W lim [ P ( i , i ) x i Q ( i , i ) y i ]. 0
L
L
0 i 1
P ( M )dx Q ( M )dy lim
[ P ( i , i )x i Q( i , i )y i ]. 0
i 1
n
其中P ( x , y ), Q( x , y )叫做被积函数 , L叫积分弧段.
2.存在条件：
当P ( x , y ), Q( x , y )在光滑曲线弧 L
x y 1
A
C dx dy dx dy 0 解： AB 1 [1 ( 1)]dx 0 AB x y 1 x y 1
x y 1
D
dx dy dx dy 1 BC 0 [1 1]dx 2. BC x y 1 dx dy dx dy 0 CD 1 [1 ( 1)]dx 0 CD x y 1 dx dy dx dy 1 DA 0 [1 1]dx 2. DA x y 1
对坐标的曲面积分
1.1 曲面的侧
本节中，我们假定所研究曲面皆为双侧曲面，并规定其中一侧为正侧，另一侧为负 侧．我们将选定侧的双侧曲面称为有向曲面，侧的选定与该曲面法向量的指向相关．例 如，对于曲面 z z(x ，y) ，若法向量指向朝上，则正侧为曲面的上侧；若法向量指向朝 下，则正侧为曲面的下侧，其余情况类推．我们规定曲面上侧、前侧、右侧为曲面的正 侧，而曲面下侧、后侧、左侧为负侧．
二类曲面积分），记作
P(x ，y ，z)dydz Q(x ，y ，z)dzdx R(x ，y ，z)dxdy ，
即
P(x ，y ，z)dydz Q(x ，y ，z)dzdx R(x ，y ，z)dxdy
n
lim
0
{P(i
i 1
，i
， i )(Si ) yz
Q(i
，i
， i )(Si )zx
3
1 y2 dz
1
3
dx
1 x2 dz 2 3 1
1 x2 dx 3 π ．
0
0
0
0
0
2
1.2 对坐标的曲面积分的概念与性质
例 2 计算曲面积分 zdxdy ，其中 为上半球面 x2 y2 z2 R2 的上侧．
解 则有
的方程是 z R2 x2 y2 ， 在 xOy 面上的投影区域为
Dxy {(x ，y) | x2 y2 R2}，
zdxdy R2 x2 y2 dxdy．
Dxy
因为将 Dxy 表示为极坐标形式时有 0 R ， 0 2 ，
故
zdxdy
R2 2 dd 1
2π
d
R
R2 2 d(R2 2 ) 2π R3 ．
Dxy
20
高数--对坐标的曲线积分
y
• B(1,1) y2 = x
x = y 2 dx = 2 ydy , y从− 1到1 到
∫L
xy d x = ∫ y 2 ⋅ y ⋅ 2 ydy
−1
1
O
x
• A(1,−1)
= 2 ∫ y4 dy −
1
1
4 = 5
15
对坐标的曲线积分
例 计算 ∫ xdx + ydy + ( x + y − 1)dz
17
对坐标的曲线积分
计算 ∫ x 2dx + ( y − x )dy , 其中
L
(2) L是x轴上由点 A(a ,0) 到点B( − a ,0) 的线段 的线段. 是 轴上由点 (2) L的方程为 y = 0, x从a到− a. 的方程为 原式= 原式
∫a
−a
x dx
2
y
2 3 =− a 3
B(−a,0) O
Γ
其中Γ是由点 到点B(2,3,4)的直线段 的直线段. 其中 是由点A(1,1,1)到点 是由点 到点 的直线段
x −1 y −1 z −1 = = 直线AB的方程为 解 直线 的方程为 1 2 3
化成参数式方程为 x = 1+ t, y = 1 + 2t, z = 1+ 3t + A点对应 t = 0, B点对应 t = 1, 于是 点对应 点对应
i =1
n
取极限 W = lim [ P (ξ i ,η i ) ⋅ ∆xi + Q(ξ i ,η i ) ⋅ ∆yi ] ∑
λ→0i =1
精确值
3
对坐标的曲线积分
二、对坐标的曲线积分的概念
1. 定义 面内从点A到点 的一条有向 设L为xOy面内从点 到点 的一条有向光滑 为 面内从点 到点B的一条有向光滑 曲线弧, 曲线弧 函数P ( x , y ), Q ( x , y )在L上有界 用L上的点 上的点: 上的点 上有界. 上有界 M 1 ( x1 , y1 ), M2 ( x2 , y2 ), LM n −1 ( x n −1 , y n−1 ) 分成n个有向小弧段 把L分成 个有向小弧段 Mi −1 Mi (i = 1,2,L, n; 分成
• B(1,1) y2 = x
x = y 2 dx = 2 ydy , y从− 1到1 到
∫L
xy d x = ∫ y 2 ⋅ y ⋅ 2 ydy
−1
1
O
x
• A(1,−1)
= 2 ∫ y4 dy −
1
1
4 = 5
15
对坐标的曲线积分
例 计算 ∫ xdx + ydy + ( x + y − 1)dz
17
对坐标的曲线积分
计算 ∫ x 2dx + ( y − x )dy , 其中
L
(2) L是x轴上由点 A(a ,0) 到点B( − a ,0) 的线段 的线段. 是 轴上由点 (2) L的方程为 y = 0, x从a到− a. 的方程为 原式= 原式
∫a
−a
x dx
2
y
2 3 =− a 3
B(−a,0) O
Γ
其中Γ是由点 到点B(2,3,4)的直线段 的直线段. 其中 是由点A(1,1,1)到点 是由点 到点 的直线段
x −1 y −1 z −1 = = 直线AB的方程为 解 直线 的方程为 1 2 3
化成参数式方程为 x = 1+ t, y = 1 + 2t, z = 1+ 3t + A点对应 t = 0, B点对应 t = 1, 于是 点对应 点对应
i =1
n
取极限 W = lim [ P (ξ i ,η i ) ⋅ ∆xi + Q(ξ i ,η i ) ⋅ ∆yi ] ∑
λ→0i =1
精确值
3
对坐标的曲线积分
二、对坐标的曲线积分的概念
1. 定义 面内从点A到点 的一条有向 设L为xOy面内从点 到点 的一条有向光滑 为 面内从点 到点B的一条有向光滑 曲线弧, 曲线弧 函数P ( x , y ), Q ( x , y )在L上有界 用L上的点 上的点: 上的点 上有界. 上有界 M 1 ( x1 , y1 ), M2 ( x2 , y2 ), LM n −1 ( x n −1 , y n−1 ) 分成n个有向小弧段 把L分成 个有向小弧段 Mi −1 Mi (i = 1,2,L, n; 分成
高等数学第一节对弧长的曲线积分第二节对坐标的曲线积分
(1)沿圆弧, (2)沿X轴.
解(1)沿圆 L1弧 :
Bo
x acos y asin
:0
L 1y 2 d x 0 a 2 s2 in a s in d
4 3
a
3
.
Ax
(2)沿X轴,
L2 :
x t y 0
t:a a.
L 2y2dxa a0dt0. 积分路径,积 不分 同值.不 24
例 8I L x 2 d x xy ,L 是 dy由 y x 抛 2 从 (0 ,0 物 )
两类曲线积分之间的关系 :
L F d L P d x Q d y R d z
前页公式:
d
t d
LF
t
d
第二类曲线积分
L F
t
d L P co Q c so R c so d s
zm 1 Lz(x,y,z)ds
m 10 2 k t a 2 k 2 t2 a 2 k 2dt
15
如果 L是平面(极 曲坐 线 ):标
r r ( )
则 xy rr(())csions
L
rd
dr d
d r
o
x
d ( r co r ss i ) 2 n ( r si r n c) o 2 ds
W 1 L y d x x d y ( x y z ) d z
终点B 起点A
0 2 y x x y (x y z )z d t
19
W1 0 2 0 2 (a y s x ti) x ( n y a s (x ti) n y (a c z )z to ) ( d a tc sto ) L : s x yz aa 2cc st in o tt
高等数学对坐标的曲面积分
cos
1 1 x2 y2
(z2 x)( x)dxdy
dS
1
z
2 x
z
2 y
dxdy
dxdy
cos
对坐标的曲面积分
(z2 x)dydz (z2 x)( x)dxdy
(z2 x)由dy对dz称性zdxdy
z 1(x2 y2)
[(z2 x14)x((xx2 )yz2 )]d2dxxddyy 0
Q( x, y, z)dzdx Q( x, y, z)cos dS
两类曲面积分之间的联系
Pdydz Qdzdx Rdxdy
(P cos Q cos Rcos )dS
其中cos、cos 、cos 是有向曲面Σ在点 ( x, y, z)
处的法向量的方向余弦. 不论哪一侧都成立.
对坐标的曲面积分
xyzdxdy xyzdxdy xyzdxdy
2
1
xy 1 x2 y2dxdy xy( 1 x2 y2 )dxdy
Dxy
Dxy
对坐标的曲面积分
Dxy : x2 y2 1( x 0, y 0)
xy 1 x2 y2dxdy xy( 1 x2 y2 )dxdy
对坐标的曲面积分 Mobius(1790--1868) 19世纪德国数学家
(2) 单侧曲面
莫比乌斯(Mobius)带.
它是由一张长方形纸条ABCD, 扭转一下,
将A、D粘在一起，B、C 粘在一起形成的环
行带.小毛虫在莫比乌斯带上,不通过边界可以
爬到任何一点去.
这在双侧曲面上是不能实现的.
决定了侧的曲面称为 有向曲面.
i 1
2. 存在条件
当P( x, y, z),Q( x, y, z), R( x, y, z) 在有向光滑
11-2 对坐标的曲线积分
第二讲 对坐标的曲线积分
对坐标的曲线积分
一、 对坐标的曲线积分的概念 二 、对坐标的曲线积分的性质 三 、对坐标的曲线积分的计算 四 、对坐标的曲线积分的应用 五 、两类曲线积分之间的联系
对坐标的曲线积分
一、 对坐标的曲线积分的概念 二 、对坐标的曲线积分的性质 三 、对坐标的曲线积分的计算 四 、对坐标的曲线积分的应用 五 、两类曲线积分之间的联系
P
[
x,j
(
x)]
+
Q
[
x,j
(
x)]j
¢(
x
)}
dx
(2) L：x =y ( y) （y=c 对应L的起点，y=d 对应L的终点）
òL
P(
x,
y
)dx
+
Q(
x,
y)dy
=
d
òc
{P
[y
(
y),
y
]y
¢(
y)
+
Q
[y
(
y
),
y]}
dy
Ø推广
空间曲线弧Γ： x = j(t), y =y (t), z = w(t)
一、 对坐标的曲线积分的概念
（一）引例 （二）对坐标的曲线积分的定义
一、 对坐标的曲线积分的概念
（一）引例 （二）对坐标的曲线积分的定义
变力沿曲线作功
y
B
设一质点在xoy面内从点A沿曲线
L移动到点B
Dyi
力F! ( x,
y)
=
P( x,
! y)i
+
Q( x,
y)
! j
变力所作的功 ?
A o
L
对坐标的曲线积分
一、 对坐标的曲线积分的概念 二 、对坐标的曲线积分的性质 三 、对坐标的曲线积分的计算 四 、对坐标的曲线积分的应用 五 、两类曲线积分之间的联系
对坐标的曲线积分
一、 对坐标的曲线积分的概念 二 、对坐标的曲线积分的性质 三 、对坐标的曲线积分的计算 四 、对坐标的曲线积分的应用 五 、两类曲线积分之间的联系
P
[
x,j
(
x)]
+
Q
[
x,j
(
x)]j
¢(
x
)}
dx
(2) L：x =y ( y) （y=c 对应L的起点，y=d 对应L的终点）
òL
P(
x,
y
)dx
+
Q(
x,
y)dy
=
d
òc
{P
[y
(
y),
y
]y
¢(
y)
+
Q
[y
(
y
),
y]}
dy
Ø推广
空间曲线弧Γ： x = j(t), y =y (t), z = w(t)
一、 对坐标的曲线积分的概念
（一）引例 （二）对坐标的曲线积分的定义
一、 对坐标的曲线积分的概念
（一）引例 （二）对坐标的曲线积分的定义
变力沿曲线作功
y
B
设一质点在xoy面内从点A沿曲线
L移动到点B
Dyi
力F! ( x,
y)
=
P( x,
! y)i
+
Q( x,
y)
! j
变力所作的功 ?
A o
L
高等数学10-2
y
F (ξ k , η k ) M x−1 Δk k My k Δk
W = ∑ ΔWk
k =1
n
B
L A
x 有向小弧段 M k −1 M k 用有向线段 M k −1 M k = ( Δ xk , Δ yk ) 近似代替, 在 M k −1 M k 上任取一点 ( ξ k , ηk ), 则有
ΔWk ≈ F (ξk , ηk ) ⋅ M k −1 M k = P (ξk , ηk )Δ xk + Q (ξk , ηk )Δ yk
0 2π
( t : 2π → 0 ) z
+ ( −2 + 2 cos t − sin t ) cos t + (cos t − sin t )(cos t + sin t ) ]d t = ∫ (1 − 4 cos 2 t ) d t = −2π
0
机动
Γ
o x
目录 上页 下页
2π
y
返回 结束
【例6】设在力场 F = ( y , − x , z ) 作用下, 质点由 A(R, 0, 0) z 沿Γ移动到 B( R , 0 , 2π k ), 其中Γ为 B ( 1) x = R cos t , y = R sin t , z = k t ;
n
(其中λ 为 n 个小弧段的 最大长度)
y
F (ξ k , η k )
L A
Mx k−1 Δk
My k Δk
B
x
机动 目录 上页 下页 返回 结束
二、对坐标的曲线积分的概念
1. 【定义】 设L为 xoy面内从点 A到点 B的一条有 向光滑曲线弧 , 函数 P ( x , y ), Q( x , y )在 L
《对坐标的曲线积分》课件
理解坐标曲线积 分在物理、工程 等领域的应用
掌握坐标曲线积 分与微积分、线 性代数等课程的 联系
培养解决问题的 能力和创新思维
THANK YOU
汇报人：
曲线积分是微积分的一个重要分支，广泛应用于物理、工程等领域
曲线积分可以帮助我们理解和解决许多实际题，如流体力学、电磁学等
曲线积分在数学、物理、工程等领域都有广泛的应用价值 曲线积分是微积分的一个重要工具，可以帮助我们理解和解决许多实际问 题
为后续学习打下基础
掌握坐标曲线积 分的概念、性质 和计算方法
例题解析与练习
典型例题解析
例题1：求曲线积分，积分区间为[0,1]，积分曲线为y=x^2 例题2：求曲线积分，积分区间为[0,1]，积分曲线为y=x^3 例题3：求曲线积分，积分区间为[0,1]，积分曲线为y=x^4 例题4：求曲线积分，积分区间为[0,1]，积分曲线为y=x^5
练习题及答案解析
曲线积分概念引入
曲线积分的定义：对曲线上的函数 进行积分
曲线积分的特点：与直线积分不同， 需要考虑曲线的弯曲程度
添加标题
添加标题
添加标题
添加标题
曲线积分的应用：物理、工程、经 济等领域
曲线积分的分类：第一类曲线积分 和第二类曲线积分
本次PPT课件的目的和内容
目的：介绍坐 标的曲线积分 的概念、方法
对坐标的曲线积分的注意事项 及常见错误分析
参数方程和直角坐标系转换时的注意事项
转换时注意参数方程和直角坐标系的转换关系 转换过程中注意参数方程的取值范围 转换过程中注意参数方程的连续性和可微性 转换过程中注意参数方程的积分区间和积分限
计算曲线积分时的常见错误及解决方法
错误：积分区间错误 解决方法：正确选择积分区间， 确保积分区间包含曲线的全部长度 解决方法：正确选择积分区间，确保积分区间包含曲线的全部长 度
对坐标的曲线积分
都存在, 则称此极限为函数
在有向曲线弧 L 上
对坐标的曲线积分, 或第二类曲线积分. 其中,
称为被积函数 , L 称为积分弧段 或 积分曲线 .
称为对 x 的曲线积分;
若记
称为对 y 的曲线积分. , 对坐标的曲线积分也可写作
类似地, 若 为空间曲线弧 , 记
说明： (1) 变力做功 W P(x, y)dx Q(x, y)dy. L (2) 与定积分比较
解: (1) 取L的参数方程为
则
(2) 取 L 的方程为
则
例29.3. 计算 (1) 抛物线 (2) 抛物线 (3) 有向折线
解: (1) 原式
(2) 原式 (3) 原式
其中L为
例29.4. 设在力场 沿移动到
作用下, 质点由 其中为
试求力场对质点所作的功. 解: (1)
(2) 的参数方程为
例29.5. 求
ቤተ መጻሕፍቲ ባይዱ
到点B.
问：F做功W多少？
解决的方法：微积分思想
大化小，常代变，近似和，取极限
n
W
lim
0
i 1
P(i ,i )xi
Q(i ,i )yi
３. 定义. 设 L 为xoy 平面内从 A 到B 的一条有向光滑 弧, 在L 上定义了一个向量函数
若对 L 的任意分割和在局部弧段上任意取点, 极限
记作
b
W a F (x)dx.
F ( x)
A(•a) B(•b) x
2.引例 （变力沿平面曲线所作的功）
设L AB是平面上的一条光滑曲 线,
F (x, y) P(x, y)i Q(x, y) j (P(x, y), Q(x, y))
是定义在 L上的变力，质点在 F的作用下沿 L从点A移动
高数10章第2节对坐标曲线积分
06 曲线积分在实际问题中应 用
面积、体积和弧长计算
01
02
03
面积计算
通过曲线积分可以计算由 平面曲线所围成的面积， 例如计算不规则图形的面 积。
体积计算
在空间中，曲线积分可以 用来计算由曲线旋转或平 移所生成的立体体积。
弧长计算
曲线积分还可以用来计算 曲线的弧长，特别是对于 那些无法直接通过几何方 法求解的曲线。
质心、形心和转动惯量计算
质心计算
在物理学和工程学中，经常需要 计算物体的质心位置，曲线积分 可以帮助我们找到由曲线构成的
物体的质心。
形心计算
形心是描述物体几何形状的一个重 要参数，曲线积分同样可以用来计 算由曲线构成的物体的形心。
转动惯量计算
转动惯量是描述物体旋转运动特性 的物理量，曲线积分可以用来计算 由曲线构成的物体绕某轴的转动惯 量。
斯托克斯公式在电磁学、流体力学等 领域有着广泛的应用，可以用来计算 磁场、电场、流场等物理量。
在使用斯托克斯公式时，需要注意被积 函数在包含曲面Σ的空间区域内是否满 足具有一阶连续偏导数的条件，以及曲 面Σ和边界曲线Γ的取向是否正确。
其他求解方法
01
直接计算法
对于一些简单的第二类曲线积分问题，可以直接通过参数化曲线并代入
面积等。
培养分析问题和解决问题的能力，提高数学素养和思维水平。
03
内容概述
本节主要介绍对坐标的曲线积分，包括曲线积分的定义、性质和计算方法。 通过具体例题，讲解如何运用定积分求解曲线积分，并介绍一些常用的计算技巧。
讨论曲线积分在实际问题中的应用，如计算平面曲线的长度、空间曲线的质量等。
02 对坐标曲线积分基本概念
高数10章第2节对坐标曲线积分
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
A
在 xoy 平面内从点 A 沿光滑曲线弧 L 移动到点 B,求移x
动过程中变力所作的功W.
常力沿直线所作的功
F W F | AB | cos
A
B F AB
解决办法: “大化小” “常代变” “近似和”
“取极限”
机动 目录 上页 下页 返回 结束
1) “大化小”. 把L分成 n 个小弧段,F 沿
例1. 计算L x yd x , 其中L 为沿抛物线 y2 x 从点
A(1, 1 )到 B(1, 1) 的一段.
y B(1,1)
解法1 取 x 为参数, 则 L : AO OB AO : y x, x :1 0
y x
OB : y x, x : 0 1
o y x x
机动 目录 上页 下页 返回 结束
• 对空间有向光滑弧 :
x (t) y (t), z (t)
t :
P [ (t ), (t ) , (t )] (t )
Q [ (t ), (t ) , (t )] (t )
R [ (t ), (t ) , (t )] (t )d t
机动 目录 上页 下页 返回 结束
3. 计算
•
对有向光滑弧
L
:
x y
(t) (t)
,
t :
P
[
(t ),
(t )] (t)
Q
[
(t ),
(t )]
(t )d
t
• 对有向光滑弧 L : y ( x ) , x : a b
ab P [ x, ( x )] Q [ x, ( x )] (x)d x
(1 x)
机动 目录 上页 下页 返回 结束
四、小结
1. 定义
2. 性质
lim
n
0 k1
P (k
,k ) xk
Q(k , k ) yk
(1) L可分成 k 条有向光滑曲线弧
k
i1
Li
P(
x,
y)d x
Q(
x,
y d
y
(2) L－ 表示 L 的反向弧
L P ( x, y)d x Q( x, y)d y 对坐标的曲线积分必须注意积分弧段的方向!
机动 目录 上页 下页 返回 结束
例7.将积分
化为对弧长的积
分,其中L 沿上半圆周
解： y
2x x2,d y
1 x dx 2x x2
y
ds 1 y2 dx 1 dx
2x x2
o
Bx
2x x2,
1 x
L P( x, y)dx Q( x, y)d y 2x x2
令 A (P , Q , R), d s (d x , d y , dz)
t (cos , cos , cos )
Ad s At ds
记 A 在 t 上的投影为 At
Ad s
机动 目录 上页 下页 返回 结束
例6. 设 续, 曲线段 L 的长度为s, 证明
lim
0
Q(k
k 1
,
k
) yk , 称为对
y
的曲线积分.
若记 d s (d x , d y ), 对坐标的曲线积分也可写作
L F d s L P ( x , y )d x Q ( x , y )d y 类似地, 若 为空间曲线弧 , 记 d s (d x , d y , d z )
L
c
x (t)
(3) 推广
:
y
(t
),
t起点 ,终点 .
z (t)
Pdx Qdy Rdz
{
P[
(t
),
(t
),
(t
)]
(t
)
Q[ (t ), (t ), (t )] (t )
R[ (t ), (t ), (t )] (t )}dt
2 0
(1
4
cos
2
t
)
d
t
2
o y
x
机动 目录 上页 下页 返回 结束
三、两类曲线积分之间的联系
设有向平面曲线弧为L：
x y
(t) ,
(t)
L上点( x, y)处的切线向量的方向角为, ,
则L Pdx Qdy L(P cos Q cos)ds
B
A
a o a x
(2) 从点 A ( a , 0 )沿 x 轴到点 B (– a , 0 ).
解: (1) 取L的参数方程为
则
L y2 dx
0
a2
sin
2
t
( a sin t )d t
2a 3 2 1 4 a3
3
3
(2) 取 L 的方程为y 0, x : a a ,则
在L上连
证:
| L P c o s Q c o s ds |
L | P cos Q cos |ds
设 A (P , Q ), t (cos ,cos )
二者夹角为
L A t ds L A t cos ds
说明: 上述证法可推广到三维的第二类曲线积分.
机动 目录 上页 下页 返回 结束
例3. 计算
其中L为 y
B (1 ,1 )
(1) 抛物线 L : y x 2 , x : 0 1; x y 2
(2) 抛物线
y x2
(3) 有向折线 L : OA AB .
o
A(1,0 ) x
解: (1) 原式
4
1 0
x
3
d
x
(2) 原式 01( 2 y2 y 2 y y4 )d y
2、设LP( x, y)dx Q( x, y)dy 0,则
P( x, y)dx Q( x, y)dy
L
____________；
L x yd x AO x yd x OB x yd x 解法2 取 y 为参数, 则
A(1,1)
2
1 0
x
3 2
d
x
4 5
L x yd x 11 y 2 y( y 2 ) d y
机动 目录 上页 下页 返回 结束
例2. 计算
其中 L 为
y
(1) 半径为 a 圆心在原点的 上半圆周, 方向为逆时针方向;
M xk k1
A
x
机动 目录 上页 下页 返回 结束
2. 定义. 设 L 为xoy 平面内从 A 到B 的一条有向光滑 弧, 在L 上定义了一个向量函数
若对 L 的任意分割和在局部弧段上任意取点, 极限
lim
0
n
k 1
P (k
,k
) xk
Q (k
,k
)
yk
记作
L P ( x , y )d x Q ( x , y )d y
特殊情形 (1) L : y y( x) x起点为a，终点为b.
则
b
Pdx Qdy {P[ x, y( x)] Q[ x, y( x)]y( x)}dx.
L
a
(2) L : x x( y) y起点为c，终点为d .
则
d
Pdx Qdy {P[x( y), y]x( y) Q[x( y), y]}dy.
所做的功为
则
n
W Wk
k 1
2) “常代变”
y F ( k , k )
L
M yk k B
Mxk k1
A
x
有向小弧段
用有向线段
近似代替, 在
上任取一点
则有
W k F (k , k ) M k 1M k P (k , k ) xk Q (k , k ) yk
( i
),
(
i
)]
(
i ) ti
因为L 为光滑弧 ,
n
lim
0
P [
i1
(
i
),
( i
)]
(
i
)ti
P [ (t ), (t )] (t)dt
同理可证
Q [ (t ), (t )] (t)d t
机动 目录 上页 下页 返回 结束
向（如 L 表示为顺时针方向、逆时针方向）？
思考题解答
曲线方向由参数的变化方向而定.
例如L：x a cos t ，y a sin t ，t [0,2 ]中
当t 从 0 变到2 时，L取逆时针方向; 反之当t 从2变到 0 时，L取顺时针方向.
练习题
一、 填空题:
1、 对______________的曲线积分与曲线的方向有关；
F ( x, y, z) (P ( x, y, z), Q ( x, y, z), R( x, y, z))
机动 目录 上页 下页 返回 结束
3. 性质
(1) 若 L 可分成 k 条有向光滑曲线弧
则 L P ( x , y )d x Q ( x , y )d y
k