双线性插值Matlab程序
Matlab插值

(2)由图形可见,若可由 散点图得到时间和温度 的函数关系(一元函 数),则问题得解!
35
30
散
25
点
20
图
15
10
5
0
2
4
6
8 10 12
显然,找时间和温度间的函数关系是很难的!
那我们是否可以找到一条经过每一个点的简单函数 作为它的近似呢?
3
插值
在离散数据的基础上补插连续函数,使得 这条连续曲线通过全部给定的离散数据点。插 值是离散函数逼近的重要方法,利用它可通过 函数在有限个点处的取值状况,估算出函数在 其他点处的近似值。
返回 17
三次样条插值 是一种分段插值,比分段线性插值更光滑!
y
a
xi-1 xi
bx
在数学上,光滑程度的定量描述是:函数(曲线) 的k阶可导且连续,则称该曲线具有k阶光滑性。
光滑性的阶次越高,则越光滑。为了得到具有
较高阶光滑性的分段低次插值多项式,我们介绍三 次样条插值。
18
1、了解插值的基本内容。 2、掌握用Matlab软件包求解插值问题。
[1] 问题的提出 [2] 一维插值 [3] 二维插值
2
问题1
在1-12的11小时内,每隔1小时测量一次温度,测得的温度 依次为:5,8,9,15,25,29,31,30,22,25,27,24 试估计每隔1/10小时的温度值。
分析:
y0
x x1
x0 x0
x x2 x1 x2
y1
x x2
x0 x0
matlab图像双线性插值-最近邻插值与几何变换
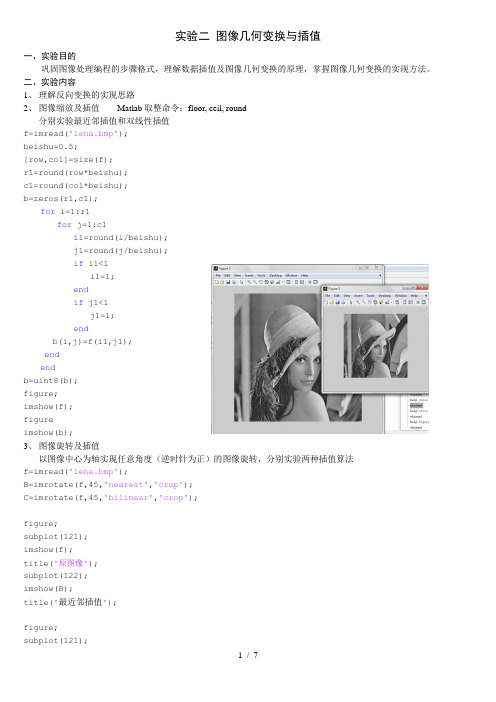
实验二图像几何变换与插值一、实验目的巩固图像处理编程的步骤格式,理解数据插值及图像几何变换的原理,掌握图像几何变换的实现方法。
二、实验内容1、理解反向变换的实现思路2、图像缩放及插值Matlab取整命令:floor, ceil, round分别实验最近邻插值和双线性插值f=imread('lena.bmp');beishu=0.5;[row,col]=size(f);r1=round(row*beishu);c1=round(col*beishu);b=zeros(r1,c1);for i=1:r1for j=1:c1i1=round(i/beishu);j1=round(j/beishu);if i1<1i1=1;endif j1<1j1=1;endb(i,j)=f(i1,j1);endendb=uint8(b);figure;imshow(f);figureimshow(b);3、图像旋转及插值以图像中心为轴实现任意角度(逆时针为正)的图像旋转,分别实验两种插值算法f=imread('lena.bmp');B=imrotate(f,45,'nearest','crop');C=imrotate(f,45,'bilinear','crop');figure;subplot(121);imshow(f);title('原图像');subplot(122);imshow(B);title('最近邻插值');figure;subplot(121);imshow(f);title('原图像');subplot(122);imshow(C);title('双线性插值');原图像最近邻插值处理原图像双线性插值处理%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% matlab练习程序(图像放大/缩小,最邻近插值)ccccl;w=0.6; %放大或缩小的宽度h=1.4; %放大或缩小的高度img=imread('Corner.png');imshow(img);[m n]=size(img);imgn=zeros(h*m,w*n);rot=[h 0 0;0 w 0;0 0 1]; %变换矩阵x=h*u,y=w*vinv_rot=inv(rot);for x=1:h*mfor y=1:w*npix=[x y 1]*inv_rot;imgn(x,y)=img(round(pix(1)),round(pix(2)));endendfigure,imshow(uint8(imgn)) %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% matlab练习程序(图像放大/缩小,双线性插值)cccm=1.8; %放大或缩小的高度n=2.3; %放大或缩小的宽度img=imread('lena.jpg');imshow(img);[h w]=size(img);imgn=zeros(h*m,w*n);rot=[m 0 0;0 n 0;0 0 1]; %变换矩阵for i=1:h*mfor j=1:w*npix=[i j 1]/rot;float_Y=pix(1)-floor(pix(1));float_X=pix(2)-floor(pix(2));if pix(1) < 1%边界处理pix(1) = 1;endif pix(1) > hpix(1) = h;endif pix(2) < 1pix(2) =1;endif pix(2) > wpix(2) =w;endpix_up_left=[floor(pix(1)) floor(pix(2))];%四个相邻的点pix_up_right=[floor(pix(1)) ceil(pix(2))];pix_down_left=[ceil(pix(1)) floor(pix(2))];pix_down_right=[ceil(pix(1)) ceil(pix(2))];value_up_left=(1-float_X)*(1-float_Y);%计算临近四个点的权重value_up_right=float_X*(1-float_Y);value_down_left=(1-float_X)*float_Y;value_down_right=float_X*float_Y;%按权重进行双线性插值imgn(i,j)=value_up_left*img(pix_up_left(1),pix_up_left(2))+ ...value_up_right*img(pix_up_right(1),pix_up_right(2))+ ...value_down_left*img(pix_down_left(1),pix_down_left(2))+ ...value_down_right*img(pix_down_right(1),pix_down_right(2));endendfigure,imshow(uint8(imgn)) %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% matlab练习程序(图像旋转,最邻近插值)ccccl;H=1; %索引pix中第一个元素,即高度W=2; %索引pix中第二个元素,即宽度jiaodu=45; %要旋转的角度,旋转方向为顺时针img=imread('Corner.png'); %这里v为原图像的高度,u为原图像的宽度imshow(img); %这里y为变换后图像的高度,x为变换后图像的宽度[v u]=size(img);theta=jiaodu/180*pi;rot=[cos(theta) -sin(theta) 0;sin(theta) cos(theta) 0;0 0 1];inv_rot=inv(rot);pix1=[1 1 1]*rot; %变换后图像左上点的坐标pix2=[1 u 1]*rot; %变换后图像右上点的坐标pix3=[v 1 1]*rot; %变换后图像左下点的坐标pix4=[v u 1]*rot; %变换后图像右下点的坐标height=round(max([abs(pix1(H)-pix4(H))+0.5 abs(pix2(H)-pix3(H))+0.5])); %变换后图像的高度width=round(max([abs(pix1(W)-pix4(W))+0.5 abs(pix2(W)-pix3(W))+0.5])); %变换后图像的宽度imgn=zeros(height,width);delta_y=abs(min([pix1(H) pix2(H) pix3(H) pix4(H)])); %取得y方向的负轴超出的偏移量delta_x=abs(min([pix1(W) pix2(W) pix3(W) pix4(W)])); %取得x方向的负轴超出的偏移量for y=1-delta_y:height-delta_yfor x=1-delta_x:width-delta_xpix=[y x 1]*inv_rot; %用变换后图像的点的坐标去寻找原图像点的坐标,%否则有些变换后的图像的像素点无法完全填充if pix(H)>=0.5 && pix(W)>=0.5 && pix(H)<=v && pix(W)<=uimgn(y+delta_y,x+delta_x)=img(round(pix(H)),round(pix(W)));endendendfigure,imshow(uint8(imgn))%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% matlab练习程序(图像旋转,双线性插值)cccjiaodu=45; %要旋转的角度,旋转方向为顺时针img=imread('lena.jpg'); %这里v为原图像的高度,u为原图像的宽度imshow(img); %这里y为变换后图像的高度,x为变换后图像的宽度[h w]=size(img);theta=jiaodu/180*pi;rot=[cos(theta) -sin(theta) 0;sin(theta) cos(theta) 0;0 0 1];pix1=[1 1 1]*rot; %变换后图像左上点的坐标pix2=[1 w 1]*rot; %变换后图像右上点的坐标pix3=[h 1 1]*rot; %变换后图像左下点的坐标pix4=[h w 1]*rot; %变换后图像右下点的坐标height=round(max([abs(pix1(1)-pix4(1))+0.5 abs(pix2(1)-pix3(1))+0.5])); %变换后图像的高度width=round(max([abs(pix1(2)-pix4(2))+0.5 abs(pix2(2)-pix3(2))+0.5])); %变换后图像的宽度imgn=zeros(height,width);delta_y=abs(min([pix1(1) pix2(1) pix3(1) pix4(1)])); %取得y方向的负轴超出的偏移量delta_x=abs(min([pix1(2) pix2(2) pix3(2) pix4(2)])); %取得x方向的负轴超出的偏移量for i=1-delta_y:height-delta_yfor j=1-delta_x:width-delta_xpix=[i j 1]/rot; %用变换后图像的点的坐标去寻找原图像点的坐标,%否则有些变换后的图像的像素点无法完全填充float_Y=pix(1)-floor(pix(1));float_X=pix(2)-floor(pix(2));if pix(1)>=1 && pix(2)>=1 && pix(1) <= h && pix(2) <= wpix_up_left=[floor(pix(1)) floor(pix(2))]; %四个相邻的点pix_up_right=[floor(pix(1)) ceil(pix(2))];pix_down_left=[ceil(pix(1)) floor(pix(2))];pix_down_right=[ceil(pix(1)) ceil(pix(2))];value_up_left=(1-float_X)*(1-float_Y); %计算临近四个点的权重value_up_right=float_X*(1-float_Y);value_down_left=(1-float_X)*float_Y;value_down_right=float_X*float_Y;imgn(i+delta_y,j+delta_x)=value_up_left*img(pix_up_left(1),pix_up_left(2))+ ...value_up_right*img(pix_up_right(1),pix_up_right(2))+ ...value_down_left*img(pix_down_left(1),pix_down_left(2))+ ...value_down_right*img(pix_down_right(1),pix_down_right(2));endendendfigure,imshow(uint8(imgn)) %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%实验一 Matlab图像基本操作一、实验目的熟悉利用Matlab进行图像处理的基本操作,了解图像数据的存储形式及进行图像处理编程的步骤方法。
matlab插值(详细 全面)

Matlab中插值函数汇总和使用说明MATLAB中的插值函数为interp1,其调用格式为: yi= interp1(x,y,xi,'method')其中x,y为插值点,yi为在被插值点xi处的插值结果;x,y为向量, 'method'表示采用的插值方法,MATLAB提供的插值方法有几种: 'method'是最邻近插值, 'linear'线性插值; 'spline'三次样条插值; 'cubic'立方插值.缺省时表示线性插值注意:所有的插值方法都要求x是单调的,并且xi不能够超过x的范围。
例如:在一天24小时内,从零点开始每间隔2小时测得的环境温度数据分别为12,9,9,10,18 ,24,28,27,25,20,18,15,13,推测中午12点(即13点)时的温度.x=0:2:24;y=[12 9 9 10 18 24 28 27 25 20 18 15 13];a=13;y1=interp1(x,y,a,'spline')结果为: 27.8725若要得到一天24小时的温度曲线,则:xi=0:1/3600:24;yi=interp1(x,y,xi, 'spline');plot(x,y,'o' ,xi,yi)命令1 interp1功能一维数据插值(表格查找)。
该命令对数据点之间计算内插值。
它找出一元函数f(x)在中间点的数值。
其中函数f(x)由所给数据决定。
x:原始数据点Y:原始数据点xi:插值点Yi:插值点格式(1)yi = interp1(x,Y,xi)返回插值向量yi,每一元素对应于参量xi,同时由向量x 与Y 的内插值决定。
参量x 指定数据Y 的点。
若Y 为一矩阵,则按Y 的每列计算。
yi是阶数为length(xi)*size(Y,2)的输出矩阵。
用MATLAB作函数插值

通过此例对最近邻点插值、双线性插值方法和双三次插值方法的插 值效果进行比较。
主程序: moutain.m
x=0:400:5600; y=0:400:4800; z=[370 470 550 600 670 690 670 620 580 450 400 300 100 150 250;... 510 620 730 800 850 870 850 780 720 650 500 200 300 350 320;... 650 760 880 970 1020 1050 1020 830 900 700 300 500 550 480 350;... 740 880 1080 1130 1250 1280 1230 1040 900 500 700 780 750 650 550;... 830 980 1180 1320 1450 1420 1400 1300 700 900 850 840 380 780 750;... 880 1060 1230 1390 1500 1500 1400 900 1100 1060 950 870 900 930 950;... 910 1090 1270 1500 1200 1100 1350 1450 1200 1150 1010 880 1000 1050 1100;... 950 1190 1370 1500 1200 1100 1550 1600 1550 1380 1070 900 1050 1150 1200;... 1430 1430 1460 1500 1550 1600 1550 1600 1600 1600 1550 1500 1500 1550 1550;... 1420 1430 1450 1480 1500 1550 1510 1430 1300 1200 980 850 750 550 500;... 1380 1410 1430 1450 1470 1320 1280 1200 1080 940 780 620 460 370 350;... 1370 1390 1410 1430 1440 1140 1110 1050 950 820 690 540 380 300 210;... 1350 1370 1390 1400 1410 960 940 880 800 690 570 430 290 210 150];
matlab插值方法

数据插值
1
实验目的
1、了解插值的基本内容。 2、掌握用数学软件包求解插值问题。
实验内容
[1]一维插值
[2]二维插值 [3]实验作业
2
一 一、插值的定义 二、插值的方法
维
插
值
拉格朗日插值
分段线性插值
三次样条插值 三、用Matlab解插值问题
返回
3
二维插值
一、二维插值定义 二、网格节点插值法
6
例 已知飞机机翼下轮廓线上数据如下,求x每改变0.1时的y 值。
X Y
0 0
3 1.2
5 1.7
7 2.0
9 2.1
y
11 2.0
12 1.8
13 1.2
14 1.0
15 1.6
机翼下 轮廓线
x
7
二维插值的定义
第一种(网格节点):
y
O
x
8
已知 mn个节点
其中 互不相同,不妨设
构造一个二元函数
通过全部已知节点,即
再用
计算插值,即
9
第二种(散乱节点):
y
0
x
10
已知n个节点
其中 互不相同,
构造一个二元函数
通过全部已知节点,即
再用
计算插值,即
返回
11
用MATLAB作网格节点数据的插值
z=interp2(x0,y0,z0,x,y,’method’)
被插值点 的函数值
插值 节点
被插值点
Matlab中插值函数汇总和使用说明

Matlab中插值函数汇总和使用说明以下内容的参考地址:/blog/article.asp?id=28904已知向量x,y,通过x,y求出向量xi的插值的值1、分段线性插值yi=interp1(x,y,xi)或yi=interp1(x,y,'linear')2、多项式插值多项式为y=p(1)*x+p(2)*x^2+...+p(n)*x^n,则可以用p=polyfit(x,y,n),(n是多项式的最高次数)求出系数向量p,然后用y=polyval(p,xi)求出向量xi的函数值y3、三次样条插值yi=interp1(x,y,xi,'spline')或yi=spline(x,y,xi)或pp=interp1(x,y,'spline','pp'),然后pp=spline(x,y)-->yi=ppval(pp,xi)4、分段三次埃尔米特yi=interp1(x,y,xi,'pchip')或yi=pchip(x,y,xi)或pp=interp1(x,y,'pchip','pp') pp=pchip(x,y)-->yi=pppval(pp.xi)以下内容的参考地址:/s/blog_6056e8800100k3xf.html命令1 interp1功能一维数据插值(表格查找)。
该命令对数据点之间计算内插值。
它找出一元函数f(x)在中间点的数值。
其中函数f(x)由所给数据决定。
x:原始数据点Y:原始数据点xi:插值点Yi:插值点格式(1)yi = interp1(x,Y,xi)返回插值向量yi,每一元素对应于参量xi,同时由向量x 与Y 的内插值决定。
参量x 指定数据Y 的点。
若Y 为一矩阵,则按Y 的每列计算。
yi 是阶数为length(xi)*size(Y,2)的输出矩阵。
(2)yi = interp1(Y,xi)假定x=1:N,其中N 为向量Y 的长度,或者为矩阵Y 的行数。
magnify matlab源程序

magnify matlab源程序以下是一个简单的 MATLAB 源程序,用于实现图片的放大功能: % 以下代码实现了图片的放大功能% 输入的变量 im 是一个三维 RGB 图像矩阵,factor 是放大因子 % 输出的变量 im_scaled 是一个放大后的三维 RGB 图像矩阵function im_scaled = magnify(im, factor)% 读取输入的图片大小[height, width, ~] = size(im);% 通过放大因子计算新的图片大小new_height = round(height * factor);new_width = round(width * factor);% 通过双线性插值法计算新的像素值,并把结果存储到输出矩阵中 for i = 1:new_heightfor j = 1:new_widthy = y_ratio * (i-1) + 1;x = x_ratio * (j-1) + 1;y1 = floor(y);y2 = ceil(y);x1 = floor(x);x2 = ceil(x);if x1 == x2x2 = x1 + 1;endif y1 == y2y2 = y1 + 1;endf11 = double(im(y1, x1, :));f12 = double(im(y2, x1, :));f21 = double(im(y1, x2, :));f22 = double(im(y2, x2, :));dx = x - x1;dy = y - y1;im_scaled(i,j,:) = uint8((1-dx)*(1-dy)*f11 + dx*(1-dy)*f21 +(1-dx)*dy*f12 + dx*dy*f22);endend% 显示原始图片和放大后的图片subplot(1, 2, 1);imshow(im);title('原始图片');subplot(1, 2, 2);imshow(im_scaled);title('放大后的图片');end该程序的功能是将输入的 RGB 图片矩阵进行放大,输出结果是放大后的图片矩阵。
双线性插值法缩放图像函数MATLAB程序(精)

% Define a function for shrinking and zooming images by bilinear interpolation% I is the original image and N is the factor for shrinking firstly and zooming later function interpolation_shrink_zoom_image(I, N% First to shrink the original image% To measure the size of original image I[P,Q]=size(I;% Rebuild the original image I to I_TEMP for bilinear interpolationI_TEMP=zeros(P+2,Q+2; I_TEMP(2:P+1,2:Q+1=I;I_TEMP(1,2:Q+1=I(1,:; I_TEMP(P+2,2:Q+1=I(P,:;I_TEMP(2:P+1,1=I(:,1; I_TEMP(2:P+1,Q+2=I(:,Q;I_TEMP(1,1=I(1,1; I_TEMP(1,P+2=I(1,P;I_TEMP(P+2,1=I(P,1; I_TEMP(P+2,Q+2=I(P,Q;I_TEMP=double(I_TEMP;% To fix the size of shrunken image% R is the number of rows and C is the number of columnsR=floor(P/N; C=floor(Q/N;% Define the shrunken imageI_S=zeros(R,C;% For bilinear interpolation f(x,y in 4 points f(x1,y1,f(x2,y1,f(x1,y2,f(x2,y2 % f(x,y = f(x1,y1*(x2-x*(y2-y/((x2-x1*(y2-y1% + f(x2,y1*(x-x1*(y2-y/((x2-x1*(y2-y1% + f(x1,y2*(x2-x*(y-y1/((x2-x1*(y2-y1% + f(x2,y2*(x-x1*(y-y1/((x2-x1*(y2-y1% For pixel matrix, x2=x1+1, y2=y1+1, x=x1+a, y=y1+b% Let x1=u, y1=v, then x2=u+1, y2=v+1, x=u+a, y=v+b% Then f(u+a, v+b = f(u,v*(1-a*(1-b + f(u+1,v*a*(1-b% + f(u,v+1*(1-a*b + f(u+1,v+1*a*b% Method: from original image I get suitable gray value by surrounding 4 pixels,% then fill the gray value into certain location in shrunken image I_S.for i=1:R;for j=1:C;% Step1: get x,y,u,v,a,b. The size of I to size of I_S ratio = N,% (x,y is pixel "in" I and (i,j is pixel in I_S, then x/i=y/j=N.x=i*N; y=j*N; u=floor(x; v=floor(y; a=x-u; b=y-v;% Step2: considering the situation on bound of I, using I_TEMP to get suitable value of f(x,y by bilinear interpolationI_S(i,j = I_TEMP(u+1,v+1*(1-a*(1-b + I_TEMP(u+2,v+1*a*(1-b +I_TEMP(u+1,v+2*(1-a*b + I_TEMP(u+2,v+2*a*b;end ;end ;% Display the original image I and the shrunken image I_SI_S=uint8(I_S;figure; imshow(I,[]; title(['Original image: ',num2str(P,'*',num2str(Q]; figure; imshow(I_S,[]; title(['Interpolation shrinking image:' ,num2str(R,'*',num2str(C];% Second to zoom the shrunken image% R*C is the size of shrunken image as shown before% Rebuild the shrunken image I_S to I_TEMP for bilinear interpolation I_TEMP=zeros(R+2,C+2; I_TEMP(2:R+1,2:C+1=I_S;I_TEMP(1,2:C+1=I_S(1,:; I_TEMP(R+2,2:C+1=I_S(R,:;I_TEMP(2:R+1,1=I_S(:,1; I_TEMP(2:R+1,C+2=I_S(:,C;I_TEMP(1,1=I_S(1,1; I_TEMP(1,R+2=I_S(1,R;I_TEMP(R+2,1=I_S(R,1; I_TEMP(R+2,R+2=I_S(R,C;I_TEMP=double(I_TEMP;% Define the zoomed imageI_Z=zeros(R*N,C*N;% Zooming the shrunken image by bilinear interpolationfor i=1:R*N;for j=1:C*N;x=i/N; y=j/N; u=floor(x; v=floor(y; a=x-u; b=y-v;% Step2: considering the situation on bound of I, using I_TEMP to get suitable value of f(x,y by bilinear interpolationI_Z(i,j = I_TEMP(u+1,v+1*(1-a*(1-b + I_TEMP(u+2,v+1*a*(1-b +I_TEMP(u+1,v+2*(1-a*b + I_TEMP(u+2,v+2*a*b;end ;end ;% Display the original image I and the shrunken image I_SI_Z=uint8(I_Z;figure; imshow(I,[]; title(['Original image: ',num2str(P,'*',num2str(Q]; figure; imshow(I_Z,[]; title(['Interpolation zooming image:' ,num2str(R*N,'*',num2str(C*N];end。
