薄膜力学8-断裂2
薄膜物理与技术-7薄膜的物理性质--(1)薄膜的力学性质

电镀膜的附着性能差(∵有一定数量的微孔)
第七章 薄膜的物理性质
7.1 薄膜的力学性质
7.1.1 薄膜的附着力
附着力的测试方法 机械方法数种如下:
扩散附着
通过中间层附着
宏观效应附着
第七章 薄膜的物理性质
7.1 薄膜的力学性质
简单附着
7.1.1 薄膜的附着力
(a)简单附着: 是在薄膜和基体之间存在一个很清楚的分界面。由两个接
触面相互吸引形成的。当两个不相似或不相容的表面相互接 触时就易形成这种附着。(如真空蒸镀)
附着能 : Wfs = Ef + Es - Efs
②静电力—薄膜和基体两种材料的功函数不同, 接触后发生电子转移→界面两边积累正负 电荷 → 静电吸引
物理吸附能:0.001eV~0.1eV
③化学键力(化学吸附能0.1-0.5eV)
共价键 离子键 金属键
价电子发生了转移, 短程力,不是普遍存在。
第七章 薄膜的物理性质
7.1 薄膜的力学性质
7.1.1 薄膜的附着力
须注意:T↑→薄膜晶粒大→热应力↑→其它性能变
第七章 薄膜的物理性质
7.1 薄膜的力学性质
7.1.1 薄膜的附着力
③引入中间过渡层 某种材料与一些物质间附着力大,与另一些物质的附
着力却可能很小。如:
(1)二氧化硅-玻璃→附着好;二氧化硅-KDP(磷酸二氢 钾)晶体→附着差 (2)金-玻璃→附着差;金-铂、镍、钛、铬等→附着好
方法:在基片Байду номын сангаас镀一层薄金属层(Ti、Mo、Ta、 Cr等).然后,在其上再镀需要的薄膜,薄 金属夺取基片中氧 中间层表面掺杂。
第七章 薄膜的物理性质
薄膜力学性能解析

19
二、残余应力的测量
1. Stoney公式
在薄膜残余应力的作用下,基底会发生挠曲,这
种变形尽管很微小,但通过激光干涉仪或者表面轮廓
仪,能够测量到挠曲的曲率半径。基底挠曲的程度反
映了薄膜残余应力的大小,Stoney给出了二者之间的
3
分类
脆性薄膜
按
脆性基底
力
学
性
质 分
脆性薄膜
类
韧性基底
韧性薄膜 脆性基底
韧性薄膜 韧性基底
4
4.1 薄膜的弹性性能
一、薄膜的弹性常数
弹性模量是材料最基本的力学性能参之一,由于 薄膜的某些本质的不同之处,其弹性模量可能完全不 同于同组分的大块材料。
5
三点弯曲
如图所示,加载和挠度的测量均在两支点中心位置,
2
y
2bdy
hs 2
hs 2h f
I f y2bdy
hs 2
(4.3)
实验中测出载荷增量与中心挠度增量的关系曲线(近似 线性),求出其斜率,用(4.1)式求出薄板的抗弯刚度,若基 体弹性模量已知,则利用(4.2)式可求得薄膜的弹性模量。
7
压痕法
纳米压痕技术可用以测定薄膜的硬度、弹性模量以
及薄膜的蠕变行为等,其理论基础是Sneddon关于轴
详细推导过程见流程图2。
15
表4.1 式(4.21)中对应于hg /R 的系数
16
17
图2 根据p-h 曲线确定应力-应变关系的流程图
4.2 薄膜的残余应力
一、残余应力的来源
通常认为,薄膜中的残余应力分为热应力和内应力两种 。
薄膜材料物理-薄膜的力学性质

塑性变形机制
屈服强度是描述材料抵抗塑性变形能力的物理量,当外力达到屈服强度时,材料开始发生不可逆的塑性变形。
应力-应变曲线是描述材料在受力过程中应力与应变关系的曲线,通过该曲线可以确定材料的弹性模量和屈服强度等力学性能参数。
屈服强度与应力-应变曲线
应力-应变曲线
屈服强度
塑性形变对薄膜物理性能的影响
断裂表面形貌与机理
温度对薄膜的力学性能产生影响,低温下材料脆性增大,高温下材料韧性增强。
温度
湿度
加载速率
湿度对薄膜材料的力学性能产生影响,湿度过高可能导致材料吸湿膨胀,降低力学性能。
加载速率越快,材料吸收的能量越少,断裂强度越低。
03
02
01
பைடு நூலகம்
环境因素对薄膜断裂性质的影响
05
薄膜的疲劳性质
薄膜在循环应力作用下,经过一段时间后发生断裂的现象。
屈服强度
断裂强度是描述材料在受到外力作用时发生断裂行为的应力值,对于薄膜材料,其断裂强度也是衡量其力学性能的重要参数之一。
断裂强度
薄膜的力学性能参数
02
薄膜的弹性性质
弹性模量
是指材料在受到外力作用时,单位面积上产生的正应力与应变之比,是衡量材料抵抗弹性变形能力的物理量。对于薄膜材料,其弹性模量决定了材料在受力时的刚度和变形程度。
疲劳现象
循环应力导致薄膜内部产生微裂纹,裂纹逐渐扩展导致薄膜断裂。
疲劳机理
循环应力的幅值、频率、温度、薄膜材料的性质等。
影响因素
疲劳现象与机理
疲劳寿命预测与实验验证
疲劳寿命预测
基于疲劳裂纹扩展速率和应力强度因子幅值,预测薄膜的疲劳寿命。
实验验证
通过实验测试薄膜的疲劳寿命,与预测结果进行对比,评估预测模型的准确性。
薄膜断裂韧性测量方法
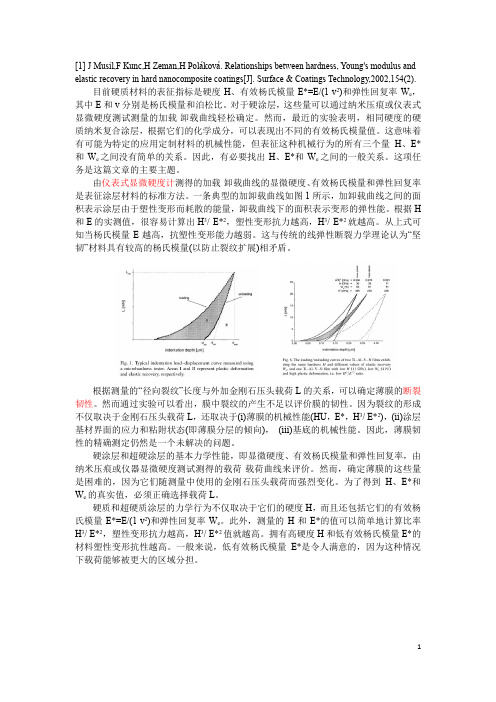
[1] J Musil,F Kunc,H Zeman,H Poláková. Relationships between hardness, Young's modulus and elastic recovery in hard nanocomposite coatings[J]. Surface & Coatings Technology,2002,154(2).目前硬质材料的表征指标是硬度H、有效杨氏模量E*=E/(1-v2)和弹性回复率W e,其中E和v分别是杨氏模量和泊松比。
对于硬涂层,这些量可以通过纳米压痕或仪表式显微硬度测试测量的加载-卸载曲线轻松确定。
然而,最近的实验表明,相同硬度的硬质纳米复合涂层,根据它们的化学成分,可以表现出不同的有效杨氏模量值。
这意味着有可能为特定的应用定制材料的机械性能,但表征这种机械行为的所有三个量H、E*和W e之间没有简单的关系。
因此,有必要找出H、E*和W e之间的一般关系。
这项任务是这篇文章的主要主题。
由仪表式显微硬度计测得的加载-卸载曲线的显微硬度、有效杨氏模量和弹性回复率是表征涂层材料的标准方法。
一条典型的加卸载曲线如图1所示,加卸载曲线之间的面积表示涂层由于塑性变形而耗散的能量,卸载曲线下的面积表示变形的弹性能。
根据H 和E的实测值,很容易计算出H3/ E*2,塑性变形抗力越高,H3/ E*2就越高。
从上式可知当杨氏模量E越高,抗塑性变形能力越弱。
这与传统的线弹性断裂力学理论认为“坚韧”材料具有较高的杨氏模量(以防止裂纹扩展)相矛盾。
根据测量的“径向裂纹”长度与外加金刚石压头载荷L的关系,可以确定薄膜的断裂韧性。
然而通过实验可以看出,膜中裂纹的产生不足以评价膜的韧性。
因为裂纹的形成不仅取决于金刚石压头载荷L,还取决于(i)薄膜的机械性能(HU,E*,H3/ E*2),(ii)涂层基材界面的应力和粘附状态(即薄膜分层的倾向),(iii)基底的机械性能。
薄膜力学测试国标

薄膜力学测试国标
薄膜力学测试的国标主要有以下几项:
1.GB/T10801-2006《塑料薄膜及片材拉伸试验》:该标准规定了对塑料薄膜及片材进行拉伸试验的方法和要求。
2.GB/T16491-2008《薄膜力学性能测量标准试验方法》:该标准规定了测量薄膜力学性能的标准试验方法和要求,包括拉伸、撕裂、切割、扭转、压缩等试验方法。
3.GB/T31318-2014《气体净化用活性炭纤维滤料》:该标准规定了气体净化用活性炭纤维滤料的物理性能、化学性能、性能测试方法等内容。
4.GB/T12706-2008《电缆用聚乙烯绝缘电力电缆》:该标准规定了电缆用聚乙烯绝缘电力电缆的物理性能、机械性能、电性能、耐热性能、耐寒性能等方面的要求和测试方法。
5.GB/T5598-2015《液晶面板用全透光同色度亚甲基蓝光谱片》:该标准规定了液晶面板用全透光同色度亚甲基蓝光谱片的外观、物理性能、光学性能、使用要求等内容。
薄膜力学性能资料

th f TsTdT
(4.22)
根据Hooke’s定律,应力为
th
E
1 f
th
(4.23)
18
薄膜—基底体系中由于晶格常数失配在薄膜中产生的内 应力由Hoffman的晶界松弛模型得到
i
1
Ef
f
xa a
1
Ef
f
Lg
(4.24)
式中 a为薄膜材料为无残余应力时的晶格常数, x 为a由于
详细推导过程见流程图2。
15
表4.1 式(4.21)中对应于hg /R 的系数
16
17
图2 根据p-h 曲线确定应力-应变关系的流程图
4.2 薄膜的残余应力
一、残余应力的来源
通常认为,薄膜中的残余应力分为热应力和内应力两种 。
热应力是由于薄膜和基底材料热膨胀系数的差异引起的, 所以也称为热失配应力。热应力对应的弹性应变为
3
分类
脆性薄膜
按
脆性基底
力
学
性
质 分
脆性基底
韧性薄膜 韧性基底
4
4.1 薄膜的弹性性能
一、薄膜的弹性常数
弹性模量是材料最基本的力学性能参之一,由于 薄膜的某些本质的不同之处,其弹性模量可能完全不 同于同组分的大块材料。
5
三点弯曲
如图所示,加载和挠度的测量均在两支点中心位置,
对称压头载荷与压头深度之间的弹性解析分析,其结果
为
S dP dh
2
Er
A
(4.4)
这里,h为压头的纵向位移,S dP为d试h 验载荷曲线的薄
膜材料刚度, 是压A头的接触面积。
8
Er 为约化弹性模量
1
8 薄膜力学性能

薄膜力学性能
沈杰 复旦大学材料科学系
薄膜力学性能
附着力 薄膜厚度一般小于1微米,本身的机械强度导致其无法单独存在, 总要附着在各种基片上。 薄膜与基片之间的附着性能直接影响到薄膜的各种性能。 附着性差,薄膜无法使用。 应力 在制作过程中,薄膜结构受到工艺条件影响很大,薄膜内部因此 而产生一定的应力。 基片材料与薄膜材料之间热膨胀系数不同,也会使薄膜产生应力。 过大的内应力将使薄膜卷曲和开裂,导致失效。 硬度
复旦大学材料科学系
薄膜材料与器件
本征应力
热应力 本征应力:薄膜形成过程中由于缺陷等原因而引起的内应力。 本征应力与薄膜厚度有关。在薄膜厚度很薄时(10nm以下) ,构成薄膜 的小岛互不相连,即使相连也呈网状结构,此时的内应力较小。随着 膜厚的增加,小岛相互连接,由于小岛之间晶格排列的差异以及小孔 洞的存在,使内应力迅速增大,并出现最大值。膜厚进一步增加,并 形成连续膜时,膜中不再有小孔洞存在,此时应力减小并趋于稳定值。
复旦大学材料科学系
薄膜-基片界面
简单附着 (突变界面 ):薄膜与基片之间存在清 楚的分界面,相互作用为范德瓦尔斯力 扩散附着 (扩散界面 ):在薄膜和基片之间通过 基片加热、离子注入、离子轰击等方法实现原 子的互扩散,形成一个渐变界面,使薄膜与基 片的接触面积明显增加,附着力相应增加。 中间层附着 (复合界面 ):薄膜与基片之间形成 化合物中间层,薄膜通过中间层与基片形成牢 固的附着。 宏观效应附着: 机械锁合:基片表面的微观的凹凸、微孔 或微裂缝。在沉积薄膜时,部分原子进入 凹凸之中或微孔、微裂缝中,增加附着力。 双电层吸引:两种功函数不同的材料互相 接触时会发生电子转移,在界面两边聚集 起电荷,形成双电层,具有静电吸引能。 复旦大学材料科学系
薄膜 抗剪切 标准-概述说明以及解释

薄膜抗剪切标准-概述说明以及解释1.引言1.1 概述薄膜是一种具有特殊性能和广泛应用领域的材料。
它们通常由聚合物、金属或陶瓷等材料制成,具有较薄的厚度和柔软的性质。
薄膜被广泛用于包装、电子产品、医疗设备、太阳能电池等各个行业。
在薄膜的制造和应用过程中,抗剪切力是一个非常重要的性能指标。
抗剪切力是指在外界施加剪切力时,薄膜的抵抗力。
这个性能对于薄膜的稳定性、可靠性和使用寿命起着至关重要的作用。
为了确保薄膜的品质和性能达到要求,需要对薄膜抗剪切力进行测试和评估。
目前,国际上已经相继制定了一系列的测试方法和标准,用于衡量薄膜抗剪切力的各项指标,如剪切模量、剪切强度等。
然而,目前存在一些问题和挑战。
首先,现有的薄膜抗剪切力测试方法和标准还不够完善,存在一定的局限性和不足。
其次,在实际应用中,薄膜抗剪切力的要求和标准也存在差异,需要进一步加强统一和规范。
因此,本文将围绕薄膜抗剪切力展开深入研究,旨在总结薄膜抗剪切力的重要性和应用,对目前的测试方法和标准进行评估,提出改进建议,并展望未来薄膜抗剪切力的研究方向。
通过这些努力,我们希望能够推动薄膜抗剪切力领域的发展,提高薄膜的品质和性能,为相关领域的应用提供更好的支持和保障。
1.2文章结构1.2 文章结构本文主要分为引言、正文和结论三个部分。
下面将对每个部分的内容进行介绍。
引言部分包括概述、文章结构和目的三个方面。
首先,我们将概述薄膜抗剪切力的重要性和应用。
通过引入薄膜在工程和科学领域中的广泛应用和对剪切力的敏感性,突出薄膜抗剪切力的研究价值。
接着,明确本文的结构,说明文章将分为引言、正文和结论三个部分。
最后,说明本文的目的,即探讨薄膜抗剪切力的定义、测试方法和标准,以及对标准的建议和未来的研究方向。
正文部分将详细介绍薄膜的定义和特性、抗剪切力的概念和重要性,以及薄膜抗剪切力的测试方法和标准。
在2.1节中,我们将对薄膜进行定义,并讨论其在各个领域中的应用。
同时,我们将介绍薄膜的一些特性,如柔韧性、透明性和可塑性,以便更好地理解薄膜的抗剪切力。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
GSS
l
2 0
2E f
Z ( , )
02 h f
Ef
l 2Z ( , )h f
For a thin substrate with the lower surface fixed:
ks ~
s
hs
l2
E f h f hs
s
Effect of substrate constraint
1 When = = 0, s = 0.5; 0.5 For < 0, s < 0.5 (less singular); For > 0, s > 0.5 (more singular); For 1, s 1.
-1 0 1
Penetration or deflection?
Elastic shear-lag approximation
0 0
x h f
u Ef x
ksu
(x)
0
S
0
ks 2u u 2 x E f hf
u(0) 0 ( S / 2) 0
Average cgth
From the shear-lag model,
S GSS tanh 2E f l
2 0 l
l2
E f hf ks
For thick substrates, compare the steady-state energy release rate with numerical solutions. For S :
h xx (r ,0) C r
s
The stress singularity exponent, s, depends on the elastic mismatch (Zak and Williams, 1963): 2 2 cos( s ) 2 (1 s) 0 2 s 1 1
Film Substrate
G p s
Gd i
When both conditions are satisfied, the crack is likely to penetrate into the substrate if
Gp s Gd 1 i
Both the energy release rates depend on the elastic mismatch between the film and the substrate.
A three-dimensional process: crack grows in both parallel and perpendicular directions, with a curved crack front.
Cutting and Channeling
Cutting: a crack growing perpendicular to the interface; a plane strain problem, assuming long in the parallel direction.
35 30 25 20 15 10 5 0 -1
Beuth [21] XFEM = /4
GSS Z ( , )
02 h
Ef
Z 1.976
-0.5 0 Elastic mismatch, 0.5 1
Beuth, IJSS 29, 1657-1675 (1992); Huang et al., Engineering Fracture Mech. 70, 2513-2526 (2003).
Dundurs parameters: f s 1 s f 1 E f Es f s 1 s f 1 E f Es
0.25
f s 1 s f 1 f s 1 s f 1
When = = 0 or a/h 0:
F
0
0
K I 1.12 a
• Stiff film on compliant substrate: SIF increases monotonically; • Compliant film on stiff substrate: SIF attains a maximum near the interface
Ratcheting underlayer: the constraint is gradually lost over thermal cycles, analogous to creep.
Crack growth modulated by creep
Tensile Film
Creeping layer
Steady-state channeling cracks
The channel front maintains its shape as it advances, and the cross section (opening) profile behind the front attains the equilibrium shape of a plane-strain crack. Thus, the steady-state energy release rate of a channeling crack can be obtained from the plane strain problem, and the fracture resistance is the film toughness.
S 2u ( S / 2) tanh Ef l
Energy release rate:
0l
l2
E f hf ks
02l 1 S GSS 0 tanh 2 2E f l
Xia and Hutchinson, JMPS 48, 1107-1131 (2000).
Rigid substrate
For a stationary long crack: When t 0, Steady-state velocity:
~a Free-standing film
a
h
G1 ~
2
E
a
a h
Film on elastic substrate
G2 ~
2
E
h
~h
The energy release rate increases if the crack penetrates into the substrate or if the film debond.
1 h GSS 0 ( z )dz 0 2h
From dimensional analysis:
or
1 h GSS G(a)dz h 0
GSS Z ( , )
02 h
Ef
Numerical results
40
Dimensionless energy release rate, (G E *)/(2h) 0 SS 1
Film
h
0
Substrate
Steady-state energy release rate
z Film
0
Film
(z)
x
0
h
Substrate Substrate (b)
Ahead of the channel front
Far behind the channel front
Energy release rate:
E E 1 2
Plane strain:
3 4
No mismatch: = = 0;
-1
1 -0.25
Stiff film on compliant substrate: > 0;
Compliant film on stiff substrate: < 0;
If f = s = 0.5, = 0; If f = s = 1/3, = /4;
Film
h
0
Substrate
Three-dimensional analysis is required to determine the shape of the channel front (Nakamura and Kamath, 1992).
The crack reaches a steady state when the length exceeds a few times the film thickness.
Both and change signs when the materials are switched.
Partially cracked films
Film Substrate
Stress intensity factor at the crack tip:
a K I F , , h h
Channeling: crack(s) growing parallel to the interface, assuming a constant depth in the perpendicular direction.
Elastic mismatch
For elastic films and substrates, the crack behavior depends on the elastic mismatch between them.
EM 397: Thin Film Mechanics
VIII. Film Cracking under Tension
