2019-2020学年度高中数学第三讲圆锥曲线性质的探讨二平面与圆柱面的截线课堂探究
2019_2020学年高中数学第三讲圆锥曲线性质的探讨3.2平面与圆柱面的截线课件新人教A版选修4_1

C.60° D.90°
解析设平面 β 与圆柱母线的夹角是 θ,则 cos θ= 23,故 θ=30°. 答案 A
首页
X D 新知导学 INZHIDAOXUE
答疑解惑
AYIJIEHUO
D当堂检测 ANGTANGJIANCE
12345
1.圆柱形物体的截口可能是( )
A.抛物线
B.双曲线
C.直线 D.椭圆或圆
心率为 e=cos 30°= 23. 答案 B
首页
X D 新知导学 INZHIDAOXUE
答疑解惑
AYIJIEHUO
D当堂检测 ANGTANGJIANCE
12345
4.已知一个平面截圆柱体所得的截口椭圆的离心率等于13,长轴长等
于 12,则圆柱底面半径为
.
解析设圆柱半焦距为 c,半长轴长为 a,半短轴长为 b,则 2a=12,于是
AYIJIEHUO
D当堂检测 ANGTANGJIANCE
探究一
探究二
解析 当 θ=30°时,φ=90°-30°=60°.
连接 O2G2,在 Rt△O2G2C 中,
由已知及 O2,F2,G2,C 四点共圆
可求得∠G2O2C=30°.
∴G2C=O2C·tan∠G2O2C=2tan 30°=233. 连接 O1G2,则在 Rt△O1BG2 中,
答疑解惑
AYIJIEHUO
D当堂检测 ANGTANGJIANCE
探究一
探究二
首页
X D 新知导学 INZHIDAOXUE
答疑解惑
AYIJIEHUO
D当堂检测 ANGTANGJIANCE
变式训练 已知平面 β 与一圆柱斜截口(椭圆)的离心率为 23,
2019-2020学年度高中数学第三讲圆锥曲线性质的探讨三平面与圆锥面的截线课堂探究

——教学资料参考参考范本——2019-2020学年度高中数学第三讲圆锥曲线性质的探讨三平面与圆锥面的截线课堂探究______年______月______日____________________部门课堂探究探究一利用Dandelin双球研究圆锥曲线讨论圆锥曲线的几何性质时,要注意结合图形进行.【典型例题1】如图,讨论其中双曲线的离心率.其中π′是Dandelin球与圆锥交线S2所在平面,与π的交线为m.解:P是双曲线上任意一点,连接PF2,过P作PA⊥m于A,连接AF2,过P作PB⊥平面π′于B,连接AB,过P作母线交S2于Q2.∵PB平行于圆锥的轴,∴∠BPA=β,∠BPQ2=α.在Rt△BPA中,PA=.在Rt△BPQ2中,PQ2=.由切线长定理,得PF2=PQ2,∴PF2=.∴e==.∵0<β<α<,∴cos β>cos α.∴e>1.同理,另一分支上的点也具有同样的性质,综上所述,双曲线的准线为m,离心率e=.探究二圆锥曲线几何性质应用根据定义,结合平面截圆锥面,正确解决有关圆锥曲线几何性质应用问题.【典型例题2】已知双曲线两个顶点间的距离为2a,焦距为2c,求两条准线间的距离.解:如图,l1,l2是双曲线的准线,F1,F2是焦点,A1,A2是顶点,O为中心.由离心率定义知=,∴A1H1=A1F1.又A1F1=OF1-OA1=c-a,∴A1H1=.∴OH1=OA1-A1H1,∴OH1=a-=.由对称性,得OH2=,∴H1H2=.点评已知圆锥曲线的结构特点,解决有关计算等问题时,通常利用圆锥曲线结构特点中的数量等式关系,如e=等,列出方程来解决.如本题中,由OH1=OA1-A1H1得到了a-=.。
2019_2020学年高中数学第三讲圆锥曲线性质的探讨3.3平面与圆锥面的截线课件新人教A版选修4_1

1234
思考辨析 判断下列说法是否正确,正确的在后面的括号内画“ ”,错误的画 “×”. (1)用一个不经过圆锥顶点的平面截圆锥面,截线只可能是椭圆、 双曲线、抛物线. ( ) (2)在圆锥的两部分分别嵌入Dandelin球,与平面π的两个切点分 别为F1,F2,则F1,F2即为平面π截圆锥所得双曲线的焦点. ( ) (3)所有圆锥曲线都有两个焦点和两条准线. ( ) (4)平面截圆锥面,所得圆锥曲线的离心率等于截面和圆锥的轴的 交角的余弦与圆锥的母线和轴所成角的余弦之比. ( ) 答案(1)× (2) (3)× (4)
1234
首页
X D 新知导学 INZHIDAOXUE
答疑解惑
AYIJIEHUO
D当堂检测 ANGTANGJIANCE
做一做1 已知圆锥的母线与轴的夹角为50°,一个平面与圆锥轴的
夹角为40°,则该平面与圆锥面的截线为 ( )
A.椭圆
B.圆 C.双曲线 D.抛物线
解析因为α=50°,β=40°,β<α,所以该平面与圆锥面的截线为双曲
3 3
B.
3 2
C.12
D.1
解析依题意,圆锥的母线与轴的夹角为 α=30°,平面与轴的夹
角为 β=60°,所以该平面与圆锥面的截线的离心率 e=ccooss6300° ° = 33. 答案 A
首页
X D 新知导学 INZHIDAOXUE
答疑解惑
AYIJIEHUO
D当堂检测 ANGTANGJIANCE
在截口上任取一点P,连接PF1,PF2.过P和圆 锥的顶点O作母线,分别与两个球相切于Q1,Q2, 则PF1=PQ1,PF2=PQ2,所以|PF1-PF2|=|PQ1PQ2|=Q1Q2.由于Q1Q2为两圆S1,S2所在平行平 面之间的母线线段长,因此Q1Q2为定值.故由双 曲线的定义知,平面与圆锥的交线是双曲线.
高中数学第三讲圆锥曲线性质的探讨3.2平面与圆柱面的截线练习含解析新人教A版选修41092358

高中数学第三讲圆锥曲线性质的探讨3.2平面与圆柱面的截线练习含解析新人教A版选修41092358课时过关·能力提升基础巩固1下列说法不正确的是()A.圆柱面的母线与轴线平行B.圆柱面的某一轴截面垂直于直截面C.圆柱面与斜截面截得的椭圆的离心率与圆柱面半径无关,只与母线和斜截面的夹角有关D.平面截圆柱面的截线椭圆中,短轴长即为圆柱面的半径A正确;由于任一轴截面过轴线,故轴截面与圆柱的直截面垂直,B正确;C显然正确;D中短轴长应为圆柱面的直径长,故不正确.2已知平面β与一圆柱斜截口(椭圆)的离心率为√32,则平面β与圆柱母线的夹角是() A.30° B.60° C.45° D.90°β与母线夹角为φ,则cosφ=√32,故φ=30°.3如果椭圆的两个焦点将长轴分成三等份,那么,这个椭圆的两条准线间的距离是焦距的() A.9倍 B.4倍 C.12倍 D.18倍2a,2b,2c,由已知,得2a3=2c,即a=3c,故两条准线间的距离为2a2a =18a2a=18c.4一组底面为同心圆的圆柱被一平面所截,截口椭圆具有() A.相同的长轴 B.相同的焦点C.相同的准线D.相同的离心率,所以长轴不同.嵌入的Dandelin球不同,则焦点不同,准线也不同,而平面与圆柱的母线夹角相同,故离心率相同.5若椭圆的一个顶点与两个焦点构成等边三角形,则此椭圆的离心率是()A.15B.√34C.√33D.122a,2b,2c,由已知a=2c,得aa =12,即e=12.6两个圆柱的底面半径分别为R,r(R>r),平面π与它们的母线的夹角分别为α,β(α<β<90°),斜截口椭圆的离心率分别为e1,e2,则()A.e1>e2B.e1<e2C.e1=e2D.无法确定e1=cosα,e2=cosβ,又α<β<90°时,cosα>cosβ,∴e1>e2.7已知圆柱的底面半径为2,平面π与圆柱的斜截口椭圆的离心率为12,则椭圆的长半轴是() A.2 B.4C.163D.4√332a,2b,2c.由题意,知b=2,aa =√a2-a2a=12,则√a 2-4a=12,解得a=4√33.8已知平面π截圆柱体,截口是一条封闭曲线,且截面与底面所成的角为45°,此曲线是 ,它的离心率为 .√229已知椭圆两条准线间的距离为8,离心率为12,则Dandelin 球的半径是 .{a 2a =4,a a =12, 解得{a =2,a =1,∴b=√a 2-a 2=√3.∴Dandelin 球的半径为√3.√310如图,设两个焦点的距离F 1F 2=2c ,两个端点的距离G 1G 2=2a ,求证:l 1与l 2之间的距离为2a 2a.,设椭圆上任意一点P ,过点P 作PQ 1⊥l 1于点Q 1,过点P 作PQ 2⊥l 2于点Q 2.连接PF 1,PF 2.∵e=aa 1aa 1=aa 2aa 2=aa ,∴PF 1=a a PQ 1,PF 2=aa PQ 2.由椭圆定义,知PF 1+PF 2=2a ,∴aa PQ1+aaPQ2=2a.∴PQ1+PQ2=2a2a,即l1与l2之间的距离为2a2a.能力提升1如图,过点F1作F1Q⊥G1G2,若△QF1F2为等腰直角三角形,则椭圆的离心率为()A.√22B.√2-12C.2-√2D.√2-12a,2b,2c.∵△QF1F2是等腰直角三角形,∴QF1=F1F2=2c,QF2=2√2c.由椭圆的定义,得QF1+QF2=2a,∴e=2a2a===√2-1.2已知圆柱的底面半径为r,平面α与圆柱母线的夹角为30°,则它们截口椭圆的焦距是() A.2√3r B.4√3r C.√3r D.3r,过点G2作G2H⊥AD,H为垂足,则G2H=2r.在Rt △G 1G 2H 中,G 1G 2=a 2acos60°=2r ×2=4r ,∴长轴2a=G 1G 2=4r ,短轴2b=2r. ∴焦距2c=2√a 2-a 2=2×√3r=2√3r.3一平面截圆柱(圆柱底面半径为1,高足够长)的侧面,得到一个离心率是√32的二次曲线,该曲线两焦点之间的距离为( ) A.√2B.2√3C.3√2D.√3e=√32<1,∴曲线是椭圆,且e=cos θ=√32,θ=30°,φ=60°(φ是底面与截面的夹角).∴cos60°=22a ,∴2a=212=4,∴a=2.又a a =√32,∴c=√3.∴2c=2√3.★4如图,已知A 为左顶点,F 是左焦点,l 交OA 的延长线于点B ,点P ,Q 在椭圆上,有PD ⊥l 于点D ,QF ⊥AO ,则椭圆的离心率是①aaaa ; ②aaaa ; ③aaaa ; ④aaaa ; ⑤aaaa .其中正确的是( )A.①②B.①③④C.②③⑤D.①②③④⑤①aaaa 符合离心率定义;②过点Q 作QC ⊥l 于C ,∵QC=FB ,∴aa aa =aaaa 符合离心率定义; ③∵AO=a ,BO=a 2a ,∴aa aa =aa a=a a ,故aaaa也是离心率; ④∵AF=a-c ,AB=a 2a -a , ∴aa aa =a -a a a-a=a a ,∴aaaa是离心率; ⑤∵FO=c ,AO=a ,∴aaaa =aa 是离心率. ∴①②③④⑤的表述均正确,故选D .5已知圆柱底面半径为b ,平面π与圆柱母线的夹角为30°,在圆柱与平面交线上有一点P 到一准线l 1的距离是√3b ,则点P 到另一准线l 2对应的焦点F 2的距离是 .,椭圆短轴长为2b ,长轴长2a=2asin30°=4b ,∴c=√22=√3b.∴e=√3a2a =√32或e=cos30°=√32.设点P 到焦点F 1的距离为d , 则√3a=√32,∴d=32b. 又PF 1+PF 2=2a=4b ,∴PF 2=4b-PF 1=4b-32b=52b.6如图,已知PF 1∶PF 2=1∶3,AB=12,G 1G 2=20,求PQ 的长.2a,短轴长为2b,焦距为2c,由已知可得a=10,b=6,c=√a2-a2=8,e=aa =45.由椭圆定义,知PF1+PF2=G1G2=20,又PF1∶PF2=1∶3,则PF1=5,PF2=15.由离心率定义,得aa1aa =45,∴PQ=254.★7如图,在圆柱O1O2内嵌入双球,使它们与圆柱面相切,并且和圆柱的斜截面相切,切点分别为F1,F2.求证:斜截面与圆柱面的截线是以点F1,F2为焦点的椭圆.,设点P为曲线上任一点,连接PF1,PF2,则PF1,PF2分别是两个球面的切线,切点分别为F1,F2,过点P作母线,与两球面分别相交于点K1,K2,则PK1,PK2分别是两球面的切线,切点为K1,K2.根据切线长定理的空间推广,知PF1=PK1,PF2=PK2,所以PF1+PF2=PK1+PK2=K1K2.由于K1K2为定值,故点P的轨迹是以F1,F2为焦点的椭圆.。
2019-2020年高中数学 第三讲 圆锥曲线性质的探讨 三 平面与圆锥面的截线课堂探究 新人教A版选修4-1
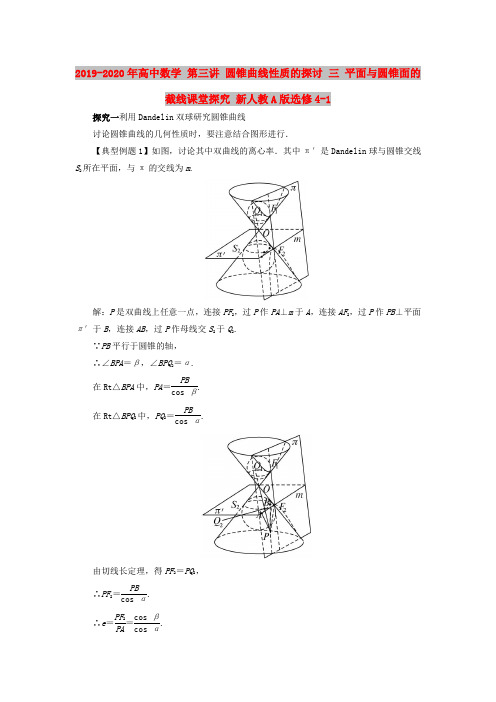
2019-2020年高中数学 第三讲 圆锥曲线性质的探讨 三 平面与圆锥面的截线课堂探究 新人教A 版选修4-1探究一利用Dandelin 双球研究圆锥曲线讨论圆锥曲线的几何性质时,要注意结合图形进行.【典型例题1】如图,讨论其中双曲线的离心率.其中π′是Dandelin 球与圆锥交线S 2所在平面,与π的交线为m .解:P 是双曲线上任意一点,连接PF 2,过P 作PA ⊥m 于A ,连接AF 2,过P 作PB ⊥平面π′于B ,连接AB ,过P 作母线交S 2于Q 2.∵PB 平行于圆锥的轴, ∴∠BPA =β,∠BPQ 2=α. 在Rt △BPA 中,PA =PBcos β. 在Rt△BPQ 2中,PQ 2=PBcos α.由切线长定理,得PF 2=PQ 2, ∴PF 2=PBcos α.∴e =PF 2PA =cos βcos α.∵0<β<α<π2,∴cos β>cos α.∴e >1.同理,另一分支上的点也具有同样的性质, 综上所述,双曲线的准线为m ,离心率e =cos βcos α.探究二圆锥曲线几何性质应用根据定义,结合平面截圆锥面,正确解决有关圆锥曲线几何性质应用问题.【典型例题2】已知双曲线两个顶点间的距离为2a ,焦距为2c ,求两条准线间的距离. 解:如图,l 1,l 2是双曲线的准线,F 1,F 2是焦点,A 1,A 2是顶点,O 为中心.由离心率定义知A 1F 1A 1H 1=ca, ∴A 1H 1=a cA 1F 1.又A 1F 1=OF 1-OA 1=c -a , ∴A 1H 1=a c -ac. ∴OH 1=OA 1-A 1H 1,∴OH 1=a -a c -a c =a 2c .由对称性,得OH 2=a 2c,∴H 1H 2=2a2c.点评 已知圆锥曲线的结构特点,解决有关计算等问题时,通常利用圆锥曲线结构特点中的数量等式关系,如e =ca等,列出方程来解决.如本题中,由OH 1=OA 1-A 1H 1得到了a -a c -a c =a 2c.2019-2020年高中数学 第三讲 圆锥曲线性质的探讨 二 平面与圆柱面的截线自我小测 新人教A 版选修4-11.已知平面β与一圆柱斜截口(椭圆)的离心率为32,则平面β与圆柱母线的夹角是( )A .30°B .60°C .45°D .90°2.如果椭圆的两个焦点将长轴分成三等份,那么,这个椭圆的两条准线间的距离是焦距的( )A .9倍B .4倍C .12倍D .18倍3.在圆锥内部嵌入Dandelin 双球,一个位于平面π的上方,一个位于平面π的下方,并且与平面π及圆锥均相切,若平面π与双球的切点不重合,则平面π与圆锥面的截线是( )A .圆B .椭圆C .双曲线D .抛物线4.已知圆柱的底面半径为r ,平面α与圆柱母线的夹角为60°,则它们截口椭圆的焦距是( )A .23rB .43rC .3rD .3r5.如图所示,已知A 为左顶点,F 是左焦点,l 交OA 的延长线于点B ,P ,Q 在椭圆上,有PD ⊥l 于D ,QF ⊥AO ,则椭圆的离心率是①PF PD ; ②QF BF ; ③AO BO ; ④AF AB ; ⑤FO AO.其中正确的是( )A .①②B .①③④C .②③⑤D .①②③④⑤6.已知平面π截圆柱体,截口是一条封闭曲线,且截面与底面所成的角为45°,此曲线是__________,它的离心率为__________.7.已知椭圆两准线间的距离为8,离心率为12,则Dandelin 球的半径是__________.8.已知圆柱底面半径为b ,平面π与圆柱母线的夹角为30°,在圆柱与平面交线上有一点P 到一准线l 1的距离是3b ,则点P 到另一准线l 2对应的焦点F 2的距离是__________.9.如图所示,已知PF 1∶PF 2=1∶3,AB =12,G 1G 2=20,求PQ .参考答案1.解析:设平面β与圆柱母线的夹角为φ,则cos φ=32, 故φ=30°. 答案:A2.解析:设椭圆的长轴长、短轴长、焦距分别为2a,2b,2c , 由已知,得2a3=2c ,即a =3c ,故两条准线间的距离为2a 2c =18c2c=18c .答案:A 3.B4.解析:如图,过点G 2作G 2H ⊥AD ,H 为垂足,则G 2H =2r .在Rt △G 1G 2H 中,G 1G 2=G 2Hcos 60°=2r ×2=4r ,∴长轴2a =G 1G 2=4r ,短轴2b =2r . ∴焦距2c =2a 2-b 2=2×3r =23r . 答案:A5.解析:①PF PD符合离心率定义;②过点Q 作QC ⊥l 于C , ∵QC =FB ,∴QF BF =QFQC符合离心率定义;③∵AO =a ,BO =a 2c,∴AO BO =a a2c=c a ,故AO BO也是离心率;④∵AF =a -c ,AB =a 2c-a ,∴AF AB =a -c a 2c-a =c a ,∴AFAB是离心率; ⑤∵FO =c ,AO =a , ∴FO AO =c a是离心率. 答案:D 6.答案:椭圆227.解析:由题意知⎩⎪⎨⎪⎧a 2c=4,c a =12,解得⎩⎪⎨⎪⎧a =2,c =1,∴b =a 2-c 2= 3.∴Dandelin 球的半径为 3. 答案: 38.解析:由题意知,椭圆短轴为2b ,长轴长2a =2bsin 30°=4b ,∴c =4b 2-b 2=3b . ∴e =3b 2b =32或e =cos 30°=32. 设P 到F 1的距离为d , 则d3b=32,∴d =32b . 又PF 1+PF 2=2a =4b , ∴PF 2=4b -PF 1=4b -32b =52b .答案:52b9.解:设椭圆长轴为2a ,短轴为2b ,焦距为2c ,由已知可得a =10,b =6,c =a 2-b 2=8,e =c a =45.由椭圆定义,知PF 1+PF 2=G 1G 2=20, 又PF 1∶PF 2=1∶3,则PF 1=5,PF 2=15.由离心率定义,得PF 1PQ =45,∴PQ =254.。
高中数学 第三讲 圆锥曲线性质的探讨 二 平面与圆柱面的截线自我小测 新人教A版选修41
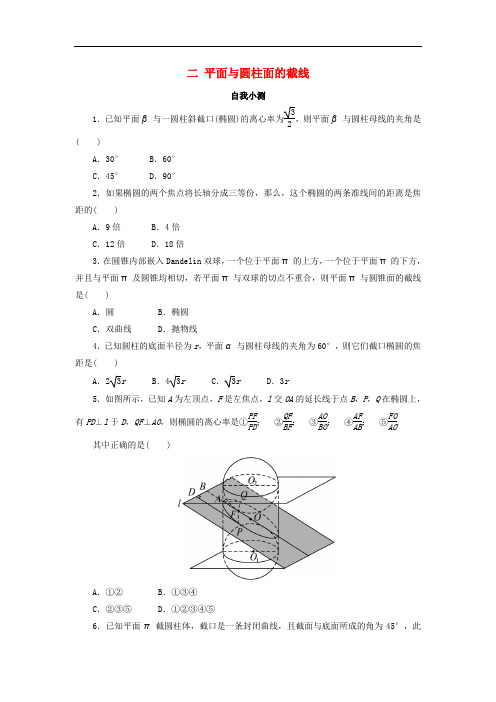
二 平面与圆柱面的截线自我小测1.已知平面β与一圆柱斜截口(椭圆)的离心率为32,则平面β与圆柱母线的夹角是( )A .30°B .60°C .45°D .90°2.如果椭圆的两个焦点将长轴分成三等份,那么,这个椭圆的两条准线间的距离是焦距的( )A .9倍B .4倍C .12倍D .18倍3.在圆锥内部嵌入Dandelin 双球,一个位于平面π的上方,一个位于平面π的下方,并且与平面π及圆锥均相切,若平面π与双球的切点不重合,则平面π与圆锥面的截线是( )A .圆B .椭圆C .双曲线D .抛物线4.已知圆柱的底面半径为r ,平面α与圆柱母线的夹角为60°,则它们截口椭圆的焦距是( )A .23rB .43rC .3rD .3r5.如图所示,已知A 为左顶点,F 是左焦点,l 交OA 的延长线于点B ,P ,Q 在椭圆上,有PD ⊥l 于D ,QF ⊥AO ,则椭圆的离心率是①PF PD ; ②QF BF ; ③AO BO ; ④AF AB ; ⑤FO AO.其中正确的是( )A .①②B .①③④C .②③⑤D .①②③④⑤6.已知平面π截圆柱体,截口是一条封闭曲线,且截面与底面所成的角为45°,此曲线是__________,它的离心率为__________.7.已知椭圆两准线间的距离为8,离心率为12,则Dandelin 球的半径是__________.8.已知圆柱底面半径为b ,平面π与圆柱母线的夹角为30°,在圆柱与平面交线上有一点P 到一准线l 1的距离是3b ,则点P 到另一准线l 2对应的焦点F 2的距离是__________.9.如图所示,已知PF 1∶PF 2=1∶3,AB =12,G 1G 2=20,求PQ .参考答案1.解析:设平面β与圆柱母线的夹角为φ,则cos φ=32, 故φ=30°. 答案:A2.解析:设椭圆的长轴长、短轴长、焦距分别为2a,2b,2c , 由已知,得2a3=2c ,即a =3c ,故两条准线间的距离为2a 2c =18c2c=18c .答案:A 3.B4.解析:如图,过点G 2作G 2H ⊥AD ,H 为垂足,则G 2H =2r .在Rt △G 1G 2H 中,G 1G 2=G 2Hcos 60°=2r ×2=4r ,∴长轴2a =G 1G 2=4r ,短轴2b =2r . ∴焦距2c =2a 2-b 2=2×3r =23r . 答案:A5.解析:①PF PD符合离心率定义;②过点Q 作QC ⊥l 于C , ∵QC =FB ,∴QF BF =QFQC符合离心率定义;③∵AO =a ,BO =a 2c,∴AO BO =a a2c=c a ,故AO BO也是离心率;④∵AF =a -c ,AB =a 2c-a ,∴AF AB =a -c a 2c-a =c a ,∴AFAB是离心率; ⑤∵FO =c ,AO =a , ∴FO AO =c a是离心率. 答案:D 6.答案:椭圆227.解析:由题意知⎩⎪⎨⎪⎧a 2c=4,c a =12,解得⎩⎪⎨⎪⎧a =2,c =1,∴b =a 2-c 2= 3.∴Dandelin 球的半径为 3. 答案: 38.解析:由题意知,椭圆短轴为2b ,长轴长2a =2bsin 30°=4b ,∴c =4b 2-b 2=3b . ∴e =3b 2b =32或e =cos 30°=32. 设P 到F 1的距离为d , 则d3b=32,∴d =32b . 又PF 1+PF 2=2a =4b , ∴PF 2=4b -PF 1=4b -32b =52b .答案:52b9.解:设椭圆长轴为2a ,短轴为2b ,焦距为2c ,由已知可得a =10,b =6,c =a 2-b 2=8,e =c a =45.由椭圆定义,知PF 1+PF 2=G 1G 2=20, 又PF 1∶PF 2=1∶3,则PF 1=5,PF 2=15.由离心率定义,得PF 1PQ =45,∴PQ =254.。
高中数学 第三讲 圆锥曲线性质的探讨 第二节 平面与圆
第二节 平面与圆柱面的截线课堂导学三点剖析一、椭圆的度量性质【例1】已知平面α与一圆柱的母线成60°角,那么该平面与圆柱截口图形的离心率是( ) A.23 B.1 C.22 D.21 解析:∵平面与圆柱截口图形为椭圆,其离心率e=cos60°=21. 答案:D温馨提示椭圆是圆柱与平面的截口,因此,椭圆的度量性质与底面半径、截面及母线夹角密切相关.二、探讨椭圆的性质【例2】如图3-2-2,已知球O 1、O 2分别切平面β于点F 1、F 2.G 1G 2=2a,Q 1Q 2=2b,G 1G 2与Q 1Q 2垂直平分,求证:F 1F 2=222b a .图3-2-2证明:过G 1作G 1H⊥BG 2,H 为垂足,则四边形ABHG 1是矩形.∴G 1H=AB.∵Q 1、Q 2分别是P 1、P 2的平行射影,∴P 1Q 1P 2Q 2.∴P 1Q 1Q 2P 2是平行四边形.∴Q 1Q 2=P 1P 2,即Q 1Q 2等于底面直径.∴G 1H=AB=Q 1Q 2=2b.又由切线长定理,G 1A=G 1F 1=G 2F 2,G 2F 1=G 2B,∴G 2F 1-G 2F 2=G 2B-G 1A.又G 1A=BH,∴G 2F 1-G 2F 2=G 2B-BH.∴F 1F 2=G 2H.在Rt△G 1G 2H 中,G 2H=2222212212)2()2(b a b a H G G G -=-=-.温馨提示探究圆柱体的斜截口——椭圆的性质,要仔细考查Dandlin 双球与圆柱及其截平面的关系,综合应用切线长定理、三角形的相似与全等、解直角三角形,以及平行射影的性质等等.三、数形结合——椭圆的解析性质【例3】已知圆柱底面半径为3,平面β与圆柱母线夹角为60°,在平面β上以G 1G 2所在直线为横轴,以G 1G 2中点为原点,建立平面直角坐标系,求平面β与圆柱截口椭圆的方程. 解:过G 1作G 1H⊥B C 于H.∵圆柱底面半径为3,∴AB=32.∵四边形ABHG 1是矩形,∴AB=G 1H=32.在Rt△G 1G 2H 中,G 1G 2=2332sin 211=∠H G G H G =4.又椭圆短轴长等于底面圆的直径32,∴椭圆的标准方程为3422y x +=1.图3-2-4各个击破类题演练1已知圆柱的底面半径为r,平面α与圆柱母线的夹角为60°,则它们截口椭圆的焦距是( )A.r 32B.r 34C.r 3D.3r 解析:如图3-2-1,过G 2作G 2H⊥AD,H 为垂足,则G 2H=2r.图3-2-1在Rt△G 1G 2H 中,G 1G 2=︒60cos 2H G =2r×2=4r, ∴长轴2a=G 1G 2=4r,短轴2b=2r.∴焦距2c=2r r b a 323222=⨯=-.答案:A类题演练2如图3-2-3,设两焦点的距离F 1F 2=2c,两端点距离G 1G 2=2a,截面β与圆柱母线的二面角为φ. 求证:P 到F 1的距离与到l 1的距离之比等于a c,即e=cosφ=a c .图3-2-3证明:过G 1作G 1H⊥BC 于H,则G 1A=BH.由切线长定量得G 2F 1=G 2B, G 1A=G 1F 1=G 2F 2,∴G 2F 1-G 2F 2=G 2B-BH.∴G 2H=F 1F 2=2c.在△PQK 1和△G 2G 1H 中,∠QPK 1=∠G 1G 2H=φ,∠QK 1P=∠G 1HG 2=90°,∴△PQK 1∽△G 2G 1H.∴ac a c G G H G PQ PK ===221221=cosφ=e.又由内切线长定理得PK 1=PF 1,∴a cPQ PK PQ PF ==11=cosφ=e.类题演练3在例3题设下,截面β与α、γ交线各为l 1、l 2,如图3-2-4,求l 1、l 2的方程. 解析:设P 是椭圆的顶点.过P 作PQ⊥l 1于Q.过P 作平面α的垂线,垂足为K 1,连结K 1Q.∵OP=3,OF 1=1)3(222=-,∴PF 1=212OF OP +=2.由切线长定理,PK 1=PF 1.在Rt△PK 1Q 中,PQ=︒=∠60cos 2cos 11QPK PK =4.又OE=PQ,∴OE=4.∴l1的方程为x=-4,l2的方程为x=4.温馨提示椭圆的平面坐标系内的解析方程及解析性质来源于几何性质,它们是统一的,是从不同侧面对它的描述.。
高中数学第三讲圆锥曲线性质的探讨第二节平面与圆柱面的截线课后导练
高中数学第三讲圆锥曲线性质的探讨第二节平面与圆柱面的截线课后导练课后导练基础达标1.已知平面β与一圆柱斜截口(椭圆)的离心率为,则平面β与圆柱母线的夹角是( )23 A.30° B.60° C.45° D.90°解析:设β与母线夹角为φ,则cos φ=,∴φ=30°.23 答案:A2.椭圆的一个顶点与两个焦点构成等边三角形,则此椭圆的离心率是( )A. B. C. D.51433321解析:由a=2c,得=,即e=.a c 2121答案:D3.两圆柱底面半径分别为R 、r(R >r),平面π与它们的母线的夹角分别为α、β(α<β<90°),斜截口椭圆的离心率分别为e1、e2,则( )A.e1>e2B.e1<e2C.e1=e2D.无法确定解析:∵e1=cos α,e2=cos β,又∵α<β<90°时,cos α>cos β,∴e 1>e2. 答案:A4.已知圆柱的底面半径为2,平面π与圆柱斜截口的离心率为,则椭圆的长半轴是( )21 A.2 B.4 C.D.31634解析:由题意知短半轴b=2,==,∴=,解得a=.aca b a 22-21a a 42-2134答案:D5.一组底面为同心圆的圆柱被一平面所截,截口椭圆具有( ) A.相同的长轴 B.相同的焦点 C.相同的准线 D.相同的离心率解析:因为底面半径大小不等,所以长轴不同.嵌入的Danlin 球不同,焦点不同,准线也不同.平面与圆柱的母线夹角相同,故离心率相同. 答案:D 综合运用6.如图3-2-5,已知∠PF1F2=30°,=,OP⊥F1F2,求⊙O1的半径.21F PF S ∆23 图3-2-5解析:设椭圆的长半轴为a,短半轴为b,焦距为c.根据题意得⎪⎪⎩⎪⎪⎨⎧+==∙︒=,,2321,30sin 222c b a bc a b 解得即OP=1,∴⊙O1的半径为1.⎪⎩⎪⎨⎧===,3,1,2c b a7.如图3-2-5,过F1作F1Q⊥G1G2,△QF1F2为等腰直角三角形,则椭圆的离心率为( )A. B. C.2- D.-122212-22 解析:∵△QF1F2是等腰直角三角形, ∴QF1=F1F2=2c,QF2=22c.由椭圆的定义得QF1+QF2=2a, ∴e=.12211222222-=+=+=c c c a c 答案:D8.如图3-2-6,已知PF1∶PF2=1∶3,AB=12,G1G2=20,求PQ.图3-2-6解析:设椭圆长轴为2a,短轴为2b,焦距为2c.由已知可得a=10,b=6,c==8,e==.22b a-a c 54由椭圆定义PF1+PF2=K1K2=G1G2=20. 又∵PF1∶PF2=1∶3, ∴PF1=5,PF2=15. 由离心率定义, ∴=.∴PQ=.PQ PF 1544259.如图3-2-7,已知设两焦点的距离F1F2=2c,两端点G1G2=2a,求证:l1与l2之间的距离为.ca 22图3-2-7证明:设椭圆上任意一点P,过P 作PQ1⊥l1于Q1,过P 作PQ2⊥l2于Q2. ∵e=,==2211PQ PF PQ PF a c ∴PF1=PQ1,PF2=PQ2.a c ac由椭圆定义PF1+PF2=2a,∴PQ1+PQ2=2a.a c ac∴PQ1+PQ2=,ca 22即l1与l2之间的距离为.ca 22拓展探究10.如图3-2-8,已知A 为左顶点,F 是左焦点,l 交OA 的延长线于点B,P 、Q 在椭圆上,有PD⊥l 于D,QF⊥AO,则椭圆的离心率是①;②;③;④;⑤.其中正确的序号是_______________.PD PF BF QF BO AO AB AF AOFO图3-2-8解析:①符合离心率定义.PDPF②过Q 作QC⊥l 于C,∵QC=FB,∴=符合离心率定义.BF QF QCQF③∵AO=a,BO=,ca 2∴==.BO AO ca a 2ac故也是离心率.BOAO④∵AF=a -c,AB=-a,ca 2∴==.∴是离心率.AB AF a ca c a --2a c ABAF⑤∵FO=c,AO=a, ∴=是离心率.AO FO ac答案:①②③④⑤ 备选习题11.椭圆的焦距、短轴长、长轴长组成一个等比数列,则椭圆的离心率为_____________.解析:由(2b)2=2c·2a,得b2=ac. 又b2=a2-c2,∴a2-c2=ac. ∴a2-c2-ac=0.两边同除ac, ∴--1=0.∴-e-1=0.c a a c e1∴e2+e -1=0. ∴e=或(舍去).215-215--答案:215- 12.椭圆一轴长为2,离心率为,则另一轴长为_________________.21 解析:设另一轴长为m,若m <2,则a2=4,b2=m2,c2=4-m2,e2=,4144222=-=m ac∴m=.3若m >2,同理,e2==,224mm -41解得m=.34答案:或33413.已知圆柱底面半径为b,平面π与圆柱母线夹角为30°,在圆柱与平面交线上有一点P 到一准线l1的距离是b,则点P 到另一准线l2对应的焦点F2的距离是_____________.3 解析:由题意知,椭圆短轴为2b,长轴长2a==4b,︒30sin 2b∴c=.b b b 3422=-∴e=或e=cos30°=.2323=b b 23设P 到F1的距离为d,则=,b d323∴d=b.23又PF1+PF2=2a=4b, ∴PF2=4b -PF1=4b-b=b.2325答案:b25 14.如果椭圆的两个焦点将长轴分成三等份,那么,这个椭圆的两准线间的距离是焦距的( )A.9倍B.4倍C.12倍D.18倍解析:由已知,得=2c,即a=3c.32a ∴两准线间的距离为==18c.c a 22cc 218答案:A15.已知椭圆两准线间的距离为8,离心率为,则Dandlin 球的半径是____________.21解析:由题意知解得⎪⎪⎩⎪⎪⎨⎧==,21,42a c ca ⎩⎨⎧==,1,2c a ∴b=.322=-c b∴Dandlin 球的半径为.3。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
——教学资料参考参考范本——
2019-
2020学年度高中数学第三讲圆锥曲线性质的探讨二平面与圆
柱面的截线课堂探究
______年______月______日
____________________部门
课堂探究
探究一椭圆的度量性质
圆柱形物体的斜截口是椭圆,因此,椭圆的度量性质与底面半径、截面及母线夹角密切相关.
【典型例题1】已知一圆柱面的半径为3,圆柱面的一截面的两焦球的球心距为12,求截面截圆柱面所得的椭圆的长轴长、短轴长、两焦点间距离和截面与母线所夹的角.
思路分析:根据题意可知长轴长及短轴长,进而求出离心率,从而得出截面与母线的夹角.
解:易知长半轴长a==6,短半轴长b=r=3,两焦点间距离2c =2=2=6.
椭圆离心率e==.
设截面与母线的夹角为φ,
则cos φ=.∴φ=.
综上,截面截圆柱面所得的椭圆的长轴长为12,短轴长为6,两焦点间距离为6,截面与母线所夹的角为.
探究二探讨椭圆的性质
探究圆柱体的斜截口——椭圆的性质,要熟知Dandelin双球与圆柱及其截平面的关系,综合应用切线长定理、三角形的相似与全等,解直角三角形,以及平行射影的性质.
【典型例题2】如图所示,已知球O1,O2分别切平面β于点F1,F2,P1P2为⊙O1的一条直径,Q1,Q2分别为P1,P2在平面β内的平行射影,G1G2=2a ,Q1Q2=2b ,G1G2与Q1Q2垂
直平分,求证:F1F2=2.
证明:如图,过G1作G1H⊥BG2,H 为垂足,
则四边形ABHG1是矩形.
∴G1H =AB.
∵Q1,Q2分别是P1,P2的平行射影,
∴P1Q1P2Q2.∴P1Q1Q2P2是平行四边形.
∴Q1Q2=P1P2,即Q1Q2等于底面直径.
∴G1H =AB =Q1Q2=2b.
又由切线长定理,知G1A =G1F1=G2F2,G2F1=G2B ,
∴G2F1-G2F2=G2B -G1A.
又G1A =BH ,∴G2F1-G2F2=G2B -BH.
∴F1F2=G2H.
在Rt△G1G2H 中,G2H ===2,22121G G G H
故F1F2=2.。
