基于LQR最优调节器的平面二级倒立摆的建模与仿真
基于SimulinkS-Function倒立摆仿真和实时控制研究(新)

摘要倒立摆是机器人技术、控制理论、计算机控制等多个领域、多种技术的有机结合,其被控系统本身又是一个不稳定、高阶次、多变量、强耦合的非线性系统,可以作为一个典型的控制对象对其进行研究。
本文阐述了倒立摆控制系统的研究背景和发展现状,研究了二级直线式倒立摆系统的物理结构,采用拉格朗日方程建立系统的数学模型,对数学模型在平衡位置进行了线性化,从而得到倒立摆系统的线性状态空间方程,同时分析了系统的稳定性和能控能观性。
在此基础上研究了极点配置,LQR控制理论,设计了二级倒立摆系统的极点配置控制器和LQR控制器,并利用Matlab软件的Simulink平台对倒立摆模型及控制器进行仿真,通过调试参数,使倒立摆倒立。
最后利用C语言编写控制器S-Function对倒立摆进行了实时控制。
关键词:倒立摆;极点配置;LQR;S-FunctionABSTRACTInverted pendulum is a combination of robotics techniques, control theory and computer control, the controlled system itself is an unstable, higher-order, multivariable, strongly coupled nonlinear system, which can be used as a typical control object to study it.This paper demonstrates the research background of inverted pendulum control system and the current development tendency, investigates the physical structure of 2-order linear-type inverted pendulum, adopts Lagrange's Equation to build the mathematical model, linearize the model in the balance position, achieves the linear state space equation of inverted pendulum, analyzes the stability, controllability and observability of the system.Furthermore, this paper investigates Pole Placement and LQR control theory, introduces a design of controller based on Pole Placement and LQR control theory for two-order inverted pendulum, simulates the performance of the controller through Simulink in Matlab and adjusts the parameters so that inverted pendulum could be inverted. Finally, a C-langrage controller is designed in S-Function of Matlab for real-time control of inverted pendulum.Key word:Inverted pendulum; pole placement; LQR; S-Function目录第1章绪论 (1)1.1课题研究的目的及意义 (1)1.2倒立摆系统简介 (1)1.3倒立摆的国内外研究情况 (3)1.4本文研究的主要内容及本文思路 (6)第2章二级直线式倒立摆系统建模和分析 (8)2.1系统建模 (8)2.1.1二级直线式倒立摆的结构 (8)2.1.2拉格朗日法建立系统数学模型 (9)2.1.3二级倒立摆系统数学模型的线性化 (14)2.2二级倒立摆系统分析 (16)2.2.1二级倒立摆系统的能控性 (17)2.2.2二级倒立摆系统的能观性 (17)2.2.3二级倒立摆系统的稳定性 (18)2.3本章小结 (18)第3章二级直线式倒立摆的极点配置控制 (19)3.1极点配置原理 (19)3.2单输入状态反馈极点配置算法 (20)3.3二级倒立摆极点配置控制仿真 (21)3.4本章小结 (24)第4章二级直线式倒立摆的LQR控制 (26)4.1线性二次最优控制LQR控制原理简介 (26)4.2直线二级倒立摆LQR控制器的设计和仿真 (29)4.3本章小结 (35)第5章利用S-Function对倒立摆进行实时控制 (36)5.1S-函数的基本概念 (36)5.2S-函数工作的基本原理 (36)5.2.1S-函数的数学模型 (36)5.2.2仿真阶段 (37)5.2.3S-函数的回调方式 (38)5.2.4S-函数的实现 (39)5.3用C语言编写S-Function对倒立摆进行实时控制 (40)5.3.1开头部分的预处理 (40)5.3.2S-函数例程的实现 (41)5.3.3倒立摆实时控制的实现过程 (45)5.4本章小结 (45)结论 (46)参考文献 (47)致谢 (49)附录 (50)第1章绪论1.1课题研究的目的及意义倒立摆是一个高阶次、非线性、快速、多变量、强耦合、不稳定的系统。
二级倒立摆系统的最优控制

∞
ut
+
B
+
1 /S
x
C
y
A
R-1BT
P
五、仿真分析
将某二级倒立摆系统模型各参数代入式1-8,得出系数矩阵 设, 写出Matlab程序如下:
A=[0,0,0,1,0,0;0,0,0,0,1,0;0,0,0,0,0,1; 0,-2.57163,0.164291,-16.6674,0.0124145,0.005; 0,29.9499,-15.1957,40.3167,-0.204856,0.17380; 0,29.9499,65.4455,-49.3949,0.463474,-0.59148]; B=[0;0;0;8.64636;-20.9146;25.9146]; C=[1 0 0 0 0 0;0 1 0 0 0 0;0 0 1 0 0 0];D=[0;0;0]; %求开环特征值 r1=eig(A) %加入最优反馈器 q1=100;q2=10;q3=5000;q4=0;q5=0;q6=0; Q=[q1 0 0 0 0 0;0 q2 0 0 0 0;0 0 q3 0 0 0;0 0 0 q4 0 0;0 0 0 0 q5 0;0 0 0 0 0 q6];R=1; %求最优增益矩阵、黎卡提方程的解、闭环特征值 [K,P,r2]=lqr(A,B,Q,R) Ac=[(A-B*K)];Bc=[B];Cc=[C];Dc=[D]; T=0:0.02:20;U=zeros(size(T)); x0=[0;-0.05;0.1;0;0;0]; [Y,X]=lsim(Ac,Bc,Cc,Dc,U,T,x0); %绘制下摆偏离垂直方向的角度变化曲线 figure(1);plot(T,Y(:,1)); xlabel('Time/sec');ylabel('01/rad');grid; %绘制上下摆角度之差的曲线 figure(2);plot(T,Y(:,2)); xlabel('Time/sec');ylabel('02-01/rad');grid; %绘制小车位移曲线 figure(3);plot(T,Y(:,3)) xlabel('Time/sec');ylabel('x(小车)/m');grid;
直线二级倒立摆建模与matlab仿真LQR
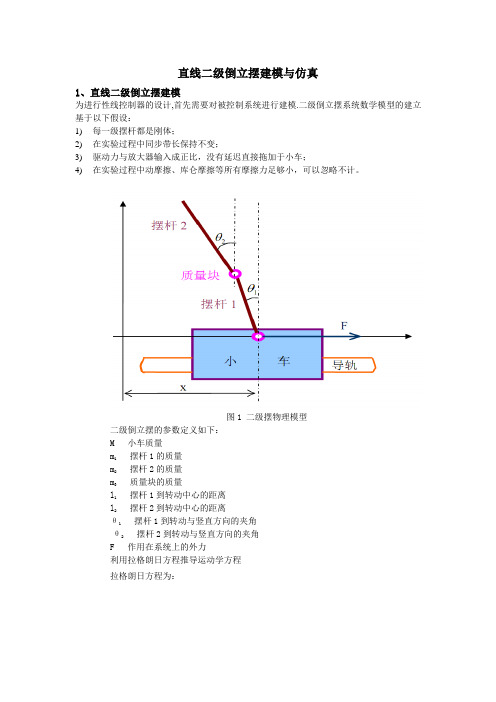
直线二级倒立摆建模与仿真1、直线二级倒立摆建模为进行性线控制器的设计,首先需要对被控制系统进行建模.二级倒立摆系统数学模型的建立基于以下假设:1)每一级摆杆都是刚体;2)在实验过程中同步带长保持不变;3)驱动力与放大器输入成正比,没有延迟直接拖加于小车;4)在实验过程中动摩擦、库仑摩擦等所有摩擦力足够小,可以忽略不计。
图1 二级摆物理模型二级倒立摆的参数定义如下:M 小车质量m1摆杆1的质量m2摆杆2的质量m3质量块的质量l1摆杆1到转动中心的距离l2摆杆2到转动中心的距离θ1摆杆1到转动与竖直方向的夹角θ2摆杆2到转动与竖直方向的夹角F 作用在系统上的外力利用拉格朗日方程推导运动学方程拉格朗日方程为:其中L 为拉格朗日算子,q 为系统的广义坐标,T 为系统的动能,V 为系统的势能其中错误!未找到引用源。
,错误!未找到引用源。
为系统在第i 个广义坐标上的外力,在二级倒立摆系统中,系统有三个广义坐标,分别为x,θ1,θ2,θ3。
首先计算系统的动能:其中错误!未找到引用源。
,错误!未找到引用源。
,错误!未找到引用源。
,错误!未找到引用源。
分别为小车的动能,摆杆1的动能,摆杆2的动能和质量块的动能。
小车的动能:错误!未找到引用源。
,其中错误!未找到引用源。
,错误!未找到引用源。
分别为摆杆1的平动动能和转动动能。
错误!未找到引用源。
,其中错误!未找到引用源。
,错误!未找到引用源。
分别为摆杆2的平动动能和转动动能。
对于系统,设以下变量: xpend1摆杆1质心横坐标 xpend2摆杆2质心横坐标 yangle1摆杆1质心纵坐标 yangle2摆杆2质心纵坐标 xmass 质量块质心横坐标 ymass 质量块质心纵坐标 又有:(,)(,)(,)L q q T q q V q q =-则有:系统总动能:系统总势能:则有:求解状态方程:可解得:使用MATLAB对得到的系统进行阶跃响应分析,执行命令:A=[0 0 0 1 0 0;0 0 0 0 1 0;0 0 0 0 1 01;0 0 0 0 0 0;0 86.69 -21.62 0 0 0;0 -40.31 39.45 0 0 0];B=[0;0;0;1;6.64;-0.808];C=[1 0 0 0 0 0;0 1 0 0 0 0;0 0 1 0 0 0];D=[0;0;0];sys=ss(A,B,C,D);t=0:0.001:5;step(sys,t)求取系统的单位阶跃响应曲线:图2 二级摆阶跃响应曲线由图示可知系统小车位置、摆杆1角度和摆杆2角度均发散,需要设计控制器以满足期望要求。
二级倒立摆的建模与MATLAB仿真

二级倒立摆的建模与 MATLAB 仿真 刘文斌,等
二级倒立摆的建模与MATLAB仿真
刘文斌,干树川 (四川理工学院电子与信息工程系 四川自贡,643000)
取为最小值。设控制输入函数形式为: U(t)= -Kx(t) (11) 状态反馈矩阵: K = R -1B T P ( 12) 其中,P 可由 Riccati 微分方程: (13) 其中, 性能指标函数: (14)
[J].计算机测量与控制,2006,14(12):1641 - 1642 5 张 春,江 明,陈其工等.平行单级双倒立摆系统的建模与滑
模变结构控制[J].2008.1
23
图1 二级倒立摆模型
(1)
(2)
(3) 经过线性化如下: (4)
(上接第 7 页) 0; 0; 0; 0]; p=eig(A) [num,den]=ss2tf(A,B,C,D,1); printsys(num,den) Q=[1000 0 0 0 0 0; 0 0 0 0 0 0; 0 0 10 0 0 0; 0 0 0 0 0 0; 0 0 0 0 10 0; 0 0 0 0 0 0]; Tc=ctrb(A,B); rank(Tc) To=obsv(A,C); rank(To) R=1; K=lqr(A,B,Q,R); Ac=[(A-B*K)]; Bc=[B]; Cc=[C]; Dc=[D]; T=0:0.005:20; U=0.2*ones(size(T)); [Y,X]=lsim(Ac,Bc,Cc,Dc,U,T); plot(T,Y(:,1),':',T,Y(:,2),' -',T,Y(:,3),'
基于LQR的二级倒立摆的模糊控制

Ab ta t T e u z c n r l t o y s n r d c d o t d t e o t o l n p o l m o t e o b n i e t d e d l m i t i a e . n r e s r c : h f z y o t o he r i i t o u e t s u y h c n r li g r b e f h d u i nv r e p n u u n h s p p r I o d r
Ke W od Do be i v re p nd l m; J y rs: u l n e td e u u I QR; uz y o t o ; u in un to qu ntfc t0 f co s F z c n rl f so f ci n; a ii ai n a tr
基于LQR最优调节器的二级倒立摆控制系统

维普资讯
2 o 年 5月 O7
安度师范学院学报 (自熊科学版)
J u l f n i e c esC l g ( a r c n eE i n o ma o A q gT a h r o e e N t a S i c d i ) n l u l e t o
收 稿 日期 : 06 0 — 8 2 0 — 7 2
作者简 介: 吴文进 ( 95 , , 17 一) 男 安徽安庆人 , 安庆师范学 院物理 与电气工程学院教 师, 硕士 , 主要研究现代控制理论及其应用 。
维普资讯
锁 良: 基于 L R最优调节器的二级倒立摆控制系统 Q 得
摘 要: 倒立摆是一个典 型的快速、 多变量 、 非线性 、 绝对不稳定系统 。 对倒立摆 系统 的稳定性研究在理论
上和方法上具有深远的意义。本文建立了二级倒立摆 的数学模型 。 并推导 出模型的状态空间表达式, 分析了系
统 的稳定性 , 能控性和能观性 。 利用 了线性 二次 型最优调节器 ( QR) L 方法实现对二级倒立摆的最优控制 , MA L B T A 仿真结果表明了该方法的有效性 。 关键词 : 二级倒立摆; 最优调节器; 最优控制
基于LQR二级倒立摆控制系统研究论文
基于LQR的二级倒立摆控制系统研究摘要倒立摆系统是一个典型的多变量、非线性、强耦合和快速运动的高阶不稳定系统,它是检验各种新的控制理论和方法有效性的典型理想模型。
在其控制过程中,能有效地反映诸如镇定性、鲁棒性、随动性以及跟踪等许多关键问题。
本文主要研究二级倒立摆LQR控制方法。
首先建立了二级倒立摆的数学模型,然后对二级倒立摆的数学模型进行控制设计,应用遗传算法确定系统性能指标函数中的加权阵Q,R得到系统状态反馈控制矩阵。
最后,用MATLAB进行了系统仿真。
在几次凑试Q矩阵值后系统的响应结果都不尽如人意,于是采用遗传算法对Q矩阵优化。
仿真结果证明:经过遗传算法优系统响应能更加满足设计要求。
关键词二级倒立摆;LQR控制;遗传算法Research on double inverted pendulum controlsystem based on LQRAbstractThe inverted pendulum is a typical high order system, with multi- variable, non-linear, strong-coupling, fleet and absolutely instable. It is representative as an ideal model to prove new control theory and techniques. During the control process, pendulum can effectively reflect many key problems such as equanimity, robust, follow-up and track, therefore.This paper studies a control method of double inverted pendulum LQR. First of all, the mathematical model of the double inverted pendulum is established, then make a control design to double inverted pendulum on the mathematical model, and determine the system performance index weight matrix Q, R by using genetic algorithm in order to attain the system state feedback control matrix. Finally, the simulation of the system is made by MATLAB. After several test matrix Q value the results are not satisfactory response, then we optimize Q matrix by using Genetic Algorithm. Simulation results show: The system response can meet the design requirements effectively after Genetic Algorithm optimization.Key words Double inverted pendulum; LQR control; Genetic Algorithm.目录摘要 (I)Abstract (II)第1章绪论 (1)1.1引言 (1)1.2倒立摆设备简介 ..................................... 错误!未定义书签。
毕业设计 二级倒立摆建模
四川理工学院毕业设计(论文)二级倒立摆系统建模与仿真学生:学号:专业:自动化班级:自动化指导教师:四川理工学院自动化与电子信息学院二O一一年六月摘要常规的PID控制从理论上可以控制二级倒立摆,但在实际中对PID控制器参数的整定为一难点。
本文针对二级倒立摆系统单输入三输出的不稳定系统,通过三回路PID 控制方案,来完成对倒立摆的控制。
利用状态反馈极点配置的方法来对参数进行整定,解决PID参数整定的难点。
然后借助于MATLAB中的Simulink模块对所得的参数进行仿真,结果表明三回路PID控制是成功的,参数的有效性,也证实了这种参数整定方法简单实用。
并通过配置不同位置的极点,对其结果进行分析得到极点配置的最佳配置方案。
关键词:倒立摆;PID;状态反馈; MATLABABSTRACTDouble Inverted Pendulum System Modeling and SimulationConventional PID control theory to control the inverted pendulum, but in practice the parameters of PID controller tuning is a difficult. In this paper, double inverted pendulum system, the instability of single-input three-output system, through the three-loop PID control program to complete the inverted pendulum control.Pole placement using state feedback approach to setting the parameters to resolve the difficulties PID parameter tuning. With MATLAB and Simulink in the module parameters obtained from simulation results show that the three-loop PID control is successful, the effectiveness of the parameters, but also confirms this tuning method is simple and practical.Different locations through the pole configuration, the results were too extreme configuration of the best configuration.Key words:pendulum;PID control ;state feedback;MATLAB目录摘要............................................................... ABSTRACT (I)第1章引言 01.1 倒立摆研究的目的及意义 01.2 倒立摆的发展史和研究现状 01.3本文的主要工作 (3)第2章倒立摆的建模 (3)2.1 二级倒立摆的简介及物理模型 (3)2.2 二级倒立摆计算机控制系统结构 (4)2.3 二级倒立摆的数学模型 (5)2.4根据牛顿力学、刚体动力学列写二级倒立摆的数学模型 (6)第3章控制策略的选择 (11)3.1 MATLAB简介 (11)3.2该系统的能控、能观及稳定性的分析 (14)3.2.1系统的能控性 (14)3.2.2系统能观性 (16)3.2.3系统的稳定性 (16)3.3 确定控制策略 (17)3.4 控制器参数整定方法 (17)3.5 通过状态反馈极点配置法来整定参数 (19)第4章计算机仿真及结果分析 (22)4.1 Matlab下Simulink模块简介 (22)4.2 在Simulink下的仿真 (23)4.3对仿真结果的分析 (31)第5章结束语 (32)致谢 (33)参考文献 (34)第1章引言1.1 倒立摆研究的目的及意义在控制理论发展的过程中, 一种理论的正确性及在实际应用中的可行性,往往需要一个典型对象来验证, 并比较各种控制理论之间的优劣, 倒立摆系统就是这样的一个可以将理论应用于实际的理想实验平台。
二阶倒立摆的稳定性控制
二阶倒立摆的稳定性控制摘要:本文研究了二阶倒立摆系统的控制方法,采用极点配置、LQR最优控制设计了控制器,通过仿真,分析指出各种方法的优缺点。
在极点配置法中,通过仿真实验寻优,得到具有较好稳定性的初始值。
在LQR最优控制器的设计中,采用仿真结果表明:该控制策略能满足系统的控制要求,系统具有良好的动态性能。
关键词:二阶倒立摆极点配置LQR最优控制倒立摆系统是应用于自动控制理论的经典实验装置,是一个复杂的多变量、高度非线性、强耦合和快速运动的绝对不稳定系统,对于倒立摆的稳定性控制,不仅有重要的理论意义,而且还有很重要的工程意义。
一方面倒立摆系统成本低廉,结构简单,物理参数和结构容易调整的优点,在实验条件下容易实现。
对于倒立摆的控制会涉及控制中的许多关键问题,如镇定问题、跟踪问题、随动问题、非线性问题、及鲁棒性问题。
另一方面,任何重心在上,支点在下的控制问题都可以近似于倒立摆系统,如机器人行走的平衡问题,火箭发射的垂直控制和卫星飞行中的姿态控制等。
1 二阶倒立摆系统二阶倒立摆系统的机械部分主要由小车、摆杆1,2、导轨、皮带轮、传动皮带等组成,电气部分由电机、功率放大器、PWM、传感器、驱动电路以及保护电路组成。
1.1 二阶倒立摆的数学模型[1]假设:摆杆及小车为刚体;皮带轮及皮带间无相对滑动,皮带无伸长;小车的驱动力与直流放大器的输入成正比,且无滞后;忽略电极电枢绕组中的电感、库仑摩擦、动摩擦。
系统各参数如下。
M(小车质量)为1.32kg;m1(摆杆1质量)为0.04kg;m2(摆杆2质量)为0.132kg;m3(质量快的质量)为0.208kg;l1(摆杆1转动中心到杆心的距离)为0.09m;l2(摆杆2转动中心到杆心的距离)为0.27m;(摆杆1与垂直方向的夹角);(摆杆2与垂直方向的夹角);F(作用在系统上的外力);g(重力加速度)为9.8。
2 控制设计及仿真2.1 用极点配置设计伺服系统设计要求:二阶倒立摆尽可能的保持倒立垂直()。
基于PSO的二级倒立摆LQR最优控制器设计
倒 立摆 作 为 控 制 系 统 的被 控 对 象 ,许 多 抽 象 的控 制 概 念 都 可 以 通 过它 直 观 的表 现 出 来 , 因此 成 为 检 验 各 种 新 型 控 制 理 论 和 方 法 有效 性 的典 型 装 置 。 年 来 , 多 学 者 对 倒 立摆 系统 进 行 近 许 广 泛 地 研 究 。 文 献 [— ] 出 了 基 于 模 糊 神 经 网 络 的 倒 立 摆 控 12提 制 系 统 , 方 法 由 于模 糊 神 经 网 络 系 统 的 自适 应 能 力 , 效 地 克 该 有 服 了 系 统存 在 的非 线 性 和 不 确 定 性 ,但 该 方 法 过 分 依 赖 人 类 直 接 控 制 被 控 对 象 的 经 验 。文 献 [ — ] 出 了倒 立 摆 拟 人 控 制 方 34提
优 控 制 器 比 较 , 真 结 果表 明 : 方 法 所 设 计 的 最 优 控 制 器 能 使 系统 的 响 应 时 间更 快 , 调 量 更 小 , 二 级 倒 立 摆 的 控 制 效 仿 该 超 对
果更理想。
关 键 词 : 级 倒 立摆 ,QR P 0, 二 L ,S 最优 控 制 器
基 于 P O 的 二级 倒 立 摆 L S QR最 优 控 制器 设 计
基于 P O的二级倒立摆 L S QR最优控制器设计
P O a e L S b s d QR Op i lCo t l r De i n f r t ma n r l sg o Do bl n e t d P n uu oe u e Iv r e d lm e
,
L QR tmal o r l op i c nt erdesgn ol i metod h ba ed n s o PS O i su e whi o er m e te hoc bl dn s f s tdid ch v co s h c ie i es o wei ig n ght m ar n ti x of QR i t e L n h de i prce s. i m e h d sgn o s Ths t o mak s s o PS e u e f O al i m wi h r t gl l t iat n o gorh t t eu i i h s c oba op i z i t ge Q 、 m o t R a nd s ae e t t fedb k co tol aw K. ubl ivet d ac n r l Do e n re pen lm o i c tol a duu pt mal onr l er ppl a in h metod s i to oft e c h i de i e whi o er sgn d ch v .
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
基于LQR最优调节器的平面二级倒立摆的建模与仿真第一章绪论
Ll研究背景
1.2研究目的
1.3论文结构
第二章平面二级倒立摆建模与仿真
2.1动力学分析
2.2时间域仿真
2.3LQR最优调节器
第三章非线性系统仿真
3.1平面二级倒立摆参数识别
3.2平面二级倒立摆非线性特性仿真
第四章强化学习控制技术
4.1强化学习控制技术原理
4.2平面二级倒立摆强化学习仿真
第五章改进PlD控制技术
5.1PlD控制器参数确定
5.2平面二级倒立摆改进PID控制仿真
第六章结论
6.1总结
6.2展望第一章绪论
当今社会,智能化机械系统的使用日渐普及,为了使其更好地实现所求的功能,对控制策略的设计和研究发挥了重要作用。
倒立摆系统是很常见的控制问题,具有时变不可知的结构,因而其调节过程十分复杂。
考虑到倒立摆的重要性,本文以平面二级倒立摆为研究对象,建立了基于LQR最优调节器的平面二级倒立摆的建模与仿真。
本文通过对平面二级倒立摆的动力学分析、时间域仿真、LQR最优调节器、平面二级倒立摆非线性特性仿真、强化学习控制和改进PID控制的实验性研究, 研究了最优调节系统的建模与仿真方法。
本文的研究目的是建立平面二级倒立摆系统的动力学模型,并以此模型为基础进行研究,研究和比较LQR最优调节器和强化学习技术在此系统中的控制效果,同时提出改进PlD控制技术。
研究希望能够有效地控制平面二级倒立摆系统,针对实际工程情况应用。
本文框架如下:第一章绪论,阐述研究的背景、研究的目的以及本文的结构;第二章介绍了平面二级倒立摆系统的建模与仿真,包括动力学分析、时间域仿真和LQR最优调节器;第三章介绍了平面二级倒立摆参数识别和非线性特性仿真;第四章介绍了强化学习控制;第五章介绍了改进PlD控制;最后,第六章总结出本文的研究结果,并对未来的工作进行展望。
第二章平面二级倒立摆建模与仿真本章首先介绍了平面二级倒立摆系统的动力学分析,然后进行仿真,在此基础上利用LQR最优调节技术进行控制。
平面二级倒立摆系统的动力学分析表明,其运动方程可以用以下的形式表示:
$$ M∖left ( q ∖right )∖ddot{q}+C∖left ( q,∖dot{q}
∖right )+G∖left ( q ∖right )=u $$
其中,M (q)为惯性矩阵;C (q, $\dot{q}$)为雅可比摩擦力矩;G (q)
为作用在系统上的重力力矩,u为控制力。
根据给定的参数,可以解出系统的非线性动力学方程,以便进行仿真。
时间域仿真可以使用MatIab/Simulink进行建模。
由于该系统具有时变不可知的结构,因此需要对系统参数进行参数识别,以保证仿真精度。
止匕外,针对平面二级倒立摆的非线性特性,本文采用MATLAB 中ode45函数计算其非线性特性,以保证仿真精度。
LQR (Linear Quadratic Regulator)最优调节器是用来控制线性系统的一种常用技术。
在本文中,LQR最优调节器结合了平面二级倒立摆系统的动力学模型,以使最优调节器能够高效调节系统状态,从而实现最佳控制效果。
本文通过仿真的方法证明了LQR最优调节器在平面二级倒立摆系统中可以显著提高系统稳定性并较好地满足控制要求。
第三章平面二级倒立摆参数识别与非线性特性仿真
本章首先进行平面二级倒立摆参数识别,然后进行非线性特性仿真。
首先,本文针对平面二级倒立摆系统的参数进行识别。
识别过程主要包括步态参数识别、动力学参数反解和模型标定三个步骤。
此外,针对平面二级倒立摆的非线性特性,本文采用MATLAB中ode45函数计算其非线性特性,以提高仿真精度。
ODE45函数是一
种灵活的方法,尤其适用于计算非线性系统的解析解,可以按照系统的实际特性很好地仿真非线性特性。
同时,本文对ode45函数进行了不同参数设置,以反映系统的实际运动特性,如:弹性元件模型、空气阻尼模型和湿滑模型等,从而进一步改善仿真精度。
第四章平面二级倒立摆的LQR最优调节
本章通过LQR最优调节技术,对平面二级倒立摆进行控制, 以实
现其最佳控制效果。
LQR (Linear Quadratic Regulator)最优调节器是用来控制线性系统的一种常用技术。
在本文中,本文采用LQR最优调节器结合平面二级倒立摆的动力学模型,以使最优调节器能够高效调节系统状态,从而实现最佳控制效果。
具体而言,LQR最优调节器通过建立一个复杂的动态系统状态空间模型,分析系统的特性,从而得出最优控制策略。
为此, 本文采用MATLAB中的Iqrd函数,采用最小二乘法求解LQR 最优调节器;此外,还将LQR控制器与平面二级倒立摆系统的动力学方程相结合,以实现最优控制效果。
本文还将LQR最优调节器的效果进行仿真,并且与简单PID 控制器结果进行了对比。
结果表明,LQR最优调节器可以显著提高系统稳定性,且在限定控制时间的情况下,仍可以在较短的时间内达到稳态状态,从而满足控制要求。
第五章平面二级倒立摆系统的控制实验
平面二级倒立摆实验中,主要采用基于双向DC伺服电机的控制系统,通过位置开环和速度闭环控制来对倒立摆系统的位置和频率进行调节。
实验中采用的控制算法包括PID控制器、LQR最优调节器和特定控制算法,以及模糊控制算法,并作为实验的对比组。
通过平面二级倒立摆的控制实验,首先我们比较不同控制器,发现LQR最优调节器在追踪误差、抗扰力性能方面表现优异, 比PlD控制器和特定控制算法更胜一筹;此外,模糊控制器也具有很好的调节性能,使系统控制更加精准,并在跟踪误差方面取得较好的性能。
最后,通过平面二级倒立摆的实验,本文验证了LQR最优调节技术和模糊控制技术在平面二级倒立摆控制中的有效性,使系统实现了较好的稳定性,从而满足控制要求。
第六章结论本文在研究后控制方法的基础上,提出了LQR最优调节器结合平面二级倒立摆的动力学模型,以实现最优控制效果。
主要结论如下:
(1)采用LQR最优调节器,可以获得最优控制效果,使系统能够实现较高的稳定性;
(2)模糊控制器也具有很好的调节性能,使系统控制更加精准。
最后,本文在实验中得到了多方面的认识,尤其是普遍认可的
PlD控制算法在不用采取保护措施的情况下无法满足系统控制的要求,同时也发现LQR最优调节器及模糊控制器在平面二级倒立摆控制中的有效性,使系统实现了较好的稳定性,从而满足控制要求。
