Friedman秩和检验
Friedman秩和检验的使用注意事项(八)

在统计学中,Friedman秩和检验是一种非参数检验方法,用于比较三个或三个以上配对样本的均值是否存在显著差异。
它是Wilcoxon符号秩检验的推广,适用于样本量较小或不满足正态分布的情况。
然而,在使用Friedman秩和检验时,有一些注意事项需要我们特别关注。
首先,我们需要注意样本的配对性。
Friedman秩和检验要求样本是配对的,也就是说,每个被试者都需要参与所有的处理条件,或者与其他被试者配对。
如果样本不满足配对条件,那么Friedman秩和检验就不适用。
因此,在进行实验设计时,需要特别注意样本的配对情况,确保满足Friedman秩和检验的前提条件。
其次,我们需要注意样本的独立性。
虽然Friedman秩和检验是一种非参数检验方法,对样本分布的假设要求相对较低,但是它依然要求样本是相互独立的。
也就是说,每个样本的取值不会受到其他样本取值的影响。
在实际应用中,我们需要特别注意样本的独立性,确保数据的有效性。
另外,我们需要注意样本量的大小。
Friedman秩和检验对样本量的要求相对较高,一般来说,每个处理条件至少需要有5个样本。
如果样本量过小,那么Friedman秩和检验的统计结果可能不准确,缺乏说服力。
因此,在进行实验设计时,需要根据样本量的要求,合理安排实验的样本数量。
此外,我们还需要注意对Friedman秩和检验统计结果的解释。
在进行Friedman秩和检验之后,我们需要对统计结果进行正确的解释。
一般来说,如果Friedman秩和检验的p值小于显著性水平(通常取),我们可以拒绝原假设,认为不同处理条件的均值存在显著差异。
如果p值大于显著性水平,我们则无法拒绝原假设,认为不同处理条件的均值没有显著差异。
在解释统计结果时,需要注意不要过度解读,要根据具体情况进行分析。
最后,我们需要注意Friedman秩和检验的局限性。
虽然Friedman秩和检验是一种有用的非参数检验方法,但是它也有一定的局限性。
4.5 完全区组设计:Friedman 秩和检验

例 某田径队对新入队的学员要进行四个部分的技术训练, 以提高学员的身体素质。为检验这四个部分的技术训练是否确实 有效,随机抽选了14 名新学员,分别接受四个部分的训练。 每个训练结束后,均进行该部分的测试,成绩以 10 分为最高。 检测结果如下表所示:
Z10.0167 Z0.09833 2.13
SE 4 4 5 4 12 3.266. 6 63
比较式 A vs B A vs C A vs D B vs C B vs D C vs D
Ri-Rj的绝对值 15-8=7 15-11.5=3.5 15-5.5=9.5 8-11.5=3.5 8-5.5=2.5 11.5-5.5=6
6(k 1)
这是大样本时基于 Friedman 秩和检验的一个方法.
如果零假设 H 0 为 i 处理和 j 处理没有区别, 那么,双边检验的统计量为 Ri R j .
对于置信水平 ,如果 Ri R j Z * 2 bk (k 1) / 6, 则拒绝零假设,这里
*
总共可比较的对数
4.5 Friedman 检验
Friedman 检验又称弗利德曼 2 检验或弗利德曼 两因素秩方差分析. 它是由 Friedman 于 1937 年提出的,后来又被 Kendall 和 Smith 发展到多元度量的协同系数相关问题上.
它是针对完全区组设计而提出的检验方法.
Friedman 检验的问题是 k 个样本的位置参数 (用1 , 2 , , k 表示)是否相等.
技术训练A
4 1 2 3 1 2 3 3 4 3 3 1 1 2 33
技术训练B
Friedman秩和检验
概率论
拒绝域的形式:
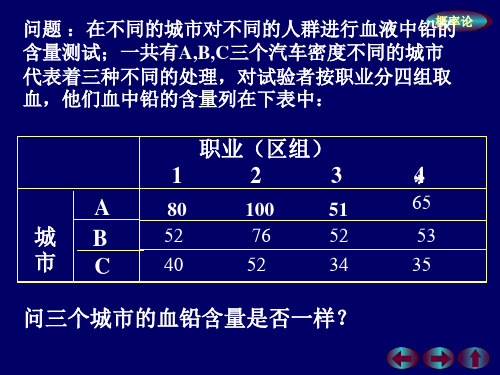
问题 :在不同的城市对不同的人群进行血液中铅的 含量测试;一共有A,B,C三个汽车密度不同的城市 代表着三种不同的处理,对试验者按职业分四组取 血,他们血中铅的含量列在下表中:
概率论
职业(区组) 3 1 2 城 市 A B C
80 52 40 100 76 52 51 52 34
ห้องสมุดไป่ตู้
65
53 35
4 *
问三个城市的血铅含量是否一样?
概率论
Descriptive Statistics N city1 city2 city3 4 4 4 Mean 74.0000 58.2500 40.2500 Std. Deviation 20.99206 11.84272 8.26136 Minimum 51.00 52.00 34.00 Maximum 100.00 76.00 52.00
概率论
Ranks city1 city2 city3 Mean Rank 2.75 2.25 1.00
Test Statisticsa N Chi-Square df Asymp. Sig. Exact Sig . Point Probability a. Friedman Test 4 6.500 2 .039 .042 .037
问三个城市的血铅含量是否一样?
§5.5
完全区组设计:Friedman秩和检验
概率论
1.适用条件:完全区组设计 2.统计假设:设各总体的位置参数为
3.基本原理:与Kruskal-Wallis检验类似 由于区组的影响,首先在每一个区组中计算各个处理 的秩,再把每个处理在各区组中的秩相加。
概率论
4.检验统计量:
问题 :在不同的城市对不同的人群进行血液中铅的 含量测试;一共有A,B,C三个汽车密度不同的城市 代表着三种不同的处理,对试验者按职业分四组取 血,他们血中铅的含量列在下表中:
Friedman秩和检验的使用注意事项(七)

Friedman秩和检验的使用注意事项Friedman秩和检验是一种非参数统计方法,通常应用于重复测量设计的数据分析中。
它的主要作用是检验不同处理条件下的观测值是否存在显著差异。
但是在使用Friedman秩和检验时,我们需要注意一些事项,以确保结果的准确性和可靠性。
首先,我们需要确保样本的独立性。
在进行Friedman秩和检验之前,我们需要确保样本是独立的,即每个观测值之间的相关性较小。
如果样本之间存在较大的相关性,可能会影响Friedman秩和检验的结果。
因此,在进行实验设计时,我们需要尽量避免使用相关性较大的样本。
其次,我们需要注意样本的大小。
Friedman秩和检验对样本大小有一定的要求,通常需要每个处理条件下的观测值不少于5个。
如果样本大小过小,可能会导致Friedman秩和检验的结果不够可靠。
因此,在进行实验设计时,我们需要尽量保证每个处理条件下的观测值数量足够。
此外,我们还需要注意数据的分布情况。
Friedman秩和检验对数据的分布情况没有要求,即使数据不符合正态分布也可以进行分析。
但是如果数据的分布情况非常偏斜或者存在明显的异常值,可能会影响Friedman秩和检验的结果。
因此,在进行数据分析时,我们需要对数据的分布情况进行检查,并在有必要的情况下进行适当的数据变换或异常值处理。
另外,我们还需要注意Friedman秩和检验的假设条件。
Friedman秩和检验的主要假设包括独立性、同质性和对称性。
在进行Friedman秩和检验之前,我们需要对这些假设条件进行检验,以确保满足这些条件。
如果这些假设条件不满足,可能会影响Friedman秩和检验的结果。
因此,在进行数据分析时,我们需要对Friedman秩和检验的假设条件进行检验,并在有必要的情况下进行适当的调整。
最后,我们需要注意Friedman秩和检验的结果解释。
在进行Friedman秩和检验之后,我们需要对结果进行适当的解释。
特别是当Friedman秩和检验的结果显著时,我们需要进行进一步的事后分析,以确定不同处理条件下的观测值之间的具体差异。
friedman秩和检验公式

friedman秩和检验公式Friedman 秩和检验公式是统计学中用于多组相关样本比较的一种非参数检验方法。
咱们先来说说啥是秩和检验。
想象一下,有几个小组在参加比赛,每个小组的表现数据不太符合常规的正态分布,这时候普通的参数检验方法可能就不太好使了,秩和检验就闪亮登场啦!Friedman 秩和检验主要就是给每个数据排个名次,然后再进行计算和分析。
比如说,咱们有三组小朋友参加画画比赛,评委根据他们的画作给出了分数。
但这些分数不是那种整齐规律的数字,那咋办?就把它们按照从高到低的顺序排个队,第一名给 1 分,第二名给 2 分,以此类推。
那这个公式具体长啥样呢?Friedman 秩和检验公式是这样的:\[\chi_{R}^{2} = \frac{12}{bk(k + 1)} \sum_{j=1}^{k} R_{j}^{2} - 3b(k + 1)\]这里面,b 是组数,k 是每个组的样本量,\(R_{j}\) 是第 j 组的秩和。
我给您举个例子来说明一下。
比如说有三个班级,每个班级 5 个同学参加数学小测验。
成绩出来后,乱糟糟的不好直接比,那就排个名次。
一班同学的名次分别是1、2、4、3、5;二班同学是2、3、1、5、4;三班同学是 5、4、3、2、1。
接下来,咱们算一下每个班的秩和。
一班是 1 + 2 + 4 + 3 + 5 = 15;二班是 2 + 3 + 1 + 5 + 4 = 15;三班是 5 + 4 + 3 + 2 + 1 = 15。
然后把这些值代入公式里算算。
\[\chi_{R}^{2} = \frac{12}{3×5(5 + 1)}×(15^{2} + 15^{2} + 15^{2}) -3×3×(5 + 1)\]算出来后,再和对应的临界值比较,如果计算出来的值大于临界值,那就说明这几个班级的成绩有显著差异;要是小于临界值,就说明没啥大差别。
在实际应用中,Friedman 秩和检验可有用啦!比如说研究不同教学方法对学生成绩的影响,或者比较不同药物对病人症状的改善效果。
Friedman秩和检验的使用注意事项(Ⅱ)

Friedman秩和检验的使用注意事项引言Friedman秩和检验是非参数统计方法中常用的一种方法,通常用于比较三个或三个以上相关样本的均值是否存在显著差异。
在实际应用中,需要注意一些使用的注意事项,以确保结果的准确性和可靠性。
样本的选择在使用Friedman秩和检验时,首先要确保所选择的样本符合相关性的要求。
即各组之间的样本是相关的,例如同一组受试者在不同时间点或不同条件下的观测值。
如果样本之间不存在相关性,则不适合使用Friedman秩和检验。
另外,样本的大小也要足够大,以确保检验结果的可靠性。
数据的测量其次,在进行Friedman秩和检验时,需要对数据的测量方式进行仔细考量。
确保所采用的测量方式是准确且可靠的,否则将会影响到检验结果的有效性。
同时,还要注意统计分析中是否存在异常值或缺失值,需要进行必要的处理。
检验的假设条件Friedman秩和检验是基于一些假设条件进行的,包括独立性、同方差性和正态性等。
在进行检验之前,需要对这些假设条件进行检查,以确保所得到的结论是可靠的。
如果假设条件不成立,可能需要采用其他的统计方法进行分析。
多重比较的问题在进行Friedman秩和检验之后,通常需要进行多重比较来确定具体哪些组之间存在显著差异。
在进行多重比较时,需要注意选择合适的校正方法,以控制错误发现率。
常用的方法包括Bonferroni校正、Tukey校正等,选择合适的校正方法对结果的解释非常重要。
结果的解释与报告最后,在得到Friedman秩和检验的结果后,需要对结果进行合理的解释和报告。
除了报告检验的统计值和显著性水平外,还需要对检验结果进行实际意义的解释,以便读者能够清晰地理解结果的含义。
另外,还要对检验结果的局限性和可能存在的偏差进行说明。
结论Friedman秩和检验是一种常用的非参数统计方法,适用于比较三个或三个以上相关样本的均值是否存在显著差异。
在使用该方法时,需要注意样本的选择、数据的测量、假设条件的检查、多重比较的问题以及结果的解释与报告等方面。
friedman秩和检验原理
friedman秩和检验原理
Friedman检验,也被称为Friedman双向秩方差分析,是一种用于多个配对样本的非参数检验方法。
其原理假设是多个配对样本来自的多个总体分布无显著差异。
Friedman检验的基本步骤如下:
将每个样本在各个组别中的观察值按照从小到大的顺序进行排序,并赋予相应的秩次。
如果有相同的观察值,则平分秩次。
计算各个组别的平均秩次,即将每个组别中的所有样本的秩次相加,然后除以样本数。
计算Friedman统计量,该统计量反映了各个组别的平均秩次之间的差异。
计算Friedman检验的P值,该值表示观察到的数据与原假设之间的差异程度。
如果P值小于给定的显著性水平(通常为0.05),则拒绝原假设,认为各个组别的分布存在显著差异。
总之,Friedman检验是一种利用秩实现对多个总体分布是否存在显著差异的非参数检验方法。
通过比较各个组别的平均秩次,可以判断多个配对样本来自的多个总体的分布是否存在显著差异。
friedman秩和检验临界值表
根据您的要求,我会深入探讨friedman秩和检验临界值表这个主题。
让我们来了解一下什么是friedman秩和检验。
friedman秩和检验是一种用于检验多组相关样本均值是否相同的非参数检验方法。
在实际应用中,我们经常需要比较多组相关样本的均值,例如在医学研究中比较不同药物对同一个疾病的疗效,或者在教育研究中比较不同教学方法对学生成绩的影响等等。
而friedman秩和检验可以有效地应用于这些问题的研究中。
接下来,让我们来看一下friedman秩和检验的临界值表。
在进行friedman秩和检验时,我们需要根据样本量和显著水平来确定临界值。
临界值表提供了在不同样本量和显著水平下,所对应的临界值以及拒绝域的边界。
通过查阅临界值表,我们可以判断我们的检验统计量是否落在拒绝域内,从而进行假设检验的判断。
在实际撰写文章时,我会首先从介绍friedman秩和检验的原理和应用场景开始,然后引入相关的临界值表。
我会逐步深入讨论临界值表的内容,包括不同样本量和显著水平下的具体数值,以及如何根据临界值表来进行假设检验的步骤和方法。
在文章的结尾部分,我会对整个主题进行回顾性的总结,总结出各种情况下应该如何应用friedman秩和检验临界值表,以及我个人对这个主题的理解和观点。
文章中会反复提及friedman秩和检验临界值表,以确保您能够全面、深入地理解这个主题。
文章的总字数将超过3000字,并且会采用普通文本的格式,遵循知识文章的格式要求。
希望这篇文章能够帮助您更好地理解friedman秩和检验临界值表这个主题。
现在,我将开始着手撰写这篇文章,以满足您的要求。
谢谢!Friedman秩和检验临界值表是进行非参数检验时非常重要的工具。
在统计学中,非参数检验是一种不对总体分布进行假设的检验方法,通常用于不满足正态性、独立性和方差齐性等假设条件的数据。
Friedman秩和检验就是一种典型的非参数检验方法,它适用于比较多组相关样本的均值,并且不对总体分布进行具体假设。
4.5 完全区组设计:Friedman 秩和检验
B 3 5 10 3 4 4 10 10 5 9 4 5 5 5
C 6 9 3 10 10 6 6 3 7 7 2 4 10 8
D 8 4 8 4 6 7 5 5 6 6 6 7 9 10
1 2 3 4 5 6 7 8 9 10 11 12 13 14
试问在5%的显著性水平下四个部分技术训练的有效性有无 显著差异?
接下来的做法与 Kruskal Wallis 检验相同. 计算处理平方和(SSt )
k b 2 k 2 i 1 j 1 k i 1
SSt ( Ri R ) b (Ri R ) Ri2 b R2 bk
i 1 2 R i i 1
大样本时基于 Friedman 秩和检验的一个方法.
如果零假设 H 0 为 i 处理和 j 处理没有区别, 那么,双边检验的统计量为 Ri R j .
对于置信水平 ,如果 Ri R j Z * 2 bk (k 1) / 6, 则拒绝零假设,这里 *
总共可比较的对数
在表中加上各处理在每个区组(职业) 中的秩,得
区组(职业) 处理(城市)
I 80(3) 52(2) 40(1)
II 100(3) 76(2) 52(1)
III 51(2) 52(3) 34(1)
IV 65(3) 53(2) 35(31)
Ri 11 9 4
A B C
Q 由此算出 Q 6.5, 对于 k 3 和 b 4,W 0.815. 4 3 1
2 当 Q (k 1) 时,在水平 上拒绝 H 0; 2 当 Q (k 1) 时,不能拒绝 H 0 .
当数据有相同秩时,秩取平均值, 在某区组存在结时,此时需要对 Q 统计量进行修正: Q Qc . k b ( i3, j i , j ) 1 i 1 j 1 2 bk (k 1) 其中 i , j 为第 j 个区组的第 i 个结统计量 .
4.5 完全区组设计:Friedman 秩和检验解析
k
b
k 1 k 1 . 12
• Friedman 检验统计量 Q 为: SSt 12 k 2 2 Q Ri b bk (k 1) 4 . Var Rij (k 1)(k 1) i 1
• Friedman 建议用 k 1 k 乘 Q 得校正式 Q.
k 个样本是匹配的,可以由 k 个条件下同一组受试者构成, 也可以将受试者分为 n 组,每组均有 k 个匹配的受试者, 随机地将 n 组受试者置于 k 个条件下.
在不同受试者匹配的样本中,应尽量使不同受试者的有关 因素匹配即相似.
1. 建立假设检验
假设检验问题:
H0 : 1 2 ... k H1 : 不是所有的位置参数都相等.
3. 作出决策
对于有限的 k 和 b,有零假设下的分布表可查, Q 查的时候要作变换 W . b k 1
当查不到时,可用自由度为 k 1的 2 分布近似. 对于固定的 k,当 b 时,在零假设下有 Q ~ 2 (k 1).
4. 小结
检验步骤: ( 1 )提出假设 H 0: k 个样本间无显著差异. H1: k 个样本间有显著差异. (2)计算检验统计量 Q. (3)作出决策
2 当 Q (k 1) 时,在水平 上拒绝 H 0; 2 当 Q (k 1) 时,不能拒绝 H 0 .
当数据有相同秩时,秩取平均值, 在某区组存在结时,此时需要对 Q 统计量进行修正: Q Qc . k b ( i3, j i , j ) 1 i 1 j 1 2 bk (k 1) 其中 i , j 为第 j 个区组的第 i 个结统计量 .
Friedman 检验统计量为:
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Ranks
Mean Rank
ci ty1
2.75
ci ty2
2.25
ci ty3
1.00
概率论
Test Statistics a
N
4
Chi-Sq uare
6.500
df
2
Asymp. Sig.
.039
Exact Sig.
.042
Point Probability
.037
a. FriedmanTest
职业(区组)
1
2
3
*4
A
80
100
51
65
城B
52
34
35
问三个城市的血铅含量是否一样?
概率论
Descriptive Statistics
N MeSatnd. DeviaMtiionnimM um aximum city1 744.000200.99206 51.00100.00 city2 548.250101.84272 52.00 76.00 city3 440.25008.26136 34.00 52.00
概率论
4.检验统计量:
概率论
Qbk(1k21)i k( 1 Rib(K 21))2
12
bk(k1)
k
R2i3b(k1)
i1
对 于 固 定 的 k , 当 b 时 , 在 原 假 设 下 , Q :2 ( k 1 )
拒绝域的形式: {Q c)
问题 :在不同的城市对不同的人群进行血液中铅概的率论 含量测试;一共有A,B,C三个汽车密度不同的城市 代表着三种不同的处理,对试验者按职业分四组取 血,他们血中铅的含量列在下表中:
问题 :在不同的城市对不同的人群进行血液中铅概的率论 含量测试;一共有A,B,C三个汽车密度不同的城市 代表着三种不同的处理,对试验者按职业分四组取 血,他们血中铅的含量列在下表中:
职业(区组)
1
2
3
*4
A
80
100
51
65
城B
52
76
52
53
市C
40
52
34
35
问三个城市的血铅含量是否一样?
概率论
