截面的静矩和形心位置
惯性矩、静矩,形心坐标公式
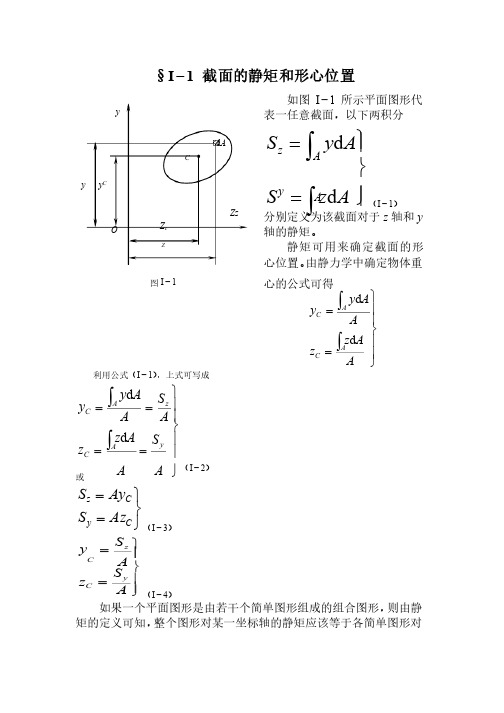
§I −1 截面的静矩和形心位置如图I −1所示平面图形代表一任意截面,以下两积分表一任意截面,以下两积分ïþïýü==òòA z S A y S A y Az d d (I −1)分别定义为该截面对于z 轴和y 轴的静矩。
轴的静矩。
静矩可用来确定截面的形心位置。
由静力学中确定物体重心的公式可得心的公式可得ïïþïïýü==òòA A z z A A y y AC ACd d利用公式(I −1),上式可写成,上式可写成ïïþïïýü====òòA S A A z z A SA Ay y y A C z A C d d (I −2) 或þýü==C y C z Az S Ay S (I −3)ïïþïýü==A S z A S y y C z C(I −4)如果一个平面图形是由若干个简单图形组成的组合图形,则由静矩的定义可知,整个图形对某一坐标轴的静矩应该等于各简单图形对d A C Zz y y y C Z c O 图I −1 Z 同一坐标轴的静矩的代数和。
即:同一坐标轴的静矩的代数和。
即:ïïþïïýü==åå==ni ci i y ni ci i z z A S y A S 11(I −5)式中A i 、y ci 和z ci 分别表示某一组成部分的面积和其形心坐标,n 为简单图形的个数。
单图形的个数。
将式(I −5)代入式(I −4),得到组合图形形心坐标的计算公式为ïïïïïþïïïïýü==åååå====ni ini c iic ni ini c i i c AzA z A y A y 1111(I −6)例题I −1 图a 所示为对称T 型截面,求该截面的形心位置。
惯性矩、静矩,形心坐标公式
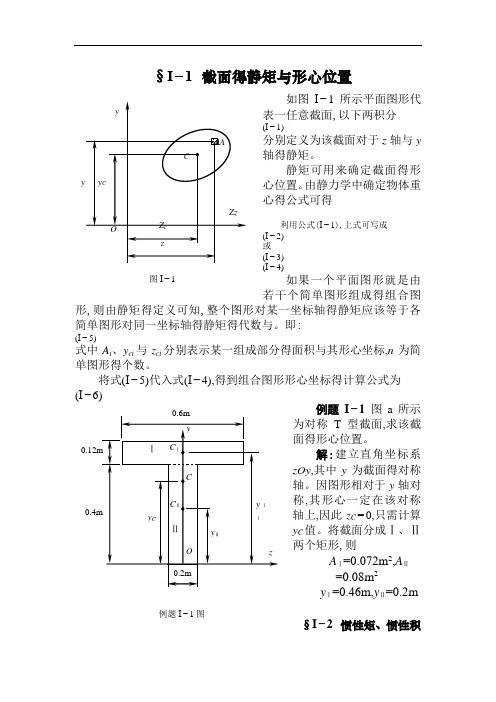
§I−1 截面得静矩与形心位置如图I −1所示平面图形代表一任意截面,以下两积分(I −1)分别定义为该截面对于z 轴与y 轴得静矩。
静矩可用来确定截面得形心位置。
由静力学中确定物体重心得公式可得利用公式(I −1),上式可写成 (I −2) 或 (I −3) (I −4)如果一个平面图形就是由若干个简单图形组成得组合图形,则由静矩得定义可知,整个图形对某一坐标轴得静矩应该等于各简单图形对同一坐标轴得静矩得代数与。
即:(I −5)式中A i 、y ci 与z ci 分别表示某一组成部分得面积与其形心坐标,n 为简单图形得个数。
将式(I −5)代入式(I −4),得到组合图形形心坐标得计算公式为 (I −6)例题I −1 图a 所示为对称T 型截面,求该截面得形心位置。
解:建立直角坐标系zOy ,其中y 为截面得对称轴。
因图形相对于y 轴对称,其形心一定在该对称轴上,因此z C =0,只需计算y C 值。
将截面分成Ⅰ、Ⅱ两个矩形,则 A Ⅰ=0.072m 2,A Ⅱ=0.08m 2y Ⅰ=0.46m,y Ⅱ=0.2m§I −2 惯性矩、惯性积例题I −1图图I −1与极惯性矩如图I −2所示平面图形代表一任意截面,在图形平面内建立直角坐标系zOy 。
现在图形内取微面积d A ,d A 得形心在坐标系zOy 中得坐标为y 与z ,到坐标原点得距离为ρ。
现定义y 2d A 与z 2d A 为微面积d A 对z 轴与y 轴得惯性矩,ρ2d A 为微面积d A 对坐标原点得极惯性矩,而以下三个积分(I −7)分别定义为该截面对于z 轴与y 轴得惯性矩以及对坐标原点得极惯性矩。
由图(I −2)可见,,所以有(I −8) 即任意截面对一点得极惯性矩,等于截面对以该点为原点得两任意正交坐标轴得惯性矩之与。
另外,微面积d A 与它到两轴距离得乘积zy d A 称为微面积d A 对y 、z 轴得惯性积,而积分(I −9)定义为该截面对于y 、z 轴得惯性积。
截面的形心静矩

形心静矩具有方向性,其方向与形心 位置有关。
形心静矩的应用
01
在结构设计中,形心静矩可用于计算截面的抗弯能 力,从而评估结构的稳定性。
02
在机械设计中,形心静矩可用于计算转动惯量,从 而评估机械设备的动态性能。
03
在船舶与海洋工程中,形心静矩可用于计算浮力与 稳性,确保船舶的安全航行。
03
截面形心静矩的计算
截面形心静矩与其他力学性能的关系研究
总结词
材料属性影响
详细描述
材料属性对截面形心静矩的影响也是未来的 研究方向之一。研究不同材料属性(如弹性 模量、泊松比等)对截面形心静矩的影响规 律,有助于更好地理解材料的力学行为,并 为新型材料的开发和优化提供理论支持。
截面形心静矩在新型材料和结构中的应用研究
05
截面形心静矩的未来研究 方向
截面形心静矩的优化计算方法
总结词
优化计算方法
详细描述
随着计算机技术的不断发展,截面形心静矩的优化计算方法成为了一个重要的研究方向。目前,研究 者们正在探索更高效、精确的数值计算方法,以解决复杂截面形状和材料属性对形心静矩计算的影响 。
截面形心静矩的优化计算方法
总结词
截面的形心静矩
contents
目录
• 截面形心静矩的定义 • 截面形心静矩的性质 • 截面形心静矩的计算 • 截面形心静矩的实例分析 • 截面形心静矩的未来研究方向
01
截面形心静矩的定义
形心
定义
形心是截面图形的几何中心,通 常用于描述截面的质量分布情况 。
计算方法
对于规则图形,形心位置可以通 过几何计算得出;对于不规则图 形,可以通过积分计算得出。
详细描述
对于圆形截面,形心静矩可以通过以 下公式计算:$I = frac{pi d^4}{64}$, 其中$d$为截面的直径。这个公式适 用于圆形截面,其中形心静矩表示截 面对其轴线的惯性矩。
材料力学课件-10截面的静矩和形心位置

静矩在结构设计中的应用
抗弯设计
在结构设计时,需要考虑到截面的抗弯能力。静矩是计算 抗弯能力的重要参数,通过计算截面的静矩,可以确定截 面的抗弯刚度,从而优化结构设计。
稳定性分析
在分析结构的稳定性时,静矩也是一个重要的参数。通过 比较不同截面的静矩,可以判断结构的稳定性,并优化截 面设计。
材料选择
优化设计
通过深入了解静矩和形心位置, 可以更好地优化结构设计,提高 结构的稳定性和安全性践
静矩和形心位置不仅是理论上的 概念,更是指导实践的重要工具 。在实际工程中,这些概念的应 用有助于确保结构的可靠性和安 全性。
THANK YOU
感谢观看
静矩的计算方法
直接积分法
适用于规则截面,通过积分计算得到静矩。
表格法
根据已知的规则截面尺寸和载荷分布,查找表格 中的静矩值。
近似法
对于不规则截面,可以采用近似法估算静矩值。
静矩的性质
静矩具有方向性
根据右手定则判断矩心的方向。
静矩与截面尺寸和形状有关
不同尺寸和形状的截面具有不同的静矩值。
静矩是内力分布的面积分
03
位置,形心位置与截面的形状密切相关。
截面尺寸对形心位置的影响
01
同一形状的截面,尺寸不同时,其形心位置也会发生变化 。
02
例如,矩形截面长度和宽度不同时,其形心位置会有所偏 移。
03
截面尺寸对形心位置的影响:同一形状的截面,尺寸不同时, 其形心位置也会发生变化,但总是位于截面的面积中心。
04
在选择材料时,静矩也是重要的参考因素。不同材料的截 面静矩不同,选择合适的材料可以保证结构的稳定性和安 全性。
形心位置在结构设计中的应用
材料力学 截面的几何性质

1、矩形截面 h
Iz
y2dA
A
2 h
y 2bdy
h
2
dy y
b y 3 2 1 bh3 3 h 12
2
同理
Iy
z2dA 1
A
12
hb3
b h z
y
26
2、实心圆截面
y
已知
IP
A2dA
D 4 32
D
z
则 I P A2 d A A y 2 d A A z 2 d I A z I y
A
Iz Iy
此式说明了极惯性矩与轴惯性矩之间的关系。
z
y
o
A dA
z
y
惯性积
定义
Iyz
yzdA
A
z y
A dA
为图形对y、z轴的惯性积 。
z
o
y
惯性积的数值可正,可负,也可为零。惯性积的量纲是[长 度]4 ,常用单位为m4和mm4。
定理:若有一个轴是图形的对称轴,则图形对这对轴 的惯性积必然为零。
4.3 形心主惯性轴和形心主惯性矩
若主惯性轴通过形心,则该轴称为形心主惯性轴(principal centroidal axis)。
图形对形心主惯性轴的惯性矩称为形心主惯性矩。 由于图形对于对称轴的惯性积等于零,而对称轴又过形心,所以,图形 的对称轴就是形心主惯性轴。
形心主惯性轴的特点可归纳为以下几点: ⑴形心主惯性轴是通过形心,由角定向的一对互 相垂直的坐标轴。
32
32
圆环形对y(或z)轴的惯性矩为
IyIz1 2Ip6 D4414
由于y轴为对称轴,故
Iyz 0
z
y
d D
截面的静矩和形心位及惯性矩的计算
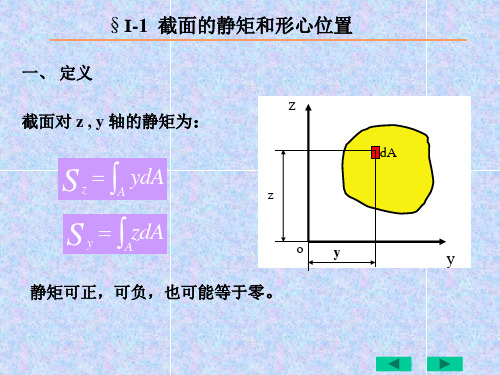
y
dA
x
x 0
截面对 x , y 轴的惯性积为
Ixy A xydA
惯性矩的数值恒为正,惯性积则可能为正值,负值,
也可能等于零。
y
若 x , y 两坐标轴中有一个为
dA y
截面的对称轴,则截面对 x , y 轴的 惯性积一定等于零 。
dx dx x
截面对 x , y 轴的惯性半俓为
iy
Z1 80 Z2 0
所以截面的形心坐标为
ZC
A1 Z1 A1
A2 Z2 A2
46.7mm
20 140
zc
20
1
yc
ZC
2
y
100
I1yC
1 12
20 1403
20 140
(8046.7)2
I
2 yC
1 12
100
203
100
20
(46.7)2
zc
120 103 152 120 10
1 12
703
10
(25)2
70
10
100.4 104 mm 4
Iy 278.4 104 mm4
70 20 10
120
y
80
c
x
10
y
I xy 0 15 20 120 10 0 (25) (35) 70 10
x2
10
70 2
45mm
y2 5mm
y 10
1 x1
y1
截面的静矩和形心位置及惯性矩的计算

x 0
截面对 x , y 轴的惯性积为
Ixy A xydA
惯性矩的数值恒为正,惯性积则可能为正值,负值,
也可能等于零。
y
若 x , y 两坐标轴中有一个为
dA y
截面的对称轴,则截面对 x , y 轴的 惯性积一定等于零 。
dx dx x
截面对 x , y 轴的惯性半俓为
iy
Iy , A
二 、 截面的主惯性轴和主惯性矩
I x1y1
Ix
2
Iy
sin 2α
I xy cos 2α
主惯性轴 —— 总可以找到一个特定的角 0 , 使截面对新坐标 轴 x0 , y0 的惯性积等于 0 , 则称 x0 , y0 为主惯轴。
主惯性矩——截面对主惯性轴的惯性矩。
形心主惯性轴 ——当一对主惯性轴的交点与截面的形心 重合时,则称为形心主惯性轴。
x
80
§ І -2 极惯性矩 惯性矩 惯性积
定义:
z dA
z
截面对 o 点的极惯性矩为
y
Ip Aρ2dA
y 0
截面对 y ,z 轴的惯性矩分别为
Iy A z2dA Iz A y2dA
因为 ρ2 y2 z2
I p Aρ2 dA
所以 Ip = Ix + Iy
y
y
dA
ix
Ix A
例 2 _ 1 求矩形截面对其对称轴 x , y 轴的惯性矩。
解:
dA = b dy
Ix
A y2dA
h
2h
by2dy
2
bh3 12
Ix A y2dA
惯性矩、静矩,形心坐标公式

惯性矩、静矩,形心坐标公式-CAL-FENGHAI.-(YICAI)-Company One1§I?1 截面的静矩和形心位置如图I ?1所示平面图形代表一任意截面,以下两积分⎪⎭⎪⎬⎫==⎰⎰A z S A y S A y Az d d (I ?1)分别定义为该截面对于z 轴和y 轴的静矩。
静矩可用来确定截面的形心位置。
由静力学中确定物体重心的公式可得⎪⎪⎭⎪⎪⎬⎫==⎰⎰A A z z A A y y AC A Cd d利用公式(I ?1),上式可写成⎪⎪⎭⎪⎪⎬⎫====⎰⎰A S A A z z A S A Ay y y AC z A C d d (I ?2)或⎭⎬⎫==C y C z Az S Ay S (I ?3)⎪⎪⎭⎪⎪⎬⎫==A S z A S y yCz C (I ?4)图I ?1如果一个平面图形是由若干个简单图形组成的组合图形,则由静矩的定义可知,整个图形对某一坐标轴的静矩应该等于各简单图形对同一坐标轴的静矩的代数和。
即:⎪⎪⎭⎪⎪⎬⎫==∑∑==ni ci i y ni ci i z z A S y A S 11(I ?5)式中A i 、y ci 和z ci 分别表示某一组成部分的面积和其形心坐标,n 为简单图形的个数。
将式(I ?5)代入式(I ?4),得到组合图形形心坐标的计算公式为⎪⎪⎪⎪⎪⎭⎪⎪⎪⎪⎪⎬⎫==∑∑∑∑====ni i ni ci i c ni i ni ci i c A z A z A y A y 1111(I ?6)例题I ?1 图a 所示为对称T 型截面,求该截面的形心位置。
解:建立直角坐标系zOy ,其中y 为截面的对称轴。
因图形相对于y 轴对称,其形心一定在该对称轴上,因此z C =0,只需计算y C 值。
将截面分成Ⅰ、Ⅱ两个矩形,则A Ⅰ=0.072m 2,A Ⅱ=0.08m 2y Ⅰ=0.46m ,y Ⅱ=0.2m例题I ?1图m323.008.0072.02.008.046.0072.0III II II I I 11=+⨯+⨯=++==∑∑==A A y A y A AyA y ni ini cii c§I ?2 惯性矩、惯性积和极惯性矩如图I ?2所示平面图形代表一任意截面,在图形平面内建立直角坐标系zOy 。
