空间几何体测试题
空间几何体测试题

空间几何体测试题一、选择题1、下列说法中正确的是( )A.棱柱的侧面可以是三角形B.正方体和长方体都是特殊的四棱柱C.所有的几何体的表面都能展成平面图形D.棱柱的各条棱都相等2、将一个等腰梯形绕着它的较长的底边所在的直线旋转一周,所得的几何体包括( ) A.一个圆台、两个圆锥 B.两个圆台、一个圆柱 C.两个圆台、一个圆柱 D.一个圆柱、两个圆锥 3、过球的一条半径的中点,作垂直于该半径的平面,则所得截面的面积与球的表面积的比为( ) A. B. C. D.4、如图所示的直观图是将正方体模型放置在你的水平视线的左上角而绘制的,其中正确的是( )5、长方体的高等于h,底面积等于S,过相对侧棱的截面面积为S′,则长方体的侧面积等于( ) A. B. C. D. 6、设长方体的对角线长度是4,过每一顶点有两条棱与对角线的夹角都是60?,则此长方体的体积是( ) A. B. C. D.7、棱锥被平行于底面的平面所截,当截面分别平分棱锥的侧棱、侧面积、体积时,相应的截面面积分别为S、S、S,则( ) 123A.S,S,SB.S,S,SC.S,S,SD.S,S,S 1233212131328、正四面体的内切球球心到一个面的距离等于这个正四面体高的( )A. B. C. D.9、若圆台两底面周长的比是1?4,过高的中点作平行于底面的平面,则圆台被分成两部分的体积比是( ) A.1?16 B.3?27 C.13?129 D.39?12910、在棱长为1的正方体上,分别用过共顶点的三条棱中点的平面截该正方体,则截去8个三棱锥后,剩下的凸多面体的体积是( )A. B. C. D.11、已知高为3的直棱柱ABCABC的底面是边长为1的正三角形(如图),则三棱锥B-ABC的体积为( ) 1111A. B. C. D.12、向高为H的水瓶中注水,注满为止.如果注水量V与水深h的函数关系如图,那么水瓶的形状是图中的( )二、填空题1、下列有关棱柱的说法:?棱柱的所有的面都是平的;?棱柱的所有的棱长都相等;?棱柱的所有的侧面都是长方形或正方形;?棱柱的侧面的个数与底面的边数相等;?棱柱的上、下底面形状、大小相等(正确的有__________.2、一个横放的圆柱形水桶,桶内的水占底面周长的四分之一,那么当桶直立时,水的高度与桶的高度的比为_________.3、一个正三棱柱的三视图如图所示,则这个正三棱柱的表面积为_________.4、一圆台上底半径为5 cm,下底半径为10 cm,母线AB长为20 cm,其中A 在上底面上,B在下底面上,从AB中点M,拉一条绳子,绕圆台的侧面一周转到B 点,则这条绳子最短长为____________.三、解答题1、画出图中两个几何体的三视图.2、在图中,M、N是圆柱体的同一条母线上且位于上、下底面上的两点,若从M点绕圆柱体的侧面到达N,沿怎么样的路线路程最短,3、倒圆锥形容器的轴截面是正三角形,内盛水的深度为6 cm,水面距离容器口距离为1 cm,现放入一个棱长为4 cm的正方体实心铁块,让正方体一个面与水平面平行,问容器中的水是否会溢出,4、棱长为2 cm的正方体容器盛满水,把半径为1 cm的铜球放入水中刚好被淹没.然后再放入一个铁球,使它淹没水中,要使流出来的水量最多,这个铁球的半径应该为多大,5、小迪身高1.6 m,一天晚上回家走到两路灯之间,如图所示,他发现自己的身影的顶部正好在A路灯的底部,他又向前走了5 m,又发现身影的顶部正好在B 路灯的底部,已知两路灯之间的距离为10 m,(两路灯的高度是一样的)求:(1)路灯的高度. (2)当小迪走到B路灯下,他在A路灯下的身影有多长,6、如图,在透明塑料做成的长方体容器中灌进一些水,固定容器的一边将其倾倒,随着容器的倾斜度不同,水的各个表面的图形的形状和大小也不同.试尽可能多地找出这些图形的形状和大小之间所存在的各种规律(不少于3种).。
(完整版)空间几何体练习题含答案
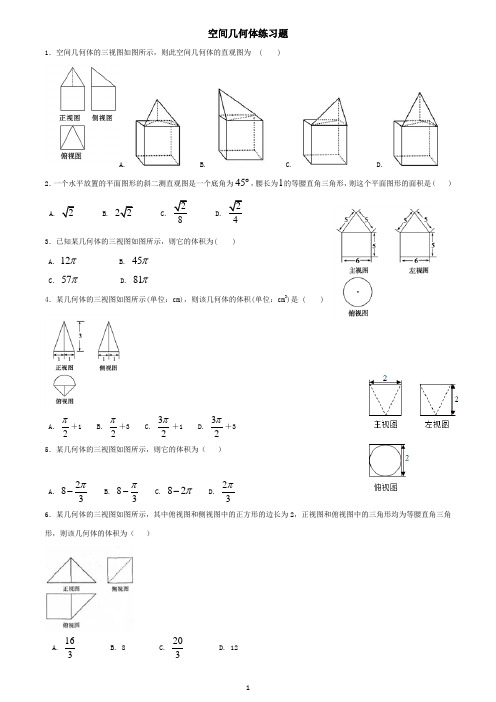
空间几何体练习题1.空间几何体的三视图如图所示,则此空间几何体的直观图为 ( )A. B. C. D.2.一个水平放置的平面图形的斜二测直观图是一个底角为45︒,腰长为1的等腰直角三角形,则这个平面图形的面积是( ) A. 2 B. 22 C. 28 D. 243.已知某几何体的三视图如图所示,则它的体积为( )A. 12πB. 45πC. 57πD. 81π4.某几何体的三视图如图所示(单位:cm),则该几何体的体积(单位:cm 3)是 ( )A. 2π+1B. 2π+3C. 32π+1D. 32π+35.某几何体的三视图如图所示,则它的体积为( )A. 283π- B. 83π- C. 82π- D. 23π6.某几何体的三视图如图所示,其中俯视图和侧视图中的正方形的边长为2,正视图和俯视图中的三角形均为等腰直角三角形,则该几何体的体积为( )A. 163B. 8C. 203D. 127.某空间几何体的三视图如图所示,则该几何体的体积为()A. 16+2πB. 16+πC. 8+πD. 8+2π8.某空间几何体的三视图如图所示,则该几何体的体积为()A. 4B. 6C. 8D. 169.将棱长为2的正方体削成一个体积最大的球,则这个球的体积为( )A. 163π B.43πC.323π D. 4π10.如图是三棱锥D ABC-的三视图,则该三棱锥的外接球体积为( )A. 92πB.33πC. 62πD.23π11.某空间几何体的正视图是三角形,则该几何体不可能是( )A. 圆锥B. 圆柱C. 四面体D. 三棱锥12.若一个正三棱柱的三视图如下图所示,则这个正三棱柱的高和底面边长分别为().A. 2,22B. 2,4C. 23,2D. 4,313.某几何体的三视图如图所示,则该几何体的表面积是()A.322++ B.5322++ C.332++ D.7322++14.一个球的内接正方体的表面积为54,则球的表面积为( )A. 27πB. 18πC. 19πD. 54π15.将一个直角边长为1的等腰直角三角形绕其一条直角边旋转一周所形成几何体的侧面积为( )A. 4πB. 22πC. 2πD. 2π16.把球的表面积扩大到原来的2倍,那么体积扩大到原来的( )A. 2倍B. 22倍C. 2倍D. 32倍17.如果一个几何体的主视图与左视图是全等的长方形,边长分别是4,2,如图所示,俯视图是一个边长为4的正方形.(1)求该几何体的表面积;(2)求该几何体的外接球的体积.18.如图是一建筑物的三视图(单位:m),现需将其外壁用油漆粉刷一遍,已知每平方米用漆0.2kg,问需要油漆多少千克?(无需求近似值)cm. 19.一个棱柱的侧面展开图是三个全等的矩形,矩形的长和宽分别为6cm,4cm,则该棱柱的侧面积为________2 20.一个几何体的三视图如图所示,则该几何体的体积为______.21.一个几何体的三视图如图所示,则该几何体的表面积为_______.22.体积为52的圆台,一个底面积是另一个底面积的9倍,那么截得这个圆台的圆锥的体积是________.23.已知正三棱锥的高为1,底面边长为26,则该三棱锥的表面积为________.-的所有棱长都为2,则该三棱锥的外接球的表面积为________.24.已知三棱锥A BCD25.若正三棱锥的底面边长为3,侧棱长为2,则其外接球的表面积为__________.26.已知高与底面直径之比为2:1的圆柱内接于球,且圆柱的体积为500π,则球的体积为________.cm).27.某几何体的三视图如图所示(单位:cm),则该几何体的体积是_____(单位:3参考答案1.A2.A3.C4.A5.A6.C7.D8.C9.B10.A11.B12.B13.D14.A15.C16.B17.(1)64;(2)36π.18.()()4.87.8kg π+19.7220.2π321.5π22.5423.24.3π25.4π26π+27.12。
(完整版)空间几何体练习题含答案
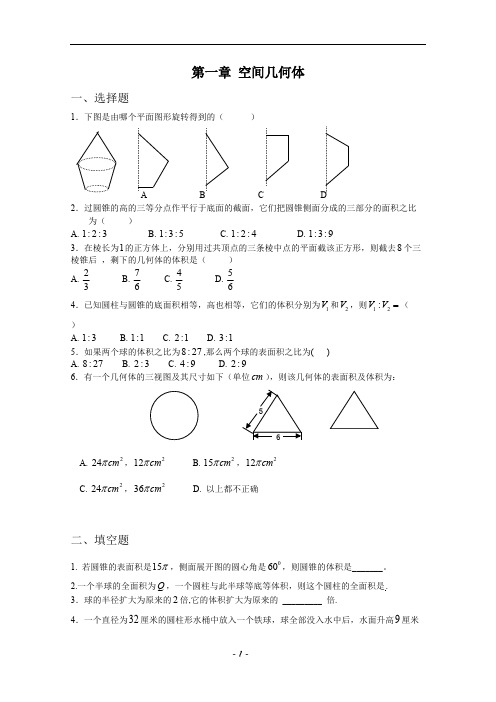
第一章空间几何体一、选择题1.下图是由哪个平面图形旋转得到的()A B C D2.过圆锥的高的三等分点作平行于底面的截面,它们把圆锥侧面分成的三部分的面积之比为()A. B. C. D.1:2:31:3:51:2:41:3:93.在棱长为的正方体上,分别用过共顶点的三条棱中点的平面截该正方形,则截去个三18棱锥后,剩下的几何体的体积是()A. B. C. D.237645564.已知圆柱与圆锥的底面积相等,高也相等,它们的体积分别为和,则(1V2V12:V V=)A. B. C. D.1:31:12:13:15.如果两个球的体积之比为,那么两个球的表面积之比为( )8:27A. B. C. D.8:272:34:92:96.有一个几何体的三视图及其尺寸如下(单位),则该几何体的表面积及体积为:cmA. ,B. ,224cmπ212cmπ215cmπ212cmπC. ,D. 以上都不正确224cmπ236cmπ二、填空题1. 若圆锥的表面积是,侧面展开图的圆心角是,则圆锥的体积是_______。
15π0602.一个半球的全面积为,一个圆柱与此半球等底等体积,则这个圆柱的全面积是.Q3.球的半径扩大为原来的倍,它的体积扩大为原来的_________ 倍.24.一个直径为厘米的圆柱形水桶中放入一个铁球,球全部没入水中后,水面升高厘米329则此球的半径为_________厘米.5.已知棱台的上下底面面积分别为,高为,则该棱台的体积为___________。
4,163三、解答题1. (如图)在底半径为,母线长为的圆柱,求圆柱的表面积242.如图,在四边形中,,,,,ABCD 090DAB ∠=0135ADC ∠=5AB =CD =,求四边形绕旋转一周所成几何体的表面积及体积.2AD =ABCD AD参考答案一、选择题1.A 几何体是圆台上加了个圆锥,分别由直角梯形和直角三角形旋转而得2.B 从此圆锥可以看出三个圆锥,123123::1:2:3,::1:2:3,r r r l l l == 12312132::1:4:9,:():()1:3:5S S S S S S S S =--=3.D 111115818322226V V -=-⨯⨯⨯⨯⨯=正方体三棱锥4.D 121:():()3:13V V Sh Sh ==5.C 121212:8:27,:2:3,:4:9V V r r S S ===6.A 此几何体是个圆锥,23,5,4,33524r l h S πππ====⨯+⨯⨯=表面 2134123V ππ=⨯⨯=二、填空题1. 设圆锥的底面半径为,母线为,则,得,r l 123r l ππ=6l r =,得,圆锥的高226715S r r r r ππππ=+⋅==r =h =21115337V r h ππ==⨯=2. 109Q 22223,S R R R Q R πππ=+===全 32222221010,,2233339V R R h h R S R R R R Q πππππ==⋅==+⋅==3. 821212,8r r V V ==4. 12234,123V Sh r h R R ππ=====5. 28'11()(416)32833V S S h =++=⨯+⨯= 三、解答题1.解:圆锥的高,h ==1r =22(2S SS πππ=+=+=侧面表面底面 2.解:S S S S=++表面圆台底面圆台侧面圆锥侧面25(25)2πππ=⨯+⨯+⨯⨯⨯1)π=+ V V V=-圆台圆锥222112211()331483r r r r h r h πππ=++-=。
空间几何体单元测试+详答(实验班用)
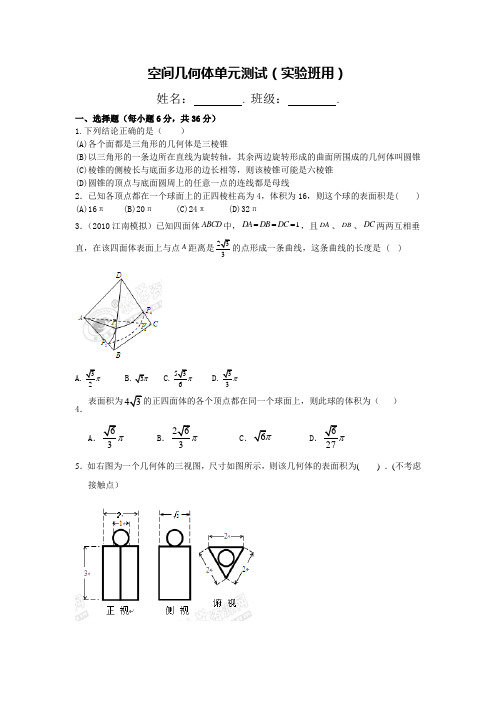
空间几何体单元测试(实验班用)姓名: .班级: .一、选择题(每小题6分,共36分)1.下列结论正确的是( )(A)各个面都是三角形的几何体是三棱锥(B)以三角形的一条边所在直线为旋转轴,其余两边旋转形成的曲面所围成的几何体叫圆锥(C)棱锥的侧棱长与底面多边形的边长相等,则该棱锥可能是六棱锥(D)圆锥的顶点与底面圆周上的任意一点的连线都是母线2.已知各顶点都在一个球面上的正四棱柱高为4,体积为16,则这个球的表面积是( )(A)16π (B)20π (C)24π (D)32π3.(2010江南模拟)已知四面体ABCD 中,1DA DB DC ===,且DA 、DB 、DC 两两互相垂直,在该四面体表面上与点A ( )4.表面积为 )A B C D 5.如右图为一个几何体的三视图,尺寸如图所示,则该几何体的表面积为( ) .(不考虑接触点)π4π+ D. 18+πC. 32π6.某几何体的一条棱长为,在该几何体的主视图中,这条棱的投影是长为的线段,在该几何体的左视图与俯视图中,这条棱的投影分别是长为a和b的线段,则a+b的最大值为________.二、填空题(每小题6分,共18分)7.如图所示两组立体图形都是由相同的小正方体拼成的。
(1)图(1)的正(主)视图与图(2)的___________相同.(2)图(3)的___________图与图(4)的___________图不同.8.一个几何体的三视图如图所示,则该几何体的体积等于_______.9.如图1,一个正四棱柱形的密闭容器水平放置,其底部镶嵌了同底的正四棱锥形实心装饰块,容器内盛有a升水时,水面恰好经过正四棱锥的顶点P.如果将容器倒置,水面也恰好过点P(图2).有下列四个命题:(A)正四棱锥的高等于正四棱柱高的一半;(B)将容器侧面水平放置时,水面也恰好过点P;(C)任意摆放该容器,当水面静止时,水面都恰好经过点P;(D)若往容器内再注入a升水,则容器恰好能装满.其中真命题的代号是:_____________(写出所有真命题的代号).三、解答题(10、11、12题每题12分,13题13分,共46分)10.如图所示,长方体ABCD—A′B′C′D′中,用截面截下一个棱锥C—A′DD′,求棱锥C —A′DD′的体积与剩余部分的体积之比.11.如图所示,半径为R的半圆内的阴影部分以直径AB所在直线为轴,旋转一周得到一几何体,求该几何体的表面积(其中∠BAC=30°).12.已知四面体的四个面都是边长分别是5、6、7的全等三角形,求这个四面体的体积。
空间几何体的综合计算测试题

空间几何体的综合计算测试题1. 综合计算题求以下空间几何体的表面积和体积:1.1 直方体已知直方体的长、宽、高分别为10 cm、6 cm、8 cm,求其表面积和体积。
解答:该直方体的表面积可通过公式2*(长×宽 + 长×高 + 宽×高)计算,代入数值计算得:表面积 = 2*(10 × 6 + 10 × 8 + 6 × 8) = 2*(60 + 80 + 48) = 376 cm²。
该直方体的体积可通过公式长×宽×高计算,代入数值计算得:体积 = 10 × 6 × 8 = 480 cm³。
1.2 正方体已知正方体的边长为5 cm,求其表面积和体积。
解答:该正方体的表面积可通过公式6×边长²计算,代入数值计算得:表面积 = 6×5² = 6×25 = 150 cm²。
该正方体的体积可通过公式边长³计算,代入数值计算得:体积 = 5³ = 125 cm³。
1.3 圆柱体已知圆柱体的底面半径为4 cm,高为10 cm,求其表面积和体积(π取3.14)。
解答:该圆柱体的表面积可分为两部分计算:侧面积和底面积。
侧面积可通过公式2×π×半径×高计算,代入数值计算得:侧面积 = 2×3.14×4×10 = 251.2 cm²。
底面积为圆的面积,可通过公式π×半径²计算,代入数值计算得:底面积 = 3.14×4² = 50.24 cm²。
因此,该圆柱体的表面积为251.2 + 50.24 = 301.44 cm²。
该圆柱体的体积可通过公式π×半径²×高计算,代入数值计算得:体积 = 3.14×4²×10 = 502.4 cm³。
(完整版)空间几何体测试题及答案,推荐文档

而 l12 l22 4a2 , 即152 52 92 52 4a2 , a 8, S侧面积 ch 4 8 5 160
7.D
V1
: V2
(Sh) : (1 3
Sh)
3:1
8.C
V1 :V2 8 : 27, r1 : r2 2 : 3, S1 : S2 4 : 9
9.A
二、10、 3 R3
、
、
的几何体构成的组合体.
13.正方体 ABCD A1B1C1D1 中, O 是上底面 ABCD 中心,若正方体的棱长为 a ,
则三棱锥 O AB1D1 的体积为____________ 三、解答题(每小题 13 分,共 26 分) 14.将圆心角为1200 ,面积为 3 的扇形,作为圆锥的侧面,求圆锥的表面积和体积
空间几何体测试题
(满分 100 分)
一、选择题(每小题 6 分,共 54 分)
1.有一个几何体的三视图如下图所示,这个几何体应是一个( )
A.棱台
B.棱锥
C.棱柱
D.都不对
主视图
左视图
俯视图
3.对于一个底边在 x 轴上的三角形,采用斜二测画法作出其直观图,其直观图面积是原三
角形面积的( )
A. 2 倍
C.1: 2
D.1:4
二、填空题(每小题 5 分,共 20 分) 10.半径为 R 的半圆卷成一个圆锥,则它的体积为________.
11.右面三视图所表示的几何体是
.
正视图
侧视图
俯视图
12.已知,ABCD 为等腰梯形,两底边为 AB,CD 且 AB>CD,绕 AB 所在的直线旋转一周
所得的几何体中是由
11、 2 :1 12、 六棱锥
空间几何体的体积与表面积测试题
空间几何体的体积与表面积测试题一、选择题(每题5分,共10题)1. 下列哪个几何体的体积公式不正确?A. 球体:V = (4/3)πr³B. 圆柱体:V=πr²hC. 圆锥体:V= (1/3)πr²hD. 正方体:V= a³2. 以下哪个几何体没有表面积?A. 圆柱体B. 球体C. 圆锥体D. 三棱柱3. 一个球体的直径为10cm,求其体积和表面积分别是多少?A. 523.6cm³, 314cm²B. 314cm³, 523.6cm²C. 523.6cm³, 628.3cm²D. 628.3cm³, 523.6cm²4. 一个立方体的边长为5cm,求其体积和表面积分别是多少?A. 125cm³, 150cm²B. 25cm³, 150cm²C. 125cm³, 100cm²D. 100cm³, 125cm²5. 以下哪个几何体的表面积公式不正确?A. 正方体:S = 6a²B. 圆柱体:S = 2πrh + 2πr²C. 球体:S = 4πr²D. 圆锥体:S = πrl + πr²6. 一个圆柱体的半径为4cm,高为10cm,求其体积和表面积分别是多少?A. 502.4cm³, 251.2cm²B. 100.48cm³, 251.2cm²C. 502.4cm³, 100.48cm²D. 100.48cm³, 502.4cm²7. 一个正方体的体积为64cm³,求其边长和表面积分别是多少?A. 8cm, 96cm²B. 4cm, 96cm²C. 8cm, 64cm²D. 4cm, 64cm²8. 一个圆锥体的半径为6cm,高为8cm,求其体积和表面积分别是多少?A. 301.4cm³, 301.4cm²B. 150.7cm³, 150.7cm²C. 301.4cm³, 200.96cm²D. 200.96cm³, 301.4cm²9. 下列哪个公式可以用来计算棱柱的体积?A. V = (1/3)πr²hB. V = (1/2)πr²hC. V = BhD. V = (1/3)Bh10. 一个棱柱的底面积为12cm²,高为8cm,求其体积是多少?A. 96cm³B. 84cm³C. 96cm²D. 84cm²二、解答题(每题15分,共2题)1. 一个正方体的表面积是96cm²,求其体积。
空间几何体练习题
空间几何体练习题一、选择题1. 下列几何体中,属于多面体的是:A. 球体B. 圆锥C. 立方体D. 圆柱2. 一个正方体的棱长为2,其表面积为:A. 12B. 24C. 36D. 483. 一个圆柱的底面半径为r,高为h,其体积公式为:A. πr^2hB. πr^2 + hC. 2πrhD. πrh4. 一个圆锥的底面半径为r,高为h,其体积公式为:A. 1/3πr^2hB. πr^2hC. πr^2 + hD. 1/3πrh5. 一个棱锥的底面积为S,高为h,其体积公式为:A. S*hB. S/hC. 1/3ShD. 3Sh二、填空题6. 一个长方体的长、宽、高分别为a、b、c,其体积公式为__________。
7. 一个正四面体的每个面都是等边三角形,其边长为a,其体积公式为_________。
8. 若一个圆锥的底面半径为2,高为3,则其体积为_________。
9. 若一个圆柱的底面半径为1,高为4,则其体积为_________。
10. 若一个棱锥的底面积为9,高为4,则其体积为_________。
三、简答题11. 描述如何计算一个正十二面体的体积。
12. 说明如何确定一个几何体是否为凸多面体。
13. 给出一个正二十面体的顶点数、边数和面数。
14. 解释什么是欧拉公式,并给出其在凸多面体中的表达形式。
15. 假设有一个棱柱,其底面为正六边形,高为h,求其体积公式。
四、计算题16. 一个棱柱,其底面为正三角形,边长为3,高为5,计算其体积。
17. 一个圆锥,其底面半径为4,高为6,计算其体积。
18. 一个圆柱,其底面半径为5,高为10,计算其表面积和体积。
19. 一个球体,其半径为7,计算其表面积和体积。
20. 一个棱锥,其底面为正六边形,边长为2,高为3,计算其体积。
五、证明题21. 证明一个正四面体的体积是其底面积与高的乘积的三分之一。
22. 证明欧拉公式V - E + F = 2对于所有凸多面体都成立,其中V 是顶点数,E是边数,F是面数。
空间几何体测试题打印版.doc
空间几何体测试题1、若一个三角形,采用斜二测画法作出其直观图,其直观图面积是原三角形面积的()丄V|A ★咅B〒倍 C 2倍D血倍2、一个圆柱的侧面展开图是一个正方形,这个圆柱的全面积与侧面积的比是()1 + 2龙 1 + 4龙 1 + 2龙 1 + 4龙A 2龙B 4龙C 7iD 2龙3、已知圆锥的母线长为8,底面圆周长为6®则它的体积是()A 9^55^ g g 755 Q 3^55^p 3^554、若圆台的上下底面半径分别是1和3,它的侧而积是两底面而积的2倍,则圆台的母线长是()A 2B 2.5C 5D 105、若圆锥的侧面展开图是圆心角为1200,半径为/的扇形,则这个圆锥的表面积与侧面积的比是()A 3: 2B 2: 1C 4: 36、如图,在棱长为4的正方体ABCD-A1B1C1D1 中,P 是A1B1 ±一点、,丄J@LPB1=4A1B1,则多面体P-BCC1B1的体积为()8 |6A 3 B亍7、两个平行于C 4 D 16圆锥底面的平面将圆锥的高分成相等的三部分,则圆锥被分成的三部分的体积的比是()A 1: 2: 3B 1: 7: 19C 3: 4: 5D 1: 9: 278、等边圆柱(轴截面是正方形)、球、正方体的体积相等,它们的表面积的大小关系是()A $正方体v *球v S圆柱B $球< $圆柱< S正方体c S岡柱v s球v S正方体 D $球v S正方体v S岡柱9、将一个等腰梯形绕着它的较长的底边所在的直线旋转一周,所得的几何体包括()A 一个圆台,两个圆锥B两个圆台、一个圆柱C两个圆台、一个圆柱 D —个圆柱、两个圆锥10、中心角为1350,面积为B的扇形围成一个圆锥,若圆锥的全面积为A,则A:B等于()A 11: 8B 3: 8C 8: 4D 13: 811、设正方体的表面积为24, —个球内切于该正方体,则这个球的体积为()32 h届 B 38 4-71 —71 C 3 D 312、若干毫升水倒入底面半径为2期的圆柱形器皿中,量得水面高度为6加,若将这些水倒入轴截面是正三角形的倒圆锥形器皿中,且恰好装满,则水面高度是()A 6迟cmB 6cmC 2V18cm 3V12cma13、64个直径都为忆的球,记它们的体积之和为⑰,表面积之和为S甲,一个直径为。
空间几何体测试题及答案
第六章空间几何体测试题一、选择题(15x4=60分)1、面数最少的多面体的顶点的个数为( B ) A 3 B 4 C 5 D 62、设集合M={正四棱柱},N={长方体},P={直四棱柱},Q={正方体},下列关系正确的是( D ) A Q M N P ⊃⊃⊃ B Q M N P ⊂⊂⊂ C Q N M P ⊃⊃⊃ D Q N M P ⊂⊂⊂3、下列命题正确的是( D ) A 三条侧棱相等的三棱锥是正三棱锥 B 侧面都是梯形的多面体是棱台C 平行于坐标轴的线段长度在直观图仍保持不变D 两点的球面距离就是过两点的大圆在这两点间的劣弧的长度 4、经过球面上两点的平面截球面所得的图形是( A ) A 圆 B 椭圆 C 三角形 D 正方形5、已知正方体的体积为64,则它的棱长为(B ) A 8 B 4 C 2 D 166、正三棱锥的底面边长为a ,高为2a ,则它的侧面积为( B )A24B 24C 2D 26a 7、正四棱台的上、下底面边长为分别为2、8,斜高为4,则它的侧面积为( B ) A 100 B 80 C 60 D 208、正三棱锥侧面都是直角三角形,其体积为3,则其底面边长为(B )A 1B 2C 3D 4 9、下面棱柱是正四棱柱的是( C )A 底面是正方形,有两个侧面是矩形B 底面是正方形,有两个侧面垂直于底面C 底面是矩形,两个相邻侧面分别是矩形和正方形D 四个侧面是全等的矩形 10、过球面上任意两点,可以做大圆的个数为( D )A 1个B 2个C 无数个D 1个或无数个 11、在斜棱柱的侧面中矩形最多有( A ) A 2个 B 3个 C 4个 D 6个12、正四棱锥的侧面是正三角形,则它的高与底面边长之比为( D )13、球的半径为2,则球的表面积与体积分别为( B ) A 4,8ππ B 3216,3ππ C 88,3ππ D 816,3ππ 14、圆锥的侧面展开图是半径为1,圆心角是270°的扇形,则它的底面积为( B ) A34π B 916π C 2116π D 316π15、长方体的长、宽、高的比为1:2:3,对角线长为,其体积为( C ) A 16 B 24 C 48 D 96 二、填空题:(5x4=20分)16、把一个圆锥截成圆台,已知圆台的上、下底面半径比为1:3,母线长为10,则圆锥的母线长为_15___.17、球的体积与其表面积的数值相等,则球的半径为___3______________. 18、正六棱柱的底面边长为2,高为2,则其体积为19、用一张长宽分别为8cm 与4cm 的矩形硬纸板,折成正四棱柱的侧面,则此四棱柱的对角线长为20、正方体的体积为64,它的全面积为_____96____________ 三、解答题:(2x10=20分)21、如果一个正三棱锥的底面边长为6解:S 底=26⨯=在直角三角形SMB 中'h = ∴S 侧 =1236⨯⨯= S 全= S 底 + S 侧 =22、一个平面截一个球得到直径为6cm 的圆面,球心到这个圆面的距离为4cm ,求该球的表面积与体积。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
空间几何体测试题
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共150分,测试时间120分钟
第Ⅰ卷(选择题共50分)
一.选择题:本大题共10小题,每小题5分,共50分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.下面几何体的轴截面一定是圆面的是
A.圆柱B.圆锥C.球D.圆台
2.下列说法正确的是
A.有两个面平行,其余各面都是四边形的几何体叫棱柱.
B.有两个面平行,其余各面都是平行四边形的几何体叫棱柱.
C.有一个面是多边形,其余各面都是三角形的几何体叫棱锥.
D.棱台各侧棱的延长线交于一点.
3.一个几何体的某一方向的视图是圆,则它不可能是
A.球体B.圆锥C.长方体D.圆柱
4.利用斜二测画法得到的:①三角形的直观图是三角形;②平行四边形的直观图
是平行四边形;③正方形的直观图是正方形.正确的说法有
A.3个B.2个C.1个D.0个
5.下列四个命题中,正确的命题是
A.矩形的平行投影一定是矩形
B.梯形的平行投影一定是梯形
C.两条相交直线的投影可能平行
D.如果一个三角形的平行投影仍是三角形,那么它的中位线的平行投影一定是这个三角形的平行投影的对应的中位线
6.下面的四个图中不能围成正方体的是
A.B.C.D.
7.长方体的三个面的面积分别是2,3,6,则长方体的体积是
A.6 B.12 C.24 D.36
8.如果圆锥的轴截面是正三角形(此圆锥也称等边圆锥),则这圆锥的侧面积
与全面积的比是
A.1:2 B.2:3 C.D.
9.一个三角形用斜二测画法画出来是一个正三角形,边长为2,则原三角形的面
积为
A.B.C.D.
10.若球的半径为1,则这个球的内接正方体的全面积为
A.8 B.9 C.10 D.12
第Ⅱ卷(非选择题共100分)
二.填空题:本大题共7小题,每小题4分,共28分。
11.以等腰直角梯形的直角腰所在的直线为轴,其余三边旋转形成的面所围成的
旋转体是_____.
12.三视图都为圆的几何体是__________.
13.两个半径为1的铁球,熔化后铸成一个球,这个大球的半径为.
14.矩形长6,宽4,以其为圆柱侧面卷成圆柱,则圆柱体积为________.
15.圆台上,下底半径分别为r,R,侧面面积等于两底面积之和,圆台的母线长为
________.
16.圆柱的底面直径与高都等于球的直径,则球的表面积______圆柱的侧面
积.(填>,<,=)
17.平行于锥体底面的截面截得锥体的体积与原锥体的体积之比为8:27,则它们
的侧面积之比为_______.
三.解答题:本大题共5小题,共72分。
解答应写出文字说明,证明过程或演算步骤。
18.(本题14分)
画出底面半径为2cm,高3cm的圆柱的三视图.
19.(本题14分)
用斜二测画法画出边长为2cm的正方体的直观图.
20.(本题14分)
等腰直角三角形的直角边为2,求以斜边所在的直线为旋转轴,其余二边旋转形成的面所围成的旋转体的体积和表面积.
21.(本题15分)
正方体ABCD-A1B1C1D1的边长为a.
(1)求三棱锥A-A1BD的表面积和体积.
(2)求三棱锥B-A1C1D的体积.
22. (本题15分)
棱长均为a的三棱锥容器内装水,若顶点向下倒立时,水面高在容器高的中点处.
(1)求水的体积和棱锥的体积比.
(2)若棱锥顶点向上正立时,水面高是容器高的几分之几?
空间几何体测试题参考答案
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共150分,测试时间120分钟
第Ⅰ卷(选择题 共50分)
一.选择题:本大题共10小题,每小题5分,共50分。
在每小题给出的四个选
第Ⅱ卷(非选择题 共100分)
二.填空题:本大题共7小题,每小题4分,共28分。
11.圆台; 12.球; 14.
24ππ
36,;
15.22r R r R
++ 16. >; 17. 4:9.
三.解答题:本大题共5小题,共72分。
解答应写出文字说明,证明过程或演算步骤。
18.(本题14分) (略)
19. (本题14分) (略)
20. (本题14分)
解:旋转成的几何体为2的圆锥底部重合而成. (4分)
体积为:22r h π=; (9分)
表面积为:222rl π==. (14分) 21. (本题15分)
解(1)表面积为:)
2
22
11
33sin 6022
2
a +⋅⋅+⋅
⋅=
o (5分) 体积为:23111
326a a a ⋅⋅=. (10分)
(2)体积为3
3
31463
a a a -⋅=. (15分)
22.(本题15分)
(1) 1:4 (7分)
(2)3
4
V V =空
全2H H ⇒=空
全22H H ⇒=全水:( (15分)。
