3节电力系统状态估计(WLS算法)
第五章 电力系统运行的状态估计汇总
1、电力系统运行状态主要研究 （1）系统的结点电压；
（2）系统的注入功率；
（3）线路潮流计算等。 2、解决方法 列写运动状态方程。首先必须确定状态变量 及其维数。在列出方程组后，为了求解最优估计 值的需要，还应求出各量测量的导数表示式。 3、测量方法 同步矢量测量技术。一般的测量方法不行。
i 1 n 2
var z E z Ez E z
2 2
z p z dz
2
三、无偏量测条件下，仪表准确度与方差的关系
无偏量测时，方差与准确度的关系可举一误 差概率分布密度曲线加以说明。 1、正态密度分布
1 2
p z
1 2
确度就愈高。列举上述，仅仅是为了说明最小二
乘法的算法，丝毫也不能根据这种极其简单的算
例，来评定最小二乘法的真实价值。
三、加权最小二乘法估计
加权二乘法估计为
J x z j hj x
j 1 k
2
/ Rvj
式中，Rvj——zj的随机量方差，并Rvj=Evj2。 最小加权二乘法估计为
第五章 电力系统运行的状态估计
电力系统运行的状态变量应该分为两种，一 种是结构变量，另一种是运行变量。
结构变量就是常说的接线图与线路参数。
运行变量就是电力系统的运行参数，如电压、潮 流、有功功率与无功功率等。
=======基本知识点======= • 测量系统误差的随机性质 • 最小二乘法估计
• 电力系统运行状态的数学模型
一、对估计值的要求 1、估计应该是无偏的，即满足
E z hx Ev 0
电力系统自动化 第四章 电力系统状态估计
第二节 状态估计的数学 模型及算法
一、状态估计的数学描述
Pij Qij z = Pi Qi Vi
数学模型
量测量
待求的 状态量
θ i x= Vi
数学模型
一、状态估计的数学描述
Pij (θ ij , Vij ) Qij (θ ij , Vij ) 量测方程 h(x) = Pi (θ ij , Vij ) Qi (θ ij , Vij ) Vi (Vi )
(l ) (l )
, θ (l )
, θ (l )
] ]
不良数据
第三节 不良数据的检测与辨识
不良数据：误差大于某一标准（ 不良数据：误差大于某一标准（如3~10 倍标准方差）的量测数据。 倍标准方差）的量测数据。 不良数据的检测： 不良数据的检测：对SCADA原始量测数据 原始量测数据 的状态估计结果进行检查， 的状态估计结果进行检查，判断是否存在 不良数据并指出具体可疑量测数据的过程。 不良数据并指出具体可疑量测数据的过程。 不良数据的辨识： 不良数据的辨识：对检测出的可疑数据验 证真正不良数据的过程。 证真正不良数据的过程。
不良数据
三、不良数据的辨识方法
3、零残差辨识法：既然辨识不良数据的 零残差辨识法： 过程就是削弱和排除不良数据对状态估 计结果影响的过程，那么不改变权重， 计结果影响的过程，那么不改变权重， 将可疑量测的残差置0也可以达到目的。 将可疑量测的残差置0也可以达到目的。 总体型估计辨识法： 4、总体型估计辨识法：根据残差方程将 残差看成是对不良数据的量测， 残差看成是对不良数据的量测，那么由 残差就可以估计出不良数据。 残差就可以估计出不良数据。
一、不良数据检测与辨 识的基本原理
电力系统状态估计概述
电力系统状态估计研究综述摘要：电力系统状态估计是当代电力系统能量管理系统(EMS)的重要组成部分。
本文介绍了电力系统状态估计的概念、数学模型，阐述了状态估计的必要性及其作用，系统介绍了状态估计的研究现状，最后对状态估计的研究方向进行了展望。
关键词：电力系统；状态估计；能量管理系统0引言状态估计是当代电力系统能量管理系统(EMS)的重要组成部分，尤其在电力市场环境中发挥更重要的作用。
它是将可用的冗余信息(直接量测值及其他信息) 转变为电力系统当前状态估计值的实时计算机程序和算法。
准确的状态估计结果是进行后续工作(如安全分析、调度员潮流和最优潮流等)必不可少的基础。
随着电力市场的发展，状态估计的作用更显重要⑴o状态估计的理论研究促进了工程应用，而状态估计软件的工程应用也推动了状态估计理论的研究和发展。
迄今为止，这两方面都取得了大量成果。
然而，状态估计领域仍有不少问题未得到妥善解决，随着电力系统规模的不断扩大，电力工业管理体制向市场化迈进，对状态估计有了新要求，各种新技术和新理论不断涌现，为解决状态估计的某些问题提供了可能。
本文就电力系统状态估计的研究现状和进一步的研究方向进行了综合阐述。
1电力系统状态估计的概念1.1电力系统状态估计的基本定义状态估计也被称为滤波，它是利用实时量测系统的冗余度来提高数据精度，自动排除随机干扰所引起的错误信息，估计或预报系统的运行状态(或轨迹)o 状态估计作为近代计算机实时数据处理的手段，首先应用于宇宙飞船、卫星、导弹、潜艇和飞机的追踪、导航和控制中。
它主要使用了六十年代初期由卡尔曼、布西等人提出的一种递推式数字滤波方法，该方法既节约内存，又大大降低了每次估计的计算量[2,4]o电力系统状态估计的研究也是由卡尔曼滤波开始。
但根据电力系统的特点，即状态估计主要处理对象是某一时间断面上的高维空间(网络)问题，而且对量测误差的统计知识又不够清楚，因此便于采用基于统计学的估计方法如最小方差估计、极大验后估计、极大似然估计等方法，目前很多电力系统实际采用的状态估计算法是最小二乘法。
第五讲电力系统状态估计概述
第五讲电力系统状态估计概述电力系统状态估计指的是通过对电力系统的监测和测量数据进行处理，推算出电力系统相关参数的过程。
通俗的说，就是在电力系统的运行过程中，通过监测数据估计电力系统的状态，以便于运行员做出更好的决策。
电力系统状态估计的意义电力系统状态估计是电力系统自动化的重要组成部分。
在电力系统运行过程中，状态估计系统可以帮助运行员迅速掌握系统状态，及时调整电力系统的运行方式，保证电力系统的安全运行。
同时，状态估计系统还能够优化系统的经济性，提高电力系统的可靠性。
电力系统状态估计的原理电力系统状态估计是基于电力系统监测数据的处理和分析而实现的。
电力系统监测数据主要包括电压、电流、功率等参数。
通过对这些参数的监测和测量，可以获取电力系统的当前状态。
状态估计系统主要是通过对监测数据的处理和分析，以及对电力系统的模型建立和分析来推算电力系统的状态。
电力系统状态估计的原理和方法很多，但基本流程是相似的。
首先需要对电力系统的模型进行建立和分析，然后根据监测数据和运行状态信息，结合电力系统模型，对电力系统的状态进行估计。
最后根据状态估计结果，进行决策和调整。
电力系统状态估计的关键技术为了实现电力系统状态估计，需要涉及到诸多技术。
其中，关键技术包括：变电站数据采集系统变电站是电力系统中起到极为重要作用的环节，所以变电站的监测数据是状态估计的重要来源之一。
因此，变电站数据采集系统的高可靠性和高稳定性是保证状态估计准确性的关键。
现代电力系统常用的数据采集系统包括智能终端设备、数字遥测与遥控设备等。
电力系统模型状态估计需要基于电力系统模型来进行推算。
电力系统模型就是对电力系统运行模式进行建模和仿真得到的电力系统模拟实验环境。
常见的电力系统模型主要有潮流计算模型、电容器模型和风电模型等。
数据预处理电力系统的监测数据通常包含了大量的噪声，因此需要对数据进行预处理。
常用的数据预处理方法包括滤波、降噪、数据插补等等。
非线性方程组求解电力系统状态估计需要根据监测数据在电力系统模型的基础上求解非线性方程组，所以求解非线性方程组是状态估计的关键技术。
3节电力系统状态估计(WLS算法)
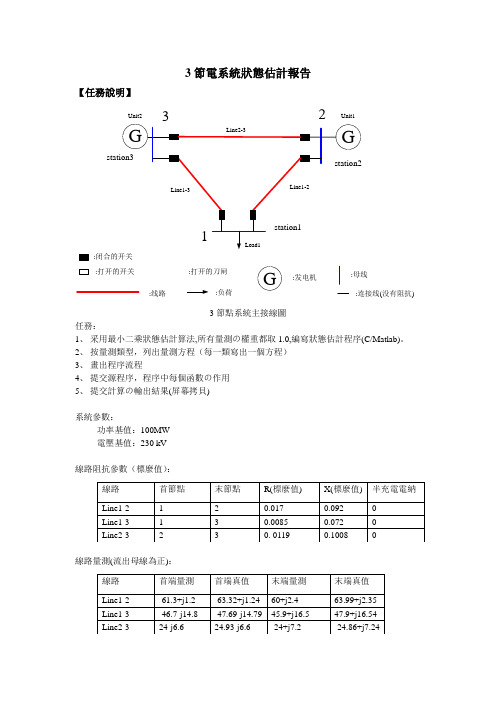
3節電系統狀態估計報告【任務說明】:闭合的开关:打开的开关:打开的刀闸:线路:负荷G:发电机:母线:连接线(没有阻抗) Unit2Unit13節點系統主接線圖任務：1、采用最小二乘狀態估計算法,所有量測の權重都取1.0,編寫狀態估計程序(C/Matlab)。
2、按量測類型，列出量測方程（每一類寫出一個方程）3、畫出程序流程4、提交源程序，程序中每個函數の作用5、提交計算の輸出結果(屏幕拷貝)系統參數：功率基值：100MW電壓基值：230 kV線路阻抗參數（標麼值）：線路量測(流出母線為正)：母線電壓量測：負荷量測(流出母線為正)：發電量測(流入母線為正)：注：量測存在誤差【數據預處理】首先根據基值將已知の量測值均轉換為標么值，並將功率值轉換為流入量，得到如下數據：線路導納參數（標麼值）：線路注入功率量測(標么值)：負荷點注入功率量測(標么值)：發電機節點注入量測(流入母線為正)：母線電壓量測（標么值）：【量測方程】選擇節點1の電壓相角為參考，為0度，以vi表示誤差值。
1）節點1電壓量測方程：Vi=Vi+v1即1.0087=V1+v12）1-3支路1號節點處注入有功功率功率：P ij=V i2g ij-V i V j(g ij cos+b ij sin)+v20.613=V12g13-V1V3(g13cos+b13sin)+v2即0.613=-1.6171V12-V1V3(-1.6171cos +13.698sin)+v2 3）1號節點注入功率：P i=V i2G ii +G ij cos+B ij sin+v3P1=V12G11+G1j cos+B1j sin+v3即-1.11=3.5613V12+V1V2(-1.9442cos -10.5107sin)+V1V3(-1.6171 cos -13.698 sin)+v3【流程圖】其中iterations 為迭代次數，可見本例の迭代次數為4，收斂較快，狀態估計得到の節點1、2、3電壓分別為：234.0144444444444444444444444444444444444444444444，，A X=b,得X+Xmax|X|<【程序說明】1、計算h矩陣の函數cal_hfunction h=cal_h(V,th0,B,G) %其中，V為節點電壓估計值，th0為節點電壓相角估計%值，B為節點電導矩陣，G為節點電納矩陣b=-B; %線路電導矩陣g=-G; %線路電納矩陣P=zeros(3,1); %初始化，節點注入功率Q=zeros(3,1);PP=zeros(3,3); %線路注入功率QQ=PP;th=[0;th0]; %節點1の電壓相角為0for i=1:3P_P=0;Q_Q=0;for j=1:3if(j~=i)P_P=P_P+V(i)*V(j)*(G(i,j)*cos(th(i)-th(j))+B(i,j)*sin(th(i)-th(j)));Q_Q=Q_Q+V(i)*V(j)*(G(i,j)*sin(th(i)-th(j))-B(i,j)*cos(th(i)-th(j)));PP(i,j)=(V(i)^2)*g(i,j)-V(i)*V(j)*(g(i,j)*cos(th(i)-th(j))+b(i,j)*sin(th(i)-th(j)));QQ(i,j)=-(V(i)^2)*b(i,j)-V(i)*V(j)*(g(i,j)*sin(th(i)-th(j))-b(i,j)*cos(th(i)-th(j)));endendP(i)=(V(i)^2)*G(i,i)+P_P;Q(i)=-(V(i)^2)*B(i,i)+Q_Q;endVV=[V(1);V(2);V(3)];h=[P;Q;PP(1,2);PP(2,3);PP(3,1);QQ(1,2);QQ(2,3);QQ(3,1);PP(1,3);PP(2,1);P P(3,2);QQ(1,3);QQ(2,1);QQ(3,2);VV];2、計算H矩陣の函數cal_HHfunction H=cal_HH(V,th0,G,B,P,Q) %其中，P，Q為根據電壓估計值計算得到の節點%注入電壓b=-B;g=-G;PV=zeros(3,3); %節點注入功率對電壓幅值の偏導數QV=zeros(3,3);Pth=zeros(3,3); %節點注入功率對電壓相角の偏導數Qth=zeros(3,3);PPV=zeros(3,3); %P ij對V jの偏導數QQV=zeros(3,3); %Q ij對V jの偏導數PPth=zeros(3,3); %P ij對th jの偏導數QQth=zeros(3,3); %Q ij對th jの偏導數PPV1=zeros(3,3); %P ij對V iの偏導數QQV1=zeros(3,3); %Q ij對V iの偏導數PPth1=zeros(3,3); %P ij對th iの偏導數QQth1=zeros(3,3); %Q ij對th iの偏導數VV=eye(3);Vth=zeros(3,2);th=[0;th0];for i=1:3for j=1:3if (i~=j)PV(i,j)=V(i)*(G(i,j)*cos(th(i)-th(j))+B(i,j)*sin(th(i)-th(j)));QV(i,j)=V(i)*(G(i,j)*sin(th(i)-th(j))-B(i,j)*cos(th(i)-th(j)));PPV(i,j)=-V(i)*(g(i,j)*cos(th(i)-th(j))+b(i,j)*sin(th(i)-th(j)));QQV(i,j)=-V(i)*(g(i,j)*sin(th(i)-th(j))-b(i,j)*cos(th(i)-th(j)));PPV1(i,j)=2*V(i)*g(i,j)-V(j)*(g(i,j)*cos(th(i)-th(j))+b(i,j)*sin(th(i)-th(j)));QQV1(i,j)=-2*V(i)*b(i,j)-V(j)*(g(i,j)*sin(th(i)-th(j))-b(i,j)*cos(th(i)-th(j)));if (j~=1)Pth(i,j)=V(i)*V(j)*(G(i,j)*sin(th(i)-th(j))-B(i,j)*cos(th(i)-th(j)));Qth(i,j)=-V(i)*V(j)*(G(i,j)*cos(th(i)-th(j))+B(i,j)*sin(th(i)-th(j)));PPth(i,j)=-V(i)*V(j)*(g(i,j)*sin(th(i)-th(j))-b(i,j)*cos(th(i)-th(j)));QQth(i,j)=-V(i)*V(j)*(-g(i,j)*cos(th(i)-th(j))-b(i,j)*sin(th(i)-th(j)));endif(i~=1)PPth1(i,j)=V(i)*V(j)*(g(i,j)*sin(th(i)-th(j))-b(i,j)*cos(th(i)-th(j))); QQth1(i,j)=-V(i)*V(j)*(g(i,j)*cos(th(i)-th(j))+b(i,j)*sin(th(i)-th(j)));endelsePV(i,j)=(G(i,i)*(V(i)^2)+P(i))/V(i);QV(i,j)=(Q(i)-(V(i)^2)*B(i,i))/V(i);if (j~=1)Pth(i,j)=-B(i,i)*(V(i)^2)-Q(i);Qth(i,j)=P(i)-(V(i)^2)*G(i,i);endendendendH=[[PV,Pth(:,2:3)];[QV,Qth(:,2:3)];...[PPV1(1,2),PPV(1,2),0,PPth(1,2),0;...0,PPV1(2,3),PPV(2,3),PPth1(2,3),PPth(2,3);...PPV(3,1),0,PPV1(3,1),0,PPth1(3,1)];...[QQV1(1,2),QQV(1,2),0,QQth(1,2),0;...0,QQV1(2,3),QQV(2,3),QQth1(2,3),QQth(2,3);...QQV(3,1),0,QQV1(3,1),0,QQth1(3,1)];...[PPV1(1,3),0,PPV(1,3),0,PPth(1,3);...PPV(2,1),PPV1(2,1),0,PPth1(2,1),0;...0,PPV(3,2),PPV1(3,2),PPth(3,2),PPth1(3,2)];...[QQV1(1,3),0,QQV(1,3),0,QQth(1,3);...QQV(2,1),QQV1(2,1),0,QQth1(2,1),0;...0,QQV(3,2),QQV1(3,2),QQth(3,2),QQth1(3,2)];...[VV,Vth]];3、主程序calculate_all.m文件format longG=[3.5613,-1.9442,-1.6171;...-1.9442,3.0993,-1.1551;...-1.6171,-1.1551,2.7722]; %B為節點電導矩陣B=[-24.2087,10.5107,13.698;...10.5107,-20.295,9.7843;...13.698,9.7843,-23.4832]; %G為節點電納矩陣P=[-1.11;0.88;0.23]; %節點注入功率量測值Q=[-0.135;-0.0424;0.24];PP=[0.613;-0.24;-0.459]; %線路1-2,2-3,3-1注入功率在首端の量測值QQ=[-0.012;0.066;-0.165];PP1=[0.467;-0.6;0.24]; %線路1-3,2-1,3-2注入功率在首端の量測值QQ1=[0.148;-0.024;-0.072];V=[1.0087;1.0198;1.0281]; %節點電壓幅值量測值R=diag(ones(21,1)); %權重都取為1Z=[P;Q;PP;QQ;PP1;QQ1;V]; %量測值矩陣V0=[1;1;1]; %初值th0=[0;0];delta=100;iterations=0; %迭代次數while delta>0.000001iterations=iterations+1;h=cal_h(V0,th0,B,G); %計算h矩陣H=cal_HH(V0,th0,G,B,h(1:3,1),h(4:6,1)); %計算H矩陣A=H'*inv(R)*H;b=H'*inv(R)*(Z-h);d=A\b; %求解修正值delta=max(abs(d));V0=V0+d(1:3,1); %修正估計值th0=th0+d(4:5,1);enditerationsV0=V0*230; %轉換為有名值th0=th0*180/pi; %轉換為度for i=1:3j=num2str(i);v=num2str(V0(i));show1=strcat('The voltage magnitude of node ',j,' is', v,' kV');disp(show1);endfor i=1:2j=num2str(i+1);th=num2str(th0(i));show1=strcat('The phase angle of node ',j,' is ',th,' degrees');disp(show1);end。
电力系统运行的状态估计
• 平方根因子分解法
• 最小二乘法的程序框图
第五节 P-Q分解法的状态估计
=======基本知识点======= • P-Q分解法的估计公式 • P-Q分解法的状态估计程序框图
第六节 电力系统运行 状态估计框图
=======基本知识点=======
• 正常时的估计功能
• 电力系统运行方式的方程组
• 变压器运行方式的方程组
1、电力系统运行状态主要研究 （1）系统的结点电压； （2）系统的注入功率； （3）线路潮流计算等。 2、解决方法
列写运动状态方程。首先必须确定状态变量 及其维数。在列出方程组后，为了求解最优估计 值的需要，还应求出各量测量的导数表示式。 3、测量方法
Z x H V
J x ˆ Z x ˆH T R v 1 Z x ˆH
其中，
v121
Rv
v222
vk2k
Rv为随机向量的方差阵。
证明最小二乘估计是一种无偏估计。
J x ˆ Z x ˆ H T R v 1 Z x ˆ H
对上式求关于 xˆ 导。
同步矢量测量技术。一般的测量方法不行。
一、输电线运行方式的方程组
I i j U ij Y G G j B U i U j
YG为线路对地电容构成的电纳的二分之一； G+jB为线路阻抗的倒数。
第四节 电力系统最小二乘法 状态估计
=======基本知识点=======
• 最小二乘法估计的矩阵形式
=======基本知识点======= • 测量系统误差的随机性质 • 最小二乘法估计 • 电力系统运行状态的数学模型 • 电力系统最小二乘法状态估计 • P-Q分解法的状态估计 • 电力系统运行状态估计框图
第四章 电力系统状态估计.ppt
不良数据
三、不良数据的辨识方法
1、残差搜索法：将量测按残差（加权残 差或标准化残差）由大到小排队，去掉 残差最大的量测重新进行状态估计。再 进行残差检测，还有可疑数据时继续上 述过程。
2、非二次准则辨识法：在迭代中按残差 的大小修改其权重，残差大者降低其权 重，进一步削弱其影响得到较准确的状 态估计结果。
第2类基尔霍夫型伪量测量：0阻抗支路
i j 0 (i, j ZBR)
Vi V j 0 (i, j ZBR)
x
Pij
Qij
(i, j ZBR)
二、基本加权最小二乘 数学模型 法状态估计
迭代修正式
xˆ (l) H T ( xˆ (l) )R1H ( xˆ (l) ) H T ( xˆ )(l) R1 z h( xˆ (l) )
不良数据
二、不良数据的检测方法
1、粗检测 2、残差型检测
加权残差检测 标准残差检测
rw,i rw rN,i rN
3、量测突变检测
Ci c
Ci
z
( i
k
)
z (k 1) i
不良数据
二、不良数据的检测方法
4、残差与突变联合检测
Si k
Si rw,i K rw Cw,i Kcw
Pij Qij
z
Pi
Qi
Vi
待求的 状态量
x
i
Vi
数学模型
一、状态估计的数学描述
量测方程
Pij (ij ,Vij )
第二章电力系统状态估计
一．概述 二．电力系统运行状态的数学描述与可观察性 三．最小二乘估计 四．静态最小二乘估计的改进 五．支路潮流状态估计法 六．电力系统的递推状态估计 七．不良数据的检测与辨识
八. 电力系统网络拓扑分析及网络结构辨识的基本概念
一．概述
一 状态估计的概念 如果已知目标状态 x 的运动规律，则可
一．概述
有
网络结构处理
可观察性检验
状态估计器
不良数据检测 与辨识
无
负荷预计
实时数据库
图2-1电力系统状态估计的功能流程框图
一．概述 电力系统的测量向量 z 包括支路功率、 节点注入功率、节点电压模值等测量量， 待求的系统状态量 x 是各节点的电压模 值与电压相角。通过网络方程从估计出的 状态量xˆ 求出支路功率、节点注入功率 zhx等ν 的估计计算zˆ 值 。如果测量有误差， 则计zˆ 算值 与实z 际值 之间有z 误zˆ 差 ， 称为残差向量。
二．电力系统运行状态的数学描述与可观察性
（2）测量系统的系统误差。这是由于仪 表不精确，通道不完善所引起的。它的特 点是误差恒为正或负而没有随机性。一般 这类数据属于不良数据。清除这类误差的 方法，主要是依靠提高测量系统的精确性 与可靠性，也可以用软件方法来检测与辨 识出不良数据，并通过增加测量系统的冗 余度来补救，但这仅是一种辅助手段。
一．概述 为了满足状态估计的上述需要，对电力 系统的测量量在数量上要有一定的裕度。 通常将全系统中独立测量量的数目与状态 量数目之比，称为冗余度。只有具有足够 冗余度的测量条件，才能通过电力系统调 度中心的计算机以状态估计算法提高实时 信息的可靠性与完整性，建立实时数据库。
一．概述 由于电力系统远动装置的工作情况经常 变化，当远动信息量严重不足时，状态估 计无法工作。因此，在状态估计之前应先 进行可观察性检验。如果系统中某些部分 被判定是不可观察的，无法通过状态估计 建立实时数据库，则应把它从状态估计的 计算中退出来，或用增加人工设置的虚拟 测量或称伪测量数据来使它变成可观察的。
一种基于WLS的电网分层状态估计方法研究
一种基于WLS的电网分层状态估计方法研究朱彬【期刊名称】《《中国设备工程》》【年(卷),期】2019(000)022【总页数】2页(P16-17)【关键词】状态估计; 加权; 最小二乘法; WLS【作者】朱彬【作者单位】上海恒合电力工程有限公司上海 200000【正文语种】中文【中图分类】TM7441 引言电力系统遥信遥测可能存在不良数据。
例如，某一个节点有3条支路，流向该节点的电流实际值为i1、i2、i3，测量值为，根据基尔霍夫电流定律，有i1+i2+i3=0；但是由于测量存在误差，一般--≠0。
这样的测量数据不能直接用于计算，必须要经过适当的处理。
这个处理的过程就称为状态估计。
电力系统状态估计即在测量误差时，运用实时量测系统的冗余度提高测量精度，排除随机干项导致的数据错误，最终通过数学计算估计出系统的运行状态，得到可靠的并且为数最少的系统状态变量值。
2 电网分层网络状态估计思想如图1所示，是一段配电网的简单模型。
图1 小型配电网模型对这个电网的模型进行网络拓扑可以得到：图2 配电网拓扑结构由于配电网呈辐射形、树枝状，单源而且没有回路。
考虑到电网的分层，可以采用从叶子节点一层一层地往根节点推进的方式进行状态估计。
如图2所示，共有8个节点，每个节点都有测量仪器的测量数据。
以各节点注入的有功功率为例，在不考虑损耗的情况下，各点的有功功率应该满足：但是测量得到往的数据往往不能满足这样的条件。
本文采用的方法是从网络拓扑图的最底层开始，逐层向上使用加权最小二乘法进行优化求解，并将得到的新数据作为往上一层进行加权最小二乘法求解时的伪量测量。
由于伪量测量是经过一次初次处理的数据，权重不再是该点量测数据的原来的权重，故应该对这个权重进行修正。
3 节点权重的修正3．1 二层二叉树节点权重修正考虑一棵简单的二层二叉树，它有3个节点：父亲节点Z以及2个儿子节点X、Y。
3个节点的关系方程为z=x+y。
设3个点的量测平均值分别为x0、y0、z0，量测方差分别为D(x0)、D(y0)、D(z0)。
状态估计算法说明
配电网状态估计的作用是充分利用量测数据，辅以历史负荷数据，利用数据的冗余性，通过一定方法计算出全网状态，剔除不良数据，补足缺乏量测，提高量测数据的一致性和精度，为其他配网高级应用软件提供全面可靠的数据。
该三相状态估计算法是通过对传统的输电系统的状态估计算法进展改良得到，主要采用加权最小二乘算法。
由于量测数据都有一定误差，该算法对量测做了局部简化假定：1〕随机量测噪声的均值为0；2〕量测误差平方的期望值服从标准差为σ的正态分布； 3〕不同量测之间互不相关。
在给定系统网络接线、支路参数和量测系统的条件下，设系统状态变量的个数为n ，量测量的个数为m ，那么反映量测量与系统状态变量之间关系的非线性量测方程可写为(4-1)式中，为量测量向量〔简称量测向量〕，，其中，为系统的第i 个量测量，；为状态变量向量〔简称状态向量〕，，其中，为系统的第i 个状态变量，；为非线性量测函数，描述了量测向量与状态向量之间的关系；为量测误差向量，，其中，为第i 个量测量的量测误差。
根本加权最小二乘状态估计法是以计算得到的状态变量的估计值所对应的量测估计值和量测值之差的加权平方和最小为目标准那么的估计方法。
它是许多状态估计算法的根底方法。
给定量测向量z 和量测方程式，可建立基于加权最小二乘法的系统状态估计的目标函数(4-2)式中，为量测权重矩阵，，其中，为第i 个量测量的权值。
假定量测误差向量服从高斯分布，那么，，其中，R 为量测误差协方差矩阵。
由于通常可假定各个量测误差之间相互独立，因而(4-3)()x =+z h v z 12[,,...,]Tm z z z =z i z 1,...i m =x 12[,,...]T n x x x =x i x 1,...i n =()h x z x v 12[,,...]T m v v v =v i v ()(())(())T J =--x z h x W z h x W 12[,,...]Tm w w w =W i w i z v ()=0E v ()=TE R vv 21222m R σσσ⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎣⎦式中，为第i 个量测量的量测误差方差，i=1,2,…,m 。
3 电力系统状态估计算法
量测雅克比矩阵 信息矩阵 H R H 状态估计误差方差阵
T 1
h( x ) H x
ˆ(k ) x x
T T 1 ˆ x x ˆ E x x H R H
1
量测估计误差
ˆ) H(x ˆ )x ˆ H(x ˆ )( x x ˆ) ˆ z h( x zz
收敛条件
ˆi ( l ) x
max i
x
ˆ (l ) ) J ( x ˆ ( l 1) ) J J(x ˆ (l ) x
三个收敛条件 任选其一即可
概述
WLS
FDSE
变换量测
比较
1
示例
ˆ (k ) ) z ( k ) z h( x
R 1 H H T R 1z ( k ) x ˆ ( k 1) x ˆ ( k ) x ˆ (k ) x
WLS与FDSE 求解方法的 区别？
l＝l+1
计算b；求解△ v( l ) v 否 是
Q-V迭代
vi( l )
max
v ?
KQ=1 v(l+1)=v(l)+△v(l) 否
KQ=0 KP=0? 是
概述
WLS
FDSE
变换量测
比较
示例
WLS与FDSE的区别
算法 求解方式 方程维数 系数矩阵 WLS 同时求解 θ 和 v n=na+nr 变化的 FDSE 分别求解 θ 和 v na和nr 常数
采用PQ分解法求解潮流 的思想，将有功和无功 解耦以及雅克比矩阵常 数化的方法用在加权最 小二乘法中，形成了快 速分解状态估计算法。
电力系统自动化5 电力系统运行的状态估计
• 协方差 co v( v i , v j ) ：有多个测量量的情况，如电压、电流与功率
第五章 电力系统运行的状态估计
第二节 最小二乘法估计
第二节 最小二乘法估计
真值已知时，测量值具有随机误差性质 z h x v 。
实践中真值为待求量，要通过多次测量进行科学估计得到。
1.对估计的要求
应为无偏估计： E ( z hx ) E v 0 ˆ 估计值应有很高的精确度：J(z) 或 varz 最小
第五章 电力系统运行的状态估计
第三节 电力系统运行状态的数学模型
2.复杂电网方程
节点导纳矩阵
Y1 1 Y 21 Y M Yn1
Y1 2 Y2 2 M Yn 2
L L O L
Y1 n Y2 n M Ynn
对角元 Yii 称为自导纳，数值上等于该节点直接连接的所有 支路导纳的总和； 非对角元 Yij 称为互导纳，数值上等于连接节点 i ，j 支路 导纳的负值。
联立并将下二式代入
& U i U i i U i (co s i j sin i ) & U j U j j U j (co s j j sin j )
% & S ij Pij j Q ij U i Iˆij I& ij
Pij j Q ij
( z ) p ( z )d z
2
记作 R v
二者区别：J(z)只需Ez，varz还需概率密度分布曲线p(z)。
第五章 电力系统运行的状态估计
第一节 测量系统误差的随机性质
3.无偏量测条件下，仪表准确度与方差的关系
电力系统状态估计算法研究与实现
电力系统状态估计算法研究与实现电力系统是现代社会的重要组成部分，负责将发电厂产生的电能传输到用户端。
为了保证电力系统的可靠性和稳定性，精确的状态估计是必不可少的。
本文将就电力系统状态估计算法进行研究与实现，分析其重要性、算法原理、实现方法和应用前景。
一、电力系统状态估计的重要性电力系统状态估计是通过测量值和部分预测值，利用估计算法分析电力系统的运行状态和电力设备的参数，从而提供准确、可靠的状态信息。
电力系统状态估计的重要性体现在以下几个方面：1. 改善系统可靠性：通过准确估计电力系统的状态，可以及时发现故障和异常，并进行相应的调整和处理，从而提高系统的可靠性和鲁棒性。
2. 优化系统运行：基于准确的状态估计结果，可以进行系统优化调度和负荷预测，以最小化系统的能耗和成本，并实现电力资源的合理利用。
3. 实时监控和故障诊断：准确的状态估计可以为系统提供实时监控和故障诊断能力，提高故障的检测和诊断精度，并促进对故障的及时处理和恢复。
二、电力系统状态估计的算法原理电力系统状态估计的算法原理主要包括以下几个方面：1. 滤波算法：电力系统中存在测量误差和噪声，滤波算法可以对测量值进行平滑处理，提高估计结果的准确度和稳定性。
常见的滤波算法包括卡尔曼滤波、粒子滤波等。
2. 优化算法：通过对状态估计问题建立优化模型，采用优化算法求解最优解，优化算法可以提高估计结果的精度和收敛速度。
常见的优化算法包括最小二乘法、最大似然估计、遗传算法等。
3. 数据挖掘算法：电力系统数据量大、维度高，数据挖掘算法可以从大量的数据中挖掘出隐藏的规律和模式，并应用于状态估计问题。
常见的数据挖掘算法包括人工神经网络、支持向量机、决策树等。
三、电力系统状态估计的实现方法电力系统状态估计的实现方法可以分为离线估计和在线估计两种。
离线估计是指通过历史的测量数据和预测数据，使用离线计算方法进行状态估计。
该方法的优点是计算量较小，可以进行详细的数据分析和处理，但缺点是无法满足实时性的要求。
电力系统信息理论状态估计
电⼒系统信息理论状态估计电⼒系统信息理论状态估计1.1研究⽬的电⼒系统中的任何控制决定，⽆论是⾃动还是⼿动，均依赖于实时访问系统的实际状态。
由于状态从未直接可⽤，所以有⼀个称为状态估计的过程来估计状态变量，并从SCADA周期性获取的测量中得出其值。
因此，传统上通过求解表征操作点的⾮线性⽅程组来解决问题。
需要实时实现的准确性和鲁棒性对于这⼀过程⾄关重要，因为关于真实系统的知识是能源管理系统（EMS）功能效率的先决条件，⽽来⾃真实的国家可能导致不恰当或甚⾄危险的控制决定。
尽管有数⼗年的合理成功的努⼒，开发了可靠地被业界⽤于⼤规模系统的强⼤的⽅法，但电⼒系统状态估计（PSSE或简称SE）的问题仍然是研究⼈员关注的焦点。
在传输系统实践的多年中，PSSE中已经接受了标准实践：基于加权最⼩⼆乘法（WLS）标准（最⼩均⽅误差准则或MSE的变体）和⽜顿算法作为求解器的回归模型。
在垂直整合的电⼒系统中，⾼⽔平的监控，⾃动化和远程控制传统上限于传输⽹格，⽽配电⽹并不是运营有效性的重点。
只要分配⽹络根据其性质被认为是准静态，即具有良好理解和可预测的负载和电压分布，并且在某些正常情况下不需要重新配置或改变保护和控制设置，这种⽅法是可接受的。
现代电⼒系统概念受到放松管制的电⼒市场状况和电⼒系统对⾮电⼒企业的开放的影响。
因此，通过新的监管框架实现了⼀些基本的业务变化。
这些新的情况特别影响分布式发电⼚正在开始爆炸式安装的分销⽹络，以及对服务质量和运营效率的不断提出的要求。
这是从单向能量流的静态径向配置迁移到⽀持分布式资源和⼀些新类型负载的系统（考虑⼤规模实施电动汽车使⽤的实际趋势）。
这种类型的⽹络⽆疑将需要更复杂的控制和⾃动化，这在⽬前⼏乎不可实施，主要是由于监控基础设施⾮常差。
因此，为了应对新的挑战，⼤量投资主要是将系统监控扩展到全⾯的配电⽹。
需要通过分销管理系统（DMS）来处理这样丰富的新数据流，这将通过复杂的⾃动化应⽤程序满⾜分销系统功能的新要求。
电力系统状态估计
a. 基于GPS相位角量测的PMU技术应用于实 时状态 估计算法的研究； b. 面向大系统，开发计算速度快和数值稳定性 好的算法，缩短状态估计执行周期； c. 各种类型和多个相关坏数据条件下，状态估 计算法的研究； d. 量测误差相关情况下估计算法研究； e. 抗差估计理论应用于状态估计算法进一 步 研究； f. 新理论应用于电力系统状态估计算法的探讨 和研究。
2）雅克比矩阵常数化：一般来说，雅克比矩阵 在迭代中仅有微小的变化，若作为常数处理 仍能得到收敛的结果。 利用上述两项简化假设，推导出快速分解法状 态估计的迭代修正公式： -1 (l) (l) ( l ) -1 (l) T (l) T [H (x ) R H(x )]∆x =H (x )R (z -h(x )) 将状态量 x分为电压相角θ和幅值v ，同时将 雅克比矩阵对相角、幅值进行分解并简化， 只要给出状态量初始值，经迭代就可以得到 状态量估计值。
ˆ J (x) = min ∑ (z − z ) = min ∑ z = h(x) ˆ
k 2 k i =1 i =1
[
]
2
五、状态估计的作用
（1）发现、修正不良数据和结构误差，滤去各 种误差，得到统计意义上的最佳估计值。 （2）计算出不能直接测量的状态变量。（如相 角） （3）补足没有测量的量。 （4）离线的状态估计计算可以用来模拟各种信 息收集系统方案，以得到经济上和技术上的 最佳方案。
下图表示状态估计在电力调度自动化中的作用
六、状态估计的基本步骤
七、状态估计算法简介及介绍
1、加权最小二乘法 加权最小二乘估计法在状态估计中应用最 为广泛。 目标函数如下：
ˆ ˆ J (x ) = z − Hx R
T
[
]
现代电力系统分析-状态估计
现代电力系统分析 ----状态估计
电力系统状态估计
概述 运行状态的表征与可观察性 状态估计的模型与算法 不良数据的检测与辨识 网络拓扑结构及参数辨识
电力系统状态估计
概述 运行状态的表征与可观察性 状态估计的模型与算法 不良数据的检测与辨识 网络拓扑结构及参数辨识
Yik Qik= ei ( ei − ek ) + fi ( fi − f k ) bik + ei ( fi − f k ) − fi ( ei − ek ) gik − ( e + fi ) 2
2 i 2
θi = arctan ( fi ei )
u= e + fi
2 i 2 i
多余m-n个方程为矛盾方程，找不到常规意义上的 解，只能用拟合的方法求在某种估计意义上的解。
潮流有研究方式和实时方式两种，而 状态估计仅有实时方式
概述
静态状态估计
利用单一量测断面进行估计
状态追踪法（有时也称为动态估计）
带有预测功能的SE，实为准稳态SE 一般利用多个量测断面进行估计 可实现预防性分析和预防性控制
∂H T ( x ) −1 T −1 ∂ [ z − h( x ) ] = R [ z − h( x ) ] + H ( x ) R T ∂x ∂x T
状态估计的模型与算法
= = ( x )] 0 f ( x ) H T ( x ) R −1 [ z − h ∂f ( x ) T T −1 ∂ [ z − h( x ) ] −1 = = − ( ) ( ) H x R H x R H ( x) T T ∂x ∂x
3节电力系统状态估计（WLS算法）
3节电力系统状态估计（WLS算法）3节电系统状态估计报告【任务说明】:闭合的开关:打开的开关:打开的刀闸:线路:负荷G:发电机:母线:连接线(没有阻抗) Unit2Unit13节点系统主接线图任务：1、采用最小二乘状态估计算法,所有量测的权重都取1.0,编写状态估计程序(C/Matlab)。
2、按量测类型，列出量测方程（每一类写出一个方程）3、画出程序流程4、提交源程序，程序中每个函数的作用5、提交计算的输出结果(屏幕拷贝)系统参数：功率基值：100MW电压基值：230 kV线路阻抗参数（标么值）：线路量测(流出母线为正)：母线电压量测：负荷量测(流出母线为正)：发电量测(流入母线为正)：注：量测存在误差【数据预处理】首先根据基值将已知的量测值均转换为标幺值，并将功率值转换为流入量，得到如下数据：线路导纳参数（标么值）：线路注入功率量测(标幺值)：负荷点注入功率量测(标幺值)：发电机节点注入量测(流入母线为正)：母线电压量测（标幺值）：【量测方程】选择节点1的电压相角为参考，为0度，以vi表示误差值。
1）节点1电压量测方程：Vi=Vi+v1即1.0087=V1+v12）1-3支路1号节点处注入有功功率功率：P ij=V i2g ij-V i V j(g ij cos+b ij sin)+v20.613=V12g13-V1V3(g13cos+b13sin)+v2即0.613=-1.6171V12-V1V3(-1.6171cos +13.698sin)+v2 3）1号节点注入功率：P i=V i2G ii +G ij cos+B ij sin+v3P1=V12G11+G1j cos+B1j sin+v3即-1.11=3.5613V12+V1V2(-1.9442cos -10.5107sin)+V1V3(-1.6171 cos -13.698 sin)+v3【流程图】其中iterations 为迭代次数，可见本例的迭代次数为4，收敛较快，状态估计得到的节点1、2、3电压分别为：234.0144444444444444444444444444444444444444444444 【程序说明】，，A X=b,得X+Xmax|X|<1、计算h矩阵的函数cal_hfunction h=cal_h(V,th0,B,G) %其中，V为节点电压估计值，th0为节点电压相角估计%值，B为节点电导矩阵，G为节点电纳矩阵b=-B; %线路电导矩阵g=-G; %线路电纳矩阵P=zeros(3,1); %初始化，节点注入功率PP=zeros(3,3); %线路注入功率QQ=PP;th=[0;th0]; %节点1的电压相角为0for i=1:3P_P=0;Q_Q=0;for j=1:3if(j~=i)P_P=P_P+V(i)*V(j)*(G(i,j)*cos(th(i)-th(j))+B(i,j)*sin(th(i)-th(j)));Q_Q=Q_Q+V(i)*V(j)*(G(i,j)*sin(th(i)-th(j))-B(i,j)*cos(th(i)-th(j)));PP(i,j)=(V(i)^2)*g(i,j)-V(i)*V(j)*(g(i,j)*cos(th(i)-th(j))+b(i,j)*sin(th(i)-th(j)));QQ(i,j)=-(V(i)^2)*b(i,j)-V(i)*V(j)*(g(i,j)*sin(th(i)-th(j))-b(i,j)*cos(th(i)-th(j)));endendP(i)=(V(i)^2)*G(i,i)+P_P;Q(i)=-(V(i)^2)*B(i,i)+Q_Q;endVV=[V(1);V(2);V(3)];h=[P;Q;PP(1,2);PP(2,3);PP(3,1);QQ(1,2);QQ(2,3);QQ(3,1);PP(1, 3);PP(2,1);P P(3,2);QQ(1,3);QQ(2,1);QQ(3,2);VV];2、计算H矩阵的函数cal_HHfunction H=cal_HH(V,th0,G,B,P,Q) %其中，P，Q为根据电压估计值计算得到的节点%注入电压b=-B;g=-G;PV=zeros(3,3); %节点注入功率对电压幅值的偏导数Pth=zeros(3,3); %节点注入功率对电压相角的偏导数Qth=zeros(3,3);PPV=zeros(3,3); %P ij对V j的偏导数QQV=zeros(3,3); %Q ij对V j的偏导数PPth=zeros(3,3); %P ij对th j的偏导数QQth=zeros(3,3); %Q ij对th j的偏导数PPV1=zeros(3,3); %P ij对V i的偏导数QQV1=zeros(3,3); %Q ij对V i的偏导数PPth1=zeros(3,3); %P ij对th i的偏导数QQth1=zeros(3,3); %Q ij对th i的偏导数VV=eye(3);Vth=zeros(3,2);th=[0;th0];for i=1:3for j=1:3if (i~=j)PV(i,j)=V(i)*(G(i,j)*cos(th(i)-th(j))+B(i,j)*sin(th(i)-th(j)));QV(i,j)=V(i)*(G(i,j)*sin(th(i)-th(j))-B(i,j)*cos(th(i)-th(j)));PPV(i,j)=-V(i)*(g(i,j)*cos(th(i)-th(j))+b(i,j)*sin(th(i)-th(j))); QQV(i,j)=-V(i)*(g(i,j)*sin(th(i)-th(j))-b(i,j)*cos(th(i)-th(j))); PPV1(i,j)=2*V(i)*g(i,j)-V(j)*(g(i,j)*cos(th(i)-th(j))+b(i,j)*sin(th(i)-th(j)));QQV1(i,j)=-2*V(i)*b(i,j)-V(j)*(g(i,j)*sin(th(i)-th(j))-b(i,j)*cos(th(i)-th(j)));if (j~=1)Pth(i,j)=V(i)*V(j)*(G(i,j)*sin(th(i)-th(j))-B(i,j)*cos(th(i)-th(j))); Qth(i,j)=-V(i)*V(j)*(G(i,j)*cos(th(i)-th(j))+B(i,j)*sin(th(i)-th(j))); PPth(i,j)=-V(i)*V(j)*(g(i,j)*sin(th(i)-th(j))-b(i,j)*cos(th(i)-th(j))); QQth(i,j)=-V(i)*V(j)*(-g(i,j)*cos(th(i)-th(j))-b(i,j)*sin(th(i)-th(j)));endif(i~=1)PPth1(i,j)=V(i)*V(j)*(g(i,j)*sin(th(i)-th(j))-b(i,j)*cos(th(i)-th(j))); QQth1(i,j)=-V(i)*V(j)*(g(i,j)*cos(th(i)-th(j))+b(i,j)*sin(th(i)-th(j)));endelsePV(i,j)=(G(i,i)*(V(i)^2)+P(i))/V(i);QV(i,j)=(Q(i)-(V(i)^2)*B(i,i))/V(i);if (j~=1)Pth(i,j)=-B(i,i)*(V(i)^2)-Q(i);Qth(i,j)=P(i)-(V(i)^2)*G(i,i);endendendendH=[[PV,Pth(:,2:3)];[QV,Qth(:,2:3)];...[PPV1(1,2),PPV(1,2),0,PPth(1,2),0;...0,PPV1(2,3),PPV(2,3),PPth1(2,3),PPth(2,3);...PPV(3,1),0,PPV1(3,1),0,PPth1(3,1)];...[QQV1(1,2),QQV(1,2),0,QQth(1,2),0;...0,QQV1(2,3),QQV(2,3),QQth1(2,3),QQth(2,3);...QQV(3,1),0,QQV1(3,1),0,QQth1(3,1)];...[PPV1(1,3),0,PPV(1,3),0,PPth(1,3);...PPV(2,1),PPV1(2,1),0,PPth1(2,1),0;...0,PPV(3,2),PPV1(3,2),PPth(3,2),PPth1(3,2)];...[QQV1(1,3),0,QQV(1,3),0,QQth(1,3);...QQV(2,1),QQV1(2,1),0,QQth1(2,1),0;...0,QQV(3,2),QQV1(3,2),QQth(3,2),QQth1(3,2)];...[VV,Vth]];3、主程序calculate_all.m文件format longG=[3.5613,-1.9442,-1.6171;...-1.9442,3.0993,-1.1551;...-1.6171,-1.1551,2.7722]; %B为节点电导矩阵B=[-24.2087,10.5107,13.698;...10.5107,-20.295,9.7843;...13.698,9.7843,-23.4832]; %G为节点电纳矩阵P=[-1.11;0.88;0.23]; %节点注入功率量测值Q=[-0.135;-0.0424;0.24];PP=[0.613;-0.24;-0.459]; %线路1-2,2-3,3-1注入功率在首端的量测值QQ=[-0.012;0.066;-0.165];PP1=[0.467;-0.6;0.24]; %线路1-3,2-1,3-2注入功率在首端的量测值QQ1=[0.148;-0.024;-0.072];V=[1.0087;1.0198;1.0281]; %节点电压幅值量测值R=diag(ones(21,1)); %权重都取为1Z=[P;Q;PP;QQ;PP1;QQ1;V]; %量测值矩阵V0=[1;1;1]; %初值th0=[0;0];delta=100;iterations=0; %迭代次数while delta>0.000001iterations=iterations+1;h=cal_h(V0,th0,B,G); %计算h矩阵H=cal_HH(V0,th0,G,B,h(1:3,1),h(4:6,1)); %计算H矩阵A=H'*inv(R)*H;b=H'*inv(R)*(Z-h);d=A\b; %求解修正值delta=max(abs(d));V0=V0+d(1:3,1); %修正估计值th0=th0+d(4:5,1);enditerationsV0=V0*230; %转换为有名值th0=th0*180/pi; %转换为度for i=1:3j=num2str(i);v=num2str(V0(i));show1=strcat('The voltage magnitude of node ',j,' is', v,' kV'); disp(show1);endfor i=1:2j=num2str(i+1);th=num2str(th0(i));show1=strcat('The phase angle of node ',j,' is ',th,' degrees'); disp(show1);end。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
3节电系统状态估计报告【任务说明】
:闭合的开关
:打开的开关:打开的刀闸
:线路:负荷
G:发电机:母线
:连接线(没有阻抗) Unit2Unit1
3节点系统主接线图
任务：
1、采用最小二乘状态估计算法,所有量测的权重都取1.0,编写状态估计程序(C/Matlab)。
2、按量测类型，列出量测方程（每一类写出一个方程）
3、画出程序流程
4、提交源程序，程序中每个函数的作用
5、提交计算的输出结果(屏幕拷贝)
系统参数：
功率基值：100MW
电压基值：230 kV
线路阻抗参数（标么值）：
线路量测(流出母线为正)：
母线电压量测：
负荷量测(流出母线为正)：
发电量测(流入母线为正)：
注：量测存在误差
【数据预处理】
首先根据基值将已知的量测值均转换为标幺值，并将功率值转换为流入量，得到如下数据：
线路导纳参数（标么值）：
线路注入功率量测(标幺值)：
负荷点注入功率量测(标幺值)：
发电机节点注入量测(流入母线为正)：
发电机量测真值
unit2 0.88-j0.0424 0.8892-j0.0424
unit3 0.23+j0.24 0.2304+j0.2378
母线电压量测（标幺值）：
母线电压量测真值(幅值/角度)
1 1.0087 1.0130/0
2 1.0198 1.0242/3.23
3 1.0281 1.0281/1.82
【量测方程】
选择节点1的电压相角为参考，为0度，以vi表示误差值。
1）节点1电压量测方程：
Vi=Vi+v1
即1.0087=V1+v1
2）1-3支路1号节点处注入有功功率功率：
P ij=V i2g ij-V i V j(g ij cos+b ij sin)+v2
0.613=V12g13-V1V3(g13cos+b13sin)+v2
即0.613=-1.6171V12-V1V3(-1.6171cos +13.698sin)+v2 3）1号节点注入功率：
P i=V i2G ii +G ij cos+B ij sin+v3
P1=V12G11+G1j cos+B1j sin+v3
即-1.11=3.5613V12+V1V2(-1.9442cos -10.5107sin)
+V1V3(-1.6171 cos -13.698 sin)+v3。