马尔科夫随机场
马尔可夫随机场能量函数

马尔可夫随机场能量函数马尔可夫随机场是一种概率图模型,它用于建模空间中的复杂结构,并对这些结构进行分析和预测。
在马尔可夫随机场中,每个节点代表一个变量,它们之间的关系由一组能量函数确定。
本文将重点介绍马尔可夫随机场中的能量函数。
一、能量函数的定义马尔可夫随机场中的能量函数是一种用于描述节点之间关系的函数。
它指定了每个节点的状态之间的相互作用,这些状态可以是二元的(如0和1)或多元的(如红、绿和蓝)。
每个节点的状态取值和它周围节点的状态取值的组合将决定整个系统的能量。
一个马尔可夫随机场的能量函数由如下形式的数学公式来表示:$E(X) = \sum_{C \in cliques}V_C(X_c)$其中,$X$为所有节点的状态向量,$C$是随机场中的一个团,$cliqes$表示所有的团,$X_c$表示团$C$中节点的状态向量,$V_C$则是团$C$的能量函数。
二、团在马尔可夫随机场中,团是指由多个节点组成的子集。
这些节点之间的关系可以是可访问的也可以是无序的。
每个团都有一个本质的最高节点,被称为扩展变量。
一个团可能包含一个或多个变量,但对于任何一个团,它所包含的任意两个变量之间都必须是有边相连的。
能量函数的主要作用是为随机场模型提供一个数学上的描述,以便于我们利用统计学的理论和方法进行建模和分析。
它指示了节点之间的相互作用,使得我们可以根据相应的统计规律进行预测和决策。
在马尔可夫随机场中,能量函数的值越低,它们所描述的状态就越合理。
这是由于能量函数的值衡量了整个系统的不确定性。
一个低能量状态表示系统的状态更加确定;而一个高能量状态,则表示系统更加不确定。
常见的马尔可夫随机场能量函数包括:二元势函数、高斯势函数、指数势函数等。
1. 二元势函数二元势函数是最基本的马尔可夫随机场能量函数之一。
它仅仅关注两个随机变量之间的相互作用,并确定它们之间的相互作用方式,通常形式如下:$V(x_i, x_j)=\begin{cases}1, & x_i=x_j \\0, & \text{otherwise}\end{cases}$高斯势函数是一种在马尔可夫随机场中刻画相邻节点之间相似性的能量函数。
马尔可夫随机场中应用蚁群系统的红外图像分割

引 言
图像 分 割是 低 层 次 图像 处 理 的 重要 步 骤 之 一 ,
法 的 抗 噪 能 力 就 显 得 稍 差 ; 于 马 尔 可 夫 随 机 场 基
( r o a d m il , F) 图像 分 割 方 法 是 Mak vR n o F ed MR 的
一
种 利用 图 像局 部 相关 特性 的统计 分 割 方 法 , 可 其
Ab t a t I or to stv e db c n h urs i s a c s r c : nf ma i n po ii e f e a k a d e itc e r h,t e ha a t r o n h c r c e s f A t Col ny Sys e o t m
( C A S) we e a p i d o t e m a e s g n a i n i h s p p r Th M AP l b l e t o u i n f , r p l f r h i g e me t to s n t i a e . e e g o a b s s l t o o s g n a i n l b o h u h M a k v Ra d m ed ( RF) e me t to s wi e g tt o g r o n o Fil M l ,wh c e c i e ma e d t e a i n y ih d s rb s i g a a r l to s b
维普资讯
Vo . 1. 1 3 No. 7
火 力 与 指 挥 控 制
Fie Co t o n mm a d Co r l r n r la d Co n nto
J l 2 0 uy, 0 6
第 3 1结 果 。
机器学习——马尔可夫随机场(Ma...

机器学习——马尔可夫随机场(Ma...最近刚好在调研马尔可夫随机场,发现可以参考的资料少之⼜少,中⽂外⽂⽂献资料都相对较少。
按照仅有的知识稍作稍作整理⾃留以免之后⽤到再作查询。
有需要的也可以简单参考,但。
根据已有资料确实不太好理解,有简单明了易理解的还望推荐。
马尔可夫随机场(MRF):是关于⼀组有马尔可夫性质的随机变量X的全联合概率分布模型。
换句话说,若⼀组随机变量是马尔可夫随机场,那么其⼀定满⾜马尔可夫性质。
马尔可夫⽹络或是MRF在依赖性的表⽰上类似于贝叶斯⽹络。
两者的区别在于:贝叶斯⽹络是有向⽆环的,⽽马尔可夫⽹络是⽆向可以有环的。
因此,马尔可夫是可以表⽰某些贝叶斯⽹络⽆法表述的依赖关系,⽐如循环依赖。
另⼀⽅⾯,它也不能表⽰贝叶斯⽹络可以表述的依赖,⽐如诱发依赖。
马尔可夫随机场的底图可以是有限的也可以是⽆限的。
1.定义给定⼀个⽆向图G=(V,E),其中每个顶点v∈V表⽰⼀组随机变量X=(Xv),每条边{u,v}∈E表⽰随机变量u和v之间的⼀种依赖关系。
(1)成对马尔可夫性质:任意两个不相邻的变量相对给定的其他全部变量都是条件独⽴的。
(2)局部马尔可夫性质:所有其他变量的邻居变量都是条件独⽴的。
(3)全局马尔可夫性质:对于给定⼀个分离⼦集,任何两组变量都是条件独⽴的以上三个马尔可夫性质并不等价:全局马尔可夫性质强于局部马尔可夫性质,同样的,局部马尔可夫性质也强于成对马尔可夫性质。
Markov⽹Markov⽹也称 Markov 随机场(Markov random field,简称 MRF),是⼀个变量集合 X=(X1,X2,…,X n)∈χ的联合分布模型.它由⼀个⽆向图 G 和定义于 G 上的⼀组势函数φk组成.其中,⽆向图的每个节点都代表⼀个随机变量,⽽ G 中的每⼀个“团(clique)”都对应着⼀个势函数(为⾮负实函数),表⽰团的⼀个状态.Markov ⽹所代表的变量集的联合分布表⽰为P ( X = x ) =1/ Z ∏kφk(X{k}) (1)其中,X{k}表⽰Markov⽹中第k团的状态,即对应于第k个团中所有变量的取值状态。
马尔可夫随机场在可见光图像分割中的应用

理特征 的MR 模型。 F 利用纹理 的MR 模 型 , F 将参数 的期望最大化用于该模型 中的参数估 计。最后将 图像 中的所有像素经该模 型
计算 后 得 到纹 理 信 息并 分 割 图像 。通 过 实验 取 得 了较 好 的效 果 。 关 键 词 图像 分 割 MR 模 型 纹 理 分 析 F
⑥ 2 0 S iT c . nn . 0 6 c eh E g g .
马尔可夫随机场在可见光图像分割中的应用
柴震海 秦 琴 王汝笠
( 国科 学 院上 海 技 术 物 理 研 究 所 , 海 20 8 ) 中 上 00 3
摘
要
在可见光图像 生成红外 图像 的过程 中, 图像分 割至关重要 。马尔 可夫 随机场 ( F 具有局部 特性 ,Ji ̄性 建立了纹 MR ) gl t
中图法分类号
T 3 1 1 文献标识码 P9. ; 4
B
图像 分 割技 术 几乎 与 计算 机 技术 同步 产 生 , 并 且 随着计算 机技 术 的发展 不断 进步 。它也成 为 计算
机视 觉领域 里极 为重 要 的内容 。图像 分割 技术 根据
示 连 接. s 中任 意 两点 所 成 的线 段 之集 , 称 f, } 则 . 为 s
s G ;( ) EG r s s 2 s , ∈G 。
针对具 体 应用有 实际意 义 的区域 。 因此 , 不 同 的 针对
应用 . 同一 副 图像 可 以有不 同的划 分方法 。 图 像分 割方 法 分 为结 构 分 割 和非 结 构 分 割 , 利
型 : 图(, ) 设 . , s 如果X= ,∈X) 某概 率空 间的一 s 为 簇 随机 变量 , 空 间 为 。称X为关 于 的马 尔 可夫 相 随机 场 ( 简记MR )需 满足 F,
【国家自然科学基金】_马尔可夫随机场(mrf)_基金支持热词逐年推荐_【万方软件创新助手】_20140730
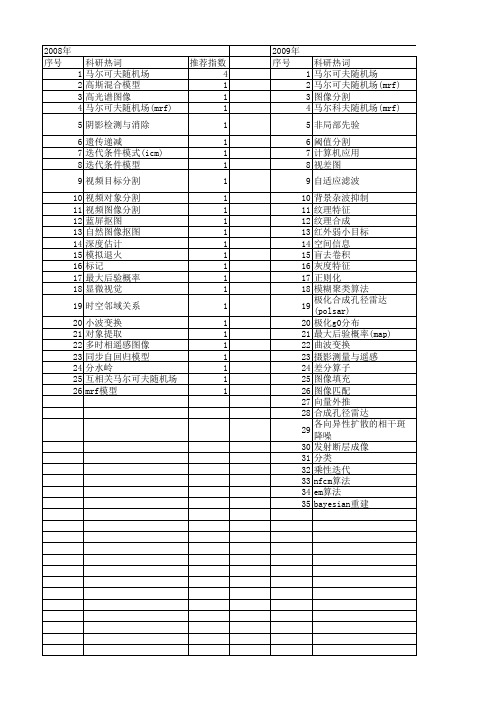
科研热词 马尔可夫随机场 马尔可夫随机场(mrf) 图像分割 马尔科夫随机场(mrf) 非局部先验 阈值分割 计算机应用 视差图 自适应滤波 背景杂波抑制 纹理特征 纹理合成 红外弱小目标 空间信息 盲去卷积 灰度特征 正则化 模糊聚类算法 极化合成孔径雷达(polsar) 极化g0分布 最大后验概率(map) 曲波变换 摄影测量与遥感 差分算子 图像填充 图像匹配 向量外推 合成孔径雷达 各向异性扩散的相干斑降噪 发射断层成像 分类 乘性迭代 nfcm算法 em算法 bayesian重建
科研热词 马尔可夫随机场 图像分割 合成孔径雷达 马尔科夫随机场 计算机应用 海冰 最大边缘概率(mpm) 最大期望值(em) 彩色图像 几何划分 像斑 高阶马尔可夫随机场 马氏链蒙特卡罗方法 面向对象 运动矢量 边缘惩罚 车辆跟踪 贝叶斯分析 语义层次 自适应马尔可夫随机场 自适应邻域系统 自适应权 置信度传播 纳什均衡 红外系统 空间关系 目标识别 目标地图 标记 标值点过程 极化白化滤波 极化合成孔径雷达 条件迭代 有形目标检测 循环置信度传播 归一化割 弱小目标检测 局部统计特性 地物类别邻接矩阵 图割 图像处理 图像分类 吉布斯参数 参数估计 事件检测 voronoi几何划分 st-mrf sar em/mpm算法 bp神经元网络
2012年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52
科研热词 推荐指数 马尔可夫随机场 9 图像分割 5 马尔科夫随机场 2 离散小波变换 2 合成孔径雷达 2 高分辨率 1 马尔可夫随机场模型 1 马尔可夫随机场(mrf)模型 1 马尔可夫随机场(mrf)样本修补 1 隐马尔可夫随机场模型 1 重要性采样 1 遥感图像分割 1 道路网 1 边缘检测 1 轮廓波变换 1 超像素 1 贝叶斯方法 1 视觉跟踪 1 行人 1 自然图像抠图 1 自助法 1 聚类 1 结构信息 1 线段 1 纹理信息 1 红外图像 1 粒子滤波 1 磁共振成像 1 目标检测 1 疲劳断口 1 消隐点 1 比率 1 模糊c均值(fcm)算法 1 植被覆盖 1 样本修补 1 最大后验概率估计 1 显著区域 1 弥散张量 1 广义高斯马尔可夫随机场 1 层次合并 1 小波变换 1 多目标跟踪 1 墙面分割 1 基于学习的超分辨率 1 图割算法 1 图像重构 1 图像提取 1 图像内容层次表征 1 变化检测 1 双树复小波变换 1 参数估计 1 区域邻接图 1
基于马尔可夫随机场的运动分割研究

M a k v r n o fedCo u e gn e ig a d Ap l a in 。 0 8。4 1 : 6 8 . r o a d m l. mp tr En ie rn n pi t s 2 0 4 ( 1)8 - 8 i c o
Abtat Sg e t i fm v g ojcsi a asa m ot trsacig sbeti m g rcsi n o p trvs n src: em na o o oi bet s l y n ip r n eerhn ujc n iae poes g ad cm ue io . tn n w a n i T i pp rue a l rh fm t n sg ett nc m ie o o smao i ro ad m Fe ( F . e ojci hs a e ss n a o tm o oi em nao o bnd m t n et tn wt Makv R n o il MR ) bet e gi o i i i i h d h T v
f n to o moi n si to c nsss f ro mo l nd o us saitc l e hn l g . fn mo l s h s n s u c in f to e tma in o it o er r de a r b t t tsia t c o o Af e y i de i c o e a mo in to m o e dl wh s pa a tr a e oe r mee s r de v d i r e by v r l c ag it I ta rgins a e o t i d a c r i g o mi m u o e -sa k lor hm.niil e o r b ane c o d n t ni m e o c tro r r r e in t n i he s ohe by M RF fa e t r mo e n ieTh e p rme t l r s t o c m mo — e i g s qu nc s o t s m eh d ae mo t d rm o e v os. e x e i n a e uls n o n us d ma e e e e f hi to r p e e td n he a r t a t r s n e i t p pe a ls.
自适应先验马尔可夫随机场模型的图像分割算法

于 图像 中的噪声或 者 纹理特 征 等具有 较好 的 分割 , 分割 结果 明显优 于全局 同 态先验 MR F模 型 ; 提
出的 自适应 先验 MR F模 型 对于 图像 的噪 声或 者 纹理 突 变信 号 的干 扰 具 有较 强 的鲁棒 性 ; 算 法 具 有 较 少的迭 代 次数 和 较好 的分 割结 果 , 且 分割 时 间较短 。
该 算法基 于贝叶斯 理论 , 利 用局部 先 验 P o t t s 模 型描 述 图像 的局 部 特征 , 建 立 了一种 局部 自适 应 先 验 MR F模 型 ; 提 出 了基 于 区域 的 置 信度 传 播 ( B e l i e f P r o p a g a t i o n , B P ) 算法, 把 图像 的 局 部 区域特 征 传递 到 全局 , 最终基 于最 大后 验 准 则( MAP ) 得 到 图像 的分 割 结果 。 实验 结果 表 明 : 所提 模 型 对
LI U Gu a n g h u i , REN Qi n g c h a n g ,M ENG Yu e b o ,XU S h e n g j u n ・
( 1 .I n f o r ma t i o n a n d Co nt r o l Eng i n e e r i n g S c h o o l ,Xi ’ a n Uni v e r s i t y o f Ar c h i t e c t ur e a n d Te c h n o l o g y,Xi ’ a n 7 1 0 0 5 5,Chi n a ;
mod e l i s p r op os e d t O s o l ve t he p r ob l e m t ha t t h e g l o b a l ho mo ge ne o us p r i or M RF mo de l i s i ne f f i c i e nt t o ut i l i z e t he l oc a 1 s t a t i s t i c f e a t u r e o f na t ur e i ma g e s f o r i ma ge s e gme n t a t i o n. The a l g or i t h m i s ba s e d on Ba y e s i a n t h e o r y,ut i l i z e s l o c a l pr i o r Po t t s mo d e l t o r e p r e s e nt i ma ge l o c a l f e a t ur e s,a n d bu i l ds a l o c a l a d a p t i v e pr i o r M RF mo de 1 .A mod i f i e d l o c al r e gi o n b e l i e f pr o pa g a t i on ( BP)a l go r i t h m i s p r op o s e d o ve r t h e M RF mo d e l , he nc e ,l o c a l r e g i o n f e a t ur e s o f a n i ma ge a r e
无向图模型(马尔科夫随机场)

19 无向图模型(马尔科夫随机场)19.1 介绍在第十章,我们讨论了图形化模型(DGMs),通常称为贝叶斯网。
然而,对于某些域,需要选择一个方向的边即(DGM), 例如,考虑建模一个图像。
我们可能会假设相邻像素的强度值是相关的。
我们可以创建一个DAG模型的2D拓扑如图19.1所示。
这就是所谓的因果MRF或马尔可夫网。
然而,它的条件独立性通常不好。
另一种方法是使用anundirected图形化模型(UGM),也称为马尔可夫随机场(MRF)或马尔可夫网络。
这些不需要我们指定边缘方向,在处理一些问题,如图像分析和空间统计数据时显得更自然。
例如,一个无向二维点阵显示(如图19.1(b));现在每个节点的马尔科夫Blanket只是最近邻节点,正如我们在19.2节所示的那样。
粗略地讲,在建立在DGMs上的UGMs的主要优点是:(1)它们是对称的,因此对某些领域更“自然”,如空间或关系数据;(2)Discriminativel UGMs(又名条件随机域,或CRFs),它定义了条件概率密度p(y|x),要比Discriminativel UGMs更好,我们在19.6.1节中解释原因。
相比于DGMs,UGMs的主要缺点是:(1)参数是可很难解释及模块化程度较差,我们在19.3节解释原因;(2)参数估计计算代价更高,原因我们在19.5节解释。
19.2 UGMs的条件独立性19.2.1UGMs通过简单的图分离定义CI关系如下:对于节点集的A,B,C,我们说X A ⊥G X B | X C,如果从在图G中把A从B中分离出来。
这意味着,当我们删除所有C 中的节,如果在A上没有任何连接的路径到B,那么CI 属性holds。
这就是所谓的UGMs的全局马尔可夫性质。
例如,在图19.2(b),有{ 1,2 }⊥{ 6、7 } | { 3、4、5 }。
图19.1节点的节点集呈现t有条件地独立于所有其他节点图为t的马尔科夫blanket;我们将表示通过mb(t)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
马尔科夫随机过程的分类
按照参数集和状态空间分成四类 时间和状态都是离散的马尔科夫过程。 也成为马尔科夫链 时间连续、状态离散的马尔科夫过程。 通常称为纯不连续马尔科夫过程。 时间和状态都是连续的马尔科夫过程。 时间连续、状态离散的马尔科夫过程。
马尔科夫随机场
马尔科夫随机场包含两层意思 马尔科夫性质 随机场
ቤተ መጻሕፍቲ ባይዱ
对于一幅给定的图像,Y已知,所以p(Y)为常数, 故上式等价于:arg max p(Y | X ) p( X )
X
由于随机场X是MRF,具有正概率性和Markov性。 由MRF与Gibbs分布的等价性可知 exp Vc ( xi ) M *N cC p(X)= p ( xi ) i 1 L i 1 1 exp Vc ( xi ) xi cC 式中Vc ( xi )是包含xi的基团c的势函数,C是所有基团的集合
马尔科夫随机场与图像处理
随机过程
在当代科学与社会领域里,人们都可以看到一 种叫作随机过程的数学模型:从分子的布朗运 动到原子的蜕变过程,从化学反应动力学到电 话通讯理论、从谣言的传播到传染病的流行、 从市场预测到密码破译,随机过程理论及其应 用几乎无所不在。人类历史上第一个从理论上 提出并加以研究的过程模型是马尔科夫链,它 是马尔科夫对概率论乃至人类思想发展作出的 又一伟大贡献。
刘爱平,付琨,尤红建,刘忠.基于MARMRF的SAR图像分割方法[J].电子与信息 学报 李旭超,朱善安.图像分割中的马尔可夫 随机场方法综述[J].中国图像图形学报 张鹏,张桂林.Markov随机场在图像处理 中应用的研究[D].华中科技大学
随机场
当给每一个位置中按照某种分布随机赋予相空 间的一个值之后,其全体就叫做随机场。其中 有两个概念:位置(site),相空间(phase space)。我们不妨拿种地来打个比方。“位 置”好比是一亩亩农田;“相空间”好比是要 种的各种庄稼。我们可以给不同的地种上不同 的庄稼,这就好比给随机场的每个“位置”, 赋予相空间里不同的值。所以,俗气点说,随 机场就是在哪块地里种什么庄稼的事情。
一维马尔科夫过程
设有随机过程 X n , n T , 若对于任意正整数n T 和任意的 i0 , i1 ,, in 1 I , 条件概率满足 P{ X n 1 in 1 | X 0 i0, , X n in } P{ X n 1 in 1 | X n in } 就称 X n , n T 为马尔科夫过程,该随机过程的统计特性 完全由条件概率所决定
s s
( ys um ) 2 exp 2 2 m 2 m 1
其中参数um和 m分别是第m区域的均值和方差,可以 根据其在概率论中的公式计算 根据上面得到的p(x)和p(Y|X)的计算公式就可 求得最优分割结果 X。
MRF图像分割的关键点
马尔科夫性质
马尔科夫性质指的是一个随机变量序列 按时间先后关系依次排开的时候,第 N+1时刻的分布特性,与N时刻以前的随 机变量的取值无关。拿天气来打个比方。 如果我们假定天气是马尔可夫的,其意 思就是我们假设今天的天气仅仅与昨天 的天气存在概率上的关联,而与前天及 前天以前的天气没有关系。其它如传染 病和谣言的传播规律,就是马尔可夫的。
的联合概率分布具有如下形式: P( X x ) (1 / Z ) exp{U ( x)} 即X在格点集S上的一组态。 U ( x) Vc ( x)称为能量函数,Vc ( x)是仅与子团c内各
cC
则称X为吉布斯随机场,式中x是随机场X的一“实现”,
象元值有关的子团势函数 Z e U ( x ) 称为配分函数,是一个归一化常数
基团的选取 势函数 Vc ( x) 的定义 先验概率p(X)的确定(图像预分割) 选取合适的条件分布 条件分布中参数的估计 分割算法的选取
参考文献
匡锦瑜.吉布斯随机场模型及其在图像处 理中的应用[J].通信学报 王玲,逯贵祯,肖怀宝.基于马尔科夫随机 场的合成孔径雷达图像分割方法[J].中国 传媒大学学报自然科学版 卢晓东,周军,周凤岐.基于可能性FMRF 的红外图像分割算法及其参数估计[J].红 外与激光工程
上式解决了求MRF中概率分布的难题,使 对MRF的研究转化为对势函数Vc(x)的研 究,使Gibbs分布与能量函数建立了等价关 系,是研究邻域系统δ(s)MRF的一个重要 里程碑。
基于MRF的图像分割模型
基于马尔科夫随机场模型的图像分割算法假设待分割图像 的像素只与其邻域内的像素相关,与邻域外的像素无关; 基于该假设我们能定量计算图像局部的先验结构信息, 并根据最大后验概率准则(MAP),有效的利用像素间 结构信息分割图像。
马尔科夫随机过程
通俗的讲,马尔科夫随机过程就是,下 一个时间点的状态只与当前的状态有关 系,而与以前的状态没有关系,即未来 的状态决定于现在而不决定于过去。
用前苏联数学家辛钦(1894-1959〕的话来说, 就是承认客观世界中有这样一种现象,其未来 由现在决定的程度,使得我们关于过去的知识 丝毫不影响这种决定性。这种在已知 “现在” 的条件下,“未来”与“过去”彼此独立的特 性就被称为马尔科夫性,具有这种性质的随机 过程就叫做马尔科夫过程
MRF与Gibbs分布的等价关系
由于标号场先验概率和标号场的邻域局 部关系在实际应用中很难确定,20世纪 80年代Hammersley-Clifford给出了Gibbs 分布与MRF的关系,从而用Gibbs分布求 解MRF中的概率分布
MRF与Gibbs分布的等价关系
Gibbs分布:
是定义在S上的邻域系统,当且仅当随机场X={x s , s S }
马尔科夫随机场
拿种地打比方,如果任何一块地里种的庄 稼的种类仅仅与它邻近的地里种的庄稼 的种类有关,与其它地方的庄稼的种类 无关,那么这些地里种的庄稼的集合, 就是一个马尔可夫随机场。
马尔科夫随机场与图像的关系
一维马尔科夫随机过程很好的描述了随 机过程中某点的状态只与该点之前的一 个点的状态有关系。对于定义在二维空 间上的图像,也可以将它看为一个二维 随机场。自然也存在二维马尔科夫随机 场,此时必须考虑空间的关系,二维MRF的 平面网格结构同样可以较好的表现图像 中像素之间的空间相关性。
在图像中 格点集S表示像素的位置 X称为标号场,也可以表示像素值的集合 或图像经小波变换后的小波系数集合 Λ为标号随机变量 x s 的集合 L表示将图像分割为不同区域的数目
邻域系统
设 ={ ( s) | s S}是定义在S上的通用邻域系统的集合, 其满足如下特性:
(1) ( s ) S (2) s ( s ) (3)s, r S , s (r ) r ( s ) 则位置r ( s )称作s的邻点, ( s)称作s的邻点集
对于一幅给定的M*N的图像Y, 其中任意一个像素yi , 分割后对应的标记为x i , 定义两个随机场: X={x i , i S }是图像分割后的类别标号场, xi 1, 2, L表示分割成L个区域, 但其类别状态不能直接观察到。 Y={yi , i S }是可观测的随机场, 即图像的观测灰度场, 那么分割问题可以描述为:
(1)P{X=x}>0,x
邻域系统 的MRF的含义:在任意格点s的其余格点位置上 随机变量xs 取值已知的条件下,随机场在格点s处的取值概率 只与格点s的 相邻点有关。
在图像中,P()表示标号场的先验概率, P(|)表示邻域系统标号的局部作用关系
在数字图像中,一个像元的灰度值仅与 其邻域系统内各象元的灰度值有关,因 而可以利用马尔科夫随机场来模拟数字 图像。当邻域系统 足够大时,任何定 义在S上的图像数据均可看成马尔科夫随 机场的一个实现
分阶邻域系统与子团
在图像模型中,可以根据对象元的距离建 立一种分阶邻域系统,定义如下:
(n)
( s) {r | d ( s, r ) n, r s}, 式中n为邻域系统的阶次,
d ()表示距离函数,经常使用欧氏距离,市区距离, 棋盘距离等函数。 对n 0, 满足特性 ( s)
x
MRF与Gibbs分布的等价关系
Gibbs分布与MRF的等价条件:一个随机场 是关于邻域系统的MRF,当且仅当这个 随机场是关于邻域系统的Gibbs分布,表 示为: exp ( Vc (xs | xr )) cC P(xs | xr , r ( s )) L 1 exp (Vc ( xs | xr )) xs cC
(n) ( n +1)
( s)
子团
S中有不同的邻域结构,在S上由单个像 元或由象元与其邻点组成的子集 c S 称为一个子团。子团c的集合用C来表示。
分阶邻域系统与子团示例
马尔科夫随机场
设 为S上的邻域系统,若随机场X={x s ,s S}满足如下条件: (2) P{X s =x s | X r xr , r s, r ( s)} P{X s =x s | X r xr , r ( s)} 则称X为以 为邻域系统的马尔科夫随机场, 上式称为马尔科夫随机场的局部特性
i t arg et1 1 2 i t arg et 2 yi Y xi xi X , i {1, 2, M * N } L i t arg etL 根据贝叶斯准则,最优分割准则为: p (Y | X ) p ( X ) X arg max p ( X | Y ) arg max p (Y ) X X
基本定义
设S {(i, j ) |1 i M ,1 j N }表示MN位置的有限格点集 即随机场中的位置
