金属塑性变形理论习题集
《金属塑性成形基础原理》习题集标准答案
《金属塑性成形原理》习题答案一、填空题1. 衡量金属或合金的塑性变形能力的数量指标有伸长率和断面收缩率。
2. 所谓金属的再结晶是指冷变形金属加热到更高的温度后，在原来变形的金属中会重新形成新的无畸变的等轴晶，直至完全取代金属的冷变形组织的过程。
3. 金属热塑性变形机理主要有：晶内滑移、晶内孪生、晶界滑移和扩散蠕变等。
4. 请将以下应力张量分解为应力球张量和应力偏张量＝＋5. 对应变张量，请写出其八面体线变与八面体切应变的表达式。
＝；＝。
6.1864 年法国工程师屈雷斯加（H.Tresca ）根据库伦在土力学中研究成果，并从他自已所做的金属挤压试验，提出材料的屈服与最大切应力有关，如果采用数学的方式，屈雷斯加屈服条件可表述为。
7. 金属塑性成形过程中影响摩擦系数的因素有很多，归结起来主要有金属的种类和化学成分、工具的表面状态、接触面上的单位压力、变形温度、变形速度等几方面的因素。
8. 变形体处于塑性平面应变状态时，在塑性流动平面上滑移线上任一点的切线方向即为该点的最大切应力方向。
对于理想刚塑性材料处于平面应变状态下，塑性区内各点的应力状态不同其实质只是平均应力不同，而各点处的最大切应力为材料常数。
9. 在众多的静可容应力场和动可容速度场中，必然有一个应力场和与之对应的速度场，它们满足全部的静可容和动可容条件，此唯一的应力场和速度场，称之为真实应力场和真实速度场，由此导出的载荷，即为真实载荷，它是唯一的。
10. 设平面三角形单元内部任意点的位移采用如下的线性多项式来表示：，则单元内任一点外的应变可表示为＝。
11、金属塑性成形有如下特点：、、、。
12、按照成形的特点，一般将塑性成形分为和两大类，按照成形时工件的温度还可以分为、和三类。
13、金属的超塑性分为和两大类。
14、晶内变形的主要方式和单晶体一样分为和。
其中变形是主要的，而变形是次要的，一般仅起调节作用。
15、冷变形金属加热到更高的温度后，在原来变形的金属中会重新形成新的无畸变的等轴晶，直至完全取代金属的冷变形组织，这个过程称为金属的。
《金属学原理》各章习题及解答(晶体的塑性变形)
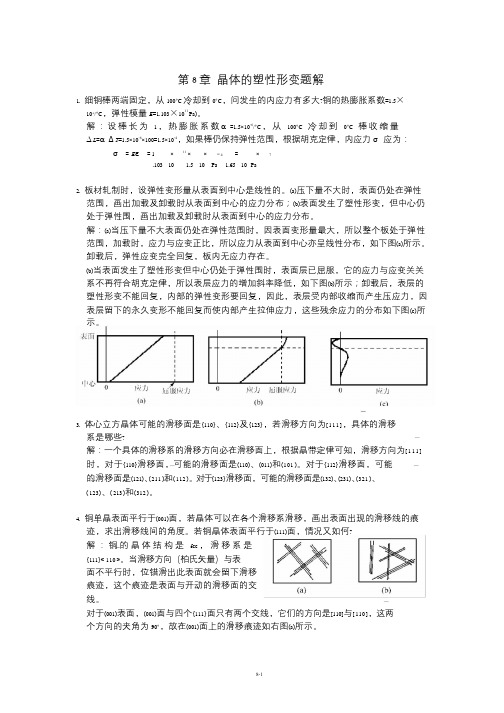
第8 章晶体的塑性形变题解1. 细铜棒两端固定，从100°C 冷却到0°C，问发生的内应力有多大?铜的热膨胀系数=1.5×10-6/°C，弹性模量E=1.103×1011 Pa)。
解：设棒长为 1 ，热膨胀系数α=1.5×10-6/°C ，从100°C 冷却到0°C 棒收缩量∆L=α∆T=1.5×10-6×100=1.5×10-4，如果棒仍保持弹性范围，根据胡克定律，内应力σ应为：σ=Eε=1 ×11 ××−4 =×7.103 10 1.5 10 Pa 1.65 10 Pa2. 板材轧制时，设弹性变形量从表面到中心是线性的。
(a)压下量不大时，表面仍处在弹性范围，画出加载及卸载时从表面到中心的应力分布；(b)表面发生了塑性形变，但中心仍处于弹性围，画出加载及卸载时从表面到中心的应力分布。
解：(a)当压下量不大表面仍处在弹性范围时，因表面变形量最大，所以整个板处于弹性范围，加载时，应力与应变正比，所以应力从表面到中心亦呈线性分布，如下图(a)所示。
卸载后，弹性应变完全回复，板内无应力存在。
(b)当表面发生了塑性形变但中心仍处于弹性围时，表面层已屈服，它的应力与应变关关系不再符合胡克定律，所以表层应力的增加斜率降低，如下图(b)所示；卸载后，表层的塑性形变不能回复，内部的弹性变形要回复，因此，表层受内部收缩而产生压应力，因表层留下的永久变形不能回复而使内部产生拉伸应力，这些残余应力的分布如下图(c)所示。
3. 体心立方晶体可能的滑移面是{110}、{112}及{123}，若滑移方向为[111]，具体的滑移系是哪些?解：一个具体的滑移系的滑移方向必在滑移面上，根据晶带定律可知，滑移方向为[111] 时，对于{110}滑移面，可能的滑移面是(110)、(011)和(101 )。
第五章塑性变形与回复再结晶--习题集
psi是一种压力单位，定义为英镑/平方英寸，145psi=1MpaPSI英文全称为Pounds per square inch。
P是磅pound，S是平方square，I 是英寸inch。
把所有的单位换成公制单位就可以算出：1bar≈14.5psi1 KSI = 1000 lb / in.2 = 1000 x 0.4536 x 9.8 N / (25.4 mm)2 = 6.89 N / mm2材料机械强度性能单位，要用到试验机来检测Density of Slip PlanesThe planar density of the (112) plane in BCC iron is 9.94 atoms/cm2. Calculate the planar density of the (110) plane and the interplanar spacings for both the (112) and the (110) planes. On which type of plane would slip normally occur?(112) planar density:The point of this problem is that slip generally occurs in high density directions and on high density planes. The high density directions are directions in which the Burgers' vector is short, and the high density planes are the "smoothest" for slip.It will help to visualize these two planes as we calculate the atom density.The (110) plane passes through the atom on the lattice point in the center of the unit cell. The plane is rectangular, with a height equal to the lattice parameter a0and a width equal to the diagonal of the cube face, which is 2 a0.Lattice parameter (height):Width:Thus, according to the geometry, the area of a (110) plane would beThere are two atoms in this area. We can determine that by counting the piece of atoms that lie within the circle (1 for the atom in the middle and 4 times 1/4 for the corners), or using atom coordinates as discussed in Chapter 3. Then the planar density isThe interplanar spacing for the (110) planes isFor the (112) plane, the planar density is not quite so easy to determine. Let us draw a larger array of four unit cells, showing the plane and the atoms it passes through.This plane is also rectangular, with a base width of √2 a0 (the diagonal of a cube face), and a height of √3 a0 (the body diagonal of a cube). It has four atoms at corners, which are counted as 1/4 for the portion inside the rectangle (4 x 1/4) and two atoms on the edges, counted as 1/2 for the portion inside the rectangle (2 x 1/2). This is a total of 2 atoms.Base width:Height:Hence, we can calculate the area and density as for the (110) plane.The planar density and interplanar spacing of the (110) plane are larger than that of the (112) plane, thus the (110) plane would be the preferred slip plane1．有一根长为5 m，直径为3mm的铝线，已知铝的弹性模量为70GPa，求在200N的拉力作用下，此线的总长度。
塑性成形原理
《金属塑性成形原理》习题集第一章 金属的塑性和塑性变形1．什么是金属的塑性？什么是变形抗力？2．简述变形速度、变形温度、应力状态对金属塑性和变形抗力的影响。
如何提高金属的塑性？3．什么是附加应力？ 附加应力分几类？试分析在凸形轧辊间轧制矩形板坯时产生的附加应力？4．什么是最小阻力定律？最小阻力定律对分析塑性成形时的金属流动有何意义？5．塑性成形时，影响金属变形和流动的因素有哪些？各产生什么影响？6．为什么说塑性成形时金属的变形都是不均匀的？不均匀变形会产生什么后果？7．什么是残余应力？残余应力有哪几类？会产生什么后果？如何消除工件中的残余应力？8．摩擦在金属塑性成形中有哪些消极和积极的作用？塑性成形中的摩擦有什么特点？9．塑性成形中的摩擦机理是什么？10． 塑性成形时接触面上的摩擦条件有哪几种？各适用于什么情况？11． 塑性成形中对润滑剂有何要求？12． 塑性成形中常用的液体润滑剂和固体润滑剂各有哪些？石墨和二硫化钼 如何起润滑作用？第二章 应力应变分析1．什么是求和约定？张量有哪些基本性质？2．什么是点的应力状态？表示点的应力状态有哪些方法？3．什么是应力张量、应力球张量、应力偏张量和应力张量不变量？4．什么是主应力、主剪应力、八面体应力？5．什么是等效应力？有何物理意义？6．什么是平面应力状态、平面应变的应力状态？7．什么是点的应变状态？如何表示点的应变状态？8．什么是应变球张量、应变偏张量和应变张量不变量？9．什么是主应变、主剪应变、八面体应变和等效应变？10． 说明应变偏张量和应变球张量的物理意义？11． 塑性变形时应变张量和应变偏张量有和关系？其原因何在？12． 平面应变状态和轴对称状态各有什么特点？13． 已知物体中一点的应力分量为⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---=30758075050805050ij σ，试求方向余弦为21==m l ，21=n 的斜面上的全应力、正应力和剪应力。
14． 已知物体中一点的应力分量为⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---=10010010010010ij σ，求其主应力、主剪应力、八面体应力、应力球张量及应力偏张量。
金属塑性成形原理复习题
一、名词解释1. 主应力：只有正应力没有切应力的平面为主平面，其面上的应力为主应力。
2. 主切应力：切应力最大的平面为主切平面，其上的切应力为主主切应力。
3. 对数应变 答：变形后的尺寸与变形前尺寸之比取对数4. 滑移线 答：最大切应力的方向轨迹。
5. 八面体应力：与主平面成等倾面上的应力6. 金属的塑性：在外力作用下使金属材料发生塑性变形而不破坏其完整性的能力。
7. 等效应力：又称应力强度，表示一点应力状态中应力偏张量的综合大小。
8. 何谓冷变形、热变形和温变形：答冷变形：在再结晶温度以下，通常是指室温的变形。
热变形：在再结晶温度以上的变形。
温变形在再结晶温度以下，高于室温的变形。
9. 何谓最小阻力定律：答变形过程中，物体质点将向着阻力最小的方向移动，即做最少的功，走最短的路。
10.金属的再结晶 答：冷变形金属加热到一定的温度后，在原来变形的金属中会重新形成新的无畸变的等轴晶，直至完全取代金属的冷变形组织的过程。
11. π平面 答：是指通过坐标原点并垂于等倾线的平面。
12.塑性失稳 答：在塑性加工中，当材料所受的载荷达到某一临界后，即使载荷下降，塑性变形还会继续，这种想象称为塑性失稳。
13.理想刚塑性材料：在研究塑性变形时，既不考虑弹性变形，又不考虑变形过程中的加工硬化的材料。
P13914.应力偏张量：应力偏张量就是应力张量减去静水压力，即：σij ′ =σ－δij σm二、填空题1. 冷塑性变形的主要机理:滑移和孪生2. 金属塑性变形的特点：不同时性、相互协调性和不均匀性。
3. 由于塑性变形而使晶粒具有择优取向的组织称为：变形织构 。
4. 随着变形程度的增加,金属的强度 硬度增加,而塑性韧性降低,这种现象称为：加工硬化。
5. 超塑性的特点:大延伸率、低流动应力、无缩颈、易成形、无加工硬化 。
6. 细晶超塑性变形力学特征方程式中的m 为:应变速率敏感性指数。
7. 塑性是指金属在外力作用下,能稳定地发生永久变形而不破坏其完整性的能力 。
金属塑性成形原理模拟题
⾦属塑性成形原理模拟题⼀、填空题：（每题 3 分，共计 30 分）1. 塑性是指： _ 在外⼒作⽤下使⾦属材料发⽣塑性变形⽽不破坏其完整性的能⼒。
2. ⾦属的超塑性可分为细晶超塑性和相变超塑性两⼤类。
3. ⾦属单晶体变形的两种主要⽅式有：滑移和孪⽣。
4. 影响⾦属塑性的主要因素有：化学成份，组织，变形温度，应变速率，变形⼒学条件。
5. 等效应⼒表达式：。
6. 常⽤的摩擦条件及其数学表达式：库伦摩擦条件，常摩擦条件。
7.π平⾯是指：通过坐标原点并垂于等倾线的平⾯，其⽅程为 __。
8.⼀点的代数值最⼤的 __ 主应⼒ __ 的指向称为第⼀主⽅向，由第⼀主⽅向顺时针转所得滑移线即为线。
9. 平⾯变形问题中与变形平⾯垂直⽅向的应⼒σ z =10. 在有限元法中：应⼒矩阵 [S]= ，单元内部各点位移 {U}=⼆、简答题（共计 30 分）1. 提⾼⾦属塑性的主要途径有哪些？（ 8 分）答：提⾼⾦属塑性的途径有以下⼏个⽅⾯：(1) 提⾼材料成分和组织的均匀性；…… 2'(2) 合理选择变形温度和应变速率；…… 2'(3) 选择三向压缩性较强的变形⽅式；…… 2'(4) 减⼩变形的不均匀性。
…… 2'2. 纯剪切应⼒状态有何特点？（ 6 分）答：纯剪切应⼒状态下物体只发⽣形状变化⽽不发⽣体积变化。
…… 2'纯剪应⼒状态下单元体应⼒偏量的主⽅向与单元体应⼒张量的主⽅向⼀致，平均应⼒。
…… 2'其第⼀应⼒不变量也为零。
…… 2'3. 塑性变形时应⼒应变关系的特点？（ 8 分）答：在塑性变形时，应⼒与应变之间的关系有如下特点：(1) 应⼒与应变之间的关系是⾮线性的，因此，全量应变主轴与应⼒主轴不⼀定重合。
…… 2'(2) 塑性变形时，可以认为体积不变，即应变球张量为零，泊松⽐。
……2'(3) 对于应变硬化材料，卸载后再重新加载时的屈服应⼒就是报载时的屈服应⼒，⽐初始屈服应⼒要⾼。
金属塑性成形原理习题集
金属塑性成形原理习题集Document serial number【KKGB-LBS98YT-BS8CB-BSUT-BST108】《金属塑性成形原理》习题集运新兵编模具培训中心二OO九年四月第一章 金属的塑性和塑性变形1．什么是金属的塑性什么是变形抗力2．简述变形速度、变形温度、应力状态对金属塑性和变形抗力的影响。
如何提高金属的塑性3．什么是附加应力 附加应力分几类试分析在凸形轧辊间轧制矩形板坯时产生的附加应力4．什么是最小阻力定律最小阻力定律对分析塑性成形时的金属流动有何意义5．塑性成形时，影响金属变形和流动的因素有哪些各产生什么影响6．为什么说塑性成形时金属的变形都是不均匀的不均匀变形会产生什么后果7．什么是残余应力残余应力有哪几类会产生什么后果如何消除工件中的残余应力8．摩擦在金属塑性成形中有哪些消极和积极的作用塑性成形中的摩擦有什么特点9．塑性成形中的摩擦机理是什么10． 塑性成形时接触面上的摩擦条件有哪几种各适用于什么情况11． 塑性成形中对润滑剂有何要求12． 塑性成形中常用的液体润滑剂和固体润滑剂各有哪些石墨和二硫化钼 如何起润滑作用第二章 应力应变分析1．什么是求和约定张量有哪些基本性质2．什么是点的应力状态表示点的应力状态有哪些方法3．什么是应力张量、应力球张量、应力偏张量和应力张量不变量4．什么是主应力、主剪应力、八面体应力5．什么是等效应力有何物理意义6．什么是平面应力状态、平面应变的应力状态7．什么是点的应变状态如何表示点的应变状态8．什么是应变球张量、应变偏张量和应变张量不变量9．什么是主应变、主剪应变、八面体应变和等效应变10． 说明应变偏张量和应变球张量的物理意义11． 塑性变形时应变张量和应变偏张量有和关系其原因何在12． 平面应变状态和轴对称状态各有什么特点13． 已知物体中一点的应力分量为⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---=30758075050805050ij σ，试求方向余弦为21==m l ，21=n 的斜面上的全应力、正应力和剪应力。
金属塑性成形力学课后答案
金属塑性成形力学课后答案【篇一：金属塑性成形原理习题】述提高金属塑性变形的主要途径有哪些？(1)提高材料成分和组织的均匀性(2)合理选择变形温度和应变速率(3)合理选择变形方式(4)减小变形的不均匀性2. 简答滑移和孪生变形的区别相同点：都是通过位错运动来实现, 都是切应变不同点：孪生使一部分晶体发生了均匀切变，而滑移只集中在一些滑移面上进行；孪生的晶体变形部分的位向发生了改变，而滑移后晶体各部分位向未改变。
3. 塑性成型时的润滑方法有哪些？(1) 特种流体润滑法。
(2) 表面磷化-皂化处理。
(3) 表面镀软金属。
4. 塑性变形时应力应变关系的特点？在塑性变形时，应力与应变之间的关系有如下特点（1）应力与应变之间的关系是非线性的，因此，全量应变主轴和应力主轴不一定重合。
（2）塑性变形时，可以认为体积不变，即应变球张量为零，泊松比??0.5。
、（3）对于应变硬化材料，卸载后再重新加载时的屈服应力就是卸载时的屈服应力，比初始屈服应力要高。
（4）塑性变形是不可逆的，与应变历史有关，即应力－应变关系不再保持单值关系。
5. levy－mises理论的基本假设是什么？（1）材料是刚塑性材料，级弹性应变增量为零，塑性应变增量就是总的应变增量。
（2）材料符合米塞斯屈服准则。
（3）每一加载瞬时，应力主轴和应变增量主轴重合。
（4）塑性变形上体积不变。
6. 细化晶粒的主要途径有哪些？（1）在原材料冶炼时加入一些合金元素及最终采用铝、钛等作脱氧剂。
（2）采用适当的变形程度和变形温度。
（3）采用锻后正火等相变重结晶的方法。
7. 试从变形机理上解释冷加工和超塑性变形的特点。
冷塑性变形的主要机理：滑移和孪生。
金属塑性变形的特点：不同时性、相互协调性和不均匀性。
由于塑性变形而使晶粒具有择优取向的组织，称为变形织构。
随着变形程度的增加，金属的强度、硬度增加，而塑性韧性降低，这种现象称为加工硬化。
超塑性变形机理主要是晶界滑移和原子扩散（扩散蠕变）。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
《金属塑性变形理论》习题集张贵杰编河北联合大学金属材料与加工工程系2013年10月前言《金属塑性变形理论》是关于金属塑性加工学科的基础理论课，也是“金属材料工程”专业大学本科生的主干课程，同时也是报考材料科学与工程专业方向硕士研究生的必考科目。
《金属塑性变形理论》总学时为72，内容上分为两部分，即“金属塑性加工力学”（40学时）和“塑性加工金属学”（32学时）。
为使学生能够学好本课，以奠定扎实的理论基础，提高分析问题和解决问题的能力，编者集20余年的教学经验特编制本习题集，一方面作为学生在学习本课程时的辅导材料，供课下消化课堂内容时使用，另一方面也可供任课教师在授课时参考，此外对报考研究生的学生还具有指导复习的作用。
本“习题集”在编写时，充分考虑了学科内容的系统性、学生学习的连贯性以及与教材顺序的一致性。
该“习题集”中具有前后关联的一个个题目，带有由浅入深的启发性，能够引导学生将所学的知识不断深化。
教师也可根据教学进程从中选题，作为课外作业指导学生进行练习。
所有这些都会有助于学生理解和消化课堂上所学习的内容，从而提高课下的学习效率。
编者2013年10月第一部分 金属塑性加工力学第一章 应力状态分析1． 金属塑性加工中的外力有哪几种？其意义如何？2． 为什么应力分量的表达需用双下标？每个下标都表示何物理意义？ 3． 已知应力状态如图1-1所示，写出应力分量，并以张量形式表示。
4． 已知应力状态的六个分量7-=x σ，4-=xy τ，0=y σ，4=yz τ，8-=zx τ，15-=z σ(MPa)，画出应力状态图，写出应力张量。
5． 作出单向拉伸、单向压缩、三向等值压缩、平面应力、平面应变、纯剪切应力状态的应力Mehr 圆。
6． 已知应力状态如图1-2所示，当斜面法线方向与三个坐标轴夹角余弦31===n m l 时，求该斜面上的全应力S 、全应力在坐标轴上的分量x S 、y S 、z S 及斜面上的法线应力n σ和切应力n τ。
图1-1⎪⎪⎪⎭⎫ ⎝⎛------=1548404847σT xyz 图1-2x107． 将下列应力状态用单元体表示。
（1）⎪⎪⎪⎭⎫ ⎝⎛---=6040504050705070100σT N/mm 2 （用直角坐标系）（2）⎪⎪⎪⎭⎫ ⎝⎛-=2007090701000900120σT N/mm 2 （用柱面坐标系） 8． 单元体上各面所作用的应力分量如图1-3所示。
根据应力分量的正负规定，在相应的圆圈内填上适当的“+”、“－”。
9． 何谓求和约定？什么是哑标？什么是自由标？10． 已知jn mn im ijβσασ='，找出哑标和自由标，并写出12σ'的展开式。
33332333232233132132322332222232122131312331212231112123βσαβσαβσαβσαβσαβσαβσαβσαβσασ++++++++=' 11． 任举一例利用求和约定对公式进行展开和合并。
12． 你是如何理解“应力张量”这一概念的？试用自己的语言描述之。
13． 试分别用单元体和张量来表达一般三向应力状态（要求采用直角、圆柱两种不同的坐标系）。
14．怎样将一个张量分解为一个对称张量和一个反对称张量？试举例。
15．应力张量有何性质？xy±yxz± 图1-316．若已知过变形体内任一点三个坐标面上的九个应力分量，如何求过该点任意斜面上的应力分量？ 17．已知变形体内某点的应力状态⎪⎪⎪⎭⎫ ⎝⎛=105851538320σT N/mm 2 ，试求外法线与x 、y 、z 坐标轴夹角分别为 45=α、 50=β、8.72=γ的斜面上的全应力n S 、正应力n σ、切应力n τ。
18．应力边界条件方程与任意斜面上的应力计算式有何区别？试述应力边界条件方程的物理意义。
19．若已知过变形体内任一点三个坐标面上的九个应力分量，如何求该点的三个主应力及其方向余弦、方向角？20．应力张量不变量有何特性？其用途何在？21．试求图1-4中主应力状态的1σ、2σ、3σ，并计算最大主切应力m ax τ，八面体正应力8σ与八面体切应力8τ，画出最大主切应力平面与八面体应力作用平面。
22．已知变形体内某点的应力状态⎪⎪⎪⎭⎫ ⎝⎛--=80027060027050σT N/mm 2 ，试求：（1）主应力及其方向余弦； （2）偏差应力与球应力。
23．判别下列应力状态是否表示同一点的应力状态。
图1-43⎪⎪⎪⎭⎫ ⎝⎛=513162324AT σ⎪⎪⎪⎭⎫ ⎝⎛=27.100073.40009BT σ 24．分别阐述偏差应力张量第一、第二不变量的物理意义。
25．试证：（1）()()()[]213232221261σσσσσσ-+-+--='I （2）2832I '=τ 26．可否利用向量合成定理将三个主应力合成为一个应力？为什么？ 27．说明图1-5中的应力状态图示是哪种特殊应力状态（即平面应力、平面应变、轴对称）。
28．什么是球应力、偏差应力？它们的物理意义为何？如何计算？ 29．什么是主应力图示、主偏差应力图示、主应变图示？各有几种？试画之，并说明其用途。
30．如图1-6所示，凸锤头在滑动摩擦条件下进行平面变形压缩，试给出当凸角βαβαβα<=> , ,三种不同情况时，A 点处的主应力图有什么不同？对单位变形力有什么影响？图1-5(a)(b)(c)(d)图1-6αT x aP P f T x sin cos '<'=ααβ=αβ>αβ<31．试画出挤压、拉拔和轧制过程的主应力图示。
32．根据主应力状态图，试分析拉拔与单向拉伸有何异同？33．为什么主应力图示和主应变图示不能一一对应，而主偏差应力图示和主应变图示却能一一对应？34．试画出主切应力，最大切应力及八面体应力的作用面在主坐标系中的位置。
35．已知变形体内某点的应力状态⎪⎪⎪⎭⎫ ⎝⎛---=3007508007500500800500500σT N/mm 2 ，试求方向余弦21==m l ，21=n 的斜面上的全应力、正应力和切应力。
36．已知变形体内某点的应力状态⎪⎪⎪⎭⎫ ⎝⎛----=200150550150100σT N/mm 2 ，试求：（1）最大主应力1σ与x 、y 、z 轴正向所成的夹角； （2）画图表示1σ的方位与指向； （3）最大切应力平面上所作用的应力；（4）给出最大切应力平面在主坐标系中的位置，并在该平面上标出m ax τ和13σ。
37．若已知过变形体内某一点的应力状态，⎪⎪⎪⎭⎫ ⎝⎛--=00100001000σT N/mm 2 ， 试求过该点的主平面，主切应力平面，最大切应力平面以及八面体平面上所作用的各个应力分量。
38．若已知过变形体内某一点的应力状态，⎪⎪⎪⎭⎫⎝⎛=p pp p p pp p p T σ N/mm 2 ， 试求过该点的主应力，主切应力平面上所作用的应力。
39．试求以下两种复杂切应力情况下的主应力和八面体切应力值。
1）τττ==yz xy 2）ττττ===zx yz xy40．试用求和约定写出用偏差应力和球应力表达的应力分量计算式。
41．八面体切应力有何物理意义？42．什么是静水压力？怎样计算？它与球应力有何关系？43．已知一点处的主应力状态为1σ=60(MPa)，2σ=50(MPa)，3σ=40(MPa)，试判断该点处所产生的主应变图示为何？并说明该主应变图示对产品性能有何影响？44．已知应力状态图如图1-7所示，试进行应力状态分解，写出应力张量分解形式，画出应力状态分解图，并计算等效应力值。
45．已知应力张量如下，试进行应力张量分解，画出应力状态分解图，并计算等效应力值。
⎪⎪⎪⎭⎫ ⎝⎛=1050515000201σT ⎪⎪⎪⎭⎫ ⎝⎛--=100500050102σT ⎪⎪⎪⎭⎫ ⎝⎛=1000020000303σT 46．在其他条件均相同的情况下，拉拔和单向拉伸哪种工艺过程所需的变形力更小？为什么？4图1-7(a)(b)(c)(d)47．金属塑性加工的基本过程有哪五种？试分别画出变形区内及边界上的应力状态图。
48．试证明平面变形时，在02=ε的方向上，其应力()2312σσσ+=，且有m σσ=2第二章 应变状态分析1．什么是相对应变、真应变？二者如何计算、有何区别？ 2．试证明真应变就是对数应变。
3．若相对应变超过10％，则须用真应变来计算变形程度，试说明理由。
4．什么是正应变（线应变）、切应变（角应变）、工程应变？ 5．什么是位移体积？它与应变有何关系？6．如何表达变形体内某点的应变状态？若相应的一对切应变分量不对称则表明应变中存在刚性转动，此时怎样才能得到纯切应变？ 7．什么是应变速度？锻压矩形件时应变速度与工具移动速度有何区别？8．试以平砧压缩为例，导出平均应变速度的表达式。
9．试证明塑性变形时应满足体积不变条件，即工件的长、宽、高三方向的真应变之和为零。
10．什么是应变张量？什么是应变张量不变量？它们各有何物理意义？ 11．已知应力状态如图2-1所示。
试求：1）对应力状态进行分解，写出应力张量分解形式； 2）画出应力状态分解图并计算等效应力值。
12．若已知应变状态如图2-2所示，画出该应变状态可能对应的主应力状态有几种？13．试用求和约定写出用偏差应变和球应变表达的应变分量计算式。
14．什么是主应变图示？为什么金属塑性加工中主应变图示只有三种，而主应力图示却有九种？15．已知应变张量如下，试求主应变张量，画出主应变图。
图2-1图2-2ε12⎪⎪⎪⎭⎫ ⎝⎛=0000101001020εT16．判断图2-3所示主应变图示中，哪个是最大主应变方向，并注明1ε、2ε、3ε。
17．已知应力状态图如图2-4所示，试根据应力状态图画出应变状态图。
18．对内径为d ，壁厚为t 的薄壁管施加扭矩M 。
当管内充气单位压力为p 时，其应力状态与应变状态如何？19．试证明对变形体内任一点，若有0=++z y x εεε（或0=i i ε）则表明满足体积不变条件。
20．轧制板带时，其厚度的变化为10→8→6.5→6.2→6.0mm，试求：1） 各道的压下率； 2） 总压下率；3）各道厚度方向的真应变；图2-3图2-44） 厚度方向总的真应变。
21．已知轧辊直径为300mm ，轧辊圆周速度为3m/s ，轧制前后工件的厚度分别为6mm 和4mm ，试计算该道次轧制时的平均应变速度。
22．已知尺寸为H=40mm 、B=70mm 、L=90mm 的长方形坯料，沿高向压下⊿h=8mm，压下速度0.5mm/s ，变形后工件宽度增加到b=82mm ，变形均匀。