自动齿轮变速箱齿比的计算与实例
齿比计算!
齿比计算！配比技巧！最后最重要！齿轮比计算所谓的齿轮比，就是以前齿盘的齿数除以后飞轮的齿数，所得到的数值就等于齿轮比，假设前齿盘齿数为44，后飞轮齿数为11，那踩踏的齿轮比就为44/11=4，所得到的数字4就是目前所踩踏的齿轮比。
若以纯粹的理论计算，当用44齿盘踩踏一圈，将带动后面11齿的后飞轮旋转四圈，若再乘以后轮(26寸)的轮径，便可以发现，踩踏一圈，车子就可以前进8.3公尺(26*2.54*3.14*4=829，大约等于8.3公尺)。
不过齿轮比4，并不算轻的齿轮比，需要相当的腿力才能踩动，而且大齿轮比，容易耗损链条，齿盘，飞轮甚至是变速器的寿命。
变速自行车是单速上发展来的,一般牙盘有两片，三片的，也有单片的。
飞轮有5、6、7、8、9、10片的，现在已有11片的。
目前山地车最常见的变速系统为前3速配后8速或9速，共24或27段变速即通常所说的几速车。
前齿盘的齿片规格多为22，32，42或22,32,44,而后面飞轮的规格则为飞轮为11-13-15-17-20-23-26-30，9速的为11、13、15、17、20、23、26、30、34）。
而车友们也可以数数看爱车的齿数各为多少，不过各位车友仔细来算算这其中的齿轮比，您会发现有些齿轮比是相当接近，一台27段变速的登山车，实际上可能只有20段左右的变速而已，所以变速时要有些技巧，若是变到相同的齿轮比，那就丧失变速的功效。
下面来看看一般27段变速的各段速度的齿轮比：当在骑乘爬坡时，若想要从大齿盘降低为中齿盘，又不希望突然将蹬踏频率提高太多，可在降低齿盘后，将后飞轮顺势变重两片，这样会得到比原来轻一点的齿轮比，又不会让蹬踏频率一下拉高太多，导致车友们踩得太急，呼吸与节奏都失去平衡。
山地车骑乘除了机械上的齿轮比运用之外，当然要靠骑乘者的腿部配合了，而两者结合起来就是蹬踏频率的概念，而适当的蹬踏频率也是重要关键之一。
蹬踏频率的计算方式就是以10秒钟为一个单位,计算在10秒钟以内,一只脚踩踏了几圈,所得的权数再乘以六便得到自己每分钟的蹬踏频率了。
各种齿轮系传动比的计算
各种齿轮系传动比的计算齿轮传动是常见的机械传动形式之一，通过不同齿数的齿轮之间的啮合，实现输出轴的转速和转矩的传递。
传动比是指输入轴和输出轴的转速之比，常用于计算机械系统的传动效率和输出速度。
齿轮传动比的计算需要确定输入轴和输出轴的齿轮齿数，并根据齿数的关系得出传动比。
以下是常见的四种齿轮传动形式及其传动比的计算方法：1.平行轴齿轮传动平行轴齿轮传动是最常见的传动形式，通过两个平行轴上的啮合齿轮实现转速的传递。
传动比计算公式如下：传动比=输出齿轮齿数/输入齿轮齿数例如，如果输入齿轮齿数为20，输出齿轮齿数为40，则传动比为40/20=22.穿轴齿轮传动穿轴齿轮传动是指两个轴不平行的齿轮传动形式，通过一个或多个齿轮对实现转速的传递。
传动比计算公式如下：传动比=输出齿轮齿数之积/输入齿轮齿数之积例如，如果输入轴上的齿轮齿数为20和30，输出轴上的齿轮齿数为40和60，则传动比为(40*60)/(20*30)=43.内外啮合齿轮传动内外啮合齿轮传动是指一个齿轮位于另一个齿轮的内部并与其啮合的传动形式，通过齿轮的运动将旋转轴方向转换为轴线的转速和转矩。
传动比计算公式如下：传动比=1/(输入齿轮齿数/输出齿轮齿数)例如，如果输入齿轮齿数为40，输出齿轮齿数为20，则传动比为1/(40/20)=0.54.斜齿轮传动斜齿轮传动是通过斜齿轮的啮合实现转速传递的传动形式，常用于垂直传动和传递大转矩的场合。
传动比计算公式如下：传动比=输出齿轮齿数/输入齿轮齿数*齿数系数齿数系数是考虑斜齿轮齿面压力角的修正系数。
以上是常见齿轮传动形式的传动比计算方法，根据实际情况选择适合的传动形式，并根据齿轮齿数和齿数系数计算传动比。
对于复杂的齿轮系统，可以通过级联多个传动，将多个传动比相乘来得到整个系统的传动比。
可以通过合理的设计和计算，实现满足机械系统性能要求的传动比。
齿轮传动比计算公式【大全】
齿轮传动比计算公式内容来源网络，由“深圳机械展（11万㎡，1100多家展商，超10万观众）”收集整理！更多cnc加工中心、车铣磨钻床、线切割、数控刀具工具、工业机器人、非标自动化、数字化无人工厂、精密测量、3D打印、激光切割、钣金冲压折弯、精密零件加工等展示，就在深圳机械展.传动比=从动轮齿数/主动轮齿数=主动轮转速/从动轮转速i=z2/z1=n1/n21、传动比是机构中两转动构件角速度的比值，也称速比。
构件a和构件b的传动比为i=ωa/ ωb=na/nb，式中ωa和ωb分别为构件a和b的角速度（弧度/秒）；na和nb分别为构件a和b的转速（转/分）。
2、当式中的角速度为瞬时值时，则求得的传动比为瞬时传动比。
当式中的角速度为平均值时，则求得的传动比为平均传动比。
理论上对于大多数渐开线齿廓正确的齿轮传动，瞬时传动比是不变的；对于链传动和摩擦轮传动，瞬时传动比是变化的。
对于啮合传动，传动比可用a和b轮的齿数Za和Zb表示，i=Zb/Za；对于摩擦传动，传动比可用a和b轮的直径Da和Db表示，i=Db/Da。
3、多级减速器各级传动比的分配，直接影响减速器的承载能力和使用寿命，还会影响其体积、重量和润滑。
传动比一般按以下原则分配：使各级传动承载能力大致相等；使减速器的尺寸与质量较小；使各级齿轮圆周速度较小；采用油浴润滑时，使各级齿轮副的大齿轮浸油深度相差较小。
4、低速级大齿轮直接影响减速器的尺寸和重量，减小低速级传动比，即减小了低速级大齿轮及包容它的机体的尺寸和重量。
增大高速级的传动比，即增大高速级大齿轮的尺寸，减小了与低速级大齿轮的尺寸差，有利于各级齿轮同时油浴润滑；同时高速级小齿轮尺寸减小后，降低了高速级及后面各级齿轮的圆周速度，有利于降低噪声和振动，提高传动的平稳性。
故在满足强度的条件下，末级传动比小较合理。
5、传动比=使用扭矩÷9550÷电机功率×电机功率输入转数÷使用系数6、传动比=主动轮转速除以从动轮转速的值=它们分度圆直径比值的倒数。
齿轮系传动比计算
齿轮系传动比计算齿轮是一种常用的机械传动装置，通过齿轮之间的啮合来实现转速和力矩的传递。
齿轮传动比（也称齿数比）是指驱动齿轮（一般称为主动轮）的齿数与被驱动齿轮（一般称为从动轮）的齿数之比。
传动比的计算是基于齿轮的齿数和齿轮的直径来进行的。
在传动系统中，驱动轮（A轮）与被驱动轮（B轮）之间的传动比可以通过以下公式来计算：传动比=驱动轮（A轮）的齿数/被驱动轮（B轮）的齿数首先，我们需要知道驱动轮（A轮）和被驱动轮（B轮）的齿数。
对于两个齿轮之间的传动，齿数通常是个整数，并且它们的比值可以是任何正整数。
但是，为了实现更好的齿轮传动效果，通常希望齿轮的齿数比尽可能接近1，这样可以减小传动误差和冲击。
接着，我们需要知道齿轮的直径。
齿轮的直径是齿轮的外直径，即从一个齿顶到另一个齿顶的距离。
齿轮的直径与齿轮的齿数之间存在一定的关系，可以通过以下公式来计算：齿轮的直径=齿轮的模数×齿数其中，模数是指齿轮的每齿宽度的单位长度。
模数的选择与齿数和精度有关，通常选择合适的模数能够实现更好的齿轮传动效果。
通过上述公式计算得出驱动轮（A轮）和被驱动轮（B轮）的直径后，可以进一步计算出驱动轮（A轮）和被驱动轮（B轮）之间的传动比。
传动比=驱动轮（A轮）的直径/被驱动轮（B轮）的直径需要注意的是，在实际应用中，为了增加传动稳定性并减小齿轮传动误差，通常会使用多个齿轮组成的齿轮箱进行传动，这就需要逐级计算各级齿轮的传动比。
此外，还需要考虑齿轮的齿形，根据齿轮的齿形不同，可能会出现齿轮传动误差、噪声和振动等问题。
因此，在进行齿轮传动比计算之前，还需要对齿轮的齿形、精度和材料等进行充分的分析和选择。
总之，齿轮系传动比的计算是基于齿轮的齿数和直径的。
按照一定的规则和公式，可以准确地计算出齿轮传动系统中各级齿轮之间的传动比，并根据实际需要进行合理的调整和优化，以实现稳定、高效的机械传动。
通用自动变速器行星齿轮机构的速比计算
增 大到
２２５ｒ／ｍｉｎ，
因此无法
滑行。第一 排太阳轮
未参与工
图１０通用６档变速器结构示意图
万方数据
蔡瓤湃痊
ＡＵＴＯＭＯＢＩＬＥ ＭＡＩＮＴＥＮＡＮＣＥ
Ｏｔ，相等，且等于整数２，即以ａ＝２、 （１＋仅）＝３代入方程：
Ｎ２２＝Ｎ１３＝（Ｎ１１＋２Ｎ１２）÷３
又因为Ｎ。；＝０，所以：
Ｎ１３＝（０＋２Ｎ１２）＋３＝２／３Ｎ１２
２档滑行的另一种方法是，在第 三排太阳轮制动路线上配置自由轮 （右面三列方程）。在第一排行星齿轮 机构中，由于齿圈提速，太阳轮相对 固定，使行星架也提速到７３３ｆｆｍｉｎ。 因而在第二排行星齿轮机构中，由于 齿圈提速，太阳轮相对固定，使行星 架也提速到１５４４ｒ／ｒａｉｎ。最终，在第二 排行星齿轮机构中，由于齿圈提速， 太阳轮提速到２１２ｒ／ｍｉｎ。因此，在第 三排太阳轮制动路线上配置自由轮， 才能够使２档滑行。
又因为Ｎ１ｌ＿Ｎ２。，二者都是主动元 件，可以将它们合并为Ｎ：。；Ｎ。＝Ｎ。２， 二者都是输出元件，可以将它们合并 为Ｎ，，，解得：
（５／３）Ｎ２ｌ＝（９，２—“３）Ｎ３３ Ｎ２１＝（１９／６）Ｘ（３／５）Ｎ３３＝５７／３０Ｎ３３＝
１．９００Ｎ３３
即：１１＝１．９００ ３档工作时三排行星齿轮机构 中各元件的转速计算如下： １９００＋２ｘ（１０００）一３ｘ（１３００）＝Ｏ
ＮＩ Ｌ＋ｄＩＮｌ２一（１＋ｏｑ）Ｎ１３＝０
动器Ｂ３增配自由轮比较合理。
Ｎ２１＋ｃ￡２Ｎ笠一（１＋ｃｘ２）Ｎ２ａ＝０
１０％，为１ ｌＯＯｄｍｉｎ时，第二排行星架 和第三排齿圈转速也增加１０％，达到 １６５０ｆｆｍｉｎ。为此，第一排行星架和第 二排齿圈也从１５００ｄｍｉｎ提速到 １７２５ｒ／Ⅱｌｉｎ。第一排太阳轮必须随之从 ２５００ｒ／ｍｉｎ提速到２９７５ｄｍｉｎ才能保 证滑行，应配置自由轮，否贝Ｕ ４档无 滑行。从左、右两边方程分析右边制
自动变速器行星齿轮机构的速比计算
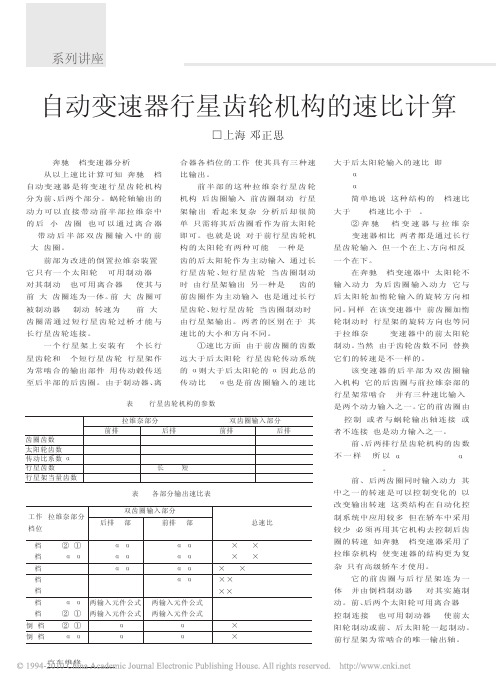
大于后太阳轮输入的速比， 即： α２＝（ １１４＋８６） ／８６＝２．２７９ α１＝（ ４２＋８６） ／８６＝１．４８８ 简单地说， 这种结构的 １ 档速比
大于 ２， ２ 档速比小于 ２。 ②奔驰 ７ 档变速器与拉维奈
ＡＧ４ 变速器相比， 两者都是通过长行 星齿轮输入， 但一个在上、方向相反， 一个在下。
６．作者应对所投稿件负责， 避免抄袭和一稿多投， 稿 件 发 生 版权纠纷等问题， 责任由作者自负。
汽车维修编辑部
%%%%%%%%%%%%%%%%%%&
%%%%%%%%%%%%%%%%%%&
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%&
４７ 汽车维修 ２００８．４
３．电子邮件的主题请用文章的标题， 以避免稿件丢失 ， 并 方 便编辑选稿。希望作者不要重复投稿， 在收到稿件后， 编辑部会 及时回复电子邮件， 告诉作者稿件已收到。若没有得到回复， 可 用 电 子 邮 件 或 电 话 （ ０４３１－ ８５９０１０９７、０４３１－ ８５９０１３１０） 查 询 。 另 外， 有些作者将同一篇稿件分别投在两个信箱里， 这样做没有必 要， 还易造成混乱， 所以请投在一个信箱即可。
超速档为后齿圈转速低于前齿
档位
拉维奈部分
Ｋ１
Ｂ１
Ｂ３
速比
Ｋ２
１档
○ ２．２７９
双齿圈输入部分
Ｋ３
Ｂ２
ＢＲ
○○
总速比 速比
１．９２１ ４．３７７
圈（ ６ 档、７ 档） ， 先在后排中两元件输 入， 由于齿圈降速， 由后排方程可知， 后太阳轮必须提高转速。进而， 前排
２档
○
自动变速器传动比的计算方法
图 7 4 挡动力传递路线
由上述计算实例可知 ,混合行星齿轮机构的传 动比计算需根据具体情况具体分析 ,但计算方法基 本相同 。即根据固定元件的转速为零 、相互连接的
(下转第 13 页)
2 单排单级行星齿轮机构传动比的计算
最简单的行星齿轮机构由一个太阳轮 (亦称中 心轮) 、一个内齿圈和一个带行星轮的行星架组成 , 称之为单排单级行星排 (如图 1 所示) 。由于单排行 星齿轮机构具有 2 个自由度 ,即需对太阳轮 、齿圈和 行星架三者之一施加制动 (使其转速为零) 或约束 (使其以某一固定的转速旋转) ,以获得某一所需的 传动比 ;如果将三者中的任何两个连接为一体 ,则整 个行星齿轮机构以同一速度旋转 。
为行星架假想齿数 。
下面就汽车自动变速器中单排单级行星齿轮机
构的几种运动状态进行分析 。
1) 太阳轮固定 ( n心 = 0) 、行星架驱动 、内齿圈输 出时 ,将 n心 = 0 代入式 (1) 、(2) ,则其传动比 i = n架 / n圈 = Z圈 / ( Z心 + Z圈 ) , 传动比小于 1 , 即为同向增速
iR = n后心 / n前架 = n后心 / n后圈 = - Z后圈 / Z后心 =
- 98/ 37 = - 2. 648 648 6
件被同时驱动 ,则整个行星齿轮机构以一个整体同 向等速旋转 , 为直接传动挡 , 即后排齿圈/ 前排行星 架同向等速输出 , i3 = 1 。因动力传动过程没有单向 离合器参与 ,故发动机制动 (见图 6) 。
图 6 3 挡动力传递路线
6) 4 挡时 , 3 、4 挡离合器接合 , 驱动后排行星 架/ 前排齿圈 。同时 2 、4 挡制动带工作 ,固定后排太 阳轮 ,则后排齿圈/ 前排行星架同向增速输出 。因动 力传动过程没有单向离合器参与 ,故发动机制动 (见 图 7) ,即 n后心 = 0 ,代入式 (4) ,得 :
变速器传动比的计算方法及其原理
变速器传动比的计算方法及其原理传动比是指变速器输出轴的转速与输入轴的转速之比，是汽车变速器的重要性能指标。
它决定了汽车在不同速度下的运行状态和动力输出情况。
为了实现高效、平稳的行驶，驾驶员需要了解变速器传动比的计算方法及其原理。
本文将介绍变速器传动比的计算方法和相关原理。
一、传动比的定义传动比是通过变速器来调节输出轴转速与输入轴转速之间的比值。
以手动变速器为例，传动比由使用者通过操纵换挡杆控制。
不同挡位会导致不同的传动比，进而实现不同的车速。
二、传动比的计算方法传动比的计算方法根据变速器的设计和构造不同而异。
下面将介绍两种常见的传动比计算方法。
1. 简单计算法对于一些简单的变速器结构，可以通过输出轴转速与输入轴转速之比直接计算传动比。
传动比 = 输出轴转速 / 输入轴转速例如，一台汽车变速器的输出轴转速为4000转/分钟，输入轴转速为2000转/分钟，则传动比为：传动比 = 4000 / 2000 = 22. 齿轮比法对于复杂的齿轮传动系统，传动比的计算可以通过齿轮比来实现。
变速器中齿轮的设计决定了传动比的变化。
传动比 = Z2 / Z1其中，Z2为输出轴上的齿轮的齿数，Z1为输入轴上的齿轮的齿数。
例如，一台汽车变速器的输出轴上的齿轮齿数为30，输入轴上的齿轮齿数为15，则传动比为：传动比 = 30 / 15 = 2三、传动比的原理传动比的原理是通过不同齿轮组合或输入输出轴间的直接比例关系实现的。
1. 齿轮传动原理在齿轮传动中，通过不同大小的齿轮组合来改变传动比。
齿轮的齿数与直径成反比，因此齿轮半径越大，齿数越小，传动比越大。
2. 偏心齿轮原理在偏心齿轮传动中，通过离心力的作用，使齿轮在轴上产生偏心运动，从而改变传动比。
通过调整齿轮的偏心程度，可以实现不同的传动比。
3. 液力变速器原理在液力变速器中，通过油流的流动和涡轮的转动来改变传动比。
液力变速器根据需要自动调整液压传动比，从而实现平稳的变速。
传动比计算举例范文
传动比计算举例范文
传动比是指在机械装置中，输出轴和输入轴之间的角速度比值，用于
衡量装置的扭矩放大或减小情况。
传动比计算的基本原理是根据轴上连续
的齿轮、皮带、链条等传动装置，通过计算齿轮关系或被动轮的齿数比、
牵引辊的直径比等，得到输出轴和输入轴之间的速度比或直径比来计算。
下面我将以两个实际例子来说明传动比的计算方法。
案例一：齿轮传动
假设有一组带动齿轮装置，输入轴上有一个齿轮A，输出轴上有一个
齿轮B。
已知齿轮A的齿数为20，齿轮B的齿数为40。
求传动比。
根据齿轮的传动原理，可以得知输出轴与输入轴之间的传动比为齿轮
B的齿数与齿轮A的齿数的比值，即40/20=2
因此，传动比为2:1，即输出轴每转动2圈，输入轴转动1圈。
案例二：皮带传动
假设有一组带动皮带装置，输入轴上有一个驱动轮，其直径为10cm，输出轴上有一个被动轮，其直径为20cm。
求传动比。
根据皮带传动的原理，可以得知输出轴与输入轴之间的传动比为被动
轮的直径与驱动轮的直径的比值，即20cm/10cm = 2
因此，传动比为2:1，即输出轴每转动2圈，输入轴转动1圈。
从以上两个实例可以看出，传动比是通过输入轴与输出轴上的传动装
置的几何关系得出的，不同的传动装置有不同的计算方法。
在实际应用中，可根据传动装置的类型选择相应的计算方法进行传动比的计算。
自动变速器速比计算
自动变速器速比的计算为适应人们日益提高的对汽车安全与舒适度的要求，自动变速器在轿车上逐渐普及。
随着自动变速器的广泛应用，轿车驾驶变得轻松，乘坐变得舒适。
但由于自动变速器的结构相对复杂，自动变速器速比计算在很多教材中暂未涉及，这给汽车维修类专业学习者理解自动变速器的传动性能和档位分析造成了一定的困难。
下面，我们对典型的单排行星齿轮机构的传动比计算原理及方法作出仔细分析。
一、自动变速器动力传递概述自动变速器由液力元件、变速机构、控制系统、主传动部件等几大部分组成。
变速机构可分为固定平行轴式、行星齿轮式和金属带式无级自动变速器（CVT）三种。
在轿车上，自动变速器都采用行星齿轮式变速机构。
行星齿轮机构一般由2个或2个以上行星齿轮组按不同的组合方式构成，其作用是通过对不同构件的驱动或制动，产生不同速比的前进挡、倒挡和空挡。
换挡执行元件是指约束行星齿轮机构的某些构件，其作用包括固定并使其转速为0，或连接某部件使其按某一规定转速旋转。
通过适当选择行星齿轮机构被约束的基本元件和约束方式，就可以得到不同的传动比，形成不同的挡位。
换挡执行元件包括离合器、制动器和单向离合器三种不同的元件。
其中，离合器的作用是连接或驱动，以将变速机构的输入轴（主动部件）与行星齿轮机构的某个部件（被动部件）连接在一起，实现动力传递。
制动器的作用是固定行星齿轮机构中的某基本元件，它工作时将被制动元件与变速器壳体连接在一起，使其固定不能转动。
单向离合器具有单向锁止的功能，当与之相连接元件的旋转趋势使其受力方向与锁止方向相同时，该元件被固定（制动）或连接（驱动）；当受力方向与锁止方向相反时，该元件被释放（脱离连接）。
由此可见，单向离合器在不同的状态下具有与离合器、制动器相同的作用。
二、单排单级行星齿轮机构1、单排单级行星齿轮机构的传动比。
最简单的行星齿轮机构由一个太阳轮、一个内齿圈和一个行星架组成，我们称之为一个单排单级行星排，如图1所示。
由于单排行星齿轮机构具有两个自由度，为了获得固定的传动比，需将太阳轮、齿圈或行星架三者之一制动（转速为0）或约束（以某一固定的转速旋转），以获得我们所需的传动比；如果将三者中的任何两个连接为一体，则整个行星齿轮机构以同一速度旋转。
自动变速器行星齿轮机构的速比计算
４５ 汽车维修 ２００８．６
系列讲座 ＡＵＴＯＭＯＢＩＬＥ ＭＡＩＮＴＥＮＡＮＣＥ
Ｎ１１＋α１Ｎ１２ －（ １＋α１） Ｎ１３＝０ Ｎ３１＋０－（ １＋α３） Ｎ３３＝０ 因 为 Ｎ１１＝－ Ｎ３１， 可 将 两 方 程 合 并 为单列方程： α１Ｎ１２－（ １＋α１） Ｎ１３＝（ １＋α３） Ｎ３３ α１Ｎ１２ ＝（ １ ＋α１） Ｎ１３ －（ １ ＋α３） Ｎ３３ ＝ （ α１＋α３＋２） Ｎ３３ Ｎ１２＝（ α１＋α３ ＋２） ／α１Ｎ３３ 以 此 类 推 ， 如 果 Ｎ１１＝－ ３Ｎ３１， 则 此 时 的 速 比 为（ α１＋３α３＋４） ／α１Ｎ３３； 如 果 Ｎ１１＝－ ４Ｎ３１， 则 此 时 的 速 比 为（ α１＋４α３＋ ５） ／α１Ｎ３３。 由此可见， １ 档速比是随着泵轮 和涡轮的转速差变化的， 它们的差别 越大， １ 档速比的分子值越大， １ 档速 比 也 就 越 大 。当 泵 轮 与 涡 轮 转 速 相 等 时 ， １ 档 速 比 为（ α１＋α３＋２） ／α１， 用 α１＝ α３＝２ 代入， １ 档速比为（２＋２＋２）÷２＝３。 ２） ２ 档 该变速器从 ２ 档开始只使用前 半部分， 变矩器及后半部分不参与工 作。２ 档时是离合器 Ｃ１ 工作， 使第一 排齿圈主动； 制动器 Ｂ０ 工作， 使第一 排太阳轮制动， 第一排行星架输出。 代入方程： Ｎ１１＋α１Ｎ１２－（ １＋α１） Ｎ１３＝０ 式 中 Ｎ１１＝０、Ｎ１２ 主 动 、Ｎ１３ 输 出 ， 解得： Ｎ１２＝（ １＋α１） ／α１Ｎ１３ 用 α１＝２ 代 入 ， ２ 档 速 比 为（ １＋２） ÷２＝１．５。 ３） ３ 档 离合器 Ｃ２ 工作， 使 第 二 排 齿 圈 和第一排行星架直接为主动， 第一排 行星架直接带动输出轴输出动力， 其 传动比等于 １。 ４） ４ 档 离合器 Ｃ３ 工作， 使 第 二 排 行 星 架为主动， 制动器 Ｂ０ 工作， 使第 一 排 、第 二 排 太 阳 轮 制 动 ， 第 二 排 齿 圈 和 第 一 排 行 星 架 直 接 为 输 出 。代 入 方 程： Ｎ２１＋α２Ｎ２２－（ １＋α２） Ｎ２３＝０ 式 中 Ｎ２１＝０、Ｎ２３ 主 动 、Ｎ２２ 输 出 ， 解得： Ｎ２３＝α２（／ １＋α２） Ｎ２２
自动齿轮变速箱齿比的计算与实例
a) 单一的行星齿轮组 – 表格计算法
构件(齿轮比)
行星轮速 (= P- C) (相讨干行星支架速度)
S
C
R
P
1
0
- S / R
-S / P
- S / P
対以上每个行格乘以 “- R/S” 值
- R / S
0
1
R / P
R / P
対以上每个行格 加以 “- 1” 值
B) 杠杆比例法(LEVER DIAGRAM METHOD)
单一行星齿轮组 双行星齿轮组 复合式(Compound) 行星齿轮系 辛普森行星齿轮系统(Simpson Gear train) Ravignaux 行星齿轮系统
三种常用齿轮比(Gear Ratio)的计算方法
a) 杠杆比例计算法 - 单一行星齿轮组
双行星齿轮比总结 - 杠杆比例法
*
*
C) 复合式系统齿轮比 - 杠杆比例计算法
实例 1 - 辛普森(Simpson) 行星齿轮系统 - 使用两个单一行星组 来合成一个复合式的齿轮系统
杠杆比例法
R1 C1 S1
R2 C2 S2
K1S1 K1R1
K2S2 K2R2
Pinion
大阳轮(S)
PC
R PC S
S R
需要三道力量以达到杠杆上的平衡即: 输入(I), 输出(O) 及紧固力G)
I O G O G I G O I
O I G I G O G I O
6 种可行的速度比排列 又 T.R = 1 / S.R.
SUN = 1
Ring =0
Carrier
-S / (R-S)
自动变速器行星齿轮机构的速比计算
前 、后 两 排 行 星 齿 轮 机 构 的 传 动
比系数为： α１＝１１０／４２＝２．６２（ 未采用） ， α２＝８６／４２＝２．０９。
①当 Ｂ１ 制动时， 太阳轮 Ｎ２１ 转速 为 ０。在后排行星齿轮机构中， 太阳 轮制动， 齿圈输入， 行星架输出。代入
ＢＲ
Ｂ２
公式： Ｓ１Ｎ１＋ＩＮ２－（ Ｓ１＋Ｉ） Ｎ３＝０ ０＋２．０９Ｎ２２－ ３．０９Ｎ２３＝０ Ｎ２２＝（ ３．０９／２．０９） Ｎ２３＝１．４８８ Ｎ２３ 或直接用公式： ０＋８６×Ｎ２２－（ ４２＋８６） ×Ｎ２３＝０ Ｎ２２＝（ １２８／８６） Ｎ２３ 即： 速比 Ｉ＝１．４８８ ②当 Ｂ３ 制动时， 前齿圈被 制 动 ，
结构型式和速比计算方法与其它变
速 器 均 有 所 不 同 。它 的 主 要 档 位 属 于
在行星齿轮机构中有两个输入元件、
一个输出元件的复合传递运动。
该 变 速 器 的 结 构 如 图 １３ 所 示 。
变矩器的输出动力由蜗轮轴传至变
速器输入轴， 动力输入到变速器后分
为两部分： 输入轴连接拉维奈的后内
这种双齿圈输入的行星齿轮机 构， 当两齿圈的输入转速相等时， 输 出轴以直接档输出； 当后齿圈的输 入转速发生无级变化， 与前齿圈不 同步时， 输出轴随之发生反向无级 变速； 当后齿圈输入定量减速变化 时 ， 输 出 轴 则 产 生 定 量 增 速 档 位 。奔 驰 ７ 档变速器是利用后者， 而非无 级变速。
齿比、马力和扭矩的换算
齿比、马力和扭矩的换算齿比、马力和扭矩的换算 1英制马力0.746千瓦kw1公制马力0.735千瓦kw 马力:是发动机功率单位是单位时间内发动机作功能力。
汽车驱动理论: 马力与扭力哪一项最能具体代表车辆性能有人说起步靠扭力加速靠马力有人说马力大代表极速高扭力大代表加速好其实这些都是片段的错误解释其实车辆的前进一定是靠引擎所发挥的扭力所谓的扭力在物理学上应称为扭矩因为以讹传讹的结果大家都说成扭力也就从此流传下来为导正视听本文以下皆称为扭矩。
扭矩的观念从小学时候的杠杆原理就说明过了定义是:垂直方向的力乘上与旋转中心的距离公制单位为:牛顿-米N-m除以重力加速度9.8m/sec2之后单位可换算成国人熟悉的公斤-米kg-m。
英制单位则为磅-呎lb-ft在美国车的型录上较为常见若要转换成公制只要将lb-ft的数字除以7.22即可。
汽车驱动力的计算方式: 将扭矩除以车轮半径即可由引擎马力-扭力输出曲线图可发现在每一个转速下都有一个相对的扭矩数值这些数值要如何转换成实际推动汽车的力量呢答案很简单就是除以一个长度便可获得力的数据。
举例而言一部1.6升的引擎大约可发挥15.0kg-m的最大扭力此时若直接连上185-60-R14尺寸的轮胎半径约为41公分则经由车轮所发挥的推进力量为15/0.4136.6公斤的力量事实上公斤并不是力量的单位而是重量的单位须乘以重力加速度9.8m/sec2才是力的标准单位牛顿。
36公斤的力量怎么推动一公吨的车重呢而且动辄数千转的引擎转速更不可能恰好晌痔プ俜裨虺底硬痪头善鹄戳诵液么厦鞯娜死喾?髁顺萋掷貌煌笮〉某萋窒嗔钆淇梢越乃俣冉档屯苯ぞ胤糯蟆,捎诔萋值脑仓鼙染褪前刖侗纫虼舜有〕萋执荻链蟪萋质弊乃俣冉档偷谋嚷室约芭ぞ胤糯蟮谋妒记『玫扔诹匠萋值某菔壤飧霰壤褪撬降某萋直取?举例说明以小齿轮带动大齿轮假设小齿轮的齿数为15齿大齿轮的齿数为45齿。
当小齿轮以3000rpm的转速旋转而扭矩为20kg-m时传递至大齿轮的转速便降低了1/3变成1000rpm但是扭矩反而放大三倍成为60kg-m。
齿轮系传动比计算公式
齿轮系传动比计算公式嘿，咱今儿就来好好聊聊齿轮系传动比计算公式这回事儿！齿轮这玩意儿，在咱们生活里可不少见。
就拿自行车来说吧，那链条带动的不同大小的齿轮，其实就藏着传动比的秘密。
先来说说啥是传动比。
简单讲，传动比就是主动轮转速与从动轮转速的比值，或者是主动轮齿数与从动轮齿数的反比。
比如说，主动轮转两圈，从动轮才转一圈，那传动比就是 2:1。
那齿轮系传动比计算公式是啥呢？一般来说，如果是简单的定轴齿轮系，传动比就等于所有从动轮齿数的乘积除以所有主动轮齿数的乘积。
咱举个例子啊。
有一个齿轮系，主动轮 A 有 20 个齿，从动轮 B 有40 个齿，从动轮 C 有 30 个齿。
那从 A 到 B 再到 C 的传动比就是（40×30）÷20 = 60。
这就意味着，主动轮 A 转 60 圈，从动轮 C 才转一圈。
在实际应用中，齿轮系传动比的计算可重要了。
就像汽车的变速箱，通过不同大小齿轮的组合，来改变传动比，从而实现不同的车速和扭矩输出。
我记得有一次去修车厂，看到师傅在修理一辆汽车的变速箱。
他拿着工具，仔细地检查着那些齿轮，嘴里还念叨着传动比的事儿。
我凑过去问他，师傅就很耐心地给我解释，说不同的齿轮组合会影响车子的性能。
他指着一个磨损比较严重的齿轮说，就是因为这个齿轮的问题，导致传动比不对，车子开起来就没劲儿。
那时候我才真切地感受到，这看似简单的传动比计算公式，在实际中是多么关键。
再比如说工厂里的机器设备，很多也是靠齿轮传动来工作的。
如果传动比计算不准确，那生产出来的产品可能就达不到要求，甚至会导致机器故障。
总之，齿轮系传动比计算公式虽然看起来有点复杂，但只要咱明白了其中的道理，掌握了方法，就能在很多地方派上用场。
不管是设计机械还是解决实际问题，都能让咱们更得心应手。
所以啊，同学们，可别小看这小小的齿轮和传动比，这里面的学问大着呢！。
齿轮传动比计算公式【大全】
齿轮传动比计算公式内容来源网络，由“深圳机械展（11万㎡，1100多家展商，超10万观众）”收集整理！更多cnc加工中心、车铣磨钻床、线切割、数控刀具工具、工业机器人、非标自动化、数字化无人工厂、精密测量、3D打印、激光切割、钣金冲压折弯、精密零件加工等展示，就在深圳机械展.传动比=从动轮齿数/主动轮齿数=主动轮转速/从动轮转速i=z2/z1=n1/n21、传动比是机构中两转动构件角速度的比值，也称速比。
构件a和构件b的传动比为i=ωa/ ωb=na/nb，式中ωa和ωb分别为构件a和b的角速度（弧度/秒）；na和nb分别为构件a和b的转速（转/分）。
2、当式中的角速度为瞬时值时，则求得的传动比为瞬时传动比。
当式中的角速度为平均值时，则求得的传动比为平均传动比。
理论上对于大多数渐开线齿廓正确的齿轮传动，瞬时传动比是不变的；对于链传动和摩擦轮传动，瞬时传动比是变化的。
对于啮合传动，传动比可用a和b轮的齿数Za和Zb表示，i=Zb/Za；对于摩擦传动，传动比可用a和b轮的直径Da和Db表示，i=Db/Da。
3、多级减速器各级传动比的分配，直接影响减速器的承载能力和使用寿命，还会影响其体积、重量和润滑。
传动比一般按以下原则分配：使各级传动承载能力大致相等；使减速器的尺寸与质量较小；使各级齿轮圆周速度较小；采用油浴润滑时，使各级齿轮副的大齿轮浸油深度相差较小。
4、低速级大齿轮直接影响减速器的尺寸和重量，减小低速级传动比，即减小了低速级大齿轮及包容它的机体的尺寸和重量。
增大高速级的传动比，即增大高速级大齿轮的尺寸，减小了与低速级大齿轮的尺寸差，有利于各级齿轮同时油浴润滑；同时高速级小齿轮尺寸减小后，降低了高速级及后面各级齿轮的圆周速度，有利于降低噪声和振动，提高传动的平稳性。
故在满足强度的条件下，末级传动比小较合理。
5、传动比=使用扭矩÷9550÷电机功率×电机功率输入转数÷使用系数6、传动比=主动轮转速除以从动轮转速的值=它们分度圆直径比值的倒数。
自动变速器行星齿轮机构的速比计算
２档工作时，离合器ｃ。继续工
阳轮与第二排太阳轮共体，。可被ｃ， 作，使第二、三排的太阳轮为主动；制
动器Ｂ：工作，使第
Ⅶｌ
ＩＵ 呲
¨ｎ｜ｉ｛
ｃ１
ｃ２
Ｔ Ｉ一
丰 ｌ＝
ｌ
ｌ
－Ｉ
二排齿圈与第一排 行星架制动（转速为 ０）。在第二排行星齿 轮机构中，太阳轮为 主动，齿圈制动，行 星架输出并传递给 第三排齿圈。在第三
汽车维修２００８．２
行业资讯ＡＵＴＯＭＯＢｌＬ…ＭＥＮＡＮｃＥ
吝 注的交强险费率调整听证
｜ｊ军篆妻懑兹意
即 ｊ
；Ｉ等 实
』｜彦耸 的 一
五
付相关条款的质疑，成为 人们关注的焦点，修改《道 路交通安全法》第七十六 条相关条款势在必行， ２００８年降低交强险费率 已毫无悬念。
：斡鬻篷蓄
｜｜ｊ；；囊黧巍嚣
１９０５＋２．５７×１０００－３．５７Ｎ∞＝０
万方数据
解得：Ｎ３３＝（１９０５＋２５７０）÷３．５７＝
１２５３
即５档速比１＝１０００＋１２５３＝０．７９９ ６）倒档速比 这种结构的倒档也很复杂，也需 用三排联立才能求出。倒档Ｉ作时， 改为离合器ｃ，工作，使第一排太阳 轮主动，同时制动器Ｂ，工作，使第 一、三排齿圈和第二排行星架制动 （转速为０）。同样，也是三排联立，首 先分析第一排，然后是第二排，最后 是第三排。 在第一排中，太阳轮主动，齿圈 制动，行星架输出，速比是１＋ｄ＝ ３．５７，传递给第二排齿圈。如果太阳 轮转速为１０００ｒ／ｍｉｎ，则输出转速为
图１２ ＺＦ一５ＨＰ２４变速器结构示意图
排行星齿轮机构中，
万方数据
太阳轮和齿圈均为主动，但两者的转 速不同。假定太阳轮的转速为１，则 齿圈的转速为１／（１＋仅：）。代入第三排 行星齿轮机构中：
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
-
+
I = 1, 2, 3 …; 乃系各行星齿轮组的代号
理论分析法 -- 各速度矢量方向性的规定及识别
2016/5/30
23
理论分析法 - 速度方程式的导演步骤
以下的程序系导引速度方程式的规则 - 单行星齿轮组:
1.
紧固内齿轮或太阳齿, 仅让非紧固的齿轮作 为输入件,同时也使行星架能自由転动.以此 内齿轮 导出输入轮和行星轮之间的速度 关系式 (方程式 1), 此方程式中应包含 行星架的転速; 方程式的速度矢量应 行星轮 和転动方向互相吻合.
三种常用的齿轮比(Gear Ratio)计算方法 C) 机构学分析法(KINEMATIC ANALTICAL
METHOD) a) 单一行星齿轮组 b) 双行星齿轮组 c) 复合式(Compound) 行星齿轮系
• 辛普森行星齿轮系统(Simpson Gear Train) • Ravignaux 行星齿轮系统 (见附件)
杠杆比例法
R1
R1
K1S1 C1 R2 C2 S1 S2 K2S2 K2R2 S1/S2 C1/R2 C2
由 K2 転换到 K1
K1S1 K1R1S2/(S2+R2) K1R1R2/(S2+R2) K1R1 =K2(S2+R2) K2 = K1R1 /(S2+R2)
设计要求 (R/S=?) R1/ S1 = C1
平行轴自动变速箱(DCT)的齿轮系统安排
齿轮比 - 平行轴齿轮変速箱
从动轮齿数 (T2 x T4 x….xTn-1) 齿速比(i)= ---------------------------------------主动轮齿数 (T1 x T3 x….xTn)
各种行星齿轮系的基本类型及其结构
A) 通常使用的行星齿轮系统
-S / P1
- RS / (P1 (R - S)) RS / ((P1(R-S)
-R / P1
(S+P1)/P1
(R+P1) / P1
c) 复合式系统齿轮比 - 表格计算法
实例 - 辛普森(Simpson) 行星齿 轮系统 - 使用两个单一行星组 来 合成一个复合式的齿轮系统
S2 /(S2+R2) =D
理论分析法– ANALYTICAL METOD
工程术语 ( Nomenclature)
代码符号 D M
= 齿轮节圆 (Pitch Diameter) = 模数 ( 法向)- Normal Module
R ( 半径 mm) RRi = RPi = RSi = RCi = Z ( 齿数) ZRi = ZPi = RSi = T ( 力矩 N-m) TRi =
0 -R/(R-S)
-1
- (R(S+P1) /(P1(R-S))
R(S-P2) / (P2(R-S))
- RS / (P1(R-S))
RS / (P2(R-S))
対以上每个行格乘以 “ – (R - S) / R ” 值
0
1
(R-S) /R
(S+P1) / P1
-(S-P2) / P2
(S+P1) / P1
行星齿速度比(相対行星支架) -S/P R/P R/P - RS /(P(R+S))
Carrier= 1
Carrier= 1
Sun =0
Ring =0
Ring
Sun
(R+S)/R
(R+S)/S
RS / (P(R+S))
S/P
b) 双行星齿轮组 – 表格计算法
构件
S 1 C
0
行星速度比(相対行星支架)
K1R1
R2/S2 = C2
实例 一 辛普森行星齿轮系统速度比总结 运転条件系依上图所示
R1
K 1S1
C1/R2
C2
K1R1S2/(S2+R2) K1R1R2/(S2+R2)
S1/S2
2016/5/30
19
杠杆比例计算法 ( LEVER DIAGRAM)的广泛应用
,
Chain
2016/5/30
20
a) 单一的行星齿轮组 – 表格计算法
构件(齿轮比)
S 1
-R/S
C
0
R
-S/R
P
-S / P
行星轮速 (= P- C) (相讨干行星支架速度)
-S/P R/P R/P - RS / (P (R + S)) RS/(P(R+S)
対以上每个行格乘以 “- R/S” 值
0
1
0
R/P
対以上每个行格 加以 “- 1” 值
长轴行星齿
单行星组系
双行星组系
B) 非常用行星歯轮系统
台阶式行星系 (Step Pinion)
Ravignaux 行星系
R2 R1 P2 P1
双内齿轮- 双行星轮 (DR-DP)
P2 P1 S1
S2
双太阳轮- 双行星轮 (DS-DP)
行星齿轮组的基本架抅及其传动规则
行星支架(PC) 行星轮 (P)
15
b) 杠杆比例计算法 - 双行星齿轮组
I O O I G I G O
PC
S
PC
R
G O G I
R
内齿轮[R]
P2
PC
P1
S
G O
G I O
太阳 齿(S)
I
双行星齿轮比总结 - 杠杆比例法
2016/5/30
17
C) 复合式系统齿轮比 - 杠杆比例计算法
实例 1 - 辛普森(Simpson) 行星齿 轮系统 - 使用两个单一行星组 来 合成一个复合式的齿轮系统
Ring Carrier Carrier Sun Ring Sun
行星2速度比 (相対行星支架)
S / P2 RS / (P2 (R-S)) -RS / ((P2(R-S) R / P2 -(S-P2)/P2 - (R - P2) / P2
S/R -S / (R-S) R / (R-S) R/S (R-S) / R -(R-S ) / S
杠杆
R
I O O I G I G
S
PC
内齿轮[R] PC
Pinion
G O G
R
S 需要三道力量以达到杠杆上的平 衡即: 输入(I), 输出(O) 及紧固力G)
I G
O G I O
大阳 轮(S)
O I
6 种可行的速度比排列 又 T.R = 1 / S.R.
单一行星齿轮比总结 - 杠杆比例法
2016/5/30
-(S-P2) / P2
输入(I) Sun = 1
SUN = 1 RING = 1 RING = 1 Carrier = 1 Carrier = 1
紧固(G) Carrier=0 Ring =0 Sun =0 Carrier=0 Sun =0 Ring =0
双行星齿轮比计算总结表 行星1速度比 输出端(O) 速度比 (相対行星支架)
Survey
三种常用齿轮比(Gear Ratio/s)的计算方法 A) 表格法(TABULATION METHOD)
a) 单一行星齿轮组 b) 双行星齿轮组 c) 复合式(Compound) 行星齿轮系
• 辛普森行星齿轮系统(Simpson Gear Train) • Ravignaux 行星齿轮系统
三种常用齿轮比(Gear Ratio)的计算方法 B) 杠杆比例法(LEVER DIAGRAM METHOD)
a) 单一行星齿轮组 b) 双行星齿轮组 c) 复合式(Compound) 行星齿轮系
• 辛普森行星齿轮系统(Simpson Gear train) • Ravignaux 行星齿轮系统
a) 杠杆比例计算法 - 单一行星齿轮组
-(R+S) /S
-1
S / (R+S)
(R - P) / P
対以上每个行格乘以 “ –S / (R+S)” 值
1
0 0 - S / (R - P) / ( P 格加 以 “- 1” 值
-R/(R+S)
-1
(R+S)/R
-R (S-P) / (P (R+S))
対以上每个行格乘以 “ – (R+S) / R ” 值
VCi = 行星架速度 ( I = 1,2,3…) w ( 角速度 - Radian /S)
wRi
= 内齿轮角速度 ( I = 1,2,3…) wPi = 行星齿轮角速度 ( I = 1,2,3…) wSi = 太阳轮角速度 ( I = 1,2,3…) wCi = 行星架角速度 ( I = 1,2,3…) n ( 転速 -RPM )
内齿轮节圆半径 ( I = 1,2,3…) 行星齿轮节圆半径 ( I = 1,2,3…) 太阳轮节圆半径 ( I = 1,2,3…) 行星支架半径 ( I = 1,2,3…) 内齿轮齿数 ( I = 1,2,3…) 行星齿轮齿数 ( I = 1,2,3…) 太阳轮齿数 ( I = 1,2,3…)
V (瞬 时的速度) (M/S) VRi = 内齿轮速度 ( I = 1,2,3…) Vpi = 行星齿轮速度 ( I = 1,2,3…) VSi = 太阳轮速度 ( I = 1,2,3…)
内齿轮速度 ( I = 1,2,3…) 行星齿轮速度 ( I = 1,2,3…) 太阳轮速度 ( I = 1,2,3…) 行星架速度 ( I = 1,2,3…)
速度 ( V ) 方向性的识别
FRi FCi FSi
= 内齿轮所受的传动力 ( I = 1,2,3…) 行星支架所受的传动力 ( I = = 1,2,3…) = 太阳轮所受的传动力 ( I = 1,2,3…)