结构力学三铰拱
合集下载
结构力学第4章 三铰拱

由上述的内力计算公式发现:
① 三铰拱的内力不但与荷载及三个铰的位置有关, 而且与拱轴线的形状有关。 ② 由于推力的存在,拱的弯矩比简支代梁的弯矩要小 ③ 三铰拱在竖向荷载作用下存在轴向受压。
注意: 1)该组公式仅适合平拱, 且承受竖向荷载;
2) 拱轴切线倾角k在拱的左半跨取正,右半跨取负;
三、内力图 (1)画三铰拱内力图的方法:水平基线描点法。
概述 三铰拱的计算 三铰拱的合理拱轴线
教学内容:﹡
﹡ ﹡
拱结构在工程中的应用实例 赵州桥
拱桥 (无铰拱)
超静定拱
世界上最古老的铸铁拱桥(英国科尔布鲁克德尔桥),约230年历史
1997年建成的重庆万县长江大桥:世界上跨度最大的混凝土拱桥,主拱圈 为钢管混凝土劲性骨架箱型混凝土结构,全长 856.12米,主跨420米,桥面宽 24米,为双向四车道,是世界最大跨径的混凝土拱桥。由重庆交通大学土木建 筑学院顾安邦教授主研完成,设计施工技术的研究成果获国家科技进步一等奖
甘肃灞陵桥,又名卧桥,在渭源县城南门外的清源河上,是一座古典纯木结 构伸臂曲拱型廊桥, 主跨:40米,始建于明洪武年间(公元1368-1398年), 后被洪水冲毁。1919年仿兰州卧桥改建,被称为“渭水长虹”。
§4-1
一、梁与拱的关系 F
HA=0 A
概
述
F
B
HA=0 A
B
曲梁 F
拱:杆轴线为曲线,
两拱趾不在同一水平线上的拱因为简支梁的内力计算大家非常熟练所以在计算三铰拱平拱在竖向荷载作用下的内力时和同跨度同荷载的简支代梁对应起来以找出两者在支座反力计算内力计算方面的区别加以对比便于理解和记忆
基本要求:○ 了解拱结构的分类及特点。
结构力学5三铰拱课件

拱架搭设
根据设计要求,选用合适的材料搭设拱架;
施工流程与工艺要求
02
01
03
拱体安装
按照从两端向跨中的顺序,对称安装拱体构件;
拱顶合拢
在拱顶设置临时支撑,确保拱体稳定;
施工监测
对施工过程进行实时监测,确保施工安全和质量。
施工流程与工艺要求
工艺要求 拱架搭设应符合设计要求,确保稳定性和承载力;
拱体安装应保证构件对接准确,避免出现错位和扭曲;
施工流程与工艺要求
01
临时支撑设置应合理,确保拱体 在合拢过程中保持稳定;
02
施工监测应实时进行,及时发现 和解决施工中的问题。
安装方法与注意事项
安装方法 采用分段吊装法,将拱体分成若干段,分别吊装到位;
对接安装时,应保证对接位置准确,避免出现错位和扭曲;
安装方法与注意事项
• 合拢时,应设置临时支撑,确保拱体稳定。
结构力学5三铰拱课件
目
CONTENCT
录
• 三铰拱概述 • 三铰拱的力学分析 • 三铰拱的设计与计算 • 三铰拱的施工与安装 • 三铰拱的维护与加固
01
三铰拱概述
定义与特点
定义
三铰拱是一种静定结构,由两个 固定端和三个铰链支承构成。
特点
拱顶在竖向荷载作用下主要承受 压力,并通过铰链传递水平推力 ,保持拱的平衡。
保持三铰拱的清洁,避免 积尘、腐蚀等影响其使用 寿命的因素。
紧固与润滑
对三铰拱的连接部位进行 紧固,对活动部位进行润 滑,确保其正常运转。
常见问题与处理方法
1 2
结构损伤
如发现三铰拱出现裂纹、变形等损伤,应立即采 取措施进行修复或更换。
连接松动
根据设计要求,选用合适的材料搭设拱架;
施工流程与工艺要求
02
01
03
拱体安装
按照从两端向跨中的顺序,对称安装拱体构件;
拱顶合拢
在拱顶设置临时支撑,确保拱体稳定;
施工监测
对施工过程进行实时监测,确保施工安全和质量。
施工流程与工艺要求
工艺要求 拱架搭设应符合设计要求,确保稳定性和承载力;
拱体安装应保证构件对接准确,避免出现错位和扭曲;
施工流程与工艺要求
01
临时支撑设置应合理,确保拱体 在合拢过程中保持稳定;
02
施工监测应实时进行,及时发现 和解决施工中的问题。
安装方法与注意事项
安装方法 采用分段吊装法,将拱体分成若干段,分别吊装到位;
对接安装时,应保证对接位置准确,避免出现错位和扭曲;
安装方法与注意事项
• 合拢时,应设置临时支撑,确保拱体稳定。
结构力学5三铰拱课件
目
CONTENCT
录
• 三铰拱概述 • 三铰拱的力学分析 • 三铰拱的设计与计算 • 三铰拱的施工与安装 • 三铰拱的维护与加固
01
三铰拱概述
定义与特点
定义
三铰拱是一种静定结构,由两个 固定端和三个铰链支承构成。
特点
拱顶在竖向荷载作用下主要承受 压力,并通过铰链传递水平推力 ,保持拱的平衡。
保持三铰拱的清洁,避免 积尘、腐蚀等影响其使用 寿命的因素。
紧固与润滑
对三铰拱的连接部位进行 紧固,对活动部位进行润 滑,确保其正常运转。
常见问题与处理方法
1 2
结构损伤
如发现三铰拱出现裂纹、变形等损伤,应立即采 取措施进行修复或更换。
连接松动
结构力学第五章 三铰拱讲解

• 三铰拱是一种静定的拱式结构,在大跨 度结构上用料比梁省,因而在桥梁和屋 盖中广泛应用。
• 拱的各部名称如下:
拱的基本特点是在竖向荷载作用下会产生水 平推力。水平推力的存在与否是区别拱与梁 的主要标志。
带拉杆的拱:在屋架中,为消除水平推力
对墙或柱的影响,在两支座间增加一拉杆, 由拉杆来承担水平推力,如下图。
铁路拱桥:在桥梁中为了降低桥面高度,可 将桥面吊在拱上。如下图。
拱的特点: 在竖向荷载作用下能产生水平反力。水平反力
产生负弯矩,可以抵消一部分正弯矩,与简支梁相 比拱的弯矩、剪力较小,轴力较大(压力),应力 沿截面高度分布较均匀。节省材料,减轻自重,能 跨越大跨度。宜采用耐压不耐拉的材料 ,如砖石 混凝土等。有较大的可利用空间。
g
ch
g x -1
H
A l/2
C f
B l/2
y
在填土重量作用下,三铰拱 的合理拱轴线是一悬链线。
返回
由截面法可推出三铰拱的内力计算公式为:
注:1、该组公式仅用于两底铰在同一水平线上,且承受竖向荷载; 2、在拱的左半跨φ取正右半跨取负; 3、仍有 Q=dM/ds 即剪力等零处弯矩达极值; 4、 M、Q、N图均不再为直线。 5、集中力作用处Q图将发生突变。 6、集中力偶作用处M图将发生突变。
§5.3 合理拱轴线
其缺点是: 拱对基础或下部结构施加水平推力,增加了下
部结构的 材料用量;
§5.2 反力和内力计算
• 当两支座在同一水平线上时,称为等高 拱或平拱,否则称为斜拱。
• 分析竖向荷载作用下三铰拱的内力和反 力时,与同跨度、同荷载的简支梁相对 比,以便于计算和对比分析拱的受力性 质。
P
C
↓↓↓↓↓
• 拱的各部名称如下:
拱的基本特点是在竖向荷载作用下会产生水 平推力。水平推力的存在与否是区别拱与梁 的主要标志。
带拉杆的拱:在屋架中,为消除水平推力
对墙或柱的影响,在两支座间增加一拉杆, 由拉杆来承担水平推力,如下图。
铁路拱桥:在桥梁中为了降低桥面高度,可 将桥面吊在拱上。如下图。
拱的特点: 在竖向荷载作用下能产生水平反力。水平反力
产生负弯矩,可以抵消一部分正弯矩,与简支梁相 比拱的弯矩、剪力较小,轴力较大(压力),应力 沿截面高度分布较均匀。节省材料,减轻自重,能 跨越大跨度。宜采用耐压不耐拉的材料 ,如砖石 混凝土等。有较大的可利用空间。
g
ch
g x -1
H
A l/2
C f
B l/2
y
在填土重量作用下,三铰拱 的合理拱轴线是一悬链线。
返回
由截面法可推出三铰拱的内力计算公式为:
注:1、该组公式仅用于两底铰在同一水平线上,且承受竖向荷载; 2、在拱的左半跨φ取正右半跨取负; 3、仍有 Q=dM/ds 即剪力等零处弯矩达极值; 4、 M、Q、N图均不再为直线。 5、集中力作用处Q图将发生突变。 6、集中力偶作用处M图将发生突变。
§5.3 合理拱轴线
其缺点是: 拱对基础或下部结构施加水平推力,增加了下
部结构的 材料用量;
§5.2 反力和内力计算
• 当两支座在同一水平线上时,称为等高 拱或平拱,否则称为斜拱。
• 分析竖向荷载作用下三铰拱的内力和反 力时,与同跨度、同荷载的简支梁相对 比,以便于计算和对比分析拱的受力性 质。
P
C
↓↓↓↓↓
结构力学-三铰拱

曲梁
拱
拱 (arch)
一、概述
2.拱的受力特点 拱的受力特点 拱
曲梁
P
拱比梁中的弯矩小
拱 (arch)
一、概述
3.拱的分类 拱的分类
超静定拱
静定拱
两铰拱
三铰拱 拉杆 拉杆拱
高差h 高差
超静定拱
无铰拱 斜拱
拱 (arch)
一、概述
4.拱的有关名称 拱的有关名称 顶铰 拱肋 拱趾铰 跨度 拱肋 拱趾铰 矢高
1 l l a1 b1 不再顶部,或 铰C不再顶部 或 不再顶部 FH = [Y A × − P1 ( − a1 )] f 2 2 0 b a2右边的结2 YB0 YA不是平拱 不是平拱,右边的结 l l
M c0 = [Y A0 × − P1 ( − a1 )]
YB=YB YA=YA0 XA=XB =FH
二、三铰拱的数解法 ----支反力计算 支反力计算 P1 三铰拱的竖向反 P2 C 力与其等代梁的 XB 反力相等 水平反 f FH 反力相等;水平反 A B 力与拱轴线形状0 XA Mc YA l/2 l/2 无关.荷载与跨度 无关 荷载与跨度 YB YA l 一定时, 一定时,水平推 YA0 等代梁 P1 P2 A C 力与矢高成反比. 力与矢高成反比 B 请问:有水平荷载 有水平荷载,或 请问 有水平荷载 或
32kN.m C C 32kN.m
8m B 4m 4m 2kN 2kN A 4m 4m
8m B 2kN
A 2kN
32kN.m
16kN.m
16kN.m
16kN.m
水平反力的作用:使相应水平代梁弯矩 水平反力的作用:使相应水平代梁弯矩MC0 降至为零。 降至为零。
结构力学 三铰拱

4 4 yk 2 4(16 4) 3m 求MK 16 MK 0 MK 12.5 4 10 3 20kN.m(下拉)
求MJ
yJ 3m
M
J
0
M J 7.5 4 10 3 30 30 0
3. 求FQ、FN的计算公式
拱轴任意截面D切线与水平线夹角为φ。 相应代梁中, F 设为正方向。
FP1=15kN K FHA A yk 4m
l/2
C f=4m
MC 0
FVA
4m
l l FVA FHA f FP1 0 2 4 0 MC 1 l l FHA ( FVA FP1 ) () f 2 4 f
0 上式中,M C 为代梁C截面弯矩。
M FHB () f
0 ND右 QD右 sin D H cosD 12 0.555 10.5 0.832 15.4kN
重复上述步骤,可求出各等分截面的内力,作出内力图。
三、三较拱的合理轴线
在给定荷载作用下,三铰拱任一截面弯 矩为零的轴线就线为合理拱轴。 三铰拱任一截面弯矩为 M M FH y
超静定拱
拉杆拱 静定拱
拱顶
C
拱轴线 拱高 f
B
拱趾
A
起拱线 跨度 l
f l
f
高跨比
l 通常 f l 在1-1/10之间变化,f 的值对内力有 很大影响。
工程实例
拱桥 (无铰拱)
超静定拱
世界上最古老的铸铁拱桥(英国科尔布鲁克代尔桥)
万县长江大桥:世界上跨度最大的混凝土拱桥
二、三铰拱的计算
A 12.5kN K左 Fº =12.5kN QK左 A 12.5kN
结构力学 第三章 三铰拱

B
②剪力、轴力计算公式
FQFQ 0co-sFHsin
F0yA φ FP1
M0
F0yB
FNFQ 0sin-FHcos
KM
FN
F
0 Q
—相应简支梁对应截面上的剪力
φ φ—截面处拱轴切线倾角,在左半拱
FH A
y φ FQ
为正(右半拱为负)
φ
x
FVA φ
◆ 拱截面轴力较大,且一般为压力
例3-5 作图示三铰拱的内力图,拱轴为抛物线,其方程为
1kN/m C
f=4m x
FQ0L 1kN
FV A l1=8m
4m
l=16m
4kN
D
B FH B
4m
FV B
FQ0R 5kN
1kN/m
A
C
4kN B
F0yA
F0yB
F QLF Q 0L co-sFHsin 1 0 .89 6 ( 4 0 .44 ) 4 1 .7 7k 8 2 N
F Q RF Q 0c R o -sF Hsin 5 0 .8 9 6 ( 0 4 .44 ) 4 1 7 .7k 2 8N 9
四 三铰拱的合理拱轴线(reasonable axis of arch) 1 合理拱轴线的概念 在给定荷载作用下,使拱处于无弯矩状态的拱轴线,称 为拱的合理拱轴线
2 合理拱轴线的确定 根据荷载作用下,任一截面弯矩为零条件确定。如竖向 荷载作用下的三铰拱:
MM0FHy0 y M0
FH
通过由调此整可拱见的,轴当线拱,上使荷拱载在为确已定知荷时载,作只用要下求各出截相面应上简的支弯梁 矩值的为弯零矩,方这程时,拱除截以面支上座只水有平通推过力截FH面,形即心可的求轴得向合压理力拱作轴 用,的其轴压线应方力程沿截面均匀分布,此时的材料使用最为经济
结构力学 三铰拱
9 / 13
À
第四章 静定拱
试求图示对称三铰拱在均布荷载作用下的合理拱轴线
q y A x q f C B
FH=ql2/8f M0=qlx/2-qx2 /2 =qx(l-x)/2 y=M0/FH=4fx(l-x)/l2
l
x
抛物线À
10 / 13
第四章 静定拱
荷载布置改变,合理拱轴亦 改变 荷载确定、拱脚位置确定, 则顶铰位置决定水平反力, 因此,有无限多个相似图形 可作合理拱轴 三铰位置确定,合理拱轴唯 一确定 设计时只能根据主要荷载选 择近似合理拱轴
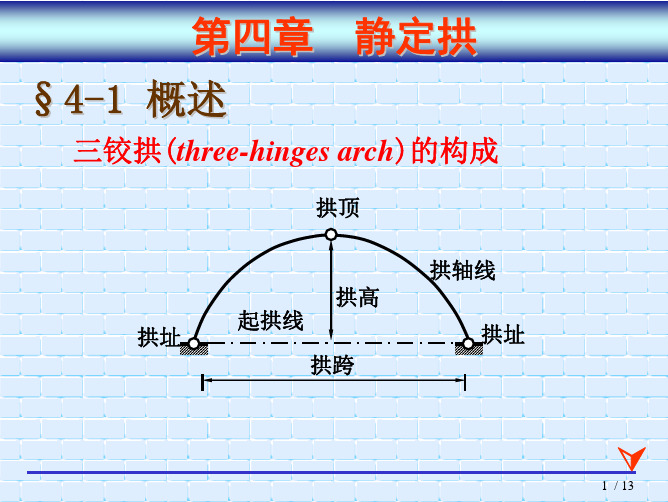
第四章 静定拱 §4-1 概述
三铰拱(three-hinges arch)的构成
拱顶 拱轴线 拱高 拱址 起拱线 拱跨 拱址
1 / 13
ÀБайду номын сангаас
第四章 静定拱
1)拱的分类
三铰拱 拉杆拱1
两铰拱
无铰拱
拉杆拱2
斜拱
2 / 13
À
第四章 静定拱
2)拱的受力特点
FP
曲梁
FP • 在竖向荷载作用下 会产生水平推力。
6 / 13
À
第四章 静定拱
拱的内力图
− y ⎤⎧M ⎫ ⎧M ⎫ ⎡1 0 ⎪ 0⎪ ⎪ ⎪ ⎢ ⎥ ⎨FS ⎬ = ⎢0 cosϕ − sinϕ⎥⎨ FS ⎬ ⎪F ⎪ ⎢0 sinϕ cosϕ ⎥⎪ F ⎪ ⎦⎩ H ⎭ ⎩ N⎭ ⎣
0
由于拱轴线是弯曲的,所以内力图都是曲线形 的,内力图要通过逐点描图的方法绘制。
拱
• 由于水平推力的存 在,使得拱内弯矩大 大减小。
3 / 13
À
第四章 静定拱 §4-2 三铰拱的计算
结构力学 三铰拱

三铰拱
一、概述
(一)工程应用
赵州桥
永定河七号铁路桥(150m)
BEH办公大楼(78m)
菜园坝长江大桥建设方案
(二)拱结构类型
(三)拱的构造
高跨比(矢跨比): 拱高与跨度之比,即 f l 。 高跨比一般为1~1/10,常用1/4 ~1/6。 拱轴线的形状可以为抛物线、 圆弧曲线等。
(四)拱的特点(拱的共性,并非三铰拱特有)
1.提出公式的目的 (1)求三铰拱内力的方法:截 取 力 平 (2)遇到类似情况,可以直接用公式计算。 2.公式的说明 (1)适用范围:对称三铰拱,任意竖向荷载。 (2)公式中各参数的含义 (3)分析拱的内力特点
M K = M K − HyK
QK = QK cos ϕ K − H sin ϕ K
N K = QK sin ϕ K + H cos Βιβλιοθήκη K例三、合理拱轴线
(一)定义
合理拱轴线:在给定荷载作用下拱所有截面上只承受轴力,弯矩为零时的拱轴线。
(二)合理拱轴线的形状
MK = M − HyK = 0
0 K
M(x) = M0 (x) − Hy(x) = 0 ⇒ y(x) = M (x) / H
0
⇒ yK = M / H
0 K
0 H = MC f
1.曲杆
2.竖向荷载作用下有水平推力 在竖向荷载作用下产生水平推力的曲杆结构称为拱。 3.由于水平推力的存在,使M<M0(可以小到100%)。 4.内力一般有M、Q、N,许多情况下N是主要内力。
(五)拱的性能
1.拱比梁更能发挥材料的作用,适用于较大的跨度和荷载。 2.拱主要受压,便于利用抗压性能好而抗拉性能差的材料。 3.三铰拱给基础施加向外的推力,所以基础比梁的基础要大。
一、概述
(一)工程应用
赵州桥
永定河七号铁路桥(150m)
BEH办公大楼(78m)
菜园坝长江大桥建设方案
(二)拱结构类型
(三)拱的构造
高跨比(矢跨比): 拱高与跨度之比,即 f l 。 高跨比一般为1~1/10,常用1/4 ~1/6。 拱轴线的形状可以为抛物线、 圆弧曲线等。
(四)拱的特点(拱的共性,并非三铰拱特有)
1.提出公式的目的 (1)求三铰拱内力的方法:截 取 力 平 (2)遇到类似情况,可以直接用公式计算。 2.公式的说明 (1)适用范围:对称三铰拱,任意竖向荷载。 (2)公式中各参数的含义 (3)分析拱的内力特点
M K = M K − HyK
QK = QK cos ϕ K − H sin ϕ K
N K = QK sin ϕ K + H cos Βιβλιοθήκη K例三、合理拱轴线
(一)定义
合理拱轴线:在给定荷载作用下拱所有截面上只承受轴力,弯矩为零时的拱轴线。
(二)合理拱轴线的形状
MK = M − HyK = 0
0 K
M(x) = M0 (x) − Hy(x) = 0 ⇒ y(x) = M (x) / H
0
⇒ yK = M / H
0 K
0 H = MC f
1.曲杆
2.竖向荷载作用下有水平推力 在竖向荷载作用下产生水平推力的曲杆结构称为拱。 3.由于水平推力的存在,使M<M0(可以小到100%)。 4.内力一般有M、Q、N,许多情况下N是主要内力。
(五)拱的性能
1.拱比梁更能发挥材料的作用,适用于较大的跨度和荷载。 2.拱主要受压,便于利用抗压性能好而抗拉性能差的材料。 3.三铰拱给基础施加向外的推力,所以基础比梁的基础要大。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
cosk
FH
sink
FN k FAy sink P1 sink FH cosk
F0 Ay
P1
sink
FH
cosk
FS
0 k
sink
FH
cosk
第二节 竖向荷载作用下三铰拱的受力分析
1 竖向荷载作用下拱反力计算
2 竖向荷载作用下指定截面内力计算
FP1
FSK
FNK
n
由 mK 0
MK
第二节 竖向荷载作用下三铰拱的受力分析
1 竖向荷载作用下拱反力计算 2 竖向荷载作用下指定截面内力计算
关于内力
M 1
FS FN
0 0
0
cos sin
y M 0
sin cos
F0 S
FH
• 内力图均不再为直线; • 集中力作用处,剪力图将发
生突变; • 集中力偶作用处,弯矩图将
FAy A
F0 Ay
a1 P1
a2 C
f
l1 l
P1
C
X 0
b1 P2
x l2
P2
b2 F l Pb Pb 0
Ay
11
22
FAy
Pb 11
l
Pb 22
B FBx
FBy
Pibi l
F0 Ay
mA 0
FBy
Pa ii l
F0 By
B
mc 0
F0 By
FAx f P1(l1 a1) FAyl1 0
带拉杆的拱: 在屋架中,为 消除水平推力 对墙或柱的影 响,在两支座 间增加一拉杆, 由拉杆来承担 水平推力
第一节 三铰拱的组成和类型
3. 三铰拱的分类
三铰拱 拉杆拱1
两铰拱 无铰拱
拉杆拱2
斜拱
第一节 三铰拱的组成和类型
4. 三铰拱的受力特点
FP
曲梁
FP
拱
拱的基本特点是在 竖向荷载作用下会 产生水平推力,从 而大大减小拱内弯 矩。水平推力的存 在与否是区别拱与 梁的主要标志。
[解] 2、求截面 3 内力
4f y l2 x(l x)
dy 4 f
dx
l2
(l 2x)
y3 3
tan3
1 2
q=2kN·m C
3 A
f=4m
l=16m
4m
q=2kN·m
FP=8kN B
FP2=8kN
M3
M
0 3
FH
y
4
kN m
FS 3
F0 S3
cos
FH
sin
0
kN
14
6
FN3
F0 S3
第二节 竖向荷载作用下三铰拱的受力分析
当两支座在同一水平线上时,称为等高拱或平拱,否 则称为斜拱。分析竖向荷载作用下三铰拱的内力和反 力时,与同跨度、同荷载的简支梁相对比,以便于计 算和对比分析拱的受力性质。
FP1
C FP2
f
A
B
l
FP1
FP2
1 竖向荷载作用下拱反力计算 mB 0
y
A FAx
例题:三铰拱所受荷载如图所示,拱的轴线为抛物线方程
y
4f l2
xl
x
计算其反力并绘制内力图
q=2kN·m C
FP=8kN
A FAy
f=4m
B
FAx
l=16m
FBx FBy
[解] 1、支座反力计算
FAy 14 kN
FBy 10 kN FAx FAy FH 12kN
第二节 竖向荷载作用下三铰拱的受力分析
sin
FH
cos
30 5
kN
40
2
10
48 40
FS(kN) M(kN.m)
第二节 竖向荷载作用下三铰拱的受力分析
曲拱计算步骤:
• 利用平衡方程求出拱的约束反力; • 绘制代梁的弯矩图和剪力图; • 利用拱的曲线方程计算拟求截面的位置(x,y, φ ); • 代入拱内力计算公式计算该截面内力。
几点说明:
M
0 K
FH y
K MK
由 F 0
FAx A
FSK FSK0cos FHsin
FAy FP1
FAy0
FSK0 MK0
由 Fn 0
FNK FSK0sin FHcos
第二节 竖向荷载作用下三铰拱的受力分析
1 竖向荷载作用下拱反力计算 2 竖向荷载作用下指定截面内力计算
关于内力
M 1
FS
赵州桥是我国隋代工匠李春建造的一个著名的范例。
第一节 三铰拱的组成和类型
1、工程上使用的拱结构实例
三铰拱是一种静定的拱式结构,在大跨度结构上用料 比梁省,因而在桥梁和屋盖中广泛应用。
第一节 三铰拱的组成和类型
2. 三铰拱的构成
拱趾
拱顶
矢高f 起拱线
拱跨L
拱轴 拱趾
第一节 三铰拱的组成和类型
2. 三铰拱的构成
• 荷载与跨度一定时,水平推力 与矢高成反比,且总是正的。
• 该组结论仅适合于平拱,且承 受竖向荷载。
二、内力的计算
P FSkMk FNk
y
a2
b2
a1
b1
P1 kk C
P2
f
yk
FH
FH A
xk
x
B
FAy
l1
l2
FH
FAy
l
FBy
F 0 F0 P
Sk
Ay
1
M 0 k
F x0 Ay k
P1
xk
a1
P1 A
P2 B
M k FAy xk P1 xk a1 FH yk
k
C
F x0 Ay k
P1
xk a1
FH yk
F0 Ay
F0 By
M0 k
FH
yk
FS k FAy cosk P1 cosk FH sink
F 0 P cos F sin
Ay
Sk
• 所求截面转角,实质是求相关函数(sin φ 和 cos φ 值),可 利用三角边的关系求出;
• 顶铰左右部分截面转角分正负; • 集中力作用点剪力图和轴力图有突变,应给予注意。
第三节 竖向荷载作用下三铰拱的内力特点
绘弯矩图
36
40 48 40
M
0 K
FH y
MK
M
0 K
FH y
综合弯矩图是两种弯矩图叠加的结果(注意是竖标的叠加, 或称代数叠加),即两个曲线所夹部分,可见弯矩很小。三 铰拱弯矩下降的原因完全是由于推力造成的。
FN
0 0
0
cos sin
y M 0 •
sin cos
F0 S
F H
•
•
•
三铰拱的内力不但与荷载及三个 铰的位置有关,而且与拱轴线的 形状有关; 由于推力的存在,拱的弯矩比相 应简支梁的弯矩要小; 三铰拱在竖向荷载作用下内力轴 压为主; 公式是以左半跨推导的,对右半 跨取角度为负即可;
发生突变; • 上述公式仅适合于平拱,且
承受竖向荷载情况; • 拱的内力仍然有FS=dM/ds
第二节 竖向荷载作用下三铰拱的受力分析
1 竖向荷载作用下拱反力计算 2 竖向荷载作用下指定截面内力计算 3 拱的内力图
由于拱轴线是弯曲的,所以内力图都是曲 线形的,内力图要通过逐点描图的方法绘制, 总的规律仍符合荷载和内力的微分关系。
FAx
FAyl1 P1(l1 a1) f
M
0 C
f
FBx
FH
第二节 竖向荷载作用下三铰拱的受力分析
1 竖向荷载作用下拱反力计算
关于反力
FAy=YAy0 FBy=YBy0 FAx=FBx =FH FH= MC0 / f
• 拱的竖向反力与其相应简支梁 的竖向反力相等;
• 水平反力只与三个铰的位置有 关而与拱轴线形状无关;
