结构力学第五章 三铰拱讲解
合集下载
结构力学-3.6 三铰拱.ppt
7.5 0.832 9.015kN
kN
9
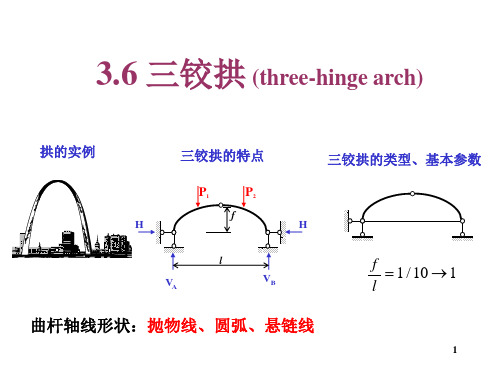
N图
13.300 10.958 9.015 7.749 7.500 7.433 1.421 6.796 3.325 11.235 11.665 11.700
0.600 0.354 0.003 0.472 1.000
3.331 1.060 0.600
Q图 kN
对于三铰拱,竖向荷载作用下任意截面上弯矩计算公式为:
M M Hy
它是由两项组成,第一项是简支梁的弯矩,而后一项与拱轴形状有关。
令
M M Hy 0
yx M x
H
在竖向荷载作用下,三铰拱的合理轴线的纵标值与简支梁
的弯矩纵标值成比例。
10
例1 设三铰拱承受沿水平方向均匀分布的竖向荷载,求其合理轴线。
qc+.f
qc q qc y
yx
f y*
d2y dx2
1 H
d 2M dx2
对简支梁来说,
d2M dx 2
qx
而 qx qc y,
d2y dx 2
1 H
qc
y
即 y y qc , 特征方程为:
HH
2 0
H
H
x
x
y C1e H C2e H
y
ex shx chx ex chx shx
q
y
C
q
A l/2
f
Bx
A
ql x
l/2
2
B
ql 2
[解] 由式 yx M x 先列出简支梁的弯矩方程
H
M x q xl x
2
拱的推力为:
H
M
C
ql 2
f 8f
kN
9
N图
13.300 10.958 9.015 7.749 7.500 7.433 1.421 6.796 3.325 11.235 11.665 11.700
0.600 0.354 0.003 0.472 1.000
3.331 1.060 0.600
Q图 kN
对于三铰拱,竖向荷载作用下任意截面上弯矩计算公式为:
M M Hy
它是由两项组成,第一项是简支梁的弯矩,而后一项与拱轴形状有关。
令
M M Hy 0
yx M x
H
在竖向荷载作用下,三铰拱的合理轴线的纵标值与简支梁
的弯矩纵标值成比例。
10
例1 设三铰拱承受沿水平方向均匀分布的竖向荷载,求其合理轴线。
qc+.f
qc q qc y
yx
f y*
d2y dx2
1 H
d 2M dx2
对简支梁来说,
d2M dx 2
qx
而 qx qc y,
d2y dx 2
1 H
qc
y
即 y y qc , 特征方程为:
HH
2 0
H
H
x
x
y C1e H C2e H
y
ex shx chx ex chx shx
q
y
C
q
A l/2
f
Bx
A
ql x
l/2
2
B
ql 2
[解] 由式 yx M x 先列出简支梁的弯矩方程
H
M x q xl x
2
拱的推力为:
H
M
C
ql 2
f 8f
结构力学5三铰拱课件

拱架搭设
根据设计要求,选用合适的材料搭设拱架;
施工流程与工艺要求
02
01
03
拱体安装
按照从两端向跨中的顺序,对称安装拱体构件;
拱顶合拢
在拱顶设置临时支撑,确保拱体稳定;
施工监测
对施工过程进行实时监测,确保施工安全和质量。
施工流程与工艺要求
工艺要求 拱架搭设应符合设计要求,确保稳定性和承载力;
拱体安装应保证构件对接准确,避免出现错位和扭曲;
施工流程与工艺要求
01
临时支撑设置应合理,确保拱体 在合拢过程中保持稳定;
02
施工监测应实时进行,及时发现 和解决施工中的问题。
安装方法与注意事项
安装方法 采用分段吊装法,将拱体分成若干段,分别吊装到位;
对接安装时,应保证对接位置准确,避免出现错位和扭曲;
安装方法与注意事项
• 合拢时,应设置临时支撑,确保拱体稳定。
结构力学5三铰拱课件
目
CONTENCT
录
• 三铰拱概述 • 三铰拱的力学分析 • 三铰拱的设计与计算 • 三铰拱的施工与安装 • 三铰拱的维护与加固
01
三铰拱概述
定义与特点
定义
三铰拱是一种静定结构,由两个 固定端和三个铰链支承构成。
特点
拱顶在竖向荷载作用下主要承受 压力,并通过铰链传递水平推力 ,保持拱的平衡。
保持三铰拱的清洁,避免 积尘、腐蚀等影响其使用 寿命的因素。
紧固与润滑
对三铰拱的连接部位进行 紧固,对活动部位进行润 滑,确保其正常运转。
常见问题与处理方法
1 2
结构损伤
如发现三铰拱出现裂纹、变形等损伤,应立即采 取措施进行修复或更换。
连接松动
根据设计要求,选用合适的材料搭设拱架;
施工流程与工艺要求
02
01
03
拱体安装
按照从两端向跨中的顺序,对称安装拱体构件;
拱顶合拢
在拱顶设置临时支撑,确保拱体稳定;
施工监测
对施工过程进行实时监测,确保施工安全和质量。
施工流程与工艺要求
工艺要求 拱架搭设应符合设计要求,确保稳定性和承载力;
拱体安装应保证构件对接准确,避免出现错位和扭曲;
施工流程与工艺要求
01
临时支撑设置应合理,确保拱体 在合拢过程中保持稳定;
02
施工监测应实时进行,及时发现 和解决施工中的问题。
安装方法与注意事项
安装方法 采用分段吊装法,将拱体分成若干段,分别吊装到位;
对接安装时,应保证对接位置准确,避免出现错位和扭曲;
安装方法与注意事项
• 合拢时,应设置临时支撑,确保拱体稳定。
结构力学5三铰拱课件
目
CONTENCT
录
• 三铰拱概述 • 三铰拱的力学分析 • 三铰拱的设计与计算 • 三铰拱的施工与安装 • 三铰拱的维护与加固
01
三铰拱概述
定义与特点
定义
三铰拱是一种静定结构,由两个 固定端和三个铰链支承构成。
特点
拱顶在竖向荷载作用下主要承受 压力,并通过铰链传递水平推力 ,保持拱的平衡。
保持三铰拱的清洁,避免 积尘、腐蚀等影响其使用 寿命的因素。
紧固与润滑
对三铰拱的连接部位进行 紧固,对活动部位进行润 滑,确保其正常运转。
常见问题与处理方法
1 2
结构损伤
如发现三铰拱出现裂纹、变形等损伤,应立即采 取措施进行修复或更换。
连接松动
5三铰拱.PPT
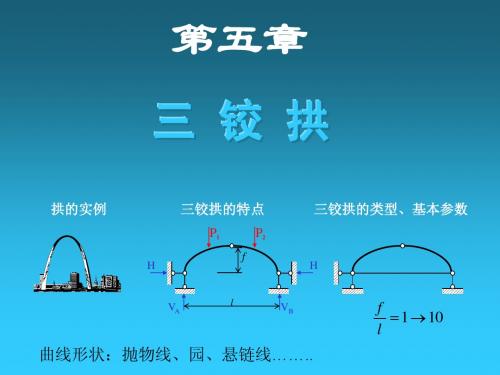
q qC y 。
q qc y
y f y
y*
因事先
M 得不到,故改用q(x)和y(x)表示:
d2y 1 d2 M 2 dx H dx 2
对简支梁来说, d M q x 2
2
e
2
qc+.f
M M H y M H f y 0 M y f H
M M Hy
它是由两项组成,第一项是简支梁的弯矩,而后一项与拱轴形状 有关。令
M M Hy 0
M x yx H
在竖向荷载作用下,三铰拱的合理轴线的纵标值与简支梁 的弯矩纵标值成比例。
例1、设三铰拱承受沿水平方向均匀分布的竖向荷载,求其合理轴线。
q y C q B l/2 B x A
H
H
y C1e
H
C2 e
x
H H q y a , 代入原方程,a c 设其特解 q y x A ch x B sh x c H H q x 0, y 0 A c 设 x 0, y 0 B 0 q y c ch x 1 悬链线 H
(1)计算支座反力
VA VA
26983 11kN 12 2 6 38 9 VB VB 9 kN 12
(2)内力计算
y2
以截面2为例
4f 44 x l x 312 3 3m l2 12 2
dy dx
x 3
MC 11 6 2 6 3 H 7.5kN f 4
A
l/2
f
M x [解] 由式 y x H
三铰拱PPT课件

F B
FS
FN FQ0sin FS cos
I
l/2
FVB
.
【例2】求图示三铰拱式屋架在竖向荷载作用下的支反力和内力。
解: (1) 计算支座反力
F H 0 , F V A F V 0 A , F V B F V 0 B
(2)计算拉杆内力:F S
M
0 C
f
(3)计算拱身内力
q
y FH
A FVA
受轴向压力FN作用。
仅在左半跨作用均布 荷载时的M图
仅在左半跨作用均布 荷载时的FQ图
仅在右半跨作用均布 荷载时的M图
仅在右半跨作用均布 荷载时的FQ图
(3) 这种在给定荷载作用下,拱处于无弯矩状态的拱轴线,是三
铰拱最合理的拱轴线( reasonable axis of arch) 。
.
• 三铰拱的合理拱轴线计算公式:
.
三铰拱压力线的求解步骤
设三铰拱所承受荷载如图4-8a所 示,现作其压力线。 第一步,作合力多边形
• 第二步,确定各截面合力的作 用线。
• 第三步,确定压力线 多边形AHIJB是由拱各段的 合力作用线构成的,称为三 铰拱在所给荷载作用下的压 力多边形,简称压力线 。 压力线应通过A、B、C三个 铰的铰心。
第五章 三铰拱( three-hinged arch )
.
内容: 三铰拱的支座反力和内力,合理拱轴。
要求: 1、了解静定拱的合理拱轴线的概念; 2、理解静定拱的基本概念及基本特点; 3、掌握静定拱的反力及内力计算。
重点:静定拱反力、内力的计算。 难点:静定拱的内力计算。
.
§5-1 概述 一、实例——拱桥(Arch Bridge)
.
结构力学 三铰拱

4 4 yk 2 4(16 4) 3m 求MK 16 MK 0 MK 12.5 4 10 3 20kN.m(下拉)
求MJ
yJ 3m
M
J
0
M J 7.5 4 10 3 30 30 0
3. 求FQ、FN的计算公式
拱轴任意截面D切线与水平线夹角为φ。 相应代梁中, F 设为正方向。
FP1=15kN K FHA A yk 4m
l/2
C f=4m
MC 0
FVA
4m
l l FVA FHA f FP1 0 2 4 0 MC 1 l l FHA ( FVA FP1 ) () f 2 4 f
0 上式中,M C 为代梁C截面弯矩。
M FHB () f
0 ND右 QD右 sin D H cosD 12 0.555 10.5 0.832 15.4kN
重复上述步骤,可求出各等分截面的内力,作出内力图。
三、三较拱的合理轴线
在给定荷载作用下,三铰拱任一截面弯 矩为零的轴线就线为合理拱轴。 三铰拱任一截面弯矩为 M M FH y
超静定拱
拉杆拱 静定拱
拱顶
C
拱轴线 拱高 f
B
拱趾
A
起拱线 跨度 l
f l
f
高跨比
l 通常 f l 在1-1/10之间变化,f 的值对内力有 很大影响。
工程实例
拱桥 (无铰拱)
超静定拱
世界上最古老的铸铁拱桥(英国科尔布鲁克代尔桥)
万县长江大桥:世界上跨度最大的混凝土拱桥
二、三铰拱的计算
A 12.5kN K左 Fº =12.5kN QK左 A 12.5kN
05三铰拱和悬索

结构力学电子教程
5 三铰拱和悬索
【例5.2】 求三铰拱在沿水平方向均匀分布竖向荷载作 用下的合理拱轴线。
【解】
M y H
0
MC0 H f
M0=qlx/2-qx2 /2 =qx(l-x)/2 MC0=ql2/8 H=ql2/8f
y=4fx(l-x)/l2
抛物线
结构力学电子教程
5 三铰拱和悬索
(1)在沿水平线均匀 分布的竖向荷载作用下 ,三铰拱的合理轴线为 二次抛物线。
结构力学电子教程
5 三铰拱和悬索
b. 截面D的内力
0 MD MD HyD =12 3-10.5 3 4.5kN m
0
1
2
3
4
5
6
7
8
0 QD左 QD 0.832-10.5 (0.555) 4.16kN 左 cos D H sin D (-2) 0 ND左 QD (0.555)-10.5 0.832 9.85kN 左 sin D H cos D =-(-2) 0 QD右 QD 0.832-10.5 (0.555) 4.16kN 右 cos D H sin D =(-12) 0 ND右 QD (0.555)-10.5 0.832 15.4kN 右 sin D H cos D -(-12)
结构力学电子教程
5 三铰拱和悬索
结构力学电子教程
5 三铰拱和悬索
结构力学电子教程
5 三铰拱和悬索
5.4 三铰拱的受力特性
一、三铰拱的受力特征:
0 0 VA VA VB VB ,与拱轴线形状及拱高无关。 (1)竖向反力, (2)H M C 0 推力只与三铰位置及荷载有关,与拱轴线无关。 f f 大,H 小。 (3)在竖向荷载作用下,拱截面上有轴力,轴力较大,是拱的 0 主要内力。 N Q sin H cos
第五章 三铰拱

为拱的跨度,拱顶到拱脚
连线的竖直距离f叫拱高,拱高f与跨度l之比f/l叫高跨 比。
5.1.2
拱的类型
拱的形式一般有无铰拱、两铰拱、三铰拱等几种, 如图3所示。其中无铰拱、两铰拱为超静定结构,三铰拱 为静定结构。
图3
5.1.3
拱的特点
拱与梁的区别主要不在于杆轴线的曲直,而是拱在 竖向荷载作用下会产生水平推力。 正是由于推力的存在, 拱的弯矩要比跨度、荷载相同的梁的弯矩小得多,而且 主要承受压力。所以拱结构可用抗压强度较高而抗拉强 度较低的砖、石、混凝土等脆性材料来建造。 另一方面,由于推力的存在,对地基和支承结构的 要求较高。三铰拱式屋架常在两支座之间设置拉杆,以 代替承受水平推力,从而消除了推力对支承结构的影响。 如图3(d)所示。
三铰拱轴线为曲线,曲杆截面的倾角φ随位置而变 化,内力亦随φ而变化。内力计算仍然将三铰拱与相应 跨度、荷载的简支梁相对应求解。
任意一截面D的内力: MD= M0D-H.yD QD= Q0DcosφD-H. sinφD ND=-Q0DsinφD-H. cosφD 截面的倾角φ由轴线方程y=f(x)求得(dy/dx=tanφ ),当X轴向右为正,Y轴向上为正时,左半拱φ取正,右 半拱φ取负。 5.3.2 三铰拱的内力图绘制 将拱沿着跨度方向等分为若干等份,逐点求出内力 值,将内力图的纵坐标垂直于杆轴线画出,然后连接各 点成曲线。
(3) 绘制内力图
图5
5.3.3 三铰拱的合理拱轴 根据三铰拱内力分析知:三铰拱截面轴力较大,弯 矩和剪力较小,为了充分发挥材料的作用,应设法减小 弯矩引起的不均匀正应力。如果使截面弯矩为零,则截 面正应力分布均匀,材料使用最经济。 在固定荷载作用下,使拱处于无弯矩状态的相应拱 轴线称为该荷载作用下的合理拱轴。 如:在某竖向荷载作用下,三铰拱任一截面的弯矩 为: M=M0-H.y 令 M0-H.y=0 则:y=M0/H 由此可见:当拱上荷载为已知时,只要求出相应简支 梁的弯矩方程,然后除以支座水平推力H,即可求得合理 拱轴的轴线方程。
结构力学——组合结构-三铰拱ppt课件

(A,B,C三铰在一直线上,成为几何瞬变体。)
.
②拱内力计算:
QM
P1
N
D
HA
VA
弯矩:受拉侧做弯矩图; 剪力:垂直于拱轴线的切线(顺时针为正); 轴力:平行于拱轴线的切线(拉为正)。
.
a1
M
P1 D
y HA x
VA
•弯矩:
由 MD0
M V A x P 1 ( x a 1 ) H y 0 M M oH y
C
Mc0q2l /8
l
Mc0 / 6
Mc0 / 6
B
A
C
B
Mc0 / 6
0.207 l 0.586 l 0.207 l
优点:方便,简单; 缺点:截面仍有弯矩。
.
②三铰曲拱:
f MM0Hy (HM c0/ f)
优点:截面弯矩很小或无弯矩; 缺点:曲线杆件施工复杂。
.
③桁架: 上弦、下弦承受弯矩;腹杆承受剪力。
其中:M o V A x P 1 (x a 1 )— 对应点的简支梁弯矩
.
Qo
Q
M
P1
φ
DH
HA
VA
•剪力:
其中:
QQ oco sH sin
Q VAP 1–– 对应点的简支梁剪力
— 切线与水平线所成锐角
(由水平向逆时针为正)
+φ -φ
左右
.
Qo M N
P1
φ
DH
y
HA x
•轴力:
VA
N Q s i n H c os
q M
qr
C
d θ
A
r
任意截面内力:
M q2r(1co )so qrdrsin () q2r(1co )sq2r(1co )s0
.
②拱内力计算:
QM
P1
N
D
HA
VA
弯矩:受拉侧做弯矩图; 剪力:垂直于拱轴线的切线(顺时针为正); 轴力:平行于拱轴线的切线(拉为正)。
.
a1
M
P1 D
y HA x
VA
•弯矩:
由 MD0
M V A x P 1 ( x a 1 ) H y 0 M M oH y
C
Mc0q2l /8
l
Mc0 / 6
Mc0 / 6
B
A
C
B
Mc0 / 6
0.207 l 0.586 l 0.207 l
优点:方便,简单; 缺点:截面仍有弯矩。
.
②三铰曲拱:
f MM0Hy (HM c0/ f)
优点:截面弯矩很小或无弯矩; 缺点:曲线杆件施工复杂。
.
③桁架: 上弦、下弦承受弯矩;腹杆承受剪力。
其中:M o V A x P 1 (x a 1 )— 对应点的简支梁弯矩
.
Qo
Q
M
P1
φ
DH
HA
VA
•剪力:
其中:
QQ oco sH sin
Q VAP 1–– 对应点的简支梁剪力
— 切线与水平线所成锐角
(由水平向逆时针为正)
+φ -φ
左右
.
Qo M N
P1
φ
DH
y
HA x
•轴力:
VA
N Q s i n H c os
q M
qr
C
d θ
A
r
任意截面内力:
M q2r(1co )so qrdrsin () q2r(1co )sq2r(1co )s0
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
• 三铰拱是一种静定的拱式结构,在大跨 度结构上用料比梁省,因而在桥梁和屋 盖中广泛应用。
• 拱的各部名称如下:
拱的基本特点是在竖向荷载作用下会产生水 平推力。水平推力的存在与否是区别拱与梁 的主要标志。
带拉杆的拱:在屋架中,为消除水平推力
对墙或柱的影响,在两支座间增加一拉杆, 由拉杆来承担水平推力,如下图。
铁路拱桥:在桥梁中为了降低桥面高度,可 将桥面吊在拱上。如下图。
拱的特点: 在竖向荷载作用下能产生水平反力。水平反力
产生负弯矩,可以抵消一部分正弯矩,与简支梁相 比拱的弯矩、剪力较小,轴力较大(压力),应力 沿截面高度分布较均匀。节省材料,减轻自重,能 跨越大跨度。宜采用耐压不耐拉的材料 ,如砖石 混凝土等。有较大的可利用空间。
g
ch
g x -1
H
A l/2
C f
B l/2
y
在填土重量作用下,三铰拱 的合理拱轴线是一悬链线。
返回
由截面法可推出三铰拱的内力计算公式为:
注:1、该组公式仅用于两底铰在同一水平线上,且承受竖向荷载; 2、在拱的左半跨φ取正右半跨取负; 3、仍有 Q=dM/ds 即剪力等零处弯矩达极值; 4、 M、Q、N图均不再为直线。 5、集中力作用处Q图将发生突变。 6、集中力偶作用处M图将发生突变。
§5.3 合理拱轴线
其缺点是: 拱对基础或下部结构施加水平推力,增加了下
部结构的 材料用量;
§5.2 反力和内力计算
• 当两支座在同一水平线上时,称为等高 拱或平拱,否则称为斜拱。
• 分析竖向荷载作用下三铰拱的内力和反 力时,与同跨度、同荷载的简支梁相对 比,以便于计算和对比分析拱的受力性 质。
P
C
↓↓↓↓↓
f
一、反力计算 H A
2
0, 得
dN 0
即拱截面上的轴力N为常数。
由于d很小,
由
n
0,
N
sin
d
2
N
dN
sin
d
2
-
qds
0,
取sin d d , 22
得 Nd - qds 0
并略去高阶微量,
故 rN
q
由于N为常数,故r也为常数。
在均匀水压力作用下,三铰拱的合理拱轴线是圆弧线。
例: 求在填土重量下三铰拱的合理拱轴线。q=q0+γy
即:
H
M
0 C
(3)
f
M
0 C
=YA×l/2-P×a
是简支梁的C截
面弯矩
返回
①该组公式仅用于:两底铰在同一水平线上 且承受竖向荷载。
②三铰拱的反力与跨度、矢高(即三铰的 位置)有关,而与拱轴线的形状无关。
③ 水平推力与矢高成反比。
二、内力计算
HA
MN
P
VA
H
xy Q
VA P
YA
d
YA M°
第五章 三铰拱
• 学习目的和要求
• 通过本章学习要求达到: 1. 熟练掌握截三铰拱的反力和内力计算。 2. 了解三铰拱的内力图绘制的步骤。 3. 掌握三铰拱合理拱轴的形状及其特征。
学习内容
1、 三铰拱的组成特点及其优缺点; 2、三铰拱的反力和内力计算及内力图的绘制; 3、三铰拱的合理拱轴线。
§5.1 三铰拱的组成与类型
Q°
M =VAA××Mxx--0 PP××dd-H×y M= M°-H×y
P
C
↓↓↓↓↓
f
a l/2
P
x da
l/2
c ↓↓↓↓↓
l
BH
VB YB
Q=(V -P)×cos-H×sin A
Q=Q°× cos - H×sin
N=-(V -P)sin-Hcos A
N=-Q°sin -Hcos
在荷载、跨度给定时,合 理拱轴线 随 f 的不同而有多 条,不是唯一的。
y(x)=M°(x)/H
M 0 (x) qx (l - x) 2
M 0(x)
=f
M
0 C
M
0 C
ql 2 8
↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓
yq
C
f
A
x
B
y(x) f
M 0 (x)
M
0 C
4f l2
x(l - x)
x l/2
l/2
三铰拱在沿水平均
匀分布的竖向荷载
q ↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓
作用下,其合理拱
轴线为一抛物线。
ql/2
l
ql/2ห้องสมุดไป่ตู้
求均匀水压力作用下的三铰拱的合理拱轴线。
q
n
r
N
t
d / 2
N+dN
d
∵拱处于无弯矩状态,∴各截面上只有轴力。
由
0,
N
cos d
2
- N
dN cos d
dy(2xy) dx2
MH1H0d((xdq2q)xM0(x2)0g
y)
q0 x
q0+γf
dd22My ddx x 2 2
0
-
g yqq(x0)
HH
y Ach
g x Bsh
H
g
H
x
-
q0
g
x 0, y 0 ;
A
q0
g
x 0 , dy 0 ; B 0 dx
y
q0
BH
对拱:∑MB=0
VA=∑MBP/l
VA
a l/2
l/2
VB
对梁:∑MB=0
P
c ↓↓↓↓↓
YA=∑MBP/l
∴ VA=YA (1)
同理 VB=YB (2) YA
a l
YB
由 ∑MC=0
得 VA×l/2 - P×a-H×f=0
其中 ∑MBP 是所 有荷载对B点的矩
H=(VA×l/2- P×a)/f
• 在给定荷载作用下使拱内各截面弯矩剪 力等于零,只有轴力的拱轴线
∵在荷载、跨度、矢高给
三铰拱的合理轴线
定时,H是一个常数.∴合理拱
在给定荷载作用下使拱内各截面弯 矩剪力等于零,只有轴力的拱轴线。
由 M(x)=M°(x)-Hy(x)=0
可得合理拱轴线方程为
轴线与相应的简支梁的弯矩图 形状相似,对应竖标成比例.
• 拱的各部名称如下:
拱的基本特点是在竖向荷载作用下会产生水 平推力。水平推力的存在与否是区别拱与梁 的主要标志。
带拉杆的拱:在屋架中,为消除水平推力
对墙或柱的影响,在两支座间增加一拉杆, 由拉杆来承担水平推力,如下图。
铁路拱桥:在桥梁中为了降低桥面高度,可 将桥面吊在拱上。如下图。
拱的特点: 在竖向荷载作用下能产生水平反力。水平反力
产生负弯矩,可以抵消一部分正弯矩,与简支梁相 比拱的弯矩、剪力较小,轴力较大(压力),应力 沿截面高度分布较均匀。节省材料,减轻自重,能 跨越大跨度。宜采用耐压不耐拉的材料 ,如砖石 混凝土等。有较大的可利用空间。
g
ch
g x -1
H
A l/2
C f
B l/2
y
在填土重量作用下,三铰拱 的合理拱轴线是一悬链线。
返回
由截面法可推出三铰拱的内力计算公式为:
注:1、该组公式仅用于两底铰在同一水平线上,且承受竖向荷载; 2、在拱的左半跨φ取正右半跨取负; 3、仍有 Q=dM/ds 即剪力等零处弯矩达极值; 4、 M、Q、N图均不再为直线。 5、集中力作用处Q图将发生突变。 6、集中力偶作用处M图将发生突变。
§5.3 合理拱轴线
其缺点是: 拱对基础或下部结构施加水平推力,增加了下
部结构的 材料用量;
§5.2 反力和内力计算
• 当两支座在同一水平线上时,称为等高 拱或平拱,否则称为斜拱。
• 分析竖向荷载作用下三铰拱的内力和反 力时,与同跨度、同荷载的简支梁相对 比,以便于计算和对比分析拱的受力性 质。
P
C
↓↓↓↓↓
f
一、反力计算 H A
2
0, 得
dN 0
即拱截面上的轴力N为常数。
由于d很小,
由
n
0,
N
sin
d
2
N
dN
sin
d
2
-
qds
0,
取sin d d , 22
得 Nd - qds 0
并略去高阶微量,
故 rN
q
由于N为常数,故r也为常数。
在均匀水压力作用下,三铰拱的合理拱轴线是圆弧线。
例: 求在填土重量下三铰拱的合理拱轴线。q=q0+γy
即:
H
M
0 C
(3)
f
M
0 C
=YA×l/2-P×a
是简支梁的C截
面弯矩
返回
①该组公式仅用于:两底铰在同一水平线上 且承受竖向荷载。
②三铰拱的反力与跨度、矢高(即三铰的 位置)有关,而与拱轴线的形状无关。
③ 水平推力与矢高成反比。
二、内力计算
HA
MN
P
VA
H
xy Q
VA P
YA
d
YA M°
第五章 三铰拱
• 学习目的和要求
• 通过本章学习要求达到: 1. 熟练掌握截三铰拱的反力和内力计算。 2. 了解三铰拱的内力图绘制的步骤。 3. 掌握三铰拱合理拱轴的形状及其特征。
学习内容
1、 三铰拱的组成特点及其优缺点; 2、三铰拱的反力和内力计算及内力图的绘制; 3、三铰拱的合理拱轴线。
§5.1 三铰拱的组成与类型
Q°
M =VAA××Mxx--0 PP××dd-H×y M= M°-H×y
P
C
↓↓↓↓↓
f
a l/2
P
x da
l/2
c ↓↓↓↓↓
l
BH
VB YB
Q=(V -P)×cos-H×sin A
Q=Q°× cos - H×sin
N=-(V -P)sin-Hcos A
N=-Q°sin -Hcos
在荷载、跨度给定时,合 理拱轴线 随 f 的不同而有多 条,不是唯一的。
y(x)=M°(x)/H
M 0 (x) qx (l - x) 2
M 0(x)
=f
M
0 C
M
0 C
ql 2 8
↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓
yq
C
f
A
x
B
y(x) f
M 0 (x)
M
0 C
4f l2
x(l - x)
x l/2
l/2
三铰拱在沿水平均
匀分布的竖向荷载
q ↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓
作用下,其合理拱
轴线为一抛物线。
ql/2
l
ql/2ห้องสมุดไป่ตู้
求均匀水压力作用下的三铰拱的合理拱轴线。
q
n
r
N
t
d / 2
N+dN
d
∵拱处于无弯矩状态,∴各截面上只有轴力。
由
0,
N
cos d
2
- N
dN cos d
dy(2xy) dx2
MH1H0d((xdq2q)xM0(x2)0g
y)
q0 x
q0+γf
dd22My ddx x 2 2
0
-
g yqq(x0)
HH
y Ach
g x Bsh
H
g
H
x
-
q0
g
x 0, y 0 ;
A
q0
g
x 0 , dy 0 ; B 0 dx
y
q0
BH
对拱:∑MB=0
VA=∑MBP/l
VA
a l/2
l/2
VB
对梁:∑MB=0
P
c ↓↓↓↓↓
YA=∑MBP/l
∴ VA=YA (1)
同理 VB=YB (2) YA
a l
YB
由 ∑MC=0
得 VA×l/2 - P×a-H×f=0
其中 ∑MBP 是所 有荷载对B点的矩
H=(VA×l/2- P×a)/f
• 在给定荷载作用下使拱内各截面弯矩剪 力等于零,只有轴力的拱轴线
∵在荷载、跨度、矢高给
三铰拱的合理轴线
定时,H是一个常数.∴合理拱
在给定荷载作用下使拱内各截面弯 矩剪力等于零,只有轴力的拱轴线。
由 M(x)=M°(x)-Hy(x)=0
可得合理拱轴线方程为
轴线与相应的简支梁的弯矩图 形状相似,对应竖标成比例.
