中考数学专题复习数学模型应用问题习题
中考数学复习满分突破(全国通用):专题13 胖瘦模型(解析版)

专题13胖瘦模型模型概述:在等腰三角形内部进行切割,利用其等腰等角的性质进行全等三角形的构造,常以等腰三角形的底边为底,在其内部再做一个等腰三角形。
模型:如图,∆ABC为等腰三角形,点P在线段BC上且点P不是BC的中点。
根据观察,S∆APC>S∆ABP,此时将∆APC看作是胖子,∆ABP看作是瘦子。
结论一:【变胖】如图,在BC上截取CQ=BP,连接AQ,则∆ABQ≌∆ACP,AP=AQ.证明:∵∆ABC为等腰三角形∴AB=AC∠B=∠C∵CQ=BP∴CQ+PQ=BP+PQ则BQ=PC在∆ABQ和∆ACP中AB=AC∠B=∠C∴∆ABQ≌∆ACP(SAS),∴AP=AQBQ=PC文字简述:∆ABP(瘦子)加上∆APQ(等腰三角形)得到新∆ABQ(变胖了),通过证明∆ABQ≌∆ACP(SAS)结论二:【变瘦】如图,在BC上截取CQ=BP,连接AQ,则∆ABP≌∆ACQ,AP=AQ.证明:∵∆ABC为等腰三角形∴AB=AC∠B=∠C在∆ABP和∆ACQ中AB=AC∠B=∠C∴∆ABP≌∆ACQ(SAS),∴AP=AQCQ=BP文字简述:∆APC(胖子)减去∆APQ(等腰三角形)得到新∆ACQ(变瘦了),通过证明∆ABP≌∆ACQ(SAS)结论三:【找中间状态】如图,过点A作AM⊥BC,垂足于点M,则∆ABM≌∆ACM证明:∵∆ABC为等腰三角形∴AB=AC∠B=∠C∵AM⊥BC,∴BM=MC在∆ABM和∆ACM中AB=ACAM=AM∴∆ABM ≌∆ACM (SSS )∴AP=AQBM=MC文字简述:∆ABP (瘦子)加上∆APM (直角三角形)得到新∆ABM (变胖了),∆APC (胖子)减去∆APM (直角三角形)得到新∆ACM (变瘦了),通过证明∆ABM ≌∆ACM (SSS )方法:见胖瘦,变胖加等腰,变瘦减等腰,中间状态加、减直角三角形。
【提高测试】1.(2023秋·广东广州·八年级统考期末)如图,BN 为∠MBC 的平分线,P 为BN 上一点,且PD ⊥BC 于点D ,∠APC +∠ABC =180°,给出下列结论:①∠MAP =∠BCP ;②PA =PC ;③AB +BC =2BD ;④四边形BAPC 的面积是△PBD 面积的2倍,其中结论正确的个数有()A .4个B .3个C .2个D .1个【答案】A 【分析】过点P 作PK ⊥AB ,垂足为点K .证明Rt △BPK ≌Rt △BPD ,△PAK ≌△PCD ,利用全等三角形的性质即可解决问题.【详解】解:过点P 作PK ⊥AB ,垂足为点K .∵PK ⊥AB ,PD ⊥BC ,∠ABP =∠CBP ,∴PK =PD ,在Rt △BPK 和Rt △BPD 中,BP BP PK PD,∴Rt △BPK ≌Rt △BPD (HL ),∴BK =BD ,∵∠APC +∠ABC =180°,且∠ABC +∠KPD =180°,∴∠KPD =∠APC ,∴∠APK =∠CPD ,故①正确,在△PAK 和△PCD 中,AKPPDC PK PD APK CPD=,∴△PAK ≌△PCD (ASA ),∴AK =CD ,PA =PC ,故②正确,∴BK ﹣AB =BC ﹣BD ,∴BD ﹣AB =BC ﹣BD ,∴AB +BC =2BD ,故③正确,∵Rt △BPK ≌Rt △BPD ,△PAK ≌△PCD (ASA ),∴S △BPK =S △BPD ,S △APK =S △PDC ,∴S 四边形ABCP =S 四边形KBDP =2S △PBD .故④正确.故选A .【点睛】本题考查全等三角形的判定和性质,角平分线的性质等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题,属于中考常考题型.2.(2022秋·山东日照·八年级期中)如图,过边长为4的等边三角形的边AB 上一点P ,作PE AC 于点E ,Q 为BC 延长线上一点,当PA CQ 时,连接PQ 交边AC 于点D ,则DE 的长为()A .2B .3C .4D .53【答案】A 【分析】根据题意,作出合适的辅助线,然后根据全等三角形的判定和性质可以求得DE 的长,本题得以解决.【详解】解:作QF ⊥AC ,交AC 的延长线于点F ,则∠QFC =90°,∵△ABC 是等边三角形,PE ⊥AC 于点E ,∴∠A =∠ACB =60°,∠PEA =90°,∴∠PEA =∠QFC ,∵∠ACB =∠QCF ,∴∠A =∠QCF ,在△PEA 和△QFC 中,∠�=∠푄�∠푃��=∠푄 �푃�=푄�,∴△PEA ≌△QFC (AAS ),∴AE =CF ,PE =QF ,∵AC =AE +EC =4cm ,∴EF =CF +EC =4cm ,∵∠PED =90°,∠QFD =90°,∴∠PED =∠QFD ,在△PED 和△QFD 中,PED QFD EDP FDQ PE QF,∴△PED ≌△QFD (AAS ),∴DE =FD ,∵DE+FD=EF=4cm,∴DE=2cm,故选:A.【点睛】本题考查了全等三角形的判定与性质、等边三角形的性质,解题的关键是明确题意,利用全等三角形的判定与性质和数形结合的思想解答.的边AB上一点P,3.(2022秋·吉林·八年级吉林省第二实验学校校考期中)如图,过边长为8的等边ABC时,DE的长为_____________.作PE AC于E,Q为BC延长线上一点,连接PQ交AC边于D,当PA CQ4.(2022秋·全国·八年级专题练习)如图,OC 平分∠MON ,A 、B 分别为OM 、ON 上的点,且BO >AO ,AC =BC ,求证:∠OAC +∠OBC =180°.【答案】见解析.【分析】如图,作CE ⊥ON 于E ,CF ⊥OM 于F .由Rt △CFA ≌Rt △CEB ,推出∠ACF =∠ECB ,推出∠ACB =∠ECF ,由∠ECF +∠MON =360°﹣90°﹣90°=180°,可得∠ACB +∠AOB =180°,推出∠OAC +∠OBC =180°.【详解】如图,作CE ⊥ON 于E ,CF ⊥OM 于F .∵OC 平分∠MON ,CE ⊥ON 于E ,CF ⊥OM 于F .∴CE =CF ,∵AC =BC ,∠CEB =∠CFA =90°,∴Rt △CFA ≌Rt △CEB (HL ),∴∠ACF =∠ECB ,∴∠ACB =∠ECF ,∵∠ECF +∠MON =360°﹣90°﹣90°=180°,∴∠ACB +∠AOB =180°,∴∠OAC +∠OBC =180°.【点睛】本题考查全等三角形的判定和性质,四边形内角和定理等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题.5.如图,在四边形ABCD 中,已知BD 平分∠ABC ,∠BAD +∠C =180°,求证:AD =CD .【答案】见解析【详解】试题分析:在边BC 上截取BE =BA ,连接DE ,根据SAS 证△ABD ≌△EBD ,推出AD =ED ,∠A =∠BED ,求出∠DEC =∠C 即可.试题解析:证明:在边BC 上截取BE =BA ,连接DE .∵BD 平分∠ABC ,∴∠ABD =∠CBD .在△ABD 和△EBD 中,BA BE ABD EBD BD BD,∴△ABD ≌△EBD (SAS ),∴AD =ED ,∠A =∠BED .∵∠A +∠C =180°,∠BED +∠CED =180°,∴∠C =∠CED ,∴CD =ED ,∴AD =CD .点睛:本题考查了等腰三角形的判定,全等三角形的性质和判定等知识点的应用,解答此题的关键是正确作辅助线,又是难点,解题的思路是把AD 和CD 放到一个三角形中,根据等腰三角形的判定进行证明,题型较好,有一定的难度.6.(2022·湖南怀化·统考中考真题)如图,在等边三角形ABC 中,点M 为AB 边上任意一点,延长BC 至点N ,使CN =AM ,连接MN 交AC 于点P ,MH ⊥AC 于点H .(1)求证:MP =NP ;(2)若AB =a ,求线段PH 的长(结果用含a 的代数式表示).∵ABC 为等边三角形,MQ ∴1AM AB AQ AC,则AM =AQ ,且∠A =60°,AMQ △为等边三角形,则又由(1)得,MQP NCP △△,则PQ =PC ,∴PH =HQ +PQ =0.5(AQ +CQ )=0.5AC =0.5a .【点睛】本题考查了等边三角形的性质与判定、三角形全等的判定,正确作出辅助线是解题的关键.7.如图,已知在四边形ABCD 中,BD 是ABC 的平分线,AD CD .2求证:180A C .【答案】见解析【分析】方法一,在BC 上截取BE ,使BE AB ,连接DE ,由角平分线的定义可得ABC DBC ,根据全等三角形的判定可证ABD △和EBD △全等,再根据全等三角形的性质可得A BED ,AD DE ,由AD =CD 等量代换可得DE DC ,继而可得C DEC ,由于180BED DEC ,可证180A C ;方法2,延长BA 到点E ,使BE BC ,由角平分线的定义可得ABD DBC ,根据全等三角形的判定可证EBD △和CBD △全等,继而可得E C ,DC DE .由AD CD ,可得DE AD ,继而求得E EAD ,由180EAD BAD ,继而可得180BAD C ;方法3,作DE BC 于点E ,DE BA 交BA 的延长线于点F ,由角平分线的定义可得,由DE BC ,DE BA ,可得90F DEB ,根据全等三角形的判定可证FBD 和EBD △全等,继而可得DF DE ,再根据HL 定理可得可证180BAD C .【详解】解:方法1截长如图,在BC 上截取BE ,使BE AB ,连接DE ,因为BD 是ABC 的平分线,所以ABC DBC .在ABD △和EBD △中,因为AB EB ABD DBC BD BD所以ABD EBD ,所以A BED ,AD DE .因为AD CD ,所以DE DC ,所以C DEC .因为180BED DEC ,所以180A C .方法2补短如图,延长BA 到点E ,使BE BC .因为BD 是ABC 的平分线,所以ABD DBC 在EBD △和CBD △中,因为BC BE EBD DBC BD BD,所以EBD CBD ,所以E C ,DC DE .因为AD CD ,所以DE AD ,所以E EAD .因为180EAD BAD ,所以180BAD C .方法3构造直角三角形全等作DE BC 于点E .DE BA 交BA 的延长线于点F因为BD 是ABC 的平分线,所以ABD DBC .因为DE BC ,DE BA ,所以90F DEB ,在FBD 和EBD △中,因为F DEB ABD DBC BD BD,所以FBD EBD ,所以DF DE .在Rt FAD △和Rt ECD △中,因为DF DE AD DC,所以Rt Rt FAD ECD ,所以FAD C .因为180FAD BAD ,所以180BAD C .8.(2022秋·广东梅州·九年级校考阶段练习)已知矩形ABCD 的一条边8AD ,将矩形ABCD 折叠,使得顶点B 落在CD 边上的P 点处.(1)如图1,已知折痕与边BC 交于点O ,连接AP ,OP ,OA .若OCP △与PDA 的面积比为1:4,求边CD 的长.(2)如图2,在(1)的条件下,擦去折痕AO 、线段OP ,连接BP .动点M 在线段AP 上(点M 与点P ,A 不重合),动点N 在线段AB 的延长线上,且BN PM ,连接MN 交PB 于点F ,作ME BP 于点E .试问当点M ,N 在移动过程中,线段EF 的长度是否发生变化?若变化,说明变化规律;若不变,求出线段EF 的长度.∥,AP AB∵,MQ AN.APB ABP MQP .MP MQBN PM∵,.BN QM9.(2021·全国·九年级专题练习)如图,在ABC 中,AD 为BAC 的平分线,如图,若2,12,7.2C B AB AC ,求线段CD 的长度.【答案】4.8【分析】在AB 上截取AE =AC ,连接DE ,证明△ACD ≌△AED (SAS ),得出∠C =∠AED ,证出∠B =∠BDE ,得出BE =DE ,即可得出答案;【详解】解:在AB 上截取AE =AC ,连接DE ,如图1所示:∵AD 为∠BAC 的平分线,∴∠DAE =∠DAC ,在△ACD 和△AED 中,AC AE DAE DAC AD AD∴△ACD ≌△AED (SAS ),∴∠C =∠AED ,∵∠C =2∠B ,∴∠AED =2∠B ,∵AED B BDE ,∴2B BDE B,∴B BDE ,∴BE =DE ,∵127.2AB AC ,,∴127.2 4.8CD DE BE AB AE AB AC ;【点睛】本题考查了全等三角形的判定与性质、等腰三角形的判定,证明三角形全等是解题的关键.10.(2021·全国·九年级专题练习)已知:如图,在△ABC 中,∠BAC =90°,AB =AC ,BD 平分∠ABC ,交AC 于D ,AE ⊥BD 于F ,交BC 于E .求证:(1)AB =BE ;(2)∠CAE =12∠ABC ;(3)AD =CE ;(4)CD +CE =AB .【点睛】本题主要考查三角形全等的判定和性质,等腰直角三角形的性质,注意观察所求线段或角之间的关系,找到所在的两个三角形,证明全等即可解决.。
中考数学专题复习常见模型方法勾股定理相关模型应用
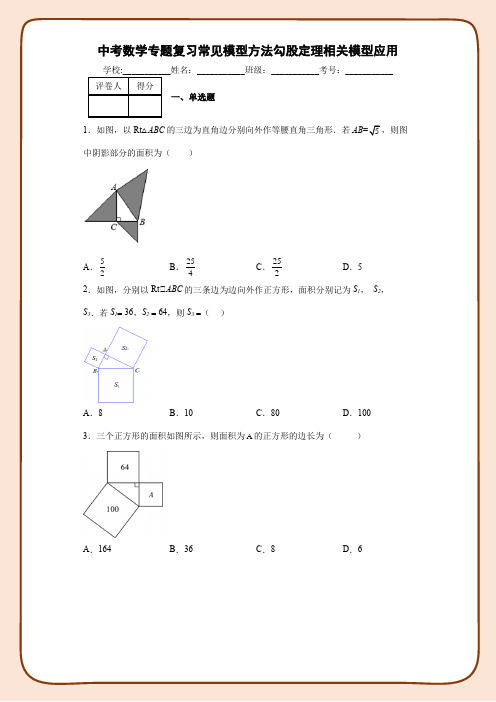
中考数学专题复习常见模型方法勾股定理相关模型应用学校:___________姓名:___________班级:___________考号:___________评卷人得分一、单选题1.如图,以Rt△ABC的三边为直角边分别向外作等腰直角三角形.若AB=5,则图中阴影部分的面积为()A.52B.254C.252D.52.如图,分别以Rt△ABC的三条边为边向外作正方形,面积分别记为S1,S2,S3.若S1= 36,S2= 64,则S3=()A.8B.10C.80D.100 3.三个正方形的面积如图所示,则面积为A的正方形的边长为()A.164B.36C.8D.64.下图是一株美丽的勾股树,其中所有的四边形都是正方形,所有的三角形都是直角三角形,若最大正方形G的边长是6cm,则正方形A,B,C,D,E,F,G的面积之和是()A.18cm2B.36cm2C.72cm2D.108cm2 5.如图,这是一株美丽的勾股树,所有的四边形都是正方形,所有的三角形都是直角三角形,若正方形A、B、C、D的边长是3、5、2、3,则最大正方形E的边长是()A.13B.47C.47D.136.有一个面积为1的正方形,经过一次“生长”后,在他的左右肩上生出两个小正方形,其中,三个正方形围成的三角形是直角三角形,再经过一次“生长”后,变成了上图,如果继续“生长”下去,它将变得“枝繁叶茂”,请你算出“生长”了2020次后形成的图形中所有的正方形的面积和是()A .1B .2021C .2020D .2019 7.设直角三角形的较长直角边长为x ,较短直角边长为y .若 xy =8,大正方形的面积为25,则小正方形的边长为( )A.9B .6 C .4 D .38.如图是“赵爽弦图”,△ABH 、△BCG 、△CDF 和△DAE 是四个全等的直角三角形,四边形ABCD 和EFGH 都是正方形,如果AB =10,EF =2,那么AH 等于( )A .8B .6C .4D .59.如图,有4个相同的直角三角形与中间的小正方形拼成一个大正方形,若大正方形的面积是17,小正方形的面积是5,直角三角形较长直角边为a ,较短直角边为b ,则 ab 的值是( )A .4B .6C .8D .10 10.“赵爽弦图”巧妙地利用面积关系证明了勾股定理,是我国古代数学的骄傲,如图所示的“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形,设直角三角形较长直角边长为a ,较短直角边长为b ,若2)21a b +=(,大正方形的面积为13,则小正方形的面积为( )A .3B .4C .5D .611.如图,一竖直的木杆在离地面4米处折断,木杆顶端落在地面离木杆底端3米处,木杆折断之前的高度为().A.7米B.8米C.9米D.12米12.一棵大树在一次强台风中于离地面6米处折断倒下,倒下部分与地面成30夹角,这棵大树在折断前的高度为()A.12米B.18米C.24米D.30米13.如图,一棵大树在离地面3米处折断,树的顶端落在离树干底部4米处,那么这棵树折断之前的高度是()A.8米B.12米C.5米D.5或7米14.如图,一棵高为16m的大树被台风刮数断,若树在地面6m处折断,则树顶端落在离树底部()处A.5m B.7m C.8m D.10m15.如图是一个饮料罐,下底面半径是5,上底面半径是8,高是12,上底面盖子的中心有一个小圆孔,则一条到达底部的直吸管在罐内部分a的长度(罐壁的厚度和小圆孔的大小忽略不计)的取值范围是()A.12≤a≤13B.12≤a≤15C.5≤a≤12D.5≤a≤1316.我国古代算书《九章算术》中第九章第六题是:今有池方一丈,葭生其中央,出水一尺,引葭赴岸,适与岸齐,问水深葭长各几何?你读懂题意了吗?请回答水深______尺,葭长_____尺.解:根据题意,设水深OB=x尺,则葭长OA'=(x+1)尺.可列方程正确的是()A.x2+52 =(x+1)2B.x2+52 =(x﹣1)2C.x2+(x+1)2 =102D.x2+(x﹣1)2=5217.如图,一根长5米的竹竿AB斜靠在竖直的墙上,这时AO为4米,若竹竿的顶端A沿墙下滑2米至C处,则竹竿底端B外移的距离BD()A.小于2米B.等于2米C.大于2米D.以上都不对18.如图,一个梯子AB斜靠在一竖直的墙AO上,测得8AO 米.若梯子的顶端沿墙面向下滑动2米,这时梯子的底端在水平的地面也恰好向外移动2米,则梯子AB的长度为()A.10米B.6米C.7米D.8米19.一架25米长的云梯,斜立在一竖直的墙上,这时梯脚距离墙底端7米.如果梯子的顶端沿墙下滑4米,那么梯脚将水平滑动()A.9米B.15米C.5米D.8米20.如图,长方体的长为3,宽为2,高为4,一只蚂蚁从点A出发,沿长方体表面到点B处吃食物,那么它爬行最短路程是()A.29B.41C.45D.5321.如图,长方体的长为3cm,宽为2cm,高为4cm,点B到点C的距离为1cm,一只蚂蚁如果要沿着长方体的表面从点A爬到点B,需要爬行的最短距离是()A.4B.5C.29D.3722.如图,正方体的棱长为2,B为一条棱的中点.已知蚂蚁沿正方体的表面从A点出发,到达B点,则它运动的最短路程为()A.10B.4C.17D.523.如图是放在地面上的一个长方体盒子,其中AB=18cm,BC=12cm,BF=10cm,点M在棱AB上,且AM=6cm,点N是FG的中点,一只蚂蚁要沿着长方体盒子的表面从点M爬行到点N,它需要爬行的最短路程为()A.20cm B.2106cm C.(12+234)cm D.18cm24.如图,圆柱的底面半径是4,高是5,一只在A点的蚂蚁想吃到B点的食物,需要爬行的最短路径是(π取3)()A.9B.13C.14D.2525.如图,一个底面直径为30cm,高为20cm的糖罐子,一只蚂蚁从A处沿着糖罐的表面爬行到B处,则蚂蚁爬行的最短距离是()A.24cm B.1013cm C.25cm D.30cm26.如图,圆柱形容器的高为0.9m,底面周长为1.2m,在容器内壁离容器底部0.3m 处的点B处有一蚊子.此时,一只壁虎正好在容器外壁,离容器上沿0.2m与蚊子相对的点A处,则壁虎捕捉蚊子的最短距离为()A.1m B.1.1m C.1.2m D.1.3m27.如图所示,有一块直角三角形纸片,△C=90°,AC=4cm,BC=3cm,将斜边AB翻折,使点B落在直角边AC的延长线上的点E处,折痕为AD,则CE的长为()A.1cm B.1.5cm C.2cm D.3cm28.如图所示的三角形纸片中,90,13,5B AC BC∠=︒==.现将纸片进行折叠,使得顶点B落在AC边上的点D处,折痕为AE,则BE的长为()A.2.4B.2.5C.2.8D.329.如图,在矩形纸片ABCD中,AB=6,AD=8,折叠该纸片,使得AB边落在对角线AC上,点B落在点F处,折痕为AE,则线段EF的长为()A.3B.4C.5D.630.如图所示,沿着AE折叠长方形,使点D落在边BC上的点F处,已知AB=8cm,BC=10cm,则EC的长为()A.3 cm B.4 cm C.5 cm D.6 cm31.如图所示,矩形纸片ABCD中,AB=6cm,BC=8cm,现将其沿EF对折,使得点C与点A重合,则AF长为()A.258cm B.254cm C.252cm D.8cm32.如图,已知矩形ABCD沿着直线BD折叠,使点C落在C'处,BC'交AD于点E,8AD=,4AB=,则DE的长为()A.3B.4C.5D.633.如图,将矩形ABCD沿EF折叠,使顶点C恰好落在AB边的中点C′上.若AB=6,BC=9,则BF的长为()A.4B.32C.4.5D.534.在△ABC中,AB=16,AC=14,BC=6,则△ABC的面积为()A.243B.563C.48D.11235.已知在△ABC中,AB=8,AC=7,BC=3,则△B=().A.45°B.37°C.60°D.90°36.已知在△ABC中,AB=7,AC=8,BC=5,则△C=().A.45°B.37°C.60°D.90°37.边长为5,7,8的三角形的最大角和最小角的和是().A.90°B.150°C.135°D.120°评卷人得分二、填空题38.《九章算术》是中国传统数学的重要著作之一,奠定了中国传统数学的基本框架.如图所示是其中记载的一道“折竹”问题:“今有竹高一丈,末折抵地,去根三尺,问折者高几何?”题意是:一根竹子原高1丈(1丈 10尺),中部有一处折断,竹梢触地面处离竹根3尺,试问折断处离地面多高?答:折断处离地面________尺高.39.如图,一架长2.5m的梯子斜靠在垂直的墙AO上,这时AO为2m.如果梯子的顶端A沿墙下滑0.5m,那么梯子的底端B向外移动_________m.40.如图,一架13m长的梯子AB斜靠在一竖直的墙AC上,这时AC为12m.如果子的顶端A沿墙下滑7m,那么梯子底端B向外移___m.41.如图,一只蚂蚁从实心长方体的顶点A出发,沿长方体的表面爬到对角顶点1C处(三条棱长如图所示),问最短路线长为_________.42.如图,圆柱体的高为8cm ,底面周长为4cm ,小蚂蚁在圆柱表面爬行,从A 点到B 点,路线如图所示,则最短路程为_____.43.如图,在Rt ABC ∆中,90B =∠,6AB =,8BC =,将ABC ∆折叠,使点B 恰好落在斜边AC 上,与点'B 重合,AE 为折痕,则'EB 的长度是__________.44.如图,在矩形ABCD 中,AB=3,BC=5,在CD 上任取一点E ,连接BE ,将△BCE 沿BE 折叠,使点C 恰好落在AD 边上的点F 处,则CE 的长为_____.45.如图,△ABC 的三边AB ,BC ,CA 的长度分别为3,7,8,则△ABC 的内切圆△的半径为_________.46.在四边形ABCD 中,,7,11,13AC BD AB CD BC ⊥===,则AD =__________.评卷人得分三、解答题47.由4个直角边长分别为a,b的直角三角形围成的“赵爽弦图”如图所示.根据大正方形的面积c2等于小正方形的面积(a-b)2与4个直角三角形的面积2ab的和证明了勾股定理a2+b2=c2,还可以用来证明结论△若a>0,b>0且a2+b2为定值,则当a ____ b时,ab取得最大值.拓展:如图所示,在正方形ABCD的四边,,,AB BC CD DA上分别取点,,,E H G F,使得BE CH GD AF===,(1)求证:四边形EHGF是正方形.(2)若//,//,//,//EQ BC HP CD GO DA FR AB,求证四边形ORQP是正方形.48.“风吹树折”问题又称为“折竹抵地”,源自《九章算术》,原文为:“今有竹高一丈,末折抵地,去本三尺.问折者高几何?”意思是:一根竹子,原高一丈,一阵风将竹子折断,其竹梢恰好抵地,抵地处离竹子底部3尺远,则折断后的竹子高度为多少尺?(1丈=10尺)49.一阵大风把一根高为9m的树在离地4m处折断,折断处仍相连,此时在离树3.9m处,一头高1m的小马正在吃草,小马有危险吗?为什么?50.读诗求解“ 出水3尺一红莲,风吹花朵齐水面,水面移动有6尺,求水深几何请你算”.51.在平静的湖面上,有一枝荷花,高出水面1米.一阵风吹过来,荷花被吹到一边,花朵齐及水面.已知荷花移动的水平距离为2米,问这里的水深多少米?52.《算法统宗》是中国古代数学名著,作者是我国明代数学家程大位.在《算法统宗》中有一道“荡秋千”的问题:“平地秋千未起,踏板一尺离地.送行二步与人齐,五尺人高曾记.仕女佳人争蹴,终朝笑语欢嬉.良工高士素好奇,算出索长有几.”(注:1步=5尺)译文:“有一架秋千,当它静止时,踏板离地1尺,将它往前推送10尺(水平距离)时,秋千的踏板就和人一样高,这个人的身高为5尺,秋千的绳索始终拉得很直,问绳索有多长.”53.如图所示,在Rt ABC中,90ACB∠=︒,已知6,8,AC BC AD==是ABC的角平分线,求DC的长.54.已知,如图所示,折叠矩形的一边AD ,使点D 落在BC 边的点F 处,如果AB =3cm ,BC =5cm ,求FC 的长.55.如图所示,矩形ABCD 沿直线EF 折叠,使点C 落在边AD 的中点C '处,点B 落在B '处,其中1812AB BC ==,,求FC '的长.56.已知:四边形ABCD 中,BD 、AC 相交于O ,且BD 垂直AC ,求证:2222AB CD AD BC +=+.57.定义,我们把对角线互相垂直的四边形叫做垂美四边形.概念理解:如图△,在四边形ABCD 中,如果AB=AD ,CB=CD ,那么四边形ABCD 是垂美四边形吗?请说明理由.性质探究:如图△,垂美四边形ABCD 两组对边AB 、CD 与BC 、AD 之间有怎样的数量关系?写出你的猜想,并给出证明.问题解决:如图△,分别以Rt△ACB 的直角边AC 和斜边AB 为边向外作正方形ACFG 和正方形ABDE ,连结CE 、BG 、GE .若AC=2,AB=5,则△求证:△AGB△△ACE ;△GE= .58.如图1,对角线互相垂直的四边形叫做垂美四边形.(1)概念理解:如图2,在四边形ABCD 中,AB AD =,CB CD =,问四边形ABCD 是垂美四边形吗?请说明理由;(2)性质探究:如图1,四边形ABCD 的对角线AC 、BD 交于点O ,AC BD ⊥.试证明:2222AB CD AD BC +=+;(3)解决问题:如图3,分别以Rt ACB 的直角边AC 和斜边AB 为边向外作正方形ACFG 和正方形ABDE ,连结CE 、BG 、GE .已知4AC =,5AB =,求GE 的长.59.问题情境:如图1,ABC 为等腰直角三角形,90,ACB E ∠=︒是AC 边上的一个动点(点E 与,A C 不重合),以CE 为边在ABC 外作等腰直角,90ECD ECD ∠=︒,连接,BE AD .猜想线段,BE AD 之间的关系.(1)独立思考:请直接写出线段,BE AD 之间的关系.(2)合作交流:“希望”小组受上述问题的启发,将图1中的等腰直角ECD 绕着点C 顺时针方向旋转至如图2的位置,BE 交AC 于点H ,交AD 于点O .(1)中的结论是否仍然成立?请说明理由.(3)拓展延伸:“科技”小组将(2)中的等腰直角ABC 改为,90,8Rt ABC ACB AC ∠=︒=△,6BC =,将等腰直角ECD 改为,90,4,3Rt ECD ECD CD CE ∠=︒==.试猜想22BD AE +是否为定值,结合图3说明理由.参考答案:1.D【解析】【分析】先用直角三角形的边长表示出阴影部分的面积,再根据勾股定理可得:AB 2=AC 2+BC 2,进而可将阴影部分的面积求出.【详解】解:()22222211112222S AC BC AB AB AC BC =++=++阴影, △在Rt△ABC 中,AB 2=AC 2+BC 2=2(5)5=,△AB 2+AC 2+BC 2=10,△S 阴影=12×10=5.故选:D .【点睛】本题考查了勾股定理的知识,能够运用勾股定理证明三个等腰直角三角形的面积之间的关系是解决本题的关键.2.D【解析】【分析】由正方形的面积公式可知S 1=AC 2,S 2=BC 2,S 3=AB 2,在Rt△ABC 中,由勾股定理得AC 2+BC 2=AB 2,即S 1+S 2=S 3,由此可求S 3.【详解】解:△在Rt△ABC 中,AC 2+BC 2=AB 2,又由正方形面积公式得S 1=AC 2,S 2=BC 2,S 3=AB 2,△S 3=S 1+S 2=100.故选:D .【点睛】本题考查了勾股定理及正方形面积公式的运用.关键是明确直角三角形的边长的平方即为相应的正方形的面积.3.D【解析】【分析】已知四边形OGMN和四边形OBCD是正方形,面积分别为64和100,即可求得OG和OD的长,再利用勾股定理即可求得GD的长.【详解】△四边形OGMN和四边形OBCD是正方形,面积分别为64和100△OG2=64,OD2=100△OG=8,OD=10△22221086GD OD OG=-=-=故面积为A的正方形的边长为:6故选:D【点睛】本题考查了正方形的基本性质,四边形各边相等,面积等于边长的平方,本题还考查了利用勾股定理解直角三角形.4.D【解析】【分析】根据正方形的面积公式,运用勾股定理可以证明:6个小正方形的面积和等于最大正方形面积的3倍.【详解】根据勾股定理得到:A与B的面积的和是E的面积;C与D的面积的和是F的面积;而E,F的面积的和是G的面积.即A、B、C、D、E、F的面积之和为3个G的面积.△M的面积是62=36 cm2,△A、B、C、D、E、F的面积之和为36×3=108 cm2.故选D.【点睛】考查了勾股定理,注意运用勾股定理和正方形的面积公式证明结论:6个小正方形的面积和等于最大正方形的面积的2倍.5.B【解析】【分析】设中间两个正方形的边长分别为x、y,最大正方形E的边长为z,根据勾股定理进行求解.【详解】设中间两个正方形的边长分别为x、y,最大正方形E的边长为z,由勾股定理得:x2=32+52=34,y2=22+32=13,z2=x2+y2=47,即最大正方形E的面积为:z2=47,边长为z=47,故选B.【点睛】本题考查勾股定理,掌握以直角三角形斜边为边长的正方形的面积等于两个以直角边为边长的正方形面积之和是解题的关键.6.B【解析】【分析】根据勾股定理求出“生长”了1次后形成的图形中所有的正方形的面积和,结合图形总结规律,根据规律解答即可.【详解】解:由题意得,正方形A的面积为1,由勾股定理得,正方形B的面积+正方形C的面积=1,△“生长”了1次后形成的图形中所有的正方形的面积和为2,同理可得,“生长”了2次后形成的图形中所有的正方形的面积和为3,△“生长”了3次后形成的图形中所有的正方形的面积和为4,……△“生长”了2020次后形成的图形中所有的正方形的面积和为2021,故选:B.【点睛】本题考查了勾股定理,如果直角三角形的两条直角边长分别是a,b,斜边长为c,那么a2+b2=c2.7.D【解析】【分析】设小正方形的边长为a,根据图形面积关系可得S大正方形=S小正方形+4S直角三角形,再根据xy =8,可列方程求解.【详解】设小正方形的边长为 a (a >0),△ S 大正方形=S 小正方形+4S 直角三角形,S 直角三角形=12x ·y , △ 25=a ²+12×4×8, 所以a =3.故选 D .【点睛】本题考查勾股定理,解题的关键是熟练运用勾股定理以及完全平方公式,本题属于基础题型.8.B【解析】【详解】根据面积的差得出a+b 的值,再利用a ﹣b=2,解得a ,b 的值代入即可.解:△AB=10,EF=2,△大正方形的面积是100,小正方形的面积是4, △四个直角三角形面积和为100﹣4=96,设AE 为a ,DE 为b ,即4×ab=96,△2ab=96,a 2+b 2=100,△(a+b )2=a 2+b 2+2ab=100+96=196,△a+b=14, △a ﹣b=2,解得:a=8,b=6,△AE=8,DE=6,△AH=8﹣2=6.故选B .9.B【解析】【分析】小正方形、大正方形的面积可以分别用a、b 表示,进而两式相减即可求出ab 的值.【详解】由勾股定理,得大正方形的面积为:2217a b +=,又小正方形的面积为2()5a b -= 即2225a b ab +-=△1725ab -=△ab =6故选:B .【点睛】本题是以弦图为背景的计算题,考查了勾股定理,图形的面积,关键是用a、b表示大小正方形的面积.10.C【解析】【详解】解:如图所示,△(a+b)2=21△a2+2ab+b2=21,△大正方形的面积为13,即:a2+b2=13,△2ab=21﹣13=8,△小正方形的面积为13﹣8=5.故选C.11.C【解析】【分析】根据勾股定理求AC的长,从而求木杆折断前的高度.【详解】解:由题意可知,AB=4,BC=3△在Rt△ABC中,225AC=AB+BC=△木杆在折断前的高度为4+5=9米故选:C.【点睛】本题考查勾股定理解直角三角形,正确理解题意进行计算是解题关键.12.B【解析】【分析】如图,由于倒下部分与地面成30°夹角,所以△BAC=30°,由此得到AB=2CB,而离地面5米处折断倒下,即BC=6米,所以得到AB=12米,然后即可求出这棵大树在折断前的高度.【详解】解:如图,△△BAC=30°,△BCA=90°,△AB=2CB,而BC=6米,△AB=12米,△这棵大树在折断前的高度为AB+BC=18米,故选B.【点睛】本题利用了直角三角形中30°的角所对的边是斜边的一半解决问题,解题关键是善于观察题目的信息,利用信息解决问题.13.A【解析】【分析】先根据勾股定理求出折断部分的长,再加上没折断的部分即可.【详解】2234=5米,3+5=8米.故选A.【点睛】本题考查了勾股定理的应用,在直角三角形中,如果两条直角边分别为a和b,斜边为c,那么a2+b2=c2.也就是说,直角三角形两条直角边的平方和等于斜边的平方.14.C【解析】【分析】首先设树顶端落在离树底部x米,根据勾股定理可得62+x2=(16-6)2,再解即可.【详解】设树顶端落在离树底部x米,由题意得:()2226166x+=-,解得:x=8.故选C.【点睛】考查勾股定理的应用,根据勾股定理列出方程是解题的关键. 15.A【解析】【分析】最短距离就是饮料罐的高度,最大距离可根据勾股定理解答.【详解】解:由题意可得:a的最小长度为饮料罐的高,即为12,当吸管斜放时,如图,此时a的长度最大,即为AB,△下底面半径是5,△AB=22512+=13,△a的取值范围是12≤a≤13,故选:A.【点睛】本题考查正确运用勾股定理.主要是运用勾股定理求得a 的最大值,此题比较常见,难度不大.16.A【解析】【分析】首先根据图形将题目中的数字对应起来,再根据题意设出未知数,用勾股定理求解即可.【详解】解:设水池的深度为x 尺,由题意得:x 2+52=(x +1)2,解得:x =12,则x +1=13,答:水深12尺,芦苇长13尺,故选A .【点睛】本题主要考查勾股定理的应用,根据勾股定理列出方程,将其化简成一元一次方程. 17.A【解析】【分析】利用勾股定理可求出OB 、OD 的长,即可得出BD 的长,再根据无理数的估算,估算出BD 的长即可得答案.【详解】△AB=5,OA=4,AC=2,AB=CD=5,△OB=22AB OA -=3,OD=22AB (OA AC)--=21,△BD=21-3,△16<21<25,△4<21<5,△1<21-3<2,即BD 的长小于2米,故选:A .【点睛】本题考查勾股定理的应用及无理数的估算,灵活运用勾股定理、熟练运用“夹逼法”估算无理数是解题关键.18.A【解析】【分析】设BO=xm,利用勾股定理用x表示出AB和CD的长,进而求出x的值,即可求出AB的长度.【详解】解:设BO=xm,依题意,得AC=2,BD=2,AO=8.在Rt△AOB中,根据勾股定理得222228AB AO OB x=+=+,在Rt△COD中,根据勾股定理22222(82)(2),DC CO OD x=+=-++△22228(82)(2),x x+=-++解得x=6,△AB=226810,+=答:梯子AB的长为10m.故选:A.【点睛】本题考查了勾股定理在实际生活中的应用,本题中找到AB=CD是解题的关键.19.D【解析】【分析】利用勾股定理进行解答.求出下滑后梯子低端距离低端的距离,再计算梯子低端滑动的距离.【详解】梯子顶端距离墙角的距离为22257-=24m,24-4=20m,梯子下滑后梯子底端距离墙角的距离为222520=15m,15m-7m=8m,即梯角水平滑动8m,故选D.【点睛】本题考查了勾股定理的应用,熟练掌握勾股定理是解题的关键,注意梯子的长度是不变的. 20.B【解析】【分析】要求长方体中两点之间的最短路径,最直接的作法,就是将长方体展开,然后利用两点之间线段最短解答.【详解】如图:根据题意,如上图所示,最短路径有以下三种情况:(1)AB2=(2+3)2+42=41;(2)AB2=32+(4+2)2=45;(3)AB2=22+(4+3)2=53;综上所述,最短路径应为(1)所示,所以AB2=41,即AB=41故选:B【点睛】此题考查的是勾股定理的应用,将长方体从不同角度展开,是解决此类问题的关键,注意不要漏解.21.B【解析】【分析】求蚂蚁爬行的最短距离,需将长方体的侧面展开,进而根据“两点之间线段最短”得出结果.【详解】解: 将长方体展开,连接A、B,根据两点之间线段最短,BD=1+2=3,AD=4,由勾股定理得:AB=22AD BD+=2234+=5.故选B.【点睛】考查了轴对称−最短路线问题,将长方体展开,根据两点之间线段最短,运用勾股定理解答是关键.22.C【解析】【分析】正方体侧面展开为长方形,确定蚂蚁的起点和终点,根据两点之间线段最短、勾股定理即可求出最短路径长.【详解】解:如图,它运动的最短路程AB=()222+21+=17故选:C【点睛】本题考查了正方体的侧面展开图、两点之间线段最短、勾股定理,掌握正方体的侧面展开图是解题关键.23.A【解析】【分析】平面展开图有两种情况,画出图形利用勾股定理求出MN的长即可.【详解】解:如图1,△AB=18cm,BC=GF=12cm,BF=10cm,点N是FG的中点,△BM=18﹣6=12 cm,BN=10+6=16 cm,△MN=221216+=20 cm;如图2,△AB=18cm,BC=GF=12cm,BF=10cm,点N是FG的中点,△PM=18﹣6+6=18 cm,NP=10 cm,△MN=221810+=424=2106cm.△20<2106,△蚂蚁需要爬行的最短路程为20 cm.故选:A.【点睛】本题考查平面展开图的最短路径问题和勾股定理的应用,解题的关键是将立体图形展为平面图形,利用勾股定理的知识求解.24.B【解析】【分析】要想求得最短路程,首先要把A和B展开到一个平面内.根据两点之间,线段最短求出蚂蚁爬行的最短路程.【详解】解:展开圆柱的半个侧面是矩形,矩形的长是圆柱的底面周长的一半,即4π≈12,矩形的宽是圆柱的高5.根据两点之间线段最短,知最短路程是矩形的对角线的长,即2251213.+=故选:B.【点睛】本题主要考查了平面展开图中最短路径求法,两个不在同一平面内的两个点之间的最短距离时,一定要展开到一个平面内.根据两点之间,线段最短.确定要求的长,再运用勾股定理进行计算.25.C【解析】【分析】根据题意首先将此圆柱展成平面图,根据两点间线段最短,可得AB最短,由勾股定理即可求得需要爬行的最短路程.【详解】解:将此圆柱展成平面图得:△有一圆柱,它的高等于20cm,底面直径等于30πcm,△底面周长=3030ππ⋅=cm,△BC=20cm,AC=12×30=15(cm),△AB=2222201525AC BC+=+=(cm).答:它需要爬行的最短路程为25cm.故选:C.【点睛】本题主要考查平面展开图求最短路径问题,将圆柱体展开,根据两点之间线段最短,运用勾股定理解答是解题关键.26.A【解析】【分析】将容器侧面展开,建立A关于EF的对称点A′,根据两点之间线段最短可知A′B的长度即为所求.【详解】解:如图,将容器侧面展开,作A关于EF的对称点A′,连接A′B,则A′B即为最短距离,由题意知,A′D=0.6m,A′E=AE=0.2m,△BD=0.9-0.3+0.2=0.8m,△A′B=22'A D BD+=220.60.8+=1(m).故选:A.【点睛】本题考查了平面展开-最短路径问题,将图形展开,利用轴对称的性质和勾股定理进行计算是解题的关键.同时也考查了同学们的创造性思维能力.27.A【解析】【分析】根据勾股定理可将斜边AB的长求出,根据折叠的性质知,AE=AB,已知AC的长,可将CE的长求出.【详解】解:在Rt△ABC中,AB=2222AC BC+=+=435根据折叠的性质可知:AE=AB=5△AC=4△CE=AE﹣AC=1即CE的长为1故选A.考点:勾股定理;翻折变换(折叠问题).28.A【解析】【分析】由△B=90°,AC=13,BC=5,可求得AB的长,设BE=x,由折叠的性质可得:△DEC是直角三角形,ED=BE=x,EC=5−x,CD=1,然后由勾股定理求得BE的长.【详解】解:△△B=90°,AC=13,BC=5,△AB=2212-=,AC BC设BE=x,-=13−12=1,由折叠的性质可得:CD=AC−AD=AC ABDE=BE=x,△ADE=△B=90°,△EC=BC−BE=5−x,在Rt△DEC中,EC2=CD2+DE2,△(5−x)2=1+x2,解得:x=2.4,△BE=2.4.故选:A.【点睛】此题考查了折叠的性质以及勾股定理.此题难度适中,注意掌握折叠前后图形的对应关系,注意数形结合思想与方程思想的应用.29.A【解析】【分析】根据矩形的性质可得BC=AD,△B=90°,利用勾股定理可求出AC的长,根据折叠的性质可得AF=AB,△B=△AFE=90°,BE=EF,在Rt△CEF中利用勾股定理列方程求出EF的长即可得答案.【详解】△四边形ABCD是矩形,AD=8,△△B=90°,BC=AD=8,△AC=22AB BC+=10,△折叠该纸片,使得AB边落在对角线AC上,点B落在点F处,折痕为AE,△BE=EF,AF=AB=6,△AFE=△B=90°,△CF=AC-AF=10﹣6=4,在Rt△CEF中,由勾股定理得,EF2+CF2=CE2,△EF2+CF2=(BC-EF)2,即EF2+42=(8-EF)2,解得:EF=3,故选:A .【点睛】本题主要考查了翻折变换的性质、勾股定理等几何知识点及其应用问题;解题的关键是灵活运用翻折变换的性质、勾股定理等几何知识点来分析、判断、推理或解答.30.A【解析】【分析】利用矩形的性质和翻折的性质求得AB =CD =8cm ,AD =BC =10cm ,△B =△C =△90°,AF =AD =10cm ,EF =DE ,在Rt、ABF 中,利用勾股定理可得BF ,在Rt、CEF 中,由勾股定理可得CE 的长.【详解】△四边形ABCD 是矩形,△AB =CD =8cm ,AD =BC =10cm ,△B =△90°由折叠的性质可得:AF =AD =10cm ,EF =DE ,在Rt、ABF 中,由勾股定理可得:22221086BF AF AB cm =-=+=在Rt、CEF 中,设EC =xcm ,则EF =DE =(8-x )cm ,FC =BC -BF =4cm , 由勾股定理得:222CE FC EF +=,即()22248x x +=-,解得:3x =△EC 的长为3cm .故选:A .【点睛】本题考查矩形的性质、翻折的性质、勾股定理的应用,解题的关键是熟练掌握上述性质,熟练掌握勾股定理解直角三角形.31.B【解析】【详解】试题解析:设AF=xcm ,则DF=(8-x )cm ,△矩形纸片ABCD 中,AB=6cm ,BC=8cm ,现将其沿EF 对折,使得点C 与点A 重合, △DF=D′F ,在Rt△AD′F中,△AF2=AD′2+D′F2,△x2=62+(8-x)2,解得:x=254(cm).故选B.考点:翻折变换(折叠问题).32.C【解析】【分析】首先根据矩形的性质知道AD△BC,所以△1=△3,由于折叠得到△1=△2,C′D=CD、BC′=BC,所以△2=△3,进而得出BE=DE,设DE=x,在Rt△DEC′中利用勾股定理即可求出DE的长.【详解】解:△四边形ABCD是矩形,△AD△BC,即△1=△3,由折叠可知,△1=△2,C′D=CD=4、BC′=BC=8,△△2=△3,即DE=BE,设DE=x,则EC′=8-x,在Rt△DEC′中,DC'2+EC'2=DE2△42+(8-x)2=x2解得:x=5,△DE的长为5.【点睛】本题主要考查了图形的折叠问题,解题的关键是掌握矩形的性质和折叠的特点,利用勾股定理解题.33.A【解析】【分析】先求出BC′,再由图形折叠特性知,C′F=CF=BC﹣BF=9﹣BF,在Rt△C′BF中,运用勾股定理BF2+BC′2=C′F2求解.。
2020年九年级数学中考复习专题专题:函数模型的应用(含答案)

专题:函数模型的应用1.超市以每千克40元的价格购进夏威夷果,计划以每千克60元的价格销售,为了让顾客得到更大的实惠,现决定降价销售,已知这种夏威夷果销售量y(千克)与每千克降价x(元)(0<x<20)之间满足一次函数关系,其图象如图所示:(1)求y与x之间的函数关系式;(2)超市要想获利2090元,则这种夏威夷果每千克应降价多少元?2.如图①,某商场在一楼到二楼之间设有上、下行自动扶梯和步行楼梯.甲、乙两人从二楼同时下行,甲乘自动扶梯,乙走步行楼梯,甲离一楼地面的高度h(单位:m)与下行时间x(单位:s)之间具有函数关系h=-310x+6,乙离一楼地面的高度y(单位:m)与下行时间x(单位:s)的函数关系如图②所示.(1)求y关于x的函数解析式;(2)请通过计算说明甲、乙两人谁先到达一楼地面.3.某智能品牌店,在销售某型号运动手环时,以高出进价的50%标价.已知按标价九折销售该型号运动手环8个与将标价直降100元销售7个获利相同.(1)求该型号运动手环的进价和标价分别是多少元?(2)若该型号运动手环的进价不变,按(1)中的标价出售,该店平均每月可售出38个;若每个运动手环每降价20元,每月可多售出2辆,求该型号运动手环降价多少元时,每月获利最大?最大利润是多少?4.一水果店以进价为每千克16元购进万荣苹果,销售中发现,销售单价定为20元时,日销售量为50千克;当销售单价每上涨1元,日销售量就减少5千克,设销售单价为x(元),每天的销售量为y(千克),每天获利为w(元).(1)求y与x之间的函数关系式;(2)求w与x之间的函数关系式;该苹果售价定为每千克多少元时,每天的销售利润最大?最大利润是多少元?(3)如果商家规定这种苹果每天的销售量不低于40千克,求商家每天销售利润的最大值是多少元?5.挂灯笼成为我国的一种传统文化. 小明在春节前购进甲、乙两种红灯笼,用3120元购进甲灯笼与用4200元购进乙灯笼的数量相同,已知乙灯笼每对进价比甲灯笼每对进价多9元.(1)求甲、乙两种灯笼每对的进价;(2)经市场调查发现,乙灯笼每对售价50元时,每天可售出98对,售价每提高1元,则每天少售出2对;物价部门规定其销售单价不高于每对65元,设乙灯笼每对涨价x元,小明一天通过乙灯笼获得利润y元.①求出y与x之间的函数解析式;②乙种灯笼的销售单价为多少元时,一天获得利润最大?最大利润是多少元?6.甲、乙两个批发店销售同一种苹果.在甲批发店,不论一次购买数量是多少,价格均为6元/kg.在乙批发店,一次购买数量不超过50 kg时,价格为7元/kg;一次购买数量超过50 kg时,其中有50 kg的价格仍为7元/kg,超出50 kg部分的价格为5元/kg.设小王在同一个批发店一次购买苹果的数量为x kg(x>0).(Ⅰ)根据题意填表:(Ⅱ)设在甲批发店花费y1元,在乙批发店花费y2元,分别求y1,y2关于x的函数解析式;(Ⅲ)根据题意填空:①若小王在甲批发店和在乙批发店一次购买苹果的数量相同,且花费相同,则他在同一个批发店一次购买苹果的数量为________kg;②若小王在同一个批发店一次购买苹果的数量为120 kg,则他在甲、乙两个批发店中的________批发店购买花费少;③若小王在同一个批发店一次购买苹果花费了360元,则他在甲、乙两个批发店中的________批发店购买数量多.7.某工厂计划生产甲乙两种产品共2500吨,每生产1吨甲产品可获得利润0.3万元,每生产1吨乙产品可获得利润0.4万元,设该工厂生产了甲产品x(吨),生产甲、乙两种产品获得的总利润为y(万元).(1)求y与x之间的函数表达式;(2)若每生产1吨甲产品需要A原料0.25吨,每生产1吨乙产品需要A原料0.5吨,受市场影响,该厂能获得的A原料至多为1000吨,其它原料充足.求出该工厂生产甲、乙两种产品各为多少吨时,能获得最大利润.8.某商场销售一批足球文化衫,已知该文化衫的进价为每件40元,当售价为每件60元时,每个月可销售出100件,根据市场行情,现决定涨价销售,调查表明,每件商品的售价每上涨1元,每月少销售出2件,设每件商品的售价为x元.每个月的销售为y件.(1)求y与x之间的函数关系式;(2)当每件商品的售价定为多少元时,每个月的利润恰好为2250元;(3)当每件商品的售价定为多少元时,每个月获得利润最大?最大月利润为多少?9.某公司计划在某地区销售一款5G产品,根据市场分析,该产品的销售价格将随销售周期的变化而变化,设该产品在第x(x为正整数)个销售周期每台的销售价格为y元,y与x 之间满足如图所示的一次函数关系.(1)求y与x之间的关系式;(2)设该产品在第x 个销售周期的销售数量为p (万台),p 与x 的关系可以用p =12x +12来描述.根据以上信息,试问:哪个销售周期的销售收入最大?此时该产品每台的销售价格是多少元?10. 某商店销售一种商品,经市场调查发现,该商品的周销售量y (件)是售价x (元/件)的一次函数,其售价,周销售量,周销售利润w (元)的三组对应值如下表:(1)①求y 关于x 的函数解析式(不要求写出自变量的取值范围);②该商品进价是________元/件;当售价是____元/件时,周销售利润最大,最大利润是______元;(2)由于某种原因,该商品进价提高了m 元/件(m >0),物价部门规定该商品售价不得超过65元/件,该商店在今后的销售中,周销售量与售价仍然满足(1)中的函数关系.若周销售最大利润是1400元,求m 的值.参考答案1. 解:(1)设一次函数解析式为y =kx +b , ∵当x =2,y =120;当x =4,y =140;∴⎩⎪⎨⎪⎧2k +b =120,4k +b =140, 解得⎩⎪⎨⎪⎧k =10,b =100.∴y 与x 之间的函数关系式为y =10x +100; (2)由题意得(60-40-x )(10x +100)=2090, 整理得x 2-10x +9=0, 解得x 1=1,x 2=9. ∵让顾客得到更大的实惠, ∴x =9,答:超市要想获利2090元,则这种夏威夷果每千克应降价9元.2. 解:(1)设y 关于x 的函数解析式为y =kx +b ,把点(0,6)(15,3)代入y =kx +b 得⎩⎪⎨⎪⎧6=b ,3=15k +b ,解得⎩⎪⎨⎪⎧k =-15,b =6,∴y 关于x 的函数解析式为y =-15x +6;(2)甲:当h =0时,得x =20.乙:当y=0时,得x=30.∵20<30,∴甲先到达一楼地面.3.解:(1)设该型号运动手环的进价为x元,根据题意得[(1+50%)x×0.9-x]×8=[(1+50%)x-100-x]×7,∴x=1000,∴(1+50%)x=1500元,∴该型号运动手环的进价为1000元,标价为1500元;(4分) (2)设该型号运动手环降价y元,利润为w元.根据题意得w=(38+y20×2)(1500-1000-y)=(38+0.1y)(500-y)=-0.1(y-60)2+19360,当y=60时,w有最大值19360.∴降价60元,每月获利最大,最大利润为19360元.4.解:(1)根据题意得y=50-5(x-20)=-5x+150;(2)根据题意得w=(x-16)(-5x+150)=-5x2+230x-2400,∴w与x的函数关系式为:w=-5x2+230x-2400=-5(x-23)2+245.∵-5 <0,∴当x=23时,w有最大值,最大值为245.(5分)答:w与x之间的函数关系式为w=-5x2+230x-2400.该苹果售价定为每千克23元时,每天销售利润最大,最大利润是245元;(3)根据题意得-5x+150≥40,解得x≤22.∵w=-5(x-23)2+245.∵-5<0,w≤23时,w随x增大而增大,∴当x=22时w有最大值,其最大值为-5×(22-23)2+245=240(元).答:商家每天销售利润的最大值是240元.5.解:(1)设甲种灯笼进价为x元/对,则乙种灯笼的进价为(x+9)元/对,由题意得3120 x=4200 x+9,解得x=26,经检验,x=26是原方程的解,且符合题意,∴x+9=26+9=35,答:甲种灯笼单价为26元/对,乙种灯笼的单价为35元/对;(2)①y=(50+x-35)(98-2x)=-2x2+68x+1470,答:y与x之间的函数解析式为:y=-2x2+68x+1470;②∵a=-2<0,∴函数y有最大值,该二次函数的对称轴为:x=-b2a=17,物价部门规定其销售单价不高于每对65元,∴x+50≤65,∴x≤15,∵x<17时,y随x的增大而增大,∴当x=15时,y最大=2040.∴15+50=65.答:乙种灯笼的销售单价为每对65元时,一天获得利润最大,最大利润是2040元.6.解:(Ⅰ)180,900,210,850;【解法提示】甲批发店花费:当x=30时,花费为30×6=180;当x=150时,花费为150×6=900.乙批发店花费:当x =30时,花费为30×7=210;当x =150时,花费为50×7+(150-50)×5=850.(Ⅱ)y 1=6x (x >0), 当0<x ≤50时,y 2=7x ;当x >50时,y 2=7×50+5(x -50),即y 2=5x +100;即y 2=⎩⎪⎨⎪⎧7x (0<x ≤50),5x +100(x >50).(Ⅲ)①100;②乙;③甲.【解法提示】①当0<x ≤50时,甲批发店和乙批发店花费不可能相同,则x >50时,令y 1=y 2,则6x =5x +100,解得x =100;②当x =120时,y 1=6×120=720,y 2=5×120+100=700,∵720>700,∴在乙批发店购买花费少;③对甲批发店而言:令y 1=360,则6x =360,解得x =60.对乙批发店而言:当x =50时,花费为350<360,则令5x +100=360,解得x =52,∵60>52,∴小王花费360元时,在甲批发店购买数量多.7. 解:(1)y =x ·0.3+(2500-x )·0.4=-0.1x +1000; (2)由题意得x ·0.25+(2500-x )·0.5≤1000,解得x ≥1000. 又∵x ≤2500, ∴1000≤x ≤2500. 由(1)可知,-0.1<0,∴y 的值随着x 的增加而减小,∴当x =1000时,y 取最大值,此时生产乙种产品2500-1000=1500(吨) 答:工厂生产甲产品1000吨,乙产品1500吨时,能获得最大利润. 8. 解:(1)根据题意得y = 100-2(x -60)=-2x +220(60≤x ≤110);(2)由题意可得:(-2x +220)(x -40)=2250. x 2-150x +5525=0, 解得x 1=65,x 2=85.答:当每件商品的售价定为65元或85元时,利润恰好是2250元; (3)设利润为W 元,∴W =(x -40)(-2x +220)=-2x 2+300x -8800=-2(x -75)2+2450. ∵a =-2<0, ∴抛物线开口向下. ∵60≤x ≤110,∴当x =75时,W 有最大值,W 最大=2450(元).答:当售价定为75元时,获得最大利润,最大利润是2450元. 9. 解:(1)设y 关于x 的函数关系式为y =kx +b (k ≠0),由图象可知,将点(1,7000),(5,5000)代入得⎩⎪⎨⎪⎧k +b =7000,5k +b =5000,解得⎩⎪⎨⎪⎧k =-500,b =7500,∴y 关于x 的函数关系式为y =-500x +7500; (2)设销售收入为W ,根据题意得 W =yp =(-500x +7500)·(12x +12),整理得W =-250(x -7)2+16000,∵-250<0,∴W 在x =7时取得最大值,最大值为16000元, 此时该产品每台的销售价格为-500×7+7500=4000元.答:第7个销售周期的销售收入最大,此时该产品每台的销售价格为4000元.10. 解:(1)①y =-2x +200; ②40,70,1800;(2)由题意可知w =(-2x +200)×(x -40-m )=-2x 2+(280+2m )x -8000-200m ,对称轴为直线x =140+m2,∵m >0,∴对称轴x =140+m2>70,∵抛物线开口向下,在对称轴左侧,y 随x 的增大而增大, ∴当x =65时,y max =1400,代入表达式解得m =5.。
专题28 截长补短模型-2023年中考数学总复习真题探究与变式训练(全国通用,含解析)(解析版)

模块二常见模型专练专题28 截长补短模型例1(2021年·四川广安·中考真题)在数学中,我们会用“截长补短”的方法来解决几条线段之间的和差问题.请看这个例题:如图1,在四边形中,,,若,求四边形的面积.解:延长线段到E,使得,连接,我们可以证明,根据全等三角形的性质得,,则,得,这样,四边形的面积就转化为等腰直角三角形面积.(1)根据上面的思路,我们可以求得四边形的面积为 cm2.(2)如图2,在中,,且,求线段的最小值.(3)如图3,在平行四边形中,对角线与相交于O,且;,则是否为定值?若是,求出定值;若不是,求出的最小值及此时平行四边形的面积.【答案】(1)12.5(2)(3)不是,,【分析】(1)根据题意,可以计算出等腰直角三角形的面积,从而可以得到四边形的面积;(2)由勾股定理可得,由配方法可求解;(3)由平行四边形的性质可得,,由勾股定理可求,由配方法可求的最小值,即可求解.【详解】(1)解:由题意可得,,,则的面积,即四边形的面积为,故答案为:12.5;(2)解:,,,,当时,取最小值,最小值为2;(3)解:如图,过点B作于H,四边形是平行四边形,,,,,,,,,,,,,,当时,有最小值,即的最小值为,此时:,,是等边三角形,.综上可知,不是定值,的最小值为,此时平行四边形的面积为.本题是四边形综合题,考查了全等三角形的判定和性质,勾股定理,平行四边形的中考真题)如图,四边形是内正方形,是圆上一点(点P与点A,B,C,D不重合),连接.(1)若点P是弧上一点,①∠BPC度数为___________;②求证:;小明的思路为:这是线段和差倍半问题,可采用截长补短法,请按小明思路完成下列证明过程(也可按自己的想法给出证明).证明:在的延长线上截取点E.使,连接.(2)探究当点P分别在,,上,求的数量关系,直接写出答案,不需要证明.【答案】(1)①,②见解析(2);;;证明见解析【分析】(1)①理由正方形的性质和圆周角的度数等于它所对弧的度数的一半解答即可;②在的延长线上截取点E.使,连接,利用全等三角形的判定与性质和等腰直角三角形的判定与性质解答即可;(2)利用截长补短法,依题意画出相应图形,按小明思路完成解答即可.【详解】(1)①解:,理由:∵四边形是正方形,∴,∴的度数为,∴,故答案为:;②证明:在的延长线上截取点E,使.连接,如图,∵四边形是内接正方形,∴,又∵点P在上,∴四边形为内接四边形∴.在和中,,∴,∴,∵,∴,∴,∴为等腰直角三角形,∴,∴;(2)当点P在上时,;在上取点E,使,连接,如图,∵四边形是内接正方形,∴,在和中,,∴,∴,∵,∴,∴,∴为等腰直角三角形,∴,∴;当点P在上时,,在上取点E,使,连接,如图,∵四边形是内接正方形,∴,在和中,,∴,∴,∵,∴,∴,∴为等腰直角三角形,∴,∴;当点P在上时,,理由:在的延长线上截取点E,使,连接,如图,∵四边形是内接正方形,∴,又∵点P在上,∴四边形为内接四边形∴.在和中,,∴,∴.∵,∴,∴.∴为等腰直角三角形,∴,∴.【点睛】本题主要考查了圆的有关性质,圆周角定理,圆的内接四边形的性质,全等三角形的判定与性质,等腰直角三角形的判定与性质,本题是阅读型题目,理解并熟练应用截长补短法,构造恰当的辅助线解答是解题的关键.模型截长补短截长补短法,是初中数学几何题中一种辅助线的添加方法,也是把几何题化难为易的一种思想。
中考数学专题复习全等三角形(公共角模型)
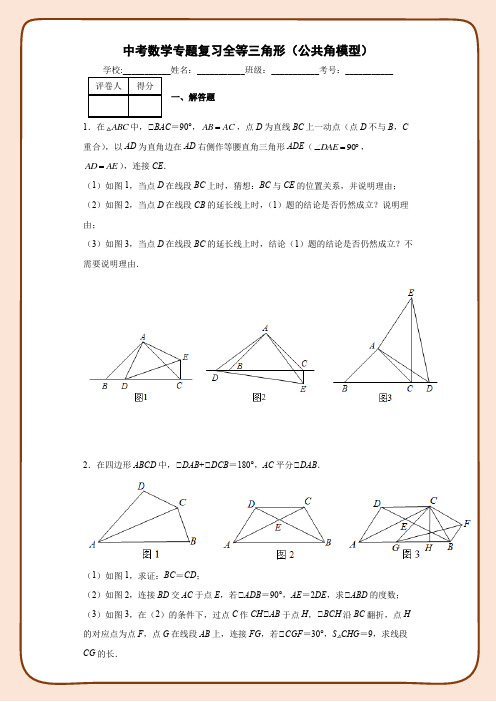
中考数学专题复习全等三角形(公共角模型)学校:___________姓名:___________班级:___________考号:___________评卷人得分 一、解答题1.在ABC 中,∠BAC =90°,AB AC =,点D 为直线BC 上一动点(点D 不与B ,C 重合),以AD 为直角边在AD 右侧作等腰直角三角形ADE (90DAE ∠=︒,AD AE =),连接CE . (1)如图1,当点D 在线段BC 上时,猜想:BC 与CE 的位置关系,并说明理由; (2)如图2,当点D 在线段CB 的延长线上时,(1)题的结论是否仍然成立?说明理由;(3)如图3,当点D 在线段BC 的延长线上时,结论(1)题的结论是否仍然成立?不需要说明理由.2.在四边形ABCD 中,∠DAB +∠DCB =180°,AC 平分∠DAB .(1)如图1,求证:BC =CD ;(2)如图2,连接BD 交AC 于点E ,若∠ADB =90°,AE =2DE ,求∠ABD 的度数; (3)如图3,在(2)的条件下,过点C 作CH ∠AB 于点H ,∠BCH 沿BC 翻折,点H 的对应点为点F ,点G 在线段AB 上,连接FG ,若∠CGF =30°,S △CHG =9,求线段CG 的长.3.如图1,在等腰直角三角形ABC中,AB=AC,∠BAC=90°,点E,F分别为AB,AC的中点,H为线段EF上一动点(不与点E,F重合),过点A作AG∠AH且AG=AH,连接GC,HB.(1)证明:AHB∠AGC;(2)如图2,连接GF,HG,HG交AF于点Q.∠证明:在点H的运动过程中,总有∠HFG=90°;∠当AQG为等腰三角形时,求∠AHE的度数.4.如图,我们把对角线互相垂直的四边形叫做“垂美四边形”.(1)性质探究:如图1.己知四边形ABCD中,AC∠BD.垂足为O,求证:AB2+CD2=AD2+BC2;(2)解决问题:已知AB=52.BC=42,分别以∠ABC的边BC和AB向外作等腰Rt∠BCE和等腰Rt∠ABD;∠如图2,当∠ACB=90°,连接DE,求DE的长;∠如图3.当∠ACB≠90°,点G、H分别是AD、AC中点,连接GH.若GH=26,则S△ABC=.5.已知,∠ABC是边长为4cm的等边三角形,点P,Q分别从顶点A,B同时出发,沿线段AB,BC运动,且它们的速度均为1cm/s.当点P到达点B时,P、Q两点停止运动.设点P的运动时间为t(s).(1)如图1,连接AQ、CP,相交于点M,则点P,Q在运动的过程中,∠CMQ会变化吗?若变化,则说明理由;若不变,请求出它的度数.(2)如图2,当t为何值时,∠PBQ是直角三角形?(3)如图3,若点P、Q在运动到终点后继续在射线AB、BC上运动,直线AQ、CP 交点为M,请直接写出∠CMQ度数.6.(1)如图(1)点P是正方形ABCD的边CD上一点(点P与点C,D不重合),点E在BC的延长线上,且CE=CP,连接BP,DE.求证:∠BCP∠∠DCE;(2)直线EP交AD于F,连接BF,FC.点G是FC与BP的交点.∠若CD=2PC时,求证:BP∠CF;∠若CD=n•PC(n是大于1的实数)时,记∠BPF的面积为S1,∠DPE的面积为S2.求证:S1=(n+1)S2.参考答案:1.(1)BC ∠CE ,见解析;(2)成立,见解析;(3)成立【解析】【分析】(1)先证∠2=∠3,再证∠ABD ∠∠ACE (SAS ),得出∠4=∠5,求出∠4=∠6=45°,∠5=45°即可;(2)先证∠2=∠3,再证∠ABD ∠∠ACE (SAS ),得出∠ABD =∠ACE ,求出∠ABC =∠ACB =45°,得出∠ABD =∠ACE =135°即可;(3)先证∠BAD =∠CAE ,再证∠ABD ∠∠ACE (SAS ),得出∠ABD =∠ACE ,再求∠ABC =∠ACB =45°,得出∠ABD =∠ACE =45°.【详解】解:(1)BC 与CE 的位置关系是BC ∠CE ,理由是:∠∠BAC =∠DAE =90°,∠∠BAC -∠1=∠DAE -∠1,即∠2=∠3,在△ABD 和△ACE 中,23AB AC AD AE =⎧⎪∠=∠⎨⎪=⎩,∠△ABD ∠△ACE (SAS ),∠∠4=∠5,∠∠BAC =90°,AB =AC ,∠∠4=∠6=45°,∠∠5=45°,∠∠BCE =∠5+∠6=45°+45°=90°,即BC ∠CE ;(2)成立.理由是:∠∠BAC =∠DAE =90°,∠∠BAC-∠1=∠DAE-∠1,即∠2=∠3,在△ABD 和△ACE 中,23AB AC AD AE =⎧⎪∠=∠⎨⎪=⎩,∠△ABD ∠△ACE (SAS ),∠∠ABD =∠ACE ,∠∠BAC =90°,AB =AC ,∠∠ABC =∠ACB =45°,∠∠ABD =∠ACE =135°,∠∠BCE =∠ACE -∠ACB =135°-45°=90°,即BC ∠CE ;(3)成立∠∠BAC =∠DAE =90°,∠∠BAC +∠CAD =∠DAE +∠CAD ,即∠BAD=∠CAE,在△ABD和△ACE中,AB ACBAD CAEAD AE=⎧⎪∠=∠⎨⎪=⎩,∠∠ABD∠∠ACE(SAS),∠∠ABD=∠ACE,∠∠BAC=90°,AB=AC,∠∠ABC=∠ACB=45°,∠∠ABD=∠ACE=45°,∠∠BCE=∠ACE+∠ACB=45°+45°=90°.【点睛】本题考查图形变换中结论问题,等腰直角三角形性质,三角形全等判定与性质,角的和差运用,直线位置关系,掌握等腰直角三角形性质,三角形全等判定与性质,角的和差运用,直线位置关系垂直的证法是解题关键.2.(1)证明见解析;(2)30ABD∠=;(3)CG=6【解析】【分析】(1)过点C作CP∠AB于点P,作CQ∠AD的延长线于点Q,证明∠CQD∠∠CPB,即可得到答案;(2)延长ED,让MD=ED,∠AME是等边三角形,然后利用等边三角形的性质和角平分线的定义即可求得答案;(3)延长GC,过点F作FK∠GC的延长线于点K,过点H作HL∠GF于点L,连接HF,通过证明∠CFK∠∠HFL,得到FK=FL,又有直角三角形中30所对的直角边是斜边的一半,求得FK=12GF,根据等腰三角形的三线合一,进一步求得∠FGH=15,从求得到∠GCH=45,然后在直角三角形中利用勾股定理求解即可得答案.【详解】解:(1)过点C作CP∠AB于点P,作CQ∠AD的延长线于点Q,如下图:∠AC平分∠DAB,CP∠AB,CQ∠AD∠CQ=CP在四边形APCQ中,∠APC=∠AQC=90∠∠QAP+∠PCQ=180又∠∠DAB+∠DCB=180°∠∠PCQ=∠DCB∠∠QCD+∠DCP=∠DCP+∠PCB∠∠QCD=∠PCB又∠∠CQD=∠CPB=90∠∠CQD∠∠CPB(ASA)∠CD=CB(2)延长ED,让MD=ED,如下图:∠∠ADB=90°∠AD∠ME又∠MD=ED∠AM=AE,ME=2DE又∠AE=2DE∠ME=AE=AM∠∠AME是等边三角形∠60AED∠=又∠∠ADE=90°∠30DAE∠=∠AC平分∠DAB∠30EAB DAE∠=∠=又∠AED EAB ABD∠=∠+∠∠30ABD∠=(3)延长GC,过点F作FK∠GC的延长线于点K,过点H作HL∠GF于点L,连接HF,如下图:∠在Rt CHB中,90,60CHB CBH ABD CBD∠=∠=∠+∠=∠∠HCB=30又∠折叠∠CH=CF, ∠HCB=∠FCB=30∠∠HCF=60∠∠CHF是等边三角形∠∠CFH=∠CHF=60,CF=HF又∠在Rt GFK△中,∠CGF=30,∠GKF=90∠∠GFK=60∠∠CFH=∠GFK∠∠CFK +∠CFG =∠CFG +∠HFL ∠∠CFK =∠HFL又∠∠CKF =∠LHF =90,CF =HF∠∠CFK ∠∠HFL∠FK =FL又∠在Rt GFK △中,∠CGF =30∠FK =12GF∠FL =12GF∠GL =FL又∠HL ∠GF∠HG =HF∠∠FGH =∠GFH又∠∠CHF =60,∠CHB =90∠∠FHB =∠CHB -∠CHF =30∠∠FGH =15∠∠CGH =∠CGF +∠FGH =45又∠∠CHG =90∠∠GCH =45∠GH =CH ,∠GCH 是等腰直角三角形又∠9CHG S =△∠192GH CH ⋅= ∠2218GH CH ==在Rt CHG 中,由勾股定理得:22236CG GH CH =+=∠CG >0∠CG =6【点睛】本题考查全等三角形的性质和判定,含30︒的直角三角形性质,等边三角形的性质和判定,直角三角形的勾股定理等知识点,能够熟练利用化归的思想和数形结合的思想去解题,是本题的重点.3.(1)见解析;(2)∠见解析;∠当∠AQG为等腰三角形时,∠AHE的度数为67.5°或90°.【解析】【分析】(1)根据SAS可证明∠AHB∠∠AGC;(2)∠证明∠AEH∠∠AFG(SAS),可得∠AFG=∠AEH=45°,从而根据两角的和可得结论;∠分两种情况:i)如图3,AQ=QG时,ii)如图4,当AG=QG时,分别根据等腰三角形的性质可得结论.【详解】(1)证明:如图1,由旋转得:AH=AG,∠HAG=90°,∠∠BAC=90°,∠∠BAH=∠CAG,∠AB=AC,∠∠ABH∠∠ACG(SAS);(2)∠证明:如图2,在等腰直角三角形ABC中,∠BAC=90°,∠∠ABC=∠ACB=45°,∠点E,F分别为AB,AC的中点,∠EF是∠ABC的中位线,∠EF∠BC,AE=12AB,AF=12AC,∠AE=AF,∠AEF=∠ABC=45°,∠AFE=∠ACB=45°,∠∠EAH=∠F AG,AH=AG,∠∠AEH∠∠AFG(SAS),∠∠AFG=∠AEH=45°,∠∠HFG=45°+45°=90°;∠分两种情况:i)如图3,AQ=QG时,∠AQ=QG,∠∠QAG=∠AGQ,∠AG∠AH且AG=AH,∠∠AHG=∠AGH=45°,∠∠AHG=∠AGH=∠HAQ=∠QAG=45°,∠∠EAH=∠F AH=45°,∠AE=AF,AH=AH,∠∠AEH∠∠AFH(SAS),∠∠AHE=∠AHF,∠∠AHE+∠AHF=180°,∠∠AHE=∠AHF=90°;ii)如图4,当AG=QG时,∠GAQ=∠AQG,∠∠AEH=∠AGQ=45°,∠∠GAQ=∠AQG=180452︒-︒=67.5°,∠∠EAQ=∠HAG=90°,∠∠EAH=∠GAQ=67.5°,∠∠AHE=∠AQG=67.5°;∠H为线段EF上一动点(不与点E,F重合),∠不存在AG=AQ的情况.综上,当∠AQG为等腰三角形时,∠AHE的度数为67.5°或90°.【点睛】本题是三角形的综合题,考查了旋转的性质,等腰直角三角形的性质和判定,等腰三角形的性质和判定,也考查了全等三角形的判定与性质,第二问要注意分类讨论,不要丢解.4.(1)见解析;(2)∠146;∠7 2【解析】【分析】(1)根据AC∠BD可以得到,AOB =∠COD=90°即可得到AB²=AO²+OB²,CD²=DO²+OC²即AB²+CD²=AO²+OB²+DO²+OC² 同理可以得到AD²+BC²=AO²+OB²+DO²+OC² 即可得到答案;(2)连DC、AE相交于点F,先证明∠ABE ∠∠DBC得到∠CDB=∠BAE 从而证得AE∠CD 再利用勾股定理和(1)中的结论求解即可得到答案;(3)连DC、AE相交于点F,作CP∠BD交DB延长线于点P,BP²+CP²=BC²=(42)²=32,DP²+PC²=DC²=(46)²=96,(DP²+PC²)-(BP²+CP²)=96-32=64,DP²-BP²=64从而求出BP=7210,再证明AB∠PC则S△ABC=12AB×BP.【详解】解:(1)证明:∠AC∠BD∠,AOB=90°在Rt∠AOB中AB²=AO²+OB²∠,COD=90°在Rt∠COD中CD² =DO²+OC²∠AB²+CD²=AO²+OB²+DO²+OC²同理AD²+BC²=AO²+OB²+DO²+OC² ∠ AB2+CD2=AD2+BC ²(2)∠解:连DC、AE相交于点F ∠Rt∠BCE和Rt∠ABD是等腰三角形∠BE=BC AB=BD∠CBE=∠ABD=90°∠∠ABE=∠DBC=90°+∠ABC∠∠ABE ∠∠DBC∠∠CDB=∠BAE∠∠ABD=90°∠∠CDB+∠CDA+∠DAB=90°∠∠BAE+∠CDA+∠DAB=90°∠∠AFD=90°∠AE∠CD∠AB=52,BC=42∠ACB=90° ∠AC=2232AB BC-=∠AB=52,BD=52∠ABD=90°∠AD=2210AB BD+=∠BC=42,BE=42∠CBE=90°∠CE=228BC BE+=由(1)中结论AD²+EC²=AC²+DE²∠(10)²+(8)²=(32)²+DE²∠DE=146∠连DC、AE相交于点F∠点G、H分别是AD、AC中点,GH=26∠ DC=2GH =46作CP∠BD交DB延长线于点PBP²+CP²=BC²=(42)²=32DP²+PC²=DC²=(46)²=96∠(DP²+PC²)-(BP²+CP²)=96-32=64∠DP²-BP²=64∠(BD+BP)²-BP²=64∠(52+BP)²-BP²=64∠BP=7210∠∠PBA=90°,∠P=90°,∠∠PBA+∠P=90°+90°=180°则S △ABC =12AB ×BP =12×52×772=102【点睛】本题主要考查了四边形的综合问题,等腰直角三角形的性质,全等三角形的性质与判定,勾股定理,垂直的定义,解题的关键在于能够熟练掌握相关知识进行求解.5.(1)不变,60°;(2)43或83;(3)120°. 【解析】【分析】(1)通过证∠ABQ ∠∠CAP 得到∠BAQ =∠ACP ,所以由三角形外角定理得到∠CMQ =∠ACP +∠CAM =∠BAQ +∠CAM =∠BAC =60°;(2)需要分类讨论:分∠PQB =90°和∠BPQ =90°两种情况;(3)通过证∠ABQ ∠∠CAP 得到∠BAQ =∠ACP ,所以由三角形外角定理得到∠CMQ =∠BAQ +∠APC =∠ACP +∠APC =180°-∠BAC =120°.【详解】(1)不变.在∠ABQ 与∠CAP 中,∠60AB AC B CAP AP BQ =⎧⎪∠=∠=︒⎨⎪=⎩,∠∠ABQ ∠∠CAP (SAS ),∠∠BAQ =∠ACP ,∠∠CMQ =∠ACP +∠CAM =∠BAQ +∠CAM =∠BAC =60°;(2)设时间为t ,则AP =BQ =t ,PB =4-t ,∠当∠PQB =90°时,∠∠B =60°,∠4-t =2t ,43t =; ∠当∠BPQ =90°时,∠∠B =60°,∠BQ =2BP ,∠ t =2(4-t ),t =83; ∠当第43秒或第83秒时,∠PBQ 为直角三角形; (3)在∠ABQ 与∠CAP 中,∠60AB AC B CAP AP BQ =⎧⎪∠=∠=︒⎨⎪=⎩,∠∠ABQ ∠∠CAP (SAS ),∠∠BAQ =∠ACP ,∠∠CMQ =∠BAQ +∠APC =∠ACP +∠APC =180°-∠BAC =120°.【点睛】本题考查了等边三角形的性质,全等三角形的判定与性质,掌握全等三角形的判定与性质是解题的关键.6.(1)证明见解析;(2)∠证明见解析;∠证明见解析.【解析】【分析】(1)由SAS 即可证明∠BCP ∠∠DCE .(2)∠在(1)的基础上,再证明∠BCP ∠∠CDF ,进而得到∠FCD +∠BPC =90°,从而证明BP ⊥CF ;∠设CP =CE =1,则BC =CD =n ,DP =CD -CP =n -1,分别求出S 1与S 2的值,得()()11112S n n =+-,()2112S n =-,所以S 1=(n +1)S 2结论成立. 【详解】证明:(1)∠在∠BCP 与∠DCE 中,90BC CD BCP DCE CP CE =⎧⎪∠=∠=︒⎨⎪=⎩∠∠BCP ∠∠DCE (SAS ).(2)∠∠CP =CE ,∠PCE =90°,∠∠CPE =45°,∠∠FPD =∠CPE =45°,∠∠PFD =45°,∠FD =DP .∠CD =2PC ,∠DP =CP ,∠FD =CP .∠在∠BCP 与∠CDF 中,90BC CD BCP CDF CP FD =⎧⎪∠=∠=︒⎨⎪=⎩∠∠BCP ∠∠CDF (SAS ),∠∠FCD =∠CBP .∠∠CBP +∠BPC =90°,∠∠FCD +∠BPC =90°,∠∠PGC =90°,即BP ⊥CF .∠设CP =CE =1,则BC =CD =n ,DP =CD -CP =n -1 易知∠FDP 为等腰直角三角形,∠FD =DP =n -1.∠()1111222BCDF BCP FDP S S S S BC FD CD BC CP FD DP ∆∆=--=+⋅-⋅-⋅梯形 ()()()()()221111111111122222n n n n n n n n =+-⋅-⋅--=-=+- ()()2111111222S DP CE n n =⋅=-⋅=- ∠S 1=(n +1)S 2.【点睛】本题是几何综合题,考查了正方形的性质、全等三角形的判定与性质、等腰直角三角形、图形的面积等知识点,试题的综合性强,难度较大.。
2024年中考专题复习++建模思想应用的常见类型归类++同步练++讲义

建模思想应用的常见类型归类点石成金数学建模思想是人类用数学知识探索自然和实际应用的一种最有效的方法,也是数学应用于科技和社会的最基本途径;它是对现象和过程进行合理的抽象和量化,然后用数学知识进行模拟和验证的一种模式化思维;初中数学建模,就是用初中所学的数学知识在数学和实际问题之间构建一个桥梁,便于把实际问题用数学问题表示出来,这个桥梁就是数学模型,构建这个桥梁的思维方法就是数学建模思想.典型例题剖析例.为解决楼房之间的挡光问题,某地区规定:两幢楼房间的距离至少为40米,中午12时不能挡光.如图,某旧楼的一楼窗台高1米,要在此楼正南方40米处再建一幢新楼.已知该地区冬天中午12时阳光从正南方照射,并且光线与水平线的夹角最小为30°,在不违反规定的情况下,请问新建楼房最高米.(结果精确到1米.√3≈1.732,√2≈1.414)分析:在不违反规定的情况下,需使阳光能照到旧楼的一楼;据此构造Rt△DCE,其中有CE=30米,∠DCE=30°,解三角形可得DE的高度,再由DB=BE+ED可计算出新建楼房的最高高度.解:过点C作CE⊥BD于E.∵AB=40米,∴CE=40米,∵阳光入射角为30°,∴∠DCE=30°,在Rt△DCE中tan∠DCE=DECE.∴DE40=√33,∴DE=40×√33=40√33米,∵AC=BE=1米,∴DB=BE+ED=1+40√33=3+40√33≈24米.答:新建楼房最高约为24米.故答案为:24分类训练类型1建立方程模型求几何图形面积1.将两张完全相同的矩形纸片ABCD,矩形纸片FBED按如图方式放置,BD为重合的对角线.重叠部分为四边形DHBG.(1)试判断四边形DHBG为何种特殊的四边形,并说明理由;(2)若四边形DHBG的面积为15,AD=3,求AB的长.分析:(1)根据矩形的性质得出∠A=∠E=90°,AD=ED,AB=EB,根据全等三角形的判定得出△DAB≌△DEB,根据全等三角形的性质得出∠ABD=∠EBD,求出DH=BH,再根据菱形的判定推出即可;(2)根据菱形的性质和已知菱形的面积求出BH,求出DH=BH=5,根据勾股定理求出AH,再求出答案即可.类型2建立几何模型解释生活中现象2.如图所示,一根长2a的木棍(AB),斜靠在与地面(OM)垂直的墙(ON)上,设木棍的中点为P,若木棍A端沿墙下滑,且B端沿地面向右滑行.请判断木棍滑动的过程中,点P到点O的距离变化(用“发生”或“不发生”填空).理由是。
2024中考数学综合复习模型篇专题08 倍长中线法和截长补短法综合应用(解析版)
专题08倍长中线法和截长补短法综合应用倍长中线类型一:直接倍长中线△ABC 中AD 是BC 边中线方法:延长AD 到E ,使DE=AD ,连接BE类型二:间接倍长中线作CF ⊥AD 于F ,作BE⊥AD 的延长线于E 连接BE 。
延长MD 到N ,使DN=MD ,连接CN截长补短常见类型及常规解题思路:①a b c ±=可采取直接截长或补短,绕后进行证明。
或者化为类型②证明。
②a b kc±=可以将a b ±与c 构建在一个三角形中,然后证明这个三角形为特殊三角形,如等边三角形,等腰直角三角形,或一个角为30 的直角三角形等。
截长法常规辅助线:(1)过某一点作长边的垂线(2)在长边上截取一条与某一短边相同的线段,再证剩下的线段与另一短边相等。
补短法常规辅助线:(1)延长短边。
(2)通过旋转等方式使两短边拼合到一起类型一:倍长中线法【典例1】如图,在△ABC中,AB=a,AC=b,a,b均大于0,中线AD=c,求c的取值范围.【解答】解:延长AD到E,使AD=DE,连接BE,∵AD=DE,∠ADC=∠BDE,BD=DC,∴△ADC≌△EDB(SAS),∴BE=AC=b,在△AEB中,AB﹣BE<AE<AB+BE,即a﹣b<2AD<a+b,∴<c<.【典例2】已知:在△ABC中,AD是BC边上的中线,E是AD上一点,且BE=AC,延长BE交AC于F,求证:AF=EF.【解答】证明:如图,延长AD到点G,使得AD=DG,连接BG.∵AD是BC边上的中线(已知),∴DC=DB,在△ADC和△GDB中,∴△ADC≌△GDB(SAS),∴∠CAD=∠G,BG=AC又∵BE=AC,∴BE=BG,∴∠BED=∠G,∵∠BED=∠AEF,∴∠AEF=∠CAD,即:∠AEF=∠FAE,∴AF=EF.【典例3】如图,△ABC中,点D是BC的中点,点E、F分别在AB、AC上,且DE⊥DF,求证:BE+CF >EF.【解答】证明:如图,延长ED使得DM=DE,连接FM,CM.∵BD=DC,∠BDE=∠CDM,DE=DM,∴△BDE≌△CDM(SAS),∴BE=CM,∵DE=DM,DF⊥EM,∴FE=FM,∵CM+CF>FM,∴BE+CF>EF.【变式1】如图,在△ABC中,AC=3,AB=5,点D为BC的中点,且AD⊥AC,则△ABC的周长为 .【解答】解:延长AD到E,使AD=DE,连接BE,∵D为BC的中点,∴BD=CD,∵∠ADC=∠BDE,∴△ADC≌△EDB(SAS),∴AC=BE=3,∠DAC=∠E,∵AD⊥AC,∴∠DAC=90°,∴∠E=90°,∴AE===4,∴AD=DE=2,∴BD===,∴BC=2BD=2,∴△ABC的周长为AB+AC+BC=5+3+2=8+2.故答案为:8+2.【变式2】如图,在△ABC中,点E是AB边的中点,D是BC延长线上一点,连接DE交AC于点F,且AF=BD,若BD=3,AC=5,则CD的长为 .【解答】解:延长DE至H,使EH=DE,连接AH,∵AF=BD,BD=3,AC=5,∴CF=AC﹣AF=5﹣3=2,在△BED和△AEH中,,∴△BED≌△AEH(SAS),∴AH=BD,∠D=∠H,∵AF=BD,∴AH=AF,∴∠AFH=∠H,∴∠CFD=∠D,∴CD=CF=2,故答案为:2.【变式3】如图,在Rt△ABC中,∠BAC=90°,点D是BC的中点,E是AB边上一点,DF⊥DE交AC于点F,连接EF,若BE=2,CF=,则EF的长为 .【解答】解:如图,延长FD到G使GD=DF,连接GE,BG,在△BDG和△CDF中,,∴△BDG≌△CDF(SAS),∴BG=CF=,∠GBD=∠C,∴BG∥CA,∴∠EBG=∠A=90°,∵BE=2,∴EG===,∵DF⊥DE,DF=DG,∴EF=EG=,故答案为:.【变式4】如图,在矩形ABCD中,AB=8,BC=9,点E为AB的中点,点F在BC上,且BF=2FC,AF 与DE,DB分别交于点G,H,求GH的长.【解答】解:如图,过点F作FM⊥AD于M,交ED于O,则FM=AB=8,∵BF=2FC,BC=9,∴BF=AM=6,FC=MD=3,∴AF===10,∵OM∥AE,∴,∵点E为AB的中点,∴OM =,∴OF =FM ﹣OM =8﹣=,∵AE ∥FO ,∴△AGE ∽△FGO ,∴=,∴AG ==,∴GH=10-4-415=49【变式5】如图,四边形ABCD 为平行四边形,点E ,F 分别为BC ,AB 上的点,且点F 为AB 的中点,连接DF ,DE .(1)如图①,若DF 平分∠ADE ,求证:AD +BE =DE ;(2)如图②,若四边形ABCD 是边长为4的正方形,当ED 平分∠FDC 时,求EC 的长.【解答】(1)证明:延长DF ,CB 交于G ,如图:∵四边形ABCD 为平行四边形,∴AD ∥CB ,∴∠ADG =∠G ,∵DF 平分∠ADE ,∴∠ADG=∠EDG,∴∠G=∠EDG,∴DE=GE=GB+BE,∵F是AB中点,∴AF=BF,在△ADF和△BGF中,,∴△ADF≌△BGF(AAS),∴AD=GB,∴DE=AD+BE;(2)解:延长AB,DE交于H,如图:∵四边形ABCD是边长为4的正方形,点F为AB的中点,∴DF===2,AB∥CD,∴∠CDE=∠H,∵ED平分∠FDC,∴∠CDE=∠FDE,∴∠FDE=∠H,∴FH=DF=2,∴BH=FH﹣BF=2﹣2,∵∠C=90°=∠HBE,∠DEC=∠HEB,∴△DCE∽△HBE,∴=,即=,解得CE=2﹣2.∴EC的长为2﹣2.【变式6】阅读下面材料,并按要求完成相应的任务.如图①,圆内接四边形的对角线AC⊥BD,垂足为G,过点G作AD的垂线,垂足为E,延长EG交BC于点F,则点F为BC的中点.下而是部分证明过程:∵AC⊥BD,EF⊥AD,∴∠EGD+∠FGC=90°,∠EGD+∠EDG=90°,∴∠EDG=∠FGC.∵∠ADB=∠ACB,…任务一:请将上述过程补充完整;任务二:如图②,在△ABC中,把边AC绕点C顺时针旋转90°得到DC,把边BC绕点C逆时针旋转90°得到EC.连接DE,取AB的中点M,连接MC并延长交DE于点N.(1)求证:MN⊥DE;(2)若AC=4,AB=6,∠CAB=30°,求DE的长.【解答】解:任务一:∵AC⊥BD,EF⊥AD,∴∠EGD+∠FGC=90°,∠EGD+∠EDG=∴∠EDG=∠FGC.∵∠ADB=∠ACB,∴∠ACB=∠CGF,∴CF=FD,同理BF=FG,∴BF=CF,∴点F为BC的中点;任务二:(1)证明:延长CM到F使MF=CM,∵AM=MB,∴ACBF是平行四边形,∴AF=BC=CE,AF∥BC,∴∠CAF+∠ACB=180°,∠DCE+∠ACB=180°,∴∠CAF=∠DCE,∵DC=AC,∴△DCE≌△CAF(SAS),∴∠D=∠ACF,∵∠ACF+∠DCN=90°,∴∠D+∠DCN=90°,∴∠DNC=90°,∴MN⊥DE;(2)解:作CG⊥AB于G,∵∠CAB=30,AC=4,∴CG=2,AG=2,∵AM=AB=3,∴GM=,∵CM2=CG2+GM2,∴CM2=22+()2,∴CM=,∵△DCE≌△CAF,∴DE=CF=2.类型二:截长补短【典例4】模型分析当题目中出现线段的和差关系时,考虑用截长补短法,该类题日中常出现等腰三角形、角平分线等关键词句,采用截长补短法进行证明.问题:如图,在△ABC中,AD平分∠BAC交BC于点D,且∠B=2∠C,求证:AB+BD=AC.截长法:在AC上截取AE=AB,连接DE,证明CE=BD即可.补短法:延长AB至点F,使AF=AC,连接DF,证明BF=BD即可.请结合右边的证明结论.求证:AB+BD=AC.请结合右边的【模型分析】证明结论.求证:AB+BD=AC.【截长法】【补短法】【解答】证明:【截长法】在AC上截取AE=AB,连接DE,∵AD平分∠BAC,∴∠BAD=∠DAC,在△ABD和△AED中,,∴△ABD≌△AED(SAS),∴∠B=∠AED,BD=DE,又∠B=2∠C,∴∠AED=2∠C,而∠AED=∠C+∠EDC=2∠C,∴∠C=∠EDC,∴DE=CE,∴AB+BD=AE+CE=AC.证明:【补短法】延长AB到F,使BF=BD,连接DF,∵BF=BD,∴∠F=∠BDF,∴∠ABC=∠F+∠BDF=2∠F,且∠ABC=2∠C,∴∠C=∠F,且∠CAD=∠BAD,AD=AD,∴△ADF≌△ADC(AAS)∴AC=AF,∴AC=AF=AB+BF=AB+BD.【变式1】如图,△ABC为等边三角形,D为△ABC外一点,连接AD,BD,CD,∠ADB=∠ADC=60°,求证:AD=BD+CD.【解答】证明:在DA上截取DE=DB,连接BE,如下图所示,∵∠ADB=60°,DE=DB,∴△ABD为等边三角形,∴∠EBD=60°,BE=BD,∵△ABC为等边三角形,∴∠ABC=60°,BA=BC,∴∠EBD﹣∠EBC=∠ABC﹣∠EBC,∴∠ABE=∠CBD,在△ABE和△CBD中,,∴△ABE≌△CBD(SAS),∴AE=CD,∴AD=AE+ED=CD+BD.【变式2】如图,Rt△ABC中,AC=BC,AD平分∠BAC交BC于点D,CE⊥AD交AD于F点,交AB于点E.求证:AD=2DF+CE.【解答】证明:在AF上截取FG=DF,连接CG,则DG=2DF,∵∠ACB=90°,∴∠DCF+∠ACF=90°,又∵CF⊥AD,∴∠ACF+∠CAF=90°,∴∠DCF=∠CAF,∵AD平分∠CAE,∴∠CAF=∠EAF,∵DF=FG,CF⊥DG,∴CD=CG,∴∠CDG=∠CGD,∵∠DGC=∠GAC+∠ACG,∠ADC=∠B+∠BAD,∴∠B=∠ACG,又∵AC=BC,∴△ACG≌△CBE(ASA),∴AG=CE,∴AD=AG+DG=CE+2DF.【变式3】如图,△ABC内接于⊙O,AC=BC,CD是⊙O的一条弦,且=,过点A作AP⊥CD,分别交CD,⊙O于点E,P,连接BP,若CD=6,△ABP的周长为13,求AE的长.【解答】解:在AE上截取AF=BP,连接CF,PC,∵AC=BC,∠CAF=∠CBP,∴△CAF≌△CBP,CF=CP,∵CD⊥PA,∴EF=PE,∴AE=AF+FE=PB+PE,∵AC=BC,∴=,∵=,∴=,∴AB=CD=6,∵△ABP的周长是13,∴AP+PB=7,∵AE=PE+PB,∴2AE=AP+PB,∴AE=.【变式4】如图,在△ABC中,AB=AC,在AB左侧作∠BDC=∠BAC=α,过点A作AE⊥DC于点E.(1)当α=90°时,①求证:AE=DE;②若BD=AE=2,请求出△ABC的面积;(2)当α≠90°时,求证:BD+DE=EC.【解答】(1)①证明:过点B作BF⊥AE,交AE的延长线于点F,∵AE⊥CD,∴∠DEF=90°,又∵∠BDE=90°,∴四边形BDEF为矩形,∴DE=BF,∵∠BAC=90°,∴∠BAF+∠EAC=90°,又∵∠EAC+∠ACE=90°,∴∠BAF=∠ACE,又∵∠AEC=∠BFA=90°,AB=AC,∴△ABF≌△CAE(AAS),∴BF=AE,∴DE=AE;②解:∵四边形BDEF为矩形,BD=AE=2,∴BD=EF=2,DE=BF=AE=,∴AF=AE+EF=+2,∴BA2=BF2+AF2==8+4,∴S==;△ABC(2)证明:过点A作AF⊥BD,交BD的延长线于F,连接AD,设CD与AB交于点O,∵∠BDC=∠BAC,∠BOD=∠AOC,∴∠ACO=∠DOB,即∠ABF=∠ACE,又∵∠AEC=∠AFB=90°,AC=AB,∴△ACE≌△ABF(AAS),∴AE=AF,BF=CE,又∵AD=AD,∴Rt△ADE≌Rt△ADF(HL),∴DE=DF,∴CE=BF=BD+DF=BD+DE.【变式5】【问题背景】如图①,在边长为1的正方形ABCD中,点E为射线BC上的一个动点(与点B,C不重合),连接AE,过点E作EF⊥AE,与正方形ABCD的外角∠DCG的平分线交于点F.李老师指出,当点E为线段BC 的中点时,AE=EF.【初步探索】(1)如图②,当点E在线段BC的延长线上时,其他条件不变,那么结论“AE=EF”是否仍然成立;【问题解决】(2)当点E在线段BC上时,设BE=x,△ECF的面积为y,求y与x之间的函数关系式;【拓展延伸】(3)如图③,将正方形ABCD放在平面直角坐标系xOy中,点O与点B重合,点C在x轴正半轴上,当点E运动到某一点时,点F恰好落在直线y=﹣2x+3上,求此时点E的坐标.【解答】解:【问题背景】如图1,取AB的中点H,连接EH,∵四边形ABCD是正方形,∴AB=BC,∠ABC=90°=∠BCD,∵CF平分∠DCG,∴∠DCF=45°,∴∠ECF=135°,∵E是BC的中点,∴BH=BE=AH=CE,∴∠BHE=∠BEH=45°,∴∠AHE=∠ECF=135°,∵AE⊥EF,∴∠AEB+∠FEC=90°,∵∠AEB+∠BAE=90°,∴∠FEC=∠BAE,∴△AHE≌△ECF(ASA),∴AE=EF;【初步探索】(1)仍然成立,理由如下:如图2,在BA的延长线上取一点N,使AN=CE,连接NE.∵AB=BC,AN=CE,∴BN=BE,∴∠N=∠FCE=45°,∵四边形ABCD是正方形,∴AD∥BE,∴∠DAE=∠BEA,∴∠NAE=∠CEF,在△ANE和△ECF中,,∴△ANE≌△ECF(ASA),∴AE=EF;【问题解决】(2)如图3,在BA上截取BH=BE,连接HE,同理得:△AHE≌△ECF,∴y=S=AH•BE=x(1﹣x)=﹣x2+x(0≤x≤1);△AHE【拓展延伸】(3)如图4,在BA上截取BH=BE,连接HE,过点F作FM⊥x轴于M,设点E(a,0),∴BE=a=BH,∴HE=a,由(1)可得△AHE≌△ECF,∴CF=HE=a,∵CF平分∠DCM,∴∠DCF=∠FCM=45°,∵FM⊥CM,∴∠CFM=∠FCM=45°,∴CM=FM=a,∴BM=1+a,∴点F(1+a,a),∵点F恰好落在直线y=﹣2x+3上,∴a=﹣2(1+a)+3,∴a=,∴点E(,0).【典例5】如图1,在Rt△ABC中,AB=BC,点D,E,F分别在AB,BC,AC边上,且DE=EF,∠DEF =∠B,∠A=45°.(1)试猜想CF与BE之间的数量关系,并证明;(2)自主探究:如图2,若将已知条件中含45°的直角三角形换成含30°的直角三角形,其余条件不变,试探究BE和CF的关系.【解答】解:(1)CF与BE之间的数量关系为:CF=BE.理由:过点F作FH⊥BC于点H,如图,∵Rt△ABC中,AB=BC,∠A=45°,∴∠C=45°,∠B=90°.∵∠DEF=∠B,∴∠DEF=90°,∴∠DEB+∠FEH=90°.∵∠BDE+∠DEB=90°,∴∠BDE=∠FEH.在△BDE和△HEF中,,∴△BDE≌△HEF(AAS),∴BE=FH.∵FH⊥BC,∠C=45°,∴△FHC为等腰直角三角形,∴FC=FH,∴FC=BE;(2)CF与BE之间的数量关系为:CF=BE.理由:过点F作FH⊥BC于点H,如图,∵Rt△ABC中,∠A=30°,∴∠C=60°,∠B=90°.∵∠DEF=∠B,∴∠DEF=90°,∴∠DEB+∠FEH=90°.∵∠BDE+∠DEB=90°,∴∠BDE=∠FEH.在△BDE和△HEF中,,∴△BDE≌△HEF(AAS),∴BE=FH.∵FH⊥BC,∠C=60°,∴sin60°=,∴FC=FH,∴FC=BE.【变式1】如图,在△ABC中,∠ABC=45°,AD⊥BC于点D,点F是AC上一点,连接BF交AD于点E,且DE=CD,连接DF,若AF=4,DF=2,则BF的长为 .【解答】解:如图,在BF上截取HF=AF,连接AH,∵∠ABC=45°,AD⊥BC,∴AD=BD,∠ADB=∠ADC=90°,在△BDE和△ADC中,,∴△BDE≌△ADC(SAS),∴∠EBD=∠CAD,∵∠BED=∠AEF,∴∠AFE=∠BDE=90°,∴∠AHF=∠HAF=45°,∴AH=AF,∴∠BAH=∠DAF,∠AHB=135°,∠AEF=∠BED,∠AFE=∠BDE=90°,∴△AFE∽△BDE,∴=,∵∠AEB=∠FED,∴△AEB∽△FED,∴∠EAB=∠EFD=45°,∴∠AFD=∠AFH+∠EFD=90°+45°=135°,∴∠AHB=∠AFD,∴△AHB∽△AFD,∴==,∴BH=DF,∴BF=BH+HF=DF+AF=2+4.故答案为:2+4.【变式2】如图,四边形ABCD内接于⊙O,BC是⊙O的直径,连接AC,BD,若AB=AC,请探究AD,BD,DC之间的数量关系.【解答】解:作AE⊥AD交BD于E,∵BC是直径,∴∠BAC=90°,∵∠BAE+∠EAC=∠DAC+∠EAC=90°,∴∠BAE=∠CAD,∵∠ABD=∠ACD,AB=AC,∴△ABE≌△ACD(SAS),∴BE=CD,∵△AED是等腰直角三角形,∴DE=AD,∵BD=DE+BE,∴BD=AD+CD.【变式3】如图,在△ABC中,∠ACB=120°,BC>AC,点E在BC上,点D在AB上,CE=CA,连接DE,∠ACB+∠ADE=180°,CH⊥AB,垂足为点H.求证:DE+AD=2CH.【解答】证明:如图,作∠FCD=∠ACB,交BA延长线于F,∵∠FCA+∠ACD=∠ACD+∠DCB,∴∠FCA=∠DCB,∵∠ACB=120°,∠ACB+∠ADE=180°,∴∠EDB=120°,∠EDA=60°,∵∠FAC=120°+∠B,∠CED=120°+∠B,∴∠FAC=∠CED,在△AFC和△EDC中,,∴△AFC≌△EDC(ASA),∴AF=DE,FC=CD,∵CH⊥FD,∴FH=HD,∠FCH=∠HCD=60°,∴DH=CH,∵AD+DE=AD+AF=FD=2DH=2CH,∴AD+DE=2CH.【变式4】如图,在△ABC中,AB=AC,∠BAC=90°,点D是平面内一点,且AD⊥CD.点O是BC的中点,连接OA,OD.(1)如图①,若点D是BC下方一点,过点O作OE⊥OD分别交AC,AD于点E,F.①求证:∠OAF=∠OCD;②若CD=1,DF=2,求BC的长;(2)如图②,若点D是AC右侧一点,试判断AD,CD,OD之间的数量关系,并说明理由.【解答】(1)①证明:∵AB=AC,O为BC的中点,∴OA=OB=OC,OA⊥OC,∵OE⊥OD,∴∠AOC=∠EOD=90°,∴∠AOF=∠COD,∵∠AOM=∠MDC=90°,∠AMO=∠CMD,∴∠OAM=∠MCD,∴△OAF≌△OCD(ASA),∴∠OAF=∠OCD;②解:∵△OAF≌△OCD,∴AF=CD=1,∵DF=2,∴AD=AF+DF=1+2=3,∵AD⊥DC,∴∠ADC=90°,∴AC===,∵AC=AB,∴BC=AC==2;(2)解:AD+CD=OD.理由:过点O作OE⊥OD,交DA的延长线于点E,∵∠DOE=∠AOC=90°,∴∠AOE=∠COD,∵∠ODC+∠+ODA=90°,∠ODA+∠OEA=90°,∴∠ODC=∠OEA,又∵OA=OC,∴△OCD≌△OAE(AAS),∴CD=AE,OD=OE,∴DE=OD,∴AD+AE=AD+CD=OD.【变式5】【问题探究】如图,△ABC是等腰三角形,AB=AC,点D是平面内一点,连接AD,BD,CD,且∠CAB=∠CDB.(1)如图①,当∠CAB=60°时,试探究BD,CD,AD之间的数量关系;(2)如图②,当∠CAB=120°时,探究是否为定值,并说明理由;【问题解决】(3)如图③,在四边形ADBC中,AB=AC,∠CAB=∠CDB=120°,若AD=2,BD=3,求CD的长.【解答】解:(1)BD,CD,AD之间的数量关系为:BD=CD+AD,理由如下:在BD上取一点E,使BE=CD,连接AE,设AC交BD于H,如图①所示:∵∠CAB=∠CDB,∠AHB=∠CHD,∴∠ABE=∠ACD,在△ABE和△ACD中,,∴△ABE≌△ACD(SAS),∴AD=AE,∠DAC=∠EAB,∴∠DAC+∠CAE=∠EAB+∠CAE=∠CAB=60°,∴△ADE是等边三角形,∴DE=AD,∴BD=BE+DE=CD+AD;(2)是定值,理由如下:在BD上取一点E,使BE=CD,连接AE,设AC交BD于H,过点A作AF⊥BD于F,如图②所示:∵∠CAB=∠CDB,∠AHB=∠CHD,∴∠ABE=∠ACD,在△ABE和△ACD中,,∴△ABE≌△ACD(SAS),∴AD=AE,∠DAC=∠EAB,∴∠DAC+∠CAE=∠EAB+∠CAE=∠CAB=120°,∴∠ADE=∠AED=(180°﹣120°)=30°,∵AF⊥DE,∴DF=EF,AF=AD,在Rt△AFD中,由勾股定理得:DF===AD,∴DE=2DF=AD,∵DE=BD﹣BE=BD﹣CD,∴BD﹣CD=AD,∴=,∴是定值;(3)在CD上取一点E,使CE=BD,连接AE,设AB交CD于H,过点A作AF⊥CD于F,如图③所示:∵∠CAB=∠CDB,∠AHC=∠BHD,∴∠ACE=∠ABD,在△ACE和△ABD中,,∴△ACE≌△ABD(SAS),∴AE=AD,∠EAC=∠DAB,∴∠EAC+∠BAE=∠DAB+∠BAE=∠CAB=120°,∴∠ADE=∠AED=(180°﹣120°)=30°,∵AF⊥DE,∴DF=EF,AF=AD,在Rt△AFD中,由勾股定理得:DF===AD,∴DE=2DF=AD,∴CD=CE+DE=BD+AD=3+×2=3+2.。
2020年中考数学专题复习:函数模型的应用(含答案)
2020年中考数学专题复习:函数模型的应用1.超市以每千克40元的价格购进夏威夷果,计划以每千克60元的价格销售,为了让顾客得到更大的实惠,现决定降价销售,已知这种夏威夷果销售量y(千克)与每千克降价x(元)(0<x <20)之间满足一次函数关系,其图象如图所示:(1)求y与x之间的函数关系式;(2)超市要想获利2090元,则这种夏威夷果每千克应降价多少元?2.如图①,某商场在一楼到二楼之间设有上、下行自动扶梯和步行楼梯.甲、乙两人从二楼同时下行,甲乘自动扶梯,乙走步行楼梯,甲离一楼地面的高度h(单位:m)与下行时间x(单位:s)之间具有函数关系h=-310x+6,乙离一楼地面的高度y(单位:m)与下行时间x(单位:s)的函数关系如图②所示.(1)求y关于x的函数解析式;(2)请通过计算说明甲、乙两人谁先到达一楼地面.3.某智能品牌店,在销售某型号运动手环时,以高出进价的50%标价.已知按标价九折销售该型号运动手环8个与将标价直降100元销售7个获利相同.(1)求该型号运动手环的进价和标价分别是多少元?(2)若该型号运动手环的进价不变,按(1)中的标价出售,该店平均每月可售出38个;若每个运动手环每降价20元,每月可多售出2辆,求该型号运动手环降价多少元时,每月获利最大?最大利润是多少?4.一水果店以进价为每千克16元购进万荣苹果,销售中发现,销售单价定为20元时,日销售量为50千克;当销售单价每上涨1元,日销售量就减少5千克,设销售单价为x(元),每天的销售量为y(千克),每天获利为w(元).(1)求y与x之间的函数关系式;(2)求w与x之间的函数关系式;该苹果售价定为每千克多少元时,每天的销售利润最大?最大利润是多少元?(3)如果商家规定这种苹果每天的销售量不低于40千克,求商家每天销售利润的最大值是多少元?5.挂灯笼成为我国的一种传统文化. 小明在春节前购进甲、乙两种红灯笼,用3120元购进甲灯笼与用4200元购进乙灯笼的数量相同,已知乙灯笼每对进价比甲灯笼每对进价多9元.(1)求甲、乙两种灯笼每对的进价;(2)经市场调查发现,乙灯笼每对售价50元时,每天可售出98对,售价每提高1元,则每天少售出2对;物价部门规定其销售单价不高于每对65元,设乙灯笼每对涨价x元,小明一天通过乙灯笼获得利润y元.①求出y与x之间的函数解析式;②乙种灯笼的销售单价为多少元时,一天获得利润最大?最大利润是多少元?6.甲、乙两个批发店销售同一种苹果.在甲批发店,不论一次购买数量是多少,价格均为6元/kg.在乙批发店,一次购买数量不超过50 kg时,价格为7元/kg;一次购买数量超过50 kg时,其中有50 kg的价格仍为7元/kg,超出50 kg部分的价格为5元/kg.设小王在同一个批发店一次购买苹果的数量为x kg(x>0).(Ⅰ)根据题意填表:(Ⅱ)设在甲批发店花费y1元,在乙批发店花费y2元,分别求y1,y2关于x的函数解析式;(Ⅲ)根据题意填空:①若小王在甲批发店和在乙批发店一次购买苹果的数量相同,且花费相同,则他在同一个批发店一次购买苹果的数量为________kg;②若小王在同一个批发店一次购买苹果的数量为120 kg,则他在甲、乙两个批发店中的________批发店购买花费少;③若小王在同一个批发店一次购买苹果花费了360元,则他在甲、乙两个批发店中的________批发店购买数量多.7.某工厂计划生产甲乙两种产品共2500吨,每生产1吨甲产品可获得利润0.3万元,每生产1吨乙产品可获得利润0.4万元,设该工厂生产了甲产品x(吨),生产甲、乙两种产品获得的总利润为y(万元).(1)求y与x之间的函数表达式;(2)若每生产1吨甲产品需要A原料0.25吨,每生产1吨乙产品需要A原料0.5吨,受市场影响,该厂能获得的A原料至多为1000吨,其它原料充足.求出该工厂生产甲、乙两种产品各为多少吨时,能获得最大利润.8. 某商场销售一批足球文化衫,已知该文化衫的进价为每件40元,当售价为每件60元时,每个月可销售出100件,根据市场行情,现决定涨价销售,调查表明,每件商品的售价每上涨1元,每月少销售出2件,设每件商品的售价为x 元.每个月的销售为y 件.(1)求y 与x 之间的函数关系式;(2)当每件商品的售价定为多少元时,每个月的利润恰好为2250元;(3)当每件商品的售价定为多少元时,每个月获得利润最大?最大月利润为多少?9. 某公司计划在某地区销售一款5G 产品,根据市场分析,该产品的销售价格将随销售周期的变化而变化,设该产品在第x (x 为正整数)个销售周期每台的销售价格为y 元,y 与x 之间满足如图所示的一次函数关系.(1)求y 与x 之间的关系式;(2)设该产品在第x 个销售周期的销售数量为p (万台),p 与x 的关系可以用p =12x +12来描述.根据以上信息,试问:哪个销售周期的销售收入最大?此时该产品每台的销售价格是多少元?10. 某商店销售一种商品,经市场调查发现,该商品的周销售量y (件)是售价x (元/件)的一次函数,其售价,周销售量,周销售利润w (元)的三组对应值如下表:售价x (元/件) 50 60 80 周销售量y (件) 100 80 40 周销售利润w (元)100016001600(1)①求y 关于x 的函数解析式(不要求写出自变量的取值范围);②该商品进价是________元/件;当售价是____元/件时,周销售利润最大,最大利润是______元;(2)由于某种原因,该商品进价提高了m元/件(m>0),物价部门规定该商品售价不得超过65元/件,该商店在今后的销售中,周销售量与售价仍然满足(1)中的函数关系.若周销售最大利润是1400元,求m的值.参考答案1. 解:(1)设一次函数解析式为y =kx +b , ∵当x =2,y =120;当x =4,y =140;∴⎩⎪⎨⎪⎧2k +b =120,4k +b =140, 解得⎩⎪⎨⎪⎧k =10,b =100.∴y 与x 之间的函数关系式为y =10x +100;(4分) (2)由题意得(60-40-x )(10x +100)=2090, 整理得x 2-10x +9=0, 解得x 1=1,x 2=9. ∵让顾客得到更大的实惠, ∴x =9,答:超市要想获利2090元,则这种夏威夷果每千克应降价9元.(7分)2. 解:(1)设y 关于x 的函数解析式为y =kx +b ,把点(0,6)(15,3)代入y =kx +b 得⎩⎪⎨⎪⎧6=b ,3=15k +b ,解得⎩⎪⎨⎪⎧k =-15,b =6,∴y 关于x 的函数解析式为y =-15x +6;(2)甲:当h=0时,得x=20.乙:当y=0时,得x=30.∵20<30,∴甲先到达一楼地面.3.解:(1)设该型号运动手环的进价为x元,根据题意得[(1+50%)x×0.9-x]×8=[(1+50%)x-100-x]×7,∴x=1000,∴(1+50%)x=1500元,∴该型号运动手环的进价为1000元,标价为1500元;(4分) (2)设该型号运动手环降价y元,利润为w元.根据题意得w=(38+y20×2)(1500-1000-y)=(38+0.1y)(500-y)=-0.1(y-60)2+19360,当y=60时,w有最大值19360.∴降价60元,每月获利最大,最大利润为19360元.(8分)4.解:(1)根据题意得y=50-5(x-20)=-5x+150;(2分)(2)根据题意得w=(x-16)(-5x+150)=-5x2+230x-2400,(4分)∴w与x的函数关系式为:w=-5x2+230x-2400=-5(x-23)2+245.∵-5 <0,∴当x=23时,w有最大值,最大值为245.(5分)答:w与x之间的函数关系式为w=-5x2+230x-2400.该苹果售价定为每千克23元时,每天销售利润最大,最大利润是245元;(6分)(3)根据题意得-5x+150≥40,解得x≤22.∵w=-5(x-23)2+245.∵-5<0,w≤23时,w随x增大而增大,∴当x=22时w有最大值,其最大值为-5×(22-23)2+245=240(元).答:商家每天销售利润的最大值是240元.(10分)5.解:(1)设甲种灯笼进价为x元/对,则乙种灯笼的进价为(x+9)元/对,由题意得3120 x=4200 x+9,解得x=26,经检验,x=26是原方程的解,且符合题意,∴x+9=26+9=35,答:甲种灯笼单价为26元/对,乙种灯笼的单价为35元/对;(4分) (2)①y=(50+x-35)(98-2x)=-2x2+68x+1470,答:y与x之间的函数解析式为:y=-2x2+68x+1470;(7分)②∵a=-2<0,∴函数y有最大值,该二次函数的对称轴为:x=-b2a=17,物价部门规定其销售单价不高于每对65元,∴x+50≤65,∴x≤15,∵x<17时,y随x的增大而增大,∴当x =15时,y 最大=2040. ∴15+50=65.答:乙种灯笼的销售单价为每对65元时,一天获得利润最大,最大利润是2040元.(10分) 6. 解:(Ⅰ)180,900,210,850;【解法提示】甲批发店花费:当x =30时,花费为30×6=180;当x =150时,花费为150×6=900.乙批发店花费:当x =30时,花费为30×7=210;当x =150时,花费为50×7+(150-50)×5=850.(Ⅱ)y 1=6x (x >0), 当0<x ≤50时,y 2=7x ;当x >50时,y 2=7×50+5(x -50),即y 2=5x +100;即y 2=⎩⎪⎨⎪⎧7x (0<x ≤50),5x +100(x >50).(Ⅲ)①100;②乙;③甲.【解法提示】①当0<x ≤50时,甲批发店和乙批发店花费不可能相同,则x >50时,令y 1=y 2,则6x =5x +100,解得x =100;②当x =120时,y 1=6×120=720,y 2=5×120+100=700,∵720>700,∴在乙批发店购买花费少;③对甲批发店而言:令y 1=360,则6x =360,解得x =60.对乙批发店而言:当x =50时,花费为350<360,则令5x +100=360,解得x =52,∵60>52,∴小王花费360元时,在甲批发店购买数量多.7. 解:(1)y =x ·0.3+(2500-x )·0.4=-0.1x +1000; (2)由题意得x ·0.25+(2500-x )·0.5≤1000,解得x ≥1000. 又∵x ≤2500,∴1000≤x ≤2500. 由(1)可知,-0.1<0,∴y 的值随着x 的增加而减小,∴当x =1000时,y 取最大值,此时生产乙种产品2500-1000=1500(吨) 答:工厂生产甲产品1000吨,乙产品1500吨时,能获得最大利润. 8. 解:(1)根据题意得y = 100-2(x -60)=-2x +220(60≤x ≤110); (2)由题意可得:(-2x +220)(x -40)=2250. x 2-150x +5525=0, 解得x 1=65,x 2=85.答:当每件商品的售价定为65元或85元时,利润恰好是2250元; (3)设利润为W 元,∴W =(x -40)(-2x +220)=-2x 2+300x -8800=-2(x -75)2+2450. ∵a =-2<0, ∴抛物线开口向下. ∵60≤x ≤110,∴当x =75时,W 有最大值,W 最大=2450(元).答:当售价定为75元时,获得最大利润,最大利润是2450元. 9. 解:(1)设y 关于x 的函数关系式为y =kx +b (k ≠0),由图象可知,将点(1,7000),(5,5000)代入得⎩⎪⎨⎪⎧k +b =7000,5k +b =5000,解得⎩⎪⎨⎪⎧k =-500,b =7500,∴y 关于x 的函数关系式为y =-500x +7500;(2)设销售收入为W ,根据题意得W =yp =(-500x +7500)·(12x +12), 整理得W =-250(x -7)2+16000,∵-250<0,∴W 在x =7时取得最大值,最大值为16000元,此时该产品每台的销售价格为-500×7+7500=4000元.答:第7个销售周期的销售收入最大,此时该产品每台的销售价格为4000元.10. 解:(1)①y =-2x +200;②40,70,1800;(2)由题意可知w =(-2x +200)×(x -40-m )=-2x 2+(280+2m )x -8000-200m ,对称轴为直线x =140+m 2, ∵m >0,∴对称轴x =140+m 2>70, ∵抛物线开口向下,在对称轴左侧,y 随x 的增大而增大,∴当x =65时,y max =1400,代入表达式解得m =5.。
中考数学专题复习全等三角形(X模型)
中考数学专题复习全等三角形(X模型)学校:___________姓名:___________班级:___________考号:___________评卷人得分一、填空题1.如图,已知AD是ABC的中线,E是AC上的一点,BE交AD于F,AC BF=,24DAC∠=︒,32EBC∠=︒,则ACB=∠__________.评卷人得分二、解答题2.问题背景:课外兴趣小组活动时,老师提出了如下问题:如图1,△ABC中,若AB=4,AC=3,求BC边上的中线AD的取值范围.小明在组内经过合作交流,得到了如下的解决方法:延长AD到点E,使DE=AD,则得到△ADC≌△EDB,小明证明△BED≌△CAD用到的判定定理是:(用字母表示);问题解决:小明发现:解题时,条件中若出现“中点”“中线”字样,可以考虑延长中线构造全等三角形,把分散的已知条件和所求证的结论集合到同一个三角形中.请写出小明解决问题的完整过程;拓展应用:以△ABC的边AB,AC为边向外作△ABE和△ACD,AB=AE,AC=AD,∠BAE=∠CAD=90°,M是BC中点,连接AM,DE.当AM=3时,求DE的长.3.如图,在△ABC中,D是BC边上的一点,E是AD的中点,过A点作BC的平行线交CE的延长线于F,且AF=BD,连接BF.(1)求证:D是BC的中点(2)如果AB=AC,试判断四边形AFBD的形状,并证明你的结论.4.【阅读理解】课外兴趣小组活动时,老师提出了如下问题:如图1,ABC中,若8AB=,6AC=,求BC边上的中线AD的取值范围.小明在组内经过合作交流,得到了如下的解决方法:延长AD到点E,使DE AD=,请根据小明的方法思考:(1)由已知和作图能得到ADC△EDB△的理由是______.(2)求得AD的取值范围是______.【感悟】解题时,条件中若出现“中点”“中线”字样,可以考虑延长中线构造全等三角形,把分散的已知条件和所求证的结论集合到同一个三角形中.【问题解决】(3)如图2,在ABC中,点D是BC的中点,点M在AB边上,点N在AC边上,若DM DN⊥,求证:BM CN MN+>.5.如图所示:ABC是等边三角形,D、E分别是AB及AC延长线上的一点,且BD CE=,连接DE交BC于点M.求让:MD ME=6.阅读下面材料【问题情境】课外兴趣小组活动时,老师提出了如下问题:如图△.在△ABC中,若AB=8,AC=6,求BC边上的中线AD取值范围,小明在组内经过合作交流,得到了如下的解决方法:延长AD到点E,使DE=AD,请根据小明方法思考:(1)由已知和作图能得到△ADC△△EDB的理由是()A.SSS B.SAS C.AAS D.HL(2)由三角形三边的关系可求得AD长的取值范围是()A.6<AD<8B.6≤AD≤8C.1<AD<7D.1≤AD≤7【解后感悟】解题时,条件中若出现“中点”“中线”字样可以考虑延长中线构造全等三角形,把分散的已知条件和所求证的结论集合到一个三角形中.【灵活运用】如图△,AD是△ABC的中线,BE交AC于E,交AD于F,且AE=EF若EF=4,7.阅读下面的题目及分析过程.已知:如图点E是BC的中点,点A在DE上,且AB DC=说明:BAE D ∠=∠分析:说明两个角相等,常用的方法是应用全等三角形或等腰三角形的性质.观察本题中说明的两个角,它们既不在同一个三角形中,而且们所在两个三角形也不全等.因此,要说明BAE D∠=∠,必须添加适当的辅助线,构造全等三角形或等腰三角形,现在提供两种添加辅助线的方法如下:如图△过点C作//CF AB,交DE的延长线于点F.如图△延长DE至点M,使ME DE=,连接BM.(1)请从以上两种辅助线中选择一种完成上题的说理过程.(2)在解决上述问题的过程中,你用到了哪种数学思想?请写出一个._______________.(3)反思应用:如图,点B是AE的中点,BC BD⊥于点B.请类比(1)中解决问题的思想方法,添加适当的辅助线,判断线段AC DE+与CD之间的大小关系,并说明理由.8.如图,在ABC中,45ABC∠=,AD,BE分别为BC,AC边上的高,连接DE,过点D 作DF DE⊥与点F,G为BE中点,连接AF,DG.(1)如图1,若点F与点G重合,求证:AF DF⊥;(2)如图2,请写出AF与DG之间的关系并证明.9.P为等边△ABC的边AB上一点,Q为BC延长线上一点,且P A=CQ,连PQ交AC边于D.(1)证明:PD=DQ.(2)如图2,过P作PE△AC于E,若AB=6,求DE的长.10.【阅读理解】课外兴趣小组活动时,老师提出了如下问题:如图1,△ABC中,若AB=8,AC=6,求BC边上的中线AD的取值范围.小明在组内经过合作交流,得到了如下的解决方法:延长AD到点E,使DE=AD,请根据小明的方法思考:(1)由已知和作图能得到△ADC△△EDB的理由是_____.A.SSS B.SAS C.AAS D.HL(2)求得AD的取值范围是______.A.6<AD<8B.6≤AD≤8C.1<AD<7D.1≤AD≤7【感悟】解题时,条件中若出现“中点”“中线”字样,可以考虑延长中线构造全等三角形,把分散的已知条件和所求证的结论集合到同一个三角形中.【问题解决】(3)如图2,AD是△ABC的中线,BE交AC于E,交AD于F,且AE=EF.求证:AC =BF.11.【问题情境】课外兴趣小组活动时,老师提出了如下问题:如图1,△ABC中,若AB=12,AC=8,求BC边上的中线AD的取值范围.小明在组内经过合作交流,得到了如下的解决方法:延长AD到E,使DE=AD,连接BE.请根据小明的方法思考:(1)由已知和作图能得到△ADC△△EDB,依据是.A.SSS B.SAS C.AAS D.HL(2)由“三角形的三边关系”可求得AD的取值范围是.解后反思:题目中出现“中点”“中线”等条件,可考虑延长中线构造全等三角形,把分散的已知条件和所求证的结论集合到同一个三角形中.【初步运用】如图2,AD是△ABC的中线,BE交AC于E,交AD于F,且AE=EF.若EF=3,EC=2,求线段BF的长.【灵活运用】如图3,在△ABC中,△A=90°,D为BC中点,DE△DF,DE交AB于点E,DF交AC 于点F,连接EF,试猜想线段BE、CF、EF三者之间的等量关系,并证明你的结论.12.如图,等边三角形ABC中,E是线段AC上一点,F是BC延长线上一点.连接BE,AF.点G是线段BE的中点,BN∥AC,BN与AG延长线交于点N.(1)若∠BAN=15°,求∠N;(2)若AE=CF,求证:2AG=AF.13.(1)【问题情境】课外兴趣小组活动时,老师提出了如下问题:如图△,在△ABC中,AD是△ABC的中线,若AB=10,AC=8,求AD的取值范围.小明在组内经过合作交流,得到了如下的解决方法:延长AD至点E,使DE=AD,连接BE.请根据小明的方法思考:△.由已知和作图能得到△ADC△△EDB,依据是________.A.SSS B.SAS C.AAS D.ASA△.由“三角形的三边关系”可求得AD的取值范围是________.解后反思:题目中出现“中点”、“中线”等条件,可考虑延长中线构造全等三角形,把分散的已知条件和所求证的结论集中到同一个三角形之中.(2)【学会运用】如图△,AD是△ABC的中线,点E在BC的延长线上,CE=AB, △BAC=△BCA, 求证:AE=2AD.14.如图,等边三角形ABC 中,E 是线段AC 上一点,F 是BC 延长线上一点.连接BE ,AF .点G 是线段BE 的中点,BNAC ,BN 与AG 延长线交于点N .(1)若15BAN ∠=︒,求N ∠; (2)若AE CF =,求证:2AG AF =.15.P 为等边△ABC 的边AB 上一点,Q 为BC 延长线上一点,且P A =CQ ,连PQ 交AC 边于D .(1)证明:PD =DQ .(2)如图2,过P 作PE △AC 于E ,若AB =6,求DE 的长.16.数学兴趣小组在活动时,老师提出了这样一个问题:如图1,在ABC 中,AB 8=,AC 6=,D 是BC 的中点,求BC 边上的中线AD 的取值范围.小明在组内经过合作交流,得到了如下的解决方法:延长AD 到E ,使DE AD =,请补充完整证明“ADC △EDB ”的推理过程.()1求证:ADC △EDB证明:延长AD 到点E ,使DE AD = 在ADC 和EDB 中AD ED(=已作),ADC EDB(∠∠=______),CD BD(=中点定义),ADC ∴△EDB(______),()2探究得出AD 的取值范围是______;【感悟】解题时,条件中若出现“中点”“中线”等字样,可以考虑延长中线构造全等三角形,把分散的已知条件和所求证的结论集合到同一个三角形中. 【问题解决】()3如图2,ABC 中,B 90∠=,AB 2=,AD 是ABC 的中线,CE BC ⊥,CE 4=,且ADE90∠=,求AE 的长.17.如图,阅读下面的题目及分析过程,并按要求进行证明.已知:如图,E 是BC 的中点,点A 在DE 上,且△BAE=△CDE . 求证:AB=CD . 分析:证明两条线段相等,常用的一般方法是应用全等三角形或等腰三角形的判定和性质,观察本题中要要证AB=CD ,必须添加适当的辅助线,构造全等三角形或等腰三18.如图,点P为等边△ABC的边AB上一点,Q为BC延长线上一点,AP=CQ,PQ交AC于D,(1)求证:DP=DQ;(2)过P作PE△AC于E,若BC=4,求DE的长.19.阅读下面的题目及分析过程,并按要求进行证明.已知:如图,E是BC的中点,点A在DE上,且∠BAE=∠CDE.求证:AB=CD.分析:证明两条线段相等,常用的一般方法是应用全等三角形或等腰三角形的判定和性质,观察本题中要证明的两条线段,它们不在同一个三角形中,且它们分别所在的两个三角形也不全等.因此,要证AB=CD,必须添加适当的辅助线,构造全等三角形或等腰三角形.现给出如下三种添加辅助线的方法,请任意选择其中一种,对原题进行证明.参考答案:1.100°【解析】【分析】延长AD到M,使得DM=AD,连接BM,证△BDM△△CDA(SAS),得BM=AC=BF,△M=△DAC=24°,△C=△DBM,再证△BFM是等腰三角形,求出△MBF的度数,即可解决问题.【详解】解:如图,延长AD到M,使得DM=AD,连接BM,如图所示:在△BDM和△CDA中,DM DABDM CDABD CD=⎧⎪∠=∠⎨⎪=⎩,△△BDM△△CDA(SAS),△BM=AC=BF,△M=△DAC=24°,△C=△DBM,△BF=AC,△BF=BM,△△M=△BFM=24°,△△MBF=180°-△M-△BFM=132°,△△EBC=32°,△△DBM=△MBF-△EBC=100°,△△C=△DBM=100°,故答案为:100°.【点睛】本题考查全等三角形的判定和性质、等腰三角形的判定和性质等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题,属于中考常考题型.2.问题背景:SAS;问题解决:完整过程见解析;拓展应用:DE=6.【解析】【分析】问题背景:先判断出BD=CD,由对顶角相等△BDE=△CDA,进而得出△ADC△△EDB (SAS);问题解决:先证明△ADC△△EDB(SAS),得出BE=AC=3,最后用三角形三边关系即可得出结论;拓展应用:如图2,延长AM到N,使得MN=AM,连接BN,同(1)的方法得出△BMN△△CMA(SAS),则BN=AC,进而判断出△ABN=△EAD,进而判断出△ABN△△EAD,得出AN=ED,即可求解.【详解】问题背景:如图1,延长AD到点E,使DE=AD,连接BE,△AD是△ABC的中线,△BD=CD,在△ADC和△EDB中,AD EDCDA BDECD BD=⎧⎪∠=∠⎨⎪=⎩,△△ADC△△EDB(SAS),故答案为:SAS;问题解决:如图1,延长AD到点E,使DE=AD,连接BE,△AD是△ABC的中线,△BD=CD,AD EDCDA BDECD BD=⎧⎪∠=∠⎨⎪=⎩,△△ADC△△EDB(SAS),△BE=AC,在△ABE中,AB﹣BE<AE<AB+BE,△AB=4,AC=3,△4﹣3<AE<4+3,即1<AE<7,△DE=AD,△AD=12AE,△12<AD<72;拓展应用:如图2,延长AM到N,使得MN=AM,连接BN,由问题背景知,△BMN△△CMA(SAS),△BN=AC,△CAM=△BNM,△AC//BN,△AC=AD,△BN=AD,△AC//BN,△△BAC+△ABN=180°,△△BAE=△CAD=90°,△△BAC+△EAD=180°,在△ABN 和△EAD 中,AB EA ABN EAD BN AD =⎧⎪∠=∠⎨⎪=⎩,△△ABN △△EAD (SAS ),△AN =DE ,△MN =AM ,△DE =AN =2AM ,△AM =3,△DE =6.【点睛】此题考查了全等三角形的判定和性质,平行线的判定与性质,补角的性质,掌握倍长中线法,构造全等三角形是解本题的关键.3.(1)见解析;(2)见解析.【解析】【分析】 (1)先由AF △BC ,利用平行线的性质可证△AFE =△DCE ,而E 是AD 中点,那么AE =DE ,△AEF =△DEC ,利用AAS 可证△AEF △△DEC ,那么有AF =DC ,又AF =BD ,从而有BD =CD ; (2)四边形AFBD 是矩形.由于AF 平行等于BD ,易得四边形AFBD 是平行四边形,又AB =AC ,BD =CD ,利用等腰三角形三线合一定理,可知AD △BC ,即△ADB =90°,那么可证四边形AFBD 是矩形.【详解】证明: (1)△AF △BC ,△△AFE =△DCE ,△E 是AD 的中点,△AE =DE ,△△AFE =△DCE , ∠AEF∠∠DEC ,AE =DE ,△△AEF △△DEC (AAS ),△AF =DC ,△AF =BD ,△BD =CD ,△D 是BC 的中点;(2)四边形AFBD 是矩形.理由: △AB =AC ,D 是BC 的中点,△AD △BC ,△△ADB =90°,△AF =BD ,过A 点作BC 的平行线交CE 的延长线于点F ,即AF △BC ,△四边形AFBD 是平行四边形,又△△ADB =90°,△四边形AFBD 是矩形.【点睛】本题利用了平行线的性质、全等三角形的判定和性质、等量代换、平行四边形的判定、等腰三角形三线合一定理、矩形的判定等知识.4.(1)SAS ;(2)17AD <<;(3)见解析【解析】【分析】(1)根据AD=DE ,△ADC=△BDE ,BD=DC 推出△ADC 和△EDB 全等即可;(2)根据全等得出BE=AC=6,AE=2AD ,由三角形三边关系定理得出8-6<2AD <8+6,求出即可;(3)延长ND 至点E ,使DE DN =,连接BE 、ME ,证明BED △()SAS CND △,得到BE CN =,根据三角形三边关系解答即可.【详解】(1)解:△在△ADC 和△EDB 中,AD DE ADC BDE BD CD =⎧⎪∠=∠⎨⎪=⎩,△△ADC△△EDB (SAS ),故答案为:SAS ;(2)解:△由(1)知:△ADC△△EDB ,△BE=AC=6,AE=2AD ,△在△ABE 中,AB=8,由三角形三边关系定理得:8-6<2AD <8+6,△1<AD <7,故答案为:1<AD <7.(3)证明:延长ND 至点E ,使DE DN =,连接BE 、ME ,如图所示:△点D 是BC 的中点,△BD CD =.在BED 和CND △中,DE DN BDE CDN BD CD =⎧⎪∠=∠⎨⎪=⎩, △BED △()SAS CND △,△BE CN =,△DM DN ⊥,DE DN =,△ME MN =, 在BEM △中,由三角形的三边关系得:BM BE ME +>,△BM CN MN +>.【点睛】本题是三角形综合题,主要考查了三角形的中线,三角形的三边关系定理,全等三角形的性质和判定等知识点,主要考查学生运用定理进行推理的能力.5.见详解【解析】【分析】过点D作DE△AC,交BC于点E,根据等边三角形和平行线的性质得△MDE=△MEC,DE=CE,从而证明∆EMD≅∆CME,进而即可得到结论.【详解】过点D作DE△AC,交BC于点E,△ABC是等边三角形,△△B=△ACB=60°,△DE△AC,△△DEB=△ACB=60°,△MDE=△MEC,△BDE是等边三角形,△BD=DE,△BD CE=,△DE=CE,又△△EMD=△CME,△∆EMD≅∆CME,△MD ME=.【点睛】本题主要考查等边三角形的性质和判定定理以及全等三角形的判定和性质定理,添加辅助线,构造等边三角形和全等三角形,是解题的关键.6.(1)B;(2)C;应用:7.【解析】【分析】(1)由已知AD是△ABC的中线,和作图延长AD到点E,使DE=AD,CD=BD,△ADC=△EDB, AD=DE得到△ADC△△EDB(SAS) 即可,(2) 由△ADC△△EDB,则BE=AC=6,AE=2AD,AB=8,在ΔABE中,AB-BE<AE<AB+BE,即则2<2AD<14即可,【灵活运用】延长AD到G,使DG=AD,连接BG,由(1)知△ADC△△GDB,BG=AC=AE+EC=7△G=△DAC可以判定BG△AC,由△BFG=△AFE,得ΔGBF△ΔAEF,由性质BG BF AE EF.【详解】(1)由已知AD是△ABC的中线,和作图延长AD到点E,使DE=AD,CD=BD,△ADC=△EDB, AD=DE得到△ADC△△EDB(SAS)故选择:B,(2) 由△ADC△△EDB,则BE=AC=6,AE=2AD,AB=8,在ΔABE中,AB-BE<AE<AB+BE,即AB-BE=8-6=2,AB+BE=14,则2<2AD<14,1<AD<7故选择:C,灵活运用延长AD到G,使DG=AD,连接BG,由(1)知△ADC△△GDB,BG=AC=AE+EC=7,△G=△DAC,BG△AC,△BFG=△AFE,ΔGBF△ΔAEF,BG BF AE EF=, 744BF =, BF=7.【点睛】本题考查中线加倍问题,由中线加倍,利用SAS 推出三角形全等,把问题转化为三角形中的问题,用三角形的三边关系,确定取值范围,由△ADC △△GDB ,△G=△DAC 可以判定BG△AC ,由△BFG=△AFE ,得ΔGBF△ΔAEF ,用相似三角形的性质解决问题. 7.(1)采用第一种方法,证明见解析(2)转化思想(3)AC+DE >CD ,证明见解析 【解析】【分析】(1)过点C 作//CF AB ,证明得到△ABE△△FCE ,得到BAE F ∠=∠,再根据AB DC =得到D F =∠∠,故可得到BAE D ∠=∠;(2)此题用到了转化思想;(3)过点E 作//EF AC ,证明得到△ABC△△EBF ,得到AC=EF,连接DF,利用等腰三角形三线合一得到CD=DF ,再根据三角形的三边关系得到EF DE +与DF 之间的大小关系即可求解.【详解】(1)采用第一种方法,过点C 作//CF AB ,交DE 的延长线于点F .△//CF AB△B ECF ∠=∠,BAE CFE ∠=∠又E 点是BC 中点,△BE=CE△△ABE△△FCE(AAS)△BAE F∠=∠,AB=CF,A,E,F在同一直线上,△AB DC=△D F=∠∠△BAED∠=∠;(2)此题用到了转化思想;故答案为:转化思想;(3)如图,过点E作//EF AC,同(1)理得到△ABC△△EBF,△AC=EF,BC=BF连接DF△BC BD⊥△△CDF是等腰三角形△CD=DF,在△DEF中,EF DE+>DF故AC+DE>CD.【点睛】此题主要考查全等三角形的判定与性质,解题的关键是熟知全等三角形的判定方法及等腰三角形的性质.8.(1)详见解析;(2)AF=2DG,且AF△DG,证明详见解析.【解析】【分析】(1) 利用条件先△DAE△△DBF,从而得出△FDE是等腰直角三角形,再证明△AEF是等腰直角三角形,即可.(2) 延长DG至点M,使GM=DG,交AF于点H,连接BM,先证明△BGM△△EGD,再证明△BDM△△DAF即可推出.【详解】解:(1)证明:设BE与AD交于点H..如图,△AD,BE分别为BC,AC边上的高,△△BEA=△ADB=90°.△△ABC=45°,△△ABD是等腰直角三角形.△AD=BD.△△AHE=△BHD,△△DAC=△DBH.△△ADB=△FDE=90°,△△ADE=△BDF.△△DAE△△DBF.△BF=AE,DF=DE.△△FDE是等腰直角三角形.△△DFE=45°.△G为BE中点,△AE=EF.△△AEF是等腰直角三角形.△△AFE=45°.△△AFD=90°,即AF△DF.(2)AF=2DG,且AF△DG.理由:延长DG至点M,使GM=DG,交AF于点H,连接BM,△点G为BE的中点,BG=GE.△△BGM△EGD,△△BGM△△EGD.△△MBE=△FED=45°,BM=DE.△△MBE=△EFD,BM=DF.△△DAC=△DBE,△△MBD=△MBE+△DBE=45°+△DBE.△△EFD=45°=△DBE+△BDF,△△BDF=45°-△DBE.△△ADE=△BDF,△△ADF=90°-△BDF=45°+△DBE=△MBD.△BD=AD,△△BDM△△DAF.△DM=AF=2DG,△FAD=△BDM.△△BDM+△MDA=90°,△△MDA+△FAD=90°.△△AHD=90°.△AF△DG.△AF=2DG,且AF△DG本题考查三角形全等的判定和性质,关键在于灵活运用性质.9.(1)证明见解析;(2)DE=3.【解析】【分析】(1)过点P作PF△BC交AC于点F;证出△APF也是等边三角形,得出AP=PF=AF=CQ,由AAS证明△PDF△△QDC,得出对应边相等即可;(2)过P作PF△BC交AC于F.同(1)由AAS证明△PFD△△QCD,得出对应边相等FD=CD,证出AE+CD=DE12=AC,即可得出结果.【详解】(1)如图1所示,点P作PF△BC交AC于点F.△△ABC是等边三角形,△△APF也是等边三角形,AP=PF=AF=CQ.△PF△BC,△△PFD=△DCQ.在△PDF和△QDC中,PDF QDCDFP QCDPF QC∠=∠⎧⎪∠=∠⎨⎪=⎩,△△PDF△△QDC(AAS),△PD=DQ;(2)如图2所示,过P作PF△BC交AC于F.△PF△BC,△ABC是等边三角形,△△PFD=△QCD,△APF是等边三角形,△AP=PF=AF.△PE△AC,△AE=EF.△AP=PF,AP=CQ,△PF=CQ.在△PFD和△QCD中,PDF QDCDFP QCDPF QC∠=∠⎧⎪∠=∠⎨⎪=⎩,△△PFD△△QCD(AAS),△FD=CD.△AE =EF ,△EF +FD =AE +CD ,△AE +CD =DE 12=AC . △AC =6,△DE =3.【点睛】本题考查等边三角形的判定与性质、全等三角形的判定(AAS )与性质、平行线的性质,熟练掌握等边三角形的性质,解题的关键是掌握等边三角形的判定与性质、全等三角形的判定(AAS )与性质、平行线的性质,熟练掌握等边三角形的性质.10.(1)B ;(2)C ;(3)证明见解析.【解析】【分析】(1)根据AD =DE ,△ADC =△BDE ,BD =DC 推出△ADC 和△EDB 全等即可;(2)根据全等得出BE =AC =6,AE =2AD ,由三角形三边关系定理得出8﹣6<2AD <8+6,求出即可;(3)延长AD 到M ,使AD =DM ,连接BM ,根据SAS 证△ADC△△MDB ,推出BM =AC ,△CAD =△M ,根据AE =EF ,推出△CAD =△AFE =△BFD ,求出△BFD =△M ,根据等腰三角形的性质求出即可.【详解】(1)解:在△ADC 和△EDB 中AD DE ADC BDE BD CD =⎧⎪∠=∠⎨⎪=⎩,△△ADC△△EDB(SAS),故选B ;(2)解:如图:△由(1)知:△ADC△△EDB,△BE=AC=6,AE=2AD,△在△ABE中,AB=8,由三角形三边关系定理得:8﹣6<2AD<8+6,△1<AD<7,故选C.(3)延长AD到M,使AD=DM,连接BM,△AD是△ABC中线,△CD=BD,△在△ADC和△MDB中DC DBADC MDBDA DM=⎧⎪∠=∠⎨⎪=⎩△△ADC△△MDB,△BM=AC,△CAD=△M,△AE=EF,△△CAD=△AFE,△△AFE =△BFD ,△△BFD =△CAD =△M ,△BF =BM =AC ,即AC =BF.【点睛】本题考查了三角形的中线,三角形的三边关系定理,等腰三角形性质和判定,全等三角形的性质和判定等知识点,主要考查学生运用定理进行推理的能力.11.(1)B ;(2)2<AD <10;【初步运用】BF =5;【灵活运用】BE 2+CF 2=EF 2,理由见解析【解析】【分析】(1)根据全等三角形的判定定理解答;(2)根据三角形的三边关系计算;初步运用 延长AD 到M ,使AD =DM ,连接BM ,证明△ADC △△MDB ,根据全等三角形的性质解答;灵活运用 延长ED 到点G ,使DG =ED ,连结GF ,GC ,证明△DBE △△DCG ,得到BE =CG ,根据勾股定理解答.【详解】解:(1)在△ADC 和△EDB 中,BD=CD BDE=CDA ED=AD ⎧⎪∠∠⎨⎪⎩, △△ADC△△EDB (SAS ),故选B ;(2)△△ADC△△EDB ,△EB=AC=8,在△ABE 中,AB ﹣BE <AE <AB+BE ,△2<AD <10,故答案为2<AD <10;【初步运用】延长AD 到M ,使AD =DM ,连接BM ,△AE =EF .EF =3,△AC =5,△AD 是△ABC 中线,△CD =BD ,△在△ADC 和△MDB 中,BD=CD BDM=CDA DM=DA ⎧⎪∠∠⎨⎪⎩, △△ADC △△MDB ,△BM =AC ,△CAD =△M ,△AE =EF ,△△CAD =△AFE ,△△AFE =△BFD ,△△BFD =△CAD =△M ,△BF =BM =AC ,即BF =5;【灵活运用】线段BE 、CF 、EF 之间的等量关系为:BE 2+CF 2=EF 2.证明:如图3,延长ED 到点G ,使DG =ED ,连结GF ,GC ,△ED △DF ,△EF =GF ,△D 是BC 的中点,△BD =CD ,在△BDE 和△CDG 中, ED=GD BDE=CDG BD=CD ⎧⎪∠∠⎨⎪⎩,△△BDE△△CDG(SAS),△BE=CG,△△A=90°,△△B+△ACB=90°,△△BDE△△CDG,EF=GF,△BE=CG,△B=△GCD,△△GCD+△ACB=90°,即△GCF=90°,△Rt△CFG中,CF2+GC2=GF2,△BE2+CF2=EF2.【点睛】本题考查全等三角形的判定和性质、三角形三边关系以及勾股定理的应用,掌握全等三角形的判定定理和性质定理是解题的关键.12.(1)45°;(2)见解析【解析】【分析】(1)由等边三角形的性质可知∠ABC=∠ACB=60°,由平行线的性质可知∠NBC=60°,进一步求出∠ABN=120°,再由三角形内角和定理即可求出∠N的度数;(2)先证△NBG≌△AEG,得到AG=NG,AE=BN,再证△ABN≌△ACF,即可推出AF =2AG.【详解】解:(1)∵△ABC是等边三角形,∴∠ABC=∠ACB=60°,∵AC∥BN,∴∠NBC=∠ACB=60°,∴∠ABN=∠ABC+∠NBC=120°,∴在△ABN中,∠N=180°﹣∠ABN﹣∠BAN=180°﹣120°﹣15°=45°;(2)∵AC∥BN,∴∠N=∠GAE,∠NBG=∠AEG,又∵点G是线段BE的中点,∴BG=EG,∴△NBG≌△AEG(AAS),∴AG=NG,AE=BN,∵AE=CF,∴BN=CF,∵∠ACB=60°,∴∠ACF=180°﹣∠ACB=120°,∴∠ABN=∠ACF,又∵AB=AC,∴△ABN≌△ACF(SAS),∴AF=AN,AN,∵AG=NG=12∴AF=2AG.【点睛】本题考查了等边三角形的性质,平行线的性质,三角形内角和定理,全等三角形的判定与性质等,解题的关键是能够熟练运用全等三角形的判定与性质.13.(1)△.B;△. 1<AD<9;(2)证明见解析.【解析】【分析】(1)△.根据全等三角形的判定定理解答;△.根据三角形的三边关系定理可得AB−BE<AE<AB+BE,结合BE=AC可确定AE的取值范围,易得AD的取值范围;(2)首先延长AD至M,使DM=AD,先证明△ABD△△MCD,进而得出MC=AB,△B =△MCD,即可得出△ACM=△ACE,再证明△ACM△△ACE,即可证明结论.【详解】解:(1)△.在△ADC和△EDB中,BD CDBDE CDA DE AD⎧⎪∠∠⎨⎪⎩===,△△ADC△△EDB(SAS),故选B;△.△△ADC△△EDB,△BE=AC,△AB−BE<AE<AB+BE,△AB− AC<AE<AB+AC,即2<AE<18,△1<AD<9,故答案为1<AD<9;(2)延长AD至M,使DM=AD,△AD是△ABC的中线,△BD=CD,在△ABD和△MCD中,BD CDADB MDC AD DM⎧⎪∠∠⎨⎪⎩===,△△ABD△△MCD(SAS),△MC=AB,△B=△MCD,△AB=CE,△CM=CE,△△BAC=△BCA,△△B+△BAC=△ACB+△MCD,即△ACE=△ACM,在△ACE和△ACM中,AC ACACE ACM CM CE⎧⎪∠∠⎨⎪⎩===,△△ACM△△ACE(SAS),△AE=AM,△AM=2AD,△AE=2AD.【点睛】本题考查的是三角形三边关系以及全等三角形的判定和性质,掌握全等三角形的判定定理和性质定理利用倍长中线得出辅助线是解题关键.14.(1)45°;(2)见解析【解析】【分析】(1)由等边三角形的性质可知△ABC=△ACB=60°,由平行线的性质可知△NBC=60°,进一步求出△ABN=120°,再由三角形内角和定理即可求出△N的度数;(2)先证△NBG△△AEG,得到AG=NG,AE=BN,再证△ABN△△ACF,即可推出AF=2AG.【详解】(1)△△ABC是等边三角形,△△ABC=△ACB=60°,△AC△BN,△△NBC=△ACB=60°,△△ABN=△ABC+△NBC=120°,△在△ABN中,△N=180°-△ABN-△BAN=180°-120°-15°=45°;(2)△AC△BN,△△N=△GAE,△NBG=△AEG,又△点G是线段BE的中点,△BG=EG,△△NBG△△AEG(AAS),△AG=NG,AE=BN,△AE=CF,△BN=CF,△△ACB=60°,△△ACF=180°-△ACB=120°,△△ABN=△ACF,又△AB=AC,△△ABN△△ACF(SAS),△AF=AN,△AG=NG=12AN,△AF=2AG.【点睛】考查了等边三角形的性质,平行线的性质,三角形内角和定理,全等三角形的判定与性质等,解题的关键是能够熟练运用全等三角形的判定与性质.15.(1)证明见解析;(2)DE=3.【解析】【分析】(1)过点P作PF△BC交AC于点F;证出△APF也是等边三角形,得出AP=PF=AF=CQ,由AAS证明△PDF△△QDC,得出对应边相等即可;(2)过P作PF△BC交AC于F.同(1)由AAS证明△PFD△△QCD,得出对应边相等FD=CD,证出AE+CD=DE12=AC,即可得出结果.【详解】(1)如图1所示,点P作PF△BC交AC于点F.△△ABC是等边三角形,△△APF也是等边三角形,AP=PF=AF=CQ.△PF△BC,△△PFD=△DCQ.在△PDF和△QDC中,PDF QDCDFP QCDPF QC∠∠∠∠=⎧⎪=⎨⎪=⎩,△△PDF△△QDC(AAS),△PD=DQ;(2)如图2所示,过P作PF△BC交AC于F.△PF△BC,△ABC是等边三角形,△△PFD=△QCD,△APF是等边三角形,△AP=PF=AF.△PE△AC,△AE=EF.△AP=PF,AP=CQ,△PF=CQ.在△PFD和△QCD中,PDF QDCDFP QCDPF QC∠∠∠∠=⎧⎪=⎨⎪=⎩,△△PFD△△QCD(AAS),△FD=CD.△AE=EF,△EF+FD=AE+CD,△AE+CD=DE 1 2=AC.△AC=6,△DE=3.【点睛】本题考查了等边三角形的判定与性质、等腰三角形的判定与性质、全等三角形的判定与性质、平行线的性质;熟练掌握等边三角形的性质,证明三角形全等是解决问题的关键.16.()1见解析;()21<AD<7;()3AE=6.【解析】【分析】(1)延长AD到点E,使DE=AD,根据SAS定理证明△ADC△△EDB;(2)根据全等三角形的性质、三角形的三边关系计算;(3)延长AD交EC的延长线于F,证明△ABD△△FCD,根据全等三角形的性质解答.【详解】()1延长AD到点E,使DE AD=,在ADC和EDB中,AD ED(=已作),ADC EDB(∠∠=对顶角相等),CD BD(=中点定义),ADC∴△()EDB SAS,故答案为对顶角相等,SAS ;()2ADC △EDB ,BE AC 6∴==,86AE 86-<<+,1AD 7∴<<,故答案为1AD 7<<;()3延长AD 交EC 的延长线于F ,AB BC ⊥,EF BC ⊥,ABD FCD ∠∠∴=,在ABD 和FCD 中,ABD FCD BD CDADB FDC ∠=∠⎧⎪=⎨⎪∠=∠⎩, ABD ∴△FCD , CF AB 2∴==,AD DF =,ADE 90∠=,AE EF ∴=,EF CE CF CE AB 426=+=+=+=,AE 6∴=.【点睛】本题考查了三角形的三边关系定理和全等三角形的性质和判定,解题关键是熟记全等三角形的判定条件.17.见解析【解析】【详解】试题分析:方法一:如图1中,作BF△DE于点F,CG△DE于点G,先证明△BFE△△CGE,得BF=CG,再证明△ABF△△DCG即可.方法二如图2中,:作CF△AB,交DE的延长线于点F,先证明CF=CD,再证明△ABE△△FCE即可.证明:方法一:如图1中,作BF△DE于点F,CG△DE于点G.△△F=△CGE=90°,在△BFE和△CGE中,,△△BFE△△CGE .△BF=CG.在△ABF和△DCG中,,△△ABF△△DCG.△AB=CD.方法二如图2中,:作CF△AB,交DE的延长线于点F.△△F=△BAE.又△△ABE=△D,△△F=△D.△CF=CD.在△ABE和△FCE中,,△△ABE△△FCE.△AB=CF.△AB=CD.18.(1)详见解析(2)ED=2【解析】【分析】(1)过P作PF△BQ,可得△APF为等边三角形,所以AP=PF,再证△DCQ△△DFP,即可得PD=DQ;(2)根据等腰三角形三线合一的性质可得AE=EF,根据全等三角形对应边相等可得FD =CD,然后求出2DE=AC,代入数据进行计算即可得解.(1)证明:如图,过点P作PF△BC,则△DPF=△Q,△△ABC为等边三角形,△△APF是等边三角形,△AP=PF,又△AP=CQ,△PF=CQ,在△DPF和△DQC中,DPF QPDF QDCPF CQ∠=∠⎧⎪∠=∠⎨⎪=⎩,△△DPF△△DQC(AAS),△DP=DQ;(2)△△P AF为等边三角形,PE△AC,可得AE=EF,由(1)知,△DPF△△DQC△FD=CD,△AC=AE+EF+FD+CD,△AC=2EF+2FD=2(EF+FD)=2ED,△AC=BC=4,△2ED=4,△ED=2.【点睛】本题考查了等边三角形的性质,全等三角形的判定与性质,等腰三角形三线合一的性质,作辅助线构造出等边三角形和全等三角形是解题的关键,也是本题的难点.19.【解析】【详解】试题分析:方法一:作BF△DE于点F,CG△DE于点G,△△F=△CGE=90°.又△△BEF=△CEG,BE=CE,△△BFE△△CGE.△BF=CG.在△ABF和△DCG中,△△F=△DGC=90°,△BAE=△CDE,BF=CG,△△ABF△△DCG.△AB=CD.方法二:作CF△AB,交DE的延长线于点F,△△F=△BAE.又△△ABE=△D,△△F=△D.△CF=CD.△△F=△BAE,△AEB=△FEC,BE=CE,△△ABE△△FCE.△AB=CF.△AB=CD.方法三:延长DE至点F,使EF=DE,又△BE=CE,△BEF=△CED,△△BEF△△CED.△BF=CD,△D=△F.又△△BAE=△D,△△BAE=△F.△AB=BF.△AB=CD.考点:1.全等三角形的判定与性质;2.阅读理解.。
中考数学总复习《构造三角形中位线模型解题》专项提升练习题(附答案)
中考数学总复习《构造三角形中位线模型解题》专项提升练习题(附答案)学校:___________班级:___________姓名:___________考号:___________一、三角形中位线的概念和性质1.连接三角形两边中点的线段叫做三角形的中位线2.三角形中位线定理:三角形的中位线平行于第三遍,且等于第三边的一半3.隐含中点的条件:等腰三角形三线合一(顶角的角平分线底边的中垂线),平行四边形对角线的交点。
例1.如图,点D、E分别为△ABC的边AB、AC的中点,点F在DE的延长线上,CF∥BA,若BC=8,则EF=( ) A.4 B.8 C.5 D.3例2.如图,在四边形ABCD中,P是对角线BD的中点,E、F分别是AB、CD的中点,AD=BC,∠EPF=136°,则∠EFP的度数是( ) A.68° B.34° C.22° D.44°二、连接两点构造三角形的中位线例3.如图,在四边形ABCD中,∠A=90°,AB=12,AD=5.点M、N分别为线段BC、AB上的动点(含端点,但点M不与点B重合),点E、F分别为DM、MN的中点,则EF的最大值是.4例4.如图1,已知点E ,F ,G ,H 分别是四边形ABCD 的边AB ,BC ,CD ,DA 的中点,根据以下思路可以证明四边形EFGH 是平行四边形:如图2,将图1中的点C 移动至与点E 重合的位置,F ,G ,H 仍是BC ,CD ,DA 的中点,求证:四边形CFGH 是平行四边形.三.已知角平分线+垂直构造中位线例5.如图,AD 为ABC 中BAC ∠的外角平分线,BD AD ⊥于D ,E 为BC 中点5DE =,3AC =则AB 长为( )A .8.5B .8C .7.5D .7例6.如图,在△ABC 中,∠ABC =90°,在边AC 上截取AD =AB ,连接BD ,过点A 作AE ⊥BD 于点E ,F 是边BC 的中点,连接EF.若AB =5,BC =12,求EF 的长度.例7.如图,在△ABC中,已知AB=6,AC=10,AD平分∠BAC,BD⊥AD于点D,点E为BC的中点,求DE的长.四.倍长法构造三角形的中位线例8.如图,在△ABC中,∠ABC=90°,BA=BC,△BEF为等腰直角三角形,∠BEF=90°,M为AF的中点.求证ME=12CF.例9.如图,在△ABC中,∠ABC=90°,AB=BC,BD⊥AC于点D,CE平分∠ACB,交AB于点E,交BD于点F.求证:(1)△BEF是等腰三角形;(2)BD=12(BC+BF).五.已知一边中点,取另一边中点构造三角形的中位线例10.如图,四边形ABCD中,点E,F分别是边AB,CD的中点,且AD=6,BC=10,则线段EF的长可能为( )A.7B.8.5C.9D.10六.已知两边中点,取第三边中点构造三角形的中位线例11.如图,菱形ABCD 的对角线AC BD ,相交于点O .E ,F 分别是AD OC ,的中点,若1207BAD EF ∠=︒=,ABCD 的周长为( )A .8B .16C .3D .3例12.如图,已知四边形ABCD 中AC BD ⊥,AC=6,8BD =点E 、F 分别是边AD 、BC 的中点,连接EF ,则EF 的长是 __.强化训练题一.选择题1.如图 在△ABC 中 AB =4 BC =5 AC =8.点D E F 分别是相应边上的中点 则四边形DFEB 的周长等于( )A .8B .9C .12D .132.如图 △ABC 中 AB =AC =12 BC =10 AD 平分∠BAC 交BC 于点D 点E 为AC 的中点 连接DE 则△CDE 的周长为( )A .11B .17C .18D .163.如图 在ABC 中 45B ∠=︒ 60C ∠=︒ AD BC ⊥于点D 6BD = 若E F 分别为AB BC 的中点 则EF 的长为( )A 2B 6C 6D 34.如图 ABCD 的对角线AC BD 交于点O AE 平分BAD ∠交BC 于点E且60ADC ∠=︒ 12AB BC = 连接OE .下列结论中不成立的是( )A .30CAD ∠=︒B .ABCD S AB AC =⋅ C .OB AB =D .14OE BC =5.如图 四边形ABCD 中 ∠B =90° AB =8 BC =6 点M 是对角线AC 的中点 点N 是AD 边的中点 连结BM MN 若BM =3MN 则线段CD 的长是( )A .53B .3C .103D .56.已知三角形三边长分别为7cm 8cm 9cm 作三条中位线组成一个新的三角形 同样方法作下去 一共做了五个新的三角形 则这五个新三角形的周长之和为( )A .46.5cmB .22.5cmC .23.25cmD .以上都不对7.如图 在ABC 中 AE 平分BAC ∠ BE AE ⊥于点E 点F 是BC 的中点 若10AB = 6AC = 则EF 的长为( )A .2B .3C .4D .58.如图 在四边形ABCD 中 点E F 分别为AD DC 的中点 连接EB BF EF △EBF 的面积为 S 1 .点G 为四边形ABCD 外一点 连接AG BG EG FG 使得AG =BC ∠GAB =∠ABC △EGF 的面积为 S 2 则 S 1 与 S 2 满足的关系是( )A .S 1 = S 2B .2 S 1 =3 S 2C .3 S 1 =4 S 2D .3 S 1 =2 S 29.如图 平行四边形ABCD 中 O 为对角线交点 DP 平分ADC ∠ CP 平分BCD ∠ 7AB = 10AD = 则OP 的长为( )A .1.5B .2C .2.5D .310.如图 ▱ABCD 的顶点A D 分别在直角∠MON 的两边OM ON 上运 动(不与点O 重合) ▱ABCD 的对角线AC BD 相交于点P 连接OP 若OP=5 则▱ABCD 的周长最小值是( )A .20B .25C .10D .15二 填空题11.如图 在平行四边形ABCD 中 E 是CD 的中点 F 是AE 的中点 CF 交BE 于点G 若BE =8 则GE = .12.如图 DE 为△ABC 的中位线 点F 在DE 上 且∠AFC 为直角 若AC =6cm BC =8cm 则DF 的长为 .13.如图已知三角形纸片ABC第1次折叠使点B落在BC边上的点B'处折痕AD交BC于点D;第2次折叠使点A落在点D处折痕MN交AB'于点P.若12BC=则MP与MN的和是_________.14.如图在▱ABCD中AC是对角线∠ACD=90°点E是BC的中点AF平分∠BAC CF⊥AF于点F连接EF.已知AB=5BC=13则EF的长为.15.如图在Rt△ABC中∠ACB=90°AC=BC=6 点D是AC边上的一点且AD=2 以AD为直角边作等腰直角三角形ADE连接BE并取BE的中点F连接CF则CF的长为.16.如图 EF是△ABC的中位线 O是EF上一点且满足OE=2OF.则△ABC的面积与△AOC的面积之比为.17.如图□ABCD的顶点C在等边△BEF的边BF上点E在AB的延长线上 G为DE的中点连接CG.若AD=5 AB=CF=3 则CG的长为.三.解答题18.如图△ABC的中线BE CF相交于G且AB=12 AC=16 BC=20 求GC的长.19.如图在平行四边形ABCD中对角线AC BD、相交于点O点E是边BC中点连接OE并延长至点F使EF OE、.连接BF CF(1)求证:四边形OBFC是平行四边形;(2)求证:OF CD∥.20.如图四边形ABCD为平行四边形 E为AD上的一点连接EB并延长使BF=BE 连接EC并延长使CG=CE连接FG H为FG的中点连接DH(1)求证:四边形AFHD为平行四边形;(2)若CB=CE∠EBC=75°∠DCE=10°求∠DAB的度数.21.如图,点B为AC上一点,分别以AB,BC为边在AC同侧作等边三角形ABD和等边三角形BCE,点P,M,N分别为AC,AD,CE的中点.(1)求证:PM=PN;(2)求∠MPN的度数.22.如图,在△ABC中,AB=AC,AD⊥BC于点D,点P是AD的中点,延长BP交AC于点N,求证:AN=13AC.23.(1)如图1 在四边形ABCD中AB=CD E F分别是AD BC的中点连接FE 并延长分别与BA CD的延长线交于点M N.求证:∠BME=∠CNE;(提示:取BD的中点H连接FH HE作辅助线)(2)如图2 在△ABC中F是BC边的中点D是AC边上一点E是AD的中点直线FE交BA的延长线于点G若AB=DC=2 ∠FEC=45°求FE的长度.24.【发现与证明】如图在四边形ABCD中 E F G H是各边中点对角线AC BD相交于点O I J是AC BD的中点连接EF EH HG GF EI GI EJ FJ IJ GJ IH.结论1:四边形EFGH是平行四边形;结论2:四边形EJGI是平行四边形;结论3:S四边形EFGH =12S四边形ABCD;……(1)请选择其中一个结论加以证明(只需证明一个结论).(2)【探究与应用】(★温馨提示:以下问题可以直接使用上述结论)①如图1 在四边形ABCD中 F H分别为边AB DC的中点连结HF.已知AD=6 BC=4线段HF的取值范围是 .②如图2 在四边形ABCD中点E F G H分别是AB BC CD DA的中点连接EG FH交于点O EG=8cm FH=6cm ∠EOF=60°求S四边形ABCD.答案部分:例1.A ∵点D E 分别为△ABC 的边AB AC 的中点 ∴DE 是△ABC 的中位线 ∴DE ∥BC ,DE =12BC =4.∴DF ∥BC ∵DF ∥BC ,CF ∥BA∴四边形BCFD 是平行四边形 ∴DF =BC =8,∴EF =DF -DE =4.例2.C ∵P 是BD 的中点,E 是AB 的中点 ∴PE =12AD ,同理,PF =12BC ∵AD =BC ,∴PE =PF∴∠EFP =12×(180°-∠EPF )=22°. 故选C.例3.答案 6.5解:如图,连接DN DB∵点E F 分别为DM MN 的中点 ∴EF 是△MDN 的中位线 ∴EF =12DN当N与点B重合时,DN最大,此时EF的值最大∵∠A=90°,AB=12,AD=5∴DB=√AD2+AB2=13,∴EF的最大值为6.5 故答案为6.5.例4.证明如图,连接BD∵C,H分别是AB,DA的中点∴CH是△ABD的中位线BD∴CH∥BD,CH=12BD同理,FG∥BD,FG=12∴CH∥FG,CH=FG∴四边形CFGH是平行四边形.例5.D解:延长BD CA交于点F∠的外角平分线∵AD为ABC中BAC∴FAD BAD∠=∠∵BD AD⊥∴90∠=∠=︒ADF ADB在ABD△和AFD△中FAD BAD AD ADADF ADB ∠=∠⎧⎪=⎨⎪∠=∠⎩∴ABD AFD △≌△ ∴AB AF = BD DF = 又E 为BC 中点 5DE = ∴210CF DE == 又3AC =∴7AF CF AC AB =-==. 故选:D .例6.解: 在△ABC 中,∠ABC =90°,AB =5,BC =12 则AC =√AB 2+BC 2=√52+122=13 ∵AD =AB =5∴DC =AC -AD =13-5=8 ∵AD =AB ,AE ⊥BD ,∴BE =ED ∵BF =FC ,∴EF =12DC =4.解:如图,延长BD 交AC 于点F ,∵AD 平分∠BAC ,∴∠BAD =∠CAD .∵BD ⊥AD ∴∠ADB =∠ADF又∵AD =AD ,∴△ADB ≌△ADF (ASA ).∴AF =AB =6,BD =FD .∵AC =10,∴CF =AC -AF =10-6=4.∵E 为BC 的中点,∴DE 是△BCF 的中位线.∴DE =12CF =12×4=2.例8.证明:如图,延长FE 至N ,使EN =EF ,连接BN ,AN ,则ME =12AN . ∵EF =EN ,∠BEF =90°,∴BE 垂直平分FN . ∴BF =BN .∴∠BNF =∠BFN . ∵△BEF 为等腰直角三角形,∠BEF =90°,∴∠BFN =45°.∴∠BNF =45°. ∴∠FBN =90°,即∠FBA +∠ABN =90°.又∠FBA +∠CBF =90° ∴∠CBF =∠ABN .在△BCF 和△BAN 中,∵BF =BN ,∠CBF =∠ABN ,BC =BA∴△BCF ≌△BAN (SAS ).∴CF =AN .∴ME =12AN =12CF .例9.(1)证明:在△ABC 中,∵AB =BC ,∠ABC =90°,∴∠ACB =45°. ∵CE 平分∠ACB ,∴∠ECB =∠ACE =22.5°.∴∠BEF =∠CFD =∠BFE =67.5°.∴BE =BF ,即△BEF 是等腰三角形. (2)解:如图,延长AB 至点M ,使得BM =AB ,连结CM .易知D 是AC 的中点∴BD ∥MC ,BD =12MC .∴∠BFE =∠MCE .由(1)得∠BEF =∠BFE ,BE =BF ,∴∠BEF =∠MCE .∴ME =MC .∵BM =AB =BC ,∴BD =12MC =12ME =12(MB +BE )=12(BC +BF ).例10.A 如图,连接BD ,取BD 的中点H ,连接HF ,HE∵点E ,H 分别是AB ,BD 的中点,∴EH 是△ABD 的中位线,∴EH =12AD =3 同理可得FH =12BC =5,∴EF ≤FH +EH =8,故选A .例11.B 解:取CD 的中点G 连接EG FG点E 为AD 的中点 点F 为OC 的中点12EG AC ∴=EG AC ∥ 12FG OD = //FG OD四边形ABCD 是菱形 120BAD ∠=︒AC BD ∴⊥ 60ADC ∠=︒ 1302ODC ADC ∠=∠=︒EG GF ∴⊥ AD DC AC ==设CD x = 则12EG x = 3FG 7EF =22213()()(7)2x ∴+= 解得4x =4CD ∴=∴菱形ABCD的周长为:44416CD=⨯=故选:B.例12解:如图取AB的中点G连接EG FG∵E F分别是边AD CB的中点∴EG BD∥且118422EG BD==⨯=FG AC且116322FG AC==⨯=∵AC BD⊥∴EG FG⊥∴2222435EF EG FG=++=.故答案为:5.强化训练题一.选择题1.如图在△ABC中AB=4 BC=5 AC=8.点D E F分别是相应边上的中点则四边形DFEB的周长等于()A.8 B.9 C.12 D.13解:∵点D F分别是AB AC的中点∴DF=BC=2.5同理EF=AB=2∴四边形DFEB的周长=EF+FD+DB+BE=9故选:B .2.解:∵AB =AC AD 平分∠BAC ∴BD =DC =BC =5 ∵点E 为AC 的中点∴CE =AC =6 DE =AB =6 ∴△CDE 的周长=CD +CE +DE =17 故选:B . 3.A 解:45B ∠=︒ AD BC ⊥ABD ∴是等腰直角三角形 6AD BD ∴=60C ∠=︒30DAC ∴∠=︒12DC AC ∴=2233AD AC DC DC AC ∴-=36AC =22AC ∴=E F 分别为AB BC 的中点1122222EF AC ∴==⨯=故选:A . 4.C解:四边形ABCD 是平行四边形60ABC ADC ∴∠=∠=︒ 120BAD ∠=︒AE 平分BAD ∠60BAE EAD ∴∠=∠=︒ABE ∴是等边三角形AE AB BE ∴==AB =12BC AE ∴=12BC90BAC ∴∠=︒30CAD ∴∠=︒ 故A 正确; AC AB ⊥∴ABCDSAB AC =⋅ 故B 正确AB =12BC OB =12BDBD BC >AB OB ∴≠ 故C 错误; CE BE = CO OA = OE ∴=12ABOE ∴=14BC 故D 正确. 故选:C . 5.【答案】C6.已知三角形三边长分别为7cm 8cm 9cm 作三条中位线组成一个新的三角形 同样方法作下去 一共做了五个新的三角形 则这五个新三角形的周长之和为( ) A .46.5cmB .22.5cmC .23.25cmD .以上都不对解:由△ABC 三边长分别为7cm 8cm 9cm 三条中位线组成一个新的三角形 可知新三角形与原三角形相似 相似比是1:2 即:后一个三角形的周长都是前一个三角形周长的∵原三角形的周长=7+8+9=24 ∴这个新三角形的周长=×24=12 ∴这个五个新三角形的周长之和=24+×24+×24+×24+×24=23.25故选:C .7.A解:延长AC BE 交于点M∵AE 平分BAC ∠ BE AE ⊥∴90AEB AEM ∠=∠=︒ CAE BAE ∠=∠∵AE AE =∴ABE AME ≌∴10AB AM == BE EM =∵6AC =∴4CM AM AC =-=∵点F 是BC 的中点 BE EM =∴EF 为BCM 中位线 ∴122EF CM ==.故选:A .8.【答案】A解:连接 AC∵∠GAB =∠ABC∴AG ∥BC .又 AG = BC可知四边形 AGBC 是平行四边形∴AC ∥BG点 E F 分别为 AD DC 的中点∴EF 是△ ADC 的中位线∴EF ∥AC∴ EF ∥BG .∴点 B 与点 G 到 EF 的距离相等△EBF 与△ EGF 是同底等高的关系∴ S △ EBF = S △ EGF 即S1=S2故选: A9.A解:如图 延长DP 交BC 于点F四边形ABCD 是平行四边形AD BC ∴∥ OD OB = 7AB CD == 10BC AD ==180ADC BCD ∴∠+∠=︒ ADF CFD ∠=∠ DP 平分ADC ∠ CP 平分BCD ∠ADF CDF ∠=∠∴ FCP DCP ∠=∠90CDP DCP ∴∠+∠=︒ CDF CFD ∠=∠7DC CF ∴== DP PF =OP ∴是DBF 的中位线()()111107 1.5222OP BF BC CF ∴==-=-= 故选:A .10.解:如图 取 AD 的中点 H ,连接 PH , OH∵四边形 ABCD 是平行四边形 ∴AP = PC又∵点 H 是 AD 中点 LAOD =90°∴PH =- AB , OH =- AD∴OH + PH ≥ OP∴AB + AD ≥2OP∴四边形 ABCD 的周长最小值为20故选: A .二.填空题11.解:取 BE 的中点 M 连接 FM , CM∵F 为AE 的中点 M 为 BE 的中点∴MF =AB , FM // AB∵四边形 ABCD 是平行四边形∴DC = AB , DC // AB∵E 为 CD 的中点∴CE =DC∴ CE = FM , CE // FM .∴四边形 EFMC 是平行四边形∴EG = GM∵BM = EM = BE =x8=4∴ EG =x4=2故答案为:212.如图 DE 为△ABC 的中位线 点F 在DE 上 且∠AFC 为直角 若AC =6cmBC =8cm则DF 的长为 1cm .解:∵DE 为△ABC 的中位线∴DE =BC =4(cm )∵∠AFC 为直角 E 为AC 的中点∴FE =AC =3(cm )∴DF =DE ﹣FE =1(cm )故答案为:1cm .13.6解:如图2 由折叠得:AM MD = MN AD ⊥ AD BC ⊥ 连接GD∴GN BC∥GN是AD的垂直平分线∴AG DG=∴GAD GDA∠=∠∵90GBD GAD GDB GDA∠+∠=︒=∠+∠∴GBD GDB∠=∠∴GB GD=∴AG BG=同理可得:AN CN=∴GN是ABC的中位线而12BC=∴162GN BC==∵PM GM=∴6 MP MN GM MN GN+=+==.故答案为:6.14.【答案】7215.解:延长AE BC交于点H∵△ADE是等腰直角三角形∴∠HAC=45°AE=AD=2∴CH=AC=BC AH=AC=6∴EH=AH﹣AE=4∵BC=CH BF=FE∴FC=EH=2故答案为:2.16.【答案】3 (或3:1)】解: EF 是△ ABC 的中位线.. EF / BC , EF = BCOE =20F: OE =BC =BC设点 A 到 BC 的距离为 h则 S △ ABC = BC · h , S △ aoc =OE · h =BC · h =BC · h:△ ABC 的面积与△ AOC 的面积之比=3:1.故选: D .17.【答案】52解答】解:∵四边形 ABCD 是平行四边形∴AD = BC , CD = AB , DC / AB∵AD =5, AB = CF =3.∴CD =3, BC =5∴BF = BC + CF =8∵△ BEF 是等边三角形 G 为 DE 的中点∴BF = BE =8, DG = EG延长 CG 交 BE 于点 H∵DC / AB∴∠CDG=∠HEG在△ DCG 和△ EHG 中∠CDG=∠HEGDG = EG∠DGC =∠ EGH∴△ DCGR △ EHG ( ASA ).∴DC = EH , CG = HG∵ CD =3, BE =8∴HE =3, BH =5∵ LCBH =60°, BC = BH =5∴△CBH 是等边三角形∴CH = BC =5∴CG = CH =52故答案为:52三.解答题18.如图△ABC的中线BE CF相交于G且AB=12 AC=16 BC=20 求GC的长.解:∵AB=12 AC=16 BC=20∴AB2+AC2=BC2∴△ABC是直角三角形∴∠A=90°∵F是AB中点∴AF=6∴CF===2∵中线BE CF相交于G∴G是△ABC重心∴CG:GF=2:1∴CG=.19.(1)证明见解析(2)证明见解析(1)证明:∵点E是边BC中点∴BE CE=又∵EF OE=∴四边形OBFC是平行四边形;(2)证明:∵四边形ABCD是平行四边形对角线AC BD、相交于点O ∴点O是BD的中点又∵点E是边BC中点∴OE是BCD△的中位线∴OE CD即OF CD∥.20.【答案】(1)证明:∵BF=BE CG=CE∴BC为△FEG的中位线FG∴BC//FG BC=12又∵H是FG的中点∴FH=1FG2∴BC=FH .又∵四边形ABCD是平行四边形∴AD//BC AD=BC∴AD//FH AD=FH∴四边形AFHD是平行四边形;(2)解:∵四边形ABCD是平行四边形∴∠DAB=∠DCB∵CE=CB∴∠BEC=∠EBC=75°∴∠BCE=180°−75°−75°=30°∴∠DCB=∠DCE+∠BCE=10°+30°=40°∴∠DAB=40° .21.解:(1)如图,连接CD,AE.由三角形中位线定理可得PM∥12CD,PN∥12AE.∵△ABD和△BCE是等边三角形,∴AB=DB,BE=BC,∠ABD=∠CBE=60°∴∠ABE=∠DBC.∴△ABE≌△DBC,∴AE=DC.∴PM=PN.(2)如图,设PM交AE于F,PN交CD于G,AE交CD于H,AE交BD于Q.由(1)知△ABE≌△DBC,∴∠BAE =∠BDC.又∵∠DQH=∠BQA,∴∠AHD=∠ABD=60°,∴∠FHG=120°.22.证明:如图,取NC的中点H,连接DH过点H作HE∥AD,交BN的延长线于E.∵AB=AC,AD⊥BC,∴D为BC的中点.∵H为NC的中点,∴DH∥BN.又∵PD∥EH,∴四边形PDHE是平行四边形.∴HE=PD.∵P为AD的中点,∴AP=PD. ∴AP=EH.又∵HE∥AD,∴∠PAN=∠EHN,∠APN=∠HEN.∴△APN≌△HEN(ASA).∴AN=NH. ∴AN=NH=HC. ∴AN=13AC.23.(1)证明:连接BD取DB的中点H连接EH FH ∵E H分别是AD BD的中点∴EH∥AB EH=AB∴∠BME=∠HEF∵F H分别是BC BD的中点∴FH∥CD FH=CD∴∠CNE=∠HFE∵AB=CD∴HE=FH∴∠HEF=∠HFE∴∠BME=∠CNE;(2)连接BD取DB的中点H连接EH FH∵E F分别是AD BC的中点∴EH=AB FH=CD FH∥AC∴∠HFE=∠FEC=45°∵AB=CD=2∴HF=HE=1∴∠HEF=∠HFE=45°∴∠EHF=180°﹣∠HFE﹣HEF=90°∴.24.【答案】(1)解:结论1:四边形EFGH是平行四边形;证明:∵在四边形ABCD中 E F G H是各边中点∴EF为∆ABD的中位线∴EF∥BD EF=12BD同理可得GH∥BD GH=12BD∴GH∥EF GH=EF∴四边形EFGH是平行四边形;结论2:四边形EJGI是平行四边形;证明:∵E J G I分别为DA DB BC AC中点∴EJ为∆ABD的中位线∴EJ∥AB EJ=12AB同理可得IG∥AB IG=12AB∴EJ∥IG EJ=IG∴四边形EJGI是平行四边形;结论3:S四边形EFGH=12S四边形ABCD;证明:由结论1证明可得 EF=12BD GH=12BD∴∆AEF的高为∆ADB高的一半∆CHG的高为∆BCD高的一半∴S�AEF=14S�ADB S�CHG=14S�CDB同理:S�DEH=14S�DAC S�BFG=14S�BCA∴S四边形EFGH=S四边形ABCD−S�AEF−S�CHG−S�DEH−S�BFG=12S四边形ABCD;(2)解:①连接AC 取AC的中点E 连接FE HE∵点E F为AC AB的中点∴EF=12BC=2同理:EH=12AD=3第 31 页 共 31 页 ∴EH-EF<FH<EF+EH即1<EH<5故答案为:1<FH<5;②如图所示 连接EFGH 由结论1可得四边形EFGH 为平行四边形如图所示 过点E 作EM ∥FH 交GH 延长线于点M 过点G 作GN ⊥EM∵EF ∥GM EM ∥FH∴四边形FHME 为平行四边形∴FH=EM=6 ∠EOF=∠GEM=60° FE=HM∴∠EGN=30°∴EN=12EG =4∴GN =√EG 2−EN 2=4√3∴S �EGM =12EM ×GN =12√3由图可得S 四边形EFGH =S �EGM =12√3由结论3可得:S 四边形ABCD =2S 四边形EFGH =24√3.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
数学模型应用问题(习题)
➢例题示范
例1:为支持抗震救灾,某市A,B,C 三地现在分别有赈灾物资100 吨、100 吨、80 吨,需要全部运往重灾地区的D,E 两县.根据灾区的情况,这批赈灾物资运往 D 县的数量比运往E 县的数量的 2 倍少 20 吨.
(1)求这批赈灾物资运往 D,E 两县的数量各是多少.
(2)若要求 C 地运往 D 县的赈灾物资为 60 吨,A 地运往 D 县的赈灾物资为x 吨(x 为整数),B 地运往D县的赈灾物资数量小于 A 地运往D 县的赈灾物资数量的2 倍.其余的赈灾物资全部运往E 县,且B 地运往 E 县的赈灾物资数量不超过
23 吨,则 A,B 两地的赈灾物资运往 D,E 两县的方案有几种?请你
写出具体的运送方案.
(3)已知 A,B,C 三地的赈灾物资运往 D,E 两县的费用如下表:
的总费用最多是多少?
1 / 7
2 / 7
【解题要点】
①理解题意,梳理信息列表
梳理信息,如下:
②辨识类型,建立模型
关键词“全部运往”、“小于”、“不超过”,确定属于方程不等式类型.
隐性条件:运送赈灾物资均为正整数.
③求解验证,回归实际
根据关键词列等式、不等式,求解.验证结果是否符合实际.
【过程示范】
解:(1)设运往 E 县的物资为 m 吨,则运往 D 县的物资为 (2m -20)吨.根据题意得,m +2m -20=100+100+80
解得,m =100
2×100-20=180(吨)
∴运往 E 县的物资为 100 吨,运往 D 县的物资为 180 吨.
120 x
2x (2)根据题意得, x
解得, 40 x ≤ 43
∵x 是正整数
∴x 可取 41,42,43
运送方案如下, 方
案一:
方案二:
A 地
B 地
C 地
运往 D 县
42 78 60 运往 E 县 58 22 20
A 地 100
B 地 100
C 地 80 180 运往
D 县 的费用 220·x 200·(120-x ) 200×60 100 运往
E 县 的费用 250·(100-x ) 220·(x -20) 210×20 A 地 B 地 C 地 运往 D 县 41 79 60
运往 E 县 59 21 20
方案三:
(3)设运送总费用为w 元,根据题意得,
w=220x+250(100-x)+200(120-x)+220(x-20)+200×60+210×20
=-10x+60 800
∵-10<0
∴w 随x 的增大而减小
∴当x=41 时,w max=60 390(元)
∴该公司承担运送物资的总费用最多是 60 390 元.
➢巩固练习
1.某服装公司招工广告承诺:熟练工人每月工资至少 3 000 元.每天工
作 8 小时,一个月工作 25 天.月工资底薪 800 元,另加计件工资.加工 1 件A 型服装计酬 16 元,加工 1 件B 型服装计酬 12 元.在工作中发现一名熟练工加工 1 件A 型服装和2 件B 型服装需 4 小时,加工 3 件A 型服装和 1 件B 型服装需 7 小时.(工人月工资=底薪+计件工资)
(1)一名熟练工加工 1 件 A 型服装和 1 件B 型服装各需要多少小时?
(2)一段时间后,公司规定:“每名工人每月必须加工 A,
B 两种型号的服装,且加工 A 型服装数量不少于 B 型服装的一半”.
设一名熟练工人每月加工 A 型服装a 件,工资总额为w 元.请你运用所学知识判断该公司在执行规定后是否违背了广告承诺?
【列表分析】
【解题过程】
3 / 7
2.在“绿满河南”行动中,某社区计划对面积为 1 800 m2 的区域进行绿
化.经投标,由甲、乙两个工程队来完成,已知甲队工作3 天,乙队工作 2 天共可完成 400 m2,甲队工作 1 天,乙队工作 4 天共可完成 300 m2.
(1)求甲、乙两工程队每天能完成绿化的面积.
(2)设甲工程队施工x 天,乙工程队施工y 天,刚好完成绿化任务,求y 与x 的函数解析式.
(3)若甲队每天绿化费用为 0.6 万元,乙队每天绿化费用为
0.25 万元,且甲、乙两队施工的总天数不超过 26 天,则如何安排甲、
乙两队施工的天数,才能使施工总费用最低?并求出最低费用.
【列表分析】
【解题过程】
4 / 7
3.某镇水库的可用水量为12 000 万立方米,假设年降水量不变,能维持该
镇 16 万人 20 年的用水量.为实施城镇化建设,新迁入了 4 万人后,水库只能维持居民 15 年的用水量.
(1)该镇年降水量以及每人年平均用水量分别是多少立方米?
(2)政府号召节约用水,希望将水库的使用年限提高到25 年,则该镇居民人均每年需节约多少立方米的水才能实现目标?
(3)某企业投入 1 000 万元购买设备,每天能淡化 5 000 立方米海水,淡化率为 70%.每淡化 1 立方米海水所需的费用为 1.5 元,政府补贴0.3 元.企业将淡化水以3.2 元/立方米的价格出售,每年还需各项支出 40 万元.按每年实际生产 300 天计算,该企业至少几年后才能收回成本?(结果精确到个位)
【列表分析】
【解题过程】
➢思考小结
应用题中建立数学模型往往要考虑两方面:
①题目当中明确指出的数学关系,常和关键词相关;
②隐含的数学关系,往往结合实际情况考虑,常见的有非负数、整数
等制约条件.
5 / 7
【参考答案】
1.(1)一名熟练工加工 1 件A 型服装需要 2 小时,加工 1 件B
型服装需要 1 小时.
(2)该公司在执行规定后违背了广告承诺,理由略.
2.(1)甲队每天能完成绿化的面积是 100 m2,乙队每天能完成绿化的面
积是 50 m2.
(2)y=-2x+36(0<x<18 且x 为整数).
(3)安排甲队施工10 天,乙队施工16 天,施工总费用最低,最低费用为10 万元.
3.(1)该镇年降水量是 200 万立方米,每人年平均用水量是 50
立方米.
(2)该镇居民人均每年需节约 16 立方米的水才能实现目标.
7 / 7。
