噪声估计的算法及MATLAB实现
matlab实现噪声中正弦信号相位估计仿真
噪声中正弦信号相位的估计问题
设观测数据为
x(n)=Acos(2πf0n+φ)+w(n),n=0,1,2,...，N-1
式中，w（n）为已知方差σ的高斯白噪声，正弦信号的幅度A和频率f0为已知。
一种估计2
φ的估计量为
N-1⎧⎡N-1⎤⎫φ=-Im⎨ln⎢∑x(n)cos(2πf0n)+j∑x(n)sin(2πf0n)⎥⎬ n=0⎦⎭⎩⎣n=0∧A2
定义信噪比为SNR=。
令A=1，f0=0.05，φ=π/3，N=256。
22σ
（1）产生服从特定概率分布的观测数据x（n）；
（2）利用估计算法计算估计量φ；
（3）上述过程重复M次，产生M个φ的实现
（4）利用μ∧=θ∧∧∧1M
1θi确定估计量的均值。
∑i=1M∧（5）利用σ∧=θ2M(θ-μθ)确定估计量的方差。
∑i∧M∧∧∧2=1
（6）利用直方图来确定PDF：首先计算落入某指定区间的次数，然后再除以总的实现次数得到概率，再除以区间长度得到PDF估计。
利用matlab仿真得到的PDF估计如图1所示。
图1 估计量φ的PDF估计
对不同的信噪比（SNR）情况进行Monte Carlo仿真，在此我们令SNR从-20（dB）取到10（dB），步进值为2。
将估计量的方差与SNR画在同一图上，如图2所示。
∧
从图中我们可以看出，估计量的结果φ的方差随着SNR增大而减小。
当SNR减小到一定程度时，方差会突然增大很多。
这是因为随着信噪比的减小，我们通过采集得到的信号主要成分为白噪声，因此其方差会很大。
∧
图2 估计量φ的方差与SNR的关系∧。
Matlab信号添加噪声及信噪比SNR的计算
Matlab信号添加噪声及信噪比SNR的计算一、MATLAB中自带的高斯白噪声的两个函数MATLAB中产生高斯白噪声非常方便，可以直接应用两个函数，一个是WGN，另一个是AWGN。
WGN用于产生高斯白噪声，AWGN则用于在某一信号中加入高斯白噪声。
1. WGN：产生高斯白噪声y = wgn(m,n,p) 产生一个m行n列的高斯白噪声的矩阵，p以dBW为单位指定输出噪声的强度。
y = wgn(m,n,p,imp) 以欧姆(Ohm)为单位指定负载阻抗。
y = wgn(m,n,p,imp,state) 重置RANDN的状态。
在数值变量后还可附加一些标志性参数：y = wgn(…,POWERTYPE) 指定p的单位。
POWERTYPE可以是'dBW', 'dBm'或'linear'。
线性强度(linear power)以瓦特(Watt)为单位。
y = wgn(…,OUTPUTTYPE) 指定输出类型。
OUTPUTTYPE可以是'real'或'complex'。
2. AWGN：在某一信号中加入高斯白噪声y = awgn(x,SNR) 在信号x中加入高斯白噪声。
信噪比SNR以dB为单位。
x的强度假定为0dBW。
如果x是复数，就加入复噪声。
y = awgn(x,SNR,SIGPOWER) 如果SIGPOWER是数值，则其代表以dBW为单位的信号强度；如果SIGPOWER为'measured'，则函数将在加入噪声之前测定信号强度。
y = awgn(x,SNR,SIGPOWER,STATE) 重置RANDN的状态。
y = awgn(…,POWERTYPE) 指定SNR和SIGPOWER的单位。
POWERTYPE可以是'dB'或'linear'。
如果POWERTYPE是'dB'，那么SNR以dB为单位，而SIGPOWER以dBW为单位。
matlab信噪比估计程序
%----------- 函数ML_Estimation -------------clc;clear all;Nt=1; %仿真次数M=8; %MPSKNsym=64; %信源仿真符号数Nss=16; %上采样点数Es=1; %每符号能量snr=1:30; %仿真信噪比范围rho=10.^(snr/10); %实际信噪比大小%sigma=sqrt(1/2)*(10.^(-snr/20)); %噪声根方差No=Es./rho;rho_ml=zeros(length(snr),Nt); %估计信噪比存储器,一列对应一次仿真，一行对应一个SNR值for time=1:Nt %仿真循环Nt次d=randint(1,Nsym,[0 M-1]); %产生Nsym个随机数作为信源符号a_n=exp(j*(2*pi/M*d+pi/M)); %构成MPSK调制符号figure(1);plot_astrology(real(a_n),imag(a_n));b_k=zeros(1,Nss*Nsym);n=1:Nss:length(b_k);b_k(n)=a_n;%b_k=upsample(a_n,Nss); %上采样，每符号取Nss个采样点%hrcos=firrcos(256,1,1,16,'sqrt'); %成型滤波器，采用RRC方式，阶数127，滚将系数0.5%gk=conv(hrcos,hrcos);hrcos=rcosflt(1,1,16,'sqrt',0.5,3);sum3=0;for i=1:length(hrcos)sum3=sum3+hrcos(i)^2;endh_k=hrcos/sqrt(sum3);m_k=conv(b_k,h_k); %序列成型L=length(m_k); %成型后的数据总长度K=Nss*Nsym;%s1=0; s2=0;for k=1:length(snr) %计算每个信噪比对应的信噪比估计值%r_k=m_k+No(k)*(randn(1,L)+j*randn(1,L));%r_k=m_k+nb(k)/sqrt(2)*(randn(1,L)+j*randn(1,L));%r_k=sqrt(Es)*m_k+sqrt(No(k))/sqrt(2)*(randn(1,L)+j*randn(1,L)); %往信号中加入高斯白噪声r_k=awgn(m_k,snr(k),'measured');y_k=conv(r_k,h_k);y_n=y_k(112+1:Nss:(length(y_k)-112));figure(2);plot_astrology(real(y_n),imag(y_n));s1=0; s2=0;for l=1:K %公式中两个求和因子计算s1=s1+real(conj(r_k(l))*m_k(l));s2=s2+abs(r_k(l))^2;endrho_ml(k,time)=(Nss^2)*(s1^2)/(K^2)/(s2/(K-1.5)-(Nss*(s1^2)/K/(K-1.5))); %代入公式计算信噪比估计值% Pe=[Pe mean((rho_ml-rho(k)).^2)/(rho(k).^2)];endendNMSE=2./rho/Nsym+1/Nss/Nsym; %克拉美罗界计算 CRBfigure(3);semilogy(snr,NMSE,'-b*');hold on,grid on;for i=1:length(snr)sum1=0;for j=1:Ntsum1=sum1+(rho_ml(i,j)-rho(i)).^2;endpe(i)=sum1./(rho(i).^2)/Nt/K; %归一化均方误差 NMSEendsemilogy(snr,pe,'-r*');grid on;（注：文档可能无法思考全面，请浏览后下载，供参考。
MATLAB对语音信号加随机噪声及去噪程序
subplot(2,2,3);plot(y_z);
title('滤波前信号的波形')
subplot(2,2,4);plot(x);
title('滤波后信号的波形')
%sound(x,fs,bits)%回放滤波后的音频
设计滤波器：
器常用的方法有：脉冲响应不变法和双线性变换法。
xlabel('时间轴')
ylabel('幅值A')
subplot(2,1,2);
plot(f,abs(y_zp(1:n/2)));%加噪语音信号的频谱图
title('加噪语音信号频谱图');
xlabel('频率Hz');
ylabel('频率幅值');
对加噪的语音信号进行去噪程序如下：
fp=1500;fc=1700;As=100;Ap=1;
%sound(y_z,fs)
%对加噪后的语音信号进行分析
n=length(y);%选取变换的点数
y_zp=fft(y_z,n);%对n点进行傅里叶变换到频域
f=fs*(0:n/2-1)/n;%对应点的频率
figure(2)
subplot(2,1,1);
plot(y_z);%加噪语音信号的时域波形图
title('加噪语音信号时域波形');
figure(3);
freqz(b,1);
（此前为低通滤波器设计阶段）——接下来为去除噪声信号的程序——
x=fftfilt(b,y_z);
X=fft(x,n);
figure(4);
有效感觉噪声级计算及MATLAB GUI实现
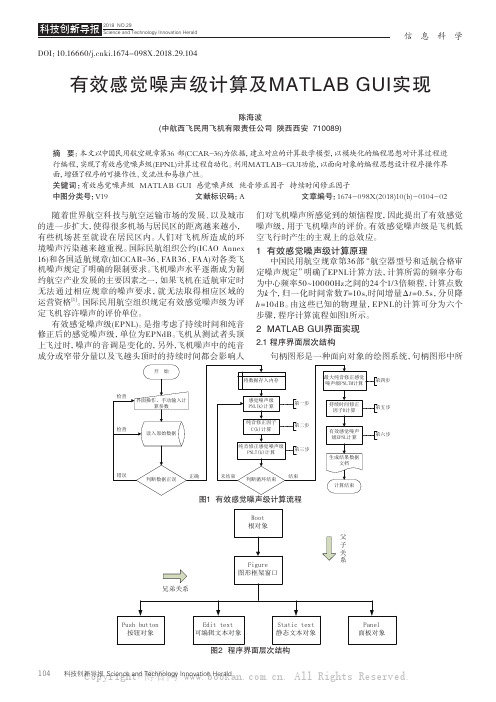
信息科学科技创新导报 Science and Technology Innovation Herald104DOI：10.16660/ki.1674-098X.2018.29.104有效感觉噪声级计算及MATLAB GUI实现陈海波(中航西飞民用飞机有限责任公司 陕西西安 710089)摘 要：本文以中国民用航空规章第36 部(CCAR -36)为依据，建立对应的计算数学模型，以模块化的编程思想对计算过程进行编程，实现了有效感觉噪声级(EPNL)计算过程自动化。
利用MATLAB-GUI功能，以面向对象的编程思想设计程序操作界面，增强了程序的可操作性、交流性和易推广性。
关键词：有效感觉噪声级 MATLAB GUI 感觉噪声级 纯音修正因子 持续时间修正因子中图分类号：V19 文献标识码：A 文章编号：1674-098X(2018)10(b)-0104-02随着世界航空科技与航空运输市场的发展、以及城市的进一步扩大，使得很多机场与居民区的距离越来越小，有些机场甚至就设在居民区内。
人们对飞机所造成的环境噪声污染越来越重视。
国际民航组织公约(ICAO Annex 16)和各国适航规章(如CCAR-36、FAR36、FAA)对各类飞机噪声规定了明确的限制要求。
飞机噪声水平逐渐成为制约航空产业发展的主要因素之一，如果飞机在适航审定时无法通过相应规章的噪声要求，就无法取得相应区域的运营资格[1]。
国际民用航空组织规定有效感觉噪声级为评定飞机容许噪声的评价单位。
有效感觉噪声级(EPNL)。
是指考虑了持续时间和纯音修正后的感觉噪声级，单位为EPNdB。
飞机从测试者头顶上飞过时，噪声的音调是变化的，另外，飞机噪声中的纯音成分或窄带分量以及飞越头顶时的持续时间都会影响人们对飞机噪声所感觉到的烦恼程度，因此提出了有效感觉噪声级，用于飞机噪声的评价。
有效感觉噪声级是飞机低空飞行时产生的主观上的总效应。
1 有效感觉噪声级计算原理中国民用航空规章第36部“航空器型号和适航合格审定噪声规定”明确了EPNL计算方法，计算所需的频率分布为中心频率50~10000Hz之间的24个1/3倍频程，计算点数为k 个，归一化时间常数T =10s,时间增量Δt =0.5s，分贝降h =10dB。
噪声方差软解调matlab -回复
噪声方差软解调matlab -回复噪声方差软解调是一种常见的信号处理技术，广泛应用于通信、雷达、图像处理等领域。
在这篇文章中，我们将详细介绍噪声方差软解调的原理和实现方法，并使用MATLAB进行演示和实践。
一、噪声方差软解调原理在通信系统中，信号的传输过程中会受到各种噪声的干扰，这些噪声将导致信号的失真和误判。
噪声方差软解调是一种基于噪声方差估计的信号解调方法，通过对接收信号进行合适的滤波和处理，可以有效地减小噪声的影响，提高信号的恢复质量。
噪声方差软解调的原理可以简单地概括为以下几个步骤：1. 接收信号采样：从信道中接收到的模拟信号首先需要进行采样，将连续的模拟信号转换为离散的数字信号。
采样过程中，要根据信号的带宽和采样频率进行适当的选择，以避免信号信息的失真。
2. 解调器设计：根据所要解调的信号类型和性质，设计相应的解调器。
解调器可以是模拟电路或数字电路，其功能是将接收到的信号转换为原始信号。
对于噪声方差软解调而言，解调器通常包括滤波和信号处理等部分。
3. 滤波处理：在接收信号中，噪声是不可避免的。
为了减小噪声对信号的干扰，需要对接收信号进行滤波处理。
滤波的基本原理是利用滤波器抑制噪声频率分量，从而增强信号的有效部分。
噪声方差软解调中常用的滤波器有FIR滤波器和IIR滤波器等。
4. 噪声方差估计：在滤波处理后，噪声仍然存在。
为了更好地进行信号解调，需要对噪声进行估计和量化。
噪声方差估计是通过一定的统计方法来对噪声进行建模和估计，从而获取噪声的统计特性和参数。
5. 软解调：基于噪声方差估计的结果，进行软解调操作。
软解调通常采用最大似然估计（Maximum Likelihood Estimation,MLE）或最小均方误差（Minimum Mean Square Error,MMSE）等方法，以降低噪声对信号恢复的影响。
软解调可以通过调整解调器的参数来实现。
二、MATLAB实现噪声方差软解调在MATLAB中，可以使用一系列信号处理工具箱和函数来实现噪声方差软解调。
数字图像去噪典型算法及matlab实现
图像去噪是数字图像处理中的重要环节与步骤。
去噪效果的好坏直接影响到后续的图像处理工作如图像分割、边缘检测等。
图像信号在产生、传输过程中都可能会受到噪声的污染，一般数字图像系统中的常见噪声主要有：高斯噪声（主要由阻性元器件内部产生）、椒盐噪声（主要是图像切割引起的黑图像上的白点噪声或光电转换过程中产生的泊松噪声）等；目前比较经典的图像去噪算法主要有以下三种：均值滤波算法：也称线性滤波，主要思想为邻域平均法，即用几个像素灰度的平均值来代替每个像素的灰度。
有效抑制加性噪声，但容易引起图像模糊，可以对其进行改进，主要避开对景物边缘的平滑处理。
中值滤波：基于排序统计理论的一种能有效抑制噪声的非线性平滑滤波信号处理技术。
中值滤波的特点即是首先确定一个以某个像素为中心点的邻域，一般为方形邻域，也可以为圆形、十字形等等，然后将邻域中各像素的灰度值排序，取其中间值作为中心像素灰度的新值，这里领域被称为窗口，当窗口移动时，利用中值滤波可以对图像进行平滑处理。
其算法简单，时间复杂度低，但其对点、线与尖顶多的图像不宜采用中值滤波。
很容易自适应化。
Wiener维纳滤波：使原始图像与其恢复图像之间的均方误差最小的复原方法，是一种自适应滤波器，根据局部方差来调整滤波器效果。
对于去除高斯噪声效果明显。
实验一：均值滤波对高斯噪声的效果代码I=imread('C:\Documents and Settings\Administrator\桌面\1.gif');%读取图像J=imnoise(I,'gaussian',0,0.005);%加入均值为0，方差为0.005的高斯噪声subplot(2,3,1);imshow(I);title('原始图像');subplot(2,3,2); imshow(J);title('加入高斯噪声之后的图像');%采用MATLAB中的函数filter2对受噪声干扰的图像进行均值滤波K1=filter2(fspecial('average',3),J)/255; %模板尺寸为3K2=filter2(fspecial('average',5),J)/255;% 模板尺寸为5K3=filter2(fspecial('average',7),J)/255; %模板尺寸为7K4= filter2(fspecial('average',9),J)/255; %模板尺寸为9 subplot(2,3,3);imshow(K1);title('改进后的图像1');subplot(2,3,4); imshow(K2);title('改进后的图像2');subplot(2,3,5);imshow(K3);title('改进后的图像3');subplot(2,3,6);imshow(K4);title('改进后的图像4');PS：filter2用法fspecial函数用于创建预定义的滤波算子，其语法格式为：h = fspecial(type)h = fspecial(type,parameters)参数type制定算子类型，parameters指定相应的参数，具体格式为：type='average'，为均值滤波，参数为n，代表模版尺寸，用向量表示，默认值为[3,3]。
matlab 中mmse 噪声方差估计
一、matlab 中MMSE 噪声方差估计的背景在数字通信系统中，噪声方差的准确估计对于信号的处理和系统性能至关重要。
MMSE（最小均方误差）是一种常用的估计方法，它可以在一定程度上降低估计误差，提高系统的性能。
二、MMSE 噪声方差估计原理1. MMSE 估计的目标MMSE 估计的目标是找到最优的估计值以最小化均方误差。
对于噪声方差的估计，我们希望找到一个估计值能够最小化观测信号与真实信号之间的均方误差。
2. MMSE 噪声方差估计的数学构建MMSE 噪声方差估计通过建立一个估计函数来得到噪声方差的估计值。
在数字通信系统中的信号通常是通过传感器采集得到的，这些信号受到了噪声的影响。
假设我们观测到的信号为 y，真实信号为 x，噪声方差为σ^2，则观测信号与真实信号的关系可以表示为 y = x + n，其中 n 表示噪声信号。
通过最小化估计信号与观测信号之间的均方误差，就可以得到最小均方误差估计。
三、matlab 中的 MMSE 噪声方差估计实现1. MMSE 估计的函数matlab 中提供了用于执行 MMSE 噪声方差估计的函数，可以使用“mmsest”命令来实现。
这个函数可以通过输入观测信号 y 来估计噪声方差的值。
该函数还可以指定其他参数，以适应不同的信号特性和系统需求。
2. MMSE 估计的实例下面是一个简单的例子，展示了如何在matlab 中使用“mmsest”函数进行噪声方差的估计：```matlab生成观测信号y = randn(100,1);估计噪声方差sigma_sq = mmsest(y);```这段代码中，我们首先生成了一个长度为 100 的观测信号 y，然后使用“mmsest”函数对观测信号进行了噪声方差的估计。
四、MMSE 噪声方差估计的应用1. 通信系统中的应用在数字通信系统中，MMSE 噪声方差估计可以用于信道估计、自适应滤波、功率分配等方面。
通过准确估计信道的噪声方差，可以提高信号的可靠性和系统的性能。
噪声估计的算法及MATLAB实现
太原理工大学毕业设计（论文）任务书噪声估计算法的研究及MATLAB仿真摘要日常的通信过程中,语音会常常受到环境噪声的干扰而使通话质量下降,严重时使得语音处理系统不能正常工作。
因此,必须采用信号处理方法通过语音增强来抑制背景噪声从而提高语音通信质量,而噪声估计的准确性又直接影响语音的增强效果。
可见,噪声估计是语音增强的一个非常重要的部分,所以研究噪声估计算法有很好的实用价值。
本文主要研究两种噪声估计算法:基于最小统计和最优平滑的噪声估计算法和最小值控制递归平均法的噪声估计算法,通过实验仿真比较最终研究了一种改进的最小值统计量控制递归平均噪声估计算法。
本文的主要工作总结归纳为以下几方面：首先,本文对几种经典的噪声估计算法进行研究,了解它们的各自优缺点,在此基础上选定两种较好的算法进行具体分析。
其次,了解最小统计和最优平滑和噪声功率谱统计跟踪的噪声估计算法的原理,它的基本思路是先用最优平滑滤波器对带噪语音的功率谱滤波,得到一个噪声的粗略估计，然后找出粗略估计噪声中的在一定时间窗内的最小值，对这个最小值进行一些偏差修正，即得到所要估计的噪声的方差。
通过MATLAB仿真看其特征。
再次,本文研究了一种改进的最小统计法。
算法采用递归平均进行噪声估计，其递归平均的平滑量控制递归平均噪声估计算因子受语音存在概率控制，而语音存在概率的计算采用了两次平滑和最小统计量跟踪。
与I．Cohen提出的IMCRA 算法相比，本文采用了一种快速有效的最小统计量跟踪算法。
仿真结果表明：在非平稳噪声条件下，该算法具有较好的噪声跟踪能力和较小的噪声估计误差，可以有效地提高语音增强系统的性能。
最后,对整体论文总结,通过研究发现改进的最小统计量控制递归平均噪声算法在IMCRA算法的基础上,采用了一种简单有效地最小统计量估计算法,在保证噪声估计准确性的同时,减小了算法的复杂度。
同时,基于这种噪声估计的语音增强系统能有效地提高增强语音的信噪比,并且能有效地消除增强语音中的音乐噪声。
Matlab中的信号加噪处理技巧
Matlab中的信号加噪处理技巧导言：在现代的信息传输、储存和处理中，信号的质量是至关重要的。
然而，在现实世界中，信号通常会受到各种噪声的干扰。
为了最大程度地提高信号的清晰度和准确性，信号加噪处理技巧在信号处理领域中起着至关重要的作用。
这篇文章将介绍Matlab中一些常用的信号加噪处理技巧，并探讨它们的原理和应用。
一、信号加噪的背景和概述1.1 什么是信号加噪？信号加噪是指在原始信号中添加噪声的过程。
噪声可以是由于电磁波、电磁辐射、传输信道等原因引起的随机干扰。
信号加噪处理的目标是去除或降低噪声对信号的影响，以提高信号的质量和可靠性。
1.2 信号加噪的意义和应用信号加噪处理技巧在很多领域都有广泛的应用。
在通信领域中，信号加噪处理可以提高通信系统的抗干扰能力和传输质量。
在音频和图像处理领域中，信号加噪处理可以提高音频和图像的清晰度和准确性。
此外，在生物医学领域和物理实验中，信号加噪处理也是必不可少的。
二、2.1 生成噪声信号在进行信号加噪处理之前，首先需要生成噪声信号。
Matlab提供了一些内置函数和工具箱，用于生成各种类型的噪声信号，如高斯噪声、均匀噪声、脉冲噪声等。
这些函数和工具箱提供了丰富的参数选项，可以根据实际需求生成符合要求的噪声信号。
2.2 信号加噪处理方法Matlab中有多种信号加噪处理方法，常用的包括滤波、降噪算法和频谱分析等。
滤波是最常用的信号加噪处理方法之一。
信号滤波可以通过去除噪声频率成分或减小噪声幅度来降低噪声的影响。
Matlab提供了多种滤波器设计工具和函数，如FIR滤波器、IIR滤波器等，可以根据具体需求选择合适的滤波器进行信号滤波。
除了滤波之外，降噪算法也是一种常用的信号加噪处理方法。
主要有小波降噪、自适应滤波等算法。
这些算法基于信号的统计特性和噪声的模型，通过一系列数学运算来估计和去除噪声成分。
Matlab提供了丰富的函数和工具箱，用于实现这些降噪算法。
频谱分析是用于分析信号频率特性的方法，也可以用于信号加噪处理。
bm3d matlab代码
bm3d matlab代码BM3D是一种基于图像处理的算法，它能够有效地去除图像中的噪声，并提取出清晰而细节丰富的图像。
本文将详细介绍BM3D算法的原理、流程和实现过程，并通过实例演示其在图像去噪中的应用。
一、BM3D算法原理BM3D算法的全称是Block Matching 3D，它利用图像中的块匹配和三维变换来消除噪声。
其原理可以分为以下几个步骤：1. 分块：将待处理的图像分成多个块状区域，每个区域包含一定数量的像素点。
2. 相似性匹配：对每个块状区域进行相似性匹配，即在图像的整个区域中寻找与当前块状区域相似的块。
这一步骤的目的是找到与当前块状区域具有相近特征的块，以便于后续的噪声估计和去噪处理。
3. 三维变换：对匹配到的相似块进行三维变换，将其转换为一个三维频域表示。
这个变换过程可以提取出块状区域中的结构信息，并将其划分为平坦信号和纹理信号。
4. 噪声估计：通过计算平坦信号的方差来估计块状区域中的噪声水平。
这一步骤的目的是准确估计出噪声的分布，并作为后续去噪处理的依据。
5. 非线性滤波：对纹理信号进行非线性滤波处理，以降低噪声的影响。
BM3D算法通过分阶段的修复方法来提高图像的质量，其中包括去除噪声和恢复细节。
二、BM3D算法流程BM3D算法的流程可以总结为以下几个步骤：1. 图像预处理：对待处理图像进行预处理，例如灰度化处理和归一化处理，以便于后续操作的进行。
2. 分块和相似性匹配：将预处理后的图像分成多个块状区域，并对每个区域进行相似性匹配，以找到与之相似的块。
3. 三维变换：对匹配到的相似块进行三维变换，将其转换为频域表示，并提取出频谱信息。
4. 噪声估计：通过计算平坦信号的方差来估计每个块状区域中的噪声水平。
5. 非线性滤波：对纹理信号进行非线性滤波处理，以降低噪声的影响，并恢复图像的细节。
6. 后处理：对滤波后的图像进行后处理操作，例如反变换、色彩空间转换等，以得到最终的去噪图像。
使用MATLAB进行图像去噪处理的基本原理
使用MATLAB进行图像去噪处理的基本原理图像去噪处理是数字图像处理的一个重要领域，它的目标是从图像中去除噪声，提高图像的质量和清晰度。
在实际应用中，图像往往会受到各种因素的影响而产生噪声，如传感器噪声、信号传输中的干扰等。
为了准确地还原图像的细节和信息，我们需要使用一些图像处理算法，而MATLAB作为一种强大的数学软件，提供了丰富的图像处理工具箱，可以帮助我们实现图像去噪处理。
在使用MATLAB进行图像去噪处理之前，首先需要了解一些基本的原理和概念。
图像噪声可以分为两种类型：加性噪声和乘性噪声。
加性噪声是指噪声与原始图像的像素值相加，而乘性噪声是指噪声与原始图像的像素值相乘。
常见的加性噪声有高斯噪声、盐噪声和椒盐噪声，而乘性噪声则包括了泊松噪声等。
对于加性噪声的去噪处理，最常用的方法是使用滤波器。
滤波器可以通过对图像进行空间域或频域的操作，抑制噪声的同时保留图像的细节。
在MATLAB中，我们可以使用各种滤波器函数，如均值滤波器、中值滤波器、高斯滤波器等。
这些滤波器可以通过对图像的像素进行加权平均、中值选取或高斯加权等方式，来实现对噪声的抑制。
而对于乘性噪声的去噪处理，一种常用的方法是使用非线性滤波器。
非线性滤波器可以通过对图像的像素进行非线性变换，来抑制噪声并保留图像的细节。
在MATLAB中，我们可以使用一些非线性滤波器函数，如中值滤波器、双边滤波器等。
这些滤波器通过对图像的像素进行排序、加权平均等方式，来实现对噪声的抑制。
除了滤波器方法，MATLAB还提供了其他一些图像去噪处理的算法。
例如，基于小波变换的去噪方法可以通过对图像的小波系数进行阈值处理，来实现对噪声的抑制。
MATLAB中的小波变换函数可以将图像分解为不同尺度的频带，然后通过对各个频带的小波系数进行阈值处理，来实现去噪处理。
此外，MATLAB还提供了一些基于统计学原理的去噪方法。
例如，基于最小均方误差的去噪方法可以通过对图像的像素进行统计分析，来估计噪声的概率分布，并通过最小化均方误差的方式，来实现对噪声的抑制。
matlab11种数字信号滤波去噪算法
matlab11种数字信号滤波去噪算法Matlab是一种强大的数学软件，广泛应用于信号处理领域。
在数字信号处理中，滤波去噪是一个重要的任务，可以提高信号的质量和准确性。
本文将介绍Matlab中的11种数字信号滤波去噪算法。
1. 均值滤波：该算法通过计算信号中一定窗口内的像素平均值来去除噪声。
它适用于高斯噪声和椒盐噪声的去除。
2. 中值滤波：该算法通过计算信号中一定窗口内的像素中值来去除噪声。
它适用于椒盐噪声的去除。
3. 高斯滤波：该算法通过对信号进行高斯模糊来去除噪声。
它适用于高斯噪声的去除。
4. 维纳滤波：该算法通过最小均方误差准则来估计信号的真实值，并去除噪声。
它适用于高斯噪声的去除。
5. 自适应滤波：该算法通过根据信号的局部特性来调整滤波器的参数，从而去除噪声。
它适用于非线性噪声的去除。
6. 小波去噪：该算法通过将信号分解为不同频率的小波系数，并对系数进行阈值处理来去除噪声。
它适用于各种类型的噪声的去除。
7. Kalman滤波：该算法通过对信号进行状态估计和观测更新来去除噪声。
它适用于线性系统的去噪。
8. 粒子滤波：该算法通过使用一组粒子来估计信号的状态，并通过重采样来去除噪声。
它适用于非线性系统的去噪。
9. 线性预测滤波：该算法通过使用线性预测模型来估计信号的未来值，并去除噪声。
它适用于平稳信号的去噪。
10. 自适应线性组合滤波：该算法通过对信号进行线性组合来估计信号的真实值，并去除噪声。
它适用于各种类型的噪声的去除。
11. 稀疏表示滤波：该算法通过使用稀疏表示模型来估计信号的真实值，并去除噪声。
它适用于各种类型的噪声的去除。
以上是Matlab中的11种数字信号滤波去噪算法。
每种算法都有其适用的场景和优缺点，根据具体的信号和噪声类型选择合适的算法进行去噪处理。
Matlab提供了丰富的函数和工具箱，可以方便地实现这些算法，并对信号进行滤波去噪。
通过合理选择和组合这些算法，可以有效提高信号的质量和准确性，为后续的信号处理任务提供更好的基础。
复高斯噪声下基于功率谱的频率估计与MATLAB仿真
复高斯噪声下基于功率谱的频率估计与MATLAB仿真摘要:频率估计是信息科学在信号处理领域的一个重要组成部分，在许多实际信号处理应用中具有非常重要的地位，且己广泛应用于雷达、地震、生物医学、语音处理和故障诊断等领域。
本文对几种常用的频率估计方法进行了回顾，简单介绍了其中两种频率估计方法的原理;并应用最大似然、MUSIC算法对复高斯白噪声下信号的频率进行估计,并给出了计算机matlaB仿真结果，并对各种方法估计结果进行了比较。
关键词:频率估计;最大似然;复高斯白噪声Frequency estimation based on power spectrum in WGN andMATLAB simulationDu Yang 201321010408(School of Communication and Information Engineering, University of Electronic Science and Technology of China Chengdu610054)Abstract: frequency estimation is a significant component in thefield of signal processing in communication science, which is rather vital in the case of processing actual signal. It has been widely applied in the field of radar, earthquake, biomedicine, speech processing, and fault diagnosis n. In this paper, some common methods of frequency estimation will be reviewed at first. Then, the principals of two of these methods will be introduced in detail. Subsequently, the writer will use maximum likelihood method and MUSIC method to estimatethe frequency of signal that is in the circumstance of complex white Gauss noise and receive some matlaB simulation results. Lastly, we will compare the consequences of different ways.Keywords: frequency estimation; maximum likelihood; WGN1 引言1.1 论文研究背景频率是参量估计中的一个重要物理量。
MATLAB中的信号噪声分析与处理方法
MATLAB中的信号噪声分析与处理方法一、引言信号噪声是在实际工程应用中普遍存在的问题，噪声会对信号的质量和准确性产生不良影响。
因此，对信号噪声进行分析和处理是非常重要的。
MATLAB作为一款强大的科学计算软件，提供了丰富的信号处理工具和算法，可以方便地进行信号噪声分析与处理。
本文将介绍一些常用的MATLAB工具和方法，帮助读者更好地处理信号噪声。
二、信号噪声分析在进行信号噪声分析之前，首先需要了解噪声的特性和类型。
常见的噪声类型有白噪声、高斯噪声、脉冲噪声等。
其中，白噪声是一种功率谱密度恒定的噪声，常用于模拟信号分析。
高斯噪声则符合正态分布特性，常用于数字信号处理。
脉冲噪声则表现为突然出现的噪声干扰。
对于信号噪声的分析，可以使用MATLAB中的频谱分析工具来实现。
例如，可以利用MATLAB中的fft函数对信号进行频谱分析，得到信号的功率谱密度。
通过观察功率谱密度图，可以清楚地看到信号的频域特性和噪声的功率分布情况。
此外，MATLAB还提供了丰富的统计工具，可以计算信号的均值、方差等统计参数，帮助进一步分析信号的噪声特性。
三、信号噪声处理1. 滤波方法滤波是一种常用的信号噪声处理方法，其目的是通过选择合适的滤波器对信号进行处理，抑制或消除噪声。
在MATLAB中，可以利用fir1、butter等函数来设计和应用滤波器。
滤波器可以分为低通滤波器、高通滤波器、带通滤波器和带阻滤波器等不同类型。
根据信号噪声的特点和需求，选择合适的滤波器类型是十分重要的。
例如，如果信号中的噪声主要集中在高频段，可以选择高通滤波器进行去噪处理。
2. 去噪算法除了滤波方法外，还有其他一些去噪算法可以应用于信号噪声处理。
例如，小波去噪算法是一种常用的信号去噪方法。
该算法通过对信号进行小波分解，并利用小波系数的特性进行噪声抑制。
MATLAB提供了丰富的小波变换函数和去噪函数，可以方便地进行信号去噪处理。
另外，独立分量分析（ICA）是一种基于统计的信号盲源分离方法，也可以用于信号噪声的降维和去噪。
matlab 环境降噪算法
matlab 环境降噪算法
在MATLAB环境中，降噪算法是一种用于处理信号的技术，可以帮助消除信号中的噪音和干扰。
在MATLAB中，有多种降噪算法可供选择，包括但不限于：
1. 统计降噪算法，包括均值滤波、中值滤波和高斯滤波等。
这些算法利用信号的统计特性来消除噪音。
2. 小波变换，小波变换是一种时频分析方法，可以将信号分解为不同频率的子信号，然后对每个子信号进行处理以实现降噪。
3. 自适应滤波，自适应滤波算法可以根据信号的特性来自动调整滤波器的参数，以适应不同的噪音类型和强度。
4. 卡尔曼滤波，卡尔曼滤波是一种递归滤波算法，常用于处理带有系统噪声的动态系统，可以用于降低噪音的影响。
在MATLAB中，这些降噪算法通常通过内置函数或者开源工具包来实现。
用户可以根据信号的特点和噪音类型选择合适的算法，并根据具体需求调整参数以实现最佳的降噪效果。
同时，MATLAB提供
了丰富的可视化和分析工具，可以帮助用户评估降噪效果并优化算法参数。
除了以上提到的算法，MATLAB还提供了各种其他降噪技术的实现，例如基于机器学习的降噪方法、频域滤波技术等。
用户可以根据具体的应用场景和信号特点选择合适的降噪算法，并利用MATLAB 强大的工具进行实现和优化。
常用的去噪方法
常用的数字图像去噪典型算法及matlab实现发表于603天前⁄图像处理⁄评论数1⁄被围观743views+图像去噪是数字图像处理中的重要环节和步骤。
去噪效果的好坏直接影响到后续的图像处理工作如图像分割、边缘检测等。
图像信号在产生、传输过程中都可能会受到噪声的污染，一般数字图像系统中的常见噪声主要有：高斯噪声（主要由阻性元器件内部产生）、椒盐噪声（主要是图像切割引起的黑图像上的白点噪声或光电转换过程中产生的泊松噪声）等；目前比较经典的图像去噪算法主要有以下三种：均值滤波算法：也称线性滤波，主要思想为邻域平均法，即用几个像素灰度的平均值来代替每个像素的灰度。
有效抑制加性噪声，但容易引起图像模糊，可以对其进行改进，主要避开对景物边缘的平滑处理。
中值滤波：基于排序统计理论的一种能有效抑制噪声的非线性平滑滤波信号处理技术。
中值滤波的特点即是首先确定一个以某个像素为中心点的邻域，一般为方形邻域，也可以为圆形、十字形等等，然后将邻域中各像素的灰度值排序，取其中间值作为中心像素灰度的新值，这里领域被称为窗口，当窗口移动时，利用中值滤波可以对图像进行平滑处理。
其算法简单，时间复杂度低，但其对点、线和尖顶多的图像不宜采用中值滤波。
很容易自适应化。
Wiener维纳滤波：使原始图像和其恢复图像之间的均方误差最小的复原方法，是一种自适应滤波器，根据局部方差来调整滤波器效果。
对于去除高斯噪声效果明显。
实验一：均值滤波对高斯噪声的效果代码I=imread('C:\Documents and Settings\Administrator\桌面\1.gif');%读取图像J=imnoise(I,'gaussian',0,0.005);%加入均值为0，方差为0.005的高斯噪声subplot(2,3,1);imshow(I);title('原始图像');subplot(2,3,2);imshow(J);title('加入高斯噪声之后的图像');%采用MATLAB中的函数filter2对受噪声干扰的图像进行均值滤波K1=filter2(fspecial('average',3),J)/255;%模板尺寸为3K2=filter2(fspecial('average',5),J)/255;%模板尺寸为5K3=filter2(fspecial('average',7),J)/255;%模板尺寸为7K4=filter2(fspecial('average',9),J)/255;%模板尺寸为9subplot(2,3,3);imshow(K1);title('改进后的图像1');subplot(2,3,4);imshow(K2);title('改进后的图像2');subplot(2,3,5);imshow(K3);title('改进后的图像3');subplot(2,3,6);imshow(K4);title('改进后的图像4');PS：filter2用法fspecial函数用于创建预定义的滤波算子，其语法格式为：h=fspecial(type)h=fspecial(type,parameters)参数type制定算子类型，parameters指定相应的参数，具体格式为：type=’average’，为均值滤波，参数为n，代表模版尺寸，用向量表示，默认值为[3,3]。
Matlab中的噪声去除算法研究
Matlab中的噪声去除算法研究引言在现代科技发展的背景下，噪声成为我们日常生活和工作中不可忽视的因素之一。
噪声的存在往往会干扰我们对信号的正确解读和处理。
因此，研究和开发高效的噪声去除算法显得尤为重要。
本文将重点讨论在Matlab平台上的噪声去除算法研究。
一、噪声的特性和类型在深入研究噪声去除算法之前，我们首先需要了解噪声的特性和类型。
噪声可以分为两种主要类型：加性噪声和乘性噪声。
加性噪声是指在原始信号上添加的一种噪声，乘性噪声则是指将原始信号与一种噪声进行乘积的结果。
噪声一般具有随机性和周期性的特点。
随机噪声是一种无规律、难以预测的噪声，往往以高斯分布或均匀分布形式出现。
周期性噪声则是指噪声信号具有明显的周期性变化，这种类型的噪声通常源于电源干扰或机械振动等外部环境。
二、常用的噪声去除算法1. 均值滤波均值滤波是最简单、最常见的噪声去除算法之一。
该算法通过计算信号邻域内像素的平均值来估计信号本身的值。
在Matlab中，可以利用imfilter函数实现均值滤波操作。
2. 中值滤波中值滤波是一种非线性滤波算法，其主要思想是通过计算信号邻域内像素的中值来估计信号的值。
中值滤波能够有效去除椒盐噪声等离群值，对于保留信号细节有良好的效果。
3. 小波去噪小波去噪是一种基于小波变换的信号去噪方法。
它利用小波变换将信号分解为低频和高频部分，然后通过对高频部分进行阈值处理来实现去噪。
小波去噪在去除高斯噪声和周期性噪声方面表现出色。
4. 自适应滤波自适应滤波算法根据输入信号的特性自动调整滤波器参数，以实现更好的去噪效果。
该算法能够动态地进行滤波器参数选择，适应不同噪声特点。
三、Matlab中的噪声去除实现在Matlab中，可以利用内置函数或自定义函数来实现不同的噪声去除算法。
下面以均值滤波和小波去噪为例，介绍它们在Matlab中的具体实现。
1. 均值滤波实现```matlabimg = imread('noisy_image.jpg');filtered_img = imfilter(img, fspecial('average', [3, 3]));```上述代码中，通过imread函数读取待处理的图像，然后利用imfilter函数对图像进行均值滤波处理。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
太原理工大学毕业设计（论文）任务书噪声估计算法的研究及MATLAB仿真摘要日常的通信过程中,语音会常常受到环境噪声的干扰而使通话质量下降,严重时使得语音处理系统不能正常工作。
因此,必须采用信号处理方法通过语音增强来抑制背景噪声从而提高语音通信质量,而噪声估计的准确性又直接影响语音的增强效果。
可见,噪声估计是语音增强的一个非常重要的部分,所以研究噪声估计算法有很好的实用价值。
本文主要研究两种噪声估计算法:基于最小统计和最优平滑的噪声估计算法和最小值控制递归平均法的噪声估计算法,通过实验仿真比较最终研究了一种改进的最小值统计量控制递归平均噪声估计算法。
本文的主要工作总结归纳为以下几方面：首先,本文对几种经典的噪声估计算法进行研究,了解它们的各自优缺点,在此基础上选定两种较好的算法进行具体分析。
其次,了解最小统计和最优平滑和噪声功率谱统计跟踪的噪声估计算法的原理,它的基本思路是先用最优平滑滤波器对带噪语音的功率谱滤波,得到一个噪声的粗略估计，然后找出粗略估计噪声中的在一定时间窗内的最小值，对这个最小值进行一些偏差修正，即得到所要估计的噪声的方差。
通过MATLAB仿真看其特征。
再次,本文研究了一种改进的最小统计法。
算法采用递归平均进行噪声估计，其递归平均的平滑量控制递归平均噪声估计算因子受语音存在概率控制，而语音存在概率的计算采用了两次平滑和最小统计量跟踪。
与I．Cohen提出的IMCRA算法相比，本文采用了一种快速有效的最小统计量跟踪算法。
仿真结果表明：在非平稳噪声条件下，该算法具有较好的噪声跟踪能力和较小的噪声估计误差，可以有效地提高语音增强系统的性能。
最后,对整体论文总结,通过研究发现改进的最小统计量控制递归平均噪声算法在IMCRA算法的基础上,采用了一种简单有效地最小统计量估计算法,在保证噪声估计准确性的同时,减小了算法的复杂度。
同时,基于这种噪声估计的语音增强系统能有效地提高增强语音的信噪比,并且能有效地消除增强语音中的音乐噪声。
关键词: 噪声估计,谱减法,语音检测,最小递归统计量NOISE ESTIMATION ALGORITHM RESEARCHAND MATLAB SIMULATIONABSTRACTThe Daily communication process, speech will often affected by environmental noise interference and make calls the quality descend, serious when make speech processing system didn't work properly. Therefore, must use signal processing methods through speech enhancement to curb background noise so as to improve the quality of voice communication, and the accuracy of the noise estimates directly affected speech enhancement effect. Visible, the speech enhancement noise estimation is a very important part, so the noise estimation algorithm has very good practical value. This paper makes a study of the two kinds of noise estimation algorithm based on least statistics and: the optimal smooth noise estimation algorithm and minimum control recursion average method noise estimation algorithm through experiment comparative simulation, finally puts forward an improved minimum statistic control recursion average noise estimation algorithm.This paper sums up the main work for the following aspects:First of all, the paper on the noise estimation algorithm several classic study, understand their respective advantages and disadvantages, based on selected two good concrete analysis algorithm.Second, understand the smallest statistics and optimal smoothing and noise power spectrum statistical tracking noise estimation algorithm of principle, it is to use the basic ideas of the optimal smoothing filter belt chirp voice power spectral filtering, get a noise a rough estimate, and then find out roughly in certain time window of noise to a minimum, within the minimum deviation correction, some of which is estimated to have the variance ofnoise. Through the simulation of MATLAB see its characteristics. noise recursively, estimates that the average recursive average smooth quantity cont Again, this paper proposes an improved minimum statistics. Algorithm for recursion average noise estimates by speech exist probability is factor control, and calculation of speech exist probability by two smooth and minimum statistic tracking. And I. Cohen proposed IMCRA algorithms, this paper adopts a kind of fast and effective minimum statistic tracking algorithm. The simulation results show that the non-stationary noise conditions, the algorithm has good noise tracking ability and smaller noise estimation error, can effectively improve the performance of the system speech enhancement.Finally, the whole thesis summed up, through the research found that improved least statistic control recursion algorithm in IMCRA average noise based on the algorithm of a simple and effective minimum statistic estimation algorithm, noise estimation accuracy in guarantee, while reducing the algorithm complexity. Meanwhile, based on this kind of noise estimates speech enhancement system can effectively improve the signal-to-noise ratio of the voice enhanced, and can effectively eliminate the music noise voice enhanced. Analytical papers deficiency and future development direction.Key words: noise estimation, the spectral subtraction, voice detection, recursive least statistic目录1 绪论 (1)1.1 噪声估计算法研究的目的和意义 (1)1.2 国内外研究的现状 (2)1.3 论文的整体安排 (3)2 几种经典的噪声估计的算法 (4)2.1 几种噪声估计算法的优点 (4)2.2 噪声估计算法 (4)3 基于语音活动性检测的噪声估计算法及MATLAB实现 (6)3.1 基于语音活动性检测的噪声估计算法 (6)3.1.1 短时能量 (6)3.1.2 短时平均过零率 (7)3.1.3 基于短时能量和短时平均过零率的语音活动性检测 (7)3.1.4 实验仿真 (9)4 最小统计递归平均的噪声估计算法及MATLAB仿真 (11)4.1 最小值统计法 (11)4.1.1 最优平滑 (11)4.1.2 最小功率谱统计跟踪 (12)4.1.3 实验仿真 (14)4.2 基于统计信息的非平稳噪声自适应算法 (15)4.2.1 概述 (15)4.2.2 非平稳噪声自适应算法 (15)4.3 最小值控制递归平均算法 (18)4.3.1 计算局部能量最小值 (19)4.3.2 估计语音存在的概率 (20)4.3.3 更新噪声谱的估计 (20)4.4 一种改进的最小统计量控制递归平均噪声估计算法 (21)4.4.1 改进的噪声估计算法 (21)4.4.2 实验仿真 (23)5 总结与展望 (24)5.1 论文的主要工作 (24)5.2 目前存在的问题及今后的发展方向 (24)参考文献 (25)致 (26)附录:外文文献 (27)1 绪论1.1 噪声估计算法研究的目的和意义语音作为语言的声学表现，是人类特有的也是最重要的思想和情感交流段，也是人机交互最自然的方式。