土力学第3章- 土的本构关系
土力学第3章- 土的本构关系
（5） （6）
求a: 将公式（1）式 1 3
a b a
a
求导，切线模量Et为：
Et
1 3 a a a b a 2
（7）
令εa＝0，则原点的切线模量，即初始切线模量为：
Ei
R
1 a
1
（8） 代入（1）、（7）式（消去a、b)，
( 1 3 ) ult
1 b
（4）
若土样破坏时的偏应力（即强度）为（σ1－σ3）f，令Rf等于破坏时的偏应 力与极限值之比，称为破坏比：
Rf
Rf （4）式代入（5）式得（消去偏应力极限值）：b 1 3 f
1 3 f 1 3 ult
2.八面体应力与应变的计算公式
可导出：
八面体法向应力
八面体剪应力
0 ( 1 2 3 ) ( x y z )
0
1 3 1 3
1 3
1 3
1 3 2 2 3 2 3 1 2
2 2 2 x
1 3
a
a b a
（ 2）
3.非线形弹性模型
1 3 a
a b a
应力－应变双曲线函数 公式（1）还可以改成：
双曲线函数坐标变换
1 3
1 a
（3）
a
b
1 3
1 a
a
通过求a、b得到弹性模量E. 求b:
b
当轴向应变εa→∞时，偏应力趋向一极限值（σ1-σ3）ult
对于加工硬化材料，屈服应力是随着荷载的提高与变形的增大而提高的。 屈服面不同于破坏面，它不是一个固定的面,图中由A点提高到B点。
土的本构关系——读书报告
邓肯-张模型的发展与特点目前描述土的应力——应变关系的数学模型有很多种，包括弹性和弹塑性两大类。
非线性弹性模型中，邓肯—张(Duncan —Chang)模型应用最为广泛的，它包括邓肯—张E-μ模型和修正后的邓肯E- B 模型，即Duncan 等提出的体积模量代替弹性模量的模型。
1、邓肯—张E-μ模型1.1 双曲线应力应变关系邓肯—张E-μ模型是邓肯等人根据大量一般土的三轴试验13()~a σσε-曲线关系而拟合出的一种应力应变关系的双曲线模型，是一种目前广泛应用的增量弹性模型。
它能反映岩土体变形的非线性特征，也可以体现应力历史对变形的影响。
13aaa b εσσε-=+ （1）式中，a 、b 为试验常数。
在常规三轴压缩试验中，1a εε=，13aaa b εσσε-=+可以写成下式：1113a b εεσσ=+- （2）将常规三轴压缩试验的结果进行整理可以得到1113~εεσσ-的关系式如下式所示：1113a b εεσσ=+- （3）由上式可以看出：1113~εεσσ-二者近似成线性关系（见图1），将实测的113εσσ-和1ε绘制在同一坐标下即可得到两个实验常数a 、b ： a 为直线的截距，b 为直线的斜率。
ε1/(σ1-σ3)1-σ3)ult图11113~εεσσ-线性关系图1.2 初始模量E i在试验的起始点，即当应变很小时，由式(1)可得初始模量E i 为：1i E a=（4） 即a 为初始弹性模量的倒数。
而当1ε→∞时，由式(1)可得到应力的极限值——右侧限抗压强度为：131()ult bσσ-=（5） 由此可以看出b 代表的是双曲线的渐近线所对应的极限偏差应力13()ult σσ-的倒数。
在土的试样中，如果应力应变曲线近似于双曲线关系，则往往是根据一定的应变值（如115%ε=）来确定土的强度13()f σσ-，而不可能在试验中使1ε无限大，求取13()ult σσ-；对于有峰值点的情况，取1313()()f σσσσ-=-峰，这样1313()()f σσσσ-<-ult 。
土体本构模型ppt
量。第三个分量常取应力罗德（Lode）参数
＝
2－ 3 － 1
1－ 3
2
＝
2
2－ 1－ 1－ 3
3
式中 2－ 3 ，1 2 ，1 3 为三个应力摩尔圆的
直径，见图5-3
还有一个参数b也反映了中主应力接近大主应力的程度。
1 3
1 2 2 2 3 2 3 1 2
＝
2q 3
它们分别与应力分量p和q有关。而点M在 π面内的方
位可反映第三个分量。将图5-4中的三个主应力坐标轴，以
及代表应力状态的点M 投影到 π面上，如图5-5所示。
§1.应力和应变
在该面上放一个二维
的直角坐标系，令Y轴与
xz yz
ij
zx zy z
在进行公式推导时，一般尽量用一种表示方 法：矩阵或张量，不宜混用
§1.应力和应变
（2）张量表示法
偏应力张量
Sij
x
yx
p
zx
xy y p
zy
xz yz
z p
注意：在进行公式推导时，一般尽量用一种表示方法： 矩阵或张量，不宜混用
3
1 2 3
1
2
一应力不变量Ｉ１相结合形成三个独立的应力分量：
第二偏应力不变量 ：
第三偏应力不变量 ：
表示一点应力状态的方法？？
§1.应力和应变
（二）应力空间和应力路径
1．应力和应变空间
为了表示应力状态，表示各应力分量的数值，常常以应 力分量为坐标轴形成一个空间，叫做应力空间。该空间内 的一点的几个坐标值就是相应的应力分量。
第3章 土的动本构关系
• 其中非弹性部分：
ε
• p ij
=γ
∂f Φ( F ) ∂σ ij
2012-2-21
广东工业大学岩土工程研究所
35
3.6 计入应变率效应的本构理论
2012-2-21 广东工业大学岩土工程研究所 21
3.3.3 Iwan模型
弹塑性元件中的应力始终等于屈服应力。根据模型的构成 特性，在全部受荷过程中，所有弹塑性元件的应变始终相 等，其应力视各弹簧的刚度和摩阻片的屈服水平的不同而 不同。 • 2.串联模型 这类模型受荷时，每个弹塑性元件所受的力是相同的， 但它们的变形不同。弹簧只有在对应的摩阻片屈服时才能 产生变形，并继续承担新的荷载。
30
3.6 计入应变率效应的动本构理论
• 2.粘塑性模型 • • • （1） Bingham模型 （2） Hohenemser-Prager方程 （3） Perzna方程
2012-2-21
广东工业大学岩土工程研究所
31
3.6 计入应变率效应的本构理论
• 1、 粘弹性模型：
• （1）Maxwell模型（弹、粘性原件串联）： • （2）Kelvin模型（弹、粘性原件并联）： • 一般的组合形式：
• 三个基本力学元件：弹性元件，粘性元件和塑性元件。 • 弹性元件：动应力应变关系曲线为过坐标原点的一条斜 直线，直线的斜率取决于弹性元件的弹性模量E，应力应 变关系曲线内的面积等于零。 • 塑性元件：动应力应变曲线为一个矩形，应力应变曲线 内的面积等于矩形的面积。
2012-2-21
广东工业大学岩土工程研究所
2012-2-21
广东工业大学岩土工程研究所
10
3.2 土的动本构关系特点
• 关系曲线将是一个滞回圈。如将不同周期动应力作用 的最大周期剪应力±τm和最大周期剪应变±γm绘出， 即得到各应力应变滞回圈顶点的轨迹，称为土的应力 应变骨干曲线。骨干曲线反映了动应变的非线性，滞 回曲线反映了应变对应力的滞后性。 • 骨干曲线表示最大剪应力与最大剪应变之间的关系。 滞回曲线表示某一个应力循环内各时刻剪应力与剪应 变的关系，二者共同反映了应力应变关系的全过程。
6. 土的本构关系(2)
特点：破坏与2无关，三轴压缩和 伸长具有相同强度。
试验表明，3相同情况下，伸长试验所 得的强度常高于压缩试验测得的强度。
7/22
1.2 常用破坏准则
（4）拉德一邓肯（Lade - Duncan）准则 根据砂土真三轴试验提出
12/22
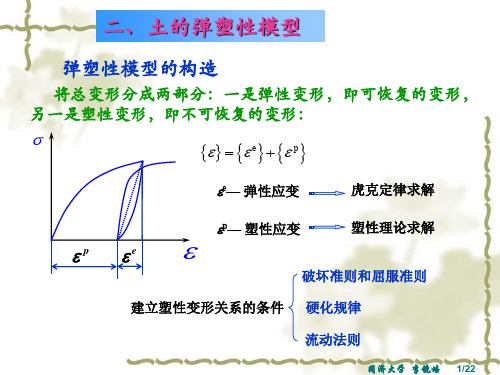
3.硬化规律
当材料达到屈服后，屈服的标准将发生改变，即k值发生变化。 k值随何种因素而变，如何变化，即为硬化规律。
k F (H )
H为硬化参数，包括 塑性变形或塑性功
屈服准则： f ( ij ) k F ( H ) 或： f ( ij , H ) 0
硬化型
软化型
理想塑性
15/22
4.流动法则
屈服函数和硬化规律 判别屈服的标准以及屈服后这个标准如何发展
流动规则：达到屈服以后应变增量各分量之间按什么比例变化
用于确定塑性应变增量方向的假定。
几个概念
塑性势：塑性变形即塑性流动，与其他性质的流动一样，可以看成是由于某种 势的不平衡所引起的，这种势称为塑性势。 米塞斯(Mises)类比弹性应变增量可以用弹性位势函数对应力微分来表示的概 念，提出了塑性势理论：
主要硬化参数：
(1) 塑性功Wp
W p ij d e ijp W p pd e vp qd e sp
在p-q坐标系可表示为 (2) 塑性体积应变 e v
p
以塑性体积应变为硬化参数相应的屈服面总是“帽 子”形的，能较好地反映土体的体积变形特征。
14/22
(3) 塑性偏应变 e s
1 ea p e v
ep ln p0 ln pa 得到 e 1 ea 1 ea
土的本构结构
土的本构关系土体是天然地质材料的历史产物。
土是一种复杂的多孔材料,在受到外界荷载作用后,其变形具有以下特性：①土体的变形具有明显的非线性,如:土体的压缩试验e～p 曲线、三轴剪切试验的应力—应变关系曲线、现场承载板试验所得的p～s曲线等; ②土体在剪切应力作用下会产生塑性应变,同时球应力也引起塑性应变; ③土体尤其是软粘土,具有十分明显的流变特性;④由于土体的构造或沉积等原因,使土具有各向异性; ⑤紧砂、超固结粘土等在受剪后都表现出应变软化的特性; ⑥土体的变形与应力路径有关,证明不同的加载路径会出现较大的差别; ⑦剪胀性等。
为了更好地描述土体的真实力学—变形特性,建立其应力、应变和时间的关系,在各种试验和工程实践经验的基础上提出一种数学模型,即: 土体的本构关系。
自从Roscoe等人首次建立了剑桥模型以来, 土的本构关系的研究经历了一个蓬勃发展的阶段, 出现了一些具有实用价值的本构模型。
虽然很多的理论为建立土的本构关系提供了有力的工具, 但是由于土是一种三相体材料, 在性质上既不同于固体也不同于液体, 是介于两者之间的特殊材料, 所以人们常借助于固体力学或流体力学理论, 同时结合工程实践经验来解决土工问题, 从而研究土的本构关系形成了自己一套独特的方法—半理论半经验的方法。
建立一个成功的本构关系关键有两点：第一要建立一个函数能较好地反映土在受力下的响应特征；第二要充分利用试验结果提供的数据比较容易地确定模型参数。
模型都需要满足以下基本条件：（1）不违背更高一级的基本物理原理（如热力学第一、第二定律）。
（2）建立在一定的力学理论基础之上（如弹性理论、塑性理论等）。
（3）模型参数能够通过常规试验求取。
从工程应用的角度出发，研究问题的精度就需要进行合理的控制，从而在计算精度与计算设备、计算难度、计算时间以及计算成本之间获得平衡。
另外，任何理论、方法都应以实践应用为目的，这样才具有价值。
综合上述两点，从工程应用的角度去分析各种土的本构关系是非常有必要的。
土的本构
ij
e ij
p ij
F 2 2 F ij
p ij
2015/10/16
广东工业大学岩土工程研究所
34
3.6 计入应变率效应的本构理论
• (3)Perzyna方程：
1 1 2 ij S ij ij 2G E
30
3.6 计入应变率效应的动本构理论
• 2.粘塑性模型
• • • （1） Bingham模型 （2） Hohenemser-Prager方程 （3） Perzna方程
2015/10/16
广东工业大学岩土工程研究所
31
3.6 计入应变率效应的本构理论
• 1、 粘弹性模型：
• （1）Maxwell模型（弹、粘性原件串联）：
2015/10/16
广东工业大学岩土工程研究所
26
3.4 土的动力屈服、破坏条件及本构理论
• 1、土的动力屈服：砂土与粘土的区别 • • 屈服条件 强化现象
•
强化条件、加载条件
• 2、破坏条件 • 3、屈服条件与破坏条件的关系
•
•
特例：理想塑性状态
（1）应变率效应：⑴不计～；⑵计入～
• 4、土的动本构理论分类
2015/10/16 广东工业大学岩土工程研究所 29
3.6 计入应变率效应的本构理论
2
据此可建立土的动本构关系，
包括粘弹性和粘塑性两类：
• 1.粘弹性模型 • • （1）加载速度单调增加的粘弹性模型 （2）Maxwell和Kelvin模型
2015/10/16
广东工业大学岩土工程研究所
土的本构模型ppt课件
土的本构关系
1 概述
体积力 面力 静(动) 力平衡
应力
本构方程
位移
几何 相容
应变
本构关系在应力应变分析中的作用
土的本构关系
1 概述
传统土力 学分析方法
变形问题 （地基沉降量）
稳定问题 （边坡稳定性）
• 弹性理论计算应力 • 压缩试验测定变形参数 • 弹性理论+经验公式计算变形
• 土体处于极限平衡状态 • 滑动块体间力的平衡 • 刚体+理想塑性计算安全系数
常用的三个应力不变量
土的本构关系
2 应力和应变 – 应变
与应力的情况相似
体应变 广义剪应变 应变洛德角
v k k 1 2 3 I 1
3 2(12)2(23)2(31)2
tg
22 1 3 3(1 3)
应变
土的本构关系
3 土的应力变形特性
土的应力变形特性
基本特性
非线性 压硬性 剪胀性 摩擦性
第二章 土的本构关系
2.5 土的弹塑性模型的一般原理
屈服函数 (yield function, yield equation))
屈服准则的数学表达式
一般应力状态 fij,H0
• 对于弹塑性模型；H是塑性应变的函数
屈服准则与屈服面
土的本构关系
5 土的弹塑性模型的一般原理
1) f<0 屈服面之内，只产生弹性应变
土的基本变形特性- 剪胀性
土的本构关系
3 土的应力变形特性
饱和重塑粘 土应力比与 塑性应变增 量比的关系
试验规律 剪胀方程
-4
-3
-2
q 1.5 p
1
0.5 0
土的本构关系
本 构 关 系“本构关系”是英文Constitutive Relation 的意译。
在力学中，本构关系泛指普遍的应力—应变关系。
因为在变形固体力学中，应力不只与应变有关．而且还与物体的加载历时(应力历史)、加载方式(或应力路径)以及温度和时间有关。
因此材科的本构关系或普遍的应力—应变关系可以表示为；应力路径等）,,,(T t f ij ij εσ= 式中t 为加载历时，T 为温度。
例如，弹性力学中的广义定律就是最简单的材料本构关系，它不计时间、温度和应力路径及应力历史的影响。
因此应力和应变之间存在着唯一对应的关系。
当材料应力超出弹性范围而进入塑性阶段时，应力和应变之间就没有唯一的对应关系，而是要受应力历史或应力路径的影响，这时材料的应力—应变关系就称为塑性本构关系。
塑性本构关系要比弹性本构关系复杂得多。
如果再考虑材科应力—应变关系随时间和温度的变化，本构关系持更加复杂。
本书所要讲的岩土本构关系主要是指与时间和温度无关的塑性本构关系。
各种本构关系的特点1.弹性本构关系类型和分类弹性本构关系可分为线弹性本构关系和非线性弹性本构关系如图1所示，线弹性本构关系即一般的弹性力学，其应力—应变关系服从广义Hooke 定律。
非线性本构关系的应力—应变曲线是非线性的，但是加卸载仍然沿着一条曲线。
弹性本构关系的基本特征是：1) 应力和变形的弹性性质或可逆性；2) 应力与应变的单值对应关系或与应力路径相应力历史的无关性。
即无论材料单元在历史上受过怎样的加卸载过程或不同的应力施加路径，只要应力不超过弹性限度，应力与应变都是一一对应的；3) 应力与应变符合叠加原理；4) 正应力与剪应变、剪应力和正应变之间没有耦合关系。
因此，根据广义Hooke 定律有γτεσG K m m ==3 （1）式中，σm和τ分别为正应力和剪应力，εm和γ分别为平均应变和剪应变，K、G为体积弹性模量和剪切弹性模量。
(1)式说明：正应力只产生正应变或体应变，而对剪应变没有贡献。
土力学知识点.
土力学知识点1、课程性质土力学是一门专业基础课。
土力学研究的对象课概括为：研究土的本构关系以及土与结构的物相互作用的规律。
2、土的本构关系即土的应力、应变、强度和时间这四个变量之间的内在关系。
3、为确保建筑物的安全和使用良好，在地基与基础设计中必须满足哪两个技术条件？1、地基的强度条件：要求建筑物地基保持稳定型，不发生滑动破坏，必须有一定的地基强度安全系数2、地基的变性条件：要求建筑物的变形不能大于地基变形允许值。
4、组成岩石的矿物称为造岩矿物5、矿物的种类：原生矿物和次生矿物6、矿物的主要物理性质？形态、色泽、光泽、硬度、解理、断口解理：矿物在受外力作用时，能沿一定的方向裂开成光滑平面的性能。
断口：矿物在受外力打击后断裂成不规则的形态。
7、矿物的鉴定方法：肉眼鉴定法和偏光显微镜法8、岩石分类？按成因分：岩浆岩、沉积岩、变质岩按坚固性分：硬质岩石、软质岩石按风化程度分：未风化、微风化、中等风化、强风化9、第四纪沉积层：地表的岩石，经物理化学风化、剥蚀成岩屑、粘土矿物及化学溶解物质；又经搬运、沉积而成的沉积物，年代不长，未压密硬结成岩石之前，呈松散状态，称为第四级沉积层，即“土”10、第四纪沉积层分类：残积层、坡积层、洪积层、冲击层、海相沉积层、湖沼沉积层11、常见的不良地质条件有？断层、岩层节理发育的场地、滑坡、河床冲淤、岸坡失稳、河沟侧向位移12、地下水分类：上层滞水、潜水、承压水13、初见水位：工程勘察钻孔时，当钻头带上水时所测的水位稳定水位：钻孔完毕，讲将钻孔的孔口保护好，待二十四小时后再测得的水位14、土是由岩石，经物理化学风化、剥蚀、搬运、沉积，形成固体矿物、流体水和气体的一种集合体。
15、土的结构：土颗粒之间的互相排列和联结形式称为土的结构分类：单粒结构、蜂窝结构、絮状结构16、土的构造：同一层土中，土颗粒之间相互关系的特征称为土的构造。
分类：层状构造、分散构造、结核状构造、裂隙状构造17：土与其它连续介质的建筑材料相比，具有哪三个显著的工程特性？1、压缩性高2、强度低3、透水性大18、土粒中的矿物分为三类：原生矿物、次生矿物、腐殖质19、工程中常用的土中各粒径的含量占总质量的百分比称为土的粒径级配。
土的基本特性及本构关系与强度理论
土的基本特性及本构关系与强度理论一、本文概述本文旨在深入探讨土的基本特性、本构关系以及强度理论，以增进对土壤力学行为的理解，并为土木工程、地质工程、环境工程等领域提供理论基础和实践指导。
土作为自然界中广泛存在的介质，其力学特性对于工程结构的稳定性和安全性至关重要。
因此，研究土的基本特性、建立合理的本构关系以及探索强度理论，对于预防地质灾害、优化工程设计、提高施工效率等方面都具有重要的意义。
本文首先对土的基本特性进行概述，包括土的分类、物理性质、化学性质以及力学性质等方面。
在此基础上，进一步探讨土的本构关系，即土的应力-应变关系，包括弹性、弹塑性和塑性等方面。
通过对土的本构关系的深入研究，可以更准确地描述土的力学行为，为工程实践提供理论支持。
本文还将重点介绍土的强度理论，包括土的抗剪强度、抗压强度等方面。
土的强度理论是土力学中的核心内容之一，它对于评估土的承载能力、预测土的变形和破坏等方面具有重要的指导作用。
通过对土的强度理论的深入研究，可以为工程实践提供更加准确、可靠的理论依据。
本文将系统介绍土的基本特性、本构关系以及强度理论，以期为提高土木工程、地质工程、环境工程等领域的理论水平和实践能力做出贡献。
二、土的基本特性土是一种由固体颗粒、液体水和气体组成的三相体，其特性受到这些组成部分的性质、相对含量以及它们之间的相互作用的影响。
土的基本特性主要包括其物质组成、物理性质、力学性质和环境特性。
物质组成：土主要由固体颗粒（如砂粒、粘土粒等）、水和气体组成。
固体颗粒的大小、形状和分布决定了土的粒度特征和结构特性。
物理性质：土的物理性质包括密度、含水率、孔隙率、饱和度等。
这些性质对于理解土的力学行为和环境响应至关重要。
例如，密度反映了土体的紧实程度，含水率则影响了土的塑性和流动性。
力学性质：土的力学性质是指在外部荷载作用下土的应力-应变关系和强度特性。
土的力学性质受到其物质组成、物理状态和环境条件的影响。
土体本构模型-高等土力学03-2013
σ１和σ２增加得少，而后期反
过来。对于某种加荷方式，代表 应力状态的点将从Ａ沿某种轨迹 移动到Ｂ。加荷过程中，不同的 图9
岩土工程研究所
加荷方式可以用不同的应力路径 来表示。
§1.应力和应变
更常用的是用p-q平面的应力路径
q
普通三轴应力状态下
A
p＝ q＝
p
O
B
与其相应，当然也有应变路径。
岩土工程研究所
用到这种ｐ－ｑ平面。
岩土工程研究所
图5-6
§1.应力和应变
二维问题中，
1 p ( 1 3 ) 2
1 q ( 1 3 ) 2
p~q
表示应力状态或应力路径也有优点 P204
岩土工程研究所
图5-6
§1.应力和应变
与应力空间相应，以应变分量为坐标轴形成一个空间，
叫做应变空间。该空间内的一点的几个坐标值就是应变分量 。图5-8所示为主应变空间。它的三个坐标轴分别为 ， 2 1 和 3 。
图5-8
岩土工程研究所
§1.应力和应变
2.应力路径 在应力空间内，代表应力状态的点移动的轨迹， 叫应力路径。它表示应力变化的过程，或者加荷的方 式。
岩土工程研究所
§1.应力和应变
设土体中一点初始应力状态如图 5-9应力空间内Ａ点所示，受力
后变化到Ｂ。从Ａ到Ｂ，可以有
各种方式，如σ１、σ２和σ３按 比例增加；初期σ３增加得多，
应力空间还可以用其他形式的应力分量为坐标。 如果以σｘ，σｙ，σｚ，τｘｙ，τｙｚ和τｚｘ六个应力分量为 坐标，则应力空间是六维空间，无法用图形表示，仅可以 作抽象的理解。
p-q 平面
岩土工程研究所
第1次
土的本构关系及其模型
Et
1
Rf
1 1 3
3 f
2
Ei
（a ）
根据简布（Janbu）对压缩试验的研究。
n
Ei
k
i
Pa
3
Pa
式中，
（b）
log Ei
ki , n 试验确定参数，由Ei和 3
的关系求得，如图示；
Pa 大气压力，单位与Ei相同；
2.2 数学模型
数学模型：直接用数学关系表达应力应 变关系。
数学模型的前提是要有应力应变关系的 曲线。目前常用的数学模型就是根据试 验曲线整理得到。
2.2.1 线性弹性模型
线性弹性模型是假设土的应力与应变成正比， 强度是无限的。
线性弹性模型对计算地基中的垂直应力分布是 很有用的，得到的结果比较符合实际，但是计 算地基的位移和沉降，该模型只适用于不排水 加荷的情况，并且对破坏要有较大的安全系数， 不能发生屈服。
渐近线1
3 ult
1 b
Ei
1 a
1 3 f
3 常数
1
3
a
a ba
轴向应变 a
如果将纵坐标修改，则：
a 1 3
1
a 1 Ei
1
3
1 Ei
a aRf
1 3 f
b
3 常数
轴向应变 a
曲线上任一点的切线模量：
对于模型，一是要比较形象地表示不同材料的 各种性能；二是研究起来比较方便，能找出规 律性。
对于土体来讲，它通常是各向异性、非匀质、 非线性弹性体，其应力应变是非常复杂的，如 土体既具有弹性、塑性、又具粘滞性等。许多 情况下又是这些性状的组合，基于这一点，人 们相继提出了许多不同的力学模型或数学模型， 但哪一种模型都不能如实地表达土体的真实情 况，只能说在一定的条件下，当解题满足工程 精度要求时，才可用某种模型来解决工程的实 际问题。
土的本构关系
如图c所示。
1
-
3
(
砂性土
1
-
3) f
粘性土
1 O
图c 破坏时的偏应力值
②由摩尔－库仑准则，破坏时 表示为 c 函数：
( 1 3 ) f
可
( 1 3 ) f
2 c co s 2 3 sin 1 sin
（5）
③根据Janbu（1963）建议，土体初始模量 可表示为：
c Rf、 、k、n为确定Et的五个参数。
（4）D-C模型的切线泊松比方程应用很少。 （5）适用性和优缺点 ①D-C模型适用于荷载不太接近破坏的条件 下模型土的 非线性情况。
地 下 水 位 总 应 力有 中 和 应 力
砂 土不
效 应 力
透 水 粘 土
总 应 力有
中 和 应 力
砂 土
6.加上工程经验，作出判断、预测、评价及处理 方案。 7.检验及修正认识。
二、 土的本构关系
• 土的本构关系又称为本构模型，即描 述土的应力－应变－关系的数学表达式。 土的 关系很复杂，具有非线性、 粘弹塑性，同时强度发挥程度、应力历 史以及土的组成状态和结构等对其都有 影响。目前，已建立的本构模型很多， 重要的有以下几类：
q
p
'
k
( N ln p ')
式 中 ， q 为 主 应 力 差 （ 1 3） ； p为平均有效应力；
'
6 sin
'
3 sin
， 为 p ' q 平 面 上 临 界 状 态 线 斜 率 ， 为 有 效 内 摩 擦 角 ； '
'
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
称为应力水平。
根据摩尔－库仑破坏准则：
sin
1 1 3 f 3 c cos 2 sin
（12）
1 3 f
2c cos 2 3 sin 1 sin
代入（11）式
Et 1 R f S Ei
1 3
2
2
1 3
2
sin
2
1
2 1 2 sin 2 2 3 2 3
2 3 1 3 1 sin
Rf a 1 Ei 1 3 f
a
代入（10）
Et
1 Ei 1 Rf a Ei 1 3 f
2
式：
（消去轴向应变 a ）
Et 1 R f S Ei
2
（11）
其中
S
1 3 1 3 f
f
i
3 pa
（18） G、F－试验常数。
代入（17）式
t
3 f 1 1 1d 2
3 G F lg p a t 1 1d 2
利用（1）式最后可得到：
(19)
3 G F lg p a t 1 A2
( 1 3 ) ult
1 b
（ 4）
若土样破坏时的偏应力（即强度）为（σ1－σ3）f，令Rf等于破坏时的偏应 力与极限值之比，称为破坏比：
Rf
Rf （4）式代入（5）式得（消去偏应力极限值）：b 1 3 f
1 3 f 1 3 ult
（2－13）
3 1 2ct
2 3 2ct
（2－14）
1 3 2ct
如果有一个式子为等号时，则材料进入塑性状态。 或
2c .
2 2 1 2 t
3 1 2ct 0 2 3 2ct .
（2－8） （2－9）
M 0 3K
剪切模量
G
0 E （2－10） 0 2(1 )
3.强度理论
达到强度条件时的应力轨迹线称为强度包线。主要强度理论有三种。
3.1 最大八面体剪应力强度理论，也叫V.Mises条件
当八面体剪应力τ0达到极限值c0时，就是破坏条件。
0 c0
强度包络面为不通过原点 的不等顶角的六边形锥面。
3.强度理论
三种破坏条件的比较
§2. 土的应力－应变关系
1．材料的应力－应变关系
材料的应力－应变关系
2．土的三轴压缩试验应力－应变曲线 基本形态
常用土工试验仪
直剪仪 单向固结仪 常规三轴压缩（σ2＝σ3）试验 仪
非常规试验仪
（2－3）
0
1 2 0 E
或
0
E 0 1 2
（2－4）
八面体弹性模量
M0
E 1 2
（2－5） （2－6）
31 2 v 1 2 3 0 E
0 E V 3 1 2
体积弹性模量
K
（2－7）
E 31 2
μt推导
ε1与ε3的关系为双曲线：
1
f d 3
3
（16）
f、d为两个待定常数。
3 f d 3 1
3 f 1 1 1d
3 f t 1 1 1d 2
（17）
过原点的初始切线泊桑比为
i f
初始切线泊桑比与σ3有如下关系
i G F lg
2.八面体应力与应变的计算公式
可导出：
八面体法向应力
八面体剪应力
0 ( 1 2 3 ) ( x y z )
0
1 3 1 3
1 3
1 3
1 3 2 2 3 2 3 1 2
2 2 2 x
n
（20）
式中
A
3 kpa p a
1 2c cos 2 sin 3
1 3 d 2 R f 1 sin 1 3
Duncan－Chang模型其有8个参数：c、φ、Rf、k、n、d、F、G,试验
3.3 散体极限平衡理论，也叫Mohr－ Coulomb条件
破坏时的最大与最小主应力之间的关系有
max K P min
（ 1 K P 3）（2－17）
K P tg 2 45 2
KP－按朗肯理论的被动土压力系数，
1 1 sin 3 1 sin
2
消去S后
R f 1 sin 1 3 Et 1 Ei 2c cos 2 3 sin
2
（13）
试验常数：Rf、c、φ、Ei
3 Ei kP a P a
n
（14）
Lg Ei～lg σ3为一直线，截距k，斜率n
1 3
a
a b a
（2）
3.非线形弹性模型
1 3 a
a b a
应力－应变双曲线函数 公式（1）还可以改成：
双曲线函数坐标变换
1 3
1 a
（3）
a
b
1 3
1 a
a
通过求a、b得到弹性模量E. 求b:
b
当轴向应变εa→∞时，偏应力趋向一极限值（σ1-σ3）ult
i
f 将（6）式 b 、（8）式 a 1 3 f 得到
E
1 3
Rf a 1 Ei 1 3 f
a
（9）
Et
1 Ei 1 Rf a Ei 1 3 f
2
（10）
（9）式
1 3
为3组常规三轴压缩试验.
Duncan－Chang模型试验常数 上海粉 质粘土 c 0 φ 39.0 Rf 0.68 k 125 n 0.52 d 8.48 F -0.127 G -0.16
（2）K－G模型
用体积模量k与剪切模量G代替E、μ。
八面体应力的基本公式： 应力与应变关系为：
1 0 1 2 3 3 1 1 2 2 2 3 2 3 1 2 0 3 v 1 2 3
（5） （6）
求a: 将公式（1）式 1 3
a b a
a
求导，切线模量Et为：
Et
1 3 a a a b a 2
（7）
令εa＝0，则原点的切线模量，即初始切线模量为：
Ei
R
1 a
1
（8） 代入（1）、（7）式（消去a、b)，
第三章 土的本构关系
§1. 八面体应力的基本知识
1.八面体及八面体应力的意义
边长为2的立方体，主应力σ1、σ2、σ3分别与x、y、z轴平行， a,b,c,d,e,f点为六个面的中心点。
把立方体六个面的中心点连接起来，就成为八面体单元。
1.八面体及八面体应力的意义
八面体应力和八面体应变：指八面体任意面上的法向应力σ0及剪应力 τ0；相应的法向应变ε0及剪应变γ0。他们分别是三个主应力σ1、σ2、 σ3和三个主应变的函数，能够综合反映空间应力状态。
即
塑性增量理论包括三个部分
① 屈服面理论
② 流动规则理论 ③ 加工硬化规律理论
①屈服面理论
在屈服面范围内，土体只发生弹性应变，超越屈服面则同时发生弹性和塑 性应变。
弹性变形与塑性变形
对于理想弹塑性材料，当应力的组合，使材料达到屈服状态时，就可以 认为是破坏了，屈服面与破坏面重合，同是一个固定的面。
对于加工硬化材料，屈服应力是随着荷载的提高与变形的增大而提高的。 屈服面不同于破坏面，它不是一个固定的面,图中由A点提高到B点。
0 K v 0 G 0
E 3(1 2 ) E G 2(1 ) K
0
2 3
1 2 2 2 3 2 3 1 2
4．弹塑性模型
（1）塑性增量理论
土的应变分为弹性应变εeij和塑性应变εpij，
e ij ij ijp
0
3.3 散体极限平衡理论，也叫Mohr－ Coulomb条件
强度包络面为通过 原点的不等顶角的 六边形锥面。
扩展了的Mohr－Coulomb条件
max KP min 2 KP c
或
1 1 sin 3 1 sin 2c cos
或
1 3
1 2 2 2 3 2 3 1 2 9c02
（2－11）
(
0
1 3 2 2 3 2 3 1 2
)
3.强度理论
强度包络面为一垂直于等倾斜面的圆柱面。
3.强度理论
如土的强度与八面体法向应力有关（扩展了的V.Mises条件）
2 2 2 2
（2－15）
3.2 最大剪应力强度理论，也叫Tresca条件
强度包络面是一个垂直 于八面体平面的正六角 柱体面，而屈服面在π
平面上的轨迹是一个正
六边形。
Tresca扩展情况：
max 0tgt
max [ct 0tgt ]
（2－16）
相应的强度包络面为通过原点和不通过原点的正六角形锥面。
0 [c0 0tg ]
0 0tg