模糊聚类分析例子
模糊聚类分析ppt课件

k 1
1 2
m k 1
(
xik
x jk )
m
( xik x jk )
rij
k 1 m
xik .x jk
k 1
5. 求模糊等价矩阵
用上述方法建立起来的模糊矩阵 R ,一般说来只 满足自反性和对称性,不一定满足传递性,即 R 不一 定是模糊等价关系,需要将 R改造成模糊等价矩阵R,
然后再在适当的阈值上进行截取,便可得所需分类。
根据需要可同时选择不同准则分别进行聚类分析,然后 通过综合取交的方法,以做到兼顾多目标,使分类结果更科学。
3、建立数据矩阵
设论域U { x1, x2 ,, xn }为被分类对象, 每个对象又由m 个指标表示其性状:
xi { xi1, xi2 ,, xim } (i 1,2,, n) 则得到原始数据矩阵为 X ( xij )nm .
1, 2,..., m
构造下列形式的F统计量,
r
i
2
ni x x /(r 1)
F i1 r ni
xij
i
x
2
/(n r)
i1 jn1
x x 其中, 为 i x x
m
i
(xk
xk )2
i
与
的距离, xij x i
i 为第
k 1
类中样本
xij 与
i
x 的距离。
F 统计量分子表征类与类之间的距离, 分母表示类内样本间距离,因此 F 值越大,说
改造的方法是将 R 自乘得 R R R2,再自 乘 R2 R2 R4 ,如此继续下去,得 R8 , R16 ……,至某 一步出现 R2k Rk 为止。则 Rk便是一个模糊等价关系。 这个方法是由所谓“传递闭包”理论而来,我们在此 拿来直接应用,不再作详细介绍。
模糊聚类分析实验报告
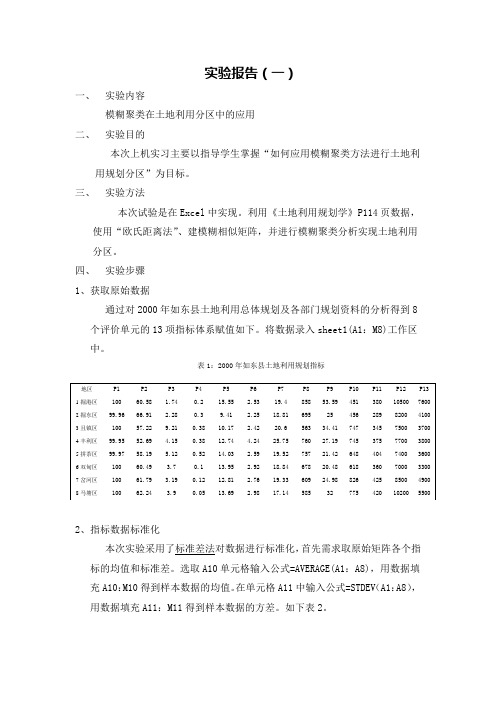
实验报告(一)一、实验内容模糊聚类在土地利用分区中的应用二、实验目的本次上机实习主要以指导学生掌握“如何应用模糊聚类方法进行土地利用规划分区”为目标。
三、实验方法本次试验是在Excel中实现。
利用《土地利用规划学》P114页数据,使用“欧氏距离法”、建模糊相似矩阵,并进行模糊聚类分析实现土地利用分区。
四、实验步骤1、获取原始数据通过对2000年如东县土地利用总体规划及各部门规划资料的分析得到8个评价单元的13项指标体系赋值如下。
将数据录入sheet1(A1:M8)工作区中。
表1:2000年如东县土地利用规划指标2、指标数据标准化本次实验采用了标准差法对数据进行标准化,首先需求取原始矩阵各个指标的均值和标准差。
选取A10单元格输入公式=AVERAGE(A1:A8),用数据填充A10:M10得到样本数据的均值。
在单元格A11中输入公式=STDEV(A1:A8),用数据填充A11:M11得到样本数据的方差。
如下表2。
表2:13个指标值得均值和标准差选取A13单元格输入公式=(A1-A$10)/A$11,并用数据填充A13:M20区域得到标准化矩阵如下表3。
表3:标准化数据矩阵3、求取模糊相似矩阵本次试验是通过欧氏距离法求取模糊相似矩阵。
其数学模型为:mr ij=1−c√∑(x ik−x jk)2k=1选取A23单元格输入公式=SQRT((A$13-A13)^2+(B$13-B13)^2+(C$13-C13)^2+(D$13-D13)^2+(E$13-E13)^2+(F$13-F13)^2+(G$13-G13)^2+(H$13-H13)^2+(I$13-I13)^2+(J$13-J13)^2+(K$13-K13)^2+(L$13-L13)^2+(M$13-M13)^2)求的d11,B23中输入公式=SQRT((A$14-A13)^2+(B$14-B13)^2+(C$14-C13)^2+(D$14-D13)^2+(E$14-E13)^2+(F$14-F13)^2+(G$14-G13)^2+(H$14-H13)^2+(I$14-I13)^2+(J$14-J13)^2+(K$14-K13)^2+(L$14-L13)^2+(M$14-M13)^2)q 求的d12。
模糊聚类分析

模糊聚类分析壹、何谓聚类分析聚类分析是研究事物分类的一种多元分析方法。
在日常生活中,我们时常要把所接触到的事物(样本),按其性质、用途等进行分类,这种分类过程我们称为聚类分析。
(阙颂廉,民83)贰、聚类分析的应用模糊聚类分析是当前在模糊数学中应用最多的几个方法之一,可以将研究的样本进行合理的分类,如产品的分类就常常用聚类分析来进行,另聚类分析也可用来进行判别分析和预测(林杰斌等。
民76)。
所以,也被广泛地应用于天气预报、地震预测、地质探勘、运动员心理素质分类、河川水质污染程度等方面。
参、普通的等价关系在谈聚类分析之前,应先介绍相似关系和等价关系:一.自反性对任意Uu∈,都有Ru,u(∈,即集合中任一个元素u都)与自身有某相同性质的关系,则称R是自反关系,相对应的矩阵称为自反矩阵。
另数学表示意义为:A中的元素关于R具有”自反性”,即。
例:若U 为同一种族的集合,而集合中每一个人u ,皆与自身有同一种族之关系,这种性质则称为自反性。
二. 对称性如果ji ,R )u ,u (,R )u ,u(i j j i≠∈∈必有。
即u i 与u j 有存在某种关系,若将两个元素之位置对调,则即u j 与u i 也必有符合这层关系,则称R 有对称关系,相对应的矩阵为对称矩阵。
另数学表示意义为:A 中的元素关于R 具有”对称性”,即yRx xRy ,A y ,x 且若∈∀。
例:若甲和乙是同学关系,则乙和甲必也是同学关系,这种关系则称为对称性。
三. 传递性如果能由R)w u (R )w v (R )v u (∈∈∈,,推導出,及,。
即u与v 有存在某一关系,而v 与w 也有这同一种关系存在,则即u 与w 也必有符合这层关系存在,则称R 有传递关系,相对应的矩阵为传递矩阵。
另数学表示意义为:A 中的元素关于R 具有”传递性”,即。
例:若甲和乙是同一种族关系,而乙和丙也是同一种族关系,则甲和丙必有同一种族关系,这种则称为具有传递性关系。
模糊聚类分析

1 2 m
x11 x21 xm1
x12 x22 xm 2
x1n x2 n xmn
2 .模糊聚类分析的一般步骤
实际问题中,不同的数据可能有不同的量 纲。为了使不同量纲的数据也能进行比较,需 要对数据进行适当的变换。根据模糊矩阵的要 求将数据压缩到区间 【0,1】。通常使用平移极差标准化: xik min{xik } 1im xik (k 1,2,, n) max{xik } min{xik }
取=0.8,得 :
~ R0.8 1 0 0 0 0 0 1 0 0 1 0 0 0 0 1 0 0 0 0 1 0 0 0 0 1
X分为4类:{X1,,X3},{X2},{X4 }, { X5 }。
2 .模糊聚类分析的一般步骤
取=0.5,得 :
~ R0.5 1 0 0 0 0 0 1 1 0 1 0 0 0 0 1 0 0 0 0 1 1 0 0 0 1
3 .应用实例
通过聚类分析,该矿决定在房柱法的基础 上增加采矿费用的投入,采用无底柱上向干式 充填采矿法。
谢
谢!
模糊聚类分析步骤可以分为:数据标准化、建立 模糊相似矩阵、聚类
2 .模糊聚类分析的一般步骤
2.1 数据标准化 设论域 X {x , x ,, x } 为被分类的对象,每个对像 又由n个指标表示其性状,即:xi (xi1, xi2 ,, xin ) (i 1,2,, m) 于是,得到原始数据矩阵为:
rij
m in (x
k 1
n
ik
, x jk )
1 2
(x
k 1
n
ik
模糊聚类分析在生活中的运用

模糊聚类分析在生活中的运用
模糊聚类分析是一种基于模糊数学技术的数据分析方法,它能够有效地将数据分类,让用户能够更加清楚的获得信息。
自20世纪70年代以来,模糊聚类分析在许多学科和行业中都得到了广泛的应用,其中包括社会学、医学、金融、商业等多个领域。
模糊聚类分析在生活中也有非常多的运用,下面就让我们来看看模糊聚类分析在生活中的运用。
首先,模糊聚类分析在精准医疗领域中有着重要的应用。
例如,数据挖掘技术可以利用模糊聚类分析,从海量的医疗数据中快速分析出病人的病变模式。
对于上述模式的发现,可以帮助医生更有针对性地采取临床治疗方法,为病人提供更加靶向性的治疗,从而提高治疗效果。
其次,模糊聚类分析还在社会调查领域占据了重要的地位。
比如,社会学家可以利用模糊聚类分析对大量的调查结果进行分析,对社会现象进行归纳概括,分出不同的群体,如性别、年龄等。
这有助于社会学家们把握社会现象的发展趋势,从而更好地为政府提供决策依据,给社会发展提供建议。
此外,模糊聚类分析还在智能推荐系统中得到了广泛的运用。
比如,当我们在电商网站上购买商品时,模糊聚类分析可以根据用户的浏览记录、购买记录等进行分析,为用户推荐商品,从而提高购买效率。
以上就是模糊聚类分析在生活中的运用。
可以看出,模糊聚类分
析是一种强大的数据分析工具,能够有效地提取出大量的信息,为各个领域的发展提供有力的支撑。
未来,模糊聚类分析将在更多领域发挥作用,为人类社会作出更大的贡献。
模糊聚类分析

模糊聚类分析定义:根据具体的标准和性质对事物进行分类的方法称为聚类分析 根据模糊标准对事物进行分类的方法称为模糊聚类分析基本思想:根据分类对象之间的模糊相似程度来衡量相互的异同程度,进而实现模糊分类。
传统聚类分析VS 模糊聚类分析1. 传统聚类分析: 设有n 个对象12,,...nx x x,每个对象有m 种特性12,,...my y y。
1>首先对每个对象的特性进行数量化:用ijz代表第i 个对象的第j 个性质的数值。
则对象ix 的性质形成的一个向量()12,,...i i im z zz2>考察对象之间相近的程度:引入“欧式距离”和“夹角余弦”。
1欧式距离:设对象()()1212,,...,,,....i i im j j jm ijy x z zz z zz ==则欧式距离为:ijyx -=这与我们所熟知的向量的欧式距离是一样的!2夹角余弦:设α是对象ix和jy之间的夹角,0180α≤≤,则夹角余弦为:(),cos ijijy x yx α=其中:()11,...i j im jm ijy x z zz z =++ix=iy=有了这些基础认识之后,下面我们通过一个例子来说明传统聚类分析 设有5个对象125,,...x x x,不妨设每个对象只有一个性质,数量化后分别为1,2,4.5,6,8.现使用传统聚类法进行聚类。
1 欧式距离:5个对象,共有25c个欧式距离。
计算可得121x x-=133.5x x-= 145x x-= 157x x-= 232.5x x-= 244x x -= 256x x-=341.5x x-=35 3.5x x-=452x x-=根据聚类的思想,差异最小的对象属于一类 从而1x 和2x为一类,并记为1G2 将1G 看成新的对象,其特征值为1x 和2x 的平均值1.5。
此时对象为1345,,,G x x x 。
再次计算欧式距离。
可知34,x x之间的距离最小。
模糊聚类分析实验报告

专业:信息与计算科学 姓名: 学号:实验一 模糊聚类分析实验目的:掌握数据文件的标准化,模糊相似矩阵的建立方法,会求传递闭包矩阵;会使用数学软件MATLAB 进行模糊矩阵的有关运算实验学时:4学时实验内容:⑴ 根据已知数据进行数据标准化.⑵ 根据已知数据建立模糊相似矩阵,并求出其传递闭包矩阵.⑶ (可选做)根据模糊等价矩阵绘制动态聚类图.⑷ (可选做)根据原始数据或标准化后的数据和⑶的结果确定最佳分类. 实验日期:20017年12月02日实验步骤:1 问题描述:设有8种产品,它们的指标如下:x 1 = (37,38,12,16,13,12)x 2 = (69,73,74,22,64,17)x 3 = (73,86,49,27,68,39)x 4 = (57,58,64,84,63,28)x 5 = (38,56,65,85,62,27)x 6 = (65,55,64,15,26,48)x 7 = (65,56,15,42,65,35)x 8 = (66,45,65,55,34,32)建立相似矩阵,并用传递闭包法进行模糊聚类。
2 解决步骤:2.1 建立原始数据矩阵设论域},,{21n x x x X 为被分类对象,每个对象又有m 个指标表示其性状, im i i i x x x x ,,,21 ,n i ,,2,1 由此可得原始数据矩阵。
于是,得到原始数据矩阵为323455654566356542155665482615645565276285655638286384645857396827498673176422747369121316123837X 其中nm x 表示第n 个分类对象的第m 个指标的原始数据,其中m = 6,n = 8。
2.2 样本数据标准化2.2.1 对上述矩阵进行如下变化,将数据压缩到[0,1],使用方法为平移极差变换和最大值规格化方法。
(1)平移极差变换:111min{}max{}min{}ik ik i n ik ik ik i n i n x x x x x ,(1,2,,)k m L显然有01ikx ,而且也消除了量纲的影响。
基于模糊C均值的聚类分析

• U = initfcm(cluster_n, data_n); %初始 化模糊分割矩阵
%以下为主循环: • for i = 1:max_iter, • [U, center, obj_fcn(i)] =
stepfcm(data, U, cluster_n, expo); • if display, • fprintf('Iteration count = %d, obj.
基于模糊C均值的聚类分析
1 模糊c均值聚类(FCM)方法
模糊C均值聚类(FCM)方法是一种在已 知聚类数的情况下,利用隶属度函数和迭 代算法将有限的数据集分别聚类的方法。 其目标函数为:
式中, 为样本数; 为聚类数; 为第 个 样本相对于第 个聚类中心的隶属度; 为
第 个类别的聚类中心; 为样本到聚类 中心的欧式距离。聚类的结果使目标函 数 最小,因此,构造如下新的目标函 数:
(2)
这里 , =1,⋯ ,n,是等式的n个约束 式的拉格朗日乘子。对所有输入参量求 导,使式(1)达到最小的必要条件为:
(3)
(4)
由上述两个必要条件,模糊c均值聚类算 法是一个简单的迭代过程。在批处理方 式运行时,FCM采用下列步骤确定聚类中 心 和隶属矩阵 U:
步骤1 用值在0,1间的随机数初始 化隶属矩阵U,使其满足式(2)中的约束 条件。
1735.33; 2421.83; 2196.22; 535.62; 584.32; 2772.9; 2226.49; 1202.69;
2949.16 1692.62 1680.67 2802.88 172.78 2063.54 1449.58 1651.52 341.59 291.02
3244.44 1867.5 1575.78 3017.11 3084.49 3199.76 1641.58 1713.28 3076.62 3095.68
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1. 模糊聚类分析模型环境区域的污染情况由污染物在4个要素中的含量超标程度来衡量。
设这5个环境区域的污染数据为1x =(80, 10, 6, 2), 2x =(50, 1, 6, 4), 3x =(90, 6, 4, 6), 4x =(40, 5, 7, 3), 5x =(10, 1, 2, 4). 试用模糊传递闭包法对X 进行分类。
解 :由题设知特性指标矩阵为: *80106250164906464057310124X ⎡⎤⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎣⎦数据规格化:最大规格化'ij ijjx x M =其中: 12max(,,...,)j j j nj M x x x =00.8910.860.330.560.10.860.6710.60.5710.440.510.50.110.10.290.67X ⎡⎤⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎣⎦构造模糊相似矩阵: 采用最大最小法来构造模糊相似矩阵55()ij R r ⨯=,10.540.620.630.240.5410.550.700.530.620.5510.560.370.630.700.5610.380.240.530.370.381R ⎡⎤⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎣⎦利用平方自合成方法求传递闭包t (R )依次计算248,,R R R , 由于84R R =,所以4()t R R =210.630.620.630.530.6310.560.700.530.620.5610.620.530.630.700.6210.530.530.530.530.531R ⎡⎤⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎣⎦,410.630.620.630.530.6310.620.700.530.620.6210.620.530.630.700.6210.530.530.530.530.531R ⎡⎤⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎣⎦=8R选取适当的置信水平值[0,1]λ∈, 按λ截矩阵进行动态聚类。
把()t R 中的元素从大到小的顺序编排如下: 1>0.70>0.63>062>053. 依次取λ=1, 0.70, 0.63, 062, 053,得11000001000()0010*******0001t R ⎡⎤⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎣⎦,此时X 被分为5类:{1x },{2x },{3x },{4x },{5x }0.71000001010()001000101000001t R ⎡⎤⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎣⎦,此时X 被分为4类:{1x },{2x ,4x },{3x },{5x }0.631101011010()001001101000001t R ⎡⎤⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎣⎦,此时X 被分为3类:{1x ,2x ,4x },{3x },{5x }0.621111011110()111101111000001t R ⎡⎤⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎣⎦,此时X 被分为2类:{1x ,2x ,4x ,3x },{5x }0.531111111111()111111*********t R ⎡⎤⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎣⎦,此时X 被分为1类:{12345,,,,x x x x x }Matlab 程序如下: %数据规格化MATLAB 程序a=[80 10 6 2 50 1 6 4 90 6 4 6 40 5 7 3 10 1 2 4]; mu=max(a) for i=1:5 for j=1:4r(i,j)=a(i,j)/mu(j); end end r%采用最大最小法构造相似矩阵r=[0.8889 1.0000 0.8571 0.3333 0.5556 0.1000 0.8571 0.6667 1.0000 0.6000 0.5714 1.0000 0.4444 0.5000 1.0000 0.5000 0.1111 0.1000 0.2857 0.6667]; b=r'; for i=1:5 for j=1:5R(i,j)=sum(min([r(i,:);b(:,j)']))/sum(max([r(i,:);b(:,j)'])); end end R%利用平方自合成方法求传递闭包t (R ) 矩阵合成的MATLAB 函数function rhat=hech(r); n=length(r); for i=1:n for j=1:nrhat(i,j)=max(min([r(i,:);r(:,j)'])); end end求模糊等价矩阵和聚类的程序R=[ 1.0000 0.5409 0.6206 0.6299 0.2432 0.5409 1.0000 0.5478 0.6985 0.5339 0.6206 0.5478 1.0000 0.5599 0.3669 0.6299 0.6985 0.5599 1.0000 0.3818 0.2432 0.5339 0.3669 0.3818 1.0000]; R1=hech (R) R2=hech (R1) R3=hech (R2) bh=zeros(5); bh(find(R2>0.7))=12. 模糊综合评判模型某烟草公司对某部门员工进行的年终评定,关于考核的具体操作过程,以对一名员工的考核为例。
如下表所示,根据该部门工作人员的工作性质,将18个指标分成工作绩效(1U )、工作态度(2U )、工作能力(3U )和学习成长(4U )这4各子因素集。
员工考核指标体系及考核表技能提高 0.1 0.4 0.3 0.1 0.1 培训参与 0.2 0.3 0.4 0.1 0 工作提供0.40.30.20.1请专家设定指标权重,一级指标权重为:()0.4,0.3,0.2,0.1A =二级指标权重为:()10.2,0.3,0.3,0.2A =()20.3,0.2,0.1,0.2,0.2A = ()30.1,0.2,0.3,0.2,0.2A = ()40.3,0.2,0.2,0.3A =对各个子因素集进行一级模糊综合评判得到:()1110.39,0.39,0.26,0.04,0.01B A R == ()2220.21,0.37,0.235,0.125,0.06B A R == ()3330.15,0.32,0.355,0.125,0.06B A R ==()4440.27,0.35,0.24,0.1,0.02B A R ==这样,二级综合评判为:()0.390.390.260.040.010.210.370.2350.1250.060.4,0.3,0.2,0.10.150.320.3550.1250.060.270.350.240.10.2B A R ⎡⎤⎢⎥⎢⎥==⎢⎥⎢⎥⎣⎦()0.28,0.37,0.27,0.09,0.04=根据最大隶属度原则,认为该员工的评价为良好。
同理可对该部门其他员工进行考核。
3. 层次分析模型你已经去过几家主要的摩托车商店,基本确定将从三种车型中选购一种,你选择的标准主要有:价格、耗油量大小、舒适程度和外观美观情况。
经反复思考比较,构造了它们之间的成对比较判断矩阵。
A=1378115531113751111853⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦三种车型(记为a,b,c )关于价格、耗油量、舒适程度和外表美观情况的成对比较判断矩阵为价格 a b c 耗油量 a b c1231/2121/31/21a b c ⎡⎤⎢⎥⎢⎥⎢⎥⎣⎦ 11/51/251721/71a b c ⎡⎤⎢⎥⎢⎥⎢⎥⎣⎦舒适程度 a b c 外表 a b c1351/3141/51/41a b c ⎡⎤⎢⎥⎢⎥⎢⎥⎣⎦ 11/535171/31/71a b c ⎡⎤⎢⎥⎢⎥⎢⎥⎣⎦根据上述矩阵可以看出四项标准在你心目中的比重是不同的,请按由重到轻顺序将它们排出。
解:用matlab 求解 层次总排序的结果如下表Matlab程序如下:clc,clearn1=4;n2=3;a=[1 3 7 81/3 1 5 51/7 1/5 1 31/8 1/5 1/3 1];b1=[1 2 31/2 1 21/3 1/2 1 ];b2=[1 1/5 1/25 1 72 1/7 1 ];b3=[1 3 51/3 1 41/5 1/4 1 ];b4=[1 1/5 35 1 71/3 1/7 1];ri=[0,0,0.58,0.90,1.12,1.24,1.32,1.41,1.45]; % 一致性指标RI[x,y]=eig(a); %x为特征向量,y为特征值lamda=max(diag(y));num=find(diag(y)==lamda);w0=x(:,num)/sum(x(:,num));w0 %准则层特征向量CR0=(lamda-n1)/(n1-1)/ri(n1) %准则层一致性比例for i=1:n1[x,y]=eig(eval(char(['b',int2str(i)])));lamda=max(diag(y));num=find(diag(y)==lamda);w1(:,i)=x(:,num)/sum(x(:,num)); %方案层的特征向量CR1(i)=(lamda-n2)/(n2-1)/ri(n2); %方案层的一致性比例endw1CR1, ts=w1*w0, CR=CR1*w0 %ts为总排序的权值,CR为层次总排序的随机一致性比例% 当CR小于0.1时,认为总层次排序结果具有较满意的一致性并接受该结果,否则对判断矩阵适当修改4. 灰色预测GM(1,1)模型某地区年平均降雨量数据如表 某地区年平均降雨量数据规定hz=320,并认为(0)()x i <=hz 为旱灾。
预测下一次旱灾发生的时间 解:初始序列如下(0)x =(390.6,412,320,559.2,380.8,542.4,553,310,561,300,632,540,406.2,313.8,576,587.6,318.5)由于满足(0)()x i <=320的(0)()x i 为异常值,易得下限灾变数列为0hz x = (320,310,300,313.8,318.5)其对应的时刻数列为t = (3,8,10,14,17)建立GM (1,1)模型(1) 对原始数据t 做一次累加,即t(1) = (3,11,21,35,52) (2) 构造数据矩阵及数据向量 (3) 计算a ,ba=-0.2536,b=6.2585 (4) 建立模型y=-24.6774+27.6774*exp(.253610*t) (5) 模型检验(6) 通过计算可以预测到第六个数据是22.0340由于 22.034 与17 相差5.034,这表明下一次旱灾将发生在五年以后。
