【高考数学】2018最新版本高考理科第一轮复习(6.5合情
2018年高考数学(理)一轮复习文档第三章三角函数、解三角形第2讲同角三角函数的基本关系与诱导公式Word版
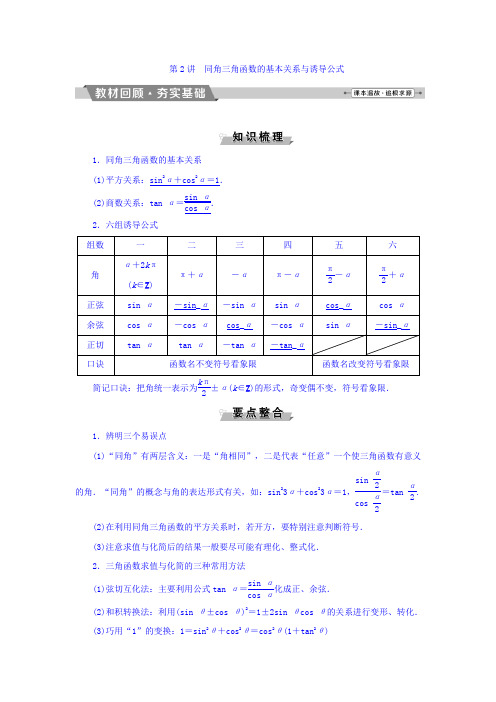
第2讲 同角三角函数的基本关系与诱导公式1.同角三角函数的基本关系 (1)平方关系:sin 2α+cos 2α=1. (2)商数关系:tan α=sin αcos α.2.六组诱导公式简记口诀:把角统一表示为k π2±α(k ∈Z )的形式,奇变偶不变,符号看象限.1.辨明三个易误点(1)“同角”有两层含义:一是“角相同”,二是代表“任意”一个使三角函数有意义的角.“同角”的概念与角的表达形式有关,如:sin 23α+cos 23α=1,sinα2cosα2=tan α2.(2)在利用同角三角函数的平方关系时,若开方,要特别注意判断符号. (3)注意求值与化简后的结果一般要尽可能有理化、整式化. 2.三角函数求值与化简的三种常用方法(1)弦切互化法:主要利用公式tan α=sin αcos α化成正、余弦.(2)和积转换法:利用(sin θ±cos θ)2=1±2sin θcos θ的关系进行变形、转化. (3)巧用“1”的变换:1=sin 2θ+cos 2θ=cos 2θ(1+tan 2θ)=tan π4=….1.cos ⎝ ⎛⎭⎪⎫-20π3=( ) A.12 B.32 C .-12D .-32C2.已知sin ⎝ ⎛⎭⎪⎫π2+α=35,α∈⎝⎛⎭⎪⎫0,π2,则sin(π+α)等于( )A.35 B .-35C.45D .-45D 因为sin ⎝⎛⎭⎪⎫π2+α=35,α∈⎝ ⎛⎭⎪⎫0,π2, 所以cos α=35,所以sin α=45,所以sin(π+α)=-sin α=-45.3.若sin θcos θ=12,则tan θ+cos θsin θ的值是( )A .-2B .2C .±2D.12B tan θ+cos θsin θ=sin θcos θ+cos θsin θ=1cos θsin θ=2.4.若sin θ=-45,tan θ>0,则cos θ=________.由已知,θ在第三象限, 所以cos θ=-1-sin 2θ=-1-(-45)2=-35.-355.教材习题改编 已知tan θ=2,则sin θ·cos θ=________. sin θcos θ=sin θ·cos θsin 2θ+cos 2θ=tan θtan 2θ+1=222+1=25. 25同角三角函数的基本关系式(高频考点)同角三角函数的基本关系式的应用很广泛,也比较灵活.高考中常以选择题、填空题的形式出现.高考对同角三角函数基本关系式的考查主要有以下三个命题角度: (1)知弦求弦; (2)知弦求切; (3)知切求弦.(1)(2016·高考全国卷丙)若tan α=34,则cos 2α+2sin 2α=( )A.6425 B.4825C .1D.1625(2)已知sin α+2cos α=3,则tan α=( ) A.22 B. 2 C .-22D .- 2【解析】 (1)法一:由tan α=sin αcos α=34,cos 2α+sin 2α=1,得⎩⎪⎨⎪⎧sin α=35,cos α=45或⎩⎪⎨⎪⎧sin α=-35,cos α=-45,则sin 2α=2sin αcos α=2425,则cos 2α+2sin 2α=1625+4825=6425. 法二:cos 2α+2sin 2α=cos 2α+4sin αcos αcos 2α+sin 2α=1+4tan α1+tan 2α=1+31+916=6425. (2)因为sin α+2cos α=3, 所以(sin α+2cos α)2=3,所以sin 2α+22sin αcos α+2cos 2α=3, 所以sin 2α+22sin αcos α+2cos 2αsin 2α+cos 2α=3,所以tan 2α+22tan α+2tan 2α+1=3, 所以2tan 2α-22tan α+1=0,所以tan α=22. 【答案】 (1)A (2)A同角三角函数关系式及变形公式的应用(1)利用sin 2α+cos 2α=1可以实现角α的正弦、余弦的互化,利用sin αcos α=tan α可以实现角α的弦切互化.(2)应用公式时注意方程思想的应用:对于sin α+cos α,sin αcos α,sin α-cos α这三个式子,利用(sin α±cos α)2=1±2sin αcos α,可以知一求二.角度一 知弦求弦1.(2017·雅安模拟)已知sin θ+cos θ=43,θ∈(0,π4),则sin θ-cos θ的值为( )A.23 B.13 C .-23D .-13C (sin θ+cos θ)2=169,所以1+2sin θcos θ=169,所以2sin θcos θ=79,由(sin θ-cos θ)2=1-2sin θ·cos θ=1-79=29,可得sin θ-cos θ=±23.又因为θ∈(0,π4),sin θ<cos θ,所以sin θ-cos θ=-23.角度二 知弦求切2.已知cos ⎝ ⎛⎭⎪⎫π2+α=35,且α∈⎝ ⎛⎭⎪⎫π2,3π2,则tan α=( )A.43 B.34 C .-34D .±34B 因为cos ⎝⎛⎭⎪⎫π2+α=35,所以sin α=-35,显然α在第三象限,所以cos α=-45,故tan α=34.角度三 知切求弦3.若sin α=2sin β,tan α=3tan β,则cos α=________. 因为sin α=2sin β,① tan α=3tan β, tan 2α=9tan 2β.②由①2÷②得:9cos 2α=4cos 2β.③ 由①2+③得sin 2α+9cos 2α=4. 又sin 2α+cos 2α=1, 所以cos 2α=38,所以cos α=±64. ±64诱导公式的应用(1)sin(-1 200°)cos 1 290°+cos(-1 020°)·sin(-1 050°)=________.(2)已知cos α是方程3x 2-x -2=0的根,且α是第三象限角,则sin (-α+3π2)cos (3π2+α)tan 2(π-α)cos (π2+α)sin (π2-α)等于________.(3)已知cos(π6-α)=23,则sin(α-2π3)=________.【解析】 (1)原式=-sin 1 200°cos 1 290°-cos 1 020°·sin 1 050°=-sin(3×360°+120°)cos(3×360°+210°)-cos(2×360°+300°)sin(2×360°+330°)=-sin 120°cos 210°-cos 300°sin 330°=-sin(180°-60°)cos(180°+30°)-cos(360°-60°)·sin(360°-30°) =sin 60°cos 30°+cos 60°sin 30° =32×32+12×12=1. (2)因为方程3x 2-x -2=0的根为x 1=1,x 2=-23,由题知cos α=-23,所以sin α=-53,tan α=52. 所以原式=-cos αsin αtan 2α-sin αcos α=tan 2α=54.(3)因为⎝ ⎛⎭⎪⎫π6-α+⎝ ⎛⎭⎪⎫α-2π3=-π2,所以α-2π3=-π2-⎝ ⎛⎭⎪⎫π6-α,所以sin ⎝ ⎛⎭⎪⎫α-2π3=sin ⎣⎢⎡⎦⎥⎤-π2-⎝ ⎛⎭⎪⎫π6-α=-cos ⎝ ⎛⎭⎪⎫π6-α=-23.【答案】 (1)1 (2)54 (3)-23(1)诱导公式用法的一般思路 ①化大角为小角.②角中含有加减π2的整数倍时,用公式去掉π2的整数倍.(2)常见的互余和互补的角①常见的互余的角:π3-α与π6+α;π3+α与π6-α;π4+α与π4-α等.②常见的互补的角:π3+θ与2π3-θ;π4+θ与3π4-θ等.(3)三角函数式化简的方向 ①切化弦,统一名. ②用诱导公式,统一角.③用因式分解将式子变形,化为最简.1.(2017·福建省毕业班质量检测)若sin(π2+α)=-35,且α∈(π2,π),则sin(π-2α)=( )A.2425 B.1225C .-1225D .-2425D 由sin(π2+α)=cos α=-35,且α∈(π2,π),得sin α=45,所以sin(π-2α)=sin 2α=2sin αcos α=-2425,选项D 正确.2.sin(-1 071°)si n 99°+sin(-171°)sin(-261°)=________. 原式=(-sin 1 071°)·sin 99°+sin 171°·sin 261°=-sin (3×360°-9°)sin(90°+9°)+sin(180°-9°)·sin(270°-9°)=sin 9°cos 9°-sin 9°cos 9°=0.故填0.3.已知cos(π+α)=-12,求sin[α+(2n +1)π]+sin (π+α)sin (π-α)·cos (α+2n π)(n ∈Z ).因为cos(π+α)=-12,所以-cos α=-12,cos α=12.sin[α+(2n +1)π]+sin (π+α)sin (π-α)cos (α+2n π)=sin (α+2n π+π)-sin αsin αcos α=sin (π+α)-sin αsin αcos α=-2sin αsin αcos α=-2cos α=-4.——方程思想求解三角函数值已知sin θ+cos θ=713,θ∈(0,π),则tan θ=________.【解析】 法一:因为sin θ+cos θ=713,θ∈(0,π),所以(sin θ+cos θ)2=1+2sin θcos θ=49169,所以sin θcos θ=-60169.由根与系数的关系,知sin θ,cos θ是方程x 2-713x -60169=0的两根,所以x 1=1213,x 2=-513.又sin θcos θ=-60169<0,所以sin θ>0,cos θ<0.所以sin θ=1213,cos θ=-513.所以tan θ=sin θcos θ=-125.法二:同法一,得sin θcos θ=-60169,所以sin θcos θsin 2θ+cos 2θ=-60169. 齐次化切,得tan θtan 2 θ+1=-60169,即60tan 2θ+169tan θ+60=0, 解得tan θ=-125或tan θ=-512.又θ∈(0,π),sin θ+cos θ=713>0,sin θcos θ=-60169<0.所以θ∈(π2,3π4),所以tan θ=-125.【答案】 -125(1)本题利用方程思想法一:由sin θ+cos θ、sin θcos θ的值构造一元二次方程,把sin θ与cos θ看作此方程的两根,即可求出sin θ与cos θ的值,便可求解.法二:利用三角函数的基本关系转化为关于tan θ的一元二次方程求解.(2)所谓方程思想就是在解决问题时,用事先设定的未知数沟通问题中所涉及的各量间的等量关系,建立方程或方程组,求出未知数及各量的值,或者用方程的性质去分析、转化问题,使问题获得解决.已知sin(3π-α)=-2sin(π2+α),则sin αcos α等于( )A .-25 B.25C.25或-25D .-15A 因为sin(3π-α)=sin(π-α)=-2sin(π2+α),所以sin α=-2cos α,所以tan α=-2,当α在第二象限时,⎩⎪⎨⎪⎧sin α=255cos α=-55,所以sin αcos α=-25;当α在第四象限时,⎩⎪⎨⎪⎧sin α=-255cos α=55,所以sin αcos α=-25,综上,sin αcosα=-25,故选A.1.tan(-233π)的值为( )A. 3 B .- 3 C.33D .-33A A tan(-233π)=tan(-8π+π3)=tan π3= 3.2.已知sin(π+θ)=-3cos(2π-θ),|θ|<π2,则θ等于( )A .-π6B .-π3C.π6D.π3D 因为sin(π+θ)=-3cos(2π-θ), 所以-sin θ=-3cos θ,所以tan θ= 3. 因为|θ|<π2,所以θ=π3.3.(2017·福建省毕业班质量检测)已知cos(α+π2)=13,则cos 2α的值等于( )A.79 B .-79C.89D .-89A 法一:因为cos(α+π2)=13,所以sin α=-13,所以cos α=±223,所以cos 2α=cos 2α-sin 2α=(±223)2-(-13)2=79,故选A.法二:因为cos(α+π2)=13,所以sin α=-13,所以cos 2α=1-2sin 2α=1-2×19=79,故选A.4.已知sin α+3cos α3cos α-sin α=5,则sin 2α-sin αcos α的值为( )A .-15B .-25C.15D.25D 依题意得tan α+33-tan α=5,所以tan α=2.所以sin 2α-sin αcos α=sin 2α-sin αcos αsin 2α+cos 2α=tan 2α-tan αtan 2α+1=22-222+1=25. 5.已知f (x )=a sin(πx +α)+b cos(πx +β)+4,若f (2 016)=5,则f (2 017)的值是( )A .2B .3C .4D .5B 因为f (2 016)=5.所以a sin(2 016π+α)+b cos(2 016π+β)+4=5, 即a sin α+b cos β=1.所以f (2 017)=a sin(2 017π+α)+b cos(2 017π+β)+4=-a sin α-b cos β+4=-1+4=3.6.已知sin α+3cos α+1=0,则tan α的值为( ) A.43或34 B .-34或-43C.34或-43D .-43或不存在D 由sin α=-3cos α-1,可得(-3cos α-1)2+cos 2α=1,即5cos 2α+3cos α=0,解得cos α=-35或cos α=0,当cos α=0时,tan α的值不存在,当cos α=-35时,sin α=-3cos α-1=45,tan α=sin αcos α=-43,故选D.7.化简sin (π2+α)cos (π2-α)cos (π+α)+sin (π-α)cos (π2+α)sin (π+α)=________. 原式=cos αsin α-cos α+sin α(-sin α)-sin α=-sin α+sin α=0. 08.在△ABC 中,若tan A =23,则sin A =________. 因为tan A =23>0,所以A 为锐角,于是1+tan 2A =1+29=119=1cos 2A ,cos 2A =911,cos A =31111,sin A =tan A cos A =2211. 2211 9.sin 43π·cos 56π·tan(-43π)的值是________. 原式=sin(π+π3)·cos(π-π6)·tan(-π-π3) =(-sin π3)·(-cos π6)·(-tan π3) =(-32)×(-32)×(-3)=-334. -33410.已知sin ⎝ ⎛⎭⎪⎫7π12+α=23,则cos ⎝⎛⎭⎪⎫α-11π12=________. cos ⎝ ⎛⎭⎪⎫α-11π12=cos ⎝ ⎛⎭⎪⎫11π12-α =cos ⎣⎢⎡⎦⎥⎤π-⎝ ⎛⎭⎪⎫π12+α=-cos ⎝ ⎛⎭⎪⎫π12+α, 而sin ⎝ ⎛⎭⎪⎫7π12+α=sin ⎣⎢⎡⎦⎥⎤π2+⎝ ⎛⎭⎪⎫π12+α =cos ⎝ ⎛⎭⎪⎫π12+α=23, 所以cos ⎝⎛⎭⎪⎫α-11π12=-23. -2311.已知sin θ=45,π2<θ<π. (1)求tan θ的值;(2)求sin 2θ+2sin θcos θ3sin 2θ+cos 2θ的值.(1)因为sin 2θ+cos 2θ=1,所以cos 2θ=925.又π2<θ<π,所以cos θ=-35.所以tan θ=sin θcos θ=-43.(2)由(1)知,sin 2θ+2sin θcos θ3sin 2θ+cos 2 θ=tan 2θ+2tan θ3tan 2θ+1=-857.12.已知α为第三象限角,f (α)=sin (α-π2)·cos (3π2+α)·tan (π-α)tan (-α-π)·sin (-α-π).(1)化简f (α);(2)若cos(α-3π2)=15,求f (α)的值.(1)f (α)=sin (α-π2)·cos (3π2+α)·tan (π-α)tan (-α-π)·sin (-α-π)=(-cos α)·sin α·(-tan α)(-tan α)· sin α=-cos α.(2)因为cos(α-3π2)=15,所以-sin α=15,从而sin α=-15.又α为第三象限角,所以cos α=-1-sin 2α=-265,所以f (α)=-cos α=265.13.已知sin αcos α=18,且5π4<α<3π2,则cos α-sin α的值为() A .-32 B.32C .-34 D.34B 因为5π4<α<3π2,所以cos α<0,sin α<0且|cos α|<|sin α|,所以cos α-sin α>0.又(cos α-sin α)2=1-2sin αcos α=1-2×18=34, 所以cos α-sin α=32. 14.化简1-2sin 40°cos 40°cos 40°-1-sin 250°=________. 原式=sin 240°+cos 240°-2sin 40°cos 40°cos 40°-cos 50°=|sin 40°-cos 40°|sin 50°-sin 40° =|sin 40°-sin 50°|sin 50°-sin 40° =sin 50°-sin 40°si n 50°-sin 40° =1.115.已知在△ABC 中,sin A +cos A =15. (1)求sin A cos A 的值;(2)判断△ABC 是锐角三角形还是钝角三角形;(3)求tan A 的值.(1)因为sin A +cos A =15,① 所以两边平方得1+2sin A cos A =125, 所以sin A cos A =-1225. (2)由sin A cos A =-1225<0,且0<A <π, 可知cos A <0,所以A 为钝角,所以△ABC 是钝角三角形.(3)因为(sin A -cos A )2=1-2sin A cos A =1+2425=4925, 又sin A >0,cos A <0,所以sin A -cos A >0,所以sin A -cos A =75,② 所以由①,②可得sin A =45,cos A =-35,所以tan A =sin A cos A =45-35=-43. 16.已知f (x )=cos 2(n π+x )·sin 2(n π-x )cos 2[(2n +1)π-x ](n ∈Z ). (1)化简f (x )的表达式; (2)求f ⎝ ⎛⎭⎪⎫π2 016+f ⎝ ⎛⎭⎪⎫1 007π2 016的值. (1)当n 为偶数,即n =2k (k ∈Z )时,f (x )=cos 2(2k π+x )·sin 2(2k π-x )cos 2[(2×2k +1)π-x ]=cos 2x ·sin 2(-x )cos 2(π-x )=cos 2x ·(-sin x )2(-cos x )2 =sin 2x (n =2k ,k ∈Z );当n 为奇数,即n =2k +1(k ∈Z )时,f (x )=cos 2[(2k +1)π+x ]·sin 2[(2k +1)π-x ]cos 2{[2×(2k +1)+1]π-x }=cos 2[2k π+(π+x )]·sin 2[2k π+(π-x )]cos 2[2×(2k +1)π+(π-x )]=cos 2(π+x )·sin 2(π-x )cos 2(π-x )=(-cos x )2sin 2x (-cos x )2 =sin 2x (n =2k +1,k ∈Z ).综上得f (x )=sin 2x . (2)由(1)得f ⎝ ⎛⎭⎪⎫π2 016+f ⎝ ⎛⎭⎪⎫1 007π2 016 =sin2π2 016+sin 21 007π2 016 =sin2π2 016+sin 2⎝ ⎛⎭⎪⎫π2-π2 016 =sin2π2 016+cos 2π2 016=1.。
2018届高考数学理科全国通用一轮总复习课件:第五章

感悟考题
试一试
3.(2016·滨州模拟)已知等比数列{an}的公比q大于1,
a3a7=72,a2+a8=27,则a12= ( A.96 B.64 C.72 ) D.48
(n}是公比大于1的等比数列,Sn为数列{an}的前n 项和.已知S3=7,且a1+3,3a2,a3+4构成等差数列,则 an=________.
【解题导引】(1)根据a3+a5+a7与a1+a3+a5的联系求解. (2)将已知条件转化为a2的方程组,求得a2,再利用S3=7 求得公比q,进而求解.
(2)由an+1=qan(q≠0),并不能断言{an}为等比数列,还 要验证a1≠0.
(3)等比数列中奇数项的符号相同,偶数项的符号相同.
2.等比数列{an}的单调性 (1)满足
a1 0, q 1 0 q 1 a1 0, 或 a1 0, 时,{a }是递减数列. (2)满足 n q 1 0 q 1 a1 0, 时,{a }为常数列. (3)当 n q 1 a1 0, 或
解得a2=2.设数列{an}的公比为q,由a2=2,可得a1= 2 ,
q
a3=2q.又S3=7,可知 2 +2+2q=7,即2q2-5q+2=0,解得
q1=2,q2= 1 .由题意得q>1,所以q=2,所以a1=1.
所以插入的两个数分别为3×4=12,12×4=48.
答案:12,48
2.(必修5P62习题2.5B组T2改编)设等比数列{an}的前n 项和为Sn,若 S6 1 , 则 S9 =________________.
2018高考数学一轮复习第6章不等式推理与证明第4节归纳与类比教师用书文北师大版

第四节归纳与类比[考纲传真] 1.了解合情推理的含义,能利用归纳和类比等进行简单的推理,了解合情推理在数学发现中的作用.2.了解演绎推理的重要性;掌握演绎推理的基本模式,并能用它们进行一些简单推理.3.了解合情推理和演绎推理之间的联系和差异.1.归纳推理(1)定义:根据一类事物中部分事物具有某种属性,推断该类事物中每一个事物都有这种属性的推理方式.(2)特点:①是由部分到整体,由个别到一般的推理.②利用归纳推理得出的结论不一定是正确的.2.类比推理(1)定义:由于两类不同对象具有某些类似的特征,在此基础上,根据一类对象的其他特征,推断另一类对象也具有类似的其他特征的推理过程.(2)特点:①是两类事物特征之间的推理.②利用类比推理得出的结论不一定是正确的.3.合情推理(1)定义:是根据实验和实践的结果,个人的经验和直觉,已有的事实和正确的结论(定义、公理、定理等),推测出某些结果的推理方式.(2)归纳推理和类比推理是最常见的合情推理.4.演绎推理(1)定义:是根据已知的事实和正确的结论,按照严格的逻辑法则得到新结论的推理过程.(2)“三段论”是演绎推理的一般模式,包括:①大前提——已知的一般原理;②小前提——所研究的特殊情况;③结论——根据一般原理,对特殊情况做出的判断.1.(思考辨析)判断下列结论的正误.(正确的打“√”,错误的打“×”)(1)归纳推理与类比推理都是由特殊到一般的推理.( )(2)在类比时,平面中的三角形与空间中的平行六面体作为类比对象较为合适.( )(3)“所有3的倍数都是9的倍数,某数m 是3的倍数,则m 一定是9的倍数”,这是三段论推理,但其结论是错误的.( )(4)在演绎推理中,只要符合演绎推理的形式,结论就一定正确.( )[答案] (1)× (2)× (3)√ (4)×2.由“半径为R 的圆内接矩形中,正方形的面积最大”,推出“半径为R 的球的内接长方体中,正方体的体积最大”是( )A .归纳推理B .类比推理C .演绎推理D .以上都不是B [类比推理的一般步骤是:(1)找出两类事物之间的相似性或一致性.(2)用一类事物的性质去推测另一类事物的性质,得出一个明确的命题(猜想).所以,由“半径为R 的圆内接矩形中,正方形的面积最大”,推理出“半径为R 的球的内接长方体中,正方体的体积最大”是类比推理.]3.(教材改编)已知数列{a n }中,a 1=1,n ≥2时,a n =a n -1+2n -1,依次计算a 2,a 3,a 4后,猜想a n 的表达式是( )A .a n =3n -1B .a n =4n -3C .a n =n 2D .a n =3n -1 C [a 1=1,a 2=4,a 3=9,a 4=16,猜想a n =n 2.]4.“因为指数函数y =a x 是增函数(大前提),而y =⎝ ⎛⎭⎪⎫13x 是指数函数(小前提),所以函数y =⎝ ⎛⎭⎪⎫13x 是增函数(结论)”,上面推理的错误在于( ) A .大前提错误导致结论错误B .小前提错误导致结论错误C .推理形式错误导致结论错误D .大前提和小前提错误导致结论错误A [“指数函数y =a x是增函数”是本推理的大前提,它是错误的.因为实数a 的取值范围没有确定,所以导致结论是错误的.]5.(2014·全国卷Ⅰ)甲、乙、丙三位同学被问到是否去过A ,B ,C 三个城市时, 甲说:我去过的城市比乙多,但没去过B 城市;乙说:我没去过C 城市;丙说:我们三人去过同一城市.由此可判断乙去过的城市为________.A [由题意可推断:甲没去过B 城市,但比乙去的城市多,而丙说“三人去过同一城市”,说明甲去过A ,C 城市,而乙“没去过C 城市”,说明乙去过城市A ,由此可知,乙去过的城市为A.](1)(2016·武汉4月调研)数列12,13,23,14,24,34,…,1m +1,2m +1,…,mm +1,…的第20项是( )A.58B .34C .57D .67(2)(2016·山东高考)观察下列等式:⎝ ⎛⎭⎪⎫sin π3-2+⎝ ⎛⎭⎪⎫sin 2π3-2=43×1×2; ⎝ ⎛⎭⎪⎫sin π5-2+⎝ ⎛⎭⎪⎫sin 2π5-2+⎝ ⎛⎭⎪⎫sin 3π5-2+⎝ ⎛⎭⎪⎫sin 4π5-2=43×2×3; ⎝ ⎛⎭⎪⎫sin π7-2+⎝ ⎛⎭⎪⎫sin 2π7-2+⎝ ⎛⎭⎪⎫sin 3π7-2+…+⎝ ⎛⎭⎪⎫sin 6π7-2=43×3×4; ⎝ ⎛⎭⎪⎫sin π9-2+⎝ ⎛⎭⎪⎫sin 2π9-2+⎝ ⎛⎭⎪⎫sin 3π9-2+…+⎝ ⎛⎭⎪⎫sin 8π9-2=43×4×5; ……照此规律,⎝ ⎛⎭⎪⎫sin π2n +1-2+⎝ ⎛⎭⎪⎫sin 2π2n +1-2+⎝ ⎛⎭⎪⎫sin 3π2n +1-2+…+⎝⎛⎭⎪⎫sin 2n π2n +1-2=________. (1)C (2)43n (n +1) [(1)数列m m +1在数列中是第1+2+3+…+m =m m +1 2项,当m =5时,即56是数列中第15项,则第20项是57,故选C. (2)通过观察已给出等式的特点,可知等式右边的43是个固定数,43后面第一个数是等式左边最后一个数括号内角度值分子中π的系数的一半,43后面第二个数是第一个数的下一个自然数,所以,所求结果为43×n ×(n +1),即43n (n +1).] [规律方法] 1.常见的归纳推理分为数的归纳和形的归纳两类:(1)数的归纳包括数字归纳和式子归纳,解决此类问题时,需要细心观察,寻求相邻项及项与序号之间的关系,同时还要联系相关的知识,如等差数列、等比数列等;(2)形的归纳主要包括图形数目归纳和图形变化规律归纳,合理利用特殊图形归纳推理得出结论,并用赋值检验法验证其真伪性.2.归纳推理的一般步骤:(1)通过观察个别情况发现某些相同性质;(2)从相同性质中推出一个明确表述的一般性命题.[变式训练1] (1)已知x ∈(0,+∞),观察下列各式:x +1x ≥2,x +4x 2=x 2+x 2+4x 2≥3,x +27x 3=x 3+x 3+x 3+27x 3≥4,…,类比得x +a x n ≥n +1(n ∈N *),则a =__________. (2)下面图形由小正方形组成,请观察图641(1)至图(4)的规律,并依此规律,写出第n 个图形中小正方形的个数是__________.【导学号:66482303】图641(1)n n (n ∈N *) (2)n n +1 2(n ∈N *) [(1)第一个式子是n =1的情况,此时a =11=1;第二个式子是n =2的情况,此时a =22=4;第三个式子是n =3的情况,此时a =33=27,归纳可知a =n n .(2)由题图知第n 个图形的小正方形个数为1+2+3+…+n .所以总个数为n n +1 2(n∈N *).]n 数列,则数列{b n }⎝ ⎛⎭⎪⎫b n =a 1+a 2+…+a n n 也是等差数列,类比这一性质可知,若正项数列{c n }是等比数列,且{d n }也是等比数列,则d n 的表达式应为( )A .d n =c 1+c 2+…+c n nB .d n =c 1·c 2·…·c n nC .d n =n c n 1+c n 2+…+c n n nD .d n =n c 1·c 2·…·c n(2)(2016·贵州六校联考)在平面几何中,△ABC 的∠C 的平分线CE 分AB 所成线段的比为AC BC =AE BE.把这个结论类比到空间:在三棱锥A BCD 中(如图642),DEC 平分二面角A CD B 且与AB 相交于E ,则得到类比的结论是________________.【导学号:66482304】图642(1)D (2)AE EB =S △ACD S △BCD[(1)法一:从商类比开方,从和类比到积,则算术平均数可以类比几何平均数,故d n 的表达式为d n =n c 1·c 2·…·c n .法二:若{a n }是等差数列,则a 1+a 2+…+a n =na 1+n n -1 2d ,∴b n =a 1+ n -1 2d =d 2n +a 1-d 2,即{b n }为等差数列;若{c n }是等比数列,则c 1·c 2·…·c n =c n 1·q 1+2+…+(n -1)=c n 1·q n n -1 2,∴d n =n c 1·c 2·…·c n =c 1·q n -12,即{d n }为等比数列,故选D.(2)由平面中线段的比转化为空间中面积的比可得AE EB =S △ACD S △BCD.] [规律方法] 1.进行类比推理,应从具体问题出发,通过观察、分析、联想进行对比,提出猜想,其中找到合适的类比对象是解题的关键.2.类比推理常见的情形有:平面与空间类比;低维与高维类比;等差数列与等比数列类比;运算类比(和与积、乘与乘方,差与除,除与开方).数的运算与向量运算类比;圆锥曲线间的类比等.[变式训练2] 给出下面类比推理(其中Q 为有理数集,R 为实数集,C 为复数集): ①“若a ,b ∈R ,则a -b =0⇒a =b ”类比推出“a ,c ∈C ,则a -c =0⇒a =c ”; ②“若a ,b ,c ,d ∈R ,则复数a +b i =c +d i ⇒a =c ,b =d ”类比推出“a ,b ,c ,d ∈Q ,则a +b 2=c +d 2⇒a =c ,b =d ”;③“a ,b ∈R ,则a -b >0⇒a >b ”类比推出“若a ,b ∈C ,则a -b >0⇒a >b ”;④“若x ∈R ,则|x |<1⇒-1<x <1”类比推出“若z ∈C ,则|z |<1⇒-1<z <1.”其中类比结论正确的个数为( )A .1B .2C .3D .4B [类比结论正确的有①②.]数列{a n }的前n 项和记为S n ,已知a 1=1,a n +1=nS n (n ∈N *).证明: (1)数列⎩⎨⎧⎭⎬⎫S n n 是等比数列; (2)S n +1=4a n .【导学号:66482305】[证明] (1)∵a n +1=S n +1-S n ,a n +1=n +2nS n , ∴(n +2)S n =n (S n +1-S n ),即nS n +1=2(n +1)S n . 2分∴S n +1n +1=2·S n n ,又S 11=1≠0,(小前提) 故⎩⎨⎧⎭⎬⎫S n n 是以1为首项,2为公比的等比数列.(结论)(大前提是等比数列的定义,这里省略了)5分(2)由(1)可知S n +1n +1=4·S n -1n -1(n ≥2), ∴S n +1=4(n +1)·S n -1n -1=4·n -1+2n -1·S n -1 =4a n (n ≥2),(小前提)8分又a 2=3S 1=3,S 2=a 1+a 2=1+3=4=4a 1,(小前提)∴对于任意正整数n ,都有S n +1=4a n .(结论)(第(2)问的大前提是第(1)问的结论以及题中的已知条件)12分[规律方法] 演绎推理的一般模式为三段论,三段论推理的依据是:如果集合M 的所有元素都具有性质P ,S 是M 的子集,那么S 中所有元素都具有性质P .应用三段论解决问题时,首先应该明确什么是大前提,小前提,然后再找结论.[变式训练3] 如图643所示,D ,E ,F 分别是BC ,CA ,AB 上的点,∠BFD =∠A ,且DE ∥BA .求证:ED =AF (要求注明每一步推理的大前提、小前提和结论,并最终把推理过程用简略的形式表示出来).图643【导学号:66482306】[证明] (1)同位角相等,两条直线平行,(大前提)∠BFD 与∠A 是同位角,且∠BFD =∠A ,(小前提)所以DF ∥EA .(结论)5分(2)两组对边分别平行的四边形是平行四边形,(大前提)DE ∥BA 且DF ∥EA ,(小前提)所以四边形AFDE 为平行四边形.(结论)8分(3)平行四边形的对边相等,(大前提)ED 和AF 为平行四边形的对边,(小前提)所以ED =AF .(结论)上面的证明可简略地写成:⎭⎪⎬⎪⎫∠BFD =∠A ⇒DF ∥EA DE ∥BA ⇒ 四边形AFDE 是平行四边形⇒ED =AF . 12分[思想与方法]1.合情推理的过程概括为从具体问题出发→观察、分析、比较、联想→归纳、类比→提出猜想2.演绎推理是从一般的原理出发,推出某个特殊情况的结论的推理方法,是由一般到特殊的推理,常用的一般模式是三段论.数学问题的证明主要通过演绎推理来进行.[易错与防范]1.在进行类比推理时要尽量从本质上去类比,不要被表面现象迷惑,否则只抓住一点表面现象的相似甚至假象就去类比,那么就会犯机械类比的错误.2.合情推理是从已知的结论推测未知的结论,发现与猜想的结论都要经过进一步严格证明.3.演绎推理是由一般到特殊的推理,它常用来证明和推理数学问题,注意推理过程的严谨性,书写格式的规范性.。
【课堂新坐标】2018版高考数学(人教A版理)一轮复习课件第6章第1节不等式的性质与一元二次不等式

1 1 1 1 1 C 正确;函数 y=x 在(0,+∞)上为减函数,由 x>y>0⇒x < y⇒x-y<0,
故 A 错误;函数 y=sin x 在(0,+∞)上不单调,当 x>y>0 时,不能比较 sin x 与 sin y 的大小,故 B 错误;x>y>0⇒xy>0⇒/ ln(xy)>0⇒/ ln x+ln y>0,故 D 错误.]
-3x+4>0 的解集为(-4,1).]
上一页 返回首页 下一页
高三一轮总复习
5.若不等式 mx2+2mx+1>0 的解集为 R,则 m 的取值范围是__________. 【导学号:01772195】
[0,1) [①当 m=0 时,1>0 显然成立;
m>0, 时,由条件知 2 Δ = 4 m -4m<0,
1 ac<bd, 故②不正确; 因为函数 y=x3是单调递增的, 所以③正确; 对于④, 由 a>b>0 1 1 可知 a >b >0,所以a2<b2,所以④不正确.]
2 2
上一页
返回首页
下一页
高三一轮总复习
3.(2016· 吉林长春二模)若 a,b∈R,且 a>b,则下列不等式恒成立的是( A.a >b
上一页
返回首页
下一页
高三一轮总复习
1 1 ①当 a=1 时,a=1,x-a(x-1)<0 无解; 1 1 1 ②当 a>1 时,a<1,解 x-a (x-1)<0 得a<x<1; 1 1 1 ③当 0<a<1 时,a>1,解 x-a(x-1)<0 得 1<x<a.10 分
高考数学新人教A版(理科)一轮复习课件:第二篇函数、导数及其应用第5节对数函数

则需 22<a<1(如图所示).
当
a>1
时,不符合题意,舍去.所以实数
a
的取值范围是
22,1.故
选 B.
返回导航
考点三 对数函数的性质及应用 考查角度 1:比较大小.
设 a=log3π,b=log2 3,c=log3 2,则( )
(A)a>b>c
(B)a>c>b
(C)b>a>c
(D)b>c>a
返回导航
返回导航
(2)B 由题意得,当 0<a<1 时,要使得 4x
<logax0<x≤12,即当 0<x≤12时,函数 y=4x 的图 象在函数 y=logax 图象的下方.
又当 x=12时,412=2,即函数 y=4x 的图象过
点12,2,把点12,2代入函数 y=logax,得 a= 22, 若函数 y=4x 的图象在函数 y=logax 图象的下方,
返回导航
【反思归纳】 (1)logaf(x)>logag(x) ⇔
或
.
(2)有关形如 y=logaf(x)的单调性:先求定义域,根据复合函数 y=
logau,u=f(x)的单调性(判断)求解.
(3)对于形如 y=logaf(x)(a>0 且 a≠1)的复合函数的值域的求解步骤
为:①分解成 y=logau,u=f(x)两个函数;②求 f(x)的定义域;③求 u
返回导航
考查角度 4:与对数函数有关的参数取值(范围)问题. 高考扫描:2013 高考新课标全国卷Ⅰ
函数 (A)(-∞,2) (C)(2,3)∪(3,+∞)
的定义域是( ) (B)(2,+∞) (D)(2,4)∪(4,+∞)
返回导航
C 解析:要使函数有意义就满足
,
高考数学一轮复习 第六章 数列 第5讲 数列的综合应用 理(2021年最新整理)

2018版高考数学一轮复习第六章数列第5讲数列的综合应用理编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望(2018版高考数学一轮复习第六章数列第5讲数列的综合应用理)的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为2018版高考数学一轮复习第六章数列第5讲数列的综合应用理的全部内容。
第5讲数列的综合应用一、选择题1.已知{a n}为等比数列.下面结论中正确的是 ( ).A.a1+a3≥2a2B.a2,1+a错误!≥2a错误!C.若a1=a3,则a1=a2D.若a3>a1,则a4〉a2解析设公比为q,对于选项A,当a1〈0,q≠1时不正确;选项C,当q=-1时不正确;选项D,当a1=1,q=-2时不正确;选项B正确,因为a错误!+a错误!≥2a1a3=2a错误!.答案B2.满足a1=1,log2a n+1=log2a n+1(n∈N*),它的前n项和为S n,则满足S n>1 025的最小n值是 ( ).A.9 B.10 C.11 D.12解析因为a1=1,log2a n+1=log2a n+1(n∈N*),所以a n+1=2a n,a n=2n-1,S n=2n-1,则满足S n〉1 025的最小n值是11.答案C3.某化工厂打算投入一条新的生产线,但需要经环保部门审批同意方可投入生产.已知该生产线连续生产n年的累计产量为f(n)=错误!n(n+1)(2n+1)吨,但如果年产量超过150吨,将会给环境造成危害.为保护环境,环保部门应给该厂这条生产线拟定最长的生产期限是 ( ).A.5年B.6年C.7年D.8年解析由已知可得第n年的产量a n=f(n)-f(n-1)=3n2。
系统集成2018高考数学理一轮总复习教案:第一章 集合
第一章集合与常用逻辑用语高考导航知识网络1.1 集合及其运算考点诠释重点:集合的表示、集合间的基本关系与基本运算.难点:自然语言,图形语言,集合语言之间的相互转化,集合元素确定性,互异性的理解及运用.典例精析题型一 集合的基本概念【例1】设a ,b ∈R ,集合{1,a +b ,a }=⎩⎨⎧⎭⎬⎫0,b a ,b ,则b -a 等于( ) A.1 B.-1 C.2 D.-2【思路分析】解题时根据集合中的对应元素相等,列出方程组,求出a ,b 的值,注意集合中元素的互异性.【解析】C.解法一:因为1≠0,所以a +b 和a 中必有一个为0,当a =0时,b a无意义,故a +b =0,所以两个集合分别为{1,0,a },{0,-1,b },所以a =-1,b =1,所以b -a =2.解法二:由{1,a +b ,a }=⎩⎨⎧⎭⎬⎫0,b a ,b ,得a ≠0, 所以⎩⎨⎧1+a +b +a =0+b a +b ,1·(a +b )·a =0·b a ·b ,解得⎩⎪⎨⎪⎧a =-1,b =1.所以b -a =2. 【方法归纳】(1)根据集合相等的定义,首先分析已知元素与另一个集合中的哪一个元素相等,有几种可能,然后列方程组求解;(2)对于含有字母的集合,在求出字母的值后,要检验是否满足集合中元素的互异性.【举一反三】1.(1)已知集合A ={0,1,2},则集合B ={x -y |x ∈A ,y ∈A }中元素的个数是( C )A.1B.3C.5D.9 (2)已知集合A ={-4,2a -1,a 2},B ={a -5,1-a ,9},若9∈(A ∩B ),则实数a 的值为 5或-3 .【解析】(1)C.B ={-2,-1,0,1,2}.(2)5或-3.因为9∈(A ∩B ),所以9∈A 且9∈B ,所以2a -1=9或a 2=9,所以a =5或a =±3.当a =5时,A ={-4,9,25},B ={0,-4,9},符合题意;当a =3时,A ={-4,5,9},B ={-2,-2,9},不满足集合中元素的互异性,所以a ≠3; 当a =-3时,A ={-4,-7,9},B ={-8,4,9},符合题意.所以a =5或a =-3.题型二 集合间的关系【例2】已知集合A ={1,3,m },B ={1,m },A ∪B =A ,则m 等于( )A.0或 3B.0或3C.1或 3D.1或3【思路分析】将A ∪B =A 转化为B ⊆A ,用分类讨论的方法求解.注意集合中元素互异性的检验.【解析】B.因为A ∪B =A ,所以B ⊆A ,所以m =3或m =m .若m =3,则A ={1,3,3},B ={1,3},满足A ∪B =A .若m =m ,解得m =0或m =1.若m =0,则A ={1,3,0},B ={1,0},满足A ∪B =A .若m =1,则A ={1,3,1},B ={1,1},显然不成立.综上,m =0或m =3,故选B.【方法归纳】已知两集合的关系求参数时,关键是将两集合的关系转化为元素的关系,进而转化为参数满足的关系,解决这类问题常常要合理利用数轴、Venn 图帮助分析,而且经常要对参数进行分类讨论.【举一反三】2.若集合A ={x |-2≤x ≤5},B ={x |m +1≤x ≤2m -1},且B ⊆A ,则由m 的可取值组成的集合为 {m |m ≤3} .【解析】当m +1>2m -1,即m <2时,B =,满足B ⊆A ;若B ≠,且满足B ⊆A ,如图所示,则⎩⎪⎨⎪⎧ m +1≤2m -1,m +1≥-2,2m -1≤5,即⎩⎪⎨⎪⎧ m ≥2,m ≥-3,所以2≤m ≤3.m ≤3,故m <2或2≤m ≤3,即所求集合为{m |m ≤3}.题型三 集合的运算【例3】已知全集U ={0,1,2,3,4,5,6,7,8,9},集合A ={0,1,3,5,8},集合B ={2,4,5,6,8},则(∁U A )∩(∁U B )为( )A.{5,8}B.{7,9}C.{0,1,3}D.{2,4,6}【思路分析】根据补集的定义求出∁U A ,∁U B ,再根据交集的定义得出结论,也可利用Venn 图解决.【解析】B.解法一:因为全集U ={0,1,2,3,4,5,6,7,8,9},集合A ={0,1,3,5,8},集合B ={2,4,5,6,8},所以∁U A ={2,4,6,7,9},∁U B ={0,1,3,7,9},所以(∁U A )∩(∁U B )={7,9}.故选B.解法二:集合(∁U A )∩(∁U B )=∁U (A ∪B )={7,9}.如图所示:【方法归纳】解决这类问题常见的思路有三种:一是利用交、并、补的定义求解;二是利用Venn 图;三是如果与不等式有关,常用数轴解决.【举一反三】3.已知全集为R ,集合A =,B ={x |x 2-6x +8≤0},则A ∩∁RB 等于(C )A.{x |x ≤0}B.{x |2≤x ≤4}C.{x |0≤x <2,或x >4}D.{x |0<x ≤2,或x ≥4}【解析】A =={x |x ≥0}, B ={x |2≤x ≤4},所以∁R B ={x |x <2,或x >4},此时A∩∁R B={x|0≤x<2,或x>4}.题型四以集合为载体的新定义问题【例4】设集合S={0,1,2,3,4,5},集合A是S的子集,若当x∈A时,都有x-1A 且x+1A,则称x为A的一个“孤立元素”,那么S中无“孤立元素”的4元素子集的个数为()A.4B.5C.6D.7【思路分析】先研究“孤立元素”的定义,再判断集合S中无“孤立元素”的4元素子集的个数.【解析】C.依据题中新定义的规定可知:当x∈A时,都有x-1A且x+1A,则称x 为A的一个“孤立元素”,那么x∈A时,如果x-1∈A或x+1∈A,则称x为A的一个非“孤立元素”,集合S中的4元素子集A中无“孤立元素”,需满足条件当x∈A 时,有x-1∈A或x+1∈A,依此要求可得符合条件的集合A为{0,1,2,3},{0,1,3,4},{0,1,4,5},{1,2,3,4},{1,2,4,5},{2,3,4,5},故符合条件的集合的个数为6,故选C.【方法归纳】集合新定义问题近年来经常出现在高考选择题与填空题中,这类试题的特点是通过给出新的概念或运算方法,在新的情境下完成某种推理证明,常见的有定义新概念、新公式、新运算和新法则等类型.【举一反三】4.在整数集Z中,被5除所得余数为k的所有整数组成一个“类”,记为[k],即[k]={5n+k|n∈Z},k=0,1,2,3,4.给出如下四个结论:①2 016∈[1];②-3∈[3];③Z=[0]∪[1]∪[2]∪[3]∪[4];④“整数a,b属于同一‘类’”的充要条件是“a-b∈[0]”.其中,正确结论的个数是( C )A.1B.2C.3D.4【解析】2 016=2 015+1=403×5+1∈[1],①正确;由-3=-5+2∈[2]可知②不正确;根据题意可知③正确;若整数a,b属于同一类,不妨设a,b∈[k]={5n+k|n∈Z},则a =5n+k,b=5m+k,n,m为整数,a-b=5(n-m)+0∈[0],反之也成立,④正确,故①③④正确.体验高考(2015新课标Ⅱ)已知集合A={-2,-1,0,1,2},B={x|(x-1)(x+2)<0},则A∩B等于()A.{-1,0}B.{0,1}C.{-1,0,1}D.{0,1,2}【解析】A.因为B={x|(x-1)(x+2)<0}={x|-2<x<1},A={-2,-1,0,1,2},所以A∩B ={-1,0}.故选A.【举一反三】(2015湖北)已知集合A={(x,y)|x2+y2≤1,x,y∈Z},B={(x,y)||x|≤2,|y|≤2,x,y∈Z},定义集合A B={(x 1+x2,y1+y2)|(x1,y1)∈A,(x2,y2)∈B},则A B中元素的个数为( C )A.77B.49C.45D.30【解析】当x1=0时,y1∈{-1,0,1},而x2,y2∈{-2,-1,0,1,2},此时x1+x2∈{-2,-1,0,1,2},y1+y2∈{-3,-2,-1,0,1,2,3},则A B中元素的个数为5×7=35.当x1=±1时,y1=0,而x2,y2∈{-2,-1,0,1,2},此时x1+x2∈{-3,-2,-1,0,1,2,3},y1+y2∈{-2,-1,0,1,2}.由于x1+x2∈{-2,-1,0,1,2},y1+y2∈{-2,-1,0,1,2}时,A B中的元素与前面重复,故此时与前面不重复的元素个数为2×5=10,所以A B中元素的个数为35+10=45.1.2命题及其关系、充分条件与必要条件考点诠释重点:四种命题的真假判定,充分条件、必要条件与充要条件的判定及其应用.难点:充分条件、必要条件、充要条件的判定,等价命题的转化.典例精析题型一四种命题的关系及其真假判断【例1】给出命题:若函数y=f(x)是幂函数,则函数y=f(x)的图象不过第四象限.在它的逆命题、否命题、逆否命题三个命题中,真命题的个数是()A.3B.2C.1D.0【思路分析】先写出原命题的逆命题、否命题和逆否命题,再判断其是否正确.【解析】C.易知原命题是真命题,则其逆否命题也是真命题,而逆命题、否命题是假命题,故它的逆命题、否命题、逆否命题三个命题中,真命题只有一个.【方法归纳】四种命题的关系及其真假判断(1)在判断四种命题之间的关系时,首先要分清命题的条件与结论,再分析每个命题的条件与结论之间的关系,要注意四种命题关系的相对性.(2)判断命题真假的关键:一是识别命题的构成形式;二是将命题简化,对等价的简化命题进行判断.要判断一个命题是假命题,只需举出反例.【举一反三】1.设原命题是“当c>0时,若a>b,则ac>bc”,写出它的逆命题、否命题与逆否命题,并分别判断它们的真假.【解析】“当c>0时”是大前提,写其他命题时应该保留,原命题的条件是a>b,结论是ac>bc.因此它的逆命题:当c>0时,若ac>bc,则a>b.它是真命题;否命题:当c>0时,若a≤b,则ac≤bc.它是真命题;逆否命题:当c>0时,若ac≤bc,则a≤b.它是真命题.题型二充分必要条件的判定【例2】(2015北京)设α,β是两个不同的平面,m是直线且mα.“m∥β”是“α∥β”的()A.充分而不必要条件B.必要而不充分条件C.充分必要条件D.既不充分也不必要条件【思路分析】m∥β并不能得到α∥β,根据面面平行的判定定理,只有α内的两相交直线都平行于β,才能得到α∥β,而α∥β,并且mα,显然能得到m∥β,这样即可找出正确选项.【解析】B.由两平面平行的判定定理可知,当一个平面内的两条相交直线均平行于另一平面时,两平面平行,所以“m∥β”不能推出“α∥β”;若两平面平行,则其中一个平面内的任意一条直线平行于另一个平面,所以“α∥β”可以推出“m∥β”.因此“m∥β”是“α∥β”的必要而不充分条件.故选B.【方法归纳】充分条件、必要条件、充要条件的判定方法(1)定义法①分清条件和结论:分清哪个是条件,哪个是结论;②找推式:判断“p⇒q”及“q⇒p”的真假;③下结论:根据推式及定义下结论.(2)等价转化法条件和结论带有否定性词语的命题,常转化为其逆否命题来判断.【举一反三】2.(2015重庆)“x>1”是“(x+2)<0”的( B )A.充要条件B.充分而不必要条件C.必要而不充分条件D.既不充分也不必要条件【解析】当x>1时,x+2>3>1,又y=x是(0,+∞)上的减函数,所以(x+2)<1=0,则x>1⇒(x+2)<0;当(x+2)<0时,x+2>1,即x>-1,则(x+2)<0x>1.故“x>1”是“(x+2)<0”的充分而不必要条件.故选B.题型三充分必要性的证明【例3】设数列{a n}的各项都不为零,求证:对任意n∈N*且n≥2,都有1a1a2+1a2a3+…+1 a n-1a n =n-1a1a n成立的充要条件是{a n}为等差数列.【思路分析】首先清楚条件是“{a n}为等差数列”,结论是“对任意n∈N*且n≥2,都有1a1a2+1a2a3+…+1a n-1a n=n-1a1a n成立”,充分性证条件⇒结论,必要性证结论⇒条件.【证明】(1)(充分性)若{a n}为等差数列,设其公差为d,则1a1a2+1a2a3+…+1a n-1a n=1d⎣⎡⎦⎤⎝⎛⎭⎫1a1-1a2+⎝⎛⎭⎫1a2-1a3+…+⎝⎛⎭⎫1a n-1-1a n=1d⎝⎛⎭⎫1a1-1a n=a n-a1da1a n=n-1a1a n.(2)(必要性)若1a1a2+1a2a3+…+1a n-1a n=n-1a1a n,则1a1a2+1a2a3+…+1a n-1a n+1a n a n+1=na1a n+1,两式相减得1a n a n+1=na1a n+1-n-1a1a n⇒a1=na n-(n-1)a n+1.①于是有a1=(n+1)a n+1-na n+2,②由①②得na n-2na n+1+na n+2=0,所以a n+1-a n=a n+2-a n+1(n≥2).又由1a1a2+1a2a3=2a1a3⇒a3-a2=a2-a1,所以对任意n∈N*,2a n+1=a n+2+a n,故{a n}为等差数列.【方法归纳】按照充分必要条件的概念,分别从充分性和必要性两方面进行探求.【举一反三】3.已知p:-4<x-a<4,q:(x-2)(x-3)<0,且q是p的充分而不必要条件,则a的取值范围为[-1,6].【解析】设p,q表示的范围分别为集合A,B,则A=(a-4,a+4),B=(2,3).由于q是p的充分而不必要条件,则有B A,即解得-1≤a≤6.体验高考1.(2015四川)设a,b都是不等于1的正数,则“3a>3b>3”是“log a3<log b3”的()A.充要条件B.充分不必要条件C.必要不充分条件D.既不充分也不必要条件【解析】B.“3a>3b>3”等价于“a>b>1”,“log a3<log b3”等价于“a>b>1或0<a<1<b或0<b<a<1”,从而“3a>3b>3”是“log a3<log b3”的充分不必要条件.故选B.2.(2015陕西)“sin α=cos α”是“cos 2α=0”的()A.充分不必要条件B.必要不充分条件C.充分必要条件D.既不充分也不必要条件【解析】A.由sin α=cos α,得cos 2α=cos 2α-sin 2 α=0,即充分性成立.由cos 2α=0,得sin α=±cos α,即必要性不成立.故选A.【举一反三】(2015安徽)设p :1<x <2,q :2x >1,则p 是q 成立的( A )A.充分不必要条件B.必要不充分条件C.充分必要条件D.既不充分也不必要条件【解析】由2x >1,得x >0,因为{x |1<x <2}{x |x >0},所以p 是q 成立的充分不必要条件.1.3 简易逻辑联结词、全称量词与存在量词考点诠释重点:复合命题的真假判断,对含有一个量词的命题的否定.难点:对全称命题、特称命题的真假判断和对含有一个量词的命题的否定的理解. 典例精析题型一 含有逻辑联结词的命题的真假判断【例1】已知命题p :(a -2)2+|b -3|≥0(a ,b ∈R ),命题q :x 2-3x +2<0的解集是{x |1<x <2},给出下列结论:①命题“p ∧q ”是真命题;②命题“p ∧⌝q ”是假命题;③命题“⌝p ∨q ”是真命题;④命题“⌝p ∨⌝q ”是假命题.其中正确的是( )A.②③B.①②④C.①③④D.①②③④【思路分析】先判断命题p ,q 的真假,然后对其与逻辑联结词构成的复合命题进行真假判断.【解析】D.命题p :(a -2)2+|b -3|≥0(a ,b ∈R )是真命题,命题q :x 2-3x +2<0的解集是{x |1<x <2}也是真命题,故①命题“p ∧q ”是真命题;②命题“p ∧⌝q ”是假命题;③命题“⌝p ∨q ”是真命题;④命题“⌝p ∨⌝q ”是假命题,故选D.【方法归纳】判断“p ∧q ”“p ∨q ”“ ⌝p ”形式命题真假的步骤(1)准确判断简单命题p ,q 的真假;(2)根据真值表判断“p ∧q ”“p ∨q ”“ ⌝p ”命题的真假.【举一反三】1.已知命题p :函数y =e |x -1|的图象关于直线x =1对称,q :函数y =cos ⎝⎛⎭⎫2x +π6的图象关于点⎝⎛⎭⎫π6,0对称,则下列命题中的真命题为( A ) A.p ∧q B.⌝p ∧qC.p ∧⌝qD.⌝p ∨⌝q【解析】函数y =e |x -1|=的图象如图所示.由图形可知图象关于直线x =1对称,所以命题p 正确;y =cos ⎝⎛⎭⎫2×π6+π6=0,所以函数y =cos ⎝⎛⎭⎫2x +π6的图象关于点⎝⎛⎭⎫π6,0对称,所以命题q 正确,所以p ∧q 正确.题型二 全称命题、特称命题的真假判断【例2】下列命题中的假命题是( )A.∀x ∈R ,2x -1>0B.∀x ∈N *,(x -1)2>0C.∃x 0∈R ,lg x 0<1D.∃x 0∈R ,tan x 0=2【思路分析】理解“∀”“ ∃”的含义,依据相关数学知识进行分析、判断.【解析】B.A 正确;对于B ,当x =1时,(x -1)2=0,错误;对于C ,当x 0=1时,lg x 0=0<1,正确;对于D ,∃x 0∈R ,tan x 0=2,正确.故选B.【方法归纳】1.判断全称命题真假的方法(1)定义法:对给定的集合中的每一个元素x ,p (x )都为真,则全称命题为真;(2)特值法:在给定的集合内找到一个x 0,使p (x 0)为假,则全称命题为假.2.判定特称命题真假的方法(1)定义法:对给定的集合中的每一个元素x ,P (x )都为假,则命题为假;(2)特值法:在给定的集合中找到一个x 0,使p (x 0)为真,则特称命题为真.【举一反三】2.下列命题中,真命题是( C )A.∃x 0∈R ,sin 2x 02+cos 2x 02=12B.∀x ∈(0,π),sin x >cos xC.∀x ∈(0,+∞),e x >1+xD.∃x 0∈R ,x 20+x 0=-1【解析】对于选项A ,∀x ∈R ,sin 2x 2+cos 2x 2=1,故A 为假命题; 对于选项B ,当x =π6时,sin x =12,cos x =32,sin x <cos x ,故B 为假命题; 对于选项C ,构造函数g (x )=e x -1-x ,g ′(x )=e x -1,当x ∈(0,+∞)时,g ′(x )>0,所以g (x )在(0,+∞)上为增函数,则g (x )>g (0)=0,得e x >1+x 在(0,+∞)上恒成立,故C 为真命题;对于选项D ,x 2+x +1=⎝⎛⎭⎫x +122+34>0恒成立,所以不存在x 0∈R ,使x 20+x 0=-1,故D 为假命题.综上可知,C 为真命题,故选C.题型三 含有一个量词的命题的否定【例3】(1)命题“所有能被2整除的整数都是偶数”的否定是( )A.所有不能被2整除的整数都是偶数B.所有能被2整除的整数都不是偶数C.存在一个不能被2整除的整数是偶数D.存在一个能被2整除的整数不是偶数(2)命题“存在x0∈R,2≤0”的否定是()A.不存在x0∈R,2>0B.存在x0∈R,2≥0C.对任意的x∈R,2x≤0D.对任意的x∈R,2x>0【思路分析】首先弄清楚是全称命题还是特称命题,再针对不同形式加以否定.【解析】(1)D.全称命题的否定是特称命题,“所有”对应“存在一个”,同时否定结论“能被2整除的整数都是偶数”,变为“存在一个能被2整除的整数不是偶数”,故选D.(2)D.根据特称命题的否定是全称命题知,命题“存在x0∈R,2≤0”的否定是“对任意的x∈R,都有2x>0”.【方法归纳】(1)全(特)称命题的否定与命题的否定有着一定的区别,全(特)称命题的否定是将其全称量词改为存在量词(或存在量词改为全称量词),并把结论否定.而命题的否定,则直接否定结论即可;(2)要判断⌝p的真假,可以直接判断,也可以判断p的真假,利用p与⌝p的真假相反作出判断.【举一反三】3.(1)已知命题p:∀x1,x2∈R,[f(x2)-f(x1)](x2-x1)≥0,则⌝p为( C )A.∃x1,x2∈R,[f(x2)-f(x1)](x2-x1)≤0B.∀x1,x2∈R,[f(x2)-f(x1)](x2-x1)≤0C.∃x1,x2∈R,[f(x2)-f(x1)](x2-x1)<0D.∀x1,x2∈R,[f(x2)-f(x1)](x2-x1)<0(2)命题“∃x∈R,x3-2x+1=0”的否定是( D )A.x∈R,x3-2x+1≠0B.不存在x∈R,x3-2x+1≠0C.x∈R,x3-2x+1=0D.∀x∈R,x3-2x+1≠0【解析】(1)由于对任意的x1,x2∈R,都有[f(x2)-f(x1)]·(x2-x1)≥0,要否定这个命题,则只要存在x1,x2∈R,使[f(x2)-f(x1)](x2-x1)≥0不成立即可,即使得[f(x2)-f(x1)](x2-x1)<0,故已知命题的否定是“∃x1,x2∈R,[f(x2)-f(x1)](x2-x1)<0”.故选C.(2)“∃x∈R,x3-2x+1=0”属于特称命题,它的否定为全称命题,从而其否定为:∀x∈R,x3-2x+1≠0.故选D.题型四命题真假的综合运用【例4】已知命题p:“∀x∈[1,2],x2-a≥0”,命题q:“∃x 0∈R,+2ax0+2-a=0”,若命题“p且q”是真命题,则实数a的取值范围是()A.{a|a≤-2或a=1}B.{a|a≥1}C.{a|a≤-2或1≤a≤2}D.{a|-2≤a≤1}【思路分析】解答本题的关键是根据“p且q”是真命题来确定关于a的不等式,从而求出a的取值范围.【解析】A.由“p且q”是真命题,则p为真命题,q也为真命题.若p为真命题,则a≤x2恒成立,因为x∈[1,2],所以a≤1.若q为真命题,即x2+2ax+2-a=0有实根,则Δ=4a2-4(2-a)≥0,即a≥1或a≤-2.综上可知,所求实数a的取值范围为{a|a≤-2或a=1}.【方法归纳】解决这类问题时,应先根据题目条件,即复合命题的真假情况,推出每一个命题的真假(有时不一定只有一种情况),然后再求出每个命题是真命题时参数的取值范围,最后根据每个命题的真假情况,求出参数的取值范围.【举一反三】4.已知命题p:对任意x∈R,存在m∈R,使4x+2x m+1=0.若命题⌝p 是假命题,则实数m的取值范围是( C )A.[-2,2]B.[2,+∞)C.(-∞,-2]D.[-2,+∞)【解析】因为⌝p 为假,故p 为真,即求原命题为真时m 的取值范围.由4x +2x m +1=0,得-m =4x +12x =2x +12x ≥2. 所以m ≤-2.体验高考(2015新课标Ⅰ)设命题p :∃n ∈N ,n 2>2n ,则⌝p 为( )A.∀n ∈N ,n 2>2nB.∃n ∈N ,n 2≤2nC.∀n ∈N ,n 2≤2nD.∃n ∈N ,n 2=2n【解析】C.命题的否定是:∀n ∈N ,n 2≤2n ,故选C.【举一反三】(2015山东)若“∀x ∈⎣⎡⎦⎤0,π4,tan x ≤m ”是真命题,则实数m 的最小值为1 .【解析】因为0≤x ≤π4,所以0≤tan x ≤1, 因为“∀x ∈⎣⎡⎦⎤0,π4,tan x ≤m ”是真命题, 所以m ≥1,所以实数m 的最小值为1.。
2018届高考数学理科全国通用一轮总复习课件:第五章 数列 5-5 精品
考向二 数列中的图表问题 【典例2】(1)(2016·德州模拟)将全体正整数排成一 个三角形数阵:
1 23 456 7 8 9 10 …………… 按照以上排列的规律,第n行(n≥3)从左向右的第3个数 为________.
(2)(2016·太原模拟)下表是一个由正数组成的数表,
数表中各行依次成等差数列,各列依次成等比数列,且
【解题导引】10次还款连同利息之和等于本金10年后 的本息.
【规范解答】设每年还款x元,需10年还清,那么各年还 款利息情况如下: 第10年付款x元,这次还款后欠款全部还清; 第9年付款x元,过1年欠款全部还清时,所付款连同利息 之和为x(1+10%)元;
第8年付款x元,过2年欠款全部还清时,所付款连同利息 之和为x(1+10%)2元; … 第1年付款x元,过9年欠款全部还清时,所付款连同利息 之和为x(1+10%)9元. 10年后应还款总数为20000(1+10%)10.
91
又b13=
2 ,所以q=2.
1314
记表中第k(k≥3)行所有项的和为S,
则 S bk 1 qk 2 1 2k
1 q
k k 1 1 2
k
2
k 1
1
2k
(k
3).
考向三 数列的实际应用问题 【典例3】(2016·日照模拟)某大学张教授年初向银行 贷款2万元用于购车,银行贷款的年利息为10%,按复利 计算(即本年的利息计入次年的本金生息).若这笔款要 分10年等额还清,每年年初还一次,并且以贷款后次年 年初开始归还,问每年应还多少元?
【变式训练】(2016·青岛模拟)下面给出了一个三角 形数阵,已知每一列的数成等差数列,从第3行起,每一 行的数成等比数列,每一行的公比都相等.记第i行第j 列数为aij(i,j∈N*),则a43=______.
2018届高考数学理科全国通用一轮总复习课件:第六章
明“1+2+22+…+2n-1=2n-1(n∈N*)”的过程中,第二步
n=k时等式成立,则当n=k+1时,应得到 A.1+2+22+…+2k-2+2k-1=2k+1-1 B.1+2+22+…+2k+2k+1=2k-1+2k+1 C.1+2+22+…+2k-1+2k+1=2k+1-1 ( )
D.1+2+22+…+2k-1+2k=2k+1-1
【小题快练】 链接教材 练一练
1.(选修2-2P99习题B组T1改编)在应用数学归纳法证
明凸n边形的对角线为 1 n(n-3)条时,第一步检验n等
2
于
(
)
A.1
B.2
C.3
D.4
【解析】选C.三角形是边数最少的凸多边形,故第一步 应检验n=3.
2.(选修2-2P96习题2.3A组T1(3)改编)用数学归纳法证
6
左边=右边,等式成立.
(2)假设n=k(k∈N*,且k≥1)时,等式成立, 即12+22+…+k2= k(k 1)(2k 1) ,
6
则当n=k+1时, 12+22+…+k2+(k+1)2
k(k 1)(2k 1) 2 = + k+ 1 6 (k 1)[(k 1) 1][2(k 1) 1] = , 6
所以当n=k+1时,等式仍然成立, 由(1)、(2)可知,对于∀n∈N*等式恒成立.
【加固训练】 1.用数学归纳法证明:对任意的n∈N*, 1 1
2018届高考数学理科全国通用一轮总复习课件:第二章 函数、导数及其应用 2.7 精品
所以选项A,C不正确.
当x∈(-1,0)时,g(x)=x- 是1 增函数,
x
因为y=lnx是增函数,
所以函数f(x)=ln(x- 1)是增函数.所以D不正确,B正确.
x
命题方向2:借助实际情景探究函数图象 【典例3】(2015·全国卷Ⅱ)如图,长方形ABCD的边 AB=2,BC=1,O是AB的中点,点P沿着边BC,CD与DA运动,记 ∠BOP=x.将动点P到A,B两点 距离之和表示为x的函数f(x), 则f(x)的图象大致为 ( )
y=f(2x)的图象的对称轴是 ( )
Hale Waihona Puke A.x=1B.x=-1
C.x=- 1
2
D.x= 1
2
【解析】选D.因为函数y=f(2x+1)是偶函数,所以其图
象关于y轴对称,而函数y=f(2x)的图象是将函数y=f(2x
+1)的图象向右平移 1 个单位,所以对称轴也向右平移
2
1 个单位,所以函数y=f(2x)的图象的对称轴为x= 1 .
【特别提醒】 1.函数对称的重要结论 (1)函数y=f(x)与y=f(2a-x)的图象关于直线x=a对称. (2)函数y=f(x)与y=2b-f(2a-x)的图象关于点(a,b)中 心对称.
(3)若函数y=f(x)对定义域内任意自变量x满足:f(a+x) =f(a-x),则函数y=f(x)的图象关于直线x=a对称.
对于B:T<2π,故a>1,所以函数y=ax是增函数,故错;
对于C:T=2π,故a=1,故错;
对于D:T>2π,故a<1,所以y=ax是减函数,正确.
4.(2016·聊城模拟)如图,点P是以O为圆心,AB为直径的 半圆上的动点,AB=2,设弦AP的长为x,△APO的面积为y, 则下列选项中,能表示y与x的函数关系的大致图象是
