参数方程化普通方程练习题有答案

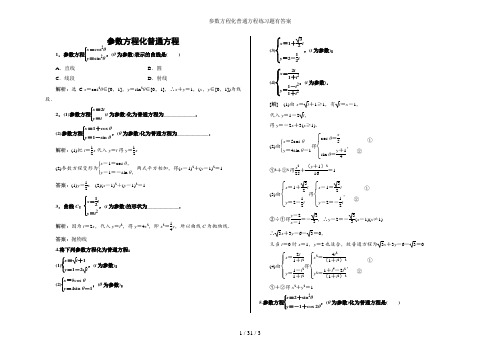
参数方程化普通方程
1．参数方程⎩
⎪⎨⎪⎧x ＝cos 2
θ
y ＝sin 2
θ，(θ为参数)表示的曲线是( ) A ．直线 B ．圆 C ．线段
D ．射线
解析：选＝cos 2
θ∈[0，1]，y ＝sin 2
θ∈[0，1]，∴x ＋y ＝1，(x ，y ∈[0，1])为线段．
2．(1)参数方程⎩
⎪⎨⎪⎧x ＝2t
y ＝t (t 为参数)化为普通方程为____________．
(2)参数方程⎩
⎪⎨⎪⎧x ＝1＋cos θ
y ＝1－sin θ，(θ为参数)化为普通方程为____________．
解析：(1)把t ＝12x 代入y ＝t 得y ＝1
2x .
(2)参数方程变形为⎩⎪⎨
⎪
⎧x －1＝cos θ，y －1＝－sin θ，
两式平方相加，得(x －1)2＋(y －1)2
＝1. 答案：(1)y ＝12
x (2)(x －1)2＋(y －1)2
＝1
3．曲线C ：⎩⎪⎨⎪⎧x ＝12t
y ＝t 2
，(t 为参数)的形状为____________．
解析：因为t ＝2x ，代入y ＝t 2
，得y ＝4x 2
，即x 2
＝1
4
y ，所以曲线C 为抛物线．
答案：抛物线
4.将下列参数方程化为普通方程：
(1)⎩⎨⎧x ＝t ＋1
y ＝1－2t
，(t 为参数)； (2)⎩
⎪⎨⎪⎧x ＝5cos θy ＝4sin θ－1，(θ为参数)； (3)⎩⎪⎨⎪⎧x ＝1＋3
2t y ＝2－1
2t ，(t 为参数)；
(4)⎩⎪⎨⎪⎧x ＝2t 1＋t 2y ＝1－t 21＋t
2
，(t 为参数)．
[解] (1)由x ＝t ＋1≥1，有t ＝x －1， 代入y ＝1－2t ， 得y ＝－2x ＋3(x ≥1)．
(2)由⎩⎪⎨⎪⎧x ＝5cos θ
y ＝4sin θ－1得⎩⎪⎨⎪⎧cos θ＝x
5sin θ＝y ＋14
， ① ②
①2
＋②2
得x 2
25＋（y ＋1）
2
16
＝1.
(3)由⎩⎪⎨⎪⎧x ＝1＋32t y ＝2－12t 得⎩⎪⎨⎪⎧x －1＝3
2t y －2＝－12t ， ① ②
②÷①得
y －2x －1＝－33，∴y －2＝－3
3
(x －1)(x ≠1) ∴3x ＋3y －6－3＝0，
又当t ＝0时x ＝1，y ＝2也适合，故普通方程为3x ＋3y －6－3＝0. (4)由⎩⎪⎨⎪
⎧x ＝2t 1＋t 2y ＝1－t 21＋t 2得⎩
⎪⎨⎪
⎧x 2＝4t 2
（1＋t 2）2
y 2＝1＋t 4－2t 2（1＋t 2）
2
，
①
② ①＋②得x 2＋y 2
＝1.
5.参数方程⎩
⎪⎨⎪⎧x ＝2＋sin 2
θ
y ＝－1＋cos 2θ，(θ为参数)化为普通方程是( )
A ．2x －y ＋4＝0
B ．2x ＋y －4＝0
C ．2x －y ＋4＝0，x ∈[2，3]
D ．2x ＋y －4＝0，x ∈[2，3]
解析：选 D.由x ＝2＋sin 2
θ，则x ∈[2，3]，sin 2
θ＝x －2，y ＝－1＋1－2sin 2
θ＝－2sin 2
θ＝－2x ＋4，即2x ＋y －4＝0，故化为普通方程为2x ＋y －4＝0，x ∈[2，3]．
6.把参数方程⎩
⎪⎨⎪⎧x ＝sin θ－cos θ
y ＝sin 2θ，(θ为参数)化成普通方程是____________．
解析：将x ＝sin θ－cos θ两边平方得x 2
＝1－sin 2θ， 即sin 2θ＝1－x 2
，代入y ＝sin 2θ，得y ＝－x 2
＋1. 又x ＝sin θ－cos θ＝2sin ⎝ ⎛⎭⎪⎫θ－π4，∴－2≤x ≤2，
故普通方程为y ＝－x 2＋1(－2≤x ≤2)． 答案：y ＝－x 2
＋1(－2≤x ≤2)
7.已知曲线C 1：⎩⎪⎨⎪⎧x ＝－4＋cos t y ＝3＋sin t ，(t 为参数)，C 2：⎩
⎪⎨⎪
⎧x ＝8cos θy ＝3sin θ.，(θ为参数)．
(1)化C 1，C 2的方程为普通方程，并说明它们分别表示什么曲线？
(2)若C 1上的点P 对应的参数t ＝π
2
，Q 为C 2上的动点，求PQ 中点M 到直线C 3：
⎩⎪⎨⎪⎧x ＝3＋2t ，y ＝－2＋t
(t 为参数)距离的最小值及此时Q 点坐标． [解] (1)由C 1：⎩⎪⎨⎪⎧x ＝－4＋cos t
y ＝3＋sin t ，(t 为参数)，
则⎩
⎪⎨⎪⎧cos t ＝x ＋4，
sin t ＝y －3， 由sin 2t ＋cos 2
t ＝1得(x ＋4)2
＋(y －3)2
＝1，即曲线C 1的普通方程．C 1表示的是
圆心为(－4，3)，半径为1的圆.2分
由C 2：⎩
⎪⎨⎪⎧x ＝8cos θ，
y ＝3sin θ.(θ为参数)，
则⎩
⎪⎨⎪
⎧cos θ＝x
8，
sin θ＝y
3，
由cos 2θ＋sin 2
θ＝1得x 264＋y 29＝1，即曲线C 2的普通方程．C 2表
示的是中心在坐标原点，焦点在x 轴上，长半轴长为8，短半轴长为3的椭圆.5分
(2)当t ＝π
2时，P (－4，4)，Q (8cos θ，3sin θ)，
故M ⎝ ⎛⎭
⎪⎫－2＋4cos θ，2＋32sin θ，6分 C 3为直线x －2y －7＝分
则点M 到直线C 3的距离d ＝55|4cos θ－3sin θ－13|＝5
5
|5cos(θ＋φ)－13|，9分
从而当cos φ＝45，sin φ＝35时，d 取得最小值85
5.
11分
此时，Q 点的坐标为⎝
⎛⎭
⎪⎫325，－95.12分
8.(2015·高考陕西卷)在直角坐标系xOy 中，直线l 的参数方程为⎩⎪⎨
⎪
⎧x ＝3＋1
2
t ，
y ＝32t
(t 为参数)．以原点为极点，x 轴正半轴为极轴建立极坐标系，⊙C 的极坐标方程为ρ＝
23sin θ.
(1)写出⊙C 的直角坐标方程；
(2)P 为直线l 上一动点，当P 到圆心C 的距离最小时，求P 的直角坐标．
解：(1)由ρ＝23sin θ，得ρ2
＝23ρsin θ，
从而有x 2＋y 2＝23y ，所以x 2＋(y －3)2
＝3. (2)设P ⎝ ⎛⎭⎪⎫3＋1
2t ，32t ，又C (0，3)，
则|PC |＝
⎝ ⎛⎭⎪⎫3＋12t 2
＋⎝ ⎛⎭
⎪⎫3
2t －32＝t 2＋12， 故当t ＝0时，|PC |取得最小值， 此时，点P 的直角坐标为(3，0)．
9．已知曲线C 1的参数方程为⎩
⎪⎨⎪⎧x ＝4＋5cos t ，
y ＝5＋5sin t (t 为参数)，以坐标原点为极点，x 轴
的正半轴为极轴建立极坐标系，曲线C 2的极坐标方程为ρ＝2sin θ.
(1)把C 1的参数方程化为极坐标方程；
(2)求C 1与C 2交点的极坐标(ρ≥0，0≤θ＜2π)． 解：(1)将⎩⎪⎨
⎪
⎧x ＝4＋5cos t ，y ＝5＋5sin t
消去参数t ，化为普通方程(x －4)2
＋(y －5)2
＝25，即
C 1：x 2＋y 2－8x －10y ＋16＝0.
将⎩⎪⎨⎪⎧x ＝ρcos θ，y ＝ρsin θ
代入x 2＋y 2
－8x －10y ＋16＝0得 ρ2－8ρcos θ－10ρsin θ＋16＝0.
所以C 1的极坐标方程为ρ2
－8ρcos θ－10ρsin θ＋16＝0. (2)C 2的普通方程为x 2
＋y 2－2y ＝0.
由⎩⎪⎨⎪⎧x 2
＋y 2
－8x －10y ＋16＝0，x 2＋y 2
－2y ＝0，解得⎩
⎪⎨⎪⎧x ＝1y ＝1或⎩⎪⎨⎪⎧x ＝0，
y ＝2. 所以C 1与C 2交点的极坐标分别为(2，
π4)，(2，π
2
)． 10.化参数方程⎩⎪⎨⎪⎧x ＝t ＋
1
t
y ＝t －1t
(t 为参数)为普通方程，并求出该曲线上一点P ，使它到y ＝
2x ＋1的距离为最小，并求此最小距离．
解：化参数方程为普通方程为x 2－y 2
＝4.
设P (t ＋1t ，t －1
t
)，则点P 到直线2x －y ＋1＝0的距离
d ＝|t ＋3t
＋1|
5
.
(1)当t >0时，d ≥23＋1
5.
(2)当t <0时，∵－t －3
t
≥23，
∴t ＋3
t
＋1≤－23＋1.
∴|t ＋3t ＋1|≥23－1，∴d ≥23－15
.
∵
23＋15>23－1
5
， ∴d 的最小值为23－15，即215－55，
此时点P 的坐标为(－433，－2
3
3)．。