误差原理第四章 最小二乘法
最小二乘法原理

最小二乘法原理:等精度测量的有限测量系列,寻求一个真值, 最小二乘法原理 使得误差的平方和达到最小。
xi 现在来证明 证明,只有按公式(1-16) x = ∑ n = x0 计算得到 证明 i =1 的最佳估计值,才具有最小的残差(或偏差)平方和。
n
设有一独立等精度的测量列xi(i=1,2,…,n),其残差为 vi = xi − x 残差的平方和为:
2 2 i =1 i =1
n
2
n
2
= n x + n x − 2n • x • x = n( x − + x − 2 • x • x) = n( x − x) 2 > 0
所以
n n
2
由此证明了: 算术平均值具有残差平 方和最小值的特性
∑ d <∑ v
2 i =1 i i =1
2
n
i
即
∑ vi 为最小值。
8
d i = x i − x ,则残差的平方和为
n
∑d
i =1
2 i
= ∑ ( xi − x ) = ∑ ( xi − 2xi x + x )
2 2 i =1
n
n
n
2
i =1
= ∑ xi − 2 x ∑ xi + n x
2 i =1 n i =1
2
n
2
2 1 n = ∑ xi − 2n • x • ∑ xi + n x n i =1 i =1
= ∑ xi − 2n • x • x + n x
2 i =1
n
2
(1: i =1 m
m
xi ∑ n+k i =1
最小二乘法的原理及其应用

最小二乘法的原理及其应用1. 最小二乘法的原理最小二乘法是一种常用的数学优化方法,其原理是通过最小化残差平方和来寻找数据的最佳拟合线或曲线。
当数据存在随机误差时,最小二乘法可以有效地估计模型参数。
最小二乘法的基本原理可以概括为以下几个步骤:1.首先,假设模型的形式,如线性模型:y=mx+b。
2.然后,定义一个衡量模型拟合程度的误差函数,通常采用残差的平方和:$E(m, b) = \\sum_{i=1}^{n} (y_i - (mx_i + b))^2$。
3.接下来,根据最小二乘法的原理,我们需要通过对误差函数求偏导数,得出使误差函数最小化的模型参数。
4.最后,通过优化算法,如梯度下降法等,迭代地调整模型参数,使误差函数达到最小值,从而获得最佳拟合模型。
最小二乘法的原理非常简单和直观,因此被广泛应用于各个领域,如统计学、经济学、工程学等。
2. 最小二乘法的应用最小二乘法在实际问题中有着广泛的应用,下面将介绍其中的几个应用场景。
2.1 线性回归线性回归是最小二乘法最常见的应用之一。
在线性回归中,最小二乘法用于估计自变量与因变量之间的线性关系。
通过最小化残差平方和,我们可以找到一条最佳拟合直线,从而对未知的因变量进行预测。
线性回归广泛应用于经济学、社会学等领域,帮助研究者探索变量之间的相互关系。
2.2 曲线拟合最小二乘法还可以用于曲线拟合。
当我们需要拟合一个非线性模型时,可以通过最小二乘法来估计参数。
通过选择适当的模型形式和误差函数,可以得到最佳拟合曲线,从而准确地描述数据的变化趋势。
曲线拟合在信号处理、图像处理等领域具有重要的应用。
2.3 数据降维数据降维是指将高维度的数据转化为低维度表示,以便于可视化和分析。
最小二乘法可以用于主成分分析(PCA)等降维方法中。
通过寻找投影方向,使得在低维度空间中的数据点到其投影点的平均距离最小化,可以实现数据的有效降维。
2.4 系统辨识在控制工程中,最小二乘法经常被用于系统辨识。
误差原理第四章-最小二乘法知识分享
解 列出误差方程
式中
t l i
——在温度 下铜捧长度的测得值;
i
——铜棒的线膨胀系数。
令 y0x1,y0x2为两个待求估计参数,则误差方程可写为
根据误差方程,我们可列出正规方程 又
将以上计算的相应系数值代入上面的正规方程得 解得 即 因此铜棒长度随温度的线性变化规律为
三、不等精度测量线性参数最小二乘法处理 不等精度误差方程转化为等精度误差方程为
例4-2 已知测量方程
对 Y i 的测量数据及其相应的标准差为
试列出最小二乘估计的正规方程。 解 列出残余误差方程
确定各测量数据的权。
根据误差方程及各测量数据的权,我们写出正规方程 式中
则正规方程为
四、非线性参数最小二乘法 非线性转化为线性:
的近似值,即
将函数在 R10 , R20 处展开,取一次项,有
代入残差方程,得线性残差方程 五、对同一量重复测量数据的最小二乘法
4.2精度估计 一、测量数据的精度估计 1. 等精度测量数据的精度估计
例4-4 试求例4-1中铜棒长度的测量精度。 解 已知残余误差方程
可得残余误差为
则标准差为 2.不等精度测量数据的精度估计
4、最小二乘原理
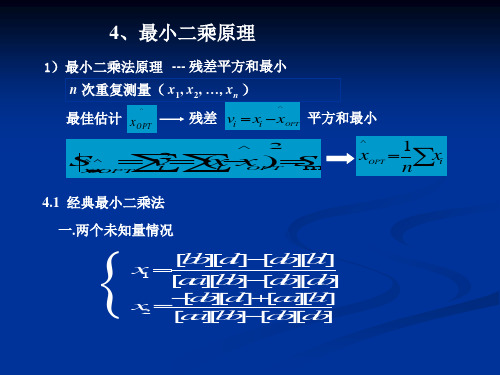
1)最小二乘法原理 --- 残差平方和最小
n 次重复测量( x1, x2, …, xn )
最佳估计
^
xOPT
^
残差 vi xi xOPT 平方和最小
^ 2
S^ ^ xxOPT
vi2
(xixOP )TSmin
^
1
xOPT n
xi
4.1 经典最小二乘法
一.两个未知量情况
第四章-最小二乘参数辨识方法及原理

脉冲传递函数描述:
Y ( z ) b0 b1 z 1 bn z n B( z 1 ) G( z) = 1 n 1 U ( z ) 1 a1 z an z A( z )
2.随机模型
v(k )
u(k )
G (k )
x(k )
y(k )
观测值可表示为:
本章的学习目的
1、掌握最小二乘参数辨识方法的基本原理
2、掌握常用的最小二乘辨识方法 3、熟练应用最小二乘参数辨识方法进行模型参数辨识 4、能够编程实现最小二乘参数辨识
回
顾
辨识目的:根据过程所提供的测量信息,在某种准则意 义下,估计模型的未知参数。 Input
Process 目 的
Output
工程实践
88 1010
95.7 1032
表 1 热敏电阻的测量值
t (C ) R ()
20.5 765
26 790
32.7 826
40 850
51 873
61 910
73 942
80 980
88 1010
95.7 1032
R a bt
N N N N ˆ Ri 2 R a 702ti.762i ti ti i 1 i 1 a i 1 i 1 ˆ 2 N N ˆ N. t i2 t i b 3 4344 i 1 i 1 N N N N Ri t i Ri t i i 1 i 1 b i 1 ˆ R 943 .1682 N N 2 N ti ti i 1 i 1
上述N个方程可写成下列向量-矩阵形式
y (n) y (1) u (n 1) y (n 1) y (n 2) y (n 1) y (2) u ( n 2) y (n N ) y (n N 1) y ( N ) u (n N )
误差理论与测量平差四章

引用参数 X=H1
X%
h%1 h%4 h%5 0
h%1 h%2 h%6 0
h%3 h%4 h%6 0
h%1
1 0
1
1
0 0
1 0
X% HA
011 000 110 000
0
0
1
1
0
hh%%12
1
2
x
2 m in
1
nE(
1
2
)
2
n
得证
二、最小二乘原理 1.最小二乘法
例:匀速运动的质点在时刻的位置y表示为:
yˆ ˆ ˆ
实际上: y v ˆ ˆ
为了求ˆ 与
ˆ, 在
1, 2,L
测定其位置,
n
得y1, y2 L yn ,则:
vi ˆ ˆ yi , (i 1, 2L n)
W AL A0
二、附有参数的条件平差函数模型 例 引用参数 X=SAB 参数的个数 U=1 n=5, t=3
r=n-t=5-3=2 条件方程个数:
C=r+U=3 可以列出三个条件方程:
S%12 S%22 X%2 2S%2 X%cos L%1 0 S%12 S%22 X%2 2S%1X%cos L%2 0 S%12 S%22 X%2 2S%1 S%2 X%cos L%3 0
hh%%34
hh%%56
0
0
0 1
X%
0
0
0
H
A
最小二乘方法

最小二乘方法:原理、应用与实现一、引言最小二乘方法是数学优化中的一种重要技术,广泛应用于各种实际问题中。
它的基本原理是通过最小化误差的平方和来估计未知参数,从而实现数据拟合、线性回归等目标。
本文将对最小二乘方法的原理、应用与实现进行详细介绍,并探讨其在实际问题中的应用。
二、最小二乘方法的原理最小二乘方法的基本原理可以概括为:对于一组观测数据,通过最小化误差的平方和来估计未知参数。
具体而言,设我们有一组观测数据{(xi, yi)},其中xi是自变量,yi是因变量。
我们希望找到一个函数f(x),使得f(xi)与yi之间的差距尽可能小。
为了量化这种差距,我们采用误差的平方和作为目标函数,即:J = Σ(f(xi) - yi)²我们的目标是找到一组参数,使得J达到最小值。
这样的问题称为最小二乘问题。
在实际应用中,我们通常采用线性函数作为拟合函数,即:f(x) = a + bx其中a和b是待估计的参数。
此时,最小二乘问题转化为求解a 和b的问题。
通过求解目标函数J关于a和b的偏导数,并令其为零,我们可以得到a和b的最优解。
这种方法称为最小二乘法。
三、最小二乘方法的应用数据拟合:最小二乘方法在数据拟合中有广泛应用。
例如,在物理实验中,我们经常需要通过一组观测数据来估计某个物理量的值。
通过采用最小二乘方法,我们可以找到一条最佳拟合曲线,从而得到物理量的估计值。
这种方法在化学、生物学、医学等领域也有广泛应用。
线性回归:线性回归是一种用于预测因变量与自变量之间关系的统计方法。
在回归分析中,我们经常需要估计回归系数,即因变量与自变量之间的相关程度。
通过采用最小二乘方法,我们可以得到回归系数的最优估计值,从而建立回归方程。
这种方法在经济学、金融学、社会科学等领域有广泛应用。
图像处理:在图像处理中,最小二乘方法常用于图像恢复、图像去噪等问题。
例如,对于一幅受到噪声污染的图像,我们可以采用最小二乘方法对图像进行恢复,从而得到更清晰、更真实的图像。
最小二乘法方差推导

最小二乘法方差推导导言最小二乘法是一种常用的回归分析方法,用于建立变量之间的关系模型。
在使用最小二乘法进行回归分析时,我们通常会考虑误差的大小和分布情况。
方差是一种常用的衡量误差大小的指标,通过推导最小二乘法的方差,可以更好地理解最小二乘法的原理和应用。
一、线性回归模型线性回归模型是最简单也是最常用的回归模型之一。
假设我们有一组观测数据(x1,y1),(x2,y2),...,(x n,y n),其中x i表示自变量,y i表示因变量。
线性回归模型的基本形式可以表示为:y=β0+β1x+ϵ其中y表示因变量,β0和β1分别表示截距和斜率,ϵ表示误差。
二、最小二乘法原理最小二乘法的目标是找到一条直线,使得观测数据到这条直线的距离最短。
假设观测数据的真实值为y i,模型预测值为y î,则观测数据的误差可以表示为e i=y i−y î。
最小二乘法的原理是通过最小化误差的平方和来估计回归模型的参数。
具体来说,我们希望找到一组参数β0̂和β1̂,使得观测数据的误差平方和最小。
误差平方和可以表示为:nSSE=∑(y i−y î)2i=1三、最小二乘法方差的推导最小二乘法方差是衡量观测数据与回归模型之间的离散程度的指标。
我们通过推导最小二乘法的方差,可以更好地理解模型的可靠性和拟合程度。
3.1 残差在推导最小二乘法方差之前,我们首先定义残差e i。
残差表示观测数据的真实值与模型预测值之间的差异。
对于线性回归模型,残差可以表示为e i=y i−y î。
3.2 方差推导方差是衡量观测数据与回归模型之间的离散程度的指标。
我们通过推导最小二乘法的方差,可以衡量回归模型的可靠性和拟合程度。
方差可以表示为残差平方和除以观测数据的数量。
具体来说,方差可以表示为:Var=SSE n其中,n表示观测数据的数量,SSE表示观测数据的误差平方和。
四、小结最小二乘法是一种常用的回归分析方法,可以用于建立变量之间的关系模型。
通过最小化观测数据与模型预测值之间的误差平方和,可以得到回归模型的参数估计值。
最小二乘法的原理

最小二乘法的原理
最小二乘法是一种统计学中常用的参数估计方法,用于拟合数据并找到最适合数据的数学模型。
其原理是通过最小化实际观测值与预测值之间的误差平方和,来确定模型参数的取值。
具体而言,假设有一组数据点,其中每个数据点包括自变量(即输入值)和因变量(即输出值)的配对。
我们要找到一条最佳拟合曲线(或者直线),使得曲线上的预测值尽可能接近实际观测值。
而最小二乘法的目标就是使得残差的平方和最小化。
假设要拟合的模型为一个一次多项式:y = β0 + β1*x,其中β0和β1是待估计的参数,x是自变量,y是因变量。
我们要找到
最优的β0和β1,使得拟合曲线的误差最小。
为了使用最小二乘法,我们首先需要构建一个误差函数。
对于每个数据点,误差函数定义为实际观测值与预测值之间的差,即e = y - (β0 + β1*x)。
我们的目标是最小化所有误差的平方和,即最小化Sum(e^2)。
通过对误差函数求导,并令导数为0,可以得到最小二乘法的
正规方程组。
解这个方程组可以得到最优的参数估计值,即
β0和β1的取值。
最终,通过最小二乘法,我们可以得到一条最佳拟合曲线(或直线),使得曲线的预测值与实际观测值的误差最小。
这条拟
合曲线可以用于预测新的因变量值,或者理解自变量与因变量之间的关系。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
X (C*)1 AT PL
三、待求量稻度估计 1.等精度测量 不定乘数
2.不等精度测量 不定乘数
三、不等精度测量线性参数最小二乘法处理 不等精度误差方程转化为等精度误差方程为
例4-2 已知测量方程
对 Yi 的测量数据及其相应的标准差为
试列出最小二乘估计的正规方程。 解 列出残余误差方程
确定各测量数据的权。
根据误差方程及各测量数据的权,我们写出正规方程 式中
则正规方程为
四、非线性参数最小二乘法 非线性转化为线性:
第二步,正规方程
则 解得 第三步,测量数据精度估计
则测量数据标准差为
第四步,估计量精度估计 求解不定乘数
解得 则估计量的标准差为
4.3矩阵最小二乘法 一、线性模型
二、最小二乘法解
1.等精度情况下的矩阵形式的正规方程
ATV 0
X C1AT L
2.不等精度测量时,正规方程可表示为
AT PV 0
x1
[bb][al] [ab][bl] [aa][bb] [ab][ab]
x2
[ab][al ] [aa][bl] [aa][bb] [ab][ab]
二.T个未知量的情况
注意到方程组形式上有如下特点:
(1)沿主对角线分布着平方项系数 aa,bb,L hh 都为正数。
(2)以主对角线为对称线,对称分布的各系数彼此两两相等。
的近似值,即
将函数在 R10, R20 处展开,取一次项,有
代入残差方程,得线性残差方程 五、对同一量重复测量数据的最小二乘法
4.2精度估计 一、测量数据的精度估计 1. 等精度测量数据的精度估计
例4-4 试求例4-1中铜棒长度的测量精度。 解 已知残余误差方程可得 Nhomakorabea余误差为
则标准差为 2.不等精度测量数据的精度估计
为获得非线性函数的展开式.必须首先确定待求估计量的近似 值,其方法有二个:
x (1)直接测量:若条件允许,可直接测量待求量, r 所得结果
即可作为其近似值。
(2)利用部分方程式进行计算。
例4-3 将下面的非线性残余方程组化成线性的形式。
取方程组中前二式,令 v1 0, v2 0 ,则可得 R1与 R2
4、最小二乘原理
1)最小二乘法原理 --- 残差平方和最小
n 次重复测量( x1, x2, …, xn )
最佳估计
^
xOPT
^
残差 vi xi x OPT 平方和最小
^
2
S ^ ^ x xOP T
vi2
(xi x OPT ) Smin
^
1
x OPT
n
xi
4.1 经典最小二乘法
一.两个未知量情况
二、最小二乘估计量的精度估计 1.等精度测量时最小二乘估计量的精度估计
标准差为
式中 ——测量数据的标准差
2. 不等精度测量的情况 不等精度测量的情况与等精度的类似
例4-5 试求例4-1中铜棒长度和线膨胀系数估计量的精度。 解 已知正规方程为
测量数据 li 的标准差为 求解不定乘数的方程为
解得 估计量的标准差为 因 故
例4-6 已知 x1 35.3 ,测得xi x j 的值为 lij,并已知 l12 69.5 l13 4.4, l14 28.3, l23 64.4, l24 42.1, l34 21.9 试用最小二乘法求 x2 , x3, x4及其误差。
解 第一步,残余误差方程组
已知 x1 35.3, 代入上式得
例4.1 在不同温度下.测定铜捧的长度如下表,试估计 0C
时的铜棒长度y0和铜的线膨胀系数 。
解 列出误差方程
式中
li ——在温度 ti 下铜捧长度的测得值;
——铜棒的线膨胀系数。
令 y0 x1, y0 x2为两个待求估计参数,则误差方程可写为
根据误差方程,我们可列出正规方程 又
将以上计算的相应系数值代入上面的正规方程得 解得 即 因此铜棒长度随温度的线性变化规律为
