第2章控制系统的结构图及化简-2013
合集下载
自动控制原理-第二章-控制系统的数学模型—结构图-信号流图-传递函数

(1)单位脉冲 (2)单位阶跃 (3)单位斜坡 (4)单位加速度 (5)指数函数 (6)正弦函数 (7)余弦函数
f (t)
(t)
1(t )
t t2 2
e at
sin t cos t
F (s)
1
1s 1 s2 1 s3
1 (s a)
(s2 2) s (s2 2)
2.2 线性定常微分方程的求解 拉普拉斯反变换:部分分式展开法
时域 差分方程
解析式模型
状态方程
复域
传递函数 结构图-信号流图
图模型
频域 频率特性
数学模型是一个反应变量之间关系的表达式,在不同的域中有不同的表现形式!
1.引言
解析法:依据系统及元件各变量之间所遵循的物理、化学定律列写出变量间的数学表 达式,并实验验证。
实验法:对系统或元件输入一定形式的信号(例如阶跃信号、单位脉冲信号、正弦信 号等),根据系统或元件的输出响应,经过数据处理而辨识出系统的数学模型。
k 1 v n1
s
l 1 n2
(Ti s 1)
(T
2 j
s2
2Tj
s
1)
i 1
j 1
适用于 频域分
析
3.2 传递函数的基本概念 传递函数的标准形式
K:增益
K*=根轨迹增益
K与K*的关系:
两者关系
m
zj
K K*
j 1 n
pi
i 1
3.3 典型环节及其传递函数
一个传递函数可以分解为若干个基本因子的乘积,每个基本因子就称为典型环节。常见 的几种形式有:
Y (s)
R(s)
Y (s)
f (t)
(t)
1(t )
t t2 2
e at
sin t cos t
F (s)
1
1s 1 s2 1 s3
1 (s a)
(s2 2) s (s2 2)
2.2 线性定常微分方程的求解 拉普拉斯反变换:部分分式展开法
时域 差分方程
解析式模型
状态方程
复域
传递函数 结构图-信号流图
图模型
频域 频率特性
数学模型是一个反应变量之间关系的表达式,在不同的域中有不同的表现形式!
1.引言
解析法:依据系统及元件各变量之间所遵循的物理、化学定律列写出变量间的数学表 达式,并实验验证。
实验法:对系统或元件输入一定形式的信号(例如阶跃信号、单位脉冲信号、正弦信 号等),根据系统或元件的输出响应,经过数据处理而辨识出系统的数学模型。
k 1 v n1
s
l 1 n2
(Ti s 1)
(T
2 j
s2
2Tj
s
1)
i 1
j 1
适用于 频域分
析
3.2 传递函数的基本概念 传递函数的标准形式
K:增益
K*=根轨迹增益
K与K*的关系:
两者关系
m
zj
K K*
j 1 n
pi
i 1
3.3 典型环节及其传递函数
一个传递函数可以分解为若干个基本因子的乘积,每个基本因子就称为典型环节。常见 的几种形式有:
Y (s)
R(s)
Y (s)
西工大、西交大自动控制原理 第二章 控制系统的数学模型_2

5 比较点的移动 比较点的前移:
Rs
Cs
Rs
Cs
Gs
Gs
Qs
1 Qs
Gs
若要将比较点由方框后移至方框的前面,为保持信号 的等效,要在移动后的信号线上加入一个比较点所越 过的方框的倒数。
5 比较点的移动 比较点的后移:
Rs
Cs Gs
Rs Gs
Cs
Qs
Qs
G(s)
若要将比较点由方框前移至方框的后面,为保持信号的 等效,要在移动后的信号线上加入一个比较点所越过的 方框。
2-3 控制系统的结构图与信号流图
控制系统的结构图概述
控制系统的结构图(block diagram)是描述系统各元部 件之间信号传递关系的数学图形,表示了系统中各变量 间的因果关系以及对各变量所进行的运算。通过对系统 结构图进行等效变换(equivalent transform)后,可 求出系统的传递函数。
G1(s)
-1 H(s)
R(s)=0
f
(s)
C(s) F(s)
G2 ( s) 1 G2 (s)H (s)(1)G1(s)
G2 ( s) 1 G2 (s)G1(s)H (s)
G2(s) G2(s) 1 G(s)H(s) 1 Gk (s)
单位反馈系统H(s)=1,有
f
(s)
C(s) F(s)
若令:G(s) G1(s)G2(s) 为前向通路传递函数,
则:
B(s)
Gk (s) (s) G(s)H(s)
可见:系统开环传递函数Gk(s)等于前向通路传递函 数G(s)=G1(s)G2(s)与反馈通道传递函数H(s)的乘积。
R(S) ε(s) G1(s)
F(s)
自动控制原理控制系统的结构图

比较点后移
R(s)
G(s)
比较点前移
+
Q(s)
C(s)
R(s)
+
C(s) G(s)
比较点后移
Q(s)
R(s)
+
C(s) G(s)
Q(s)
C(s) R(s)G(s) Q(s)
[R(s) Q(s) ]G(s) G(s)
R(s)
C(s) G(s)
+
Q(s)
G(s)
C(s) [R(s) Q(s)]G(s)
R(s)G(s) Q(s)G(1s6 )
(5)引出点旳移动(前移、后移)
引出点前移
R(s)
G(s)
分支点(引出点)前移
C(s) C(s)
引出点后移
R(s)
G(s)
R(s)
分支点(引出点)后移
R(s)
G(s)
C(s)
G(s)
C(s)
C(s) R(s)G(s)
G(s) R(s)
C(s) R(s)
将 C(s) E(s)G(s) 代入上式,消去G(s)即得:
E(s) R(s)
1
H
1 (s)G(s)
1
1 开环传递函数
31
N(s)
+ E(s)
++
C(s)
R(s)
G1(s)
G2 (s)
-
B(s)
H(s)
(1)
打开反馈
C(s) R(s)
1
G(s) H (s)G(s)
前向通路传递函数 1 开环传递函数
注意:进行相加减旳量,必须具有相同旳量纲。
X1 +
+
X1+X2 R1(s)
233控制系统方框图的化简及传递函数
U 2 ( s)
22
两个相加点互相交换移动
U1 ( s )
A
-
-
1 R1
1 sC1
1 R2C2 s 1
R1C2 s
U 2 ( s)
U1 ( s )
A
-
-
1 R1
1 sC1
1 R2C2 s 1
R1C2 s
U 2 ( s)
23
小回路化简
U1 ( s ) A
-
-
1 R1
1 sC1
1 R2C2 s 1
12
结论
下列闭环传递函数
(s)
F ( s)
(s)
F ( s )
具有相同的特征多项式
13
闭环特征多项式:
1 G1 (s)G2 (s) H (s)
14
G1 (s)G2 (s) (s) 1 G1 (s)G2 (s) H (s)
输出对输入 对 比
G2 (s) F ( s) 1 G1 (s)G2 (s) H (s)
R( s )
+
E ( s )
G1 ( s )
G2 (s)
Y ( s)
35
G3 ( s) G1 ( s)
R( s )
+
E ( s )
G1 ( s )
G2 (s)
Y ( s)
小回路化简
R( s )
G1 ( s) G3 ( s) G1 ( s)
G1 ( s)G2 ( s) 1 G1 ( s)G2 ( s)
1 G2 ( s)G3 ( s) 1 G1 ( s)G2 ( s)
E (s)
E ( s) 1 G2 (s)G3 (s) R(s) 1 G1 (s)G2 (s)
自动控制原理第二章3
Uc(s)
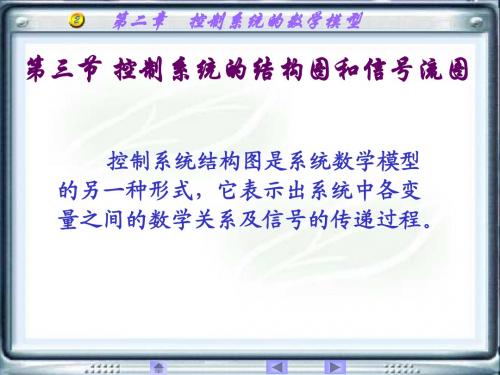
第三节控制系统的结构图和信号流图
N(s) R(s) C(s) G1(s) G2(s)
+ _
H(s) 典型反馈控制系统方框图 1)信号线:带单向箭头,表示信号流向 信号线:带单向箭头, 2)引出点:信号从引出点分开,大小和性质相同 引出点:信号从引出点分开, 3)比较点:两个或两个以上的信号相加减 比较点: 4)方框:对信号进行数学变换,方框中写入环节的传递函数 方框:对信号进行数学变换,
R1 C2S 1 C(S) 1 1 R2 +R1C R2 +1)C2S C2S2S
R(s)
_
1 R1C1S+1 R1C2S
1 R2C2S+1
C(s)
第三节控制系统的结构图和信号流图
三、控制系统的信号流图: 控制系统的信号流图:
1、定义 、 一组线性代数方程式变量间传递关系的图形表示, 一组线性代数方程式变量间传递关系的图形表示,由节 支路和支路增益组成。 点、支路和支路增益组成。 y1 典型的信号流图 x1 1 x2 a e a y2=ay1 d x3 b f x4 c x5 g 1 x6 y2
第三节控制系统的结构图和信号流图
绘制动态结构图的一般步骤为: 绘制动态结构图的一般步骤为 (1)确定系统中各元件或环节的传递函数。 )确定系统中各元件或环节的传递函数。 (2)绘出各环节的方框,方框中标出其传 )绘出各环节的方框, 递函数、输入量和输出量。 递函数、输入量和输出量。 (3)根据信号在系统中的流向,依次将各 )根据信号在系统中的流向, 方框连接起来。 方框连接起来。
p1 = abc
L1与L3
p2 = d
L3 = g L2与L3
L1 = ae
L2 = bf
第三节控制系统的结构图和信号流图
N(s) R(s) C(s) G1(s) G2(s)
+ _
H(s) 典型反馈控制系统方框图 1)信号线:带单向箭头,表示信号流向 信号线:带单向箭头, 2)引出点:信号从引出点分开,大小和性质相同 引出点:信号从引出点分开, 3)比较点:两个或两个以上的信号相加减 比较点: 4)方框:对信号进行数学变换,方框中写入环节的传递函数 方框:对信号进行数学变换,
R1 C2S 1 C(S) 1 1 R2 +R1C R2 +1)C2S C2S2S
R(s)
_
1 R1C1S+1 R1C2S
1 R2C2S+1
C(s)
第三节控制系统的结构图和信号流图
三、控制系统的信号流图: 控制系统的信号流图:
1、定义 、 一组线性代数方程式变量间传递关系的图形表示, 一组线性代数方程式变量间传递关系的图形表示,由节 支路和支路增益组成。 点、支路和支路增益组成。 y1 典型的信号流图 x1 1 x2 a e a y2=ay1 d x3 b f x4 c x5 g 1 x6 y2
第三节控制系统的结构图和信号流图
绘制动态结构图的一般步骤为: 绘制动态结构图的一般步骤为 (1)确定系统中各元件或环节的传递函数。 )确定系统中各元件或环节的传递函数。 (2)绘出各环节的方框,方框中标出其传 )绘出各环节的方框, 递函数、输入量和输出量。 递函数、输入量和输出量。 (3)根据信号在系统中的流向,依次将各 )根据信号在系统中的流向, 方框连接起来。 方框连接起来。
p1 = abc
L1与L3
p2 = d
L3 = g L2与L3
L1 = ae
L2 = bf
自动控制原理第二章方框图

R1C2s
(R1C1s 1)(R2C2s 1) R1C2s
(R1C1s 1)(R2C2s 1)
解法二:
ui (s)
-
1 I1(s) - 1 u(s)
R1
I (s) C1s
-
1
1 uo (s)
R2 I2(s) C2s
ui (s) 1
R1
ui (s) 1
R1
-
1
-
C1s
1 R1
-
1
-
C1s
1 R1
1
自动控制原理第二章方框图自动控制方框图闭环控制系统方框图串级控制系统方框图前馈控制系统方框图控制系统方框图单回路控制系统方框图过程控制系统的方框图自动调节系统方框图控制方框图
传递函数的表达形式
有理分式形式:G(s)
b0 s m a0 s n
b1s m1 a1s n1
bm1s an1s
bm an
H3
相加点移动 G3 G1
G3 G1
向同无类用移功动
G2
错!
G2
H1
G(s) G1G2 G2G3 1 G1G2 H1
G2
G1 H1
总的结构图如下:
ui (s)
-
1 I1(s) - 1 u(s)
R1
I (s) C1s
-
1
1 uo (s)
R2 I2(s) C2s
ui (s)
-
C2s
1 I1(s) - 1 u(s)
X 2 (s)
X (s) G(s) Y (s)
X 2 (s)
X1(s)
相加点和分支点在一般情况下,不能互换。
X 3 (s)
X (s)
自动控制原理 控制系统的结构图

其他变化(比较点的移动、引出点的移动)以此三种 基本形式的等效法则为基础。
12
(1)串联连接
R( s )
U (s) 1
G (s) 1
G (s) 2
C( s )
R(s)
C(s)
G(s)
(a)
(b)
特点:前一环节的输出量就是后一环节的输入量
U1(s) G1(s)R(s) C(s) G2 (s)U1(s) G2 (s)G1(s)R(s)
注意:进行相加减的量,必须具有相同的量纲。
X1 +
+
X1+X2 R1(s)
-
R1(s)R2(s)
X1
X2
R2(s)
X3
X1-X2 +X3 -
X2
4
(4) 引出点(分支点、测量点) 表示信号测量或引出的位置
R(s)
G (s) 1
X(s)
G (s) 2
C(s)
X(s) 引出点示意图
注意:同一位置引出的信号大小和性质完全一样
G(s)
分支点(引出点)前移
C(s) C(s)
引出点后移
R(s)
G(s)
R(s)
分支点(引出点)后移
R(s)
G(s)
C(s)
G(s)
C(s)
C(s) R(s)G(s)
G(s) R(s)
C(s) R(s)
C(s) R(s)
G1(s)G2
(s)
G(s)
结论:
n
G(s) Gi (s) n为相串联的环节数 i 1
串联环节的等效传递函数等于所有传递函数的乘积
13
(2)并联连接
G1 (s)
12
(1)串联连接
R( s )
U (s) 1
G (s) 1
G (s) 2
C( s )
R(s)
C(s)
G(s)
(a)
(b)
特点:前一环节的输出量就是后一环节的输入量
U1(s) G1(s)R(s) C(s) G2 (s)U1(s) G2 (s)G1(s)R(s)
注意:进行相加减的量,必须具有相同的量纲。
X1 +
+
X1+X2 R1(s)
-
R1(s)R2(s)
X1
X2
R2(s)
X3
X1-X2 +X3 -
X2
4
(4) 引出点(分支点、测量点) 表示信号测量或引出的位置
R(s)
G (s) 1
X(s)
G (s) 2
C(s)
X(s) 引出点示意图
注意:同一位置引出的信号大小和性质完全一样
G(s)
分支点(引出点)前移
C(s) C(s)
引出点后移
R(s)
G(s)
R(s)
分支点(引出点)后移
R(s)
G(s)
C(s)
G(s)
C(s)
C(s) R(s)G(s)
G(s) R(s)
C(s) R(s)
C(s) R(s)
G1(s)G2
(s)
G(s)
结论:
n
G(s) Gi (s) n为相串联的环节数 i 1
串联环节的等效传递函数等于所有传递函数的乘积
13
(2)并联连接
G1 (s)
第2章 控制系统数学模型的建立

di
Ri dt
的增量方程式:Dur
dD(i) dDi
K1 dDi
RDi dt
整理得:
Dur
K1K
dDi dt
RDi
省略偏量符号Δ得:
ur
L
di dt
Ri
13
2.3 传递函数
2.3.1 传递函数的概念
RC电路如下:根据克希霍夫定律, 可列写微分方程
Ri(t) uc (t) ur (t)
消去中间变量i(t),得 对上式进行拉氏变换
K
(线性定常二阶微分方程式)
5
举例3 电枢控制的直流电动机
电枢电压控制的直流电动机线路原理图和结构图
输入—电枢电压ua
输出—轴角位移q 或角速度w
扰动—负载转矩ML
(1)列写原始方程式。电枢回路方程式:La
dia dt
Rai
Kew
ua
根据刚体旋转定律,写出运动方程式:
J
dw
dt
ML
Md
(2)Md和ia是中间变量。由于电动机转矩与电枢电流和气 隙磁通的乘积成正比,又因磁通恒定,有M d Kmia , 联立求解,整理后得
15
2.3.1 传递函数的性质
(1)传递函数是复变量s的有理真分式函数,分子的阶数m一 般低于或等于分母的阶数n, 即m≤n ,且所有系数均为 实数。
(2)传递函数只取决于系统和元件的结构和参数,与外作用
及初始条件无关。
(3)一定的传递函数有一定的零、极点分布图与之对应,因
此传递函数的零、极点分布图也表征了系统的动态性能。
令C(s)=L[c(t)],R(s)=L[r(t)],在初始条件为零时,进行拉氏变换, 可得到s的代数方程
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Uc(s) = I2(s) sc 2
1
图1图2比较
Ur(s)
从右 到左
R1 1
1 I (s)
SC1
I2(s)
R2
I1(s) I1(s)
sc2
1
Uc(s)
sc1
(补充)
Ur(s)
从左 到右
Sc 1
sc1
R2 I2(s)
1
Uc(s)
sc2
I2(s)
R1
I(s)
绘制网络结构图(3)
R1
U1(s)
R2
I2(s)
第2章 控制系统的数学模型
2.3 控制系统的结构图及其等效变换
2013.3.26
r (s) k U r (s)
r
W1
W2
位置随动系统结构图绘制
U r (s ) U c (s ) U (s )
U (s) Ut (s) U(s) r 1 m (s) c (s) E i uε r ur uε
1 [I1 (s) I 2 (s)] U 1 (s ) sc1 1 I 2 (s) Uc (s) sc2
练习题1
描述系统动态性能的方程组如下,试绘制以R(s)为输入 信号、C(s)为输出信号、N(s)为干扰信号的系统结构图。
E(s)=R(s)-C(s) N(s)+X4(s)=C(s) X4(s)=X3(s)G2(s)
r ( t ) k r ( t )
绘制网络结构图(1)
I(s)
R1 R2 1 C 1 I1(s)
urr(t) U (s) Ur(s)
sc1
R1
sc2
I2(s) R2
I2(s) 1 C2 ucc(t) U (s) 1
1 I (s)
1
sc2
Uc(s)
从右 到左
sc1 I2(s) • sc2
a d
G1 b a(1 G 2 ) 1 G 1G 2
b (a d)G1 aG1 (a b)G 2G1
d (a b)G 2 aG 2 (a d)G1G 2
a
G2 d a(1 G 1 ) 1 G 1G 2
b
d
课上练习: 求下述控制系统的传函。
G4(s)
E(s)-X4(s)H(s)=X1(s) X2(s)=X1(s)G1(s)
X3(s)=X2(s)+R(s)G4(s)+N(s)G3(s)
G3(s) G1(s) X2(s) H(s) X3(s) X4(s) G2(s) N(s) X4(s) C(s)
R(s)
E(s) C(s)
X1(s)
结构图三种基本形式(P29-30)
先简化 红线框
注意图形等效后面的代数辅助运算
注意图形等效后面的代数辅助运算
注意图形等效后面的代数辅助运算
注意图形等效后面的代数辅助运算
注意图形等效后面的代数辅助运算
注意图形等效后面的代数辅助运算
反思:有没有更好的方法?
今天的课程内容到此! 下次课讲授第3章 控制系统的时域 分析,请同学们做好预习!
urr(t) U (s)
I1(s)
sc1
I2(s)
1 C 1
sc2
1 C 2
ucc(t) U (s)
Ur(s)
R1
U1(s)
1
I1(s)
sc1
1
U1(s)
1 1 Uc(s) R2 I2(s) sc2
Uc(s)
1 [U r (s) U1 (s)] I 1 (s ) R1
1 [U1 (s) U c (s)] I 2 (s ) R2
G2(s)
G2(s)
C(s)
C(s)
4 G1 H (s) 1 G 1G 4 H
G (s)
2反馈
H (s)
G3(s) R(s)
G 1 (s ) G1(s) 1 G1 (s)G 4 (s)H(s)
H (s) G4(s)
G2(s)
C(s)
等效变换例1 (补充)
H (s)
等效变换例2 (补充)
R(s) G1(s) G3(s) H (s) G2(s) C(s)
3 相邻引出点可互换位置、可合并…
注意事项:
1 不是典型结构不可直接用公式
2 引出点综合点相邻,不可互换位置
引出点的移动(表2-2)
a
G(s)
a
b
a
G(s)
b
b
1 a G (s )
b
a
G(s)
b
b b G(s)
a
G(s)
综合点的移动(表2-2)
a
e b
G(s)
c
c = e G(s) = (a-b) G(s)= a G(s)- b G(s)
串
R
联 G2
C R
并
联
C R
反
馈 G1
C
G1
G1 G2
G2
R
G1 G2
C
R
G1 G2
C R
G1 1+ G1 G2
C
基本练习
G1 G2 G1 G2
G1- G2
G2
1 G1 G2
相邻综合点相邻引出点(表2-2)
结构图等效变换方法(表2-2) 1 三种典型结构可直接用公式
2 相邻综合点可互换位置、可合并…
G4
G4
R(s)
作用分解(补充)
G1
H1
1并联
G2
G3 H3
G3 G 3 1 G 3H 3
C(s)
G4
G 1G 2 G1 1 G 1H1
R(s)
G2
C(s)
3串联
2反馈
H1
H1
G 1G 2 H 1H 2 3 1 G 1H1 NhomakorabeaH
H3
G3(s) R(s)
G3(s)
1并联
G1(s)
3串联
G 1 R(s) 1 G 1G 4 H
W1 k
cc (s) k U c (s)
操纵手柄
ur ( t )
u(t ) u (t ) ut (t ) max E ua ( t ) ka u( t ) uc ( t ) c ( t ) k c ( t ) max d 2 m ( t ) d m ( t ) k m ua ( t ) u ( t ) ur ( t ) uc ( t ) k [r (t ) c (t )] Tm 2 dt dt d m ( t ) 1 ut ( t ) k t c (t ) m (t ) dt i
E
m 1 + u 放大器 u 1 c J f u a m 减 SM u k a_ i f 放大器 速 电机 L L k s ( T s 1 ) ut a 器 i J L fL ut c 测速电机 kts uc + Z TG 2 _ W k2
m m
U(s) k a Ua (s) U a (s) k m m (s ) Ra La s(Tms 1) m (s) k t s Ut (s) Z
1
s C1 I1(s) I1(s) = [Uc(s)+I2(s)•R2]•sC1 I(s) = [Ur(s) – I1(s)• sc ]• R 1 1
1
Uc(s) =
I2(s) = I(s) – I1(s)
1
补充
绘制网络结构(2)
I(s) R1 R2 1 I1(s) 1
Ur(s) Ur(s)
I(s) R1
Sc1
sc1
I1(s)
sc2
1
I2(s)
Uc(s) Uc(s)
Ur(s) sc 1 sc1
1
这是不行的
sc2
从左 到右
R1 1
1
I1(s) R2 I2(s)
I2(s)
I(s)
= Ur(s)
I(s)R1+I1(s) sc
I1(s) sc
1
1
= I2(s)R2+
Uc(s)
I(s) = I1(s)+ I2(s)
R(s)
G1
H 1 G 3H
反 馈
G2
C(s)
1 1 G 3H
再 反 馈
R(s)
G1(s) G3(s)
G2(s)
C(s) R(s)
1 1 G 3 (s)H(s)
3串联
1 1 G3 (s)H(s)
G1(s) 2反馈
G2(s)
C(s)
H (s)
H (s)
1并联
H (s) G2(s)
等效变换例3(补充)
a G(s) G(s) a e c a c b c b
G(s)
G(s)
1 G (s )
b
综合点移动(补充)
G3
G1
向同类移动
G2
G4
1并联
G3 G1
3串联
2反馈
G2
G1 G4
引出点移动(补充)
G1
图2-1
H2 G2 G3 H3 H1 G4
请你写出结果,行吗?
H2 G1 G2
H1 G3 H3
1 G4
Ur(s)
R1
1
sc1
1
1
1 R2
sc2
1
Uc(s)
你把综合点与引出点互换位置了
Ur(s)
R1
1
错啦!
sc1
1
sc1
1 R2
