数学建模的万能模板
数学建模万能模板4问题分析
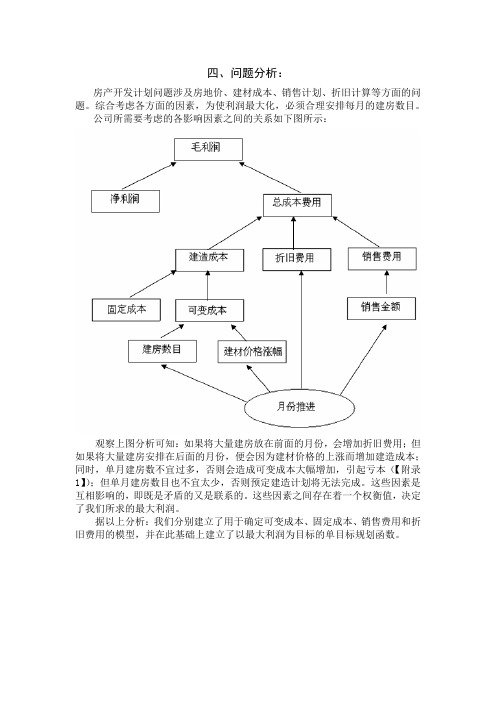
四、问题分析：房产开发计划问题涉及房地价、建材成本、销售计划、折旧计算等方面的问题。
综合考虑各方面的因素，为使利润最大化，必须合理安排每月的建房数目。
公司所需要考虑的各影响因素之间的关系如下图所示：观察上图分析可知：如果将大量建房放在前面的月份，会增加折旧费用；但如果将大量建房安排在后面的月份，便会因为建材价格的上涨而增加建造成本；同时，单月建房数不宜过多，否则会造成可变成本大幅增加，引起亏本（【附录1】）；但单月建房数目也不宜太少，否则预定建造计划将无法完成。
这些因素是互相影响的，即既是矛盾的又是联系的。
这些因素之间存在着一个权衡值，决定了我们所求的最大利润。
据以上分析：我们分别建立了用于确定可变成本、固定成本、销售费用和折旧费用的模型，并在此基础上建立了以最大利润为目标的单目标规划函数。
三、问题分析和基本思路2.1 问题分析和建模思路考虑问题的题设和要求，我们要解决的是出版社的资源优化配置问题。
资源优化配置问题是一类典型的规划问题。
对于规划问题的求解步骤基本是：第一步，找目标函数；第二步，找约束条件；第三步，对规划函数进行求解。
对题目仔细地分析后，我们确定当前经济效益和潜在经济效益为出版社资源配置的目标函数。
当前经济效益可以比较容易地用分配到的书号数表示出来，难点是潜在经济效益的表达。
我们分析关系，建立了顾客满意度量化描述潜在经济效益的模型。
当前经济效益和潜在效益描述好了，我们的目标函数也就形成了。
约束条件的寻找相对比较容易，不过我们能从题目中得到的明显约束条件很少，可想而知本题有隐含的约束条件需要自己去挖掘。
如果约束条件能够起到有效的约束作用，唯一剩下的就是借助计算机对规划模型进行最优求解。
此外，为了目标函数和约束条件的顺利表述。
我们在正式模型建立之前，做了大量完整而系统的模型准备工作，用量化的语言理清了各部分之间的关系。
2.2 思路流程图下面的思路流程图是我们文章结构的一个缩影，它完整而形象的反映了我们文章的建模思路。
数学建模范文参考实用模板
理工大学2015年数学建模竞赛论文(文样本)答卷编号（竞赛组委会填写）：题目编号：（ A ）论文题目：基于双种群遗传算法的公交路线查询问题参赛队员信息(必填)：答卷编号（竞赛组委会填写）：评阅情况（学校评阅专家填写）：评阅1.评阅2.评阅3.基于双种群遗传算法的公交路线查询问题摘要本文探讨的是公交路线选择而开发的查询系统.以两站点之间所花时间的最小值作为主要目标函数，利用双种群遗传算法的原理建立公交路线选择数学模型，再通过MATLAB程序来实现整个流程和迭代，最终求出全局近似最优解，即最优权重线路，以起点和终点查询到近似的最优公交路线，并进行了误差分析,模型的评价与推广.问题一：仅考虑公汽线路，对数据进行初步分析和处理后，考虑到数据的复杂性和数据搜索围的广度，我们应用比较成熟的双种群遗传算法建立数学模型. 通过MATLAB强大的矩阵运算功能得到站点之间的邻接矩阵，用时间加权. 其流程思想为基于双种群初始群体A、B，对染色体进行整数编码，用竞争选择法选择出较优个体作为繁殖下一代的母体，依据选择性集成思想，等概率使用两点交叉法和区域交叉法对染色体进行交叉操作与使用邻居交换变异和两点交换变异进行染色体变异操作，并结合MATLAB反复迭代，最终给出了六对起始站与终点站的六条近似最优路线. 该法扩大遗传算法的搜索围，避免过早收敛.问题二：在数据处理上用时间加权把地铁站点和汽车站点统一化，可得所有站点之间的邻接矩阵. 其求解原理与问题一相似，但由转车方式的不同生成了8种不同的适应度函数,再根据适应度函数来进行问题的求解.问题三：我们将任意两个站点之间的步行时间作为矩阵中相应位置的权，这时构建的邻接矩阵中的权就由两站点之间公汽到公汽的时间,公汽到地铁的时间,地铁到公汽的时间,地铁到地铁的时间和两点之间的步行时间构成. 但其求解原理与问题一相似，但由转车方式的不同就会生成不同的适应度函数,再根据适应度函数来进行问题的求解.双种群遗传算法提供了一种求解复杂系统优化问题的通用框架，它不依赖于问题的具体领域，对问题的种类有很强的鲁棒性，具有自组织、自适应和自学习性.关键词双种群遗传算法；竞争选择法；离散赌轮选择算子；选择性集成思想.一、问题的重述第29届奥运会明年8月将在举行，届时有大量观众到现场观看奥运比赛，其部分人将会乘坐公共交通工具（简称公汽，包括公汽、地铁等）出行. 市的公汽线路已达800条以上，使得公众的出行更加通畅、便利，但同时也面临多条线路的选择问题. 针对市场需求，某公司准备研制开发一个解决公汽线路选择问题的自主查询计算机系统.为了设计这样一个系统（核心是线路选择的模型与算法），从实际情况出发，满足查询者的各种不同需求. 需要研究的问题如下：问题一：只考虑公汽线路情况，给出任意两公汽站点之间线路选择问题的一般数学模型与算法. 并根据基本参数设定中的数据，利用其模型与算法，求出6对起始站→终问题三：假设知道所有站点之间的步行时间，给出任意两站点之间线路选择问题的数学模型.其中基本参数设定：相邻公汽站平均行驶时间(包括停站时间)：3分钟相邻地铁站平均行驶时间(包括停站时间)：2.5分钟公汽换乘公汽平均耗时：5分钟(其中步行时间2分钟)地铁换乘地铁平均耗时：4分钟(其中步行时间2分钟)地铁换乘公汽平均耗时：7分钟(其中步行时间4分钟)公汽换乘地铁平均耗时：6分钟(其中步行时间4分钟)公汽票价：分为单一票价与分段计价两种，标记于线路后；其中分段计价的票价为：0～20站：1元；21～40站：2元；40站以上：3元地铁票价：3元（无论地铁线路间是否换乘）注：以上参数均为简化问题而作的假设，未必与实际数据完全吻合.公汽线路及相关信息见数据文件B2007data.rar.二、模型的假设1.转车的次数控制在2次以；2. 相邻公汽站平均行驶时间(包括停站时间)：3分钟；3. 相邻地铁站平均行驶时间(包括停站时间)：2.5分钟；4. 公汽换乘公汽平均耗时：5分钟(其中步行时间2分钟)；5. 地铁换乘地铁平均耗时：4分钟(其中步行时间2分钟)；6. 地铁换乘公汽平均耗时：7分钟(其中步行时间4分钟)；7. 公汽换乘地铁平均耗时：6分钟(其中步行时间4分钟)；8. 公汽票价：分为单一票价与分段计价两种，标记于线路后，其中分段计价的票价为：0～20站：1元，21～40站：2元，40站以上：3元；9. 地铁票价：3元（无论地铁线路间是否换乘）；10. 知道所有站点之间的步行时间.三、符号说明C：只考虑公汽线路的情况下，每个个体对应路线总长；D：考虑公汽和地铁线路的情况下，每个个体对应路线部长；T：相邻公汽站平均行驶时间(包括停站时间)；1T：相邻地铁站平均行驶时间(包括停站时间)；2()f X：第k个个体所对应的适应度值；kA：每个个体所对应的适应度比例；P：每个个体所对应的选择概率（适应度比例）；T：所有站点之间的步行时间；abu：表示转车换乘所耗时间之和.四、模型的建立与求解（一）问题一1.1 问题分析该问题是一个组合优化问题. 对于此类问题，只有当其规模较小时，才能求其精确解. 在本文中公汽路线总数与站点数是成指数型增长的，所以一般很难精确地求出其最优解，因而寻找出有效的近似求解算法就具有重要意义.由于L406公汽线路的路线是环形的，而数据中没有标示出来，所以我们用相邻站点整体路线也相邻，判断出该公汽线路是环行的，所以应当作环行处理. 对于该问题，我们先求出其站点与站点之间的邻接矩阵（权用时间表示），其矩阵大小为39573957，数据量太多，不能输出，只能把放在存中.许多智能算法被用于求解两点间线路问题. 如禁忌搜索、模拟退火、蚁群算法等. 其中遗传算法是被研究最多的一种算法. 但标准遗传算法容易陷入局部极值解，出现“早熟收敛”现象. 为此人们提出了多种改进方法，如将遗传算子中的交叉算子进行改进，应用单亲遗传算法，将遗传算子与启发式算法结合等.遗传算法的核心思想为自然选择，适者生存. 遗传算法作为一种模拟生物进化的一种算法，提供了一种求解复杂系统优化问题的通用框架，它不依赖于问题的具体领域，对问题的种类有很强的鲁棒性，具有自组织、自适应和自学习性. 其也是一种迭代算法，从选定的初始解出发，通过不断地迭代，逐步改进当前解，直到最后搜索到最优解或满意解，其迭代过程是从一组初始解(群体)出发，采用类似于自然选择和有性繁殖的方法，在继承原有优良基因的基础上生成具有更好性能的下一代解的群体. 遗传算法的流程图见下图：遗传算法流程图标准遗传算法是针对一个宏观的种群进行选择、交叉、变异三种操作.双种群遗传算法是一种并行遗传算法，它使用多种群同时进化，并交换种群之间优秀个体所携带的遗传信息，以打破种群的平衡态达到更高的平衡态，跳出局部最优. 在双种群遗传算法中，每一种群都是按照标准算法进行操作. 在操作时，首先建立两个遗传算法群体，即种群A和种群B，分别独立地进行选择、交叉、变异操作，且交叉概率、变异概率不同. 当每一代运行结束以后，产生一个随机数n，分别从A，B中选出最优染色体和n个染色体进行杂交，以打破平衡态. 因为在双种群遗传算法中，每一种群都是按照标准算法进行操作的.算法（double populations genetic 由上分析，对于本问题，我们釆用双种群遗传[5]algorithm）在选择公汽路线问题中的应用.遗传算法的创始人美国著名学者、密西根大学教授John H.Holland认为，可以用一组编码来模拟一组计算机程序，并且定义了一个衡量每个“程序”的度量：“适应值”. Holland模拟自然选择机制对这组“程序”进行“进化”，直到最终得到一个正确的“程序”为止. 编码方式有：二进制编码、十进制编码和符号编码等方法. 整数编码与符号编码一般用于与顺序有关的组合优化方面的问题. 根据公汽路线的特点，本文的工作采编码. 染色体长度与公汽路线结点个数相同，染色体的每个基因的编码即为公用整数[6]汽路线结点的编号. 因此，每条染色体由1到n（3957）的一个全排列组成.选择时,考虑到适应度比例法(轮盘赌选择法)与最佳个体保留法在对染色体进行[6]各自的优缺点，差异性较大，依据选择性集成思想,表现好的个体学习器越精确、差异越大，集成后可以获得的结果越好. 而竞争选择法集成了上述两种的优点克服了它们的缺点，因此本文釆用竞争选择法. 其中竞争选择法是釆用适应度比例法进行选择，交叉后产生下一代，再利用最佳个体保留法将上一代的最佳个体直接保存下来，然后从新群体中淘汰一个适应度最差的个体，提高了问题求解的收敛速度，体现了遗传算法自适应环境的能力.在对染色体进行交叉[6]操作时,对于由整数编码的染色体，交叉操作会形成染色体中的非法基因，即重复基因. 所以实现染色体交叉要将重复的基因清除. 只使用一种交叉方法容易引起过早收敛，即“早熟”. 依据选择性集成思想 ,等概率使用两点交叉法和区域交叉法这两种交叉方法，扩大遗传算法的搜索围，避免过早收敛.在染色体的变异[6]操作中，与交叉方法一样，如果使用一种变异方法，同样可能会引起“早熟”. 为了避免过早收敛，依据选择性集成思想选择邻居交换变异和两点交换变异这两种个性好且差异性较大的变异方法，等概率使用以扩大搜索围.1.2 模型建立1.2.1 从起点站到终点站不转车，则双种群遗传算法的流程如下：（1）产生邻接矩阵邻接矩阵的MATLAB 程序实现见附件一.（2）基于站点序号的编码一般来说种群规模越大越容易收敛到最优解，但是要保证其初始种群中的每个个体都是互异的，m 不能设置过大，否则无法产生初始种群，且m 过大其收敛速度必然降低，也会消耗更多的计算资源,并基于一般遗传算法中初始群体大小的选择，本文中取m=30.公汽路线问题中每一种起点站到终点站的方案对应于解空间的一个解 ，解空间中的数据是遗传算法的表现形式，从表现到基因型的映射称为编码. 最初遗传算法是采用二进制编码方法，但在大量实际问题中，二进制编码操作不简便，不易进行变异交叉操作，易产生大量非可行解，所以针对特殊的问题，可以灵活采用不同的编码方法. 本文在公汽线路求解中，采用基于站点序号的实数编码，将染色体定义为公汽线路的一条解路线中的站点号序列，在MATLAB 中为一个没有重复数字的行向量来表示. 设有n 个站点的某个全排列为12(,,,)n x x x ，则个体的染色体表示为12(,,,)n X x x x ，n=3957.（3）产生初始群体种群中每一个体为n （3957）个站点的一个全排列，随机生成m （m=30）个1～n 的随机排列，得到m 个个体的初始种群，m 为种群大小，n 为染色体长度.生成初始群体的具体算法的MATLAB 程序实现见附件二.A 、B 初始群体的数据矩阵为303957，由于数据太多，文中就不给出数据（其结果可运行程序得出）.（4）适应度函数与染色体的选择在遗传算法进行搜索时只以适应度函数为依据，利用种群中个体每个的适应度值来进行搜索，适应度值是进化时优胜劣汰的依据，应用中总是根据问题的优化指标来定义.对于公汽线路问题，以个体对应路线所发的时间之和作为个体适应度，其适应度越小,表明该个体越优. 则该个体对应[7]适应度值为：11111()()(1)n i n i i k x x x x f X T C C其中1T （3（分钟））表示相邻公汽站平均行驶时间(包括停站时间)，b a x x C 表示站点a x 和b x 之间的距离，1n x x C 表示起始点与终点站之间的距离.一般来说，选择算子设计使得个体被选中并遗传到下一代群体中的概率与该个体的适应度大小有关. 适应度是越高越好，而在公汽线路问题中，如果适应度是所经过的对应路线所花的时间之和，路线所花时间之和是越小越好，为了使公汽线路问题的适应度与一般遗传算法中的适应度一致. 这里用选择概率来进行衡量. 则每个个体的选择概率（适应度比例）就是每个个体的适应度与所有个体适应度的总和之比，即： 301()(2)()k k k f X A f X 其中301()k k f X 表示所有个体适应度的总和.但当路径所花时间非常大(例如：10000)，这样其适应度比例的最高数据位将在小数点后的第四位，这样不利于计算，为此要进行尺度变换. 为确保适应度有两位整数，此处将适应度放大倍数L(本题中 L=lOOO) 因此适应度比例[8]函数的表达式为：(3)P AL遗传算法中选择算子设计经典的是用适应度成比例的概率方法 ，但是这里存在的问题是由于许多个体的适应度比例很小几乎没有机会复制个体，从而被过早地淘汰. 这样整个群体多样性就无法得到保证，这里采用一种新的赌轮选择算子——离散赌轮选择[8]算子，将有效地避免了这个问题.在本题中是由30个个体构成初始群体，即：1230,,,X X X ，其所占的适应度比例分别是1230,,,P P P ，在保持这个比例的情况下对这个取值围放大1000倍. 按照顺序在1～1000分别占不同的区间，当随机函数产生1～1000以的时，即使是适应度比例最小的也有可能被选中，从而较好的保持了群体的多样性.由上所述则可选择出适应力强的，淘汰适应力弱的个体从而得到总体适应能力强的群体.经过选择算子得出总体适应能力强的A 、B 群体数据矩阵为303957，因数据量太大，文中就不给出具体数据.（5）交叉重组依据选择性集成思想 ,等概率使用两点交叉法和区域交叉法这两种差异性较大的交叉方法，扩大遗传算法的搜索围，避免过早收敛.其中，两点交叉法是先随机设定两个基因交叉位置，将父辈两个个体在这两个交叉点之间的基因链码相互交换，从而形成新的个体；区域交叉法是随机在染色体中选择一个交叉区域，将第二条染色体的交叉区域加在第一条染色体的前面，第一条染色体的交叉区域加在第二条染色体的前面，在交叉区域后依次删除与交叉区域相同的基因，得到最后的两条子染色体.将第（3）步得到的关于A ，B 种群的数据分别用两种交叉算法来实现操作. 其中一半数据用两点交叉法，另一半的数据用区域交叉法来进行染色体的交叉重组.其具体算法的MATLAB 程序实现见附件四.经过交叉重组得出的A 、B 群体数据矩阵为303957，因数据量太大，文中就不给出具体数据.（6）染色体的变异为了避免过早收敛，依据选择性集成思想选择邻居交换变异和两点交换变异这两种个性好且差异性较大的变异方法，等概率使用以扩大搜索围.其中，邻居交换变异是产生一个随机数，将该数对应的基因和其后的基因交换；若该数对应的基因是染色体中的最后一个基因，则将该基因与染色体的第一个基因交换；两点交换变异是先产生两个不同的随机数，确定两个交换点，然后对个体在此两点的基因进行交换.经过染色体变异得出的A 、B 群体数据矩阵为303957，因数据量太大，文中就不给出具体数据.（7）种群交叉将两个种群中的最优解取出，再在每个种群中随机选取n 个染色体，将这n+1个染色体互换，进入对方种群.经过种群交叉得出的A 、B 群体数据矩阵为303957，因数据量太大，文中就不给出具体数据.（8）最佳个体保留法要把群体中适应度最高的个体不经过配对交叉直接复制到下一代中，然后从 新群体中淘汰一个适应度最差的个体. 分别对A 、B 进行独立的操作.经过最佳保留法选择后得出的A 、B 群体数据矩阵为303957，因数据量太大，文中就不给出具体数据.（9）迭代的结束条件在本文中，采用进化的代数N 作为循环迭代过程的结束，如果等于N ，则算法结束，输出适应值最高的解；否则，继续重复上述过程.重复步骤（3），（4），（5），（6），（7），（8）依次进行循环迭代，本题中设定迭代次数为N=1000. 最后得到30个近似的最优解.以上（2）—（9）流程的MATLAB 程序实现见附件二.（10）结果选出这30个近似最优解中以时间作为权值最小的那一组解作为题设中要求的近似最优解. 其中满足要求的基因链码（站点数）的顺序即是顾客所需从起始点到终点站的路线1.2.2 从起点站到终点站转一次车从起点站到终点站转一次车遗传算法流程中基于站点序号的编码，交叉重组，染色体的变异，种群交叉，迭代的结束条件和结果的原理与从起点站到终点站不转车相同.只有在适应度函数与选择流程中每一个个体所对应的适应度函数处有所改变，其函数为：11111()()5(4)n i n i i k x x x x f X T C C其中5（分钟）表示公汽换乘公汽一次耗时(其中步行时间2分钟).除这之外，这一流程中的其他的原理没变.1.2.3 从起点站到终点站转两次车从起点站到终点站转两次车遗传算法流程中基于站点序号的编码，交叉重组，染色体的变异，种群交叉，迭代的结束条件和结果的原理与从起点站到终点站不转车相同.只有在适应度函数与选择流程中每一个个体所对应的适应度函数处有所改变，其函数为：11111()()52(5)n i n i i k x x x x f X T C C其中52（分钟）表示公汽换乘公汽两次耗时(其中步行时间22分钟).除这之外，这一流程中的其他的原理没变.1.3 模型求解1.3.1从起点站到终点站不转车由程序运行最终得出：找不一条路线使从起点站到终点站不转车.1.3.2 从起点站到终点站转一次车1.3.32.1 问题分析考虑到加入地铁及公汽的交叉通道，在数据处理上用时间加权把地铁站点和汽车站点统一化，可得所有站点之间的邻接矩阵. 其求解原理与问题一相似，但由转车方式的不同就会生成相对应的适应度函数,再根据适应度函来对问题求解.2.2 模型建立2.2.1 产生邻接矩阵首先运用MATLAB 强大的矩阵运算功能把其邻接矩阵得出,该矩阵是39573957,由于数据量太大不能把其具体表示出来,只能把所得到的数据放在存中,在运用的时候再从存中调用.2.2.2 只坐地铁（不换乘）对于该问题遗传算法流程中基于站点序号的编码，交叉重组，染色体的变异，种群交叉，迭代的结束条件和结果的原理与仅考虑公汽线路从起点站到终点站不转车相同.只有在适应度函数与选择流程中每一个个体所对应的适应度函数处有所改变，其函数为：12111()()(6)m m j j j k x x x x f X T D D其中2T 表示相邻地铁站平均行驶时间(包括停站时间),a bx x D 表示站点a x 和b x 之间的距离， 1mx x D 表示起始点与终点站之间的距离. 除这之外，这一流程中的其他的原理没变.2.2.3 地铁到地铁（换乘一或两次）对于该问题遗传算法流程中基于站点序号的编码，交叉重组，染色体的变异，种群交叉，迭代的结束条件和结果的原理与仅考虑公汽线路从起点站到终点站不转车相同.只有在适应度函数与选择流程中每一个个体所对应的适应度函数处有所改变，其函数为：12111()()4(42)(7)m m j j j k x x x x f X T or D D其中2T (2.5(分钟))表示相邻地铁站平均行驶时间(包括停站时间),a bx x D 表示站点a x 和b x 之间的距离， 1mx x D 表示起始点与终点站之间的距离, 4(分钟)表示地铁换乘地铁平均耗时(其中步行时间2分钟).除这之外，这一流程中的其他的原理没变.2.2.4 地铁到公汽对于该问题遗传算法流程中基于站点序号的编码，交叉重组，染色体的变异，种群交叉，迭代的结束条件和结果的原理与仅考虑公汽线路从起点站到终点站不转车相同.只有在适应度函数与选择流程中每一个个体所对应的适应度函数处有所改变，其函数为：1112111111()()()7(8)mn m i j n i j ijk x x x x x x x x f X T T C C D D除这之外，这一流程中的其他的原理没变. 2.2.5 公汽到地铁为了简化模型，将地铁换乘公汽平均耗时与公汽换乘地铁平均耗时都假设为7分钟，因为耗时相差不大. 则地铁到公汽与公汽到地铁是一样的.对于该问题遗传算法流程中基于站点序号的编码，交叉重组，染色体的变异，种群交叉，迭代的结束条件和结果的原理与仅考虑公汽线路从起点站到终点站不转车相同.只有在适应度函数与选择流程中每一个个体所对应的适应度函数处有所改变，其函数为：1112111111()()()6(9)mn m i j n i j ijk x x x x x x x x f X T T C C D D除这之外，这一流程中的其他的原理没变. 2.2.6 公汽到地铁再到公汽对于该问题遗传算法流程中基于站点序号的编码，交叉重组，染色体的变异，种群交叉，迭代的结束条件和结果的原理与仅考虑公汽线路从起点站到终点站不转车相同.只有在适应度函数与选择流程中每一个个体所对应的适应度函数处有所改变，其函数为：1112111111()()()67(10)mn m i j n i j ijk x x x x x x x x f X T T C C D D除这之外，这一流程中的其他的原理没变. 2.2.7公汽到地铁再到地铁对于该问题遗传算法流程中基于站点序号的编码，交叉重组，染色体的变异，种群交叉，迭代的结束条件和结果的原理与仅考虑公汽线路从起点站到终点站不转车相同.只有在适应度函数与选择流程中每一个个体所对应的适应度函数处有所改变，其函数为：1112111111()()()64(11)mn m i j n i j ijk x x x x x x x x f X T T C C D D除这之外，这一流程中的其他的原理没变. 2.2.8地铁到公汽再到公汽对于该问题遗传算法流程中基于站点序号的编码，交叉重组，染色体的变异，种群交叉，迭代的结束条件和结果的原理与仅考虑公汽线路从起点站到终点站不转车相同.只有在适应度函数与选择流程中每一个个体所对应的适应度函数处有所改变，其函数为：1112111111()()()75(12)mn m i j n i j ijk x x x x x x x x f X T T C C D D 除这之外，这一流程中的其他的原理没变. 2.2.9地铁到公汽再到地铁对于该问题遗传算法流程中基于站点序号的编码，交叉重组，染色体的变异，种群交叉，迭代的结束条件和结果的原理与仅考虑公汽线路从起点站到终点站不转车相同.只有在适应度函数与选择流程中每一个个体所对应的适应度函数处有所改变，其函数为：1112111111()()()76(13)mn m i j n i j ijk x x x x x x x x f X T T C C D D 除这之外，这一流程中的其他的原理没变. 2.3 模型求解 2.3.1 只坐地铁由程序运行最终得出：对六对起点到终点找不一条路线为只做地铁. 2.3.2 地铁到地铁由程序运行最终得出：对六对起点到终点找不一条路线地铁到地铁. 2.3.3 地铁到公汽由程序运行最终得出：对六对起点到终点找不一条路线为地铁到公汽. 2.3.4 公汽到地铁由程序运行最终得出：对六对起点到终点找不一条路线为公汽到地铁. 2.3.5 公汽到公汽 1.换一次车2.换两次车由程序运行最终得出：对六对起点到终点找不一条路线为公汽到地铁再到地铁. 2.3.7 地铁到公汽再到公汽由程序运行最终得出：对六对起点到终点找不一条路线为地铁到公汽再到公汽. 2.3.8 地铁到公汽再到地铁由程序运行最终得出：对六对起点到终点找不一条路线为地铁到公汽再到地铁. （三）问题三 3.1 问题分析在该问题中假设知道所有站点之间的步行时间,即任意两个站点之间都是可以到达的,只是以步行的方式来实现. 我们以两个站点之间的步行时间作为矩阵中的权. 这时构建的邻接矩阵中的权由两站点之间公汽到公汽的时间,公汽到地铁的时间,地铁到公汽的时间,地铁到地铁的时间和两点之间的步行时间构成. 3.2 模型建立对于该问题遗传算法流程中基于站点序号的编码，交叉重组，染色体的变异，种群交叉，迭代的结束条件和结果的原理与仅考虑公汽线路从起点站到终点站不转车相同.。
数学建模：第六章建模范例三
103.133872
(3)
101.310287
(3,1)
98.472872
(5)
96.731702
(5,1)
94.787533
(5,2)
92.480158
(5,3)
90.844949
(5,3,1)
4108.656375
(5,5)
*
M=5000万元，n=10年基金使用最佳方案（单位：万元）
3
改为
4
利用
5
软件求解（程序略）M=5000万元，
6
n=10年基金使用最佳方案：（单位：万元）
7
*
M=5000万元，n=10年基金使最佳方案（单位：万元）
存1年定期
存2年定期
存3年定期
存5年定期
取款数额（到期本息和）
每年发放奖学金数额
第一年初
105.650679
103.527252
220.429705
2.255
*
由上表可得，任何最佳存款策略中不能存在以下的存款策略(1,1),(2,1),(2,2),(3,2)和（3,3）。
由1,2,3,5四种定期能够组成的策略（5年定期不重复） 只能有（1）,（2）,（3）,（3,1）,(5), (5,1), (5,2), (5,3), (5,3,1)九种，
*
根据以上的推理，可得n年的最优存储方案公式二为：
据上公式用
可以求得n=10年，M=5000万元时
基金使用的最优方案：（单位：万元）
每年奖学金：
问题三求解：
方案一：只存款不购买国库券
1
因学校要在基金到位后的第3年举行校庆，所以此年奖金应是其他年度的1.2倍，
全国大学生数学建模竞赛模板3篇
全国大学生数学建模竞赛模板第一篇：问题分析与建模问题背景与分析在我们生活中，电子商务绝对是不可避免的一个事物。
我们可以在家里通过手机或电脑上的网站购买许多我们需要的商品，这使得我们的生活更加便利。
但是，在电子商务中，涉及到的交易问题也不可忽略。
其中，一项重要的问题就是物流问题。
物流是电子商务中不可忽略的部分，对于所有电子商务交易来说，物流都是不可缺少的环节。
我们需要在电商平台上进行物流规划，使得发送仓库到达顾客地点的时间最短。
在电商平台上，从订单生成到物流出发需要一定的时间，这也就限制了物流的速度。
因此，确定出发送仓库和配送路线是保证顺利送达的重要因素。
问题描述在这个问题中，我们需要制定出一种方案，来优化电商平台上的物流配送问题。
具体来说，可以完成以下几个阶段的优化课题：1. 确定发送仓库的位置2. 确定货物的分配方式3. 确定配送路线在以上三个阶段中，配送路线是最关键的一部分。
如果能够找到最优的配送路线，可以将配送时间缩短到最短。
建模过程对于这个问题，我们可以进行如下的建模：不同的仓库可能会对应不同的快递公司，每个快递公司都有自己的服务区域。
因此，确定发送仓库的位置，也就注定了使用哪家快递公司来进行配送。
在确定仓库位置时，我们可以使用多种方法，如基于历史数据的分析，考虑客户量等因素。
2. 确定货物的分配方式电商平台中，货物的分配方式涉及到多个因素。
首先，需要考虑各个仓库的库存量和客户的需求量。
其次，还需要考虑货物的类型和性质，如食品、电子产品、生活用品等。
在确定货物的分配方式时，需要综合考虑多个因素。
3. 确定配送路线最后，需要确定配送路线。
这个过程中，需要考虑到多种因素。
首先，需要考虑路程的长度，因为路程长度对配送时间有较大的影响。
其次，需要考虑城市交通状况，如拥堵情况等。
还需要考虑到各个地点的重要性和紧急程度，这些因素也会影响到配送的速度和效率。
模型应用我们的模型可以使用多种优化算法来得到最优的配送方案。
数学建模美赛写作各部分实用模板
摘要第一段：写论文解决什么问题1．问题的重述a. 介绍重点词开头：例1：“Hand move” irrigation, a cheap but labor-intensive system used on small farms, consists of a movable pipe with sprinkler on top that can be attached to a stationary main.例2:……is a real-life common phenomenon with many complexities.例3：An (effective plan) is crucial to………b. 直接指出问题：例 1：We find the optimal number of tollbooths in a highway toll-plaza for a given number of highway lanes: the number of tollbooths that minimizes average delay experienced by cars.例2：A brand-new university needs to balance the cost of information technology security measures with the potential cost of attacks on its systems.例3：We determine the number of sprinklers to use by analyzing the energy and motion of water in the pipe and examining the engineering parameters of sprinklers available in the market.例4: After mathematically analyzing the …… problem, our modeling group would like to present our conclusions, strategies, (and recommendations )to the …….例5：Our goal is... that (minimizes the time )……….2．解决这个问题的伟大意义反面说明。
数学建模万能模板
K：学科评价模型学科的水平、地位是高等学校的一个重要指标，而学科间水平的谈论对于学科的发展有重视要的作用，它可以使得各学科能更加深入的认识本学科 ( 与其他学科对照较 ) 的地位及不足之处，可以更好的促进该学科的发展。
因此，如何给出合理的学科谈论系统或模型素来是学科发展研究的热点问题。
现有某大学（科研与授课并重型高校）的13 个学科在一段时期内的检查数据，包括各种建设见效数据和先期投入的数据。
1、依照已给数据建立学科谈论模型，要求必要的数据解析及建模过程。
2、模型解析，给出建立模型的适用性、合理性解析。
3、假设数据来自于某科研型或授课型高校，请给出相应的学科谈论模型。
承诺书页编号学科谈论大纲（一）对问题的基本认识或办理整个问题的基本框架，思路（简短简要，要点，亮点突出）研究目的，意义要求）本文研究。
问题。
即数学种类的归纳（一）（建模思路）（1. 每题数据性质等大概解析）第一，本文分别解析每个小题的特点：。
（2. 建立模型的思路：）针对第一问。
问题，本文建立。
模型；在第一个。
模型中，本文对。
问题进行简化，利用。
什么知识建立什么模型；在对。
模型改进的基础上建立了。
模型Ⅱ。
针对第二。
针对第三。
（三）算法思想，求解思路，使用方法，程序）1）针对模型求解， ( 设计。
求解思路 ) 。
本文使用。
什么算法，。
软件工具，对附件中所给的数据进行精选，去除异常数据，对残缺数据进行合适的补充，求解出什么问题，进一步求解出。
什么结果。
（方法，软件，结果清楚写出来）2）建模特点，模型检验）对模型进行合理的理论证明和推导，所给出的理论证明结果大体为。
模型优点。
，建模思想方法。
，算法特点。
，结果检验。
，。
，模型检验。
从中随机抽取了 3 组（每组 8 个采样）对理论结果进行了数据模拟，结果显示，理论结果与数据模拟结果切合。
等等3）在模型的检验模型中，本文分别谈论了以上模型的精度，牢固性，矫捷度平解析。
（四）（数据结果，结论，回答所问道全部问题）最后，归纳全文，突出亮点，指出不足，提出本文经过改进或扩展。
数学建模竞赛模板
数学建模竞赛模板
数学建模竞赛模板
一、题目背景
（介绍数学建模竞赛的背景，例如国际数学建模竞赛（IMMC）是一项全球性的数学竞赛，旨在提高学生的数学建模能力。
）
二、问题描述
（简要描述比赛题目，例如“给定一组气象数据，如何预测未来一周的天气情况？”）
三、问题分析
（对问题进行分析，明确问题的关键点和需要解决的难点。
例如，需要分析气象数据的特征，找到合适的数学模型来预测天气情况。
）
四、模型建立
1. 数据预处理
（对原始数据进行清洗和处理，例如去除异常值、填补缺失值等。
）2. 特征提取
（提取与天气预测相关的特征，例如温度、湿度、风速等。
）
3. 模型选择
（根据问题的特点选择合适的数学模型，例如线性回归、神经网络等。
）
4. 模型训练与优化
（使用训练集对模型进行训练，并进行参数优化以提高模型的预测能力。
）
5. 模型评估与调整
（使用测试集对模型进行评估，并根据评估结果进行模型的调整和改进。
）
五、结果分析与讨论
（对模型的预测结果进行分析和讨论，例如分析模型的准确率、误差等。
）
六、模型优化与改进
（根据分析的结果，对模型进行优化和改进，例如调整模型的参数、增加更多特征等。
）
七、总结与展望
（对整个建模过程进行总结，提出未来进一步改进的方向。
）
以上是一个数学建模竞赛的模板，根据实际情况可以进行适当的调整和拓展。
在实际建模过程中，还需要进行更详细的数据分析、模型训练和评估等步骤。
同时，团队合作、创新思维和良好的沟通能力也是取得好成绩的关键因素。
数学建模 -的范例
针对问题三，本文首先对主要风险因子进行了灰色预测，计算出未来几年水资源总量、降水量、平均气温、生活用水量、工业用水量。
然后采用问题二中的BP神经网络预测每年的缺水量。
最后通过整合往年的数据，运用问题二中的熵值取权的模糊评价模型预测出未来几年内水资源短缺的风险等级。
由于考虑到降水量和地下储水相关系数高，我们依据历年的降水量估测出平水年，偏枯年，枯水年三种不同年份的水资源总量，并应用问题二的风险评价模型进行评估，得到三种不同年份水资源短缺风险等级依次为高，较高，较低。
最后我们分析了南水北调工程对北京市未来两年水资源短缺的风险等级影响，风险等级依次变为低，偏低，无。
针对问题四，我们从北京市水资源现状及分析、北京市严重缺水的原因探究、北京市水资源开发利用对策三个层面向相关行政主管部门提交建议报告，以求帮助其合理规避水资源短缺风险。
关键字：水资源短缺风险、灰色关联度分析、主成分分析，模糊综合评价、BP 神经网络、熵值取权一、问题重述1.1 问题背景水是生命之源，万物之本，是人类生存和发展不可或缺的物质，是地球上最普遍、最常见同时也是最珍贵的自然资源。
水是人类一切生产活动的基础，有水的地方欣欣向荣，水资源枯竭的地方则文明消失。
长期以来，我们注重经济社会发展，却忽略了水资源的承载能力，注重水资源开发利用，却没有同等重视节约和保护。
随着经济社会发展，1.2 问题重述水资源短缺危险泛指在特定的时空环境下，由于来水和用水的不确定性，室区域水资源系统发生供水短缺的可能性以及有此产生的损失。
近年来我国水资源短缺问题日趋严重，以北京市为例，北京是世界上水资源严重缺乏的大都市之一，属严重缺水地区。
虽然政府采取了一些列措施，如南水北调工程建设, 建立污水处理厂,产业结构调整等。
但是，气候变化和经济社会不断发展，水资源短缺风险始终存在。
如何对水资源风险的主要因子进行识别，对风险造成的危害等级进行划分，对不同风险因子采取相应的有效措施规避风险或减少其造成的危害，这对社会经济的稳定、可持续发展战略的实施具有重要的意义。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
K：学科评价模型学科的水平、地位是高等学校的一个重要指标，而学科间水平的评价对于学科的发展有着重要的作用，它可以使得各学科能更加深入的了解本学科(与其他学科相比较)的地位及不足之处，可以更好的促进该学科的发展。
因此，如何给出合理的学科评价体系或模型一直是学科发展研究的热点问题。
现有某大学（科研与教学并重型高校）的13个学科在一段时期内的调查数据，包括各种建设成效数据和前期投入的数据。
1、根据已给数据建立学科评价模型，要求必要的数据分析及建模过程。
2、模型分析，给出建立模型的适用性、合理性分析。
3、假设数据来自于某科研型或教学型高校，请给出相应的学科评价模型。
承诺书页编号学科评价摘要（一）对问题的基本认识或处理整个问题的基本框架，思路（简明扼要，重点，亮点突出）研究目的，意义要求）本文研究。
问题。
即数学类型的归纳（一）（建模思路）（1.每题数据性质等粗略分析）首先，本文分别分析每个小题的特点：。
（2.建立模型的思路：）针对第一问。
问题，本文建立。
模型；在第一个。
模型中，本文对。
问题进行简化，利用。
什么知识建立什么模型；在对。
模型改进的基础上建立了。
模型Ⅱ。
针对第二。
针对第三。
（三）算法思想，求解思路，使用方法，程序）1）针对模型求解，(设计。
求解思路)。
本文使用。
什么算法，。
软件工具，对附件中所给的数据进行筛选，去除异常数据，对残缺数据进行适当的补充，求解出什么问题，进一步求解出。
什么结果。
（方法，软件，结果清晰写出来）2）建模特点，模型检验）对模型进行合理的理论证明和推导，所给出的理论证明结果大约为。
模型优点。
，建模思想方法。
，算法特点。
，结果检验。
，。
，模型检验。
从中随机抽取了3组（每组8个采样）对理论结果进行了数据模拟，结果显示，理论结果与数据模拟结果吻合。
等等3）在模型的检验模型中，本文分别讨论了以上模型的精度，稳定性，灵敏度等分析。
（四）（数据结果，结论，回答所问道所有问题）最后，归纳全文，突出亮点，指出不足，提出本文通过改进或扩展。
，得出什么。
模型。
（注意：1.具体的方法，结果，软件，名称，思想，亮点，明确详细写出来2.不要写废话，不要照抄题目的一些话，直奔主题3.不写结论一定不会获奖）关键字：结合问题方法理论概念等（1.问题背景：结合时代，社会，民生等）学科的水平、地位是高等学校的一个重要指标，而学科间水平的评价对于学科的发展有着重要的作用，它可以使得各学科能更加深入的了解本学科(与其他学科相比较)的地位及不足之处，可以更好的促进该学科的发展。
（2.需要解决的问题）因此，如何给出合理的学科评价体系或模型一直是学科发展研究的热点问题。
现有某大学（科研与教学并重型高校）的13个学科在一段时期内的调查数据，包括各种建设成效数据和前期投入的数据。
（3.问题一，问题二。
）1、根据已给数据建立学科评价模型，要求必要的数据分析及建模过程。
2、模型分析，给出建立模型的适用性、合理性分析。
3、假设数据来自于某科研型或教学型高校，请给出相应的学科评价模型。
(一) 问题1的分析对问题1研究的意义分析。
问题1属于。
数学问题，对于解决此类问题一般数学方法的分析。
对附件中所给的数据特点的分析。
对问题1所要求的结果进行分析。
由于以上原因，我们可以首先对。
问题进行简化。
并用。
数学知识。
建立一个。
数学模型Ⅰ，然后对模型Ⅰ进行改进。
将建立一个。
的数学模型Ⅱ，。
对结果分别进行预测，并将结果进行比较。
(二) 问题2的分析对问题2研究的意义分析。
问题2属于。
数学问题，对于解决此类问题一般数学方法的分析。
对附件中所给的数据特点的分析。
对问题2所要求的结果进行分析。
由于以上原因，我们可以首先对。
问题进行简化。
并用。
数学知识。
建立一个。
数学模型Ⅰ，然后对模型Ⅰ进行改进。
将建立一个。
的数学模型Ⅱ，。
对结果分别进行预测，并将结果进行比较。
（三）问题3的分析。
（要点：1.什么样的问题，什么样的要求，需要建立什么样的模型，用什么方法来求解2.善于用画图给出你对问题的理解和具体分析层次和过程3.对于一些复杂定义要给出你的理解：如满意度，平衡度，经济效益等，需要建立数学表达式来刻画）三．模型的假设（与约定）1.假设题目所给的数据真实可靠；2.（根据题目条件作出假设）；3.（跟据题目要求作出假设）；4.。
5，。
（要求：1.大量数据中筛选最能表现问题本质变量，理想化，简化关系，2.假设严格确切，不模糊，不曲解3.模型必需的，不是无关假设4．合乎常识5.假设不要太具体，不要把某些重要参数定死为只能取某些值）四．符号说明（及名词定义）1.方程符号2.编程中用到的符号3.创新名词（特别解释）（注意：1.主符号与各参考文献典型符号靠近，不要乱定义符号2.不超过15个.）五．模型的建立（5.1）第一部分：准备工作(一)5.1.1. 数据处理1.。
数据全部缺失，不予考虑。
2.对数据测试的特点，如，周期等进行分析。
3.。
数据残缺，根据数据挖掘等理论。
，根据。
变化趋势进行补充。
4.对数据特点(后面将会用到的特征)进行提取。
(二) 5.1.2.聚类分析（进行采样）用。
软件聚类分析和各个不同问题需要，采得。
组采样，每组5-8个采样值。
将采样所对应的特征值进行列表或图示。
(三) 5.1.3预测的准备工作（5.2）第二部分：问题一的。
模型(一) 5.2.1模型Ⅰ（。
的模型）1.该种模型的一般数学表达式，意义，和式中各种参数的意义。
注明参考文献。
2..。
模型Ⅰ的建立和求解(ⅰ)说明问题1使用用此模型来解决，并将模型进行改进以适应具体问题1.（2）借助准备工作的采样，（用拟合等方法）确定出模型中的参数(3)给出问题1的数学模型Ⅰ表达式和图形表达式。
（4）给出误差分析的理论估计。
3.模型Ⅰ的数值模拟将模型Ⅰ进行数值计算，并与附件中的真实采样值（进行列表或图示）比较。
对误差进行数据分析（二）5.2.2模型Ⅱ（。
模型）。
（三）5.2.3模型Ⅲ（。
模型）。
（四）5.2.4对问题1的三个模型的比较.对上述三种模型的优缺点结合原始数据和模拟预测数据进行比较。
给出各自的优点和缺点。
5.3第三部分：问题2的。
个模型。
5.4第四部分：问题3的。
个模型（要点：1.适当的分析和推导，有理有据，归纳明确的数学模型（分析问题——公式推导——基本模型——最终或简化模型，明确说明简化的思想，依据）2 .条理清晰，可以建立小标题逐层展开，善用图表3.引用参考文献，什么作者的什么理论清晰摆明4.鼓励创新但不要离题搞标新立，有效性原则）六．模型的求解6.1.问题一6.1.1.模型Ⅰ的求解.1.说明原理，算法或软件2.详细书写出算法，具体求解步骤Step1：。
Step2：。
3.用该算法的理由，算法的优点（可以采用多算法并都实现，再比较其优劣。
例如：目标算法中可以用加权算法/分层算法/遗传算法等）4.从中选出最优算法（即明确合理的数值结果）（※5.模拟方法时，用流程图形式表达算法步骤）6.2.问题二（同上）6.3.问题三。
（要点：1.明确算法，软件，合理的最优数值结果2.计算的中间步骤可以省略）七．模型的检验1）对（六步骤中）数值结果或模拟结果进行必要的检验（精度，稳定性，灵敏度）。
结果不正确，误差太大时，分析原因，再对分析方法，算法，或模型进行修正，改进。
2）题目中要求回答的问题，数值结果，结论，一一明确列出。
3）列结果，数据时，考虑是否列多组数据，或额外数据，为所得数据提供比较，分析的依据。
4)结果表示集中，一目了然，便于比较，数值结果设计表格，图形图表表示规律，趋势。
5）必要时，做定性或规律性的讨论，得一般性定理等，最后结论要明确。
八．模型评价与推广8.1.模型评价1)有点突出，适当加入缺点。
2）必要时，可以合理改变题目要求或条件，重新建模8.2模型推广1）搜索相似问题应用2）挖空心思，虽然不一定可行，大胆想象准理想化方法，模型（当然有一定合理性）九．参考文献1）引用别人的成果或公开资料（包括网上查到的资料）必须按照规定的参考文献表述方式在正文引用处和参考文献中能够均明确列出。
正文引用方括号标示参考文献的编号，如[1][3]等，引用书籍还必须指出页码。
参考文献按正文中能够的引用次序列出，其中书籍的表述方式为：[编号] 作者，书名，出版地，出版社，出版年。
参考文献中期刊杂志论文的表述方式为：[编号] 作者，论文名，杂志名，卷期号，起止页码，出版年。
参考文献中网上资源的表述方式为:[编号] 作者，资源标题，网址，访问时间（年月日）。
十．附录附表1.。
附表2.。