中考数学第一轮复习精品讲解第四单元三角形(2)(共76张PPT)
合集下载
人教版中考数学一轮复习课件第四章 第2课时 三角形的有关概念及性质

重要 线段 中线
高线
图形
性质
结论
BD=__D_C_
1.中线将三角形分割成等底同
高(即面积相等)的两个三角 形,即S△ABD=S△ACD= 12S△ABC; 2.三角形三条中线的交点,
叫做这个三角形的重心
AD⊥__B_C__, 即∠ADB= ∠ADC=90°
1.高线不一定在三角形内,遇 到高线问题应注意分类讨论; 2.三角形三条高线的交点, 叫做这个三角形的垂心
A.1.7
B.1.8
C.2.2
D.2.4
2.如图,△ABC中,AB=4,AC=3,AD,AE分别是其角平分线和中线, 过点C作CG⊥AD于点F,交AB于点G,连接EF,则线段EF的长为( A)
A. 1
B.1
C. 7
D.7
2
2
3.如图,在△ABC中,∠C=90°,AD平分∠BAC交CB于点D,过点D作
DE⊥AB,垂足恰好是边AB的中点E.若AD=3 cm,则BE的长为( A)
A. 3 3 cm
2
C.3 2 cm
B.4 cm D.6 cm
【问题情境1——示例】 1.为了探究三角形内角和,把∠B和∠A剪下后拼在一起,请你用量角器量 一量,∠BCD=____1_8_0___°,所以∠A+∠B+∠ACB=_____1_8_0__°.
1.三角形三个内角的和等于180°;特别地,当有一个内角是 90°时,其余的两个内角互余
2.三角形的外角和等于360°
3.三角形的任意一个外角等于和它不相邻的两个内角的和;三 角形的任意一个外角大于任意一个和它不相邻的内角
三角形的 边角关系 同一个三角形中,等角对等边,大角对大边
状元笔记:三角形的外角通常和三角形的内角、平行线一起考查,在解题时 要注意一个外角和与它不相邻的两个内角之间的关系
第四单元三角形(新)中考数学第一轮中考考点复习公开课PPT2
第四单元 三角形(新)中考数学第一轮 中考考点复习教学PPT- 2-PPT执教课件【推荐】
第四单元 三角形(新)中考数学第一轮 中考考点复习教学PPT- 2-PPT执教课件【推荐】
命题的真假:正确的命题是_真__命__题___,错误的命题是 _假___命__题__.判断一个命题为假命题时,只需举出一个反例;要 论证一个命题是真命题时,则需要加以推理和证明.
AC∥EF,∠C=∠F.求证:BC=DF.
证明:∵AD=BE, ∴AD-BD=BE-BD,∴AB=ED.
∵AC∥EF,∴∠A=∠E.
∠C=∠F, 在△ABC 和△EDF 中, ∠A=∠E,
AB=ED, ∴△ABC≌△EDF(AAS),∴BC=DF.
1.三角形的有关概念及分类
定 义:由不在同一条直线上的三条线段首尾顺次相接所
第四单元 三角形(新)中考数学第一轮 中考考点复习教学PPT- 2-PPT执教课件【推荐】
第四单元 三角形(新)中考数学第一轮 中考考点复习教学PPT- 2-PPT执教课件【推荐】
特 征:任意一个三角形都有三条角平分线,这三条角 平分线交于三角形内一点,这一点叫做三角形的_内__心___.
规 律:(1)三角形两条角平分线的交点一定在第三条角 平分线上.
(不添加其他字母及辅助线),你添加的条件是_A_C__=__B_C__.
【解析】添加AC=BC.∵△ABC的两条高线AD,BE, ∴∠ADC=∠BEC=90°.在△ ADC和△ BEC中,
∠ ∠AC=DC∠=C∠,BEC,∴△ADC≌△BEC(AAS). AC=BC,
5.[2019·山西]如图,已知点B,D在线段AE上,AD=BE,
逆命题:若命题2与命题1的题设、结论正好相反,则这样 的两个命题叫做互逆命题.如果把其中的一个命题叫做原命 题,那么另一个命题叫做它的逆命题.
第四单元 三角形(新)中考数学第一轮 中考考点复习教学PPT- 2-PPT执教课件【推荐】
命题的真假:正确的命题是_真__命__题___,错误的命题是 _假___命__题__.判断一个命题为假命题时,只需举出一个反例;要 论证一个命题是真命题时,则需要加以推理和证明.
AC∥EF,∠C=∠F.求证:BC=DF.
证明:∵AD=BE, ∴AD-BD=BE-BD,∴AB=ED.
∵AC∥EF,∴∠A=∠E.
∠C=∠F, 在△ABC 和△EDF 中, ∠A=∠E,
AB=ED, ∴△ABC≌△EDF(AAS),∴BC=DF.
1.三角形的有关概念及分类
定 义:由不在同一条直线上的三条线段首尾顺次相接所
第四单元 三角形(新)中考数学第一轮 中考考点复习教学PPT- 2-PPT执教课件【推荐】
第四单元 三角形(新)中考数学第一轮 中考考点复习教学PPT- 2-PPT执教课件【推荐】
特 征:任意一个三角形都有三条角平分线,这三条角 平分线交于三角形内一点,这一点叫做三角形的_内__心___.
规 律:(1)三角形两条角平分线的交点一定在第三条角 平分线上.
(不添加其他字母及辅助线),你添加的条件是_A_C__=__B_C__.
【解析】添加AC=BC.∵△ABC的两条高线AD,BE, ∴∠ADC=∠BEC=90°.在△ ADC和△ BEC中,
∠ ∠AC=DC∠=C∠,BEC,∴△ADC≌△BEC(AAS). AC=BC,
5.[2019·山西]如图,已知点B,D在线段AE上,AD=BE,
逆命题:若命题2与命题1的题设、结论正好相反,则这样 的两个命题叫做互逆命题.如果把其中的一个命题叫做原命 题,那么另一个命题叫做它的逆命题.
安徽省2024中考数学第4章三角形pptx课件

补角
若∠3+∠4=180°,则∠3与∠4互为补角.
性质
同角(或等角)的余角相等; 同角(或等角)的补角相等.
考点 2 角的相关概念及性质
6.角平分线的概念及其定理
(1)概念 在角的内部,从角的顶点引出的一条射线,把这个角分成 两个相等的角,这条射线叫做这个角的平分线.如图,OC 是从∠AOB的顶点O引出的一条射线,∠AOB被OC分成 两个角,若∠AOC=∠BOC,则OC叫做∠AOB的平分线. (2)常用结论 ∠AOC=∠BOC= ∠AOB,∠AOB=2∠AOC=2∠BOC.
图(1)
图(2)
(1)如图(1),AC交EF于点G,若α=30°,则DE与AB的位置关系为 DE∥AB ,DF
与AB的位置关系为 DF⊥AB ,∠AGE= 105 °;
(2)如图(2),AB交DF于点H,若EF∥BC,则α=
,∠AHD=
°;
45
°,AC与EF的位置关系为
AC⊥EF
75
命题角度1 平行线的判定与性质
考点 3 相交线
(4)垂线的基本性质 ①在同一平面内,过一点有且只有一条直线与已知直线垂直; ②连接直线外一点与直线上各点的所有线段中,⑪垂线段 最短. (5)线段垂直平分线的性质定理及其逆定理 ①性质定理:线段垂直平分线上的点到线段两端点的距离相等. ②逆定理:到一条线段两端点距离相等的点在这条线段的垂直平分 线上.
名称 端 1个 可向一方无限延伸
线段 2个 有一定长度,可度量
图示
表示及读法 直线AB或直线BA
射线OA 线段AB或线段BA
考点 1 直线与线段
(2)两个基本事实 ①直线的基本事实:经过两点④ 有且只有 一条直线. ②线段的基本事实:两点之间,⑤ 线段 最短.
第四单元三角形(新)中考数学第一轮中考考点复习公开课PPT

②当∠ABC为底角,∠BAC为锐角时,如答图2所示,BD= AC=12AB,∴∠BAC=30°,则∠ABC=75°;
1 2
③当∠ABC为底角,∠BAC为钝角时,如答图3所示,BD= AC=12AB,∴∠BAD=30°,∠BAC=150°,则∠ABC=15°.
1 2
综上所述,△ ABC的度数为45°或75°或15°.
1.如图,点 D 在 AC 上,点 E 在 AB 上,且 AB=AC,BC =BD,AD=DE=BE,求∠A 的度数.
解:由题意,可设∠EDB=∠DBE=x°,则∠A=∠AED= 2x°,∠BDC=∠C=∠ABC=3x°.在△ ABC中,∠A+∠ABC+∠C =180°,即2x°+3x°+3x°=180°,解得x=22.5,故∠A=45°.
类型之三 方程思想和分类讨论思想 如图,直线MN与x轴、y轴分别相交于A,C两点,分
别过A,C两点作x轴、y轴的垂线相交于B点,且OA,OC(OA>OC) 的长分别是一元二次方程x2-14x+48=0的两个实数根.
(1)求点C的坐标; (2)求直线MN的解析式; (3)在直线MN上存在点P,使以点P,B,C三点为顶点的三角 形是等腰三角形,求出点P的坐标.
核心素养专练4——方程思想和分类讨论思想
类型之一 方程思想 如图,在△ ABC中,AB=AC,点D在AC上,
且BD=BC=AD.求△ ABC各角的度数. 解:∵AB=AC,BD=BC=AD, ∴∠ABC=∠C=∠BDC,∠A=∠ABD. 设∠A=x°,则∠BDC=∠A+∠ABD=2x°, ∴∠ABC=∠C=∠BDC=2x°, ∴∠A+∠ABC+∠C=x°+2x°+2x°=180°,解得x=36, ∴在△ ABC中,∠A=36°,∠ABC=∠C=72°.
安徽省2021中考数学决胜一轮复习第4章三角形第2节三角形及其性质课件
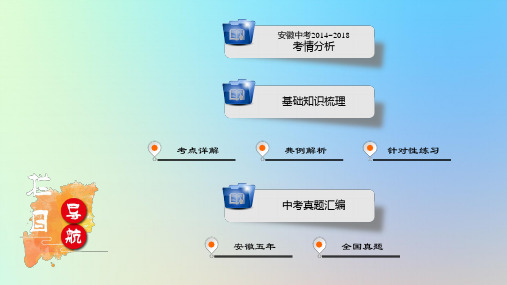
(2)如图 2,当高 CD 在△ABC 的外部,即点 D 在边 BA 的延长线上 时,BD=AB+AD=4+1=5,在 Rt△BDC 中,运用勾股定理,得 BC = BD2+CD2= 52+ 32=2 7.
【答案】 2 3或 2 7
【点拨】 遇到三角形的高的问题,假设没有给定三角形,一般需 要分锐角三角形和钝角三角形进展讨论.如此题分两种情况,分别在两 个图形中利用勾股定理求出BD和CD,从而求出BC的长.
(1)求证:CM=EM; (2)假设∠BAC=50°,求∠EMF的大小; (3)如图2,假设△DAE≌△CEM,点N为CM的中点,求证: AN∥(1E)M证.明:∵∠ACB=90°,点 M 为 BD 中点,∴CM=12BD,同理 EM =12BD,∴CM=EM; (2)解:∵∠ACB=90°,∠BAC=50°,∴∠ABC=40°,由(1)得 CM
●考点三 等腰三角形 1 . 等 腰 三 角 形 的 性 质 : 等 腰 三 角 形 的 两 腰 __相__等____ 、 两 个 底 角 __相__等____、顶角的平分线也是底边上的__中__线__和__高____(三线合一). 2.等腰三角形的判定:有两个角__相__等____的三角形是等腰三角形(等 角对等边).
3.三角形的内角和定理及其外角性质 (1)三角形的内角和等于__1_8_0_°___; (2)三角形的外角性质:三角形的任意一个外角等于和它不相邻的 _两__个__内__角__的和;三角形的外角大于和它不相邻的_任__意__一__个__内__角___.
●考点二 三角形中的重要线段
图形
结论
(1)∠ADB=∠ADC=__9_0_°____
C.85°
D.90°
3.(2021·泰州)三角形的重心是( )
中考数学第四章几何初步与三角形第二节三角形与全等三角形课件

【分析】 利用三角形中“大角对大边”及三角形的三 边关系解答即可.
讲:忽略三角形三边关系的条件 判断已知三条线段是否能够组成三角形,必须满足下列两 个条件之一:①如果选最长边作为第三边,则需判断其余 两边之和大于第三边;②如果选最短边作为第三边,则需 判断其余两边之差小于第三边.在解答此类问题时,容易 忽略三边是否满足组成三角形的条件. 练:链接变式训练2
求与三角形有关的角度时,常利用三角形的内角和定理 建立已知角与所求的角之间的数量关系,然后进行求解 即可.
3.(2017·长春)如图,在△ABC中,点D在AB上,点E在
AC上,DE∥BC.若∠A=62°,∠AED=54°,则∠B的大
小为(
)
C
A.54°
B.62° C.64° D.74°
4.(2016·大庆)如图,在△ABC中,∠A=40°,D点是 ∠ABC和∠ACB角平分线的交点,则∠BDC= _1_1_0_°__.
4.三角形的中位线:连接三角形两边的中点的线段叫做 三角形的中位线.一个三角形有3条中位线,都在三角形 的内部.三角形的中位线 _平__行__ 于第三边且等于第三边的
_一__半__ .
三角形的中线、高、角平分线、中位线都是线段,注意 区分三角形的角平分线与角的平分线的区别,前者是线 段,后者是射线.
(2)直角三角形全等的条件:除上述四种判别方法外,
还有 _H_L_ .
证明三角形全等的一般思路如下:
考点一 三角形的三边关系 (5年2考)
(2013·河北)如图1,M是铁丝AD的中点,将该铁丝
首尾相接折成△ABC,且∠B=30°,∠C=100°,如图2.
则下列说法正确的是(
)
A.点M在AB上 B.点M在BC的中点处 C.点M在BC上,且距点B较近,距点C较远 D.点M在BC上,且距点C较近,距点B较远
【中考一轮复习】特殊三角形---直角三角形课件
F (2)若AB+CD=2 3 +2,求AB.
D
A
E
B
目录
01 直角三角形性质与判定 02 勾股定理
典型例题
【例4】“赵爽弦图”奇妙地利用面积关系证明了勾股定理,是我 国古代数学的骄傲.如图所示的“赵爽弦图”是由四个全等的直 角三角形和一个小正方形拼成的一个大正方形.设直角三角形较
长直角边长为a,较短直角边长为b.若ab=8,大正方形的面积为25,
D.②③
2.如图,Rt△ABC中,∠B=90º,AB=4,BC=3,AC的垂直平分线DE分别
交AB,AC于D,E两点,则CD的长为_2_85__.
A
E D
B
C
当堂训练
3.如图,有两棵树高10米,另一棵高4米,两树相距8米. 一只小鸟从一棵树的树梢飞到另一棵树的树梢,小鸟 至飞少行飞的行距(离不)B可能是( A ) A.8米 B.10米 C.12米 D.14米
判定
定义法:有一个角是90º的三角形是直角三角形. 有一条边上的中线是这边的一半的三角形是直角三角形.
2.等面积法求斜边上的高:如图,S=0.5ab=0.5ch,
其中a,b为两个直角边,c为斜边,h为斜边上的高.
a
b
h
c
当堂训练
1.如图,在Rt△ABC中,∠ACB=90º,CD为AB边上的高,CE为AB边上
连接BE,ED,BD.若∠BAD=58º,则∠EBD的度数为_3_2__度.
6.在直角三角形ABC中,∠ACB=90º,D、E是边AB上两点,且CE所在
直线垂直平分线段AD,CD平分∠BCE,BC= 2 3,则AB=_4__.
D
A
E
C
A E D
D
A
E
B
目录
01 直角三角形性质与判定 02 勾股定理
典型例题
【例4】“赵爽弦图”奇妙地利用面积关系证明了勾股定理,是我 国古代数学的骄傲.如图所示的“赵爽弦图”是由四个全等的直 角三角形和一个小正方形拼成的一个大正方形.设直角三角形较
长直角边长为a,较短直角边长为b.若ab=8,大正方形的面积为25,
D.②③
2.如图,Rt△ABC中,∠B=90º,AB=4,BC=3,AC的垂直平分线DE分别
交AB,AC于D,E两点,则CD的长为_2_85__.
A
E D
B
C
当堂训练
3.如图,有两棵树高10米,另一棵高4米,两树相距8米. 一只小鸟从一棵树的树梢飞到另一棵树的树梢,小鸟 至飞少行飞的行距(离不)B可能是( A ) A.8米 B.10米 C.12米 D.14米
判定
定义法:有一个角是90º的三角形是直角三角形. 有一条边上的中线是这边的一半的三角形是直角三角形.
2.等面积法求斜边上的高:如图,S=0.5ab=0.5ch,
其中a,b为两个直角边,c为斜边,h为斜边上的高.
a
b
h
c
当堂训练
1.如图,在Rt△ABC中,∠ACB=90º,CD为AB边上的高,CE为AB边上
连接BE,ED,BD.若∠BAD=58º,则∠EBD的度数为_3_2__度.
6.在直角三角形ABC中,∠ACB=90º,D、E是边AB上两点,且CE所在
直线垂直平分线段AD,CD平分∠BCE,BC= 2 3,则AB=_4__.
D
A
E
C
A E D
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
·新课标
第22讲 │ 归类示例
A.3 cm C.3 2 cm
B.6 cm D.6 2 cm
图 22-1
·新课标
第22讲 │ 归类示例
[解析] 如图所示,过点 A 作 AD⊥BD,垂足为 D,所以 AB=2AD =2×3=6 cm,△ABC 是等腰直角三角形,AC= 2AB=6 2 cm.
·新课标
命题角度: 1.利用勾股定理求线段的长度 2.利用勾股定理解决折叠问题 [2011· 黄石] 将一个有 45 度角的三角板的直角顶点放在一张 宽为 3 cm 的纸带边沿上,另一个顶点在纸带的另一边沿上,测得三角 板的一边与纸带的一边所在的直线成 30 度角,如图 22-1,则三角板 的最大边的长为( D )
[解析] 两个三角形周长相等,不一定全等.
·新课标
第22讲 │ 考点随堂练
7.如图22-5,△BAC≌△DAE,AC=3 cm,AD=4 cm, 则BE的长是(cm
D.4 cm
[解析] 因为△BAC≌△DAE,所以AC=AE,AB=AD, 则BE=4-3=1(cm).
·新课标
第22讲 │ 考点随堂练
12.[2010· 宜宾]如图22-10,分别过点C、B作△ABC的BC边上 的中线AD及其延长线的垂线,垂足分别为E、F.求证:BF=CE.
图22-10
证明: ∵CE⊥AF,FB⊥AF,∴∠DEC =∠DFB=90° , 又∵AD为BC边上的中线, ∴BD=CD, 且∠EDC =∠FDB(对顶角相等), ∴△BFD≌△CED(AAS), ∴BF=CE.
·新课标
第22讲 │ 考点随堂练
8.要测量河两岸相对的两点A、B的距离,先在AB的垂线BF上 取两点C、D,使CD=BC,再作出BF的垂线DE,使A、C、E在 一条直线上(如图22-6所示),可以证明△EDC≌△ABC,得ED =AB,因此测得ED的长就是AB的长,判定△EDC≌△ABC的 理由是( B ) A.SAS B.ASA C.SSS D.AAS
图22-3
解: △ABE与△CDF全等.理由:∵CE=AF, ∴AE=CF.∵AB∥CD,∴∠DCA=∠CAB.在△ABE与
AB=CD, △CDF中,∠DCA=∠BAC, AE=CF,
∴△ABE≌△CDF(SAS).
·新课标
第22讲 │ 考点随堂练
5.[2010· 玉溪]如图22-4,在▱ABCD中,E是AD的中点,请添加 适当条件后,构造出一对全等的三角形,并说明理由.
图22-12 已知: 求作:
解: 已知:线段a、b 、角β, 求作:△ABC,使边BC=a, AC=b,∠C=β ,画图:先画一个角等于∠β,然后从角的 顶点出发,在角的两边分别截取长度为a和b的线段.
·新课标
第22讲 │ 考点随堂练
15.[2011· 綦江]为了推进农村新型合作医疗制度改革,准备 在某镇新建一个医疗点P,使P到该镇所属A村、B村、C村 的村委会所在地的距离都相等(A、B、C不在同一直线上, 地理位置如图22-13),请你用尺规作图的方法确定点P的 位置. 要求: 写出已知、求作;不写作法,保留作图痕迹.
·新课标
第22讲 │ 归类示例
[知识拓展] a+b 利用图②中的直角梯形,我们可以证明 c < 2.其证明步骤 如下:
第22讲
第23讲
全等三角形
形似三角形及其应用
第22讲 │ 全等三角形
第22讲 全等三角形
·新课标
第22讲 │ 考点随堂练 │考点随堂练│
考点1 全等三角形的定义及其性质
重合 定 如果两个三角形能够完全______,那么这两个三角形全等, 义 即对应边______,对应角______的三角形全等. 相等 相等 夹角 两个三角形有两边及其______对应相等,这两个三 SAS 角形全等. 两个三角形有两个角及其这两角的______对应相 夹边 判 ASA 等,这两个三角形全等. 定 对边 两个三角形有两个角及其中一角的______对应相 定 AAS 等,这两个三角形全等. 理 三边 SSS 两三角形______对应相等,两三角形全等. 两直角三角形,斜边和直角边对应相等,两直角三 HL 角形全等.
图22-6 [解析]∠ABC=∠EDC=90° ,∠ACB=∠ECD,BC=DC, 根据角边角定理,两三角形全等.
·新课标
第22讲 │ 考点随堂练
9.如图22-7,AC=AD,BC=BD,AB与CD相交于O.则AB 与CD的关系是__________. AB⊥CD
图22-7
[解析] 先证明△ABC≌△ABD,所以∠CAB=∠DAB,再利 用等腰三角形的性质得出AB⊥CD.
·新课标
第22讲 │ 归类示例
图 22-2
·新课标
第22讲 │ 归类示例
解: (1)如图, 木柜的表面展开图是两个矩形 ABC′1D1 和 ACC1A1. 蚂蚁能够最快到达目的地的可能路径有如图的 AC′1 和 AC1. (2)蚂蚁沿着木柜表面经线段 A1B1 到 C′1,爬过的路径的长是 l1 = 42+4+52= 97. 蚂蚁沿着木柜表面经线段 BB1 到 C1,爬过的路径的长是 l2= 4+42+52= 89. l1>l2,最短路径的长是 l2= 89. B1C1 4 20 (3)作 B1E⊥AC1 于 E,则 B1E= · 1= AA · 5= 89为所 AC1 89 89 求.
·新课标
第22讲 │ 考点随堂练
1.[2011· 江西]如图22-1,下列条件中,不能证明△ABD≌ .. △ACD的是( D ) A.BD=DC,AB=AC B.∠ADB=∠ADC,∠BAD=∠CAD C.∠B=∠C,∠BAD=∠CAD D.∠B=∠C,BD=DC
图22-1
[解析]两边和其中一边的对角对应相等的两个三角形不一 定全等.
第22讲 │ 归类示例
勾股定理的作用:(1)已知直角三角形的两边求第三边; (2)已知直角三角形的一边求另两边的关系;(3)用于证明平 方关系的问题.
·新课标
第22讲 │ 归类示例
类型之二 利用勾股定理解决生活中的实际问题
命题角度: 1.求最短路线问题 2.求有关长度问题 如图 22-2,一个长方体形的木柜放在墙角处(与墙面和地 面均没有缝隙), 有一只蚂蚁从柜角 A 处沿着木柜表面爬到柜角 C1 处. (1)请你画出蚂蚁能够最快到达目的地的可能路径; (2)当 AB=4,BC=4,CC1=5 时,求蚂蚁爬过的最短路径的长; (3)求点 B1 到最短路径的距离.
第22讲 │ 归类示例
[尝试证明] 以图 22-4①中的直角三角形为基础,可以构造出以 a、b 为底, 以 a+b 为高的直角梯形(如图 22-4②),请你利用图②,验证勾股定 理;
图 22-4
·新课标
第22讲 │ 归类示例
解:[定理表述] 如果直角三角形的两直角边长分别为 a、b,斜边长为 c, 那么 a2+b2=c2. [尝试证明] ∵AB=EC,BE=DC,AE=DE,Rt△ABE≌Rt△ECD, ∴∠AEB=∠EDC. 又∵∠EDC+∠DEC=90° , ∴∠AEB+∠DEC=90° . ∴∠AED=90° . ∵S 梯形 ABCD=SRt△ABE+SRt△DEC+SRt△AED, 1 1 1 1 ∴ (a+b)(a+b)= ab+ ab+ c2. 2 2 2 2 整理,得 a2+b2=c2.
·新课标
第22讲 │ 考点随堂练
10.如图22-8,已知AD=BC,AE⊥BD、CF⊥BD于点E、F,且 30 AE=CF,∠ADB=30° ,则∠DBC=________° .
图22-8
[解析] ∠AED=∠CFB=90° ,AD=BC,AE=CF,斜边和直 角边对应相等的两直角三角形全等,全等三角形对应角相等.
·新课标
第22讲 │ 考点随堂练
2.[2011· 上海]下列命题中,真命题是( D ) A.周长相等的锐角三角形都全等 B.周长相等的直角三角形都全等 C.周长相等的钝角三角形都全等 D.周长相等的等腰直角三角形都全等
[解析]设两个等腰直角三角形的直角边分别为a和b,那么它 们的周长分别为(2+ 2 )a,(2+ 2 )b,因为(2+ 2 )a=(2+ 2)b,则a=b,两三角形全等.
图22-4
解: 添加的条件是连接BE,过D作DF∥BE交BC于点F,构造的 全等三角形是△ABE与△CDF.理由: ∵平行四边形ABCD,AE =ED,又∵DE∥BF,且DF∥BE,∴四边形DEBF是平行四边 形,∴DE=DF.∴在△ABE与△CDF中,AB=CD,∠EAB= ∠FCD,AE=CF,∴△ABE≌△CDF.
·新课标
第22讲 │ 考点随堂练
3.已知,如图22-2,AD=AC,BD=BC,O为AB上一 三 点,那么,图中共有_______对全等三角形.
图22-2
[解析] 先证△ABC≌△ABD,由全等三角形对应角相等, 得出证明另外两个三角形全等的条件.
·新课标
第22讲 │ 考点随堂练
4.如图22-3,AB=CD,AB∥CD,CE= AF.判断△ABE与△CDF是否全等,并说明 理由.
·新课标
第22讲 │ 考点随堂练
考点3 尺规作图
·新课标
第22讲 │ 考点随堂练
13.[2011· 绍兴]如图22-11,在△ABC中,分别以 1 点A和点B为圆心,大于 AB的长为半径画弧,两 2 弧相交于点M、N,作直线MN,交BC于点D,连 接AD.若△ADC的周长为10,AB=7,则△ABC的 周长为( C ) 图22-11 A.7 C.17 B.14 D.20
·新课标
第22讲 │ 归类示例
[定理表述] 请你根据图 22-3 中的直角三角形叙述勾股定理(用文字及符号语 言叙述);
图 22-3
[解析] 先证明 Rt△ABE≌Rt△ECD, 然后利用等面积法 S 梯形 ABCD =SRt△ABE+SRt△DEC+SRt△AED,可得 a2+b2=c2.
