专项14 坐标图像题 -【专项专练】中考化学专项考点培优训练(原卷版)
2023年中考化学毕业班二轮热点题型《坐标图像题》归纳与变式演练(全国通用)原卷

专题09 坐标图像题目录一、热点题型归纳【题型一】溶液pH的变化图象【题型二】化学反应过程中的变化图象【题型三】溶解度曲线题二、最新模考题组练【题型一】溶液pH的变化图象【典例分析】【2022河北中考】向含有酚酞的氢氧化钠溶液中慢慢滴入稀硫酸,该过程中溶液的变化如图所示。
下列分析正确的是()A. 点时的溶液一定呈红色B. 点时的溶液能与纯碱发生反应C. 过程中溶液的碱性逐渐增强D. 过程中生成的硫酸钠不断增加【提分秘籍】1.酸碱稀释过程中溶液pH的变化图像(1)酸性溶液稀释:溶液pH由小于7逐渐增大,但溶液始终显酸性,溶液pH只能接近7,而不能等于或大于7。
如图1所示。
(2)碱性溶液稀释:溶液H由大干7诼渐减小,但溶液始终显碱性,溶液H只能接近7而不能等干或小干7。
如图2所示。
2中和反应过程中溶液pH的变化图像(3)向酸溶液中加入碱溶液:起点时,pH<7,随着碱溶液的加入,pH逐渐增大;当二者恰好完全反应时,pH=7;再继续加入碱溶液,溶液显碱性,pH>7。
如图3所示。
(4)向碱溶液中加入酸溶液:起点时,pH>7,随着酸溶液的加入,pH逐渐减小;当二者恰好完全反应时,pH=7;再继续加入酸溶液,溶液显酸性,pH<7。
如图4所示。
【变式演练】1.【2023山东德州一模】向某稀盐酸中逐渐加入试剂X后溶液的pH变化如图。
试剂X可能是下列物质中的( )A. H2OB. H2SO4C. NaOHD. CaCO32.【2023湖南益阳一模】某校化学兴趣小组探究稀盐酸和氢氧化钠溶液的反应过程,测得烧杯中溶液的pH 随滴加液体体积变化的曲线如图所示。
下列说法错误的是A. 向图中a 点所示溶液中滴加紫色石蕊溶液,溶液变蓝B. 图中b 点处氢氧化钠和盐酸恰好完全反应C. 图中c 点所示溶液中,溶质为NaOH 和NaClD. 该实验是将氢氧化钠溶液逐滴滴入到盛有稀盐酸的烧杯中【题型二】化学反应过程中的变化图象【典例分析】【2022广西贺州中考】下列图像不能正确反映其对应变化关系的是()A. 图①用等质量、等浓度的过氧化氢溶液在有无MnO2条件下制氧气B. 图②将一定量的浓硫酸加入适量水中C. 图③用一氧化碳气体还原一定质量的氧化铁粉末D. 图④向氯化铁和盐酸的混合溶液中加入过量的氢氧化钠溶液【提分秘籍】1.反应物的质量变化图像:贿着反应的进行,反应物的质量逐渐减小、若反应物有剩余,则如客的所示:若反应物完全反应,则如图6所示。
中考数学专项复习《二次函数图像与坐标轴的交点问题》练习题及答案

中考数学专项复习《二次函数图像与坐标轴的交点问题》练习题及答案一、单选题1.抛物线y=kx2−7x−7的图象和x轴有交点,则k的取值范围是()A.k≥−74B.k≥−74且k≠0C.k>−74D.k>−74且k≠02.下列二次函数的图象与x轴没有交点的是()A.y=-3x2+2x B.y=x2-3x-4C.y=x2-4x+4D.y=x2+4x+53.已知抛物线y=ax2+bx+c(a≠0)与x轴交点为(﹣1,0)和(3,0),与y轴交点为(0,﹣2),则一元二次方程ax2+bx+c=0(a≠0)的根为()A.x1=﹣1,x2=3B.x1=﹣2,x2=3C.x1=1,x2=﹣3D.x1=﹣1,x2=﹣24.关于x的函数y=(a−2)x2+2x−1与x轴有交点,则a的取值范围是()A.a≥1B.a>1C.a>1且a≠2D.a≥1且a≠25.抛物线y=x2﹣2x+3与x轴的交点个数是()A.0B.1C.2D.36.如图,抛物线y=−x2+bx+c的部分图象如图所示,若y>0,则x的取值范围是()A.−4<x<1B.−3<x<1C.x<−4或x>1D.x<−3或x>1 7.已知二次函数y=2(x+1)(x-a),其中a>0,若当x≤2时,y随x增大而减小,当x≥2时y随x增大而增大,则a的值是A.3B.5C.7D.不确定8.二次函数y=ax2﹣bx的图象如图,若方程ax2﹣bx+m=0有实数根,则m的最大值为()A.-3B.3C.-6D.09.二次函数y=ax2+bx+c(a≠0)的图象如图所示,对称轴为x=1.给出下列结论:①abc>0;②b2>4ac;③4a+2b+c>0;④3a+c>0,其中正确的结论有()A.1个B.2个C.3个D.4个10.二次函数y=ax2+bx+c(a、b、c为常数,且a≠0)中x与y的部分对应值如下表:x﹣2﹣101234y50﹣3﹣4﹣305y<0,则x的取值范围是0<x<2;(3)二次函数y=ax2+bx+c的图象与x轴有两个交点,且它们分别在y轴两侧,则其中正确结论的个数是()A.0B.1C.2D.311.二次函数y=ax2+bx+c的图象如图所示,则下列关系式中错误的是()A.a>0B.b>0C.c>0D.b2-4ac>012.抛物线y=ax2+bx+c(a≠0)形状如图,下列结论:①b>0;②a-b+c=0;③当x<-1或x>3时,y>0.④一元二次方程ax2+bx+c+1=0(a≠0)有两个不相等的实数根。
专项训练:函数的图像
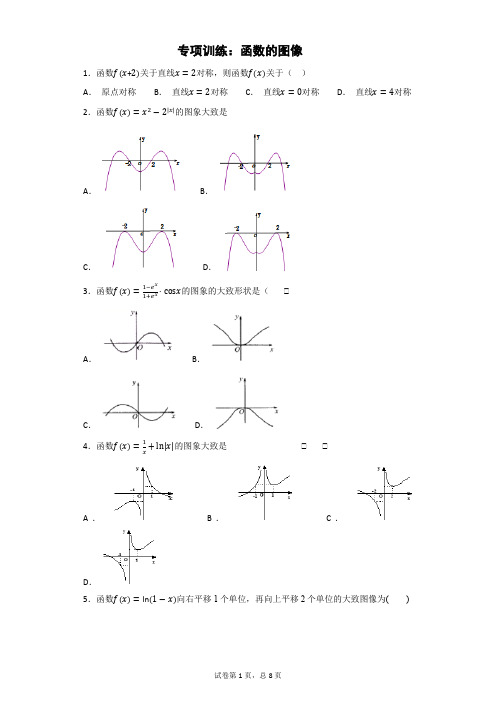
专项训练:函数的图像1.函数关于直线对称,则函数关于()A.原点对称B.直线对称C.直线对称D.直线对称2.函数的图象大致是A.B.C.D.3.函数的图象的大致形状是()A.B.C.D.4.函数的图象大致是()A.B.C.D.5.函数向右平移1个单位,再向上平移2个单位的大致图像为( )A.B.C.D.6.已知某函数图象如图所示,则图象所对应的函数可能是()A.B.C.D.﹣7.函数的图象大致为A.B.C.D.8.为了得到函数y=lg x的图象,只需将函数y=lg(10x)图象上A.所有点沿y轴向上平移10个单位长度B.所有点沿y轴向下平移10个单位长度C.所有点沿y轴向上平移1个单位长度D.所有点沿y轴向下平移1个单位长度9.函数y=的单调减区间和图象的对称中心分别为A.(–∞,0),(0,+∞);(1,1)B.(–∞,–1),(–1,+∞);(1,0)C.(–∞,1),(1,+∞);(1,0)D.(–∞,1),(1,+∞);(1,1)10.设函数在上可导,其导函数为,且函数在处取得极大值,则函数的图象可能是A.B.C.D.11.函数的图象是()A.B.C.D.12.函数的图象大致为()A.B.C.D.13.函数的图象大致是A.B.C.D.14.函数y=的大致图象只能是A.B.C.D.15.若f(x)的图象向左平移一个单位后与y=e x的图象关于y轴对称,则f(x)解析式是A.e x+1B.e x–1C.e–x+1D.e–x–116.函数的图象大致是()A.B.C.D.17.已知某函数图象如图所示,则图象所对应的函数可能是()A.B.C.D.﹣18.函数向右平移1个单位,再向上平移2个单位的大致图像为( )A.B.C.D.19.函数的图象大致为()A.B.C.D.20.若a>1,则函数y=a x与y=(1–a)x2的图象可能是下列四个选项中的A.B.C.D.21.函数与函数的图象如下图,则函数的图象可能是A.B.C.D.22.函数的图象的大致形状是()A.B.C.D.23.某学生离家去学校,一开始跑步前进,跑累了再走余下的路程.下列图中纵轴表示离校的距离,横轴表示出发后的时间,则较符合该学生走法的是( )A.B.C.D.24.直线与在同一直角坐标系中的图象可能是A.B.C.D.25.已知函数f(x)=ax2+bx+c,不等式f(x)<0的解集为,则函数y =f(-x)的图象可以为A.B.C.D.26.函数f(x)=ln(x2+1)的图象大致是( )A.B.C.D.27.设,,函数的定义域为,值域为,则的图象可以是()A.B.C.D.28.函数的图象是().A.B.C.D.29.函数f(x)=1-e|x|的图象大致是( )参考答案1.D【解析】【分析】由题意结合函数图象的变换规律确定函数的对称性即可.【详解】将函数的图象向左平移个单位长度即可得到函数的图象,结合函数关于直线对称,可知函数关于直线对称.本题选择D选项.【点睛】本题主要考查函数的对称性,函数的平移变换等知识,意在考查学生的转化能力和计算求解能力.2.B【解析】【分析】利用特殊值排排除即可【详解】∵函数,()>,故排除C,D,(),()<,故排除A,故选:B.【点睛】本题考了函数的图象的识别,充分利用排除法是解题的关键,属于基础题3.C【解析】【分析】分析函数的奇偶性,代入特殊值计算结果,排除错误答案,可得结论【详解】,函数为奇函数,排除,令,令,则故选:【点睛】本题考查的知识点是函数的图象,由于函数非基本初等函数,故用排除法,是解答的最佳选择,需要判定函数的奇偶性和单调性或者取值,属于基础题4.D【解析】【分析】当x<0时,函数f(x)=,由函数的单调性,排除A、B;当x>0时,函数f(x)=,此时,代入特殊值验证,排除C,只有D正确.【详解】当x<0时,函数f(x)=,由函数y=、y=ln(﹣x)递减知函数f(x)=递减,排除A、B;当x>0时,函数f(x)=,此时,f(1)==1,而选项A的最小值为2,故可排除C,只有D正确,故选:D.【点睛】函数图象的辨识可从以下方面入手:(1)从函数的定义域,判断图象的左右位置;从函数的值域,判断图象的上下位置;(2)从函数的单调性,判断图象的变化趋势;(3)从函数的奇偶性,判断图象的对称性;(4)从函数的特征点,排除不合要求的图象.5.C【解析】【分析】根据函数图象的平移规律:在上的变化符合“左加右减”,在上的变化符合“上加下减”.再根据复合函数的单调性即可得出结论.【详解】将函数向右平移1个单位,得到函数为,再向上平移2个单位可得函数为.根据复合函数的单调性可知在上为单调减函数,且恒过点,故C正确.故选:C.【点睛】本题主要考查函数的“平移变换”.解答本题的关键是掌握函数的平移规律“左加右减,上加下减”,属于基础题.6.D【解析】【分析】对给出的四个选项分别进行分析、讨论后可得结果.【详解】对于A,函数,当时,;当时,,所以不满足题意.对于B,当时,单调递增,不满足题意.对于C,当时,,不满足题意.对于D,函数﹣为偶函数,且当时,函数有两个零点,满足题意.故选:D.【点睛】函数图象的识辨可从以下方面入手:(1)从函数的定义域,判断图象的左右位置;从函数的值域,判断图象的上下位置;(2)从函数的单调性,判断图象的变化趋势;(3)从函数的奇偶性,判断图象的对称性;(4)从函数的周期性,判断图象的循环往复;(5)从函数的特征点,排除不合要求的图象.7.B【解析】【分析】确定函数是奇函数,利用(),()()>,即可得出结论.【详解】由题意,()()()(),函数是奇函数,(),()()>,故选:B.【点睛】本题考查函数的奇偶性,考查函数的图象,比较基础.8.D【解析】【分析】由于函数y=lg(10x)═lgx+1,把函数y=lg(10x)的图象上所有的点向下平移1个单位长度,可得函数函数y=lgx的图象,由此得出结论.【详解】由于函数y=lg(10x)═lgx+1,把函数y=lg(10x)的图象上所有的点向下平移1个单位长度,可得函数y=lgx的图象.故选:D.【点睛】本题主要考查函数的图象平移变换方法,依据x加减左右平移(左加右减),函数值加减上下平移(加向上、减向下),属于基础题.9.D【解析】【分析】先化简函数y==1+,通过图像的变换求出函数的对称中心和单调减区间.【详解】∵y==1+,x≠1,画出函数的图象如图所示,由图象可知函数的单调减区间是(–∞,1),(1,+∞).∵y=的对称中心为(0,0),∴y==1+的图象时由y=的图象先向右平移一个单位,再向上平移1个单位得到的,故对称中心为(1,1),故选D.【点睛】本题主要考查函数图像的变换,考查函数的图像和性质(单调性和对称中心),意在考查学生对这些知识的掌握水平和分析推理能力.10.D【解析】因为-1为即值点且为极小值点,故在-1的左侧<0,-1的右侧>0,所以当x>0时,排除AD,当x<-1时,故综合得选C11.C【解析】【分析】分和两种情况,将函数化为和两段考虑。
(完整word版)化学平衡图像专项练习题

化学平衡图像一、选择题(本题包括35小题,每小题2分,共70分。
每小题有一个或两个选项符合题意。
)1.一定温度下,在2L的密闭容器中,X、Y、Z三种气体的物质的量随时间变化的曲线如右图所示,下列描述正确的是()A.反应开始到10s,用Z表示的反应速率为0.158mol/(L·s)B.反应开始时10s,X的物质的量浓度减少了0.79mol/LC.反应开始时10s,Y的转化率为79.0%D.反应的化学方程式为:X(g)+Y(g)Z(g)2.T℃时,A气体与B气体反应生成C气体。
反应过程中A、B、C浓度变化如图(Ⅰ)所示,若保持其他条件不变,温度分别为T1和T2时,B的体积分数与时间的关系如图(Ⅱ)所示,则下列结论正确的是()A.在(t1+10)min时,保持其他条件不变,增大压强,平衡向逆反应方向移动B.t1+10)min时,保持容器总压强不变,通入稀有气体,平衡向逆反应方向移动C.T℃时,在相同容器中,若由0.3mol·L—1 A 0.1 mol·L—1 B和0.4 mol·L—1 C反应,达到平衡后,C的浓度仍为0.4 mol·L—1D.其他条件不变,升高温度,正、逆反应速率均增大,且A的转化率增大3.已知可逆反应aA+bB cC中,物质的含量A%和C%随温度的变化曲线如图所示,下列说法正确的是()A.该反应在T1、T3温度时达到过化学平衡B.该反应在T2温度时达到过化学平衡C.该反应的逆反应是放热反应D.升高温度,平衡会向正反应方向移动4.右图表示反应N 2(g)+3H2(g)2NH3(g);ΔH=-92.2kJ/mol。
在某段时间t0~t6中反应速率与反应过程的曲线图,则氨的百分含量最高的一段时间是()A.t0~t1B. t2~t3C. t3~t4D. t5~t65.反应过程中A(g)、B(g)、C(g)物质的量变化如图所示,根据图中所示判断下列说法正确的是()A .10~15 min 可能是加入了正催化剂B .10~15 min 可能是降低了温度C .20 min 时可能是缩小了容器体积D .20 min 时可能是增加了B 的量6.在一定条件下,将X 和Y 两种物质按不同的比例放入密闭容器中反应,平衡后测得X ,Y 的转化率与起始时两物质的物质的量之比n x /n y 的关系如图所示,则X ,Y 的反应方程式可表示为( )A . 2X +Y 3ZB . 3X +2Y 2ZC . X +3Y ZD . 3X +Y Z7.可逆反应aX (g )+bY (g )cZ (g )在一定温度下的一密闭容器内达到平衡后,t 0时改变某一外界条件,化学反应速率(v )-时间(t )图象如右图。
(化学)初三化学化学图像题汇编专项训练100(附答案)

(化学)初三化学化学图像题汇编专项训练100(附答案)一、中考化学图像题汇编1.下列所示的四个图像,能正确反映对应变化关系的是()A .常温下,相同质量的锌和铁分别与足量的溶质质量分数相同的稀硫酸反应B .向一定量的氢氧化钠溶液中滴加 pH =3 的稀盐酸C .加热一定质量的高锰酸钾D .氢气还原一定质量的氧化铜【答案】C【解析】【分析】【详解】A 、常温下,相同质量的锌和铁分别与足量的溶质质量分数相同的稀硫酸反应,锌的活动性大于铁,锌的反应速率快,根据锌和铁与足量的稀硫酸反应的质量关系:24424422Zn + H SO = ZnSO Fe+ H SO = FeSO 65+ H + 5622H ↑↑,可知,完全反应铁生成的氢气多,该图像不能正确反映对应变化关系;B 、向一定量的氢氧化钠溶液中滴加 pH =3 的稀盐酸,二者恰好反应时溶液呈中性,再滴加稀盐酸,溶液呈酸性,当盐酸无限加入时,由于反应中生成了水,则溶液的pH 接近于3且大于3,该图像不能正确反映对应变化关系;C 、加热高锰酸钾固体,开始时高锰酸钾不分解,所以Mn 元素质量分数不变;一段时间后分解生成锰酸钾、二氧化锰和氧气,Mn 元素质量不变,但是固体总重量减小, Mn 元素质量分数增大;当高锰酸钾完全分解后固体总质量不变,Mn 元素质量分数不变,该图像能正确反映对应变化关系;D、氢气还原CuO固体生成Cu和水,随着反应的进行固体质量减少,当CuO完全反应生成Cu后固体质量不变,反应后固体质量不可能为零,该图像不能正确反映对应变化关系。
故选C。
【点睛】本题是一道图像坐标与化学知识相结合的综合题,解题的关键是结合所涉及的化学知识,正确分析各变化的过程,注意分析坐标轴表示的意义、曲线的起点、折点及变化趋势,确定正确的图像。
2.下列图像能正确反映对应变化关系的是A.在一定量的硝酸银和硝酸铜的混合溶液中加入铁粉至过量B.一氧化碳还原氧化铁C.质量相同的粉末状碳酸钙和块状碳酸钙分别与足量的稀盐酸反应D.向等质量、相同质量分数的两份稀盐酸中分别加入足量的锌粉和铁粉【答案】D【解析】【详解】A.由于铁和硝酸铜反应生成铜和硝酸亚铁,随着铁的加入直至过量,硝酸铜的质量分数将变成0,故A错误;B.一氧化碳和氧化铁反应生成铁和二氧化碳,随着一氧化碳的通入,固体的质量逐渐减少直至氧化铁反应完全,固体的质量将保持不变,故B错误;C.质量相同的粉末状碳酸钙和块状碳酸钙分别与足量的稀盐酸反应生成的二氧化碳质量相同,故C错误;D.向等质量、相同质量分数的两份稀盐酸中分别加入足量的锌粉和铁粉,刚开始金属不足,相同质量的锌和铁,铁生成的氢气质量较多;金属与酸反应时氢气来源于酸中的氢元素,因为酸的量相同,最终生成的氢气应该相等,故D正确。
中考数学专项复习《二次函数图像与坐标轴的交点问题》练习题附答案

中考数学专项复习《二次函数图像与坐标轴的交点问题》练习题附答案一、单选题1.若函数y=x2−2x+b的图象与x轴有两个交点,则b的取值范围是()A.b≤1B.b>1C.0<b<1D.b<12.二次函数与y=kx2−8x+8的图象与x轴有交点,则k的取值范围是() A.k<2B.k<2且k≠0C.k≤2D.k≤2且k≠03.函数y=ax2+bx+c的图象如图所示,那么关于x的方程ax2+bx+c-3=0的根的情况是()A.有两个不相等的实数根B.有两个异号的实数根C.有两个相等的实数根D.没有实数根4.已知二次函数y=2(x+1)(x-a),其中a>0,若当x≤2时,y随x增大而减小,当x≥2时y随x增大而增大,则a的值是()A.3B.5C.7D.不确定5.在平面直角坐标系中,二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论正确的()A.ac>0B.b2﹣4ac<0C.4a+2b+c<0D.b=2a6.如图所示,二次函数y=ax2+bx+c的图象中,王刚同学观察得出了下面四条信息:(1)b2﹣4ac>0;(2)c>1;(3)2a﹣b<0;(4)a+b+c<0,其中错误的有()A.1个B.2个C.3个D.4个7.若二次函数y=(m﹣1)x2+2x+1的图象与x轴有两个不同的交点,则m的取值范围是()A.m≤2B.m<2C.m≤2且m≠1D.m<2且m≠18.如图为抛物线y=ax2+bx+c的图象,A,B,C为抛物线与坐标轴的交点,且OA=OC=1,则下列关系中正确的是()A.a+b=﹣1B.a﹣b=﹣1C.b<2a D.ac<09.已知二次函数y=ax2+bx+c(a≠0)的图象如图,在下列代数式中(1)a+b+c>0;(2)﹣4a<b<﹣2a(3)abc>0;(4)5a﹣b+2c<0;其中正确的个数为()A.1个B.2个C.3个D.4个10.如图是二次函数y=ax2+bx+c的图象,下列结论:①二次三项式ax2+bx+c的最大值为4;②4a+2b+c<0;③一元二次方程ax2+bx+c=1的两根之和为﹣1;④使y≤3成立的x的取值范围是x≥0.其中正确个数有().A.1个B.2个C.3个D.4个11.二次函数y=kx2﹣6x+3的图象与x轴有交点,则k的取值范围是()A.k<3B.k<3且k≠0C.k≤3D.k≤3且k≠012.如图,一次函数y1=2x与二次函数y2=ax2+bx+c图象相交于P、Q两点,则函数y=ax2+(b﹣2)x+c的图象可能是()A.B.C.D.二、填空题13.已知函数y= 12(m+3)x2+2x+1的图象与x轴只有一个公共点,则m的值为. 14.如图,是抛物线y=ax2+bx+c的一部分,其对称轴为直线x=1,它与x轴的一个交点为A(3,0),根据图象,可知关于x的一元二次方程ax2+bx+c=0的解是.15.如图是抛物线y=ax2+bx+c的一部分,其对称轴为直线x=1,若其与x轴一交点为B(3,0),则由图象可知,不等式ax2+bx+c>0的解集是.16.如图,我们把一个半圆与抛物线的一部分围成的封闭图形称为“果圆”.已知点A、B、C、D分别是“果圆”与坐标轴的交点,抛物线的解析式为y=x2﹣6x﹣16,AB为半圆的直径,则这个“果圆”被y 轴截得的线段CD的长为.17.已知:y关于x的函数y=k2x2−(2k−1)x+1的图象与坐标轴只有两个不同的交点A、B,P 点坐标为(3,2),则△PAB的面积为.18.抛物线y=ax2+bx+c的顶点为D(−1,2),与x轴的一个交点A在点(−3,0)和(−2,0)之间,则以下结论:①b2−4ac<0;②a+b+c<0;③c−a=2;④方程ax2+bx+c−2=0有两个不相等的实数根,其中正确结论为.三、综合题19.设二次函数y1=2x2+bx+c(b,c是常数)的图象与x轴交于A,B两点.(1)若A,B两点的坐标分别为(1,0),(2,0),求函数y)的表达式及其图象的对称轴.(2)若函数y1的表达式可以写成心=2(x-h)2-2(h是常数)的形式,求b+c的最小值.(3)设一次函数y2=x-m(m是常数),若函数y1的表达式还可以写成y1=2(x-m)(x-m-2)的形式,当函数y=y1-y2的图象经过点(x0,0)时,求x0-m的值.20.已知函数y=x2-2kx+k2+1.(1)求证:不论k取何值,函数y>0;(2)若函数图象与y轴的交点坐标为(0,10),求函数图象的顶点坐标.21.已知二次函数y=x2+2bx−3b.(1)当该二次函数的图象经过点A(1,0)时,求该二次函数的表达式;(2)在(1) 的条件下,二次函数图象与x轴的另一个交点为点B,与y轴的交点为点C,点P从点A出发在线段AB上以每秒2个单位长度的速度向点B运动,同时点Q从点B出发,在线段BC上以每秒1个单位长度的速度向点C运动,直到其中一点到达终点时,两点停止运动,求△BPQ面积的最大值;(3)若对满足x≥1的任意实数x,都使得y≥0成立,求实数b的取值范围.22.已知关于x的方程x2﹣(m+2)x+2m﹣1=0.(1)求证:此方程有两个不相等的实数根;(2)若抛物线y=x2﹣(m+2)x+2m﹣1=0与x轴有两个交点都在x轴正半轴上,求m的取值范围;(3)填空:若x2﹣(m+2)x+2m﹣1=0的两根都大于1,则m的取值范围是.23.函数y=mx2﹣2mx﹣3m是二次函数.(1)如果该二次函数的图象与y轴的交点为(0,3),那么m=;(2)在(1)的条件下,结合图象当0<x<3时,求y的取值范围.24.已知抛物线y=ax2﹣bx+3经过点A(1,2),B(2,3).(1)求此抛物线的函数解析式.(2)写出该抛物线与坐标轴的交点坐标.参考答案1.【答案】D2.【答案】D3.【答案】C4.【答案】B5.【答案】C6.【答案】A7.【答案】D8.【答案】B9.【答案】A10.【答案】B11.【答案】D12.【答案】A13.【答案】m=﹣1或m=﹣314.【答案】3或﹣115.【答案】x<﹣1或x>316.【答案】2017.【答案】1或1218.【答案】②③19.【答案】(1)解:由题意,得y1=2(x-1)(x-2).图象的对称轴是直线x= 3 2(2)解:由题意,得y1=2x2-4hx+2h2-2∴b+c=2h2-4h-2=2(h-1)2-4∴当h=1时,b+c的最小值是-4.(3)解:由题意,得y=y1-y2=2(x-m)(x-m-2)-(x-m)=(x-m)[2(x-m)-5]∵函数y的图象经过点(x0,0)∴(x0-m)[2(x0-m)-5]=0∴x0-m=0,或x0-m= 52.20.【答案】(1)解:y=(x-k)2+1∵不论k取何值,(x-k)2≥0∴(x-k)2+1>0;即不论k取何值,函数y>0;(2)解:∵二次函数图象与y轴交于点(0,10)∴当x=0时,y=10∴k2+1=10,解得k=±3∴y=x2±9x+10=(x±3)2+1∴顶点坐标为(3,1)或(﹣3,1).21.【答案】(1)解:把A(1,0)代入y=x2+2bx−3b 得:0=12+2b−3b,解得:b=1∴该二次函数的表达式为:y=x2+2x−3;(2)解:令y=0代入y=x2+2x−3得:0=x2+2x−3解得:x1=1或x2=−3令x=0代入y=x2+2x−3得:y=-3∴A(1,0),B(-3,0),C(0,-3)设运动时间为t,则AP=2t,BQ=t∴BP=4-2t过点M作MQ△x轴∵OB=OC=3∴△OBC=45°∴△BMQ是等腰直角三角形∴MQ= √22BQ= √22t∴△BPQ的面积= 12BP⋅MQ=12(4−2t)⋅√22t= −√22(t−1)2+√22∴当t=1时,△BPQ面积的最大值= √22;(3)解:抛物线y=x2+2bx−3b的对称轴为:直线x=-b,开口向上设y=f(x)=x2+2bx−3b∵对x≥1的任意实数x,都使得y≥0成立∴{−b≤1f(1)≥0或{−b>1f(−b)≥0∴-1≤b≤1或-3≤b<-1∴-3≤b≤1.22.【答案】(1)证明:∵△=[﹣(m+2)]2﹣4(2m﹣1)=m2+4m+4﹣8m+4=m2﹣4m+8=(m﹣2)2+4∵(m﹣2)2≥0∴(m﹣2)2+4>0∴无论m取何实数时,此方程都有两个不相等的实数根(2)解:设抛物线y=x2﹣(m+2)x+2m﹣1=0与x轴两个交点的横坐标是x1,x2则x1+x2=m+2,x1•x2=2m﹣1.根据题意,得{m+2>02m−1>0解得m>1 2.即m的取值范围是m>1 2(3)m>223.【答案】(1)-1(2)解:由(1)可知函数的解析式为y=−x2+2x+3∵y=−x2+2x+3=−(x−1)2+4∴顶点坐标为(1,4)列表如下:x…-2-101234…y…-503430-5…描点、连线,函数图象如下:结合图象当 0<x <3 时, 0<y <3 .24.【答案】(1)解:将点A (1,2),B (2,3)代入y =ax 2﹣bx +3得 {a −b +3=24a −2b +3=3 解得 {a =1b =2∴抛物线的函数解析式为y =x 2−2x +3 (2)解:当x=0时,y =x 2−2x +3=3 ∴抛物线与y 轴的交点坐标为(0,3) 当y =0时,x 2−2x +3=0 解得x 1=3,x 2=-1∴抛物线与x 轴的交点坐标为(3,0)和(-1,0).故抛物线与坐标轴的交点坐标为(0,3)、(3,0)、(-1,0).。
中考数学《二次函数图像与坐标轴的交点问题》专项练习题及答案

中考数学《二次函数图像与坐标轴的交点问题》专项练习题及答案一、单选题1.如图,将二次函数y=31x2-999x+892的图形画在坐标平面上,判断方程31x2-999x+892=0的两根,下列叙述何者正确()A.两根相异,且均为正根B.两根相异,且只有一个正根C.两根相同,且为正根D.两根相同,且为负根2.已知抛物线y=ax2+bx+c(a<0)过A(-3,0)、O(1,0)、B(-5,y1)、C(5,y2)四点,则y1与y2的大小关系是()A.y1>y2B.y1=y2C.y1<y2D.不能确定3.已知二次函数y=ax2+bx+c(a≠0)的图象如图,则下列结论正确的是()A.c<0B.a+b+c<0C.2a﹣b=0D.b2﹣4ac=04.已知函数y=(k-1)x2-4x+4的图象与x轴只有一个交点,则k的取值范围是() A.k≤2且k≠1B.k<2且k≠1C.k=2D.k=2或15.函数y=ax+1与抛物线y=ax2+bx+1(b≠0)的图象可能是().A.B.C.D.6.若关于x的一元二次方程(x-2)(x-3)=m有实数根x1、x2,且x1≠x2,有下列结论:①x1=2,x2=3;②m>;③二次函数y=(x-x1)(x-x2)+m的图象与x轴交点的坐标为(2,0)和(3,0).其中,正确结论的个数是()A.0B.1C.2D.37.对于每个非零自然数n,抛物线y=x2-2n+1n(n+1)x+1n(n+1)与x轴交于A n,B n两点,以A n B n表示这两点间的距离,则A1B1+A2B2+…+A2009B2009()A.20092008B.20082009C.20102009D.200920108.二次函数y=kx2-6x+3的图象与x轴有交点,则k的取值范围是()A.k<3B.k<3,且k≠0C.k≤3D.k≤3,且k≠010.如图,抛物线y=ax2+bx+c与x轴交于点(-1,0),对称轴为x=1,则下列结论中正确的是()A.a>0B.当x>1时,y随x的增大而增大C.c<0D.x=3是一元二次方程ax2+bx+c=0的一个根11.已知抛物线y=ax2+bx+c(b>a>0)与x轴最多有一个交点,现有以下四个结论:①该抛物线的对称轴在y轴左侧;②关于x的方程ax2+bx+c+2=0无实数根;③a﹣b+c≥0;3.④a+b+cb−a的最小值为其中,正确结论的个数为()A.1个B.2个C.3个D.4个12.已知抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=2,与x轴的一个交点坐标为(4,0),其部分图象如图所示,下列结论:①抛物线过原点;②4a+b+c=0;③a﹣b+c<0;④抛物线的顶点坐标为(2,b);⑤当x<2时,y随x增大而增大.其中结论正确的是()A.①②③B.③④⑤C.①②④D.①④⑤二、填空题13.已知函数y=ax2−2x+1的图象与x轴只有一个公共点,则a的值是.14.经过A(4,0),B(﹣2,0),C(0,3)三点的抛物线解析式是.15.如图,P是抛物线y=2(x﹣2)2对称轴上的一个动点,直线x=t平行y轴,分别与y=x、抛物线交于点A、B.若△ABP是以点A或点B为直角顶点的等腰直角三角形,求满足条件的t的值,则t=.16.抛物线y=x2﹣4x+c与x轴交于A、B两点,已知点A的坐标为(1,0),则线段AB的长度为.17.抛物线y= 49(x-3)2与x轴的交点为A,与y轴的交点为B,则△AOB的面积为18.已知二次函数y=﹣x2+2x+m的部分图象如图所示,则关于x的一元二次方程﹣x2+2x+m=0的解为.三、综合题19.如图,二次函数y=- 12x2+bx+c的图象经过A(2,0)、B(0,-4)两点(1)求二次函数的解析式;(2)设该二次函数的对称轴与x轴交于点C,连接BA、BC,求△ABC的面积.20.已知二次函数y=ax2+bx+8,经过点(1,9)和(6,−16).(1)求此二次函数解析式;(2)若此二次函数与x轴的交点为点A、点B,与y轴的交点为点C,求△ABC的面积. 21.在平面直角坐标系xOy中,抛物线y=﹣x2+mx+n与x轴交于点A,B(A在B的左侧).(1)若抛物线的对称轴为直线x=﹣3,AB=4.求抛物线的表达式;(2)平移(1)中的抛物线,使平移后的抛物线经过点O,且与x正半轴交于点C,记平移后的抛物线顶点为P,若△OCP是等腰直角三角形,求点P的坐标;22.已知二次函数y=(x-1)(x-m).(1)若二次函数的对称轴是直线x=3,求m的值.(2)当m>2,0≤x≤3时,二次函数的最大值是7,求函数表达式.23.已知抛物线y=ax2-2ax-3+2a2 (a<0).(1)求这条抛物线的对称轴;(2)若该抛物线的顶点在x轴上,求抛物线的函数解析式;24.已知抛物线顶点坐标为(1,3),且过点A(2,1).(1)求抛物线解析式;(2)若抛物线与x轴两交点分别为点B、C,求线段BC的长度.参考答案1.【答案】A2.【答案】A3.【答案】C4.【答案】D5.【答案】C6.【答案】C7.【答案】D8.【答案】D9.【答案】C10.【答案】D11.【答案】D12.【答案】C13.【答案】0或114.【答案】y=﹣38x2+ 34x+315.【答案】5±√52或1或316.【答案】217.【答案】618.【答案】x1=4,x2=﹣219.【答案】(1)解:分别把点A(2,0)、B(0,-4)代入y=−12x2+bx+c得{−12×22+2x+c=0c=−4解得:{b=3c=−4∴这个二次函数的解析式为:y=−12x2+3x−4(2)解:由(1)中抛物线对称轴为直线∴点C的坐标为:(3,0)∴AC=3−2=1∴△ABC的面积为:12⋅OB⋅AC=12×4×1=220.【答案】(1)解:把点(1,9)和(6,−16)代入函数解析式得{9=a+b+8−16=36a+6b+8解得a=-1, b=2. 所以二次函数的解析式为y=−x2+2x+8(2)解: 令y=0,得-x 2+2x+8=0, 解得x=-4或x=2 得A 、B 的坐标为(-4,0),(2,0) 则AB=6令x=0, 得y=8 ∴C 点坐标为(0,8),则OC=8 ∴S △ABC =12AB ×OC =12×6×8=24 .21.【答案】(1)解:∵抛物线的对称轴为直线x =﹣3,AB =4∴A 、B 两点到对称轴的距离相等,且为2 ∴A 点坐标为(-5,0),B 点坐标为(-1,0)把A 、B 两点的坐标分别代入函数解析式中,得: {−25−5m +n =0−1−m +n =0解得: {m =−6n =−5∴y =−x 2−6x −5(2)解:∵y =−x 2−6x −5 平移后过原点∴设平移后过原点的抛物线为 y =−x 2+bx 令 y =−x 2+bx =0 ,解得:x=0 ∴C (b ,0)且b>0∵y =−x 2+bx =−(x −b 2)2+b 24∴顶点P 的坐标为 (b 2,b 24) ∵△OCP 是等腰直角三角形 ∴b 2=b 24解得:b=2∴顶点P 的坐标为 (1,1)22.【答案】(1)解: 令y =0,即0=(x −1)(x −m) ,得x 1=1,x 2=m也即抛物线与x轴的交点坐标为(1,0),(m,0)∵(1,0),(m,0)关于抛物线对称轴对称,且对称轴是直线x=3∴1+m2=3,解得m=5(2)解:由(1)可知,抛物线的对称轴为直线x=1+m 2∵m>2,∴x=1+m 2>32∵a=1>0,且0≤x≤3时,二次函数的最大值是7∴当x=0时y max=7∴把(0,7)带入抛物线表达式得7=(0−1)(0−m)∴m=723.【答案】(1)解:∵抛物线y=ax2−2ax−3+2a2=a(x−1)2+2a2−a−3∴抛物线的对称轴为直线x=1;(2)解:由(1)可得y=a(x−1)2+2a2−a−3∵抛物线的顶点在x轴上∴2a2−a−3=0解得a1=32,a2=-1∵a<0∴a=-1∴抛物线的解析式为y=−x2+2x−1.24.【答案】(1)解:设抛物线解析式为y=a(x﹣1)2+3把A(2,1)代入得a•(2﹣1)2+3=1,解得a=﹣2所以抛物线解析式为y=﹣2(x﹣1)2+3(2)解:y=0时,﹣2(x﹣1)2+3=0解得x1=1+ √62,x2=1﹣√62所以BC=1+ √62﹣(1﹣√62)= √6。
化学专项2015--坐标图像题(学生版)

化学专项2015--坐标图像题(学生版)- 2 -化学专项——坐标图像题【方法指导】解决此类问题须注意:一看横纵坐标的含义,二看图像的起点,三看拐点及终点,四看图像中横纵坐标的比例关系,五看图像的走向。
然后把图像表示的意义与化学知识有效地结合起来,找出图与相关化学知识的具体关系即可。
一、金属与酸反应类型1.用相同质量的镁、铝、锌,分别跟足量的相同浓度的盐酸反应,反应情况用下列图线表示,纵坐标是氢气的质量,横坐标是反应时间,其中图线正确的是( )2.过量的Mg 、Zn 、Fe 三种金属分别与等质量等浓度的稀硫酸反应,放出H 2的质量w 与时间t 的关系曲线正确的是( )3.将质量相等的A 、B 、C 三种金属,同时分别放入三份溶质质量分数相同且足量的稀盐酸中,反应生成的H 2的质量与反应时间的关系如图所示。
(已知:A 、B 、C 在生成物中均为+2价)根据图中所提供的信息,得出的结论正确的是 ( ) A .放出H 2的质量是A>B>C B .金属活动性顺序是A>B>C C .反应速率最大的是A D .相对原子质量是C>B>A 二、溶液酸碱度的变化1.将一定浓度的硫酸加水稀释,下列图像可能符合的是(m 为加水的质量)( )- 3 -2.下图能表示18.25g 质量分数为2%的盐酸与20g 质量分数为2%氢氧化钠溶液反应的是( )三、反应速率与时间的关系1.有质量相等的两份氯酸钾,只向其中一份加入少量二氧化锰,同时放在两只试管内加热。
下列有关放出氧的质量(g )与反应时间(t )的关系图象(图中a 是纯氯酸钾的曲线,b 是混有二氧化锰的曲线)中正确的是( )A .B .C .D .四、质量守恒定律型1.红磷在密闭容器(含有空气)内燃烧,容器内有关的量随时间变化的图象正确的是( )A B C D五、与溶液相关的曲线1.农业上常用饱和的食盐水选种。
在室温保持不变的情况下,饱和食盐水露置在空气中一段时间后,有少量固体析出。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
专项14 坐标图像题
一、单选题
1.小鹏在进行电解水实验时,为增强水的导电性,加快水的分解速率,取100g 3%硫酸钠溶液(硫酸钠溶液显中性,在水通电分解前后质量不变)进行电解。
下列图像正确的是()
A. B.
C. D.
2.下列图像不能正确反映其对应关系的是()
A.向一定量且等质量的锌和镁中分别加入足量的稀盐酸
B.向一定量的稀盐酸中加入足量的不同金属
C.任何量都相同的两份硝酸铜中,分别加入过量的铁粉和锌粉(加入
的量相同)
D.向等质量的铁粉和锌粉中加入足量等浓度的稀硫酸
3.下列图像不能正确反映其对应变化关系的是()
A.分别向等质量Mg和Cu中加入足量等质量,等浓度的稀硫酸
B.用等质量、等浓度的过氧化氢溶液在有无MnO2条件下制氧气
C.一定温度下,向饱和的氯化钠溶液中加入氯化钠固体并搅拌
D.一定质量的白磷在密闭的容器(内含空气)中燃烧
4.实验小组用图1装置探究稀氢氧化钠溶液与稀盐酸能否反应,测得数据如图2。
下列说法正确的是()
A.烧杯中只能盛放稀氢氧化钠溶液
B.图2不能证明反应是放热反应
C.60s时溶液中溶质只有氯化钠
D.实验证明氢氧化钠与盐酸能反应
5.实验小组用传感器探究氢氧化钠溶液与稀盐酸反应过程中温度和pH 的变化,测定结果如图所示。
下列说法正确的是()
A.氢氧化钠与盐酸反应先放热后吸热
B.该反应的微观实质是Na+和Cl-反应生成NaCl 分子
C.30s 时溶液中的溶质为氢氧化钠和氯化钠
D.该实验是将氢氧化钠溶液滴入稀盐酸中
6.学会识图能发展科学思维,一小块未打磨的铝片和一定质量的稀盐酸反应,产生气泡的快慢和反应时间的关系如下图。
下列猜想正确的有()
①0~t1阶段,可能是铝表面有层氧化膜
②t1~t2阶段,可能是铝和稀盐酸反应放出热量
③t3时刻,可能是稀盐酸过量
④t3时刻,可能是稀盐酸不足
A.1项
B.2项
C.3项
D.4项
7.相同质量的镁、铁、锌三种金属,分别与足量的、相同质量分数的稀硫酸充分反应,生成氢气质量与反应时间关系如图,分析图像判断,下面说法正确的是()
A.镁的相对原子质量最大
B.锌反应速率最快
C.锌生成氢气质量最少
D.铁消耗稀硫酸质量最多
8.下列图像能正确反映其相应关系的有()
A.向氢氧化钠溶液中不断加水
B.向一定质量的锌粒中加入稀硫酸至过量
C.高温煅烧石灰石
D.向稀硫酸中滴加氢氧化钡溶液至过量
9.能反映相关实验过程中量的变化的图像是()
A.等质量镁、锌分别和足量等浓度的盐酸反应
B.用一氧化碳与氧化铁反应
C.镁在氧气中燃烧
D.等质量、等质量分数的双氧水完全分解
10.两支试管中分别盛有等质量、等溶质质量分数的稀盐酸,分别向其中逐渐加入两种不同的金属粉末M和N。
加入金属的质量与产生氢气的质量之间的关系如图所示。
下列说法不正确的是()
A.充分反应后,产生氢气的质量:M=N
B.由图像可推出N的相对原子质量比M的相对原子质量大
C.a点对应的溶液中的溶质只有一种
D.c点对应的溶液中的溶质一定有两种
11.将锌粉持续加入到100g含有AgNO3和Cu(NO3)2两种溶质的混合溶液中,充分反应。
当加入锌粉的质量为6.5g时,溶液质量最小;当加入锌粉的质量为13.0g时,恰好完全反应。
下列是反应中的相关量随加入锌的质量变化的关系图,其中正确的是()
A. B.
C. D.
12.煅烧石灰石样品(杂质不含钙元素且不发生反应)时,某质量随加热时间的变化关系如图所示,有关分析中正确的是()
A.若纵坐标表示固体质量,则剩余氧化钙质量为m2g
B.若纵坐标表示氧元素的质量,则杂质中一定含有氧元素
C.纵坐标不能表示固体中碳元素的质量
D.纵坐标表示固体质量或氧元素质量,都可知碳酸钙质量
13.已知:C+2CuO2Cu+CO2↑,如图表示一定量的木炭和氧化铜固体混合物受热过程中,某变量y随加热时间的变化趋势,其中纵坐标y表示()
A.固体的质量
B.固体中氧化铜的质量
C.二氧化碳的质量
D.固体中铜元素的质量分数
14.下列图像能正确反映对应变化关系的是()
A.向稀硫酸和硫酸铜的混合溶液中加入足量的氢氧化钡溶液
B.高温煅烧石灰石
C.足量的镁、铝分别同时放入等质量、等浓度的稀硫酸中
D.向饱和石灰水中加入少量的生石灰
15.下列图像能正确反映对应变化关系的是()
A.一定温度下,氧气的溶解度随压强的变化
B.向等质量的铝粉和锌粉中分别滴加足量的相同浓度的稀盐酸
C.向一定量硫酸铜溶液中加入过量铁粉
D.向一定量的饱和硝酸钠溶液中加入氯化钠固体
16.下面所示的图像能正确反映对应变化关系的是()
A.向一定浓度的NaOH溶液中加水稀释
B.浓盐酸在空气中敞口放置一段时间
C.向硫酸和硫酸铜的混合溶液中逐滴加入烧碱溶液至过量
D.加热一定质量木炭粉和氧化铜混合物
17.下列图像不能
..正确反映对应变化关系的是()
A.在一定温度下,向接近饱和的硝酸钾溶液中加入硝酸钾晶体
B.两份完全相同的稀盐酸中分别加入足量铁粉、锌粉
C.用等质量等质量分数的过氧化氢溶液制取氧气
D.向一定量的稀盐酸中不断加入NaOH溶液至过量
18.下列各个过程对应的图像正确的是()
A.将一定量KNO3的不饱和溶液恒温蒸发水分至有晶体析出
B.向足量且质量分数相同的稀硫酸中分别加入等量锌粉和铁粉
C.向等质量、等溶质质量分数的盐酸中,分别加入足量的铝粉和镁粉
D.向一定质量的AgNO3和Cu(NO3)2的混合溶液中加入足量Fe粉
19.一定质量的氢氧化钡溶液逐渐加入碳酸钠粉末(不考虑溶液体积变化),直至过量。
如图横坐标表示加入碳酸钠粉末的质量,根据图象判断,纵坐标可能表示()
A. 溶液中溶质的质量
B.溶液中溶剂的质量
C.生成沉淀的质量
D.溶液的pH
20.整理实验室时,同学们发现一瓶盐酸呈黄色,老师解释说里面含有氯化铁。
为测定这瓶工业盐酸中氯化铁的含量(假设不含其他杂质),小明做了如下实验:取20g工业盐酸加适量的水稀释后加入小烧杯中,然后向小烧杯中不断滴加溶质质量分数为10%的氢氧化钠溶液,同时不断测量溶液的pH,得出如图所示的关系(横坐标x表示
滴加氢氧化钠溶液的质量)。
则下列分析错误的是()
A.工业盐酸呈黄色是因为含有Fe3+
B.点A时溶液中所含溶质是NaCl和FeCl3
C.当16<x≤22时的实验现象是有红褐色沉淀产生
D.当x=22g时,所得沉淀为19.6g。
