4.四边形的不稳定性
四边形专项训练题(培优)

四边形专项训练题(培优)一.选择题(共10小题)1.四边形具有不稳定性,对于四条边长确定的四边形.当内角度数发生变化时,其形状也会随之改变.如图,改变正方形ABCD的内角,正方形ABCD变为菱形ABC′D′.若∠D′AB=30°,则菱形ABC′D′的面积与正方形ABCD的面积之比是()A.1B.C.D.2.如图,在▱ABCD中,一定正确的是()A.AD=CD B.AC=BD C.AB=CD D.CD=BC3.用形状、大小完全相同的一种或几种平面图形进行拼接,彼此之间不留空隙、不重叠地铺成一片,这就是平面图形的镶嵌.工人师傅不能用下列哪种形状、大小完全相同的一种地砖在平整的地面上镶嵌()A.等边三角形B.正方形C.正五边形D.正六边形4.如图,在▱ABCD中,AB=8,点E是AB上一点,AE=3,连接DE,过点C作CF∥DE,交AB的延长线于点F,则BF的长为()A.5B.4C.3D.25.如图1,在菱形ABCD中,∠C=120°,M是AB的中点,N是对角线BD上一动点,设DN长为x,线段MN与AN长度的和为y,图2是y关于x的函数图象,图象右端点F 的坐标为(2,3),则图象最低点E的坐标为()A.(,2)B.(,)C.(,)D.(,2)6.如图,在△ABC中,AB=AC,△DBC和△ABC关于直线BC对称,连接AD,与BC相交于点O,过点C作CE⊥CD,垂足为C,与AD相交于点E,若AD=8,BC=6,则的值为()A.B.C.D.7.大自然中有许多小动物都是“小数学家”,如图1,蜜蜂的蜂巢结构非常精巧、实用而且节省材料,多名学者通过观测研究发现:蜂巢巢房的横截面大都是正六边形.如图2,一个巢房的横截面为正六边形ABCDEF,若对角线AD的长约为8mm,则正六边形ABCDEF 的边长为()A.2mm B.2mm C.2mm D.4mm8.如图,在正五边形ABCDE中,以AB为边向内作正△ABF,则下列结论错误的是()A.AE=AF B.∠EAF=∠CBF C.∠F=∠EAF D.∠C=∠E9.依据所标数据,下列一定为平行四边形的是()A.B.C.D.10.如图,▱ABCD的对角线AC和BD相交于点O,下列说法正确的是()A.若OB=OD,则▱ABCD是菱形B.若AC=BD,则▱ABCD是菱形C.若OA=OD,则▱ABCD是菱形D.若AC⊥BD,则▱ABCD是菱形二.填空题(共10小题)11.四边形具有不稳定性.如图,矩形ABCD按箭头方向变形成平行四边形A'B'C'D',当变形后图形面积是原图形面积的一半时,则∠A'=.12.正十二边形的一个内角的度数为.13.如图,在Rt△ABC中,∠BAC=90°,AB=3,BC=5,点P为BC边上任意一点,连接P A,以P A,PC为邻边作平行四边形P AQC,连接PQ,则PQ长度的最小值为.14.如图,在正六边形ABCDEF中,M,N是对角线BE上的两点.添加下列条件中的一个:①BM=EN;②∠F AN=∠CDM;③AM=DN;④∠AMB=∠DNE.能使四边形AMDN是平行四边形的是(填上所有符合要求的条件的序号).15.如图,菱形ABCD的边长为2,∠ABC=60°,对角线AC与BD交于点O,E为OB 中点,F为AD中点,连接EF,则EF的长为.16.如图,CD是△ABC的角平分线,过点D分别作AC,BC的平行线,交BC于点E,交AC于点F.若∠ACB=60°,CD=4,则四边形CEDF的周长是.17.七边形一共有条对角线.18.小张同学家要装修,准备购买两种边长相同的正多边形瓷砖用于铺满地面.现已选定正三角形瓷砖,则选的另一种正多边形瓷砖的边数可以是.(填一种即可)19.如图,在四边形ABCD中,连接AC,∠ACB=∠CAD.请你添加一个条件,使AB=CD.(填一种情况即可)20.如图,将△ABC沿着BC方向平移得到△DEF,只需添加一个条件即可证明四边形ABED 是菱形,这个条件可以是.(写出一个即可)三.解答题(共8小题)21.同学们在探索“多边形的内角和”时,利用了“三角形的内角和”.请你在不直接运用结论“n边形的内角和为(n﹣2)•180°”计算的条件下,利用“一个三角形的内角和等于180°”,结合图形说明:五边形ABCDE的内角和为540°.22.如图,在▱ABCD中,点E、F分别是边AB、CD的中点.求证:AF=CE.23.小惠自编一题:“如图,在四边形ABCD 中,对角线AC ,BD 交于点O ,AC ⊥BD ,OB =OD .求证:四边形ABCD 是菱形”,并将自己的证明过程与同学小洁交流.小惠:证明:∵AC ⊥BD ,OB =OD ,∴AC 垂直平分BD .∴AB =AD ,CB =CD ,∴四边形ABCD 是菱形.小洁: 这个题目还缺少条件,需要补充一个条件才能证明.若赞同小惠的证法,请在第一个方框内打“√”;若赞成小洁的说法,请你补充一个条件,并证明.24.如图,已知五边形ABCDE 是正五边形,连接AC 、AD .证明:∠ACD =∠ADC .25.如图,四边形ABCD 为菱形,E 为对角线AC 上的一个动点(不与点A ,C 重合),连接DE 并延长交射线AB 于点F ,连接BE .(1)求证:△DCE ≌△BCE ;(2)求证:∠AFD =∠EBC .26.如图,在四边形ABCD中,AB∥CD,AC平分∠DAB,AB=2CD,E为AB中点,连结CE.(1)求证:四边形AECD为菱形;(2)若∠D=120°,DC=2,求△ABC的面积.27.如图,在四边形ABCD中,AC与BD交于点O,BE⊥AC,DF⊥AC,垂足分别为点E,F,且BE=DF,∠ABD=∠BDC.求证:四边形ABCD是平行四边形.28.如图,在△ABC中,AD⊥BC于点D,E,F分别是AC,AB的中点,O是DF的中点,EO的延长线交线段BD于点G,连结DE,EF,FG.(1)求证:四边形DEFG是平行四边形.(2)当AD=5,tan∠EDC=时,求FG的长.。
平行四边形地不稳定性

平行四边形的不稳定性
江苏省海门市海南小学周巾
侠
我们都知道三角形具有稳定性,不容易变形。
平行四边形与三角形不同,容易变形,也就是具有不稳定性。
这种不稳定性在生活中有广泛的应用。
如电动伸缩门(图1)、铁拉门(图2)、活动衣架(图3)等等。
图
1 图2
图3
那你理解平行四边形的不稳定性吗?不妨做个对比实验:(1)准备三根不同长度的小棒摆三角形。
(2)准备四根小棒(2长2短)摆平行四边形。
看看你分别有多少种不同的摆法?
可能细心的小朋友就会发现,三角形就摆出了一种。
是的,当三角形的三条边长度确定后,三角形的形状和大小也就被确定了,只是位置的不同。
如图4
图4
而摆出的平行四边形不止一种,如图5
图5
这里摆出的4个平行四边形,用了同样的2长2短四根小棒,但形状各不相同,面积也是越来越小。
这个对比试验,告诉我们三角形稳定性的实质是指边长确定,则形状、大小唯一;而平行四边形不稳定性的实质是指平行四边形边长确定,其形状、大小不能完全确定。
四边形不稳定性的思考

四边形不稳定性的思考作者:郝四柱朱金玲来源:《中学数学杂志(初中版)》2015年第05期1 问题的提出在一次活动课上,学生们探究如何让六边形实现稳定.问题是:一个六边形钢架ABCDEF,由6条钢管连接而成,为了使这一钢架稳固,请你用三条钢管做对角线使它固定,你能设计两种不同的方案吗?同学们的思路各种各样,如图1的6个图形是出现比较多的情况.前面4种容易判断.图1①不稳定,图1②—④都是稳定的,并且能够证明.老师们认为后两种方法含有四边形,不具有稳定性,因而不符合要求(解释一下,图形中对角线用虚线,突出对角线交点不存在;只保持对角线的长度不变).最后两种方法本人凭感觉它们是稳定的.几何画板演示之后,验证了这两个图确实是稳定的.但是如何解释呢?解铃还须系铃人,问题必须回到“四边形的不稳定性”上来,进行深度探究,弄清楚四边形不稳定性的内在规律.众所周知,三角形具有稳定性,四边形不具有稳定性.对于四边形不稳定性,有不少人还会产生误解:(1)有人会说,三角形有时也不具有稳定性,你看:如图2,△ABC,具有AB、AC和∠ABC确定,这样的三角形可以有两个,能稳定吗?(2)有人还会说:四边形我能让它稳定;用长度一定的四根钢筋,把四边的顶点依次焊接起来,这个四边形不就稳定了吗?以上两种想法都是不正确的.对于看法(1),把图形的两种情况和不稳定性混淆了.△ABC1和△ABC2虽然是两种情况,但是△ABC1运动变成△ABC2的过程中,AC长度和∠ABC度数至少有一个发生变化;也就是说这两情况虽然是存在的,但是不可能通过连续变化实现△ABC1和△ABC2这两种情况的相互转换.对于看法(2)涉及到顶点的连接方式问题:顶点处必须是可动的,如同四肢的关节一样.否则稳定性研究无从谈起.那么四边形不稳定性有哪些内在的规律?课本中有四边形不稳定性的明确定义:四边形具有不稳定性,也就是说,当一个四边形的四边的长度确定时,这个四边形的形状、大小不唯一确定.如图3,不妨让一边AB固定,四边长度确定,此时四边形形状变化时,点D的轨迹是以点A为圆心、AD为半径的圆(弧),点C的轨迹是以点B为圆心、BC为半径的圆(弧).在边BC、AD上的固定点的轨迹也是圆.此时四边形ABCD中,CD上的某个固定点的轨迹又是什么?是圆(弧)?显然四边形ABCD如果是平行四边形,在AB确定的情况下,图形变化过程中有cos(α-β)=1,R=r;此时点P的轨迹显然是圆.但是对于四边形ABCD不是平行四边形的时候,点P 的轨迹通过几何画板演示发现:点P在直线CD上的不同位置的点的轨迹如图4.显然轨迹不是一个圆,而是一个封闭图形.那么四边形在运动过程中除了平行四边形外,是否还有其它点的轨迹是圆?也就是说:有cos(α-β)为定值呢?答案是没有,证明如下.特别的:当四边形是梯形且BC∥AD时,那么α-β=0,随着图形的变化,那么这种平行的位置关系发生变化,α-β也不可能是定值.所以,除了平行四边形之外的其它四边形均不可能有α-β是定值.也就是说:只有平行四边形的情况下,CD边上的点P(异于C、D)的轨迹才是圆,否则,根据(1)可知:点P轨迹方程是围绕一个中心运动,但是半径不断发生变化的方程,其图形是一种有中心的封闭图形(或其一部分)不妨称之为变圆.4 问题的拓展推论1:根据结论(2)可知:当四边形ABCD以一边AB固定,其它边运动时,①直线AD、BC上的任意一点(除A、B外)运动的轨迹是:半径和圆心都固定的确定的圆.②直线CD上的点(除点C、D外)运动的轨迹是圆心确定但半径不断变化的一种似圆非圆的变圆(或变圆的一部分).③如果某个点E是以BC(或AD为定边)而被固定的点,那么这个点E的轨迹是一个圆.④如图6某个点E是以CD为定边,CE、DE边长确定三角形CDE,当四边形ABCD以AB不动其他部分运动时,点E的轨迹是圆心和半径都改变的变圆.根据推论可知:显然五边形需要且只需要任意2条对角线就能把五边形固定.那么对于六边形至少需要3条对角线才能把六边形固定.如图1①—④易于发现是否是固定的了.对于如图1的⑤⑥两图,是否稳定呢?如图7就是图1⑤,让△ABF固定不动,根据推论1③可知:当四边形BCEF图形变化时,点D的轨迹是变圆,点D到点A的距离是不断变化的,所以一旦AD长度确定,那么点D确定,整个图形就固定了了.说明这种情况下是稳定的.对于图1⑥情况,即:图8,由于一时找不到一个固定不变的三角形,故只能另用它法.我们首先画出六边形ABCDEF然后画出A′B′,使得A′B′=AB,然后以B′为圆心BC为半径画圆,在圆上找一点为对应的点C′,以A′、C′分别为圆心,AD、CD为半径确定点D′,进而确定点E′、F′,显然当点C′绕圆运动时,点F′的运动轨迹是变圆,用几何画板验证了这一点(如图9).所以点A′F′长度一旦确定,则点F′也就确定,因而六边形就是稳定的图形了.推论2:对于四边形只需增添一条对角线即可稳定.对于五边形,只需增添两条对角线即可稳定.对于六边形增添3条对角线,还需考虑放置的方法才能稳定.相应的对于n边形,至少需要(n-3)条对角线方可稳定,最简洁的放置方法是从一个顶点出发引出(n-3)条对角线即可.。
平行四边形具有稳定性不易变形对吗

平行四边形具有稳定性不易变形对吗
平行四边形的特性是不稳定性。
因为平行四边形的形状、大小不能仅由平行四边的四条边确定。
如果把两两相等的四根木条用可活动的饺钉钉成平行四边形木框,推动木条可以得出形状、大小各不相同的平行四边形,由此说明平行四边形具有不稳定性。
一个四边形是平行四边形,这个四边形的两组对边分别相等。
一个四边形就是平行四边形,这个四边形的两组对角分别成正比。
夹在两条平行线间的平行的高相等。
相连接任一四边形各边的中点税金图形就是平行四边形。
平行四边形abcd中,ac、bd是平行四边形abcd的对角线,则各四边的平方和等于对角线的平方和。
平行四边形的面积等同于相连两边与其夹角正弦的乘积。
平行四边形,是在同一个二维平面内,由两组平行线段组成的闭合图形。
平行四边形一般用图形名称加四个顶点依次命名。
特定的平行四边形:
1、矩形
定义:存有一个角就是直角的平行四边形就是矩形。
判定:有一个角是直角的平行四边形是矩形;对角线相等的平行四边形是矩形。
2、菱形
定义:有一组邻边相等的平行四边形是菱形。
认定:一组邻边成正比的平行四边形就是菱形;对角线互相横向的平行四边形就是菱形。
四年级上册数学教案-4.5.7平行四边形的不稳定性,底和高的概念∣人教新课标

四年级上册数学教案-4.5.7平行四边形的不稳定性,底和高的概念∣人教新课标一、教学目标1. 让学生了解平行四边形的不稳定性,理解底和高的概念。
2. 培养学生观察、分析、抽象、概括的能力。
3. 培养学生合作交流、动手操作的能力。
二、教学内容1. 平行四边形的不稳定性2. 底和高的概念3. 底和高的测量方法三、教学重点与难点1. 教学重点:平行四边形的不稳定性,底和高的概念。
2. 教学难点:底和高的测量方法。
四、教学过程1. 导入新课通过复习平行四边形的性质,引导学生思考:平行四边形具有哪些特性?当平行四边形的某个角度或边长发生变化时,会对整个平行四边形的形状产生什么影响?2. 探究平行四边形的不稳定性(1)分组讨论:让学生分组讨论平行四边形的不稳定性,引导学生从日常生活实例中寻找例子,如伸缩门、晾衣架等。
(2)展示实例:教师展示一些平行四边形的不稳定性实例,如推拉门、折叠桌等,让学生直观感受平行四边形的不稳定性。
(3)总结特点:引导学生总结平行四边形的不稳定性特点,如易变形、角度变化影响整体形状等。
3. 学习底和高的概念(1)定义:教师给出平行四边形的底和高的定义,让学生理解底和高分别指平行四边形的哪两条边。
(2)举例:教师通过举例,让学生明确底和高的位置关系,如底可以任意选取,高与底垂直。
(3)练习:让学生在平行四边形图中找出底和高,并标明。
4. 学习底和高的测量方法(1)讲解方法:教师讲解底和高的测量方法,如使用直尺、量角器等工具。
(2)演示操作:教师演示底和高的测量方法,让学生观察并模仿。
(3)分组练习:让学生分组进行底和高的测量练习,互相交流、合作。
5. 课堂小结教师引导学生回顾本节课所学内容,总结平行四边形的不稳定性、底和高的概念及测量方法。
6. 课后作业(略)五、教学反思本节课通过实例导入,让学生充分感受平行四边形的不稳定性,从而激发学生的学习兴趣。
在教学过程中,注重引导学生观察、分析、抽象、概括,培养学生的逻辑思维能力。
人教版平行四边形的性质(24)
D
C
A
B
D
C
A
B
D
C
A
B
课本49页习题1、2、3
2.记作: □ABCD
3.读作: 平行四边形ABCD
四边形ABCD是平行四边形
5.对边:AB、CD; AD、BC.
对角:A、 C ; B、 D .
已知:AB//CD ,AD//BC.
求证:ABCD,ADBC, DAB BC,D ABC CD. A
D
C
41
3
A
2B
大家有疑问的,可以询问和交流
可以互相讨论下,但要小声点
平行四边形的性质:
性质1:平行四边形的对边相等。
D
C
∵四边形ABCD是平行四边形 A
B
∴AB=CD,BC=AD。
性质2:平行四边形的对角相等。
D
C
A
B
∵四边形ABCD是平行四边形
∴∠A=∠C,∠B=∠D。
1、如图:在 ABCD中,根据已知 你能得到哪些结论?为什么?
A 32cm D
124°
56°
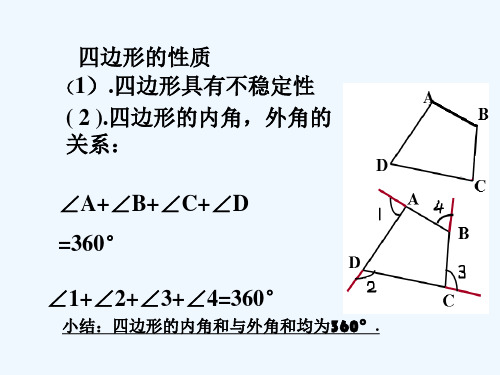
四边形的性质
(1).四边形具有不稳定性
( 2 ).四边形的内角,外角的
A
关系:
∠A+∠B+∠C+∠D =360°
D C
∠1+∠2+∠3+∠4=360°
小结:四边形的内角和与外角和均为360°.
请找出图中的平行四边形。 说明寻找的依据是什么?
D
C
A
B
平行四边形概念:两组对边分别平行的四边形叫平
行四边形。记作 ABCD。
A
∴CD=8(m),
又AB+BC+CD+AD=36,
四边形不稳定性

四边形不稳定性
平行四边形的特性是不稳定性。
因为平行四边形的形状、大小不能仅由平行四边的四条边确定。
如果把两两相等的四根木条用可活动的饺钉钉成平行四边形木框,推动木条可以得出形状、大小各不相同的平行四边形,由此说明平行四边形具有不稳定性。
一个四边形是平行四边形,这个四边形的两组对边分别相等。
一个四边形就是平行四边形,这个四边形的两组对角分别成正比。
夹在两条平行线间的平行的高相等。
相连接任一四边形各边的中点税金图形就是平行四边形。
平行四边形abcd中,ac、bd是平行四边形abcd的对角线,则各四边的平方和等于对角线的平方和。
平行四边形的面积等同于相连两边与其夹角正弦的乘积。
平行四边形,是在同一个二维平面内,由两组平行线段组成的闭合图形。
平行四边形一般用图形名称加四个顶点依次命名。
特定的平行四边形:
1、矩形
定义:存有一个角就是直角的平行四边形就是矩形。
判定:有一个角是直角的平行四边形是矩形;对角线相等的平行四边形是矩形。
2、菱形
定义:有一组邻边相等的平行四边形是菱形。
认定:一组邻边成正比的平行四边形就是菱形;对角线互相横向的平行四边形就是菱形。
四边形的不稳定性

四边形的不稳定性
四边形的不稳定性是指当四边形的边界发生变化时,它的形状也会发生变化。
这种不稳定性是由于四边形的边界是由四条直线组成的,而这四条直线之间的关系是相互依赖的,因此当其中一条直线发生变化时,其他三条直线也会发生变化,从而导致四边形的形状发生变化。
四边形的不稳定性在很多领域都有着重要的应用,比如在机械设计中,当设计者需要设计一个稳定的结构时,他们就会考虑四边形的不稳定性,以确保结构的稳定性。
此外,四边形的不稳定性也可以用来解释一些自然现象,比如地震时地壳的变形,这是由于地壳的边界是由四边形组成的,当地壳发生变形时,四边形的形状也会发生变化,从而导致地壳的变形。
总之,四边形的不稳定性是一个重要的概念,它在很多领域都有着重要的应用,比如机械设计和自然现象的解释等。
因此,我们应该加强对四边形的不稳定性的研究,以更好地理解它的作用,并利用它来解决实际问题。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1. (2011 四川省绵阳市) 王师傅用4根木条钉成一个四边形木架,如图,要使这个木架不变形,他至少要再钉上几根木条?( )
A .0根
B .1根
C .2根
D .3根
答案:B
2. (2011 河南省)
如图,在ABC Rt △中,9030B BC C ∠==∠=°,°.点D 从点C 出发沿CA 方向以每秒2个单位长的速度向点A 匀速运动,同时点E 从点A 出发沿AB 方向以每秒1个单位长的速度向点B 匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D 、E 运动的时间是()0t t >秒.过点D 作DF BC ⊥于点F ,连接DE 、EF .
(1)求证:AE DF =;
(2)四边形AEFD 能够成为菱形吗?如果能,求出相应的t 值;如果不能,说明理由.
(3)当t 为何值时,DEF △为直角三角形?请说明理由.
答案:1)在DFC △中,90302DFC C DC t ∠=∠==°,°,,
DF t ∴=.
又AE t AE DF =∴=,
. (2)能.理由如下:
AB BC DF BC ⊥⊥,,
AE DF ∴∥.
又AE DF =,∴四边形AEFD 为平行四边形.
∵tan 3053
AB BC
===·°, ∴210AC AB ==. ∴102AD AC DC t =-=-.
若使平行四边形AEFD 为菱形,则需AE AD =.即101023
t t t =-=,. 即当103
t =
时,四边形AEFD 为菱形. (3)①90EDF ∠=°时,四边形EBFD 为矩形.
在Rt AED △中,30ADE C ∠=∠=°,
∴2AD AE =.即510222
t t t -==,. ②90DEF ∠=°时,由(2)知EF AD ∥,
∴90ADE DEF ∠=∠=°.
∵90A ∠=°-60C ∠=°,
∴cos 60AD AE
=︒·. 即110242
t t t -==,. ③90EFD ∠=°时,此种情况不存在.
综上所述,当52
t =或4时,DEF △为直角三角形.
3. (2011 黑龙江省哈尔滨市) 如图,在平面直角坐标系中,点O 是坐标原点,四边形ABCD 为
菱形,AB 边在x 轴上,点D 在y 轴上,点A 的坐标是(60-,
),10AB =. (1)求点C 的坐标;
(2)连接BD ,点P 是线段CD 上一动点(点P 不与C 、D 两点重合),过点P 作PE BC ∥交BD 于点E ,过点B 作BQ PE ⊥交PE 的延长线于点Q .设PC 的长为x ,PQ 的长为y ,求y 与x 之间的函数关系式(直接写出自变量x 的取值范围);
(3)在(2)的条件下,连接AQ 、AE ,当x 为何值时,45
BQE AQE DEP S S S +=△△△?并判断此时以点P 为圆心,以5的半径的P ⊙与直线BC 的位置关系,请说明理由.
答案:解:(1)如图1,过点C 作CN x ⊥轴,垂足为N ,则四边形DONC 为矩形, ON CD ∴=.
四边形ABCD 是菱形,10AB =,
10.10.
AB BC CD AD ON ∴====∴= (6A -,0),
68OA OD ∴===,.
(108)C ∴,.
(2)如图1,过点P 作PH BC ⊥,垂足为H ,则90PHC AOD ∠=∠=.
四边形ABCD 是菱形,PCB DAO ∴∠=∠.
∴PHC DOA △∽△,
CH PH PC AO DO DA
∴==. 6810
CH PH x ∴==. 4355
PH x CH x ∴==,. 3105
BH x ∴=-. PE BC BQ PQ ⊥∥,,
90PQB QBC PHB ∴∠=∠=∠=.
∴四边形PQBH 为矩形,
3105
PQ BH x ∴==-. 310(010)5
y x x ∴=-<<.
(3)如图2,过点P 作PH BC '⊥,垂足为H ',则四边形PQBH '是矩形,
45
BQ PH x '∴==. PE BC PED CBD ∴∠=∠∥,.
CD CB CBD CDB =∴∠=∠,.
CDB PED ∴∠=∠.
2105PE PD x QE PQ PE x ∴==-=-=
,. 过点D 作DG PQ ⊥于点G ,过点A 作AF PQ ⊥交PQ 的延长线于点F ,
90DGF AFG ∴∠=∠=.
PQ BC PQ AD ∴∥,∥.
90ADG ∴∠=.
∴四边形AFGD 为矩形,
AF DG PQ BC ∴=∴,∥.
DPG C ∴∠=∠.
90DGP PH C '∠=∠=,
DGP PH C '∴△∽△.
DP DG PC PH ∴='.44(10)855
AF DG x x ∴==-=-. 111241248(8)222552555
BQE AQE S S EQ BQ EQ AF x x x x x +=+=⨯+⨯-=△△····. 21142(10)(8)8402255DEP S PE DG x x x x ==--=-+△··,45
BQE AQE DEP S S S +=△△△. 2842(840)555
x x x ∴=-+. 整理,得2
251000x x -+=. 12520x x ∴==,.
201020x x <<∴=,不符合题意舍去,5x ∴=.
5x ∴=时,45
BQE AQE DEP S S S +=△△△. 4455
PH x '==<,P ∴⊙与直线BC 相交.
4. (2011 黑龙江省绥化市) 在正方形ABCD 的边AB 上任取一点E ,作EF AB ⊥交BD 于点F ,取FD 的中点G ,连结EG CG 、,如图(1),易证EG CG 且EG CG ⊥.
(1)将BEF △绕点B 逆时针旋转90°,如图(2),则线段EG 和CG 有怎样的数量关系和位置关系?请直接写出你的猜想.
(2)将BEF △绕点B 逆时针旋转180°,如图(3),则线段EG 和CG 又有怎样的数量关系和位置关系?请写出你的猜想,并加以证明.
答案:解:(1)EG CG EG CG =,⊥.
(2)EG CG BG CG =,⊥.
证明:延长FE 交DC 延长线于M ,连MG , 909090AEM EBC BCM ∠=∠=∠=°,°,°, ∴四边形BEMC 是矩形.
90BE CM EMC ∴=∠=,°,
又BE EF =,
EF CM ∴=.
90EMC FG DG ∠==°,,
12
MG FD FG ∴==. BC EM BC CD ==,,
EM CD ∴=.
EF CM =,
.FM DM ∴=
45F ∴∠=°.
又FG DG =,
1452
CMG EMC ∠=∠=°, F GMC ∴∠=∠.
GFE GMC ∴△≌△.
EG CG FGE MGC ∴=∠=∠,.
90FMC MF MD FG DG ∠===°,,, MG FD ∴⊥.
90FGE EGM ∴∠+∠=°.
90MGC EGM ∴∠+∠=°.
即90EGC ∠=°.
EG CG ∴⊥.。
