概率论期末复习
概率论期末复习题集

概率论期末复习题集一、基本概念与原理1. 定义随机试验、样本空间、事件,并举例说明。
2. 解释概率的古典定义、频率定义和主观定义。
3. 描述概率的公理化定义,并列出概率的三个基本公理。
4. 举例说明条件概率的概念,并解释全概率公式和贝叶斯公式。
5. 描述随机变量、离散型随机变量和连续型随机变量的区别。
6. 定义数学期望、方差、标准差,并解释它们的意义。
二、离散型随机变量1. 给出离散型随机变量的概率分布列和概率质量函数。
2. 计算离散型随机变量的数学期望和方差。
3. 解释二项分布、泊松分布和几何分布,并给出它们的期望和方差公式。
4. 利用二项分布解决实际问题,例如药物测试的成功率问题。
三、连续型随机变量1. 描述连续型随机变量的概率密度函数和分布函数。
2. 计算连续型随机变量的数学期望和方差。
3. 解释均匀分布、指数分布和正态分布,并给出它们的概率密度函数和期望、方差的公式。
4. 利用正态分布解决实际问题,例如测量误差的分布问题。
四、多变量随机变量1. 定义联合分布函数和边缘分布函数,并解释它们之间的关系。
2. 描述协方差、相关系数和独立性的概念。
3. 计算两个随机变量的协方差和相关系数。
4. 利用联合分布解决实际问题,例如两个独立试验的联合成功概率。
五、大数定律和中心极限定理1. 解释切比雪夫不等式、马尔可夫不等式和切比雪夫大数定律。
2. 描述中心极限定理的内容,并解释为什么它在统计学中非常重要。
3. 利用中心极限定理估计样本均值的分布。
六、随机过程1. 定义随机过程和遍历理论。
2. 描述泊松过程和维纳过程,并解释它们在实际中的应用。
3. 解释随机过程的平稳性和遍历性。
七、应用题1. 一个袋子里有10个红球和20个蓝球,随机抽取5个球,计算以下事件的概率:至少有3个红球。
2. 某工厂生产的零件,每个零件合格的概率为0.95。
求生产100个零件中,至少有90个合格的概率。
3. 一个随机变量X服从正态分布N(μ, σ²),求X的数学期望和方差。
概率论期末考试复习题与答案

第一章1.设P(A)= 13,P(A∪B)=12,且 A 与B 互不相容,则P(B)=____16_______.2. 设P(A)= 13,P(A∪B)=12,且 A 与B 相互独立,则P(B)=______14_____.3.设事件 A 与B 互不相容,P(A )=0.2,P(B)=0.3,则P(A B)=___0.5_____.4.已知P(A)=1/2,P(B)=1/3,且A,B 相互独立,则P(A B )=________1/3________.A 与B 相互独立5.设P(A )=0.5,P(A B )=0.4,则P(B|A )=___0.2________.6.设A ,B 为随机事件,且P(A)=0.8 ,P(B)=0.4,P(B|A)=0.25 ,则P(A|B)=____ 0.5 ______.7.一口袋装有 3 只红球,2 只黑球,今从中任意取出 2 只球,则这两只恰为一红一黑的概率是________ 0.6 ________.8.设袋中装有 6 只红球、4 只白球,每次从袋中取一球观其颜色后放回,并再放入 1 只同颜色的球,若连取两次,则第一次取得红球且第二次取得白球的概率等于____12/55____.9.一袋中有 7 个3 个白球,从袋中有放回地取两次球,每次取一个,则第一次取得 红球且第二次取得白球的概率p=___ 0.21_____. 10.设工厂甲、乙、丙三个车间生产产品, 产量依次占全厂产量的 45%,35%,20%, 且各车间的次品为 4%,2%,5%.求:(1)从该厂生产的产取 1 件,它是次 品的概率; 3.5% (2)该件次品是由甲车间生产的概率 . 18 35 第二章 2),则 P{X ≤ 0}=___0.1587____. (附: Φ( 1)=0.8413) 1.设量 X~ N ( 2,2设量 X~N (2,2 2),则 P{X ≤ 0}= ( P{(X-2)/2 ≤ -1}=Φ(-1)=1-Φ(1)=0.1587 2.设连续 F (x) x>0 时, X 的概率密度 f(x)=___2xa e , x 0;则常数a =____1____. 3.X 的分布函数为 F (x )= 0, x 0, 4.设量 X ~N (1,4),已知标则常数 a<___3_________. 5.抛一枚6.X 表示 4次独立重复射击命中目标的次数, 每次命中目标的概率为 0.5,则 X~ _B(4, 0.5)____7.设量 X 服从区间 [0,5]上的均匀分布,则 P X 3 = ____0.6_______.X-1 0 1 2 2,记随机 8.设随X 的分,且 Y=X 1 3 1 7 P881616Y 的分布F Y (y F Y (3)=_____9/16____________. 9.设随X 的分布律为 P{ X=k}= a/N , k=1,2,⋯ , N ,试确定常数 a. 1 10.已知随X 的密度函数为 f(x)=Ae |x|, ∞<x<+∞,求:(1)A 值;(2)P{0< X<1}; (3) F( x ).1 2 1 2 (1-e ) F (x) 1 1 e 2 1xe2x x x 0 011.设随X 分布函数为F (x )=xtA Be , x 0,0,x 0.(0),( 1) 求常数 A ,B ;( 2) 求 P{ X ≤ 2} ,P{ X >3} ; ( 3) 求分布密度 f (x ).A=1B=-1P{ X ≤ 2}=21 eP{X >3}=e3f ( x)xe x 0 0x 012.设随X 的概率密度为x,0 x 1, f (x )=2 x, 1 x 2, 0,. 其他求 X 的分布函数 F (x ).F (x) 1 20 1 22 x 2 x 21x 1 0 1 x x x x 0212 13.设X 2 113P k1/51/61/51/1511/30求(1)X 的分布函数, (2)Y=X2的分布律 .0 x 2 1/52 x 1F (x)11/ 17 / 30 30 1 0x x0 1Y 1 49P k1/57/301/511/3019 / 30 1 x 31x 314.设随机变量 X~U (0,1),试求: (1) Y=eX的分布函数及密度函数;(2) Z= 2lnX 的分布函数及密度函数 .f Y (y) 1 y 0 1 y others e f (z) Z 1 2 e 0z 2 z0 others第三章(x y)e, x 0, y 0; 1.设二维随机变量( X ,Y )的概率密度为f (x, y)0,,其他(1)求边缘概率密度 f X (x) 和 f Y (y),(2)问 X 与 Y 是否相互独立,并说明理由 .f xyex 0 e y 0(x)f (y)X0 Yx 0y因为 f (x, y)f (x) f (y)X,所以 X 与 Y 相互独立Y2.设二维随机变量 22 (X ,Y) ~ N ( ,,,, ) ,且 X 与Y 相互独立,则 =____0______.12123.设 X~N (-1,4),Y~N (1,9)且 X 与 Y 相互独立,则 2X-Y~___ N (-3,25)____.4.设随机变量 X 和 Y 相互独立,它们的分布律分别为X -1 0 1 Y -1 0,,P 13312512P1434则P X Y 1 _____ 516_______.5.设随机变量(X,Y) 服从区域 D 上的均匀分布,其中区域 D 是直线y=x ,x=1 和x 轴所围成的三角形区域,则(X,Y) 的概率密度10 y x 1f x y( ,) 2 .0 others6.设随机变量X 与Y 相互独立,且X,Y 的分布律分别为X 0 1 Y 1 21 P 4 342P 535试求:(1)二维随机变量(X,Y)的分布律;(2)随机变量Z= X Y 的分布律.X0 1Y1 0.1 0.32 0.15 0.45Z 0 1 2P 0.25 0.3 0.457.设二维随机向量(X ,Y )的联合分布列为X0 1 2Y1 0.1 0.2 0.12 a 0.1 0.2求:(1)a 的值;(2)(X,Y)分别关于X 和Y 的边缘分布列;(3)X 与Y 是否独立?为什么?(4)X+Y 的分布列.a=0.3X 0 1 2 Y 1 2P 0.4 0.3 0.3 P 0.4 0.6因为P{ X 0,Y 1}P{ X 0} P{Y 1} ,所以X 与Y 不相互独立。
概率论与数理统计期末复习课件

置信水平
用于确定样本统计量的不 确定性范围。
置信区间
根据置信水平和抽样分布, 估计未知参数的可能值范 围。
点估计与最优性
点估计
用单一的数值估计未知参数的值。
无偏估计
样本统计量的期望值等于真实参数 值。
最小方差估计
选择一个点估计,使得预测误差的 方差最小。
假设检验与p值
假设检验
根据样本数据对未知参数 提出假设,并进行检验。
详细描述
一元线性回归是一种最简单的回归分析方 法,用于研究一个因变量和一个自变量之 间的线性关系。
一元线性回归模型通常表示为`Y = β0 + β1*X + ε`,其中Y是因变量,X是自变量, ε是误差项。β0和β1是需要估计的参数。
重要概念
适用范围
一元线性回归模型假设因变量Y和自变量X 之间存在线性关系,即Y的变化可以由X的 变化来解释。
02
置信区间
根据自助法计算的统计量的置信区间,可以用来估计总体参数的区间范
围。
03
应用
在社会科学和医学研究中,自助法和置信区间被广泛应用于估计样本参
数的可靠性和精度。例如,在估计人口平均年龄的置信区间时,自助法
可以用来确定样本大小和置信水平之间的关系。
CHAPTER 06
实验设计初步
完全随机设计
描述 马尔科夫链通常用状态转移图来表示,其中每个状态通过 箭头连接到其他状态,箭头上标记了从一个状态转移到另 一个状态的概率。
实例 例如天气预报、股票价格等都可以被视为马尔科夫链。
平稳过程与遍历性
定义
平稳过程是一类特殊的随机过程,它具有“时间齐次性”和“空 间齐次性”的性质。
描述
概率论与数理统计期末考试复习资料
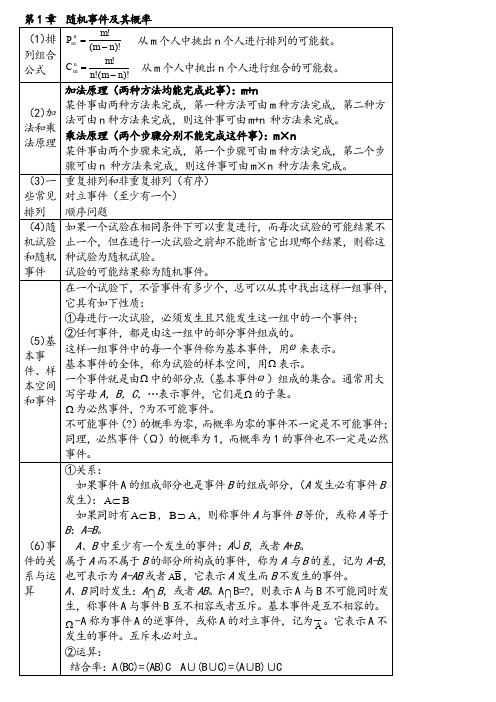
(1)排 列组合 公式
Pmn
m! (m n)!
C
n m
m! n!(m n)!
从 m 个人中挑出 n 个人进行排列的可能数。 从 m 个人中挑出 n 个人进行组合的可能数。
加法原理(两种方法均能完成此事):m+n
(2)加 法和乘 法原理
某件事由两种方法来完成,第一种方法可由 m 种方法完成,第二种方 法可由 n 种方法来完成,则这件事可由 m+n 种方法来完成。 乘法原理(两个步骤分别不能完成这件事):m×n 某件事由两个步骤来完成,第一个步骤可由 m 种方法完成,第二个步
率。分布函数F(x) 表示随机变量落入区间(– ∞,x]内的概率。
分布函数具有如下性质:
1° 0 F(x) 1, x ;
2° F(x) 是单调不减的函数,即x1 x2 时,有 F(x1) F(x2) ;
3° F() lim F(x) 0, F() lim F(x) 1;
设F(x) 是随机变量 X 的分布函数,若存在非负函数 f (x) ,对任意 实数x ,有
F (x) x f (x)dx ,
则称 X 为连续型随机变量。f (x) 称为 X 的概率密度函数或密度函 数,简称概率密度。 密度函数具有下面 4 个性质: 1° f (x) 0 。
2° f (x)dx 1。
X
| x1, x2,, xk, 。
P( X xk) p1, p2,, pk,
显然分布律应满足下列条件:
(1) pk 0 ,k 1,2,, (2) pk 1。 k 1
(2)连 续型随 机变量 的分布 密度
概率论期末复习题库答案

概率论期末复习题库答案一、选择题1. 某随机事件的概率为0.6,那么它的对立事件的概率为:A. 0.4B. 0.5C. 0.6D. 无法确定答案:A2. 假设事件A和事件B是互斥的,且P(A) = 0.3,P(B) = 0.2,那么P(A∪B)等于:A. 0.5B. 0.4C. 0.3D. 0.2答案:B3. 如果一个骰子连续投掷两次,求至少出现一次6的概率:A. 1/6B. 5/6C. 2/3D. 1/3答案:B二、填空题1. 随机变量X服从标准正态分布,那么P(X ≤ 0) = _______。
答案:0.52. 如果随机变量X的期望值为2,方差为4,那么P(X = 4) =_______。
答案:无法直接给出,需要更多信息3. 事件A发生的概率为0.3,事件B发生的概率为0.4,且P(A∩B) = 0.1,那么事件A和B是________。
答案:既不互斥也不独立三、简答题1. 什么是条件概率?请给出条件概率的公式。
答案:条件概率是指在已知一个事件已经发生的条件下,另一个事件发生的概率。
条件概率的公式为:\[ P(A|B) = \frac{P(A \cap B)}{P(B)} \]其中,\( P(A|B) \) 是在事件B发生的条件下事件A发生的条件概率,\( P(A \cap B) \) 是事件A和事件B同时发生的概率,\( P(B) \) 是事件B发生的概率。
2. 什么是大数定律?请简要说明其含义。
答案:大数定律是概率论中的一个基本概念,它描述了随机事件在大量重复试验中表现出的稳定性。
具体来说,大数定律指出,随着试验次数的增加,随机事件的相对频率会越来越接近其真实概率。
四、计算题1. 假设有一个装有红球和蓝球的袋子,其中红球有5个,蓝球有3个。
如果从袋子中随机抽取一个球,求抽到红球的概率。
答案:抽到红球的概率 \( P(\text{红球}) \) 可以通过以下公式计算:\[ P(\text{红球}) = \frac{\text{红球的数量}}{\text{总球数}} = \frac{5}{5+3} = \frac{5}{8} \]2. 假设随机变量X服从参数为λ的泊松分布,求X=2的概率。
概率论期末复习

F 0 .05 ( 7 , 8 ) 3 . 5 t 0 .05 ( 17 ) 1 . 74 t 0 .025 ( 15 ) 2 . 13
F 0 .05 ( 8 , 9 ) 3 . 23 t 0 .025 ( 17 ) 2 . 11 t 0 .05 ( 15 ) 1 . 75
F 0 .025 ( 8 , 9 ) 4 . 10
7.总体的未知参数 的点估计 ˆ 1 比 ˆ 2 有效指的是_____。
8.设 ( X , X , , X ) 为总体 X 的一个样本,则总体 X 的方差的矩估计量为_____。
1 2 n
二、(12分)甲、乙、丙三人独立的向飞机各射击一次, 命中率分别为0.5,0.6,0.7, (1) 求飞机被击中的概率; (2) 已知飞机被击中一次,求甲击中飞机的概率。
关于X的边缘概率密度
fX (x)
5.设随机变量X~N(5,4),则P{X<13/2}+P{X<7/2}=___.
6.随机变量X与Y的相关系数越接近于1,则 X,Y的 线性相关程度越 . 7.在区间(0,1)中随机的取两个数, 则事件“两数之和小于4/3”的概率为_____.
8.设总体X在区间[1,b]上服从均匀分布,b>1未知, 则对于来自总体的样本值(2.3, 1.6, 2.7, 2.2, 1.3, 1.1), b的矩估计值为____.
(B )P{ X x} f ( x )
(C ) P { X x } F ( x ) ( D ) P { X x } F ( x )
4. 设正态总体期望的置信区间长度 则其置信度为
( A)
2
L
2S n
t ( n 1)
概率论期末总复习必考题型
复习重点题目第一章p13例2、p14例5、习题一20、25第二章p34 例7、8;习题二15、24。
第三章p58 例2、例5、p61 例5、p63 例1、习题三5。
第四章习题四13、14、15、16。
第七章P139 例4、P148 例2、习题七P157 1、P159 13。
第八章例4、例5、习题八3、6。
例 1.5.2 设袋中装有r 只红球,t 只白球,每次自袋中任取一只球,观察其颜色然后放回,并再放入 a 只与所取出的那只球同色的球,若在袋中连续取球 4 次,试求第一、二次取到红球且第三、四次取到白球的概率。
解以A i(i 1,2,3,4)表示事件“第i次取到红球”,则A3, A4 分别表示事件“第三、四次取到白球” 。
所求概率为:P( A1 A2 A3 A4 ) P(A4 | A1 A2 A3)P( A3 | A1A2 )P( A2 |A1)P(A1)t a t r a rr t 3a r t 2a r t a r t例 1.5.4 八支枪中,有三支未经试射校正,五支已经试射校正。
校正过的枪射击时,中靶的概率为0.8,未校正的枪射击时,中靶的概率为0.3,今从8 支枪中任取一支射击中靶。
问所用这枪是校正过的概率是多少?解设事件8 8 10 45A ={射击中靶}B 1={ 任取一枪是校正过的 }, B 2 ={任取一枪是未校正过的 }, B 1, B 2构成完备事件组 ,则 P(B 1) 5/8,P(B 2) 3/8,P(A |B 1) 0.8,P(A|B 2) 0.3, 故所求概率为P(B 1 | A) P(B 1)P(A|B 1)/[P(B 1)P(A|B 1) P(B 2)P(A|B 2)] 40/49 0.816习题一、20.已知在 10 只晶体管中有 2 只次品,在其中取两次,每次任取一 只,作不放回抽样。
求下列事件的概率: (1)两只都是正品; (2)两只都是次品;(3)一只是正品,一只是次品; (4)第二次取出的是次品。
大学概率论期末复习题七套
试题(一)一、填空题1.设 A 、B 、C 是三个随机事件。
试用 A 、B 、C 分别表示事件 1)A 、B 、C 至少有一个发生 2)A 、B 、C 中恰有一个发生3)A 、B 、C 不多于一个发生2.设 A 、B 为随机事件, P (A)=0.5,P(B)=0.6,P(B A)=0.8。
则P(B )A =3.若事件A 和事件B 相互独立, P()=,A αP(B)=0.3,P(AB)=0.7,则α=4. 将C,C,E,E,I,N,S 等7个字母随机的排成一行,那末恰好排成英文单词SCIENCE 的概率为5. 甲、乙两人独立的对同一目标射击一次,其命中率分别为0.6和0.5,现已知目标被命中,则它是甲射中的概率为二、选择题1. 设A,B 为两随机事件,且B A ⊂,则下列式子正确的是 (A )P (A+B) = P (A); (B )()P(A);P AB =(C )(|A)P(B);P B = (D )(A)P B -=()P(A)P B -2. 以A 表示事件“甲种产品畅销,乙种产品滞销”,则其对立事件A 为 (A )“甲种产品滞销,乙种产品畅销”; (B )“甲、乙两种产品均畅销” (C )“甲种产品滞销”; (D )“甲种产品滞销或乙种产品畅销”。
3. 袋中有50个乒乓球,其中20个黄的,30个白的,现在两个人不放回地依次从袋中随机各取一球。
则第二人取到黄球的概率是(A )1/5 (B )2/5 (C )3/5 (D )4/5 4. 对于事件A ,B ,下列命题正确的是 (A )若A ,B 互不相容,则A 与B 也互不相容。
(B )若A ,B 相容,那么A 与B 也相容。
(C )若A ,B 互不相容,且概率都大于零,则A ,B 也相互独立。
(D )若A ,B 相互独立,那么A 与B 也相互独立。
5. 若()1P B A =,那么下列命题中正确的是(A )A B ⊂ (B )B A ⊂ (C )A B -=∅ (D )()0P A B -=三、计算题1. 10把钥匙中有3把能打开门,今任意取两把,求能打开门的概率。
概率论与数理统计期末复习重要知识点及公式整理
概率论与数理统计期末复习重要知识点及公式整理2010-2011学年第一学期期末复习资料概率论与数理统计期末复习重要知识点第二章知识点:1.离散型随机变量:设X是一个随机变量,如果它全部可能的取值只有有限个或可数无穷个,则称X为一个离散随机变量。
2.常用离散型分布:(1)两点分布(0-1分布):若一个随机变量XP{X x1}p,P{X x2}1p只有两个可能取值,且其分布为(0p1),则称X服从x1,x2处参数为p的两点分布。
两点分布的概率分布:两点分布的期望:(2)二项分布:P{X x1}p,P{X x2}1p(0p1) E(X)p;两点分布的方差:D(X)p(1p)若一个随机变量X的概率分布由式给出,则称X服从参数为n,p的二项分布。
记为X~b(n,p)(或B(n,p)).两点分布的概率分布:二项分布的期望:(3)泊松分布:P{x k}Cnp(1p)kkn kkkn k,k0,1,...,n. P{x k}Cnp(1p),k0,1,...,n. E(X)np;二项分布的方差:D(X)np(1p)kP{X k} e若一个随机变量X的概率分布为数为的泊松分布,记为X~P () k!,0,k0,1,2,...,则称X服从参P{X k} e泊松分布的概率分布:泊松分布的期望:4.连续型随机变量:kk!,0,k0,1,2,... E(X);泊松分布的方差:D(X)如果对随机变量X的分布函数F(x),存在非负可积函数F(x)P{X x}f(x),使得对于任意实数x,有xf(t)dt,则称X为连续型随机变量,称f(x)为X的概率密度函数,简称为概率密度函数。
2010-2011学年第一学期期末复习资料5.常用的连续型分布:(1)均匀分布:1,若连续型随机变量X的概率密度为f(x)b a 0,a x b其它,则称X在区间(a,b)上服从均匀分布,记为X~U(a,b)1,均匀分布的概率密度:f(x)b a0,a b2a xb 其它均匀分布的期望:(2)指数分布:E(X);均匀分布的方差:D(X)(b a)122e xf(x)0若连续型随机变量X的概率密度为x00,则称X服从参数为的指数分布,记为X~e ()x0e xf(x)0指数分布的概率密度:指数分布的期望:(3)正态分布:E(X)1;指数分布的方差:D(X)2f(x)(x)222x若连续型随机变量X的概率密度为则称X服从参数为和22的正态分布,记为X~N(,)(x)222f(x)正态分布的概率密度:正态分布的期望:E(X)xD(X)x22;正态分布的方差:(4)标准正态分布:0,21(x),2(x)xet22标准正态分布表的使用:(1)x0(x)1(x)2010-2011学年第一学期期末复习资料X~N(0,1)P{a x b}P{a x b}P{a x b}P{a x b}(b)(a)X~N(,),Y2(2)X(3)P{a X b}P{a~N(0,1),F(x)P{X x}P{X故b}(b)(a)x(x) Y2Y定理1:设X~N(,),则X~N(0,1)6.随机变量的分布函数:设X是一个随机变量,称分布函数的重要性质:0F(x) 1P{x1X x2}P{X x2}P{X x1}F(x2)F(x1)x1x2F(x1)F(x2)F()1,F()0F(x)P{X x}为X的分布函数。
概率论复习知识点总结
第2章要点
一、随机变量及其分布 1.随机变量的概念 2.分布函数:
➢定义:F(x)=P{X≤x} x∈R ➢性质:单调性,有界性,右连续性 ➢利用分布函数求概率:即对任意实数a, b, 有
➢例2.2,2.4,2.5 ,三1,2,4
第2章要点
二、离散型随机变量 1.离散型随机变量的分布律
➢分布律的概念;
若Xi同分布,则
作业: 三、19
第4章要点
一、随机变量的数学期望 ➢离散型随机变量的数学期望 ➢连续型随机变量的数学期望 ➢随机变量函数的数学期望
第4章要点
一、随机变量的数学期望 ➢数学期望的性质 (1) 设c是常数,则有E(c) = c. (2) E(cX) = cE(X),E(X + c) = E(X) + c. (3) E(X + Y) = E(X) + E(Y). (4) 设X,Y是相互独立的随机变量,则有
➢例2.9 ,2.11 作业:三、10,11
第2章要点
三、连续型随机变量 2.常用连续型随机变量
➢均匀分布 X~U(a, b),
➢指数分布:X~Exp(), >0,
➢正态
第2章要点
四、随机变量函数的分布 1.离散型随机变量函数的分布 2.连续型随机变量函数的分布
第1章要点
三、概率的性质 (1) P() = 0. (2) (有限可加性)
两两互不相容,则
(3) (逆事件的概率) 对任一事件A,有
(4) (单调性)若
P(A) P(B) ,且P(A–B) = P(A) - P(B).
(5) 对任意两个事件A,B有P(A–B) = P(A)–P(AB).
(6)(加法公式)对于任意两事件A,B有
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
18
• 掌握估计量的三个评价标准,能够对估计 量的无偏性和有效性进行证明和判断。 • 要求熟练掌握正态总体均值与方差的区间 估计,(能够知道在不同的情况下应该构 造什么样的统计量,然后在该情况下的置 信区间是怎么样的,懂得熟练运用)
14
第七章参数估计
• 156页第2节“基于截尾样本的最大似然估 计”不作要求; • 165页“两个总体的情况” (总体均值差) 不作要求, (总体方差比)要了解;
• 熟练掌握方差的定义,简化后的公式(计 算中经常使用),方差的性质。 • 数学期望和方差的性质最好能对比记忆, 并注意部分性质在一定的前提下成立。
10
第四章随机变量的数字特征
• 给出分布律或者概率密度函数,要求掌握其数学期 望以及方差的计算,特别是常用的分布(哪些属于 常用,请见上述第二章中的叙述的6种分布)。 • 随机变量X的分布已知,g(X)的期望如何计算要掌握 (P95页定理)
• 多个独立的正态随机变量的线性组合仍然 服从正态分布,且参数之间的对应关系 (熟练掌握和应用,书上77页中间黑体处 给出的结论) • 除了上述结论,书上76页开始的两个随机 变量函数的分布不作要求
9
第四章随机变量的数字特征
• 熟练掌握数学期望的定义,计算公式(包 括连续型和离散型),数学期望的性质。
• 记忆以及应用协方差以及相关系数的计算公式
• 清楚相关性的衡量,独立性衡量的不同方式,不要 混淆在一起。
• 知道k阶原点矩和中心矩的定义,协方差矩阵不作 要求
11
第五章大数定理及 中心极限定理(约5分)
• 了解大数定理和中心极限定理的作用;
• 掌握中心极限定理的应用
12
第六章样本及抽样分布(约5分)
– 0-1分布
– 二项分布(伯努利试验),熟练使用伯努利定 理 – 泊松分布(了解即可)
5
第二章 随机变量及其分布
• 连续型:
– 均匀分布(要求熟练,给出参数后能自行写出 其概率密度函数)
– 正态分布(非常重要,要求熟练掌握其应用, 首先是记忆其概率密度函数书上46页(4.10) 式,48页的引理的应用) – 指数分布(了解即可)
• 168页“(0-1)分布参数的区间估计”不 作要求
15
第八章假设检验(约5分)
• 假设检验的简单概念和基本思想,两类错 误的含义以及处理方式,第一节的概念理 解,可参看217页小结
16
• 此外,关于正态分布的一些定理和关系要 注意弄清楚。
17
分数大致分布
• 第五章约 5分,第六章 约5分,第八章约5分 • 除此外其它章节都差不多,均在上述描述范 围内 • 只考到第8章第1节6来自第二章 随机变量及其分布
• 分布函数的定义:F(x)=P{X<=x},理解分布函数的 几个性质
– F(x)是一个不减函数 – 0F(x)1 – F(x)右连续
• 知道离散型和连续型的情况下,如何求一个随机 变量的分布函数,确定概率密度函数的参数等。 • 随机变量的函数的分布
7
第三章多维随机变量 及其分布
• 二维随机变量,
– 离散型,当给出联合分布律,能求边缘分布律 – 连续型,当给出联合概率密度函数,能求解边 缘概率密度函数
• 当给出一个二维随机变量的联合分布律或 联合概率密度时,能判断证明两个随机变 量之间是否独立
8
第三章多维随机变量 及其分布
• 两个随机变量相互关系的数字特征有哪些, 如何计算(结合第四章)
概率论与数理统计
复习
1
题型及分值分布
• • • • 单选题(每题2分,10小题,共20分) 填空题(每空3分,10小空,共30分) 解答题(3小题,共40分) 应用题(1小题,共10分)
2
第一章 概率论的基本概念
• 事件的关系与运算;如:和事件、积事件、互 斥事件、对立事件的含义,以及基本的事件运 算规则 • 概率的定义,三个条件:非负性、规范性,可 列可加性 • 概率的重要性质:特别是加法公式及其推广的 形式(要记忆) • 古典概型的简单应用;伯努力试验概型 • 条件概率的概念以及计算
3
第一章 概率论的基本概念
• 乘法公式
• 全概率公式的应用,贝叶斯公式的应用 (看到生活当中的例子要能够对得上号, 知道该怎么求)如课后练习:1-18,1- 20,1-21,1-23型 • 独立性的含义以及简单判断 • (本章较多零散的性质和公式,要注意)
4
第二章 随机变量及其分布
• 几种重要的随机变量及其分布(要清楚他 们的概率密度和符号表示): • 离散型:
• 书上142页-143页上的定理一到定理三以 及定理四的第一小点要求掌握(注意参数) • 熟练掌握样本均值和样本方差、样本矩的 计算方法(尤其注意样本方差的系数,要 注意区分总体均值,总体方差,总体矩的 计算) • 130页第二节“直方图和箱线图”不作要求
13
第七章参数估计
• 矩估计和最大似然估计方法的掌握和熟练 运用;
