Mises屈服条件在固支圆板塑性极限分析中的应用
用加权余量法分析固支圆板和环板在Mises屈服条件下的极限荷载

用加权余量法分析固支圆板和环板在Mises屈服条件下的极
限荷载
刘福林
【期刊名称】《计算力学学报》
【年(卷),期】2002(019)003
【摘要】应用加权余量法求出了承受线性荷载的固支圆板和承受均布荷载的内边界支承环板在Mises屈服条件下的极限荷载的近似值,并与最大弯矩极限条件结果进行了比较,说明本文计算结果较合理.
【总页数】4页(P369-372)
【作者】刘福林
【作者单位】辽宁大学,数学系力学教研室,沈阳,110036
【正文语种】中文
【中图分类】O344.1
【相关文献】
1.用Mises屈服条件求固支环板的极限荷载 [J], 李茂林;雷金波
2.求固支圆板在线性荷载作用下的极限荷载用加权余量法和Mises屈服条件 [J], 洪媛;陈钢
3.Mises屈服条件在固支圆板塑性极限分析中的应用 [J], 刘磊
4.用加权余量法求圆板在Mises屈服条件下的极限荷载 [J], 赵颖;王福忠;等
5.用Mises屈服条件求内边界固支环板的极限荷载 [J], 刘福林
因版权原因,仅展示原文概要,查看原文内容请购买。
厚壁圆筒的弹塑性分析

厚壁圆筒的弹塑性分析姓名:王海萍学号:2011200147指导老师:丹丹时间:2012-2-12一、 问题描述内半径为a ,外半径为b 的厚壁圆筒,在外表面处作用有均匀压力p (如图1(a )),圆筒材料为理想弹塑性的(如图1(b ))。
随着压力p 的增加,圆筒内的θσ及r σ都不断增加,若圆筒处于平面应变状态下,其z σ也在增加。
当应力分量的组合达到某一临界值时,该处材料进入塑性变形状态,并逐渐形成塑性区,随着压力的继续增加,塑性区不断扩大,弹性区相应减小,直至圆筒的截面全部进入塑性状态时即为圆筒的塑性极限状态。
当圆筒达到塑性极限状态时,其外压达到最大值,即载荷不能继续增加,而圆筒的变形也处于无约束变形状态下,即变形是个不定值,或者说瞬时变形速度无穷大。
为了使讨论的问题得以简化,本文中限定讨论轴对称平面应变问题,并设2/1=ν。
(a ) (b )图1 厚壁圆筒二、 弹性分析1.基本方程平面轴对称问题中的未知量为r σ,θσ,r ε,θε,u ,它们应该满足基本方程及相应的边界条件,其中平衡方程为0=-+rdr d r r θσσσ (1) 几何方程为dr du r =ε,ru=θε (2) 本构方程为()()⎪⎪⎭⎪⎪⎬⎫-=-=r r r E Eνσσενσσεθθθ11(3)边界条件为r r F s =σσ ,在力的边界σS 上 (4)2.应力的求解取应力分量r σ,θσ为基本未知函数,利用平衡方程和以应力分量表示的协调方程联立求解,可以求得应力分量的表达式为⎪⎪⎭⎪⎪⎬⎫-=+=221221r C C r C C r θσσ (5)如图1(a )所示内半径为a ,外半径为b 的厚壁圆筒,在外表面处受外压p ,内表面没有压力,相应的边界条件为0==ar rσ ,p br r-==σ将以上边界条件代入式(5),则可以求得两个常数为2221a b p b C --=,22222ab pb a C -= 则应力分量为⎪⎪⎭⎪⎪⎬⎫⎪⎪⎭⎫ ⎝⎛+--=⎪⎪⎭⎫ ⎝⎛---=222222222211r a a b p b r a a b pb r θσσ (6) 上式和弹性常数无关,因而适用于两类平面问题。
塑性力学第三章-屈服条件
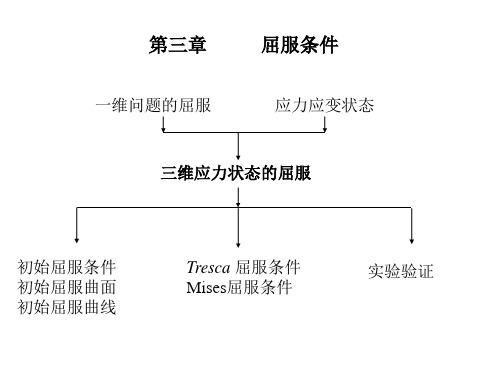
一维问题的屈服
屈服条件
应力应变状态
三维应力状态的屈服
初始屈服条件 初始屈服曲面 初始屈服曲线
Tresca 屈服条件 Mises屈服条件
实验验证
初始屈服条件
初始弹性状态的界限为初始屈服条件
ɺ φ (σ ij , ε ij , ε ij , t , T ) = 0
影响因数: 应力 影响因数: 1应力、2应变、3应变率、4时间、5温度 应力、 应变 应变、 应变率 应变率、 时间 时间、 温度
_____ p
_____ p
2 p p dε ij dε ij 3
K = ϕ ( ∫ dW p ) , dW p = σ ij dε ijp
采用Mises屈服条件,线性强化 屈服条件, 采用 屈服条件
f = σ −σ s = 0
φ =σ −K = 0
简单拉伸时, 简单拉伸时,
σ = σ s + E pε p
σ z + 4τ zθ = σ s
2 2
(σ 1 − σ 2 )2 + (σ 2 − σ 3 )2 2 + (σ 3 − σ 1 ) = 2σ s2
σ z 2 + 3τ zθ 2 = σ s2
σz σ s τ + 3 zθ = 1 σ s
2 2
σ z 2 + 4τ zθ 2 = σ s2
P = 0,
µσ = −1
µσ = 0
(θ = −300 )
(θ = 00 )
P = πR 2 q ,
P = 2πR 2 q ,
µσ = 1
(θ = 300 )
σ1 − σ 3 Tresca : =1 σs
Mises准则的圆形屈服轨迹及其在板料成形中的应用

* 华中理工大学塑性成形模拟及模具技术国家重点实验室资助项目 * * 男, 30 岁 , 讲师 收稿日期 : 1998-11-07
四、结论
通过以上分析可得到以下结论: ( 1) 本文给出的排样优化算法适用于单一冲裁件 在整体板料上的二维排样。 ( 2) 本优化数学模型是基于两参数的冲裁件二维 排样, 比文献 [ 1] 基于单参数的冲裁件二维排样求 得到的解更趋近于全局最优。 基于单参数的冲裁件二 维排样是基于两参数的冲裁件二维排样的一特例。 ( 3) 考虑到冲压工艺特点 , 冲裁排样件在板料上 平行。这样在冲裁时, 只须将冲裁模按其最优角度 ∀ j
Luo Wenbo Luo Zhonghua Peng Yanrong
Abstract T he so lv ing met hod of the ax isym metric sheet fo rming by use o f M ises yield crit erion, is close theoretically and the solut ion is ex act. In this paper, a diagr am of circular lo cus of M ises y ield criterion is intr oduced. M aking use of this diagr am , the solving pro cess is simplified and t he r esult is visual and clear . A s co mpa red w ith t he diagr am of elliptical lo cus o f M ises yield cr it erio n, the diagr am of circular yield locus is m or e available for use. Keywords A x isym metric sheet fo rming M ises y ield cr iter ion Cir cular yield lo cus Ellipt ical y ield locus
基于levy-mises本构关系及d-p屈服准则的轴对称圆巷理想弹塑性解

基于levy-mises本构关系及d-p屈服准则的轴对称圆巷理想弹塑性解
研究利用Levy-Mises本构关系及D-P屈服准则,推导出轴对称圆柱理想弹塑性解。
该解条件是假设变形对称性和保管料应力满足Lamé方程,并假设落入材料的应力-应变关系满足Levy-Mises本构关系,屈服准则采用D-P准则来表征。
按照求解思路,先是用有关轴对称变形和Levy-Mises本构关系求解得到偏心应力和半径内应力。
以D-P准则确定屈服压力之后,利用确定屈服压力及偏心应力关系,求解出应力系数,以确定等效屈服半径和弹性变形量。
综上,本文通过Levy-Mises本构关系及D-P屈服准则推导出了轴对称圆柱理想弹塑性解,这解能够用于研究轴对称圆柱结构的总体偏心应变及屈服半径分布,为结构设计提供有益的参考。
弹塑性力学课程作业 参考答案

弹塑性力学课程作业1 参考答案一.问答题1. 答:请参见教材第一章。
2. 答:弹塑性力学的研究对象比材料力学的研究对象更为广泛,是几何尺寸和形态都不受任何 限制的物体。
导致这一结果的主要原因是两者研究问题的基本方法的不同。
3. 答:弹塑性力学与材料力学、结构力学是否同属固体力学的范畴,它们各自求解的主要问题都是变形问题,求解主要问题的基本思路也是相同的。
这一基本思路的主线是:(1)静 力平衡的受力分析;(2)几何变形协调条件的分析;(3)受力与变形间的物理关系分析; 4. 答:“假设固体材料是连续介质”是固体力学的一条最基本假设,提出这一基本假设得意义是为利用数学中的单值连续函数描述力学量(应力、应变和位移)提供理论依据。
5. 答:请参见本章教材。
6. 答:略(参见本章教材)7. 答:因为物体内一点某微截面上的正应力分量 σ 和剪应力分量τ 同材料的强度分析 问题直接相关,该点微截面上的全应力则不然。
8. 答:参照坐标系围绕一点截取单元体表明一点的应力状态,对单元体的几何形状并不做 特定的限制。
根据单元体所受力系的平衡的原理研究一点的应力状态。
研究它的目的是: 首先是了解一点的应力状态任意斜截面上的应力,进一步了解该点的主应力、主方向、 最大(最小)剪应力及其作用截面的方位,最终目的是为了分析解决材料的强度问题。
9.答:略(请参见教材和本章重难点剖析。
) 10. 答:略(请参见教材和本章重难点剖析。
)11. 答:略(请参见教材和本章重难点剖析。
) 这样分解的力学意义是更有利于研究材料的塑性变形行为。
12. 答:略(请参见教材和本章重难点剖析。
)纳唯叶 (Navier) 平衡微分方程的力学意义是:只有满足该方程的应力解和体力才是客观上可能存在的。
13. 答:弹塑性力学关于应力分量和体力分量、面力分量的符号规则是不一样的。
它们的区别请参见教材。
14、答:弹塑性力学的应力解在物体内部应满足平衡微分方程和相容方程(关于相容方程详见第3、5、6章),在物体的边界上应满足应力边界条件。
2010-04-13基于Levy-Mises 本构关系及Hoek-Brown屈服准则的轴对称圆巷理想弹塑性解
z ( r ) / 2
令 1 , 3 r ,并代入式(4),可得
(13)
r m c r s c2
(5) 平衡方程为 d r r 0 dr r 将式(14)代入(15),可得
d r m c r s
1
引
言
沿用至今 [1
~ 6]
。然而,卡氏方程求解存在的不足和
缺陷是不能忽略的:(1) 对支护反力的力学处理存 20 世纪 50,60 年代,轴对称圆巷围岩的理想 弹 塑 性 分 析 解 答 —— 即 著 名 的 卡 斯 特 纳 方 程
收稿日期:2009–07–19;修回日期:2009–12–31 基金项目:中央高校基本科研业务费资助项目 作者简介:侯公羽(1965–),男,博士,1986 年毕业于西安矿业学院采矿系矿井建设专业,现任教授、博士生导师,主要从事岩土工程、岩石力学 方面的教学与研究工作。E-mail:hgyht@;hgyht@
式(2b) (2a)并整理,可得
(2b) (2c)
z ( r 2 p0 ) p0
将式(1)代入式(2c),可得
第 29 卷
第4期
侯公羽,等. 基于 Levy-Mises 本构关系及 Hoek-Brown 屈服准则的轴对称圆巷理想弹塑性解
• 767 •
z p0
(11a) (11b)
H-B 在塑性区,当原岩应力 p0>p0 时,巷道由周
边向里依次、逐渐地进入屈服状态,弹塑性界面半 径不断增大。因为假定原岩为不可压缩材料,故根 据 Levy-Mises 本构关系[11 14]有 2 z r d z 2 r z d r
M-C D-P p0 和 p0 ,即 M-C p0
关于Mises屈服准则和Tresca屈服准则的差异
9、 若变形体屈服时的应力状态为:{}ij σ=⎪⎪⎪⎭⎫⎝⎛---15332330×10MPa 试分别按Mises 和Tresca 塑性条件计算该材料的屈服应力s σ及β值,并分析差异大小。
解:由变形体屈服时的应力状态得:{}x σ=—300Mpa, {}y σ=230Mpa, {}z σ=150Mpa, {}yz σ=—30Mpa,{}zyσ=-30Mpa, {}xyσ={}xz σ{}yx σ={}zxσ=0.所以解得:I 1=x σ+y σ+z σ=80MpaI 2=—()222zxyz xy x z z y y x τττσσσσσσ+++++=8404Mpa I 3=()2222xzz zx y yz x zx yz xy z y x τστστστττσσσ++-+=100800Mpa 将上面的I 1、I 2、I 3代入应力状态的特征方程式032213=---I I I σσσ,并且另321σσσ〉〉,得:1σ=240Mpa , 2σ=140Mpa , 3σ=—300Mpa. 按Mises 塑性条件计算得:屈服应力s σ=21()()()213232221---σσσσσσ++=487.6Mpa,中间主应力系数β=s31-σσσ=1.085.按Tresca 塑性条件计算得:s σ=2K=m ax τ=max []322131,,σσσσσσ---=540Mpaβ=sσσσ31-=1关于Mises 屈服准则和Tresca 屈服准则的差异摘要:不同应力状态下,变形体某点进入塑性状态并使塑性变形继续进行,各应力分量与材料性能之间必须符合一定的关系,而不同的分析方法获得的结果也各有差异。
关键字: Mises 屈服准则、Tresca 屈服准则Tresca 屈服准则:当变形体或质点中的最大切应力达到某一定值时,材料就发生屈服。
或者说,材料处于塑性状态时,其最大切应力是一个不变的定值,该定值只取决于材料在变形条件下的性质,而与应力状态无关。
弹塑性力学之结构的塑性极限分析
塑性极限载荷
4"6
确定塑性区位置
截面的上下两塑性区相连,使 跨中左右两截面产生像结构
・特点:
-塑性较的存在是由于该截面 上的弯矩等于塑性极限弯矩; 故不能传递大于塑性极限弯 矩的弯矩。
<]
ax(x9z\ay=az= rxy=ryz= rzx=0
♦:・小挠度假设:在梁达到塑性极限状态瞬 间之前,挠度与横截面尺寸相比为一微 小量,可用变形前梁的尺寸进行计算。
二.弹性阶段
—
P1
6M
♦ Mises屈服条件:
xmax
bh2
弹性极限弯矩
二
2bh2
弹性极限载荷
三.弹塑性阶段(约束塑性变形阶段)
>Mp塑性区扩展
第十章结构的塑性极限分析
矗塑性极限分析定理和方法
❖梁的极限分析❖圆板的极限分析
❖梁模型法计算圆板和环板的塑性极限 載荷
§10-1梁的弹塑性弯曲
1.基本假定
•:•平截面假设:在变形过程中,变形 前为平面的横截面,变形后仍保持 为平面,且与变形后梁的轴线垂直。
z5=— P
・纵向纤维互不挤压:不计挤压应力, 横截面上只有正应力。
heh/2
陆=2町(yxzdz+ 2町aszdz
0he
陆
0叽he
“Me
Ms=—-
s2
h2
弹塑性区交界线:
h/2
(Jszdz
陆=
£
弹塑性区交界线:饥=±丄3
h~2\
<]
►P(lΒιβλιοθήκη 2x)2ALPl/4
四.全塑性阶段
X—6
x = 0
塑性极限弯矩
n
A
矿大(北京)高等岩石力学试题答案
1.简述岩石的强度特性和强度理论,并就岩石的强度理论进行简要评述。
答:岩石作为一种天然工程材料的时候,它具有不均匀性、各向异性、不连续等特点,并且受水力学作用显著。
在地表部分,岩石的破坏为脆性破坏,随着赋存深度的增加,其破坏向延性发展。
岩石强度理论是判断岩石试样或岩石工程在什么应力、应变条件下破坏。
当然岩石的破坏与诸多因素有关,如温度、应变率、湿度、应变梯度等。
但目前岩石强度理论大多只考虑应力的影响,其他因素影响研究并不深入,故未予考虑。
(1). 剪切强度准则a. Coulomb-Navier 准则Coulomb-Navier 准则认为岩石的破坏属于在正应力作用下的剪切破坏,它不仅与该剪切面上剪应力有关,而且与该面上的正应力有关。
岩石并不沿着最大剪切应力作用面产生破坏,而是沿其剪切应力和正应力最不利组合的某一面产生破裂。
即: ϕστtan +=C式中为岩石材料的内摩擦角,为正应力,C 为岩石粘聚力。
b. Mohr 破坏准则根据实验证明:在低围压下最大主应力和最小主应力关系接近于线性关系。
但随着围压的增大,与关系明显呈现非线性。
为了体现这一特点,莫尔准则在压剪和三轴破坏实验的基础上确定破坏准则方程,即: ()στf =此方程可以具体简化为斜直线、双曲线、抛物线、摆线以及双斜直线等各种曲线形式,具体视实验结果而定。
@虽然从形式上看,库仑准则和莫尔准则区别只是在于后者把直线推广到曲线,但莫尔准则把包络线扩大或延伸至拉应力区。
c. 双剪的强度准则Mohr 强度准则是典型的单剪强度准则,没有考虑第二主应力的作用。
我国学者俞茂宏从正交八面体的三个主应力出发,提出了双剪强度理论和适用于岩土介质的广义双剪强度理论,并得到了双剪统一强度理论:() 3211t b b σσσασ=+--αασσσ++≤1312 ()t b b σασσσ=-++31211 αασσσ++≥1312 式中和b 为两个材料常数,是岩石单轴抗拉强度。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
∞ 一一
。锰翥曹名:孰3裂絮弘h男·丹东人·硕士’从事弹塑性理论研究
万方数据
318
辽宁大学学报
自然科学版
2003年
式中k】、k2为待定系数试函数(4)式己满足边界 条件(3)式,也满足平衡方程(1)式中函数的幂次 关系.
将试函数(4)式分别代入平衡方程(1)式与屈 服条件(2)式,得相应余量:
RI=导(rMr)一%+蹇(3一_r3) =女。(3ar2-4 r3)一以护一r3)一3孚r+
presented reasonable.
Key words: Mises yield condition;method of weighted residuals;clamped supported circular plate;lin
ear】oad;unifoEm load;】imit load.
在该问题中,Mises屈服条件与边界条件仍 为(2)式与(3)式只是平衡方程与图1不同,平衡 方程为
图2圆板和荷载示意图
导(机)~%=一。(3ar2+2r3)(19)
因图2、图1两种情况中,边界条件相同,
万方数据
第4期
刘磊:Mises屈服条件在固支圆板塑性极限分析中的应用
319
(19)式右端也为r的3次函数,故仍可取(4)式和 (14)式为试函数.
(7)
j:R 2dr=o:4(女i+Ii~kl女2)n6—28klMta3+
35k2Mpa 3—210M;=0
(8)
由(7)式得
铲3 qo。_18等
(9)
代入(8)式,得
五}口6+k1(1lMpa3—3qoa5)+9q3n4一
—32r7』.”∥。口2+114M;=o
(10)
因在(10)式中有二个未知量k1与qo,所以
参考文献(3条) 1.王仁;熊祝华;黄文彬 塑性力学基础 1982 2.徐次达 固体力学加权残值法 1987 3.徐秉业;刘信声 结构塑性极限分析 1985
引证文献(1条) 1.蒋朝志 圆板和环板的统一塑性极限分析[学位论文]硕士 2006
本文链接:/Periodical_lndxxb200304007.aspx
当(3d,2一,3)
(5)
R2=M;一M朋。+M;一M:
=(女}+bi一Ⅲ2)(冉·一2∥+r6)+孚(2^。
一k2)(a2r2—3at3+2r4)
+Ma--1(2k2-k1)(a 2r2--2ar3+ra)+等∽一
3ar+3r2)一M:
(6)
应用加权余量法中的子域法消除余量‘3】:
』nRldr。o:^2n 3+18Mp一3qoa 22 0
还不能从(10)式中求出qo为此,文中还利用了
极值条件,即在(10)式对k1取极值,得
2kln6+llMfl”3qod5=0(11)
由此式求出k1,然后再将女1代回(10)式,得极限
荷载qo所满足的方程
27q5a4—261Mpqoa2+335M;=0
(12)
由此求出极限荷载为
93f≈8.142971335Mp/a2≈8.14Mp/a2(13), 1 2.2设试函数为
关键词:Mises屈服条件;加权余盘法;固支圆板;线性荷载;均布荷载;极限荷载.
中图分类号:0344
文献标识码:A
文章编号:1000—5846【2003)04—0317—03
用塑性极限分析问题在结构和机械设计中有 着广泛的应用对结构进行塑性极限分析,常用的 屈服条件有Tresca屈服条件和最大弯矩极限条 件,很少用Mises屈服条件.虽经前人多次实验证 明:对铁、铜、铝、镍及软钢等材料,Mises屈服条 件比Tresca屈服条件更接近于实验结果与实际 问题【11,但由于Mises屈服条件是非线性的,在计 算上会遇到很大困难,故Mises屈服条件很少应 用
对于固支圆板的塑性极限分析问题,主要应 用简化的最大弯矩极限条件,至今只见到在均布 荷载和环形集中力作用下的Mises屈服条件 解-2 J,还没有见到在线性荷载作用下的Mises屈 服条件解,更未见到线性荷载和均布荷载共同作 用下的Mises屈服条件解.因此,本文选择上述题 目进行探讨研究考虑到Mises屈服条件的非线 性,文中在数学方法上应用加权余量法进行分析. 圆板材料为理想刚塑性的.
如果选择(4)式为试函数,可求出与(13)式相 同的计算结果;如果选择(14)式为试函数,也可求 出与(18)式完全相同的计算结果,计算过程略
3结束语
①本文针对线性荷载的两种不同分布形式,
并选择了两种不同的试函数,用加权余量法求出
了承受线性与均布荷载共同作用的固支圆板在
Mises屈服条件下的极限荷载的近似值,且计算
。,2)+等(a2--3at+3r2)~M;06)
按E述步骤。消除余量并应用极值条件得
蔫gja4-面173啤90a2+舞M;=0 1(17)
由此求出极限荷载为 q伊≈8.141404894MpAa2≈8.14AL/a2(18)
2在线性荷载第二种分布形式下的解
设作用于固支圆板编辑郑绥乾)
万方数据
Mises屈服条件在固支圆板塑性极限分析中的应用
作者: 作者单位: 刊名:
英文刊名: 年,卷(期): 被引用次数:
刘磊 辽宁大学,数学系,辽宁,沈阳,110036
辽宁大学学报(自然科学版) JOURNAL OF LIAONING UNIVERSITY(NATURAL SCIENCES EDITION) 2003,30(4) 1次
本文结果是合理的,本文的求解方法是有效的
参考文献:
[1]王仁,熊祝华,黄文彬塑性力学基础[M].北京: 科学出版社,1982,134一140
[2] 徐秉业,劓信声结构塑性极限分析[M]北京:中国 建筑工业出版社,1985,129—173
[3]徐次达固体力学加权残值法[M].上海:同济大学 出版社,1987,1--196
辽宁大学学报 自然科学版
第30卷第4期2003年
JOURNAL OF LIAONING UNIVERSITY
Natural Sciences Edition Vol 30 No 4 2003
MiseS屈服条件在固支圆板塑性极限分析中的应用
刘 磊’
(辽宁大学数学系,辽宁沈阳110036)
摘要:应用加权余量法求出承受线性和均布荷载共同作用的固支圆支板在Misea屈服条件下的极限荷 载,计算结果较合理
1在线性荷载第一种分布形式下的解
1 1基本方程 设作用于固支圆板上的线性荷载和均布荷载
如图1所示,其中线性荷载最大值和均布荷载都 为qo,n为半径.
圈1圊板和衙载球意图
平衡方程为
导(rMr)一M0=一jqno(3 nr2一r3) (1)
式中Mr、Mo分别为板内径向和横向弯矩
Mises屈服条件[2】:
M;一M舳+M;=Mj
(2)
式中Mp为塑性极限弯矩. 板屈服时的边界条件:
fM,(o)=Mo(O)=Mp
(3)
【M,(。)=一M。,M日(n)=0 1.2用加权余量法与选择不同试函数进行求解
1.2.1设试函数为
晦 以 = h
一 口 一
+
h 一打
(4)
监。丝。 ,0●』‘【 % = b 一 口 一 一 +
结果吻合甚好,即可确定本文给出的计算结果为
口口≈8.14M。/a2
(20)
②对于本文的研究对象,如果用最大弯矩极
限条件求解,可容易求出极限荷载为
q李=8Mp/a 2
(21)
③由(20)、(21)式比较看出:本文Mises屈服 条件解q{;f与最大弯矩极限条件解q夺非常接近,
并且本文结果稍高于最大弯矩极限条件解,说明
聪慧篙?…,
R a=导(rMr)一慨+。qdo(3护_r3)=
k1(3ar2—4r3)一k2(口r—r2)一
3骂+磐(3。,z一,3)
(15)
R4=M;一M朋口+M;一M§= 七}(口2r4—2ar5+r6)+矗;(口2r2—2ar3+I-4)一
klk2(42r3~2ar4+y5)
埔孚∽r2-4矿+3r4)%等㈦r一
The Application of Mises Yield Condition in Limit Analyse of Plasticity
LIU Lei
(Mathematics Department ofLiaoning University,Shenyang 110036,China)
Abstract: With the method of weighted residuals,limit load of clamped supported circular plate simulta— neously affected by linaear and uniform loads was calculated under the condition of Mises yield.The result
