高中数学-第二章小结与复习课件-新人教A版必修1
合集下载
第二章 一元二次函数、方程和不等式复习与小结)课件-高一数学人教A版(2019)必修第一册)

常量(如1)替换,变量替换(消元)
返回
6.二次函数与一元二次方程、不等式的关系:
(1)形式上
二次函数 y=ax2+bx+c
(2)数值上 二次函数函数 y=ax2+bx+c的零点
一元二次方程 ax2+bx+c=0
右边化为0, 左边设为y
一元二次不等式 ax2+bx+c<0(或>0)
一元二次方程 ax2+bx+c=0的根
a b a b 0; 2.两个实数大小关系的基本事实: a b a b 0;
a b a b 0.
利用这个事实可以采取作差法可以对一些代数式的大小进 行了比较也可以证明不等式:
(1)作差; (2)变形;
目的:便于判定差的符号 常用的方法:因式分解、配方、通分、分子有理化等 (3)定号; 当差的符号不确定时,一般需要分类讨论 (4)作结论。 根据当差的正负与实数大小关系的基本事实作出结论 返回
1
1
ab
返回
4.基本不等式及其推导
对任意的a 0,b 0,有 ab a b 2
当且仅当a b时,等号成立
(1)基本不等式的常见变形:
① a+b≥2 ab ;
② ab≤( a+b )2 2
代数特征: 两个正数的几何平均数不大于它们的算术平均数,当且仅 当这两个正数相等时,二者相等. 几何解释: 圆O的半弦CD不大于圆的半径OD,当且仅当C与圆心O 重合时,二者相等。 (2)基本不等式的推导和证明: ①利用两个实数大小关系的基本事实用作差法得出;
求a b的最小值以及此时a的值。
解: 方法1
a0 , b0
由a b ab - 3得 a b ab - 3 ( a b )2 3
2019年最新-人教版高中数学必修一第二章小结与复习ppt课件

(ln x)' 1
x;
(loagx)'1 x;loga
(ex )' ex
;
(ax)'ax lna
。
5.导数的四则运算法则:
[ u (x ) v (x )' ] u '(x ) v '(x )
[ u ( x ) v ( x ) ] u ' ( x ) v ( x ) u (
[C u(x)]C u'(x)
练习:课本 作业:课本
P53 复习题:A组1、2、 P53 复习题:A组 5;
五、教后反思:
谢谢!
We are so hungry.How can we get to Italian restaurant?W e are in front of the cinema. Let’s go straight and turn left at the bookstore. Follow me. 加热高锰酸钾制取氧气的装置 适合用双氧水在二氧化锰作催化剂 条件下制取氧气吗?为什么?
[ 1 ( 3 x ) 3 ] 2
( 1
e2x 1(1 16x) (13x)4
例2、已知曲线C1: y, x 2 与曲线C2: y
,直线l与C1、C2都相切,, 求直线l的方程。
解:设l与C1相切于点
P1(x1, y1),l与C2相切于
,直线l的斜率为k。C1: y x,2 y 2,x k
C2: y(x2),2 y2(x2),k2
据此可得出气体的发生装置与哪些 因素有关?如何选择发生装置?如何 选择收集装置? Na2CO3 +2HCl == 2NaCl +H2O + CO2
人教A版高中数学必修1《第二章 基本初等函数(Ⅰ) 小结》_6
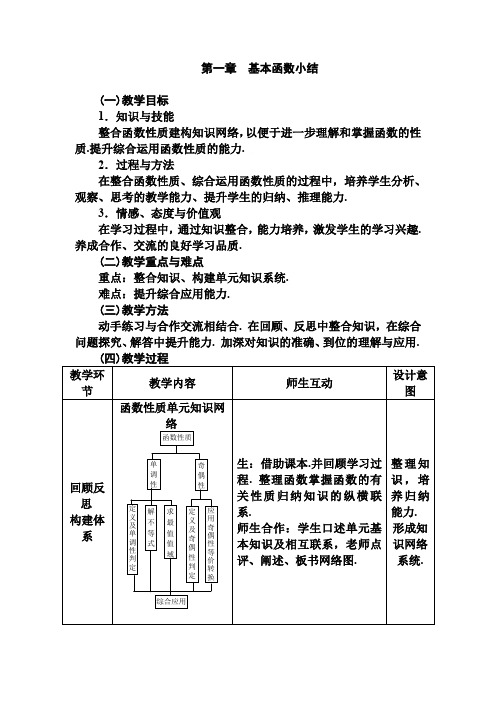
第一章基本函数小结(一)教学目标1.知识与技能整合函数性质建构知识网络,以便于进一步理解和掌握函数的性质.提升综合运用函数性质的能力.2.过程与方法在整合函数性质、综合运用函数性质的过程中,培养学生分析、观察、思考的教学能力、提升学生的归纳、推理能力.3.情感、态度与价值观在学习过程中,通过知识整合,能力培养,激发学生的学习兴趣. 养成合作、交流的良好学习品质.(二)教学重点与难点重点:整合知识、构建单元知识系统.难点:提升综合应用能力.(三)教学方法动手练习与合作交流相结合. 在回顾、反思中整合知识,在综合问题探究、解答中提升能力. 加深对知识的准确、到位的理解与应用.(四)教学过程思络..求函数值域的基本方法总结(1)观察法:一些简单函数,通过观察法求值域.(2)配方法:“二次函数类”用配方法求值域.(3)换元法:形如y=ax+b±cx+d(a、b、c、d均为常数,且a≠0)的函数常用换元法求值域.(4)分离常数法:形如y=cx+dax+b(a≠0)的函数也可用此法求值域.(5)单调性法:函数单调性的变化是求最值和值域的依据,根据函数的单调区间判断其增减性进而求最值和值域.(6)数形结合法:画出函数的图像,找出坐标的范围或分析条件的几何意义,在图上找其变化范围.判断函数单调性的方法:①根据定义;②根据图像;③利用已知函数的增减性;⑤复合函数单调性判定方法:在复合函数y=f(g(x))中,“同增异减”。
1.函数单调性的证明根据函数的单调性的定义,证明(判定)函数f(x)在其区间上的单调性,其步骤是:(1)设x1、x2是该区间上的任意两个值,且x1<x2;(2)作差f(x1)-f(x2),然后变形;(3)判定f(x1)-f(x2)的符号;(4)根据定义作出结论.。
人教A版高中数学必修第一册第二章二次函数与一元二次不等式课件

综上,当 a<0 时,不等式解集为x|x<1a,或x>1; 当 a=0 时,不等式解集为{x|x>1}; 当 0<a<1 时,不等式解集为x|1<x<1a; 当 a=1 时,不等式解集为∅; 当 a>1 时,不等式解集为x|1a<x<1.
/人A数学/ 必修 第一册
返回导航 上页 下页
解含参数的一元二次不等式的步骤 1.讨论二次项系数:讨论二次项系数是等于0,小于0,还是大于0. 2.判断方程根的个数和根的大小关系:讨论判别式Δ与0的大小关系, 判断方程根的个数,若方程存在两个实数根,要讨论根的大小关 系.确定方程无根时可直接写出解集. 3.写出不等式解集:根据方程根的情况和二次函数图象确定不等式解 集.
返回导航 上页 下页
一元二次不等式 1.一般地,我们把只含有 一个未知数,并且未知数的最高次数是 2 的 不等式,称为一元二次不等式.一元二次不等式的一般形式是 __a_x_2+__b_x_+__c_>_0__或__a_x_2+__b_x_+__c_<_0__ ,其中a,b,c均为常数,a≠0.
/人A数学/ 必修 第一册
返回导航 上页 下页
Δ>0
Δ=0
ax2 + bx + c > 0 _{_x_|_x_<__x1_,__或__x_>__x_2_}_ (a>0)的解集
__x_|x_≠__-__2_ba__
ax2 + bx + c < 0 __{_x_|x_1_<__x<__x_2_}__ (a>0)的解集
__∅___
/人A数学/ 必修 第一册
返回导航 上页 下页
[解] (1)Δ=a2-16,下面分情况讨论: ①当Δ<0,即-4<a<4时,方程2x2+ax+2=0无实根,所以原不等式 的解集为R. ②当Δ=0,即a=±4时,若a=-4,则原不等式等价于(x-1)2>0, 故x≠1;若a=4,则原不等式等价于(x+1)2>0,故x≠-1.
人教A版高中数学必修一课件:第二章章末小结

2
数;在 x∈(-∞,3]上函数 y=������-������2+3x+2为减函数.
2
数学(RA-GZ) -必修1
【小结】涉及函数 y=ax 的单调性,底数 a 为字母时,应该分 a>1 和 0<a<1 两种情况进行讨论.
数学(RA-GZ) -必修1
4
2
1
1.(2016 年全国Ⅲ卷)已知 a=23,b=45,c=253,则( ).
2
aa,log1
2
1
a,������2之间的大小关系是(
).
1
1
A.aa>������2>log1a B.������2>log1a>aa
2 1
C.log 1 a>aa>������2
2 1
D.log 1 a>������2 >aa
2
2
数学(RA-GZ) -必修1
【方法指导】先根据指数函数的单调性比较
1
������3
=������
1
3 (a -8b ������-8������
)������13
1
������3
1
������3
=a
3
b.
(2)原式=lg4 2-lg 4+lg 7 5
7
=lg(4 2×1×7
74
5)
=lg 10=1lg 10=1.
2
2
数学(RA-GZ) -必修1
【小结】根式、指数和对数的运算要注意几个方面:一是把根式 化成指数幂的形式;二是借助公式把底数化成同底;三是注意指数与
∞)上为增函数;
数学(RA-GZ) -必修1
数;在 x∈(-∞,3]上函数 y=������-������2+3x+2为减函数.
2
数学(RA-GZ) -必修1
【小结】涉及函数 y=ax 的单调性,底数 a 为字母时,应该分 a>1 和 0<a<1 两种情况进行讨论.
数学(RA-GZ) -必修1
4
2
1
1.(2016 年全国Ⅲ卷)已知 a=23,b=45,c=253,则( ).
2
aa,log1
2
1
a,������2之间的大小关系是(
).
1
1
A.aa>������2>log1a B.������2>log1a>aa
2 1
C.log 1 a>aa>������2
2 1
D.log 1 a>������2 >aa
2
2
数学(RA-GZ) -必修1
【方法指导】先根据指数函数的单调性比较
1
������3
=������
1
3 (a -8b ������-8������
)������13
1
������3
1
������3
=a
3
b.
(2)原式=lg4 2-lg 4+lg 7 5
7
=lg(4 2×1×7
74
5)
=lg 10=1lg 10=1.
2
2
数学(RA-GZ) -必修1
【小结】根式、指数和对数的运算要注意几个方面:一是把根式 化成指数幂的形式;二是借助公式把底数化成同底;三是注意指数与
∞)上为增函数;
数学(RA-GZ) -必修1
人教A版高中数学必修1 课件 :第二章 章末复习与总结

解得 x1=1,x2=1+2
3,x3=1-2
3 .
因为 1≤m<n,所以 m=1,n=1+2
3 .
2.进行等价转化有效避免讨论
有时可以将题目中的条件进行等价转化,结合一定的运算技
巧,避免分类讨论.
【例 2】 设函数 f(x)=|lg x|若 0<a<b,且 f(a)>f(b),证明:
ab<1. [ 证 明 ] 如 果 是 常 规 做 法 , 将 f(x) 写 成 分 段 函 数 形 式
章末复习与总结 创新拓展 思想方法 易错警示
有效回避分类讨论的若干策略 分类讨论是高中数学中必须掌握的数学思想之一.掌握分类 讨论的思想方法,有利于培养学生全面严谨的数学思维能力,并 能够有逻辑地分析、解决问题.然而,这种数学思想对于学生来 说,难度非常大,掌握情况并不理想.具体表现在:没有分类讨 论的意识、不知道分类讨论的标准及讨论的内容.大多数分类讨 论的问题都与参数有关,其实质是“化整为零,各个击破”,而
们分同正、同负和一正一负四类讨论.而事实上,如果运用偶函
数的性质,可以避免讨论.
因为 f(x)=f(-x)=f(|x|),所以 f(1-t)<f(t)⇔f(|1-t|)<f(|t|).因
为|1-t|与|t|都在区间[0,+∞)内,且 f(x)在[0,+∞)上单调递减,
所 以 |1 - t|>|t| 两 边 同 时 平 方 可 解 得
x-1>0, 3-x>0, [解] 由题意得a-x>0, x-13-x=a-x,
即1x<<ax<,3, -x2+5x-3=a.
设函数 f(x)=-x2+5x-3,x∈(1,3),则函数 f(x)的值域为
高中数学新人教A版必修1课件:第二章基本初等函数2.2.1对数与对数运算(第1课时)对数

• 并非所有指数式都可以直接化为对数式.如(-3)2=9就不能直接 写成log(-3)9=2,只有a>0且a≠1,N>0时,才有ax=N⇔x=logaN.
〔跟踪练习1〕
将下列指数式化为对数式,对数式化为指数式:
(1)42=16;
(2)102=100;
1
(3)42
=2;
(4)log1 32=-5. 2
(3)原式=(alogab) logbc=blogbc=c.
• 『规律方法』 运用对数恒等式时注意事项 • (1)对于对数恒等式alogaN=N要注意格式: • ①它们是同底的;②指数中含有对数情势;③其值为对数的真数. • (2)对于指数中含有对数值的式子进行化简,应充分考虑对数恒等式的应用.
〔跟踪练习3〕 求31+log36-24+log23+103lg3+(19)log34的值. [解析] 原式=3·3 log36-24·2 log23+(10lg3)3+(3 log34)-2 =3×6-16×3+33+4-2 =18-48+27+116=-4176.
• 3.对数与指数的关系
• 当a>0,且a≠1时,ax=N⇔x=____ln_N_______.
• 4.对数的基本性质 • (1)___零___和_负_数______没有对数.
• (2)loga1=_0____(a>0,且a≠1). • (3)logaa=_1____(a>0,且a≠1). • 5.对数恒等式
B.log1 9=-2 3
C.log1 (-2)=9 3
D.log9(-2)=13
[解析] 将(13)-2=9写成对数式为log13 9=-2,故选B.
• 4.若log2(log3x)=0,则x=_3____. • [解析] 由题意得log3x=1,∴x=3.
〔跟踪练习1〕
将下列指数式化为对数式,对数式化为指数式:
(1)42=16;
(2)102=100;
1
(3)42
=2;
(4)log1 32=-5. 2
(3)原式=(alogab) logbc=blogbc=c.
• 『规律方法』 运用对数恒等式时注意事项 • (1)对于对数恒等式alogaN=N要注意格式: • ①它们是同底的;②指数中含有对数情势;③其值为对数的真数. • (2)对于指数中含有对数值的式子进行化简,应充分考虑对数恒等式的应用.
〔跟踪练习3〕 求31+log36-24+log23+103lg3+(19)log34的值. [解析] 原式=3·3 log36-24·2 log23+(10lg3)3+(3 log34)-2 =3×6-16×3+33+4-2 =18-48+27+116=-4176.
• 3.对数与指数的关系
• 当a>0,且a≠1时,ax=N⇔x=____ln_N_______.
• 4.对数的基本性质 • (1)___零___和_负_数______没有对数.
• (2)loga1=_0____(a>0,且a≠1). • (3)logaa=_1____(a>0,且a≠1). • 5.对数恒等式
B.log1 9=-2 3
C.log1 (-2)=9 3
D.log9(-2)=13
[解析] 将(13)-2=9写成对数式为log13 9=-2,故选B.
• 4.若log2(log3x)=0,则x=_3____. • [解析] 由题意得log3x=1,∴x=3.
高中数学新人教A版必修1课件:第二章基本初等函数章末整合提升

[分析] 本题考查讨论方程的实根的个数,可转化为求函数图象的交点.
1<x<3
原方程等价于x<a
.
x-13-x=a-x
方程(x-1)(3-x)=a-x的解满足1<x<3,必满足x<a;反之若满足x<a,
则必满足1<x<3.
于是问题转化为在x∈(1,3)条件下解方程(x-1)(3-x)=a-x.
[解析]
之相应的几何图形,并利用图形的特征和规律,解决数的 问题,或将图形信息转化成代数信息,使解决形的问题转 化为数量关系的问题讨论.
• 典例 6 (202X·北京丰台区高一期末测试)已知等式
log2m=log3n(m>0,n>0)成立,那么下列结论:
• ①m=n;②n<m<1;③m<n<1;④1<n<m;⑤1<m<n;⑥
[解析] (1)原式=(32)2+1-(287)32
=94+1-[(32)3]
2 3
=94+1-(32)2
=94+1-94=1.
(2)原式=lg5·(3lg2+3)+( 3lg2)2-lg6+lg1600
=3lg5·lg2+3lg5+3(lg2)2-lg6+lg6-2
=3lg2·(lg5+lg2)+3lg5-2
• 3.应用指数函数y=ax和对数函数y=logax的图象和性质时, 若底数含有字母,要特别注意对底数a>1和0<a<1两种情况 的讨论.
• 4.幂函数与指数函数的主要区分:幂函数的底数为变量, 指数函数的指数为变量.因此,当遇到一个有关幂的情势 的问题时,就要看变量所在的位置从而决定是用幂函数知 识解决,还是用指数函数知识去解决.
3.图象问题
典例 4
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(2) 对称翻转变换: ①互为反函数的两个函数图象关于直线 y=f(x)对称.即y=f-1(x)的函数图象与函 数y=f(x)的图象关于y=x对称; ② y=f(x)的函数图象与函数y=f(-x)的 图象关于y轴对称;
(2) 对称翻转变换: ①互为反函数的两个函数图象关于直线 y=f(x)对称.即y=f-1(x)的函数图象与函 数y=f(x)的图象关于y=x对称; ② y=f(x)的函数图象与函数y=f(-x)的 图象关于y轴对称;
8. 图象的变换规律: (1) 平移变换 (a>0)
向右平移 y=f(x) a 个单位 向左平移 y=f(x) a 个单位 向上平移 y=f(x) a 个单位 y=f(x-a)
向下平移 y=f(x) a 个单位
8. 图象的变换规律: (1) 平移变换 (a>0)
向右平移 y=f(x) a 个单位 向左平移 y=f(x) a 个单位 向上平移 y=f(x) a 个单位 y=f(x-a) y=f(x+a)
A. f (xy)=f (x) f (y)
( C )
B. f (xy)=f (x)+f (y)
C. f (x+y)=f (x) f (y) D. f (x+y)=f (x)+f (y)
例5 方程4x+2x-2=0的解是
.
例5 方程4x+2x-2=0的解是
.
例6方程log4(3x-1)=log4(x-1)+log4(3+x)
(3) 若对任意的x、y∈(0, +∞),都有 f(xy)=f(x)+f(y), 则f(x)可与对数函数类比.
例1 设集合A和B都是坐标平面内的点集 {(x, y) | x∈R,y∈R},映射f:A→B把 集合A中的元素(x, y)映射成集合B的元 素(x+y, x-y) ,则在映射下象(2, 1)的 原象是 ( )
的解是
.
例5 方程4x+2x-2=0的解是
.
例6方程log4(3x-1)=log4(x-1)+log4(3+x)
的解是
.
例7 若关于x的方程 4x-(a+1)×2x+9=0有实数根,求a的 取值范围.
例8 比较大小
(1) 3 和 3.1 1 ( 2) 8 和 ( ) 9 ( 3) 3 和 5
1. 4 7 8
5. 函数值域的求法:
①观察法; ③图象法; ⑤反函数法; ⑦换元法. ②配方法; ④分离常数法; ⑥判别式法;
6. 函数单调性的判定法:
证明的步骤:
①取值;②作差;③定号;④作结论.
6差;③定号;④作结论. 7. 解应用题的一般步骤:
①审题;②建模;③求模;④还原.
三、本章的主要方法
1. 相同函数的判断方法: ①定义域相同; ②值域相同; ③对应法则相同.
2. 函数解析式的求法:
三、本章的主要方法
1. 相同函数的判断方法: ①定义域相同; ②值域相同; ③对应法则相同.
2. 函数解析式的求法: ①换元法; ②配方法; ③待定系数法; ④方程组法.
三、本章的主要方法
1. 相同函数的判断方法: ①定义域相同; ②值域相同; ③对应法则相同.
2. 函数解析式的求法: ①换元法; ②配方法; ③待定系数法; ④方程组法.
3. 反函数的求法: ①求解x; ②互换x,y的位置; ③注明反函数的定义域.
4. 函数定义域的求法:
(通常考虑以下六个方面) ①分式中分母不为零; ②偶次方根被开方数(式)非负; ③ x0中x≠0; ④对数中真数大于零; ⑤指、对数函数中底数大于零且不等于1; ⑥实际问题要考虑实际意义.
例4 设f(x)=ax(a>0且a≠1)对于任意的
实数x、y都有
A. f (xy)=f (x) f (y)
(
)
B. f (xy)=f (x)+f (y)
C. f (x+y)=f (x) f (y) D. f (x+y)=f (x)+f (y)
例4 设f(x)=ax(a>0且a≠1)对于任意的
实数x、y都有
向右平移 y=f(x) a 个单位 向左平移 y=f(x) a 个单位 向上平移 y=f(x) a 个单位 y=f(x-a) y=f(x+a)
y=f(x)+a
y=f(x)-a
向下平移 y=f(x) a 个单位
(2) 对称翻转变换: ①互为反函数的两个函数图象关于直线 y=f(x)对称.即y=f-1(x)的函数图象与函 数y=f(x)的图象关于y=x对称;
9. 抽象函数
(1) 若f(a+x)=f(a-x),则f(x)关于直线 x=a对称;
9. 抽象函数
(1) 若f(a+x)=f(a-x),则f(x)关于直线 x=a对称; (2) 若对任意的x、y∈R,都有 f(x+y)=f(x)·f(y), 则f(x)可与指数函数类比;
9. 抽象函数
(1) 若f(a+x)=f(a-x),则f(x)关于直线 x=a对称; (2) 若对任意的x、y∈R,都有 f(x+y)=f(x)·f(y), 则f(x)可与指数函数类比;
向下平移 y=f(x) a 个单位
8. 图象的变换规律: (1) 平移变换 (a>0)
向右平移 y=f(x) a 个单位 向左平移 y=f(x) a 个单位 向上平移 y=f(x) a 个单位 y=f(x-a) y=f(x+a)
y=f(x)+a
向下平移 y=f(x) a 个单位
8. 图象的变换规律: (1) 平移变换 (a>0)
5 2
5 2
7 8
1. 5
例9 某化工厂生产一种溶液,按市场要 求,杂质含量不能超过0.1%,若初时 含杂质2%,每过滤一次可使杂质含量 减少三分之一, 问至少要过滤几次才
能使产品达到市场要求?
(lg2=0.3010,lg3=0.4771)
谢谢观看
A. ( 3 , 1)
3 1 C. ( , ) 2 2
3 1 B. ( , ) 2 2
D. (1 , 3)
例1 设集合A和B都是坐标平面内的点集 {(x, y) | x∈R,y∈R},映射f:A→B把 集合A中的元素(x, y)映射成集合B的元 素(x+y, x-y) ,则在映射下象(2, 1)的 原象是 ( B )
C. [2,1) (1 , 2]
(
)
D. ( 2,1) (1 , 2)
例3 函数 y log 1 ( x 1) 的定义域是
2 2
A. [ 2 ,1) (1, 2 ] B. ( 2 ,1) (1, 2 )
C. [2,1) (1 , 2]
( A )
D. ( 2,1) (1 , 2)
A. ( 3 , 1)
3 1 C. ( , ) 2 2
3 1 B. ( , ) 2 2
D. (1 , 3)
例2 设A={x|0≤x≤2},B={y|0≤y≤2}, 图中表示集合A到集合B的函数关系的图 象是 ( )
y 2 A. 1
O y 3 2 C. 1
O
y 2 B. 1
1
x
O
1
2x
y 2 D. 1
③ y=f(x)的函数图象与函数y=-f(x)的 图象关于x轴对称;
(2) 对称翻转变换: ①互为反函数的两个函数图象关于直线 y=f(x)对称.即y=f-1(x)的函数图象与函 数y=f(x)的图象关于y=x对称; ② y=f(x)的函数图象与函数y=f(-x)的 图象关于y轴对称;
③ y=f(x)的函数图象与函数y=-f(x)的 图象关于x轴对称; ④ y=f(x)的函数图象与函数y=-f(-x) 的图象关于原点对称.
第二章复习
一、本章知识框架
函数的概念
函数的图象 函数的性质
反函数
对应
映射
函数
指数函数
应用
对数函数
幂函数
二、本章的主要概念
1. 映射
3. 函数的单调性 5. 分数指数幂与根式
2. 函数
4. 反函数 6. 指数函数
7. 对数
8. 对数函数
三、本章的主要方法
1. 相同函数的判断方法: ①定义域相同; ②值域相同; ③对应法则相同.
1
2x
O
1
2x
例2 设A={x|0≤x≤2},B={y|0≤y≤2}, 图中表示集合A到集合B的函数关系的图 象是 ( B )
y 2 A. 1
O y 3 2 C. 1
O
y 2 B. 1
1
x
O
1
2x
y 2 D. 1
1
2x
O
1
2x
例3 函数 y log 1 ( x 1) 的定义域是
2 2
A. [ 2 ,1) (1, 2 ] B. ( 2 ,1) (1, 2 )
