时间序列分析第二章王燕第一到第三题习题解答
时间序列分析王燕习题答案

时间序列分析王燕习题答案时间序列分析王燕习题答案时间序列分析是一门研究时间序列数据的统计学方法,它可以帮助我们理解和预测时间序列数据的趋势和模式。
王燕是这一领域的专家,在她的教材中提供了一系列的习题供学习者练习。
本文将给出一些关于时间序列分析中王燕习题的答案,希望能帮助读者更好地理解和应用这一方法。
第一题:给出一个时间序列数据,如何确定其季节性?季节性是时间序列数据中重复出现的周期性变化。
我们可以通过观察数据的图表来确定其季节性。
如果数据呈现出明显的周期性变化,且每个周期的长度相似,那么可以认为该时间序列具有季节性。
第二题:如何进行时间序列数据的平滑处理?时间序列数据的平滑处理是为了去除数据中的随机波动,使其更易于观察和分析。
常用的平滑方法有移动平均法和指数平滑法。
移动平均法是将一段时间内的数据求平均值,以此来代表整个时间段的数据。
指数平滑法则是通过对历史数据进行加权平均,赋予较近期数据更高的权重,以反映出时间序列数据的趋势。
第三题:如何进行时间序列数据的分解?时间序列数据的分解是为了将其拆解成趋势、季节性和随机成分三个部分,以便更好地理解和预测数据。
常用的分解方法有经典分解法和X-11分解法。
经典分解法是将时间序列数据拆解成趋势、季节性和随机成分,其中趋势是数据的长期变化,季节性是周期性的变化,随机成分则是无法解释的随机波动。
X-11分解法则是在经典分解法的基础上加入了一些调整和修正,使得分解结果更准确。
第四题:如何进行时间序列数据的预测?时间序列数据的预测是利用历史数据来预测未来的趋势和模式。
常用的预测方法有移动平均法和指数平滑法。
移动平均法是将时间序列数据的平均值作为未来的预测值。
指数平滑法则是通过对历史数据进行加权平均,赋予较近期数据更高的权重,以反映出时间序列数据的趋势。
此外,还可以使用ARIMA模型进行时间序列数据的预测,ARIMA模型是一种常用的时间序列预测模型,它结合了自回归、滑动平均和差分运算。
《时间序列分析》第二章 时间序列预处理习题解答

《时间序列分析》习题解答�0�2习题2.3�0�21考虑时间序列12345…201判断该时间序列是否平稳2计算该序列的样本自相关系数kρ∧k12… 6 3绘制该样本自相关图并解释该图形. �0�2解1根据时序图可以看出该时间序列有明显的递增趋势所以它一定不是平稳序列�0�2即可判断该时间序是非平稳序列其时序图程序见后。
�0�2 时间序描述程序data example1 input number timeintnxyear01jan1980d _n_-1 format time date. cards 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 proc gplot dataexample1 plot numbertime1 symbol1 cblack vstar ijoin run�0�2�0�2�0�22当延迟期数即k本题取值1 2 3 4 5 6远小于样本容量n本题为20时自相关系数kρ∧计算公式为number1234567891011121314151617181920time01JAN8001J AN8101JAN8201JAN8301JAN8401JAN8501JAN8601JAN870 1JAN8801JAN8901JAN9001JAN9101JAN9201JAN9301JAN9 401JAN9501JAN9601JAN9701JAN9801JAN99121nkttktknttX XXXXXρ�6�1∧�6�1�6�1≈�6�1∑∑ 0kn4.9895�0�2注20.05125.226χ接受原假设认为该序列为纯随机序列。
�0�2解法三、Q统计量法计算Q统计量即12214.57kkQnρ∑�0�2�0�2�0�2�0�2�0�2�0�2�0�2�0�2�0�2�0�2查表得210.051221.0261χ�6�1由于Q统计量值4.57Q小于查表临界值即可认为接受原假设即该序列可视为纯随机序列为白噪声序列 5表2——9数据是某公司在2000——2003年期间每月的销售量。
人大版应用时间序列分析(第5版)习题答案
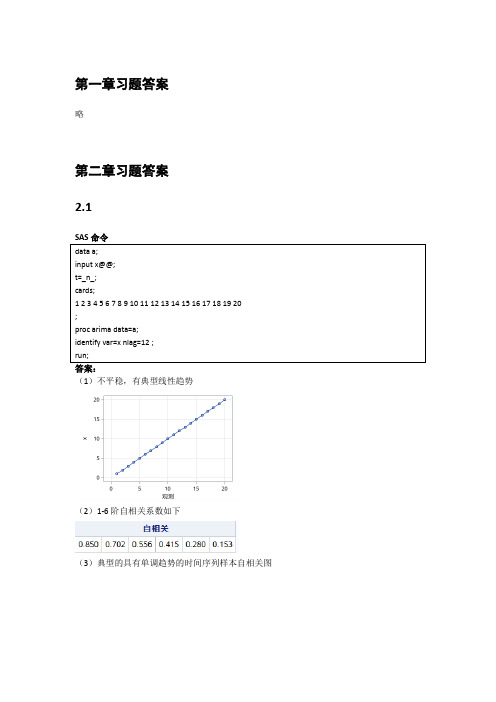
第一章习题答案略第二章习题答案2.1答案:(1)不平稳,有典型线性趋势(2)1-6阶自相关系数如下(3)典型的具有单调趋势的时间序列样本自相关图2.2答案:(1)不平稳(2)延迟1-24阶自相关系数(3)自相关图呈现典型的长期趋势与周期并存的特征2.3答案:(1)1-24阶自相关系数(2)平稳序列(3)非白噪声序列2.4计算该序列各阶延迟的Q统计量及相应P值。
由于延迟1-12阶Q统计量的P值均显著大于0.05,所以该序列为纯随机序列。
2.5答案(1)绘制时序图与自相关图(2)序列时序图显示出典型的周期特征,该序列非平稳(3)该序列为非白噪声序列2.6答案(1)如果是进行平稳性图识别,该序列自相关图呈现一定的趋势序列特征,可以视为非平稳非白噪声序列。
如果通过adf检验进行序列平稳性识别,该序列带漂移项的0阶滞后P值小于0.05,可以视为平稳非白噪声序列(2)差分后序列为平稳非白噪声序列2.7答案(1)时序图和自相关图显示该序列有趋势特征,所以图识别为非平稳序列。
(2)单位根检验显示带漂移项0阶延迟的P值小于0.05,所以基于adf检验可以认为该序列平稳(3)如果使用adf检验结果,认为该序列平稳,则白噪声检验显示该序列为非白噪声序列如果使用图识别认为该序列非平稳,那么一阶差分后序列为平稳非白噪声序列2.8答案(1)时序图和自相关图都显示典型的趋势序列特征(2)单位根检验显示该序列可以认为是平稳序列(带漂移项一阶滞后P值小于0.05)(3)一阶差分后序列平稳第三章习题答案 3.10101()0110.7t E x φφ===--() 221112() 1.96110.7t Var x φ===--() 22213=0.70.49ρφ==()12122221110.490.7=0110.71ρρρφρρ-==-(4) 3.21111222211212(2)7=0.515111=0.30.515AR φφφρφφφρφρφφφ⎧⎧⎧=⎪=⎪⎪⎪--⇒⇒⎨⎨⎨⎪⎪⎪=+=+⎩⎩⎪⎩模型有:,2115φ=3.312012(1)(10.5)(10.3)0.80.15()01t t t t t tt B B x x x x E x εεφφφ----=⇔=-+==--,22121212()(1)(1)(1)10.15=(10.15)(10.80.15)(10.80.15)1.98t Var x φφφφφφ-=+--+-+--+++=()1122112312210.83=0.70110.150.80.70.150.410.80.410.150.70.22φρφρφρφρφρφρ==-+=+=⨯-==+=⨯-⨯=() 1112223340.70.15=0φρφφφ====-()3.41211110011AR c c c c c ⎧<-<<⎧⎪⇒⇒-<<⎨⎨<±<⎪⎩⎩() ()模型的平稳条件是 1121,21,2k k k c c k ρρρρ--⎧=⎪-⎨⎪=+≥⎩() 3.5证明:该序列的特征方程为:320c c λλλ--+=,解该特征方程得三个特征根:11λ=,2λ=3λ=无论c 取什么值,该方程都有一个特征根在单位圆上,所以该序列一定是非平稳序列。
人大(王燕)时间序列课后习题解答)2 5(含上机的)

第二章P34 1、(1)因为序列具有明显的趋势,所以序列非平稳。
(2)样本自相关系数:∑∑=-=+---≅=nt tkn t k t tk x xx x x xk 121)())(()0()(ˆγγρ5.10)2021(20111=+++==∑= n t t x n x =-=∑=2201)(201)0(x x t t γ35 =--=+=∑))((191)1(1191x x x x t t t γ29.75=--=+=∑))((181)2(2181x x x x t t t γ25.9167=--=+=∑))((171)3(3171x x x x t t t γ21.75γ(4)=17.25 γ(5)=12.4167 γ(6)=7.251ρ=0.85(0.85) 2ρ=0.7405(0.702) 3ρ=0.6214(0.556) 4ρ=0.4929(0.415) 5ρ=0.3548(0.280) 6ρ=0.2071(0.153) 注:括号内的结果为近似公式所计算。
(3)样本自相关图:Autocorrelation Partial Correlation AC PACProb . |*******| . |*******| 1 0.850 0.850 16.732 0.000 . |***** | . *| . | 2 0.702 -0.07628.7610.000 . |**** | . *| . | 3 0.556 -0.07636.7620.000 . |*** | . *| . | 4 0.415 -0.07741.5000.000 . |**. | . *| . | 5 0.280 -0.07743.8000.000 . |* . | . *| . | 6 0.153 -0.07844.5330.000 . | . | . *| . | 7 0.034 -0.07744.5720.000 . *| . |. *| . |8 -0.074 -0.07744.7710.000. *| . | . *| . |9 -0.17-0.07545.9210.000 .**| . | . *| . | 10 -0.252-0.07248.7130.000 .**| . | . *| . | 11 -0.319-0.06753.6930.000 ***| . |. *| . | 12 -0.37-0.0661.2200.000该图的自相关系数衰减为0的速度缓慢,可认为非平稳。
时间序列分析基于R_习题答案
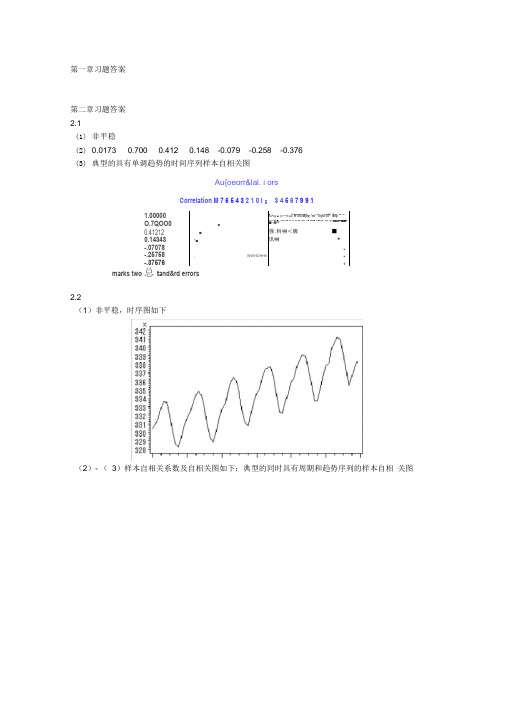
第一章习题答案第二章习题答案2.1(1)非平稳(2)0.0173 0.700 0.412 0.148 -0.079 -0.258 -0.376(3)典型的具有单调趋势的时间序列样本自相关图Au{oeorr&lal. i orsCorrelation M 7 6 5 4 3 2 1 0 I ; 3 4 5 6 7 9 9 11.00000■Hi ■ K. B H,J B ik L L1■* J.1 jA1-.IM L L*rn^rp ■ i>i™iTwin H'iTiii M[lrp i,*nfr 'TirjlvTilT'1 iBrpO.7QOO0■ill. Ii ill ■ _.ill«L■ ill iL si ill .la11 ■ fall■ 1 ■ rpTirp Tp和阳申■丽轉■晒?|•卉(ft0.41212■强:料榊<牌■0.14343'■讯榊*-.07078■-.25758, WWHOHHfi■-.375761marks two 总t and&rd errors2.2(1)非平稳,时序图如下(2)- (3)样本自相关系数及自相关图如下:典型的同时具有周期和趋势序列的样本自相关图raa rka two standard errors2.3(1) 自相关系数为: 0.20230.013 0.042-0.043 -0.179 -0.251 -0.094 0.0248 -0.068 -0.072 0.014 0.109 0.217 0.316 0.0070-0.025 0.075 -0.141 -0.204 -0.245 0.066 0.0062-0.139 -0.034 0.206 -0.010 0.080 0.118(2 )平稳序列 (3) 白噪声序列 2.4LB=4.83 , LB 统计量对应的分位点为 0.9634 , P 值为0.0363。
时间序列分析基于R——习题答案
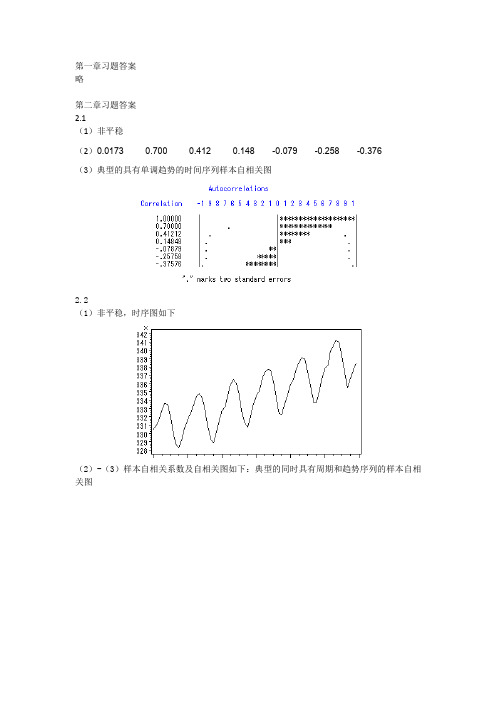
第一章习题答案略第二章习题答案2.1(1)非平稳(2)0.0173 0.700 0.412 0.148 -0.079 -0.258 -0.376(3)典型的具有单调趋势的时间序列样本自相关图2.2(1)非平稳,时序图如下(2)-(3)样本自相关系数及自相关图如下:典型的同时具有周期和趋势序列的样本自相关图2.3(1)自相关系数为:0.2023 0.013 0.042 -0.043 -0.179 -0.251 -0.094 0.0248 -0.068 -0.072 0.014 0.109 0.217 0.316 0.0070 -0.025 0.075 -0.141 -0.204 -0.245 0.066 0.0062 -0.139 -0.034 0.206 -0.010 0.080 0.118(2)平稳序列(3)白噪声序列2.4,序列LB=4.83,LB统计量对应的分位点为0.9634,P值为0.0363。
显著性水平=0.05不能视为纯随机序列。
2.5(1)时序图与样本自相关图如下(2) 非平稳 (3)非纯随机 2.6(1)平稳,非纯随机序列(拟合模型参考:ARMA(1,2)) (2)差分序列平稳,非纯随机第三章习题答案3.1 ()0t E x =,21() 1.9610.7t Var x ==-,220.70.49ρ==,220φ= 3.2 1715φ=,2115φ=3.3 ()0t E x =,10.15() 1.98(10.15)(10.80.15)(10.80.15)t Var x +==--+++10.80.7010.15ρ==+,210.80.150.41ρρ=-=,3210.80.150.22ρρρ=-=1110.70φρ==,2220.15φφ==-,330φ=3.4 10c -<<, 1121,1,2k k k c c k ρρρρ--⎧=⎪-⎨⎪=+≥⎩3.5 证明:该序列的特征方程为:32--c 0c λλλ+=,解该特征方程得三个特征根:11λ=,2c λ=3c λ=-无论c 取什么值,该方程都有一个特征根在单位圆上,所以该序列一定是非平稳序列。
时间序列第2-3章习题解答

则模型的传递形式为:
=
,确定该模型的 Green 函数,使该
故该模型的 Green 函数为: 该模型可以等价表示为无穷阶 MA 模型形式为:
13. 某 ARMR(2,2)模型为: .
解因
所以
,求 . 其中
, .
14. 证明 ARMR(1,1)序列 解 方法一 因为 所以
的自相关系数为:
第 3 章 习题(王燕)
1. 已知 AR(1)模型为 解由 . 由
。求 ,
,和 。
=
=
(常均值性),有
, ,(由平稳序列的方差常性)
又
,
,故
,
所以 =
。
根据 Yule–Walker 方程,有
,
即 ,
故 =
本题也可不要推导,由相关公式和性质直接给出结果。
2. 已知某 AR(2)模型为: 求 , 的值。
1.5
样本自相关系数图
1
0.5
0 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24
-0.5
自相关系数如下:
延迟
1
2
3
4
5
6
7
8
自相关系数 0.5060 0.5385 0.3736 0.2907 0.2578 0.1475 0.2696 0.1862
延迟
9
10
11
12
13
14
15
16
自相关系数 0.1776 0.2584 0.2070 0.2263 0.1375 -0.0268 -0.0532 -0.1124
延迟
时间序列分析课后习题答案1

时间序列分析课后习题答案(上机第二章 2、328330332334336338340342(1时序图如上:序列具有明显的趋势和周期性,该序列非平稳。
(2样本自相关系数:(3该样本自相关图上,自相关系数衰减为 0的速度缓慢,且有正弦波状,显示序列具有趋势和周期,非平稳。
3、 (1样本自相关系数:(2序列平稳。
(3因 Q 统计量对应的概率均大于 0.05,故接受该序列为白噪声的假设,即序列为村随机序列。
5、 (1时序图和样本自相关图:50100150200250300350(2序列具有明显的周期性,非平稳。
(3序列的 Q 统计量对应的概率均小于 0.05,该序列是非白噪声的。
6、 (1根据样本相关图可知:该序列是非平稳,非白噪声的。
(2对该序列进行差分运算:1--=t t t x x y {t y }的样本相关图:该序列平稳,非白噪声。
第三章:17、 (1结论:序列平稳,非白噪声。
(2 拟合 MA(2 model:VariableCoefficient Std. Error t-Statistic Prob. C 80.40568 4.630308 17.36508 0.0000 MA(1 0.336783 0.114610 2.938519 0.0047 R-squared0.171979 Mean dependent var 80.29524 Adjusted R-squared 0.144379 S.D. dependent var 23.71981 S.E. of regression 21.94078 Akaike info criterion 9.061019 Sum squared resid 28883.87 Schwarz criterion 9.163073 Log likelihood -282.4221 F-statistic 6.230976 Durbin-Watson stat 2.072640 Prob(F-statistic 0.003477Residual tests(3拟合 AR(2model:C 79.71956 5.442613 14.64729 0.0000 AR(10.2586240.1288102.0077940.0493R-squared0.154672 Mean dependent var 79.50492 Adjusted R-squared 0.125522 S.D. dependent var 23.35053 S.E. of regression 21.83590 Akaike info criterion 9.052918 Sum squared resid 27654.79 Schwarz criterion 9.156731 Log likelihood -273.1140 F-statistic 5.306195 Durbin-Watson stat 1.939572 Prob(F-statistic 0.007651Inverted AR Roots.62-.36Residual tests:(4 拟合 ARMA (2, 1 model :Variable Coefficient Std. Error t-Statistic Prob. C 79.17503 4.082908 19.39183 0.0000 AR(1 -0.586834 0.118000 -4.973170 0.0000 AR(2 0.376120 0.082091 4.581756 0.0000 MA(11.1139990.09712211.470120.0000R-squared0.338419 Mean dependent var 79.50492 Adjusted R-squared 0.303599 S.D. dependent var 23.35053 S.E. of regression 19.48617 Akaike info criterion 8.840611 Sum squared resid 21643.51 Schwarz criterion 8.979029 Log likelihood-265.6386 F-statistic9.719104Inverted AR Roots .39-.97 Inverted MA Roots-1.11Estimated MA process is noninvertible残差检验:(5拟合 ARMA (1, (2 model:Variable Coefficient Std. Error t-Statistic Prob. C 79.52100 4.621910 17.205230.0000 AR(1 0.270506 0.125606 2.153603 0.0354 R-squared0.157273 Mean dependent var 79.55161 Adjusted R-squared 0.128706 S.D. dependent var 23.16126 S.E. of regression 21.61946 Akaike info criterion 9.032242 Sum squared resid 27576.65 Schwarz criterion 9.135167 Log likelihood -276.9995 F-statistic 5.505386 Durbin-Watson stat 1.981887 Prob(F-statistic 0.006423Inverted AR Roots.27残差检验:(6优化根据 SC 准则,最优模型为 ARMA(2,1模型。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
时间序列分析习题解答
第二章 P.33 2.3 习 题
2.1 考虑序列{1,2,3,4,5,…,20}: (1) 判断该序列是否平稳;
(2) 计算该序列的样本自相关系数k ^
ρ(k=1,2,…,6); (3) 绘制该样本自相关图,并解释该图形。
解:(1) 由于不存在常数μ,使,t EX t T μ=∀∈,所以该序列不是平稳序列。
显然,该序列是按等步长1单调增加的序列。
(2) 1^
ρ=0.85000 2^
ρ=0.70150 3^
ρ=0.55602
4^ρ=0.41504 5^ρ=0.28008 6^
ρ=0.15263 (3) 样本自相关图
该图横轴表示自相关系数,纵轴表示延迟时期数。
该图的自相关系数递减的速度缓慢,在6期的延迟时期里,自相关系数一直为正,说明该序列是有单调趋势的非平稳序列。
附:SAS 程序如下: data ex2_1; input freq@@; cards;
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 ;
proc arima data=ex2_1; identify var=freq Nlag=6; run;
可得到上图的自相关图等内容, 更多结果被省略。
2.2 1975-1980年夏威夷岛莫那罗亚火山(Mauna Loa )每月释放的CO 2数据如下(单位:ppm )见下表。
330.45 330.97 331.64 332.87 333.61 333.55 331.90 330.05 328.58 328.31 329.41 330.63 331.63 332.46 333.36 334.45 334.82 334.32 333.05 330.87 329.24 328.87 330.18 331.50 332.81 333.23 334.55 335.82 336.44 335.99 334.65 332.41 331.32 330.73 332.05 333.53 334.66 335.07 336.33 337.39 337.65 337.57 336.25 334.39 332.44 332.25 333.59 334.76 335.89 336.44 337.63 338.54 339.06 338.95 337.41 335.71 333.68 333.69 335.05 336.53 337.81 338.16 339.88 340.57 341.19 340.87 339.25 337.19 335.49 336.63 337.74 338.36
(1)绘制该序列时序图,并判断该序列是否平稳; (2)计算该序列的样本自相关系数k ^
(k=1,2,…,24); (3)绘制该样本自相关图,并解释该图形。
解:(1) 该序列的时序图:
由上图可以看出,CO 2排量总体逐步上升,且以年为周期呈现出一定的周期性。
故该序列是呈现带周期性的单调上升趋势,该序列不平稳。
(2) 该序列的样本自相关系数k ^
(k=1,2,…,24) 如下图第三列Lag=1到24所示。
(3) 样本自相关图如上。
解释如下:
上图第三列数可看出样本自相关系数k ^
(k=0,1,2,…,24)。
该图形显示序列自相关系数长期位于零轴的一边,这是具有单调趋势序列的典型特征,同时自相关图呈现出明显的正弦波动规律,这是具有周期变化规律的非平稳序列的典型特征。
自相关图显示出带长期递增趋势的周期性质。
附SAS 程序如下:
data ex2_2; input CO2@@;
time=intnx('month','01jan1975'd ,_n_-1); format time date.; cards ;
330.45 330.97 331.64 332.87 333.61 333.55 331.90 330.05 328.58 328.31 329.41 330.63 331.63 332.46 333.36 334.45 334.82 334.32 333.05 330.87 329.24 328.87 330.18 331.50 332.81 333.23 334.55 335.82 336.44 335.99 334.65 332.41 331.32 330.73 332.05 333.53 334.66 335.07 336.33 337.39 337.65 337.57 336.25 334.39 332.44 332.25 333.59 334.76 335.89 336.44 337.63 338.54 339.06 338.95 337.41 335.71 333.68 333.69 335.05 336.53 337.81 338.16 339.88 340.57 341.19 340.87 339.25
337.19 335.49 336.63 337.74 338.36
;
proc gplot data =ex2_2; plot CO2*time=1;
symbol1 c =black v =star i =join; run ;
proc arima data=ex2_2; identify var=CO2 Nlag=24; run;
2.3 1945-1950年费城月度降雨量数据如下(单位:mm )见下表。
—————————————————————————————————— 69.3 80.0 40.9 74.9 84.6 101.1 225.0 95.3 100.6 48.3 144.5 128.3 38.4 52.3 68.6 37.1 148.6 218.7 131.6 112.8 81.8 31.0 47.5 70.1 96.8 61.5 55.6 171.7 220.5 119.4 63.2 181.6 73.9 64.8 166.9 48.0 137.7 80.5 105.2 89.9 174.8 124.0 86.4 136.9 31.5 35.3 112.3 143.0 160.8 97.0 80.5 62.5 158.2 7.6 165.9 106.7 92.2 63.2 26.2 77.0 52.3 105.4 144.3 49.5 116.1 54.1 148.6 159.3 85.3 67.3 112.8 59.4 ____________________________________________________________________
(1)计算该序列的样本自相关系数k ^
ρ(k=1,2,…,24); (2)判断该序列的平稳性; (3)判断该序列的纯随机性。
解:(1) 该序列的样本自相关系数k ^
ρ(k=1,2,…,24) 如下图第三列Lag=1
到24所示。
(2) 该序列基本平稳,时序图如下:
(3)白噪声检验输出结果为:
观察上面结果,由于延迟6,12,18,24时,0.14<P<0.37,所以该序列为非白噪声序列,但相关性不够显著。
附SAS程序(画时序图、计算相关系数和白噪声检验)如下:
data ex2_3;
input rainfall@@;
time=intnx('month','01jan1975'd,_n_-1);
format time MONYY5.;
cards;
69.3 80.0 40.9 74.9 84.6 101.1 225.0 95.3 100.6 48.3 144.5 128.3
38.4 52.3 68.6 37.1 148.6 218.7 131.6 112.8 81.8 31.0 47.5 70.1
96.8 61.5 55.6 171.7 220.5 119.4 63.2 181.6 73.9 64.8 166.9 48.0 137.7 80.5 105.2 89.9 174.8 124.0 86.4 136.9 31.5 35.3 112.3 143.0 160.8 97.0 80.5 62.5 158.2 7.6 165.9 106.7 92.2 63.2 26.2 77.0 52.3 105.4 144.3 49.5 116.1 54.1 148.6 159.3 85.3 67.3 112.8 59.4
;
proc gplot ;
plot rainfall*time=1;
symbol1c=black v=star i=join;
run;
proc arima ;
identify var=rainfall nlag=24;
run;。
