材料力学上册第五章梁弯曲时的位移
合集下载
材料力学第五章梁弯曲时的位移

实例3 :均布载荷
分析受均布载荷作用下梁的位移。
材料力学第五章梁弯曲时 的位移
在材料力学的第五章中,我们将学习有关梁在弯曲时的位移。掌握梁的基本 知识、位移方程和位移计算方法,以及梁的挠度与转角关系。
梁的基本知识
1 定义
梁是一种长条形结构,承受着沿其长度方向的外部力。
2 类型
常见的梁包括简支梁、悬臂梁和受力梁。
3 材料
梁可以由不同类型的材料制成,例如钢、木材或混凝土。
梁的位移方程
1 弯曲位移
2 挠度
3 转角
梁在弯曲时,沿梁的长度方 向发生位移。
挠度是梁的中点相对于其自 由状态的偏移量。
转角是指梁在弯曲时端部角 度的变化。
简支梁的位移计算方法
1
载荷和反力
计算简支梁上的载荷和反力分布。
2
弯矩方程
使用弯矩方程推导出简支梁的位移方程。
3
边界条件
应用适当的边界条件来解决位移方程中的未知量。
悬臂梁的位移计算方法
加载和支座反力
确定悬臂梁上的加载和支座反力。
弯曲力矩方程
通过推导弯曲力矩方程来解决悬臂 梁的位移问题。
解决边界条件
应用边界条件来计算悬臂梁的位移。
受力梁的位移计算方法
1
截面转动方程
2
推导出受力梁的截面转动方程。
3
确定力的分布
分析受力梁上的力分布,包括集中力和均布 力。
边界条件和位移方程
应用边界条件,求解受力梁的位移方程。ຫໍສະໝຸດ 梁的挠度与转角关系挠度
挠度是梁在弯曲时沿其长度方向上的位移。
转角
转角是梁在弯曲时端部偏离初始位置的角度。
关系公式
挠度和转角之间存在一定的关系,可以通过公式计算。
材料力学第五章梁弯曲时的位移

第五章 梁弯曲时的位移
工程实例
7-1
工程实例
工程实例
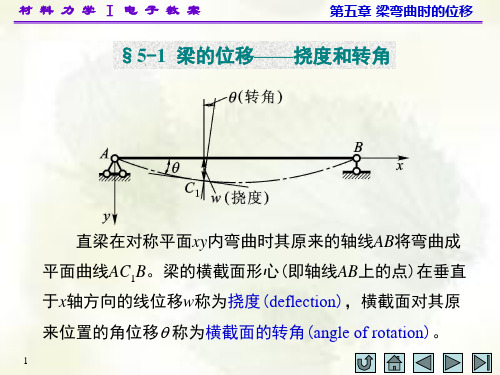
5-1 梁的位移——挠度及转角
建立坐标系,oxy为梁对称面,外力作用在对 称面内。所以,挠曲线为o xy面内的平面曲线。
挠度
y 向下为正。
y
x
y
转角
x
挠曲线
挠曲线方程:
7-2
w= f (x)
挠度
略去剪力的影响,则平面假设成立,发
y
5.2 积分法求梁的挠度和转角
例1 求梁的转角方程和挠度方程,并求最大转角和最大挠度, 梁的EI已知。
解 1)由梁的整体平衡分析可得:
2)写出x截面的弯矩方程
FAx 0, FAy F (), M A Fl (
)
A
x
l
yB
F B
B
x
M ( x ) F (l x ) F ( x l )
A
FAx 0, FAy
Fb Fa , FBy l l
2)弯矩方程
FAy x1
ymax
x2
FBy
AC 段:
M x1 FAy x1 Fb x1 ,0 x1 a l
y
a
b
CB 段:
Fb M x2 FAy x2 F ( x2 a ) x2 F ( x2 a ), l
目录
a x2 l
5.2 积分法求梁的挠度和转角
A d 2 w1 Fb EI M ( x1 ) x1 2 dx1 l FAy x1 dw1 Fb 2 EI EI ( x1 ) x1 C1 x2 dx1 2l Fb 3 a EIw1 x C1 x1 D1 6l a x2 l CB 段: y d 2 w2 Fb EI M ( x2 ) x2 F ( x2 a) 2 dx2 l dw Fb 2 F EI 2 EI ( x2 ) x 2 ( x2 a ) 2 C 2 dx2 2l 2 Fb 3 F EIw2 x 2 ( x2 a)3 C2 x2 D2 6l 6
工程实例
7-1
工程实例
工程实例
5-1 梁的位移——挠度及转角
建立坐标系,oxy为梁对称面,外力作用在对 称面内。所以,挠曲线为o xy面内的平面曲线。
挠度
y 向下为正。
y
x
y
转角
x
挠曲线
挠曲线方程:
7-2
w= f (x)
挠度
略去剪力的影响,则平面假设成立,发
y
5.2 积分法求梁的挠度和转角
例1 求梁的转角方程和挠度方程,并求最大转角和最大挠度, 梁的EI已知。
解 1)由梁的整体平衡分析可得:
2)写出x截面的弯矩方程
FAx 0, FAy F (), M A Fl (
)
A
x
l
yB
F B
B
x
M ( x ) F (l x ) F ( x l )
A
FAx 0, FAy
Fb Fa , FBy l l
2)弯矩方程
FAy x1
ymax
x2
FBy
AC 段:
M x1 FAy x1 Fb x1 ,0 x1 a l
y
a
b
CB 段:
Fb M x2 FAy x2 F ( x2 a ) x2 F ( x2 a ), l
目录
a x2 l
5.2 积分法求梁的挠度和转角
A d 2 w1 Fb EI M ( x1 ) x1 2 dx1 l FAy x1 dw1 Fb 2 EI EI ( x1 ) x1 C1 x2 dx1 2l Fb 3 a EIw1 x C1 x1 D1 6l a x2 l CB 段: y d 2 w2 Fb EI M ( x2 ) x2 F ( x2 a) 2 dx2 l dw Fb 2 F EI 2 EI ( x2 ) x 2 ( x2 a ) 2 C 2 dx2 2l 2 Fb 3 F EIw2 x 2 ( x2 a)3 C2 x2 D2 6l 6
材料力学梁弯曲时的位移
w
1 w2
3/ 2
M x
EI
由于梁的挠曲线为一平坦的曲线,上式中的w2与1相比可略
去,于是得挠曲线近似微分方程 w M x
EI
8
材料力学Ⅰ电子教案
第五章 梁弯曲时的位移
Ⅱ. 挠曲线近似微分方程的积分及边界条件
w M x
EI 求等直梁的挠曲线方程时可将上式改写为
EIw M x
后进行积分,再利用边界条件(boundary condition)确定积分 常数。
左段梁 (0 x a)
右段梁 (a x l)
q1
w1
Fb 2lEI
1 3
l2 b2
x
2
q2
w2
Fb 2lEI
l b
x
a
2
x2
1 3
l2
b2
w1
Fbx 6lEI
l2
b2
x2
w2
Fb 6lEI
l b
x
a
3
x3
l2
b2
x
30
材料力学Ⅰ电子教案
第五章 梁弯曲时的位移
于是有
C2 0
及
EIw|xl
q 2
l4 6
l4 12
C1l
0
即
C1
ql3 24
,C2
0
从而有
转角方程 q w q l3 6lx2 4x3 24EI
挠曲线方程 w qx l3 2lx2 x3 24EI
22
材料力学Ⅰ电子教案
第五章 梁弯曲时的位移
根据对称性可知,两支座处的转角qA及qB的绝对值相
F lx
x2 2
C1
EIw
材料力学课件5第五章梁弯曲时的位移5-1

F A
x
θmax
l
wmax
y
B o
F A
o
B
l
y
x
请大家将坐标原点取在固定端,练习完 整解题过程。
例题5-2 试求图示等直梁的挠曲线方程和转角方 程,并确定其最大挠度wmax和最大转角max。
解:该梁的弯矩方程为
ql 1 2 q M x x qx lx x 2 2 2 2
Fb x2 =EI w1 +C1 (1) l 2 Fb x3 EI w1 = +C1 x D1 (2) l 6
Fb x2 F(x-a) 2 EI w + +C 2 (3) 2 = l 2 2 Fb x3 F(x-a) 3 EI w 2 = + +C 2 x D2 (4) l 6 6
截面x的位移—挠度、转角 转角 θ C 1 θ w C
1
挠度
A
x y
B
x
挠曲线
梁变形前后横截面形心位置的变化称 为位移,位移包括线位移和角位移。在小 变形和忽略剪力影响(l >> h)的条件下, 略去x 方向的线位移,y 方向的线位移是截 面形心沿垂直于梁轴线方向的位移,称为 挠度,用 w 表示,单位m、mm;角位移 是横截面变形前后的夹角,称为转角,用 θ 表示,单位弧度。而变形后的轴线是一 条光滑连续平坦的曲线称为挠曲线(弹性 曲线) 。
w'(l )=0 代入(1): Fl 2 / 2+C1 = 0 得:C1=- Fl 2 / 2
w(l ) =0 代入(2): Fl 3/ 6+C1l+C2 = 0
C2= -Fl 3/ 6 -C1l = -Fl 3/ 6 + Fl 3 / 2 = Fl 3/ 3
材料力学土木类第五章 梁弯曲时的位移.ppt
M x F b x
则:
EIw1
M
x
F
b l
x
l
积分可得:
EIw1
F
b l
x2 2
C1
EIw1
F
b l
x3 6
C1x
D1
DB段: a x l M x F b x Fx a
l
F x
A
D
B
x
a
b
l
y
则:
EIw2
M
x
由此可得:1 6
Fa3
C1a
D1
1 6
Fa3
1 2
Fa3
2 3
Fa3
1 2
Fa2
C1
1 2
Fa2
Fa2
即:
C1 Fa2;
D1
7 6
Fa3
最后可得:
wA
w1
x0
D1
7 Fa 3 6EI
(向下)
A
w1 '
x0
C1
Fa 2 EI
(逆时针)
小结: (1) 两段:四个常数,每增加一段,就增加 两个积分常数;
则: D1 D2
C1 C2
(2)约束条件:a) x 0 时, w1 0 由此可得:D1 0 D2
b) x l 处, w2 0
由此可得:
C2
Fb 6l
l2
b2
C1
则梁的挠曲线和转角方程为:
材料力学第五章梁弯曲时的位移课件

qw q0 (l39lx 28x3)
4E 8I
w(0)0 q (0) q0l3
48EI
固定铰支座 活动铰支座
w(l)0 q(l) 0
固定端 活动铰支座
材料力学第五章梁弯曲时的位移
22
M (x)Ew Iq0(3lx 4x2) 抛物线 8
FS(x)ddM xq 80(3l8x)
直线
q(x)dFS dx
材料力学第五章梁弯曲时的位移
12
x
FA
x
FA
Fb l
FB
FB
Fa l
AD段( 0≤ x ≤ a ):
M1(x)
Fbx l
DB段( a ≤ x ≤ l ):
M2(x)F l b xF(xa)
材料力学第五章梁弯曲时的位移
13
x a AD段( 0≤ ≤ ):
M1(x)
Fbx l
EIw1
Fbx l
Ew I1 EqI1F l bx22C1
q0
M(0)0
FS(0)
3 8
q0l
M(l) 81q0l2
FS(l) 85q0l
材料力学第五章梁弯曲时的位移
23
q0
1 8
q0l
材料力学第五章梁弯曲时的位移
7
挠曲线上某些点的已知位移(挠度和 转角)条件 —— 边界条件
wA = 0 wB = 0
wA = 0 qA = 0
边界条件 —— 支座处的约束条件
材料力学第五章梁弯曲时的位移
8
挠曲线的任意点上,有唯一确定的挠 度和转角 —— 连续条件
错!
错!
当弯矩方程需要分段建立时,在相邻梁 段的交接处,应具有相同的挠度和转角。
4E 8I
w(0)0 q (0) q0l3
48EI
固定铰支座 活动铰支座
w(l)0 q(l) 0
固定端 活动铰支座
材料力学第五章梁弯曲时的位移
22
M (x)Ew Iq0(3lx 4x2) 抛物线 8
FS(x)ddM xq 80(3l8x)
直线
q(x)dFS dx
材料力学第五章梁弯曲时的位移
12
x
FA
x
FA
Fb l
FB
FB
Fa l
AD段( 0≤ x ≤ a ):
M1(x)
Fbx l
DB段( a ≤ x ≤ l ):
M2(x)F l b xF(xa)
材料力学第五章梁弯曲时的位移
13
x a AD段( 0≤ ≤ ):
M1(x)
Fbx l
EIw1
Fbx l
Ew I1 EqI1F l bx22C1
q0
M(0)0
FS(0)
3 8
q0l
M(l) 81q0l2
FS(l) 85q0l
材料力学第五章梁弯曲时的位移
23
q0
1 8
q0l
材料力学第五章梁弯曲时的位移
7
挠曲线上某些点的已知位移(挠度和 转角)条件 —— 边界条件
wA = 0 wB = 0
wA = 0 qA = 0
边界条件 —— 支座处的约束条件
材料力学第五章梁弯曲时的位移
8
挠曲线的任意点上,有唯一确定的挠 度和转角 —— 连续条件
错!
错!
当弯矩方程需要分段建立时,在相邻梁 段的交接处,应具有相同的挠度和转角。
材料力学 第五章 梁弯曲时的位移 A

材料力学
第五章梁弯曲时的位移
主讲:韩玉林教授
东南大学工程力学系
§5-1 梁的位移
一.工程实例
在工程实践中,对某些受弯构件,除要求具有足够的强度外,还要求变形不能过大,即要求构件有足够的刚度,以保证结构或机器正常工作,如摇臂钻床。
约束对位移的影响
没有约束无法确定位移
连续光滑曲线;铰支座对位移的限制。
边界条件:
A B w w ==约束对位移的影响
连续光滑曲线;固定端对位移的限制。
边界条件:
0,0
B B w θ==约束对位移的影响
注意:
1.分段连续弯矩方程必须从原点沿x 的正向依次写出;
2.对含(x-a)项可不展开,把它视为新变量积分,更为方便;
试绘制图示梁挠曲轴的大致形状
绘制原则
•挠曲轴是一条连续而光滑的曲线(中间铰链除外
,该处只连续而不光滑),为此必须满足连续光滑
条件。
•挠曲轴必须符合梁的边界条件
•弯矩为正的梁段是一条凹曲线;弯矩为负的梁段是一条凸曲线;弯矩为零的梁段不变形,为一条直线
•弯矩图由正变负或由负变正处,弯矩为零处,
挠曲轴出现拐点
下列图示梁的Q、M图和挠曲轴大致形状先用虚线标出,请读者自行检查是否正确,如有错,请在原图上改正
图示梁有一中间铰链,试勾画出挠曲轴大致形状,并求C处的挠度。
图示梁,左右端各作用一力偶矩m 1和m 2,要使挠曲轴的拐点位于距左端为L/3处,问m 1和m 2应保持何种比例?
作业
•5-8,5-11,5-13,5-17,5-25
谢谢大家!。
材料力学I-第5章%20梁弯曲时的位移[1]
![材料力学I-第5章%20梁弯曲时的位移[1]](https://img.taocdn.com/s3/m/a77b562e915f804d2b16c1ba.png)
T$
T%
$
Z'
Z&
'
D
)$ )%
TD[ T[ d [ d D TD [ D T[ 0 [ TD[ D d [ d D , Z c (,Zc 0 [ TD[ T[ d [ d D c (,Z TD[ T[ & (,Z TD[ T[ & [ ' Z c (,Zc 0 [ TD[ TD [ D T[ D d [ d D c (,Z TD[ TD [ D T[ & (,Z TD[ TD [ D T[ & [ ' 0 [
0H
O
0H
G Z )O )[ G[ (, GZ )O[ )[ & G[ (, Z )O[ )[ &[ ' (, T & Z '
0
)O )[
T$ T%
T O
ZPD[
)$
[ TO 0 [ )$ [ T [ [ T O[ [ O [ T O[ O
(,Zcc (,Zc (,Z
& '
O T O O
)$
$ O
%
T O
Z
[
(,Z
&
[ D
&
TD ' T Z
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
6EIl
Mechanics of Materials
wmax 在AC段
wmax
=
Fb( l 2 − b2 )3 2 9 3EIl
Mechanics of Materials
例题:已知梁的刚度EI,用奇异函数法求梁的位移
θA、θD、wB、wD。
qa
q
A
B
C Dx
FA a
y
aa
FC
解:建立图示坐标系
1、求约束反力
( ) M(x) = − EI
w′′ 1+ w′2
32
Mechanics of Materials
若挠曲线是较平坦的光滑连续曲线, w′ << 1,
可忽略不计。
则
M (x) = −w′′
EI
即
EIw′′ = − M (x)
——挠曲线近似微分方程
适用条件: 线弹性小变形; 对称弯曲的细长梁。
2、积分法确定梁的位移
一、挠曲线近似微分方程
材力 数学
1 = M(x)
ρ EI
( ) 1 = w′′
ρ 1 + w′2 3 2
x y M > 0 w′′ < 0
( ) M(x) = ± EI
w′′ 1+ w′2
32
x
( ) M(x) = − EI
w′′ 1+ w′2
32
y M < 0 w′′ > 0
☻挠曲线微分方程的正负号与选取的坐标系有关
2
Mechanics of Materials
弯矩的通用方程
∑ ∑ ∑ ∑ ( ) M x =
i
Mi < x −ai >0 +
j
Fj < x − bj > +
k
qk 2
<
x − ck
>2
−
k
qk 2
< x − dk
>2
说明:
☻Mi以顺时针为正,Fj、qk以向上为正。
☻Mi、Fj包括外载荷和约束反力。 ☻ai、bj分别是集中力偶和集中力作用点的坐标,
b2
x
EIw2=
−
Fb 6l
x3
+
F(x −
6
a)3
+
Fb
l2 − 6l
b2
x
4、最大转角和最大挠度
a Fb
( ) θA
=
Fb l 2 − b2 6EIl
= Fab(l + b)
6EIl
A FA y
lC
Bx FB
( ) θB
=
−
Fbl 2 2EIl
+
Fb2 2EI
+
Fb l 2 − b2 6EIl
= − Fab(l + a)
6EIl
若a>b,
θmax
=
Fab(l + a)
6EIl
Mechanics of Materials
( ) EIw1′
=
−
Fb 2l
x2
+
Fb
l2 − 6l
b2
( ) EIw′2
=
−
Fb 2l
x2
+
F(x −
2
a)2
+
Fb
l2 − 6l
b2
( ) ( ) EIw1
=
−
Fb 6l
x3
+
Fb
l2 − 6l
4
4
2
3、转角方程和挠度方程
EIθ = − qa x2 + qa < x − a >2 − 7qa < x − 2a >2+ q < x − 2a >3 +C
8
2
8
6
EIw = − qa x3 + qa < x − a >3 − 7qa < x − 2a >3
24 6
24
+ q < x − 2a >4 +Cx + D 24
M(x)= M < x − a >0
2、仅有F作用的情况
M(x) = F < x − b >1
3、仅有q作用的情况
M
x
x
a
y
F
bx
y
x
q
M(x)= q < x − c >2
c
x
2
x
y
4、M、F、q共同作用的情况
M(x) = M < x − a >0+ F < x − b >1 + q < x − c >2
挠度w——向下为正,向上为负。
转角θ——顺时针为正,逆时针为负。
挠度w 转角θ
x
转角θ 挠曲线
y
线弹性小变形状态,挠曲线为光滑平坦的曲 线,故挠度和转角是位置坐标的函数。
即
w = w( x ) θ = θ( x )θ很Leabharlann 时,θ≈tan
θ
=
dw dx
Mechanics of Materials
§2 挠曲线近似微分方程及其积分
θ max
=
θA
=
Fl 2 16EI
wmax
=
wl
2
=
Fl 3 48EI
Mechanics of Materials
§3 奇异函数法求梁的挠度和转角
一、奇异函数
对n≥0(n为正整数)的情况,函数
f
(x)
=<
x
−
a
>n
=
⎧
⎩⎨(x
0
− a)n
(x < a) (x ≥ a)
——称为奇异函数
奇异函数的微分 奇异函数的积分
2
2
转角方程 EIw′ = 1 ql 2 x − 1 qlx 2 + 1 qx3 + C
2
2
6
挠度方程 EIw = 1 ql 2 x2− 1 qlx 3+ 1 qx4 + Cx + D
4
6
24
Mechanics of Materials q
l
wmaxx
y
θmax
EIw′ = 1 ql 2 x − 1 qlx2 + 1 qx3 + C
x2
+
F(x −
2
a)2
+
C2
挠度 方程
EIw1
=
−
Fb 6l
x3
+
C1
x
+
D1
EIw2
=
−
Fb 6l
x3
+
F(x −
6
a)3
+
C2 x
+
D2
EIw1′
=
−
Fb 2l
x2
+
C1
EIw1
=
−
Fb 6l
x3
+
C1
x
+
D1
Mechanics of Materials
EIw′2
=
−
Fb 2l
x2
+
F(x −
2
a)2
+
C2
EIw2=
−
Fb 6l
x3
+
F(x −
6
a)3
+
C2 x
+
D2
3、利用边界条件和光滑 A 连续条件确定积分常数
a Fb
lC
Bx
FA y
FB
x=0 x=a x=a
w1 = 0 θ1 = θ2 w1 = w2
D1 = 0 C1 = C2 D1 = D2
( ) C2
=
Fb
l2 − 6l
b2
x = l w2 = 0
− Fb l 2 + F(l − a)3
6
6
+ C2l = 0
Mechanics of Materials
( ) EIw1′
=
−
Fb 2l
x2
+
Fb
l2 − 6l
b2
( ) EIw′2
=
−
Fb 2l
x2
+
F(x −
2
a)2
+
Fb
l2 − 6l
b2
( ) ( ) EIw1
=
−
Fb 6l
x3
+
Fb
l2 − 6l
M (x) = Fb x − F (x − a)
l
(a ≤ x ≤ l )
A FA y
Mechanics of Materials
a Fb
lC
Bx
FB
AC段
CB段
弯矩 方程
M1
(x)
=
Fb l
x
M2(x)
=
Fb l
x
−
F(x
−
a)
转角 方程
EIw1′
=
−
Fb 2l
x2
+
C1
EIw′2
=
−
Fb 2l
2
F lC
l2 − b2 3
b
Bx
FB
5、讨论
①当 b → 0,
Mechanics of Materials
wmax 在AC段
wmax
=
Fb( l 2 − b2 )3 2 9 3EIl
Mechanics of Materials
例题:已知梁的刚度EI,用奇异函数法求梁的位移
θA、θD、wB、wD。
qa
q
A
B
C Dx
FA a
y
aa
FC
解:建立图示坐标系
1、求约束反力
( ) M(x) = − EI
w′′ 1+ w′2
32
Mechanics of Materials
若挠曲线是较平坦的光滑连续曲线, w′ << 1,
可忽略不计。
则
M (x) = −w′′
EI
即
EIw′′ = − M (x)
——挠曲线近似微分方程
适用条件: 线弹性小变形; 对称弯曲的细长梁。
2、积分法确定梁的位移
一、挠曲线近似微分方程
材力 数学
1 = M(x)
ρ EI
( ) 1 = w′′
ρ 1 + w′2 3 2
x y M > 0 w′′ < 0
( ) M(x) = ± EI
w′′ 1+ w′2
32
x
( ) M(x) = − EI
w′′ 1+ w′2
32
y M < 0 w′′ > 0
☻挠曲线微分方程的正负号与选取的坐标系有关
2
Mechanics of Materials
弯矩的通用方程
∑ ∑ ∑ ∑ ( ) M x =
i
Mi < x −ai >0 +
j
Fj < x − bj > +
k
qk 2
<
x − ck
>2
−
k
qk 2
< x − dk
>2
说明:
☻Mi以顺时针为正,Fj、qk以向上为正。
☻Mi、Fj包括外载荷和约束反力。 ☻ai、bj分别是集中力偶和集中力作用点的坐标,
b2
x
EIw2=
−
Fb 6l
x3
+
F(x −
6
a)3
+
Fb
l2 − 6l
b2
x
4、最大转角和最大挠度
a Fb
( ) θA
=
Fb l 2 − b2 6EIl
= Fab(l + b)
6EIl
A FA y
lC
Bx FB
( ) θB
=
−
Fbl 2 2EIl
+
Fb2 2EI
+
Fb l 2 − b2 6EIl
= − Fab(l + a)
6EIl
若a>b,
θmax
=
Fab(l + a)
6EIl
Mechanics of Materials
( ) EIw1′
=
−
Fb 2l
x2
+
Fb
l2 − 6l
b2
( ) EIw′2
=
−
Fb 2l
x2
+
F(x −
2
a)2
+
Fb
l2 − 6l
b2
( ) ( ) EIw1
=
−
Fb 6l
x3
+
Fb
l2 − 6l
4
4
2
3、转角方程和挠度方程
EIθ = − qa x2 + qa < x − a >2 − 7qa < x − 2a >2+ q < x − 2a >3 +C
8
2
8
6
EIw = − qa x3 + qa < x − a >3 − 7qa < x − 2a >3
24 6
24
+ q < x − 2a >4 +Cx + D 24
M(x)= M < x − a >0
2、仅有F作用的情况
M(x) = F < x − b >1
3、仅有q作用的情况
M
x
x
a
y
F
bx
y
x
q
M(x)= q < x − c >2
c
x
2
x
y
4、M、F、q共同作用的情况
M(x) = M < x − a >0+ F < x − b >1 + q < x − c >2
挠度w——向下为正,向上为负。
转角θ——顺时针为正,逆时针为负。
挠度w 转角θ
x
转角θ 挠曲线
y
线弹性小变形状态,挠曲线为光滑平坦的曲 线,故挠度和转角是位置坐标的函数。
即
w = w( x ) θ = θ( x )θ很Leabharlann 时,θ≈tan
θ
=
dw dx
Mechanics of Materials
§2 挠曲线近似微分方程及其积分
θ max
=
θA
=
Fl 2 16EI
wmax
=
wl
2
=
Fl 3 48EI
Mechanics of Materials
§3 奇异函数法求梁的挠度和转角
一、奇异函数
对n≥0(n为正整数)的情况,函数
f
(x)
=<
x
−
a
>n
=
⎧
⎩⎨(x
0
− a)n
(x < a) (x ≥ a)
——称为奇异函数
奇异函数的微分 奇异函数的积分
2
2
转角方程 EIw′ = 1 ql 2 x − 1 qlx 2 + 1 qx3 + C
2
2
6
挠度方程 EIw = 1 ql 2 x2− 1 qlx 3+ 1 qx4 + Cx + D
4
6
24
Mechanics of Materials q
l
wmaxx
y
θmax
EIw′ = 1 ql 2 x − 1 qlx2 + 1 qx3 + C
x2
+
F(x −
2
a)2
+
C2
挠度 方程
EIw1
=
−
Fb 6l
x3
+
C1
x
+
D1
EIw2
=
−
Fb 6l
x3
+
F(x −
6
a)3
+
C2 x
+
D2
EIw1′
=
−
Fb 2l
x2
+
C1
EIw1
=
−
Fb 6l
x3
+
C1
x
+
D1
Mechanics of Materials
EIw′2
=
−
Fb 2l
x2
+
F(x −
2
a)2
+
C2
EIw2=
−
Fb 6l
x3
+
F(x −
6
a)3
+
C2 x
+
D2
3、利用边界条件和光滑 A 连续条件确定积分常数
a Fb
lC
Bx
FA y
FB
x=0 x=a x=a
w1 = 0 θ1 = θ2 w1 = w2
D1 = 0 C1 = C2 D1 = D2
( ) C2
=
Fb
l2 − 6l
b2
x = l w2 = 0
− Fb l 2 + F(l − a)3
6
6
+ C2l = 0
Mechanics of Materials
( ) EIw1′
=
−
Fb 2l
x2
+
Fb
l2 − 6l
b2
( ) EIw′2
=
−
Fb 2l
x2
+
F(x −
2
a)2
+
Fb
l2 − 6l
b2
( ) ( ) EIw1
=
−
Fb 6l
x3
+
Fb
l2 − 6l
M (x) = Fb x − F (x − a)
l
(a ≤ x ≤ l )
A FA y
Mechanics of Materials
a Fb
lC
Bx
FB
AC段
CB段
弯矩 方程
M1
(x)
=
Fb l
x
M2(x)
=
Fb l
x
−
F(x
−
a)
转角 方程
EIw1′
=
−
Fb 2l
x2
+
C1
EIw′2
=
−
Fb 2l
2
F lC
l2 − b2 3
b
Bx
FB
5、讨论
①当 b → 0,
