2019年北京各区一模理科数学分类汇编---三角函数(含答案)
2019北京各区一模数学理试题分类解析-函数

2019北京各区一模数学理试题分类解析-函数注意事项:认真阅读理解,结合历年的真题,总结经验,查找不足!重在审题,多思考,多理解!7.〔2018年海淀一模理7〕函数2,1,()1,1,x ax x f x ax x ⎧-+≤=⎨->⎩假设1212,,x x x x ∃∈≠R ,使得12()()f x f x =成立,那么实数a 的取值范围是〔A 〕A 、2a <B 、2a >C 、22a -<<D 、2a >或2a <-6.〔2018年西城一模理6〕假设2log 3a =,3log 2b =,4log 6c =,那么以下结论正确的选项是〔D 〕A 、b a c <<B 、a b c <<C 、c b a <<D 、b c a <<13.〔2018年西城一模理13〕函数122,0,(),20,x x c f x x x x ⎧≤≤⎪=⎨+-≤<⎪⎩其中0c >、那么()f x 的零点是_____;假设()f x 的值域是1[,2]4-,那么c 的取值范围是_____、 答案:1-和0;(0,4]。
6、〔2018年房山一模理6〕函数⎪⎩⎪⎨⎧≥-+<--=0,120,12)(22x x x x x x x f ,那么对任意R ∈21,x x ,假设120x x <<,以下不等式成立的是(D)A.12()()0f x f x +<B.12()()0f x f x +>C.12()()0f x f x ->D.12()()0f x f x -<8、〔2018年东城一模理8〕函数21,0,()(1),0.x x f x f x x -⎧-≤=⎨->⎩假设方程()f x x a =+有且只 有两个不相等的实数根,那么实数a 的取值范围是〔A 〕A 、(),1-∞B 、(],1-∞C 、()0,1D 、[)0,+∞8、〔2018年丰台一模理8〕定义在R 上的函数y=f(x)满足f(x+2)=f(x),当-1<x ≤1 时,f(x)=x 3、假设函数()()log a g x f x x =-恰有6个零点,那么〔D 〕A.a=5或a=15B.1(0,)[5,)5a ∈+∞C.11[,][5,7]75a ∈D.11[,)[5,7)75a ∈ 6.〔2018年朝阳一模理6〕函数()f x 是定义在R 上的偶函数,且对任意的x ∈R ,都有(2)()f x f x +=.当01x ≤≤时,2()f x x =.假设直线y x a =+与函数()y f x =的图象在[0,2]内恰有两个不同的公共点,那么实数a 的值是〔D 〕A.0B.0或12- C.14-或12- D.0或14- 13.〔2018年朝阳一模理13〕函数213(),2,()24log ,0 2.x x f x x x ⎧+≥⎪=⎨⎪<<⎩假设函数 ()()g x f x k =-有两个不同的零点,那么实数k 的取值范围是. 答案:3(,1)412.〔2018年石景山一模理12〕设函数21,,2()1log ,2x a x f x x x ⎧-+<⎪⎪=⎨⎪≥⎪⎩的最小值为1-,那么实数a的取值范围是、 答案:21-≥a 。
北京市海淀区2019届高三第二学期期中练习(一模)数学(理科)试题(解析版)

【点睛】本题主要考查三角函数值的符号判断,考查了诱导公式,三角函数的符号是解决本题的关键.
3.已知等差数列
满足
,则 中一定为零的项是( )
A.
B.
C.
D.
【答案】 A
【解析】
【分析】
利用等差数列通项公式即可得到结果 .
【详解】由
得,
,解得:
,
所以,
,
故选 A
【点睛】本题考查等差数列通项公式,考查计算能力,属于基础题
.
4.已知
,则下列各式中一定成立(
)
A.
B.
C.
D.
【答案】 D
【解析】
【分析】
利用不等式的性质与指数函数性质即可作出判断
.
【详解】 x, y 的符号不确定,当 x= 2, y=- 1 时,
,
对于 A,
不成立,所以错误;
对于 B、
也错;
对于 C,
是减函数,所以,
也错;
对于 D,因为
,所以,
,正确,
故选 D
【点睛】本题考查不等式的性质,指数函数的单调性及均值不等式,考查反例法,属于基础题
.
5.执行如图所示的程序框图,输出的
值为( )
A.
B.
C.
D.
【答案】 B 【解析】 【分析】 分析程序中各变量、各语句的作用,再根据流程图所示的顺序,即可得出结论. 【详解】 解: 第 1 步: S=2, x= 4, m= 2;
( 3)生物 B 层 1 班,政治 2 班,物理 A 层 1 班;
( 4)生物 B 层 1 班,政治 2 班,物理 A 层 4 班;
( 5)生物 B 层 1 班,政治 3 班,物理 A 层 1 班;
2019北京高三一模数学---函数理科

2019北京高三一模数学---函数理科1.2019东城一模理(13)已知函数3()4f x x x =-,若1212,[,],,x x a b x x ∀∈≠都有12122()(2)(2)f x x f x f x +>+成立,则满足条件的一个区间是________. 2.2019西城一模理11.函数()sin2cos2f x x x =+的最小正周期T =____;如果对于任意的x ∈R 都有()f x a ≤,那么实数a 的取值范围是____.13. 能说明“若sin cos αβ=,则36090k αβ+=⋅+,其中k ∈Z ”为假命题的一组α,β的值是___. 3.2019海淀一模理(2)若角α的终边在第二象限,则下列三角函数值中大于零的是(A) sin(+)2πα (B) s(+)2co πα (C) sin()πα+ (D) s()co πα+ 4.2019朝阳一模理4.若函数22,1,()log ,1x x f x x x ⎧<=⎨-≥⎩,则函数()f x 的值域是A .(,2)-∞B .(,2]-∞C .[0,)+∞D .(,0)(0,2)-∞5.如图,函数()f x 的图象是由正弦曲线或余弦曲线经过变换得到的,则()f x 的解析式可以是A .()sin(2)3f x x π=+B .()sin(4)6f x x π=+C .()cos(2)3f x x π=+D .()cos(4)6f x x π=+12.能说明“函数()f x 的图象在区间[]0,2上是一条连续不断的曲线.若(0)(2)0f f ⋅>,则()f x 在(0,2)内无零点”为假命题的一个函数是 . 5.2019丰台一模理5.下列函数中,同时满足:①图象关于y 轴对称;②1212,(0,)()x x x x ∀∈+∞≠,2121()()0f x f x x x ->-的是(A )1()f x x -=(B )2()log ||f x x =(C )()cos f x x =(D )1()2x f x +=13.已知函数()cos(2)(0)2f x x ϕϕπ=+-<<. ①函数()f x 的最小正周期为____;②若函数()f x 在区间4[,]33ππ上有且只有三个零点,则ϕ的值是____.6.2019石景山一模理7. 若1x y a b >>>>,则下列各式中一定正确的是A. x ya b >B. ln ln x y <C. sin sin x y >D.a b x y< 8.已知函数()sin f x a x x =-的一条对称轴为π6x =-,12()()0f x f x +=,且函数()f x 在12(,)x x 上具有单调性,则12||x x +的最小值为A. π6B.π3C.2π3D.4π37.2019怀柔一模理6.若函数()22-=-x x f x ,则()f xA .是奇函数,且在R 上是增函数B .是偶函数,且在R 上是增函数C .是奇函数,且在R 上是减函数D .是偶函数,且在R 上是减函数11.函数的最小正周期是________,的取值范围是__________.8.2019延庆一模理3. 已知(0,1)x ∈,令log 3x a =,sin b x =,2x c =,那么,,a b c 之间的大小关系为 (A )a b c << (B )b a c << (C )b c a << (D )c a b << 4.函数()=sin 22f x x x -在区间[,]22ππ-上的零点之和是 (A )3π-(B )6π- (C )6π(D )3π(f x )12. 设()f x 是定义在R 上的单调递减函数,能说明“一定存在0x R 使得0()1f x <”为假命题的一个函数是()f x =_____.9.2019平谷一模理2. 下列函数中,在区间(0,+∞)上为增函数的是( ) A. y=B. y=lnxC. y=sinxD. y=8. 放射性物质的半衰期T 定义为每经过时间T ,该物质的质量会衰退原来的一半,铅制容器中有两种放射性物质A ,B ,开始记录时容器中物质A 的质量是物质B 的质量的2倍,而120小时后两种物质的质量相等,已知物质A 的半衰期为7.5小时,则物质B 的半衰期为( ) A. 10小时B. 8小时C. 12小时D. 15小时13. 已知函数f(x)=sin(2x+ )(其中 为实数),若f (x )≤对x ∈R 恒成立,则满足条件的 值为 (写出满足条件的一个 值即可)。
2019年北京各区高三一模文科数学分类汇编----三角函数

2019年北京各区高三一模文科数学分类汇编----三角函数1.(2019海淀一模文科)若角α的终边在第二象限,则下列三角函数值中大于零的是 D(A) sin(+)2πα (B) s(+)2co πα (C) sin()πα+ (D) s()co πα+2.(2019海淀一模文科)在△ABC 中,14,5,cos 8a b C ===,则=c ,ABC S ∆=6,3.(2019海淀一模文科)已知函数())cos4f x x x a π=-+的图象经过点(O,l),部分图象如图所示. (I)求a 的值;(Ⅱ)求图中0x 的值,并直接写出函数()f x 的单调递增区间.解:(Ⅰ)π(0)sin()cos014f a =+=12a += 所以1a =-(Ⅱ)()cos()cos 14f x x x π=--(2sin 2cos )cos 1x x x =+-22sin cos 2cos 1x x x =+-sin2cos2x x =+π)4x =+由图象得0ππ242x += 所以0π8x = 函数()f x 的单调增区间为31(ππ,ππ)88k k -+,k ∈Z4. (2019朝阳一模文科)已知ABC △中, 120A ∠=,a =ABC 的面积且b c <.则 Bc b -=A. B. 3 C. 3-D.5.(2019朝阳一模文科)已知函数2()cos cos f x x x x =+. (Ⅰ)求()3f π的值及()f x 的最小正周期; (Ⅱ)若函数()f x 在区间[0,]m 上单调递增,求实数m 的最大值.解:(Ⅰ)由已知2()coscos 3333f ππππ=+13144=+=. 因为()fx 1cos 222x x +=+π1sin(2)62x =++, 所以函数()f x 的最小正周期为π.………………………..7分(II )由πππ2π22π262k x k -++≤≤得,ππππ36k x k -+≤≤,k ∈Z .所以,函数()f x 的单调增区间为πππ,π36k k ⎡⎤-+⎢⎥⎣⎦,k ∈Z . 当0k =时, 函数()f x 的单调增区间为ππ,36⎡⎤-⎢⎥⎣⎦, 若函数()f x 在区间[0,]m 上单调递增,则ππ[0,],36m ⎡⎤⊆-⎢⎥⎣⎦, 所以实数m 的最大值为π6. ………………………..13分 6.(2019西城一模文科)在△ABC 中,已知2a =,1sin()3A B +=,1sin 4A =,则 C (A )(B )(C )(D )7.(2019西城一模文科)能说明“在△ABC 中,若sin2sin2A B =,则A B =”为假命题的一c =438343组A ,B 的值是____.答案不唯一,如60A =,30B =8.(2019西城一模文科)已知函数()sin (cos )f x x x x =. (Ⅰ)求函数()f x 的最小正周期; (Ⅱ)求函数()f x 在区间π5π[,]312-上的最小值和最大值.解:(Ⅰ)2()sin cos f x x x x =-1sin 2cos2)2x x =-……………… 4分πsin(2)3x =+, (6)分所以函数()f x 的最小正周期πT =. ……………… 8分(Ⅱ)因为π5π312x -≤≤,所以 ππ7π2336x -+≤≤. ……………… 9分所以当ππ232x +=,即π12x =时,()f x 取得最大值1.当ππ233x +=-,即π3x =-时,()f x 取得最小值 ……………… 13分9.(2019丰台一模文科)已知函数()cos(2)(0)2f x x ϕϕπ=+-<<.①函数()f x 的最小正周期为____; ②若函数()f x 在区间4[,]33ππ上有且只有三个零点,则ϕ的值是____. .π;6π-10.(2019丰台一模文科)在锐角ABC △中,角,,A B C 所对的边分别为,,a b c .已知3cos 24C =-.(Ⅰ)求sin C ;(Ⅱ)当2c a =,且b =时,求a .解:(Ⅰ)因为 3cos24C =-,所以 2312sin 4C -=-.因为 02C π<<,所以 sin 4C =.(Ⅱ)由(Ⅰ)可知sin C =因为 ABC ∆是锐角三角形,所以 cos 4C ==. 因为 2c a =,sin sin a cA C=,所以 1sin sin 2A C ==,cos 8A =.所以 sin sin[()]sin()sin cos cos sin B A C A C A C A C =π-+=+=+=.因为sin sin a bA B=,b =, 所以 2a =.11.(2019石景山一模文科)已知2π()sin()5f x x =,则(0)(1)(2)(3)(2019)f f f f f +++++= AA. 0B. 505C. 1010D. 202012.(2019石景山一模文科)在平面直角坐标系xOy 中,角α和角β均以Ox 为始边,它们的终边关于x 轴对称.若1sin 3α=,则sin β=__________.13-13.(2019石景山一模文科)在ABC △中,角A B C ,,的对边分别为a b c ,,,b =3c=,1cos 3B =-.(Ⅰ)求sin C 的值; (Ⅱ)求ABC △的面积.解:(Ⅰ)在ABC △中,1cos 3B =-,∴sin B==,∵b=3c=,由正弦定理sin sinb cB C=3sin C=,∴sin C=(Ⅱ)由余弦定理222+2cosb=a c ac B-得2112+923()3=a a-⨯⨯-,∴2230a a=+-,解得1a=或3a=-(舍)∴1sin2ABCS=ac B11323=⨯⨯⨯14.(2019延庆一模文科)函数()=sin22f x x x在区间[,]22ππ-上的零点之和是 D(A)3π-(B)3π(C)6π(D)6π-15.(2019延庆一模文科)如图,在ABC∆中,点D在BC边上,cos ADB∠=,3cos=5C∠,7AC=.sin CAD∠(求Ⅰ)的值;(Ⅱ)若10BD=,求AD的长及ABD∆的面积.解:(Ⅰ)因为cos10ADB∠=-,所以cos10ADC∠=,………………………1分ADB Csin ADC ∠=…………………2分又因为3cos =,5C ∠4sin 5C ∠=,所以,…………………3分s i n s i n ()s i n c o s c o s s i n D A C A D C A C D A D C A C D A D C A C D∠=∠+∠=∠⋅∠+∠⋅∠……5分3455=+=…………7分 (Ⅱ)在ACD ∆中,由ADCAC C AD ∠=∠sin sin ,…………9分得47sin sin AC C AD ADC ⋅⋅∠===∠.…………11分所以11sin 102822ABD S AD BD ADB ∆=⋅⋅∠=⋅=. …………13分 16.(2019怀柔一模文科)在ABC ∆中,=b ,45∠=A ,75∠=C ,则=a __________.17.(2019怀柔一模文科)已知函数()sin cos f x x x =+. (Ⅰ)求()4f π的值;(Ⅱ)如果函数()()()g x f x f x =-,求函数()g x 的最小正周期和最大值. 解:(Ⅰ).------------------------5分 (Ⅱ),的最小正周期为. ,因此,函数的最大值是.----------------------------------------13分 18.(2019东城文科一模)在ABC ∆中,若cos sin 0b C c B +=,则C ∠= .34π 19.(2018东城文科一模)已知函数()2sin()4f x x π=+,若对于闭区间[]a b ,中的任意两()sincos444f πππ=+==()()()(sin cos )[sin()cos()]g x f x f x x x x x =-=+-+-(sin cos )(sin cos )x x x x =+-+22cos sin cos 2x x x =-=22T ππ==()g x π1cos21x ∴-≤≤()g x 1个不同的数12x x ,,都有1212()()0f x f x x x -<-成立,写出一个满足条件的闭区间 . 5[,]44ππ(答案不唯一) 20(2019东城文科一模)已知函数()4cos sin 16f x x x π⎛⎫=-+ ⎪⎝⎭. (Ⅰ)求23f π⎛⎫⎪⎝⎭的值; (Ⅱ)求()f x 的最小正周期,并画出()f x 在区间[]0,π上的图象. 解:(I )2224cos sin 13336f ππππ⎛⎫⎛⎫=-+⎪ ⎪⎝⎭⎝⎭24cos sin 132ππ=+14112⎛⎫=⨯-⨯+ ⎪⎝⎭1=-.………………………………………………………………………………………………………………. 3分(Ⅱ)()4cos sin 16f x x x π⎛⎫=-+ ⎪⎝⎭4cos sin cos cos sin 166x x x ππ⎛⎫=-+ ⎪⎝⎭14cos sin cos 122x x x ⎛⎫=-+ ⎪ ⎪⎝⎭2cos 2cos 1x x x =-+2cos2x x =-12sin 2cos 222x x ⎛⎫=- ⎪ ⎪⎝⎭2sin 26x π⎛⎫=- ⎪⎝⎭. …………………………………………………………………..9分所以()f x 的最小正周期22T π==π. ………………………………………………….10分因为[]0,x ∈π,所以112,666x πππ⎡⎤-∈-⎢⎥⎣⎦.列表如下:…………………………..13分21.(2019昌平文科一模)在锐角△ABC 中,AB =2,AC =3.若△ABC 的面积为,则∠A = 60° ;BC =.【分析】由已知利用三角形的面积公式可求sin A ,结合A 为锐角可求A 的值,根据余弦定理可求BC 的值.【解答】解:∵AB =2,AC =3. 若△ABC 的面积为=AB •AC •sin A =,∴解得:sin A =,∵A 为锐角, ∴A =60°,∴BC ===.故答案为:60°,.【点评】本题主要考查了三角形面积公式,余弦定理在解三角形中的应用,属于基础题.22.(2019昌平文科一模)已知函数.(Ⅰ)求f (x )的单调递增区间; (Ⅱ)若f (x )在区间上的最小值为﹣2,求m 的最大值.【分析】(Ⅰ)利用三角恒等变换化简函数的解析式,再利用正弦函数的单调性求出f (x )的单调递增区间;(Ⅱ)利用正弦函数的定义域和值域,求得m 的最大值. 【解答】解:(Ⅰ)==sin2x +cos2x =2sin (2x +). 由2k π﹣≤2x +≤2k π+,求得.所以f (x )的单调递增区间是.(Ⅱ)在区间上,∴2x +∈[2m +,].要使得f (x )在区间上的最小值为﹣2,2sin (2x +)在区间上的最小值为﹣1, ∴2m +≤﹣,∴m ≤﹣,即m 的最大值为﹣.【点评】本题主要考查三角恒等变换,正弦函数的单调性,定义域和值域,属于中档题. 23.(2019房山文科一模)在△ABC 中,已知6BC =,4AC =, 3sin 4A =,则B ∠=____.6π 24.(2019房山文科一模)已知函数sin 2cos21()2cos x x f x x++=.(Ⅰ)求(0)f 的值;(Ⅱ)求函数()f x 的定义域;(Ⅲ)求函数()f x 在(0,)2π上的取值范围.(Ⅰ)()sin0cos0111012cos02f +++=== ……………2分(Ⅱ) 由0cos ≠x 得,2x k k π≠+π∈Z所以 函数的定义域是 ,2x x k k ⎧⎫π≠+π∈⎨⎬⎩⎭Z ……………5分 (Ⅲ)()22sin cos 2cos 112cos x x x f x x⋅⋅+⋅-+=⋅ ……………9分()2cos sin cos 2cos x x x x⋅+=⋅sin cos x x =+4x π⎛⎫=+ ⎪⎝⎭ ……………11分0,2x π⎛⎫∈ ⎪⎝⎭即 02x π<<3sin()144424x x ππππ∴<+<<+≤1)6x π∴<+所以 函数()fx 在(0,)2π上的取值范围为 ……………14分25.(2019通州文科一模)已知函数f (x )=Asin(ωx +φ)的部分图象如图所示,则f (x )的表达式为 CA .f (x )=2sin(32 x +π4)B .f (x )=2sin(x +2π9)C .f (x )=2sin(32 x +5π4)D .f (x )=2sin(x +2518π)26.(2019通州文科一模)在△ABC中,3cos 5A =,a =5b =. (Ⅰ)求角B 的大小;(Ⅱ)求△ABC 的面积. 解:(Ⅰ)因为3cos 5A =,0A <<π, 所以02A π<<,4sin 5A =. ………………2分 3232由sin sin a b A B =得,45sin sin 2b A B a ⨯===. ………………4分 因为a b > ,所以A B >. 所以4B π=. ………………6分 (Ⅱ)因为A BC ++=π,所以()C A B =π-+. ………………7分 因为4B π=,所以sin cos B B ==. ………………8分 所以()()sin sin sin C A B A B =π-+=+⎡⎤⎣⎦ ………………9分sin cos cos sin A B A B =+ ………………10分4355==. ………………11分 所以△ABC 的面积1sin 2S ab C =1514210=⨯⨯=. ………………13分27.(2019门头沟文科一模)已知中,,则的面积为( ) A. B. C. D.【答案】C【解析】【分析】先求C ,再根据余弦定理求b ,最后根据三角形面积公式求结果. 【详解】因为,所以,因此,从而的面积为,选C.【点睛】本题考查余弦定理以及三角形面积公式,考查基本分析求解能力,属基础题.28.(2019门头沟文科一模)一半径为的水轮,水轮圆心距离水面2,已知水轮每分钟转动(按逆时针方向)3圈,当水轮上点从水中浮现时开始计时,即从图中点开始计算时间.(1)当秒时点离水面的高度_________;(2)将点距离水面的高度(单位: )表示为时间(单位: )的函数,则此函数表达式为_______________ .【答案】(1). (2).【解析】【分析】1利用直角三角形的边角关系,即可求出5秒后点P离开水面的距离;2由题意求值,结合的情况可求出的值,即得函数解析式.【详解】解:1秒时,水轮转过角度为,在中,,;在中,,,此时点离开水面的高度为;2由题意可知,,设角是以Ox为始边,为终边的角,由条件得,其中;将,代入,得,;所求函数的解析式为.故答案为:1,2.【点睛】本题考查函数的图象与应用问题,理解函数解析式中参数的物理意义,是解题的关键.29.(2019门头沟文科一模)已知函数(1)求的周期及单调增区间;(2)若时,求的最大值与最小值.【答案】(1),;(2)见解析【解析】【分析】(1)先根据二倍角公式以及辅助角公式化简,再根据正弦函数性质求周期与增区间,(2)根据正弦函数性质求最值.【详解】(1),所以的周期单调增区间:(2)【点睛】本题考查正弦函数性质、二倍角公式以及辅助角公式,考查分析求解能力,属中档题.。
北京市城六区2019届高三期末数学(理)解答题分类汇编之三角函数含答案

【海淀】15.(本小题满分13分) 已知函数()s()cos22f x aco x x π=--(Ⅰ)比较()6f π和()2f π的大小;(Ⅱ)求函数()f x 在区间[,]22ππ-的最小值.解:(Ⅰ)因为π1(),622a f =- π()12f a =+ 所以ππ13()()(1)()262222a a f f a -=+--=+因为0a >,所以3022a +>,所以ππ()()26f f >(Ⅱ)因为()sin cos2f x a x x =-2sin (12sin )a x x =--22sin sin 1x a x =+- 设sin ,t x = ππ[,]22x ∈-,所以[1,1]t ∈-, 所以221y t at =+-,其对称轴为4at =-当14at =-<-,即4a >时,在1t =-时函数取得最小值1a - 当14a t =-≥-,即04a <≤时,在4a t =-时函数取得最小值218a --【东城】(15)(本小题13分)在△ABC 2sin cos sin .c A B a C = (Ⅰ)求B ∠的大小;2cos ABC a A (Ⅱ)若的面积为△,求的值.解:sin sin sin cos sin 2ABC a C c A a C B c A ==(Ⅰ)在△中,由正弦定理得所以,=0B <∠<π又,=.4B π∠所以 .............................5分21sin ,.24S =ABC ac a c π==(Ⅱ)因为的面积所以△22282,.2b a a a b =+-⋅⋅⋅=由余弦定理所以,222cos10A ==所以 .............................13分【朝阳】15.(本小题满分13分)在ABC △中,已知312,cos 413A C π==,13.BC = (Ⅰ)求AB 的长;(Ⅱ)求BC 边上的中线AD 的长. 15. (本小题满分13分) 解:(Ⅰ)由12cos 13C =,02C π<<,所以5sin 13C =.由正弦定理得,sin sin AB BCC A =,即5sin =13sin 2C AB BC A =⋅= .……… 6分(Ⅱ)在ABD △中,3cos cos()42226B C C C π=π--=+=. 由余弦定理得,222+2cos AD AB BD AB BD B =-⋅,所以2AD 216913172292)+25242264=-⨯⨯=. 所以29AD =. ……………… 13分 【丰台】15.(本小题13分)在ABC △中,角,,A B C 的对边分别为,,a b c ,3a =,b =,1cos 3B =. (Ⅰ)求c 的值; (Ⅱ)求ABC △的面积. 15.(共13分)解:(Ⅰ)在△ABC 中,因为3a =,b =,1cos 3B =, 由余弦定理2222cos b a c ac B =+-, ……………….2分可得2230c c --=, ……………….4分所以3c =,或1c =-(舍). ……………….6分(Ⅱ)因为1cos ,(0,)3B B =∈π,所以sin B ==.所以ABC △的面积11sin 33223S ac B ==⨯⨯⨯=. …………….13分 【西城】15.(本小题满分13分)在ABC ∆中,3a =,b =2B A =. (Ⅰ)求cos A 的值;(Ⅱ)试比较B ∠与C ∠的大小. 15.(本小题满分13分)解:(Ⅰ)在ABC ∆中,由正弦定理sin sin a bA B=, ……………… 2分得3sin A =3sin A =……………… 4分解得cos A = ……………… 6分(Ⅱ)由(0,π)A ∈,得sin A ==. ……………… 7分因为2B A =,所以21cos cos22cos 13B A A ==-=.……………… 8分 所以222sin 1cos B B =-=……………… 9分 又因为πA B C ++=, 所以c o s c o s ()c o s c o ss i n n C A B A B A =-+=-+.……………… 11分 所以c o s c o s B C >.又因为函数cos y x =在(0,π)上单调递减,且,(0,π)B C ∈,所以B C ∠<∠. ……………… 13分【石景山】15. (本小题13分)函数()sin()(0,0,||)2f x A x A π=+>><ωϕωϕ的部分图象如图所示. (Ⅰ)求()f x 的最小正周期及解析式;(Ⅱ)设()()cos g x f x x =-,求函数()g x 在区间[0,]2π上的最小值.15.(本小题13分)解:(Ⅰ)由图可得1,A =4233T ππ=-=π,所以2,1T =πω=. 当3x π=时,1)(=x f ,可得sin()13π+ϕ=,||,.26ππϕ<∴ϕ=()sin()6f x x π∴=+.(Ⅱ)()()cos sin()cos sin cos cos sin cos 666g x f x x x x x x x πππ=-=+-=+-1cos sin()26x x x π=-=-. 0,2663x x ππππ∴--≤≤≤≤.当66x ππ-=-,即0=x 时,)(x g 有最小值为21-.。
2019年北京卷 理科数学真题(解析版)
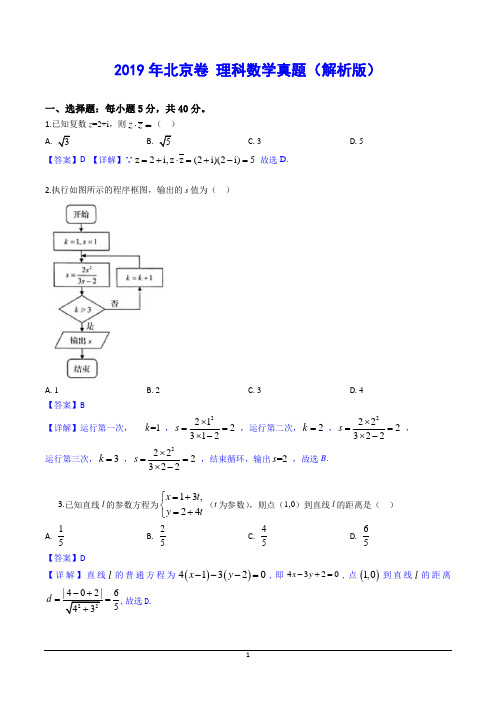
2019年北京卷 理科数学真题(解析版)一、选择题:每小题5分,共40分。
1.已知复数z =2+i ,则z z ⋅=( ) A.3B.5C. 3D. 5【答案】D 【详解】∵z 2i,z z (2i)(2i)5=+⋅=+-= 故选D.2.执行如图所示的程序框图,输出的s 值为( )A. 1B. 2C. 3D. 4【答案】B【详解】运行第一次, =1k ,2212312s ⨯==⨯- ,运行第二次,2k = ,2222322s ⨯==⨯- ,运行第三次,3k = ,2222322s ⨯==⨯- ,结束循环,输出=2s ,故选B .3.已知直线l 的参数方程为13,24x t y t =+⎧⎨=+⎩(t 为参数),则点(1,0)到直线l 的距离是( )A.15B.25C.45D.65【答案】D【详解】直线l 的普通方程为()()41320x y ---=,即4320x y -+=,点()1,0到直线l 的距离226543d ==+,故选D.4.已知椭圆2222 1x y a b+=(a >b >0)的离心率为12,则( )A. a 2=2b 2B. 3a 2=4b 2C. a =2bD. 3a =4b【答案】B 【详解】椭圆的离心率2221,2c e c a b a ===-,化简得2234a b =,故选B.5.若x ,y 满足|1|x y ≤-,且y ≥−1,则3x+y 的最大值为( ) A. −7 B. 1C. 5D. 7【答案】C 【详解】由题意1,11yy x y-≤⎧⎨-≤≤-⎩作出可行域如图阴影部分所示.设3,3z x y y z x =+=-,当直线0:3l y z x =-经过点()2,1-时,z 取最大值5.故选C.6.在天文学中,天体的明暗程度可以用星等或亮度来描述.两颗星的星等与亮度满足212152–lg E m m E =,其中星等为m k 的星的亮度为E k (k =1,2).已知太阳的星等是–26.7,天狼星的星等是–1.45,则太阳与天狼星的亮度的比值为( ) A. 1010.1 B. 10.1C. lg10.1D. 10–10.1【答案】D【详解】两颗星的星等与亮度满足12125lg 2E m m E -= , 令2 1.45m =- ,126.7m =- ,()1212221g( 1.4526.7)10.155E m m E =-=-+=,10.110.112211010E EE E -=⋅= , 故选D.7.设点A ,B ,C 不共线,则“AB 与AC 的夹角为锐角”是“||||AB AC BC +>”的( ) A. 充分而不必要条件 B. 必要而不充分条件 C. 充分必要条件 D. 既不充分也不必要条件【答案】C【详解】∵A 、B 、C 三点不共线,∴|AB +AC |>|BC |⇔|AB +AC |>|AB -AC |⇔|AB +AC |2>|AB -AC |2AB ⇔•AC >0AB ⇔与AC的夹角为锐角.故“AB 与AC 的夹角为锐角”是“|AB +AC |>|BC |”的充分必要条件,故选C.8.数学中有许多形状优美、寓意美好的曲线,曲线C :221||x y x y +=+就是其中之一(如图).给出下列三个结论:①曲线C 恰好经过6个整点(即横、纵坐标均为整数的点); ②曲线C 2; ③曲线C 所围成的“心形”区域的面积小于3. 其中,所有正确结论的序号是( ) A. ① B. ②C. ①②D. ①②③【答案】C详解】由221x y x y +=+得,221y x y x -=-,2222||3341,10,2443x x x y x ⎛⎫-=-- ⎪⎝⎭, 所以x 可为的整数有0,-1,1,从而曲线22:1C x y x y +=+恰好经过(0,1),(0,-1),(1,0),(1,1), (-1,0),(-1,1)六个整点,结论①正确.由221x y x y +=+得,222212x y x y +++,解得222x y +≤,所以曲线C 上任意一点到原点的距离都不2结论②正确.如图所示,易知()()()()0,1,1,0,1,1,,0,1A B C D -,四边形ABCD 的面积13111122ABCD S =⨯⨯+⨯=,很明显“心形”区域的面积大于2ABCD S ,即“心形”区域的面积大于3,说法③错误.故选C.二、填空题共6小题,每小题5分,共30分。
专题05---2014-2024北京三角函数选题真题汇编解析版
专题05北京高考三角函数选填真题1.【2024年北京卷06】已知()()sin 0f x x ωω=>,()11f x =−,()21f x =,12min π||2x x −=,则ω=( ) A. 1 B. 2 C. 3 D. 4【答案】B 2.【2024年北京卷12】已知ππ,63α⎡⎤∈⎢⎥⎣⎦,且α与β的终边关于原点对称,则cos β的最大值为________.由题意π2π,Z k k βα=++∈,从而()cos cos π2πcos k βαα=++=−,3.【2023年北京卷13】已知命题p:若α,β为第一象限角,且α>β,则tanα>tanβ.能说明p 为假命题的一组α,β的值为α= ,β= . 【答案】 9π4π3单位圆因为f (x )=tanx 在(0,π2)上单调递增,若0<α0<β0<π2,则tanα0<tanβ0, 取α=2k 1π+α0,β=2k 2π+β0,k 1,k 2∈Z ,则tanα=tan (2k 1π+α0)=tanα0,tanβ=tan (2k 2π+β0)=tanβ0,即tanα<tanβ, 令k 1>k 2,则α−β=(2k 1π+α0)−(2k 2π+β0)=2(k 1−k 2)π+(α0−β0), 因为2(k 1−k 2)π≥2π,−π2<α0−β0<0,则α−β=2(k 1−k 2)π+(α0−β0)>3π2>0,即k 1>k 2,则α>β.不妨取k 1=1,k 2=0,α0=π4,β0=π3,即α=9π4,β=π3满足题意.故答案为:9π4;π3. 4.【2022年北京卷05】已知函数f(x)=cos 2x −sin 2x ,则( )A .f(x)在(−π2,−π6)上单调递减B .f(x)在(−π4,π12)上单调递增C .f(x)在(0,π3)上单调递减D .f(x)在(π4,7π12)上单调递增【答案】C 5.【2022年北京卷13】若函数f(x)=Asinx −√3cosx 的一个零点为π3,则A =________;f(π12)=________. 【答案】 1 −√2 【解析】 ∵f(π3)=√32A −√32=0,∴A =1∴f(x)=sinx −√3cosx =2sin(x −π3) f(π12)=2sin(π12−π3)=−2sin π4=−√2 【三角函数性质灵活考查】(2022北京卷改编)若()sin f x A x x =关于3x π=对称,则A =________.【答案】3− 【解析】对称性运用 ∵f(2π3)=f(0),∴A =−36. 【2021年北京07】函数f(x)=cosx −cos2x ,试判断函数的奇偶性及最大值( ) A .奇函数,最大值为2 B .偶函数,最大值为2 C .奇函数,最大值为98D .偶函数,最大值为98【答案】D由题意,f(−x)=cos(−x)−cos(−2x)=cosx −cos2x =f(x),所以该函数为偶函数, 又f(x)=cosx −cos2x =−2cos 2x +cosx +1=−2(cosx −14)2+98, 所以当cosx =14时,f(x)取最大值98. 7.【2021年北京13】若点P(cosθ,sinθ)与点Q(cos(θ+π6),sin(θ+π6))关于y 轴对称,写出一个符合题意的θ=___. 【答案】5π12(满足θ=5π12+kπ,k ∈Z 即可)8. 【2020年北京卷10】2020年3月14日是全球首个国际圆周率日(π Day ).历史上,求圆周率π的方法有多种,与中国传统数学中的“割圆术”相似.数学家阿尔·卡西的方法是:当正整数n 充分大时,计算单位圆的内接正6n 边形的周长和外切正6n 边形(各边均与圆相切的正6n 边形)的周长,将它们的算术平均数作为2π的近似值.按照阿尔·卡西的方法,π的近似值的表达式是( ). A .3n (sin 30°n +tan 30°n ) B .6n (sin 30°n +tan 30°n) C .3n (sin60°n+tan60°n)D .6n (sin60°n+tan60°n)【答案】A单位圆内接正6n 边形的每条边所对应的圆周角为360°n×6=60°n,每条边长为2sin30°n,所以,单位圆的内接正6n 边形的周长为12nsin 30°n,单位圆的外切正6n 边形的每条边长为2tan 30°n,其周长为12ntan 30°n,∴2π=12nsin30°n +12ntan 30°n2=6n (sin 30°n+tan30°n),则π=3n (sin 30°n+tan30°n).9.【2020年北京卷12】若函数f(x)=sin(x +φ)+cosx 的最大值为2,则常数φ的一个取值为________. 【答案】π2(2kπ+π2,k ∈Z 均可)【解析】因为f (x )=cosφsinx +(sinφ+1)cosx =√cos 2φ+(sinφ+1)2sin (x +θ), 所以√cos 2φ+(sinφ+1)2=2,解得sinφ=1,故可取φ=π2.故答案为:π2(2kπ+π2,k ∈Z 均可). 10. 【2019年北京文科06】设函数f (x )=cosx +bsinx (b 为常数),则“b =0”是“f (x )为偶函数”的( ) A .充分而不必要条件 B .必要而不充分条件C .充分必要条件D .既不充分也不必要条件【答案】C解:设函数f (x )=cosx +bsinx (b 为常数), 则“b =0”⇒“f (x )=cosx 为偶函数”,“f (x )为偶函数”⇒()()f x f x =− ,cos sin cos sin x b x x b x ∴+=−,cos sin cos sin x b x x b x ∴+=−sin sin b x b x ∴=−,2sin 0b x ∴=对任意x 成立;∴0b =11. 【2019年北京文科08】如图,A ,B 是半径为2的圆周上的定点,P 为圆周上的动点,∠APB 是锐角,大小为β,图中阴影区域的面积的最大值为( )A.44cos ββ+B.44sin ββ+C.22cos ββ+D.22sin ββ+【答案】B解:由题意可得22AOB APB β∠=∠=,要求阴影区域的面积的最大值,即为直线QO ⊥AB ,即有QO =2,Q 到线段AB 的距离为22cos β+,224AB sin sin ββ==,扇形AOB 的面积为12•2β•4=4β,△ABQ 的面积为12(2+2cosβ)•4sinβ=4sinβ+4sinβcosβ=4sinβ+2sin2β,即有阴影区域的面积的最大值为4β+4sin β. 12. 【2019年北京理科09】函数2()2f x sin x =的最小正周期是 . 【答案】π213. 【2018年北京理科07】在平面直角坐标系中,记d 为点P(cosθ.sinθ)到直线x −my −2=0的距离.当θ、m 变化时,d 的最大值为( )A .1B .2C .3D .4【答案】C 解:法一:由题意d =|cosθ−msinθ−2|√12+m 2=|√m 2+1sin(θ+α)−2|√m 2+1,tan α=1m =yx ,∴当sin (θ+α)=−1时,d max =1+2√m 2+1≤3.∴d 的最大值为3.法二: P 点在单位圆221x y +=上动,圆心到直线距离的最大值(圆心到过定点的距离)+半径 14. 【2018年北京理科11】设函数π()cos()6f x x ω=−(0)ω>.若π()()4f x f ≤对任意的实数x 都成立,则ω的最小值为___________.ω⋅π4−π6=2kπ,k ∈Z ,解得ω=8k +23 15. 【2018年北京文科07】在平面直角坐标系中,AB ̂,CD ̂,EF ̂,GH ̂是圆221x y +=上的四段弧(如图),点P 其中一段上,角α以Ox 为始边,OP 为终边.若tan cos sin ααα<<,则P 所在的圆弧是( )A .AB ̂ B .CD ̂C .EF ̂D .GH ̂ 【答案】C解:A .在AB 段,正弦线小于余弦线,即cos α<sin α不成立,故A 不满足条件. B .在CD 段正切线最大,则cos α<sin α<tan α,故B 不满足条件. C .在EF 段,正切线,余弦线为负值,正弦线为正, 满足tan α<cos α<sin α,D .在GH 段,正切线为正值,正弦线和余弦线为负值, 满足cos α<sin α<tan α不满足tan α<cos α<sin α. 16. 【2017年北京理科12】在平面直角坐标系xOy 中,角α与角β均以Ox 为始边,它们的终边关于y 轴对称,若sinα=13,则cos (α−β)= .解:方法一:∵角α与角β均以Ox 为始边,它们的终边关于y 轴对称,方法二:∵sinα=13,当α在第一象限时,cosα=2√23, ∵α,β角的终边关于y 轴对称,∴β在第二象限时,sinβ=sinα=13,cosβ=−cosα=−2√23, ∴cos (α−β)=cosαcosβ+sinαsinβ=−2√23×2√23+13×13=−7917. 【2016年北京理科07】将函数sin(2)3y x π=−图象上的点(,)4t π向左平移s (0)s >个单位长度得到点'P .若'P 位于函数sin 2y x =的图象上,则A.12t =,s 的最小值为6πB.t =,s 的最小值为6πC.12t =,s 的最小值为3π D.t =,s 的最小值为3π【答案】A将x =π4代入得:t =sin π6=12,将函数y =sin (2x −π3)图象上的点P 向左平移s 个单位, 得到P ′(π4−s ,12)点,若P ′位于函数y =sin2x 的图象上, 则sin (π2−2s )=cos2s =12,则2s =±π3+2k π,k ∈Z , 则s =±π6+k π,k ∈Z ,由s >0得:当k =0时,s 的最小值为π618. 【2014年北京理科14】设函数()sin()(,,f x A x A ωϕωϕ=+是常数,0,0A ω>>).若()f x 在区间ππ[,]62上具有单调性,且π2ππ()()()236f f f ==−,则()f x 的最小正周期为 . 【答案】π.则x =π2离最近对称轴距离为7π12−π2=π12.又f (π2)=﹣f (π6),则f (x )有对称中心(π3,0), 由于f (x )在区间[π6,π2]上具有单调性,则π2−π6≤12T ⇒T ≥2π3,从而7π12−π3=T 4⇒T =π.。
2019年高考北京卷理科数学真题(含答案)
绝密★启用前2019年普通高等学校招生全国统一考试数学(理)(北京卷)本试卷共5页,150分。
考试时长120分钟。
考生务必将答案答在答题卡上,在试卷上作答无效。
考试结束后,将本试卷和答题卡一并交回。
第一部分(选择题共40分)一、选择题共8小题,每小题5分,共40分。
在每小题列出的四个选项中,选出符合题目要求的一项。
1.已知复数z=2+i,则z z⋅=5 C. 3 D. 5【答案】D【解析】【分析】题先求得z,然后根据复数的乘法运算法则即得.=+⋅=+-=故选D.【详解】∵z2i,z z(2i)(2i)5【点睛】本容易题,注重了基础知识、基本计算能力的考查.2.执行如图所示的程序框图,输出的s值为A. 1B. 2C. 3D. 4【答案】B根据程序框图中的条件逐次运算即可.【详解】运行第一次, =1k ,2212312s ⨯==⨯- ,运行第二次,2k = ,2222322s ⨯==⨯- ,运行第三次,3k = ,2222322s ⨯==⨯- ,结束循环,输出=2s ,故选B .【点睛】本题考查程序框图,属于容易题,注重基础知识、基本运算能力的考查.3.已知直线l 的参数方程为13,24x t y t =+⎧⎨=+⎩(t 为参数),则点(1,0)到直线l 的距离是A.15B.25 C.45D.65【答案】D 【解析】 【分析】首先将参数方程化为直角坐标方程,然后利用点到直线距离公式求解距离即可. 【详解】直线l 的普通方程为()()41320x y ---=,即4320x y -+=,点()1,0到直线l 的距离65d ==,故选D. 【点睛】本题考查直线参数方程与普通方程转化,点到直线的距离,属于容易题,注重基础知识、基本运算能力的考查.4.已知椭圆2222 1x y a b+=(a >b >0)的离心率为12,则A. a 2=2b 2B. 3a 2=4b 2C. a =2bD. 3a =4b【答案】B由题意利用离心率的定义和,,a b c 的关系可得满足题意的等式. 【详解】椭圆的离心率2221,2c e c a b a ===-,化简得2234a b =, 故选B.【点睛】本题考查椭圆的标准方程与几何性质,属于容易题,注重基础知识、基本运算能力的考查.5.若x ,y 满足|1|x y ≤-,且y ≥−1,则3x+y 的最大值为 A. −7 B. 1C. 5D. 7【答案】C 【解析】 【分析】首先画出可行域,然后结合目标函数的几何意义确定其最值即可.【详解】由题意1,11yy x y-≤⎧⎨-≤≤-⎩作出可行域如图阴影部分所示.设3,3z x y y z x =+=-, 当直线0:3l y z x =-经过点()2,1-时,取最大值5.故选C.【点睛】本题是简单线性规划问题的基本题型,根据“画、移、解”等步骤可得解.题目难度不大题,注重了基础知识、基本技能的考查.6.在天文学中,天体的明暗程度可以用星等或亮度来描述.两颗星的星等与亮度满足212152–lg Em m E =,其中星等为m 1的星的亮度为E 2(k =1,2).已知太阳的星等是–26.7,天狼星的星等是–1.45,则太阳与天狼星的亮度的比值为 A. 1010.1B. 10.1C. lg10.1D. 10–10.1【答案】D 【解析】 【分析】 先求出12lgE E ,然后将对数式换为指数式求12E E 再求12E E【详解】两颗星的星等与亮度满足12125lg 2E m m E -= , 令21.45m =- ,126.7m =- ,()1212221g( 1.4526.7)10.155E m m E =-=-+=, 10.110.112211010E EE E -=⋅= , 故选D.【点睛】考查考生的数学应用意识、信息处理能力、阅读理解能力以及指数对数运算.7.设点A ,B ,C 不共线,则“AB 与AC 的夹角为锐角”是“||||AB AC BC +>”的A. 充分而不必要条件B. 必要而不充分条件C. 充分必要条件D. 既不充分也不必要条件【答案】C 【解析】 【分析】由题意结合向量的减法公式和向量的运算法则考查充分性和必要性是否成立即可.【详解】∵A 、B 、C 三点不共线,∴|AB +AC |>|BC |⇔|AB +AC |>|AB -AC |⇔|AB +AC |2>|AB -AC |2AB ⇔•AC >0AB ⇔与AC的夹角为锐角.故“AB 与AC 的夹角为锐角”是“|AB +AC |>|BC |”的充分必要条件,故选C. 【点睛】本题考查充要条件的概念与判断、平面向量的模、夹角与数量积,同时考查了转化与化归数学思想.8.数学中有许多形状优美、寓意美好的曲线,曲线C :221||x y x y +=+就是其中之一(如图).给出下列三个结论:①曲线C 恰好经过6个整点(即横、纵坐标均为整数的点); ②曲线C 2;③曲线C 所围成的“心形”区域的面积小于3. 其中,所有正确结论的序号是 A. ① B. ②C. ①②D. ①②③【答案】C 【解析】 【分析】将所给方程进行等价变形确定x 的范围可得整点坐标和个数,结合均值不等式可得曲线上的点到坐标原点距离的最值和范围,利用图形的对称性和整点的坐标可确定图形面积的范围.详解】由221x y x y +=+得,221y x y x -=-,2222||3341,10,2443x x x y x ⎛⎫-=-- ⎪⎝⎭厔, 所以x 可为的整数有0,-1,1,从而曲线22:1C x y x y +=+恰好经过(0,1),(0,-1),(1,0),(1,1),(-1,0),(-1,1)六个整点,结论①正确.由221x y x y +=+得,222212x y x y +++…,解得222x y +≤,所以曲线C 上任意一点到原点的距. 结论②正确.如图所示,易知()()()()0,1,1,0,1,1,,0,1AB C D -,四边形ABCD 的面积13111122ABCD S =⨯⨯+⨯=,很明显“心形”区域的面积大于2ABCD S ,即“心形”区域的面积大于3,说法③错误.故选C.【点睛】本题考查曲线与方程、曲线的几何性质,基本不等式及其应用,属于难题,注重基础知识、基本运算能力及分析问题解决问题的能力考查,渗透“美育思想”.第二部分(非选择题 共110分)二、填空题共6小题,每小题5分,共30分。
2019年北京市海淀区一模数学理科
海淀区高三年级第二学期期中练习数学(理科)本试卷共4页,150分。
考试时长120分钟。
考生务必将答案答在答题卡上,在试卷上 作答无效。
考试结束后,将本试卷和答题卡一并交回。
第一部分(选择题 共40分)一、选择题共8小题,每小题5分,共40分.在每小题列出的四个选项中,选出符合题目要求的一项.(1)已知集合{|04}P x x =<<,且M P ⊆,则M 可以是 (A ){1,2}(B ){2,4}(C ){1,2}-(D ){0,5}(2)若角α的终边在第二象限,则下列三角函数值中大于零的是(A )πsin()2α+(B )πcos()2α+ (C )sin(π)α+(D )cos(π)α+(3)已知等差数列{}n a 满足3243a a =,则{}n a 中一定为零的项是 (A )6a (B )8a (C )10a (D )12a(4)已知x y >,则下列各式中一定成立的是 (A )11x y <(B )12x y+> (C )11()()22x y >(D )2+22x y ->(5)执行如图所示的程序框图,输出的m 值为(A )18(B )16(C )516(D )13(6)已知复数i z a =+(其中a ∈R ),则下面结论正确的是(A )i z a =-+(B )||1z ≥(C )z 一定不是纯虚数 (D )在复平面上,z 对应的点可能在第三象限(7) 已知椭圆22114 x C y +=:和双曲线22221(0)x y mC m -=>:的离心率之积为1,则双曲线2C 的两条渐近线的倾斜角分别为(A )ππ,66-(B )ππ,33-(C )π5π,66(D )2π2π,33(8) 某校实行选科走班制度,张毅同学的选择是物理、生物、政治这三科,且物理在A 层班级,生物在B 层班级.该校周一上午选科走班的课程安排如下表所示,张毅选择三个科目的(A )8种(B )种(C )12种(D )14种第二部分(非选择题 共110分)二、填空题共6小题,每小题5分,共30分.(9)已知,4,a c 成等比数列,且0a >,则22log log ____.a c += (10)在ABC ∆中,4,5,a b ==1cos 8C =,则___,___.ABC c S ∆== (11)已知向量(1,2)=-a ,同时满足条件①a b P ,②|||+<a b |a 的一个向量b 的坐标为___. (12)在极坐标系中,若圆2cos a ρθ=关于直线cos sin 10ρθθ++=对称,则___.a =(13)设关于,x y 的不等式组0,0,1x y y kx ≥⎧⎪≥⎨⎪≥+⎩表示的平面区域为Ω.记区域Ω上的点与点(0,1)A -距离的最小值记为()d k .则 (I)当1k =时,(1)___;d =(II )若()d k ≥时,k 的取值范围是___.(14)已知函数()f x x =,2(),g x ax x =-其中0a >.若1[1,2]x ∀∈,2[1,2]x ∃∈,使得1212()()()()f x f x g x g x =成立,则_.__a =三、解答题共6小题,共80分.解答应写出文字说明、演算步骤或证明过程. (15)(本小题满分13分)已知函数π())cos 4f x x x a=-+.(Ⅰ)求a 的值;(Ⅱ)求函数()f x 的单调递增区间.(16)(本小题满分13分)据《人民网》报道,“美国国家航空航天局(NASA )发文称,相比20年前世界变得更绿色了.卫星资料显示中国和印度的行动主导了地球变绿.”据统计,中国新增绿化面积的42%来自于植树造林.下表是中国十个地区在2017年植树造林的相关数据.(造林总面积为人工造林、飞播造林、新封山育林、退化林修复、人工更新的面积之和)单位:公顷(Ⅰ)请根据上述数据,分别写出在这十个地区中人工造林面积与造林总面积的比值最大与最小的地区;(Ⅱ)在这十个地区中,任选一个地区,求该地区人工造林面积占总面积的比值超过50%的概率是多少(Ⅲ)在这十个地区中,从新封山育林面积超过五万公顷的地区中,任选两个地区,记X 为这两个地区中退化林修复面积超过六万公顷的地区的个数,求X 的分布列及数学期望.(17)(本小题满分14分)如图,在直三棱柱111ABC A B C -中,AC BC ⊥,12AC BC CC ===,点,,D E F 分别为棱11111,,AC B C BB 的中点.(Ⅰ)求证:1AC P 平面DEF ; (Ⅱ)求证:平面1ACB ⊥平面DEF ;(Ⅲ)在线段1AA 上是否存在一点P ,使得直线DP 与平面1ACB 所成的角为30o 如果存在,求出线段AP 的长;如果不存在,说明理由.(18)(本小题满分14分) 已知函数2()ln(1).f x x x ax =+-(Ⅰ)求曲线()y f x =在点(0,(0))f 处的切线方程; (Ⅱ) 当0a <时,求证: 函数()f x 存在极小值; (Ⅲ)请直接写出函数()f x 的零点个数. (19)(本小题满分13分)已知抛物线2:2G y px =,其中0p >.点(2,0)M 在G 的焦点F 的右侧,且M 到G 的准线的距离是M 与F 距离的3倍.经过点M 的直线与抛物线G 交于不同的,A B 两点,直线OA 与直线2x =-交于点P ,经过点B 且与直线OA 垂直的直线l 交x 轴于点Q . (Ⅰ) 求抛物线的方程和F 的坐标;(Ⅱ)试判断直线PQ 与直线AB 的位置关系,并说明理由. (20)(本小题满分13分)首项为0的无穷数列{}n a 同时满足下面两个条件:1||n n a a n +-=;②12n n a -≤. (Ⅰ)请写出4a 的所有可能值;(Ⅱ)记2n n b a =,若1n n b b +<对任意n *∈N 成立,求数列{}n b 的通项公式;(Ⅲ)对于给定的正整数k ,求12k a a a +++L 的最大值.海淀区高三年级第二学期期中练习参考答案FC 1B 1BCDA 1EA数 学 (理科)阅卷须知:1.评分参考中所注分数,表示考生正确做到此步应得的累加分数。
2019年北京市各区高三一模试题分类汇编:1三角函数(理科)(含答案解析)
2019年北京市各区高三一模试题分类汇编01三角函数(理科)1 (2019年东城一模理科)2 (2019年西城一模理科)下列函数中,对于任意x ∈R ,同时满足条件()()f x f x =-和(π)()f x f x -=的函数是( D )(A )()sin =f x x(C )()cos =f x x (B )()sin cos =f x x x(D )22()cos sin =-f x x x3 (2019年朝阳一模理科) 在ABC △中,π4A =,BC =AC =π3B =”的(B )A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条 4 (2019年丰台一模理科)已知tan 2=α,则sin cos sin cos -+αααα的值为_______________. 5 (2019年顺义一模理科)已知函数()cos(2)cos 23f x x xπ=+-,其中x R ∈,给出下列四个结论 ①.函数()f x 是最小正周期为π的奇函数; ②.函数()f x 图象的一条对称轴是23x π=;③.函数()f x 图象的一个对称中心为5(,0)12π;④.函数()f x 的递增区间为2,63k k ππππ⎡⎤++⎢⎥⎣⎦,k Z ∈. 则正确结论的个数是(C)(A) 1 个 (B) 2 个 (C) 3 个 ( D) 4 个 6 (2019年延庆一模理科)同时具有性质“①最小正周期是π, ②图像关于3π=x 对称,③在]3,6[ππ-上是增函数”的一个函数是(C)A .)62sin(π+=x y B .)32cos(π+=x y C .)62sin(π-=x y D .)62cos(π-=x y7 (2019年东城一模理科)8 (2019年西城一模理科)在△ABC 中,角A ,B ,C 所对的边分别为a ,b ,c. 已知222b c a bc +=+.(Ⅰ)求A 的大小;(Ⅱ)如果cos 3=B ,2b =,求△ABC 的面积. 9 (2019年海淀一模理科)已知函数ππ()2sincos 66f x x x =,过两点(,()),(1,(1))A t f t B t f t ++的直线的斜率记为()g t .(Ⅰ)求(0)g 的值;(II )写出函数()g t 的解析式,求()g t 在33[,]22-上的取值范围.10 (2019年朝阳一模理科)已知函数22()2sin()cos sin cos f x x x x x =π-⋅+-,x ∈R .(Ⅰ)求()2f π的值及函数()f x 的最小正周期;(Ⅱ)求函数()f x 在[]0,π上的单调减区间11 (2019年丰台一模理科)已知函数2()cos(2)2sin 13f x x x =--+π.(Ⅰ)求函数()f x 的最小正周期;(Ⅱ)求函数()f x 在区间[0,]2π上的最大值和最小值.12 (2019年石景山一模理科)在△ABC 中,角A B C ,,的对边分别为a b c ,,,且a b c <<,2sin b A =.(Ⅰ)求角B 的大小;(Ⅱ)若2a =,b =c 边的长和△ABC 的面积 13 (2019年顺义一模理科)已知ABC 中,角A ,B ,C 所对的边分别 为a ,b ,c,且满足3sin sin )2A A A +=(Ⅰ)求角A ;(Ⅱ)若a =,ABC S =,求b ,c 的值. 14 (2019年延庆一模理科)在三角形ABC 中,角C B A ,,所对的边分别为c b a ,,,且2=a ,4π=C ,53cos =B .(Ⅰ)求A sin 的值;(Ⅱ)求ABC ∆的面积2019年北京市各区高三一模试题汇编--三角函数(理科) 答案:1.D ;2.D ;3.B ;4.13;5.C ;6.C ; 7.8.(Ⅰ)解:因为 222b c a bc +=+,所以 2221cos 22b c a A bc +-==,…………… 3分 又因为 (0,π)∈A ,所以 π3A =. ……………… 5分(Ⅱ)解:因为cos 3=B ,(0,π)∈B ,所以sin 3B ==.…………7分由正弦定理 sin sin =a b A B , ……………9分 得 sin 3sin ==b Aa B. ………………10分 因为 222b c a bc +=+, 所以 2250--=c c , 解得1=c 因为 0>c ,所以1=c . ………………11分 故△ABC的面积1sin 22S bc A ==……………13分 9.解:(Ⅰ)π()sin3f x x =———————————————2分 (1)(0)(0)1f fg -=——————3分πsin sin 03=-=.————5分(Ⅱ)(1)()π()sin()sin 1333f t f tg t t t t t ππ+-==+-+-——————————6分 πππsin cos cos sin sin 33333t t t ππ=+-—————————————————7分1ππsin 233t t =-————————————————8分ππsin()33t =--————————————————10分因为33[,]22t ∈-,所以ππ5ππ[,]3366t -∈-,————————————————11分 所以π1sin()[1,]332t π-∈-,———————————————12分所以()g t 在33[,]22-上的取值范围是1[,1]2-————————————————13分10.解:()f x =sin 2cos 2x x-)4x π-.(Ⅰ)())1224f πππ=⋅-==.显然,函数()f x 的最小正周期为π……… 8分 (Ⅱ)令ππ3π2π22π242k x k +-+≤≤得37ππππ88k x k ++≤≤,k ∈Z .又因为[]0,πx ∈,所以3π7π,88x ⎡⎤∈⎢⎥⎣⎦.函数()f x 在[]0,π上的单调减区间为3π7π,88⎡⎤⎢⎥⎣⎦…13分11.解:(Ⅰ)()cos 2cossin 2sincos 233f x x x x ππ=++1cos 22cos 222x x x =++32cos 222x x =+13(sin 22)22x x =+2coscos 2sin )33x x ππ=+)3x π=+----------------------------------------------5分所以()f x 的最小正周期为π.----------------------------------------------7分(Ⅱ)由(Ⅰ)知())3f x x π=+因为[0,]2x π∈,所以ππ4π2[,]333x +∈,当ππ232x +=,即π12x =时,函数()f x取最大值,当π4π233x +=,即π2x =时,函数()f x 取最小值32-. 所以,函数()f x 在区间[0,]2π32-.--------------13分 12.解:2sin b A =,2sin sin A B A =,……………2分 因为0A π<<,所以sin 0A ≠,所以sin 2B =, …………………… 4分 因为0B π<<,且a b c <<,所以60B =.…………………………6分 (Ⅱ)因为2a =,b =22212222c c =+-⨯⨯⨯,即2230c c --=,解得3c =或1c =-(舍),所以c 边的长为3.…………………………10分11=sin 232222ABC S ac B ∆=⨯⨯⨯=.…………………………13分 13.14.解:(Ⅰ) 53cos =B ,∴54sin =B ……………………1分∴)sin(sin C B A +=……………………2分C B C B sin cos cos sin +=……………………4分102722532254=⨯+⨯=……………………6分 (Ⅱ) AaB b sin sin =……………………8分 1027254=∴b ,728=∴b ……………………10分C ab S ABC sin 21=∴∆,……………………11分22728221⨯⨯⨯=78=………………………………13分。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2019年北京各区一模理科数学分类汇编----三角函数(含答案)一、选择、填空题1、(朝阳区2019届高三一模)如图,函数()f x 的图象是由正弦曲线或余弦曲线经过变换得到的,则()f x 的解析式可以是A .()sin(2)3f x x π=+B .()sin(4)6f x x π=+C .()cos(2)3f x x π=+ D .()cos(4)6f x x π=+2、(东城区2019届高三一模)在平面直角坐标系xOy 中,角α以Ox 为始边,终边经过点(1,)(0)P m m -≠,则下列各式的值一定为负的是 (A)sin cos αα+ (B) sin cos αα- (C) sin cos αα (D)sin tan αα3、(丰台区2019届高三一模)已知函数()cos(2)(0)2f x x ϕϕπ=+-<<. ①函数()f x 的最小正周期为____; ②若函数()f x 在区间4[,]33ππ上有且只有三个零点,则ϕ的值是____. 4、(海淀区2019届高三一模)若角α的终边在第二象限,则下列三角函数值中大于零的是(A) sin(+)2πα (B) s(+)2co πα (C) sin()πα+ (D) s()co πα+5、(怀柔区2019届高三一模)函数21()sin cos s 2=+-f x x x co x 的最小正周期是________,(f x)的取值范围是__________.6、(门头沟区2019届高三一模)一半径为4m 的水轮,水轮圆心O 距离水面2m ,已知水轮每分钟转动(按逆时针方向)3圈,当水轮上点P 从水中浮现时开始计时,即从图中点0P 开始计算时间. (Ⅰ)当5t =秒时点P 离水面的高度 ;(Ⅱ)将点P 距离水面的高度h (单位: m )表示为时间t (单位: s )的函数,则此函数表达式为yx1234–1–2–3–4–1–2–3–41234P0OP7、(石景山区2019届高三一模)已知函数()sin 23cos f x a x x =-的一条对称轴为π6x =-,12()()0f x f x +=,且函数()f x 在12(,)x x 上具有单调性,则12||x x +的最小值为A.π6B.π3C.2π3D.4π38、(顺义区2019届高三第二次统练(一模))已知α为锐角,5s i n 25α=,则c o s ()2πα+= .9、(西城区2019届高三一模)函数()sin2cos2f x x x =+的最小正周期T =____;如果对于任意的x ∈R 都有()f x a ≤,那么实数a 的取值范围是____.10、(延庆区2019届高三一模)函数()=sin 23cos 2f x x x -在区间[,]22ππ-上的零点之和是 (A )3π-(B )6π-(C )6π(D )3π11、(房山区2019届高三一模)在△ABC 中,已知6BC =,4AC =, 3sin 4A =,则B ∠= . 12、(平谷区2019届高三一模)已知函数 f (x ) = sin(2x +ϕ) (其中ϕ为实数),若 ()|()|6f x f π≤对 x ∈R 恒成立,则满足条件的ϕ值为______________(写出满足条件的一个ϕ值即可) 参考答案1、A2、D3、π;6π- 4、D 5、π ,22[,]22-; 6、232;(4sin()2106h t t ππ+=-+) 7、C 8、54- 9、π;2a ≥ 10、B11、6π 12、答案不唯一,如:6π二、解答题1、(朝阳区2019届高三一模)在ABC △中,21a =,120A ∠=︒,ABC △的面积等于3,且b c <. (Ⅰ)求b 的值; (Ⅱ)求cos2B 的值.2、(东城区2019届高三一模)已知函数()4cos sin()6f x a x x π=-,且()13f π=. (Ⅰ) 求a 的值及()f x 的最小正周期;(Ⅱ) 若()f x 在区间[0,]m 上单调递增,求m 的最大值.3、(丰台区2019届高三一模)已知函数2()cos(2)2sin ()3f x x x a a π=--+∈R ,且()03f π=.(Ⅰ)求a 的值;(Ⅱ)若()f x 在区间[0,]m 上是单调函数,求m 的最大值.4、(海淀区2019届高三一模)已知函数()22cos()cos 4f x x x a π=-+的最大值为2.(Ⅱ)求a 的值;(Ⅱ)求函数()f x 的单调递增区间.5、(怀柔区2019届高三一模) 在中,角,,所的对边分别是a ,b ,c ,,.(Ⅰ)求边c 的值; (Ⅱ)若,求的面积.6、(门头沟区2019届高三一模)在ABC △中,且满足已知C b B c a cos cos )2(=-. (Ⅰ)求B ∠的大小;(Ⅱ)若ABC △的面积为3,6a c +=,求ABC △的周长.7、(石景山区2019届高三一模)在ABC △中,角A B C ,,的对边分别为a b c ,,,23b =,3c=,1cos 3B =-.(Ⅰ)求sin C 的值; (Ⅱ)求ABC △的面积.8、(顺义区2019届高三第二次统练(一模))在△ABC 中,b =8,3=c ,3π=A .(Ⅰ)求a 及C sin 的值; (Ⅱ)求BC 边上的高.9、(西城区2019届高三一模)在△ABC 中,已知222a c b mac +-=,其中m ∈R . (Ⅰ)判断m 能否等于3,并说明理由;(Ⅱ)若1m =-,27b =,4c =,求sin A .10、(延庆区2019届高三一模) 如图,在ABC ∆中,点D 在BC 边上,2cos 10ADB ∠=-,3cos =5C ∠,7AC =.sin CAD ∠(求Ⅰ)的值;(Ⅱ)若10BD =, 求AD 的长及ABD ∆的面积.11、(房山区2019届高三一模)已知函数3sin 2cos21()2cos x x f x x++=.(Ⅰ)求(0)f 的值; (Ⅱ)求函数()f x 的定义域;(Ⅲ)求函数()f x 在(0,)2π上的取值范围. 参考答案1、解:(Ⅰ)由已知得2221=sin =3,2(21)=2cos120.S bc A b c bc ⎧⎪⎨⎪+-︒⎩整理得22=4,=17.bc b c ⎧⎨+⎩ 解得=1,=4b c ⎧⎨⎩,或=4,=1.b c ⎧⎨⎩ 因为b c <,所以1b =.………………………………………………….8分(Ⅱ)由正弦定理sin sin a bA B=, 即372sin =1421B =.所以22713cos 2=12sin 12()1414B B -=-= ……………………………….13分 2、解:(Ⅰ)由已知()13f π=,得114122a ⨯⨯=,解得1a =. ()4cos sin()6f x x x π=-2314cos (sin cos )2223sin cos 2cos 3sin 2cos 21x x x x x xx x =-=-=--2sin(2)16x π=--所以()2sin(2)16f x x π=--的最小正周期为π. ..........................7分(Ⅱ)由(Ⅰ)知()2sin(2) 1.6f x x π=--当[0,]x m ∈时,2[,2],666x m πππ-∈--若()f x 在区间[0,]m 上单调递增,则有262m ππ-≤,即3m π≤. 所以m 的最大值为3π. ............................13分3、解:(Ⅰ)2()cos(2)2sin 3f x x x a π=--+13cos2sin 2cos2122x x x a =++-+ 33cos2sin 2122x x a =+-+ 313(cos2sin 2)122x x a =+-+3sin(2)13x a π=+-+.因为 ()03f π=,所以 1a =.(Ⅱ)解法1:因为 函数sin y x =的增区间为ππ[2π,2π],22k k k -+∈Z .由πππ2π22π232k x k -++≤≤,k ∈Z ,所以 5ππππ1212k x k -+≤≤,k ∈Z . 所以 函数()f x 的单调递增区间为5ππ[π,π]1212k k -+,k ∈Z . 因为 函数()f x 在[0,]m 上是单调函数,所以 m 的最大值为12π.解法2:因为[0,]x m ∈,所以ππ22333x m π++≤≤.因为 ππ[,]22-是函数sin y x =的增区间,所以 π232m π+≤.所以 π12m ≤. 所以 m 的最大值为12π. 4、解:(Ⅰ)因为()22cos()cos 4f x x x a π=-+(2sin 2cos )cos x x x a =++ 22sin cos 2cos x x x a =++sin2cos21x x a =+++π2sin(2)14x a =+++所以函数()f x 的最大值为21a ++ 所以10a += 所以1a =-(Ⅱ)因为sin y x =的单调递增区间为ππ(2π,2π)22k k -+,k ∈Z令πππ2π22π242k x k -<+<+ 所以 31ππππ88k x k -<<+函数()f x 的单调递增区间为31(ππ,ππ)88k k -+,k ∈Z5、解:(Ⅰ)由及正弦定理得,∴-----------------------------------------------------------------------------------5分 (Ⅱ)在中,由余弦定理得,所以 整理得,解得或(舍去)因为,所以。
所以面积。
---------------------------------13分6、解:(Ⅰ)由正弦定理得:1(2)cos cos 2sin sin )cos sin cos cos 2a c B b C A C B B C B -=⇒-=⇒=( 3B π∠= (Ⅱ)由三角形面积公式得:1sin 342ac B ac =⇒= 由余弦定理得:22222cos ()32426b a c ac B a c ac b =+-=+-=⇒=所以,ABC ∆的周长为626+ 7、解:(Ⅰ)在ABC V 中,1cos 3-B =, ∴22122sin 1cos 1()33--=B =B =, ∵23b =,3c=,由正弦定理sin sin =b cB C 得233sin 223=C , ∴6sin 3C =. (Ⅱ)由余弦定理222+2cos -b =a c ac B 得2112+923()3-⨯⨯-=a a ,∴2230+-a a =,解得1a=或3-a=(舍) ∴1sin 2ABC S =ac B V 12213223=⨯⨯⨯=. 8、解(Ⅰ)在△ABC 中,由余弦定理得A bc c b a cos 2222-+=,-----------------2分 所以2138238222⨯⨯⨯-+=a =49,即7=a . --------------------------- 4分 由正弦定理CcA a sin sin =, --------------------------- 6分 得14337233sin sin =⨯==aAc C . --------------------------- 8分 (Ⅱ)在△ABC 中,BC 边上的高为33123sin 8147b C =⨯=.:------------13分或法2:ABC 1=sin 2s bc A ∆=123,又ABC 1=BC h 2S ∆⋅,所以1237h = 9、解:(Ⅰ)当3m =时,由题可知 2223a c b ac +-=,由余弦定理2222cos b a c ac B =+-, ……………… 3分得2223cos 22a cb B ac +-==. ……………… 4分这与cos [1,1]B ∈-矛盾,所以m 不可能等于3 . ……………… 6分(Ⅱ)由(Ⅰ),得 1cos 22m B ==-,所以2π3B =. ……………… 7分 因为27b =,4c =,222a c b ac +-=-, 所以216284a a +-=-,解得6a =-(舍)或2a =. ……………… 9分在△ABC 中,由正弦定理sin sin a bA B=, ……………… 11分 得sin 2321sin 21427a B Ab ==⨯=. ……………… 13分 10、解:(Ⅰ)因为2cos 10ADB ∠=-, 所以2cos 10ADC ∠=,………………………1分 72sin 10ADC ∠=…………………2分又因为3cos =,5C ∠4sin 5C ∠=,所以,…………………3分sin sin()sin cos cos sin DAC ADC ACD ADC ACD ADC ACD∠=∠+∠=∠⋅∠+∠⋅∠…………5分7232421051052=⋅+⋅=. ……………7分 (Ⅱ)在ACD ∆中,由ADCACC AD ∠=∠sin sin ,…………9分得47sin 542sin 7210AC C AD ADC ⋅⋅∠===∠.…………11分72sin =10ADB ∠ …………12分所以1172sin 4210282210ABD S AD BD ADB ∆=⋅⋅∠=⋅⋅⋅=. …………13分 11、(Ⅰ)()12110cos 210cos 0sin 30=+=++⋅=f ……………2分(Ⅱ) 由0cos ≠x 得,2x k k π≠+π∈Z 所以 函数的定义域是 ,2x x k k ⎧⎫π≠+π∈⎨⎬⎩⎭Z ……………5分 (Ⅲ)()xx x x x f cos 211cos 2cos sin 232⋅+-⋅+⋅⋅⋅= ……………9分()xxx x cos 2cos sin 3cos 2⋅+⋅⋅=x x cos sin 3+⋅=2sin 6x π⎛⎫=+ ⎪⎝⎭ ……………11分0,2x π⎛⎫∈ ⎪⎝⎭ 即 02x π<<21sin()166326x x ππππ∴<+<∴<+≤ 12sin()26x π∴<+≤所以 函数()f x 在(0,)2π上的取值范围为(1,2] ……………14分。
